1 Introduction

All the giant planets in the Solar System have extensive satellite systems. These systems fall into two distinctive types. There are the regular satellites which are generally large and close to the planet and have planar and near circular orbits; and there are the irregular satellites which are usually very small and move at large distances from the planet on high eccentricity, high inclination orbits and are often retrograde in their motion. The regular satellites are most likely to have formed during the formation of the planet itself out of the primordial disc material surrounding the central star (Mosqueira and Estrada 2003). The irregular satellites with their non-planar eccentric orbits are more likely to have been captured in orbit around the planet at a late stage in the planet’s evolution (Peale 1999). The importance of moons has also become more evident as it is clear that the axial tilt (obliquity) of the Earth is stabilized by the presence of the Moon (Laskar et al. 1993). This is in contrast with the obliquity of Mars, which with only two relatively small moons, fluctuates chaotically (Laskar and Robutel 1993). The presence of moons is therefore likely to be crucial for a planet to have a stable obliquity necessary for the existence of a long-term habitable zone.

It therefore seems very likely that many of the extrasolar planets, of which there are currently 1,780 observed in 1,103 planetary systems, 460 of which are multiple planetary systems, will possess satellite systems. A list of these extrasolar planetary systems is available at the web sites http://exoplanet.org and http://exoplanet.eu/catalog.php. In this paper we will only discuss the stability of possible moons orbiting a planet in a single star system (P-type planets). So called S-type planets orbiting around one of the primaries in a binary star system will not be considered. A number of techniques have been proposed for observing possible extrasolar moons. The use of planetary transits is currently the most likely to produce a detection. One method is to look for any detectable dips in the stellar light curve produced by the planet and the moon or moons during a transit (Sartoretti and Schneider 1999). The alternative related method is to monitor any variations in the position and velocity of the planet during transits. The perturbations produced by a satellite makes two possible detectable changes in the orbit of the planet. The first effect is to alter the position of the planet so that the transit lightcurve seems to shift about. This is known as the transit time variation (TTV) and was first predicted by Sartoretti and Schneider (1999). The other change is in the velocity of the planet which is inversely proportional to the duration of the transit. So that as the velocity changes due to the dynamical interaction between the moon and planet, then so also does the transit duration. This transit duration variation (TDV) was predicted by Kipping (2009). It is the combination of these two changes which allows both the mass of the moon and its orbital distance to be calculated. It should be noted that it is not possible to find either of these physical parameters from TTV and TDV alone.

A number of searches for extrasolar moons have so far been made employing the NASA Kepler mission photometry and using the transit timing techniques outlined by Kipping (2009). They were applied to the hot Jupiters: Kepler-4b, Kepler-5b, Kepler-6b, Kepler-7b and Kepler-8b (Kipping and Bakos 2011a), and to TrES-2b (Kipping and Bakos 2011b). Both investigations produced null results but they did indicate that the observations were sensitive to the presence of sub-Earth masses. Kipping et al. (2013) analysed Kepler data for seven viable satellite hosting planetary candidates but have not yet found evidence of any dynamical variations. More recently Kipping et al. (2014b) have found “no compelling evidence” for exomoons around eight Kepler planetary candidates associated with M-dwarfs. It should noted that their project is however sensitive to Earth–Moon mass ratio moons in approximately 1 in 6 cases and to Pluto–Charon mass ratio exomoons in approximately 1 in 3 cases (Kipping 2014a). The discovery of a sub-Mercury sized exoplanet transiting Kepler 37 (Barclay et al. 2013) also suggests the presence of small bodies in extrasolar planetary systems. So far there have not been any positive detections of extrasolar moons.

Regardless of the actual mechanism of formation and evolution of such moons, they still need to satisfy certain dynamical criteria. In particular, by examining the regions of orbital stability available generally and to particular systems we can determine the long-term survival of such moons and also predict where such moons are likely to be observed. In order to proceed further we will now consider various aspects of the stability of such possible moons.

2 Stability Limits

An important aspect of these possible moons is their stability. For orbital stability, the possible satellites are assumed to have orbital radii which lie between the Roche limit as the inner boundary and the Hill radius as the outer boundary. The smallest tidally stable orbit of a moon is given by the Roche limit, \(R_{roche},\) as

$$R_{roche}=fR_{p}\left( \frac{\rho _{p}}{\rho _{s}}\right) ^{\frac{1}{3}}=f\left( \frac{3M_{P}}{4\pi \rho _{s}}\right) ^{\frac{1}{3}}, \quad {\text { where }}\quad \rho _{p}>\rho _{s}$$
(1)

where \(R_{p}\) is the radius of the planet and \(\rho _{p}\) and \(\rho _{s}\) are the mean densities of the planet and moon respectively; while \(M_{P}\) is the mass of the planet and f is a numerical factor which for a rigid spherical satellite is \(f=2^{\frac{1}{3}}=1.26\) (Scharf 2006); while for a fluid-like body it is given by f = 2.44, (Darwin 1908). A moon moving inside this limit would either collide with the planet or be torn apart very rapidly by the tidal forces exerted by the planet (see Donnison and Williams 1975 for an estimate of the likely dispersal timescale).

An important aspect of the evolution of extrasolar moons is the long term tidal stability of their orbits (Correia 2009; Namouni 2010; Brasser et al. 2013). The tidal stability of the satellites around close-in Giant planets has been investigated by Barnes and O’Brien (2002). Since the more massive satellites will be removed more quickly than the less massive ones, they derive an upper limit in mass for those satellites that might have survived to the present day. The two major uncertainties are the value of the tidal dissipation factor and, the tidal Love number. Barnes and O’Brien (2002) choose a value which corresponds to the value of a polytrope of index n = 1 (Hubbard 1984), and assumed a dissipation factor of \(10^{5}\). The results obtained suggest that only very small close-in moons could have survived. They also suggest that Earth-mass moons could exist around Jupiters for billions of years around stars of mass \(M_{star}>0.5M_{\odot }\). However this estimation neglects the effects of satellite tides on planetary rotation and is therefore only applicable to systems in which the mass of the moon is much less than that of the planet. Sasaki et al. (2012) found that the inclusion of satellite tides allowed for significantly longer lifetimes for massive moons. With the uncertainty in the main parameters and the tidal interaction largely only effective for close-in moons, it is not clear how reliable are any upper limits proposed. The tidal effects are weak and since we will only be dealing with specific values of eccentricity and inclination rather than their evolution, we will not impose these possible limits on the systems discussed later.

Estimating the outer boundary of the orbits is more problematical. In general it is only possible to follow the long-term orbital evolution of such systems and hence their long-term stability by direct numerical integration of the orbits of all three masses. Analytical approaches can however provide limits on the range of orbital elements that a system must possess if it is to remain stable and avoid disruption, exchange or collision of the components. However it is clear from numerical calculations that the straight Hill radius given by the restricted circular three-body problem as

$$R_{H}=a_{2}\left( \frac{M_{P}}{3M_{*}}\right) ^{\frac{1}{3}},$$
(2)

where \(M_{P}\) is the mass of the planet, \(M_{*}\) is the mass of the central star and \(a_{2}\) is their orbital separation distance, is not sufficiently accurate as a measure of the critical planet–satellite separation distance, \(a_{1}\). Hamilton and Krivov (1997), using the Jacobi constant found numerically for circular orbits that the critical planet–satellite separation in terms of \(R_{H}\), that is \(a_{1}/R_{H},\) is 0.53 for prograde orbits and 0.69 for retrograde orbits. Using the full three-body problem configuration with \(M_{*}\gg \;M_{P}+M_{S},\) where \(M_{S}\) is the mass of the satellite, and circular orbits Donnison (1988) found the critical Hill stability critical distance ratio for systems with prograde orbits could be approximated for different masses ratios by

$$\left( \frac{a_{2}}{a_{1}}\right) =0.7420\left( \frac{81M_{*}}{M_{P}+M_{S}}\right) ^{\frac{1}{3}}.$$
(3)

Taking the Hill radius of the binary as (see Donnison and Williams 1975)

$$R_{H}=a_{2}\left( \frac{M_{P}+M_{S}}{3M_{*}}\right) ^{\frac{1}{3}},$$
(4)

then we find on combining this equation with Eq. (3) that the critical separation in terms of this radius for prograde circular orbits, \(a_{1}/R_{H}\), is 0.449. Donnison and Mikulskis (1992) found numerically that for prograde three body systems moving on circular orbits that there was a good correspondence between the results obtained for the critical orbital or Lagrange stability and the full three-body Hill stability method employed here (see also Donnison and Mikulskis 1995 for eccentric orbits). Donnison and Mikulskis (1994) and Eggleton and Kiseleva (1995) have also shown numerically that retrograde circular orbits tend to be more stable than their prograde counterparts.

Domingos et al. (2006), using numerical simulations of the orbits using the restricted elliptic three-body problem, with the moon assumed to be massless examined the boundary of the stable regions for a fixed planet/star mass ratio of \(10^{-3}\). They found empirically for that mass ratio that for a prograde and retrograde moons the critical orbital distance can be approximated by expressions in terms of the eccentricity of the planet and the eccentricity of the moon. They found prograde moons on circular orbits \(a_{1}/R_{H}= 0.4895\), which is very similar to the values obtained previously; while for corresponding retrograde orbits \(a_{1}/R_{H}= 0.9309\). Here \(R_{H}\) is the Hill radius given by the restricted circular three-body problem as in Eq. (2). This method is in contrast to the exchangeability criteria given by full three body Hill stability(see later in Sect 4).

Weidner and Horne (2010) applied limits to possible extrasolar moons using the Rôche limit given by Eq. (1) and the empirical approximations by Domingos et al. (2006) to the 87 then currently known transiting planets. Donnison (2010a) using the full three-body Hill stability approach (to be discussed in detail later) determined the critical separation values for all the 334 then known extrasolar planet systems for a variety of possible planet/moon mass ratios, assuming that the moon moved on a circular orbit. It was found that the critical moon–planet separation did not change significantly when the planet/moon mass ratio was altered if the planet orbits its parent star on a circular orbit. However, for systems with eccentric orbits it was found that there were large changes in the critical separation as the mass ratio decreased, with the regions of stability rapidly decreasing. The effect of an eccentrically orbiting moon was only examined generally for a planet moving on a circular orbit. It was found that as the eccentricity was increased the regions of Hill stability decreased. Here we will reinvestigate all these aspects using a more easily applied approximation, which has not been applied to this problem previously, to actual systems which have more than tripled in number during the intervening period. In the present investigation the effects of the binary eccentricity and inclination on the Hill stability will also be determined for all the currently known transiting extrasolar planet systems where the mass is known. It should be noted that Weidner and Horne (2010) found that the majority of Hill radii derived from Domingos et al. (2006) agreed within better than 10 % with those derived by Donnison (2010a) for the 43 extrasolar planets common to both samples. To proceed further we now consider Hill stability in some detail.

3 Full Three Body Hill Stability

The concept of zero velocity surfaces as boundaries of possible motion was introduced by Hill (1878) in the circular restricted three-body problem in which a body of infinitesimal mass moves under the gravitational influence of two finite masses. The topology of these surfaces and hence the regions of possible motion are controlled in this case by the Jacobi constant. For full three-body systems, where all the masses have finite values, the theory of Hill stability was developed using different approaches by Gobulev (1967, 1968), Marchal and Saari (1975), Zare (1976, 1977), and Bozis (1976). For this full three-body case the important parameter is \(c^{2}E\), where E is the energy and c the angular momentum of the system of three masses. This parameter, which corresponds to the Jacobi constant in the restricted problem of three bodies, controls the topology of the zero velocity surfaces and since the bodies may not cross these surfaces determines the regions of possible motion. The value of \(c^{2}|E|\) for the actual system is compared with the critical value derived for the corresponding three-body Hill surfaces determined by the position of the collinear Lagrangian points. The system will then be stable against disruption or exchange of components if its actual value of \(c^{2}|E|\) is greater or equal to the critical value. The system is then considered to be Hill stable. If this condition is not satisfied then exchange of components, disruption or collision is possible but not inevitable. The condition for stability is a sufficient condition but not a necessary one so that exchange might not occur when the condition is violated but certainly cannot occur if the condition is satisfied.

This theory was originally applied only to coplanar systems where all three bodies moved on bound orbits (Szebehely and Zare 1977; Walker et al. 1980; Walker and Roy 1981; Marchal and Bozis 1982; Donnison and Williams 1983).The theory was extended to unbound coplanar orbits by Donnison (1984a, b) and to inclined unbound orbits by Donnison (2006, 2008) and to bound inclined orbits by Veras and Armitage (2004) and Donnison (2009). The basic theory was applied to extrasolar planetary systems. Here in this work, we will consider the situation where the binary is small in mass compared with the third mass, originally discussed for planar systems by Donnison (1988), and recently extended by Donnison (2010a, b) to inclined systems and applied to very low mass binary systems and possible circular orbiting exomoons. In this work we derive and use a more easily applicable approximation with a closed solution to the problem of binary planets and moons and investigate and extend the orbital stability discussion to possible eccentric and inclined moons of extrasolar planets. The work is new but the approach is a development of the earlier work of Szebehely and Zare (1977).We now consider the general theory first and then move on to the appropriate approximation.

4 Binary Systems Moving on Inclined Elliptic Orbits Relative to the Central Body

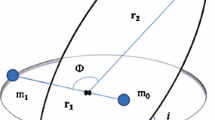
For this configuration we consider a system of three bodies with masses \(M_{1},M_{2},\) and \(M_{3}\), which can take any positive value. The masses \(M_{1}\) and \(M_{2}\) form an inner binary system with semi-major axis \(a_{1}\) and eccentricity \(e_{1},\) whose barycentre G moves on a elliptical orbit relative to the third body \(M_{3}\) with an inclination i, measured relative to the orbital axis of the inner binary with semi-major axis \(a_{2}\) and eccentricity \(e_{2}\). The total energy of the system, using a two body approximation, (see Szebehely and Zare 1977), is then

$$E=-\left( \frac{GM_{1}M_{2}}{2a_{1}}+\frac{GM_{3}\mu }{2a_{2}}\right),$$
(5)

where G is the gravitational constant and \(\mu =M_{1}+M_{2}\) is the mass of the binary. The corresponding exact angular momentum squared for the system is then

$$c^{2}=G\left\{ \frac{M_{3}^{2}\mu ^{2}}{M}a_{2}\left( 1-e_{2}^{2}\right) +\frac{M_{1}^{2}M_{2}^{2}}{\mu }a_{1}\left( 1-e_{1}^{2}\right) +2M_{1}M_{2}M_{3}\left( \frac{\mu }{M}a_{1}a_{2}\left( 1-e_{1}^{2}\right) \left( 1-e_{2}^{2}\right) \right) ^{\frac{1}{2}}\cos i\right\}$$
(6)

where \(M=M_{1}+M_{2}+M_{3}\) and \(0 {{}^{\circ} } \le i\le 180 {{}^{\circ}}\). Here \(i=0^{\circ }\) indicates that \(M_{3}\) and the binary pair are both moving in the same plane and in the same sense on coplanar prograde orbits, while \(i=180^{\circ }\) indicates that the motion of the masses is in the opposite sense that is coplanar retrograde motion. The motion is generally prograde if \(i<90^{\circ }\) and retrograde if \(i\geqslant 90^{\circ }\).

The parameter controlling the topology of the zero velocity surfaces of the actual system, \(c^{2}E,\) can now using Eqs. (5) and (6) be written as \(S_{ac}\) where

$$\begin{aligned} S_{ac}&= \left\{ \frac{c^{2}|E|}{G^{2}}\right\} _{ac}=\frac{ M_{1}M_{2}M_{3}^{2}\mu ^{2}}{2M}\left( \frac{a_{2}}{a_{1}}\right) \left( 1-e_{2}^{2}\right) +\frac{M_{1}^{3}M_{2}^{3}}{2\mu }\left( 1-e_{1}^{2}\right) \\&\quad +M_{1}^{2}M_{2}^{2}M_{3}\left( \frac{\mu \left( 1-e_{1}^{2}\right) \left( 1-e_{2}^{2}\right) }{M}\right) ^{\frac{1}{2}}\left( \frac{a_{2}}{a_{1}} \right) ^{\frac{1}{2}}\cos i+\frac{M_{3}^{3}\mu ^{3}}{2M}\left( 1-e_{2}^{2}\right) \\&\quad +\frac{M_{1}^{2}M_{2}^{2}M_{3}}{2}\left( \frac{a_{1}}{a_{2}}\right) \left( 1-e_{1}^{2}\right) +M_{1}M_{2}M_{3}^{2}\left( \frac{\mu ^{3}\left( 1-e_{1}^{2}\right) \left( 1-e_{2}^{2}\right) }{M}\right) ^{\frac{1}{2} }\left( \frac{a_{1}}{a_{2}}\right) ^{\frac{1}{2}}\cos i\end{aligned}.$$
(7)

The corresponding critical value of the \(c^{2}E\) parameter for the Hill stability surfaces at the position of the collinear Lagrange points for a central configuration \(M_{1}:M_{2}:M_{3}\), depends only on the three masses present. If the ratio of the distances \(|M_{2}M_{3}|:|M_{1}M_{2}|\) is taken to be \(1:x\), then x, the position of the appropriate collinear equilibrium point, is the real solution of the usual Lagrange quintic equation given by (see Roy 2005 for derivation)

$$\begin{aligned}&\left( M_{2}+M_{3}\right) x^{5}+\left( 3M_{3}+2M_{2}\right) x^{4}+\left( 3M_{3}+M_{2}\right) x^{3}-\left( 3M_{1}+M_{2}\right) x^{2} \\&\quad -\left( 3M_{1}+2M_{2}\right) x-\left( M_{1}+M_{2}\right) =0. \end{aligned}$$
(8)

Zare (1977) showed that the critical value of \(c^{2}|E|\) here can be conveniently computed in terms of x in the form

$$S_{cr}=\left\{ \frac{c^{2}|E|}{G^{2}}\right\} _{cr}=\frac{f^{2}(x) g(x) }{2M},$$
(9)

where

$$f(x)=M_{2}M_{3}+\frac{M_{1}M_{3}}{1+x}+\frac{M_{1}M_{2}}{x},$$

and

$$g(x) =M_{2}M_{3}+M_{1}M_{3}(1+x)^{2}+M_{1}M_{2}x^{2}.$$
(10)

It should be noted that there was a typographical error in the indices quoted for \(f(x)\) in Donnison (2010a, b). Only in certain special cases is it possible to express x in Eq. (8) and hence \(S_{cr}\) in a closed form. In general it has to be solved numerically. For the system to be Hill stable it must therefore satisfy the condition \(S_{ac}-S_{cr}\ge 0\) in order for the system not to be disrupted or any exchange of components to occur.

To solve this condition generally for the critical value of \((a_{2}/a_{1})\) in terms of the orbital elements \(e_{1},\;e_{2}\) and i, Donnison (2009) showed that the critical condition can be solved numerically as a fourth order algebraic equation of the form

$$(1+y^{2}) (\beta ^{2}y^{2}+2\beta y\cos i+1)-Ay^{2}=0,$$
(11)

where

$$y=\left( \frac{a_{1}}{a_{2}}\frac{M_{3}\mu }{M_{1}M_{2}}\right) ^{\frac{1}{2} },\quad \beta =\left( \frac{M_{1}M_{2}}{M_{3}}\right) ^{\frac{3}{2}}\left( \frac{ M}{\mu ^{4}}\right) ^{\frac{1}{2}}\left( \frac{1-e_{1}^{2}}{1-e_{2}^{2}} \right) ^{\frac{1}{2}}$$
(12)

and

$$A=\frac{2S_{cr}M}{M_{3}^{3}\mu ^{3}(1-e_{2}^{2})}.$$

It should be noted that in Donnison (2009, 2010a) this equation had a typographical error in the sign of A, which should be defined as positive. Equations (11) and (12) use the same basic parameters as Szebehely and Zare (1977) did for a completely bound coplanar three body system but now with the inclusion of the inclination. The application of this two body approximation to hierarchical systems has been shown to be very good, with disagreement between using the exact energy and this approximation being very small (Walker et al. 1980; Kiseleva et al. 1994; Veras et al. 2013). We now consider a particularly important combination of masses for which there is a closed solution.

5 Approximate Solutions for Systems Where the Third Mass M3 is Large Compared to the Binary Mass

A closed solution is possible in this case when \(M_{3}\gg M_{1}+M_{2}\). A reasonable approximation to x in the quintic Eq. (8), if we identify \(M_{3}=M_{*},\;M_{1}=M_{p},M_{2}=M_{s}\), is then given by (Walker et al. 1980; Walker 1983) as

$$x_{0}=\left( \frac{M_{P}+M_{S}}{3M_{*}}\right) ^{\frac{1}{3}}.$$
(13)

Since \(x_{0}\) is very small the critical value \(S_{cr}\), which is achieved at the Lagrangian point \(\hbox {L}_{2}\), can be expanded in terms of increasing powers of \(x_{0},\) with \(\mu =3M_{*}x_{0}^{3},\) to give

$$\begin{aligned} S_{cr}&= \beta \{(1+\lambda ) ^{3}+9\lambda (\lambda +1) x_{0}^{2}+\left( 2\lambda (\lambda -1) -3(1+\lambda ) ^{3}\right) x_{0}^{3} \\&\quad +\left( \lambda (2+5\lambda ) +\frac{21\lambda ^{2}}{\left( 1+\lambda \right) }\right) x_{0}^{4}+O(x_{0}^{5})+\cdots \}, \end{aligned}$$
(14)

where

$$\lambda =\frac{M_{P}}{M_{S}}\ge 1,\quad {\text { and}}\quad\beta =\frac{M_{*}^{2}M_{S}^{3}}{2}.$$

It should be noted that there was a typographical error in the fourth order term in Donnison (2010a, b, 2011). As this term was not used in any of the calculations the results obtained are unaffected.

Similarly, the actual value \(S_{ac}\) can be expanded in terms of \(x_{0}\) to give

$$\begin{aligned} S_{ac}&= \beta \left\{(1+\lambda ) ^{3} (1-e_{2}^{2}) +\left( 2\sqrt{3}\lambda (1+\lambda ) \left( \frac{a_{1}}{a_{2}} \right) ^{\frac{1}{2}}(1-e_{1}^{2}) ^{\frac{1}{2}}(1-e_{2}^{2}) ^{\frac{1}{2}}\cos i\right) x_{0}^{\frac{3}{2}}\right. \\&\quad +\,\left( 3\lambda (1+\lambda ) \left( \frac{a_{2}}{a_{1}} \right) (1-e_{2}^{2}) +\frac{3\lambda ^{2}}{(1+\lambda ) }\left( \frac{a_{1}}{a_{2}}\right) (1-e_{1}^{2}) -3(1+\lambda ) ^{3}\left( 1-e_{2}^{2}\right) \right) x_{0}^{3} \\ &\quad+\,\left( \frac{6\sqrt{3}\lambda ^{2}}{(1+\lambda ) }\left( \frac{a_{2}}{a_{1}}\right) ^{\frac{1}{2}}\left( 1-e_{1}^{2}\right) ^{\frac{1 }{2}}\left( 1-e_{2}^{2}\right) ^{\frac{1}{2}}\cos i\right) x_{0}^{4.5}-9\left( 1+\lambda \right) \left( 1-e_{2}^{2}\right) \left( \frac{a_{2}}{a_{1}}\right) x_{0}^{6} \\ &\quad \left. +\,O\left( x_{0}^{7.5}\right) +\cdots \right\}. \end{aligned}$$
(15)

For low mass binaries comprising a moon and a planet, it is not necessary to retain all the terms, but only those up to order \(x_{0}^{3}\). For a hierarchical triple system, such as we are considering, the distance separation ratio \(a_{2}/a_{1}\) is large and can be considered to vary as \(x_{0}^{-3}\) (Li et al. 2010). We have therefore separated out one of the terms of order \(x_{0}^{4.5},\) as this term which varies as \(\left( a_{2}/a_{1}\right) ^{\frac{1}{2}}x_{0}^{4.5}\) can be considered as of order \(x_{0}^{3}\) (see Donnison 2011), similarly the \(x_{0}^{6}\) term, omitted by Li et al. (2010), which varies as \(\left( a_{2}/a_{1}\right) x_{0}^{6}\) can be considered of order \(x_{0}^{3}\) and should also be retained By contrast the term involving \(\left( a_{1}/a_{2}\right) x_{0}^{3}\) would be of order \(x_{0}^{6}\) and all the other \(x_{0}^{4.5}\) and \(x_{0}^{6}\) terms in the expansion can be safely neglected. Therefore retaining only terms of up to order \(x_{0}^{3},\) the critical condition \(S_{ac}-S_{cr}=0\) can now be written in the slightly amended form, with decreasing powers of \(\left( a_{2}/a_{1}\right)\), as

$$\begin{aligned}&3 (1+\lambda ) \left( 1-e_{2}^{2}\right) x_{0}^{3}\left( \lambda -3x_{0}^{3}\right) \left( \frac{a_{2}}{a_{1}}\right) +\left( 6\sqrt{3 }\lambda ^{2}\left( 1+\lambda \right) ^{-1}\left( 1-e_{1}^{2}\right) ^{\frac{ 1}{2}}\left( 1-e_{2}^{2}\right) ^{\frac{1}{2}}x_{0}^{4.5}\cos i\right) \left( \frac{a_{2}}{a_{1}}\right) ^{\frac{1}{2}} \\&\quad-\left( 1+\lambda \right) ^{3}e_{2}^{2}-9\lambda \left( \lambda +1\right) x_{0}^{2}+\left( 3\left( 1+\lambda \right) ^{3}e_{2}^{2}-2\lambda \left( \lambda -1\right) \right) x_{0}^{3} \\ &\quad+\left( 2\sqrt{3}\lambda (1+\lambda ) ^{\frac{1}{2}}\left( 1-e_{1}^{2}\right) ^{\frac{1}{2}}\left( 1-e_{2}^{2}\right) ^{\frac{1}{2} }x_{0}^{\frac{3}{2}}\cos i\right) \left( \frac{a_{1}}{a_{2}}\right) ^{\frac{1 }{2}} = 0. \end{aligned}$$
(16)

Multiplying Eq. (16) through by \(\left( a_{2}/a_{1}\right) ^{\frac{1}{2} }\), enables it to be written in the form of a standard cubic equation in \(\left( a_{2}/a_{1}\right) ^{\frac{1}{2}},\) which can be solved using Viete’s variation on Cardano’s method. This cubic equation, which is slightly different to that considered previously, has a real critical solution (Li et al. 2010; Liu et al. 2012) which can be expressed in closed form by

$$\begin{aligned} \left( \frac{a_{2}}{a_{1}}\right) _{cr}&= \frac{9+\left( 1+\lambda \right) ^{2}\lambda ^{-1}e_{2}^{2}\left( x_{0}^{-2}-3x_{0}\right) +2\left( \lambda -1\right) \left( 1+\lambda \right) ^{-1}x_{0}}{\left( \frac{9}{4}\right) \left( 1-e_{2}^{2}\right) x_{0}} \\&\quad \cos ^{2}\left\{ \frac{1}{3}\cos ^{-1}\left[ \frac{3\sqrt{3}\mathcal {K} \left( 3-4e_{2}^{2}\right) }{\left( 9+\left( 1+\lambda \right) ^{2}\lambda ^{-1}e_{2}^{2}\left( x_{0}^{-2}-3x_{0}\right) +2\left( \lambda -1\right) \left( 1+\lambda \right) ^{-1}x_{0}\right) ^{\frac{3}{2}}}\right] -\frac{\pi }{3}\right\}, \end{aligned}$$
(17)

where we have set

$$\mathcal {K}=\left( 1-e_{1}^{2}\right) ^{\frac{1}{2}}\cos i,$$
(18)

and \(\ e_{2}\) is the eccentricity of the binary orbit relative to the star, \(e_{1}\) the eccentricity of the binary, \(M_{P}\) the mass of the planet, \(M_{S}\) the mass of the moon, \(M_{*}\) the mass of the central star and i the inclination of the binary orbit relative to the star,

and

$$x_{0}=\left( \frac{M_{P}+M_{S}}{3M_{*}}\right) ^{\frac{1}{3}}, \quad \lambda =\frac{M_{P}}{M_{S}}\ge 1.$$

It should be noted that this Hill criterion depends only on the eccentricity \(e_{1}\) and the inclination i through this term \(\mathcal {K},\) so that the effects of eccentricity and inclination on the critical distance \(\left( a_{2}/a_{1}\right) _{cr}\) can be studied together. The critical \(\left( a_{2}/a_{1}\right) _{cr}\) values decrease as \(\mathcal {K}\) is raised from \(-1\) to \(+1,\) which means that the Hill stable region expands with increasing \(\mathcal {K}\) for given mass ratios (Li et al. 2010).We should note that perturbation theory (Kozai 1962; Lidov 1962) has shown that \(e_{1}\) and i are subject to strong perturbations, particularly for large values of these parameters. Since the time scale of changes in these elements is long compared to the observational time scale (Mazeh 2008), it is justifiable to consider the Hill stability of a system for all given values of these elements.

For circular orbits where \(e_{2}=0,\) Eq. (17) reduces to the expression

$$\begin{aligned} \left( \frac{a_{2}}{a_{1}}\right) _{cr}&= \frac{9+2\left( \lambda -1\right) (1+\lambda )^{-1}x_{0}}{\left( \frac{9}{4}\right) x_{0}}\\&\quad\cos ^{2}\left\{ \frac{1}{3}\cos ^{-1}\left[ \frac{9\sqrt{3}\mathcal {K}}{ \left( 9+2\left( \lambda -1\right) \left( 1+\lambda \right) ^{-1}x_{0}\right) ^{\frac{3}{2}}}\right] -\frac{\pi }{3}\right\} . \end{aligned}$$
(19)

In general these equations are given in terms of \(x_{0},\lambda ,e_{1},e_{2}\) and i which enables them to be used to derive the critical value of \(a_{2}/a_{1}\) for a system.

For \(i=90^{\circ },\) that is the largest inclination for prograde orbits, the expression given by Eq. (17) simplifies and can be written in terms of the critical pericentric distance \(q_{2}=a_{2}(1-e_{2})\) as

$$\left( \frac{q_{2}}{a_{1}}\right) _{cr}=\frac{\left( 1+\lambda \right) ^{2}e_{2}^{2}\left( 1-3x_{0}^{3}\right) +9\lambda x_{0}^{2}+2\lambda \left( \lambda -1\right) \left( 1+\lambda \right) ^{-1}x_{0}^{3}}{3\lambda (1+e_{2})x_{0}^{3}}.$$
(20)

Here \(\mathcal {K}=0\), and the criterion is independent of the binary orbit eccentricity \(e_{1}\). If in addition the orbit is circular around the third massive body, then this reduces further to give

$$\left( \frac{q_{2}}{a_{1}}\right) _{cr}=\frac{3}{x_{0}}+\frac{2\left( \lambda -1\right) }{3\left( 1+\lambda \right) }.$$
(21)

Therefore \(\left( q_{2}/a_{1}\right) _{cr}\) then lies in the range

$$\frac{3}{x_{0}}-\frac{2}{3}\le \left( \frac{q_{2}}{a_{1}}\right) _{cr}\le \frac{3}{x_{0}}+\frac{2}{3},$$
(22)

the lower limit corresponding to \(\lambda \longrightarrow 0\) and the upper limit to \(\lambda \longrightarrow \infty\), with \(\left( q_{2}/a_{1}\right) _{cr}=3/x_{0}=3a_{2}/R_{H}\) for the equal mass binary case where \(\lambda =1.0\). As \(x_{0}\) is small, the term involving \(x_{0}\) is the dominant term in all these expressions. It should be noted, as mentioned earlier, that Hill stability refers only to the exchangeability of the component masses and does not correspond directly to orbital stability. So that satellites with inclinations of about \(90^{\circ }\) would be highly unstable (Kozai 1962; Lidov 1962). Harrington (1972) suggested from numerical calculations that there was little variation of stability with inclination, except close to \(90^{\circ }\), where instability was clearly present. These equations obtained can be applied to a variety of physical systems. Here we will consider extrasolar planetary systems and their possible moons.

6 Current Data on Extrasolar Planetary Systems

The binary system composed of the planet and moon has a combined mass given by \(M_{P}+M_{S}\) Since in general the system will be inclined to the line of sight of the observer, then only \(M_{p}\sin i_{p}\), can be measured where \(i_{p}\) is the inclination angle of the orbit plane to the line of sight. Currently there are 361 planets with known inclinations. These lie in the range \(0.962^{\circ }\le i\le 172.10^{\circ }\), with a mean of \(81.173^{\circ }\) and a median of \(87.25^{\circ }.\) The vast majority of these systems with known inclinations are obtained from transits and are very close to \(90^{\circ }\) as would be expected using this method. We can only apply the theory outlined if the mass of the central star, is known. Since in the earlier calculations we retain terms up to order \(x_{0}^{3}\), where \(x_{0}=\left( M_{p}\left( 1+\lambda ^{-1}\right) /3M_{*}\right) ^{ \frac{1}{3}}\), the error which is of order of \(x_{0}^{4}\) is clearly negligible.

The number of planets discovered so far is 1780. For current data see the web sites http://exoplanet.org and http://exoplanets.eu/catalog.php. maintained by Schneider. The actual extrasolar planetary systems can be divided using the methods by which they were discovered or confirmed. Originally the majority of the systems were discovered by the detection of the variation in the radial velocity measurements of the stellar component which are due to the reflex response caused by the motions of its planetary companion. Currently 419 planetary systems, with 558 planets and 98 multiple planet systems have been detected in this way. For systems solely discovered by this technique only the measurement of \(M_{p}\sin i_{p}\) is available so that the masses determined can only be considered as lower limits to the actual masses. Detection of a planet by its transit across the face of its companion star has led to the discovery of 614 planetary systems, comprising some 1,131 planets with 350 multiple planet systems. Microlensing techniques have led to the discovery of 26 planetary systems with 28 planets, only two of which are a multiple planet systems. Direct imaging has led to the detection of 43 planetary systems with 47 planets, two of which is a multiple system. The remaining 11 planetary systems with 14 planets, 2 of which are multiple systems have been detected by timing methods. Since the mass of an exoplanet is only completely determined for systems discovered by the transit method which have subsequently had follow up detections of their radial velocity, it is only those systems we consider. In addition, it should be noted that the prospects for further planetary confirmations is bright with the Kepler mission transit observations of unconfirmed extrasolar planetary candidates reaching 3601 (http://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html).

7 General Results

7.1 Comparison with Previous Results for Circular Orbits

Initially, as a first approximation we will see how the results obtained from our theory, using Eq. (17), compare with the critical numerical values for \(a_{1}/R_{H}\) determined for prograde three-body systems moving on circular orbits given in the section on stability. For comparison the critical values of \(a_{2}/a_{1}\) for all the known transiting extrasolar planets were determined using (17) and hence the critical separation ratio \(a_{1}/R_{H}\) for binary mass ratios \(\lambda =1.0, 10, 100, 1{,}000\), on the assumption that the moon moves on a circular orbit, that is \(e_{1}=0.0\). This covers masses for binary planets down to masses of small moons. Figure 1 is a plot of the orbital eccentricity \(e_{2}\) against the critical separation \(a_{1}\) in terms of the appropriate Hill radius using Eq. (4), that is \(a_{1}/R_{H}\), for all the transiting planets for which there is full data. The results for \(\lambda =1.0\) are shown in the figure as black circles, for \(\lambda =10\) as red squares, for \(\lambda =100\) as green diamonds and finally for \(\lambda =1{,}000\) as blue triangles. We find that for the four binary mass ratios that all the planets, for which the necessary data was available, lie in the ranges: \(0.001596\le a_{1}/R_{H}\le 0.4492\) for \(\lambda =1.0; 0.000356\le a_{1}/R_{H}\le 0.4477\) for \(\lambda =10; 0.000040\le a_{1}/R_{H}\le 0.4475\) for \(\lambda =100; 0.00000406\le a_{1}/R_{H}\le 0.4473\) for \(\lambda =1{,}000.\)

Fig. 1
figure 1

This shows a plot of planetary eccentricity \(e_{2}\) against the ratio of the critical separation of the moon and planet, \(a_{1}\), to the Hill radius R\(_{H},\;a_{1}/R_{H}\) for the four values of \(\lambda ,\) for all the currently known transiting extrasolar planetary systems for which there is full data. The results for \(\lambda =1.0\) are shown as black circles, for \(\lambda =10\) as red squares, for \(\lambda =100\) as green diamonds and finally for \(\lambda =1{,}000\) as blue triangles. (Color figure online)

Full size image
Fig. 2
figure 2

This figure shows a plot of the critical \(q_{2}/a_{1}\) values, where \(q_{2}=a_{2}(1-e_{2})\) is the closest approach of the binary, composed of the planet and moon, to the central star against \(e_{2}\) for different planet-moon ratios \(\lambda\). The masses satisfy the condition \(x_{0}=\left( \left( M_{1}+M_{2}\right) /3M_{3}\right) ^{\frac{1}{3}}=0.1\), which is relevant to a Jupiter mass planet with an accompanying moon

Full size image

It is clear from the graph and the above ranges, that all the systems satisfy the condition \(a_{1}/R_{H}\le 0.4492\). All of these systems have \(a_{1}/R_{H}\) values which are below the critical values for prograde systems given by the various criteria obtained for circular orbits in Sect. 2, but not those for retrograde systems. Therefore, as we can see from the figure, these moons clearly satisfy the criteria and are stable. A plot of planetary mass against \(a_{1}/R_{H}\) for the same set of planets, not shown, again indicates that all the systems considered are likely to be stable. Before considering the application of the theory to these observed systems for eccentric and inclined orbits of the moons, we will consider general trends in stability for these types of variations for different mass ratios.

7.2 Changes in the Range of Orbital Eccentricity and Inclination

Applying the theory generally to extrasolar planets which have an \(x_{0}\) value of \(x_{0}=\left( \left( M_{P}+M_{S}\right) /3M_{*}\right) ^{\frac{1 }{3}}=0.1,\) where this value of \(x_{0}\) is in the range of the expected values of extrasolar planetary systems where a solar mass star is orbited by a Jupiter mass planet with an accompanying moon. In order to clarify the regions of stability, the \(\lambda\) values have been split into a number of ranges. In Fig. 2 there is a plot of the critical \(q_{2}/a_{1}\) values where \(q_{2}=a_{2}(1-e_{2})\) is the closest approach of the binary, composed of the planet and moon, to the central star against \(e_{2}\) for different planet-moon ratios \(\lambda\). Here \(e_{2}\) lies in the range \(0.0 \le e_{2}\le 1.0\), while the value of \(\lambda\) varies in the range \(1.0\le \lambda \le 10\), that is from a moon comparable to the mass of the planet (a binary planet system) to one with a mass of 1/10 the mass of the planet. These systems are Hill stable against exchange of the components if they lie to the right of the appropriate stability curve. To the left of the curves the Hill surfaces open out and exchange or collision of the component masses of the system is possible but not inevitable. The critical distance ratios, \(q_{2}/a_{1}\) increase and the corresponding regions of stability decrease as the value of the orbit eccentricity \(e_{2}\) is increased. Increasing the value of \(\lambda\) also moves the stability curves to the right though the differences are not pronounced for circular orbits. It was also found that varying the inclination through the values \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) did not change the results for \(q_{2}/a_{1}\) very much compared to the situation where there are changes in \(e_{2}\) and \(\lambda ,\) as the different curves all merged into one line for a given value of \(\lambda\) indicating that they are of limited importance for this mass range (value of \(x_{0}\)). In Fig. 3 the range of the planet-moon ratio is increased to cover the smaller moons. The range of \(\lambda\) is \(10\le \lambda \le 500\), which extends the mass range down into the Earth and super-Earth mass range. As in the previous figure, the \(q_{2}/a_{1}\) values increase as the value of \(e_{2}\) is increased and even more rapidly as the value of \(\lambda\) is increased, with regions of stability again lying to the right of any given curve. As before the effects of inclination are secondary and do not change perceptibly compared to changes due to variations in eccentricity and hence orbital distance. Although the changes in inclination and binary eccentricity are secondary features compared the changes in orbital distance, they are still significant and will be discussed more fully in a later section.

7.2.1 Application to the Observed Systems

The main emphasis in Donnison (2010a) was on the variations of the distance of the planet–moon system from the central star critical for stability, particularly with orbital eccentricity, \(e_{2},\) while the moon was assumed to move on a circular orbit. It was found that for the sample considered when \(e_{2}=0,\) there were only small changes in the critical separation \(a_{1}\) as the planet/satellite mass ratio \(\lambda\) increased; while for orbits where \(e_{2}\ne 0\) there could be large changes in \(a_{1}\) for the larger eccentricities as \(\lambda\) increased. Since this original analysis the number of extrasolar planets discovered has more than trebled in number and many of the values of the orbital elements of the previously discovered systems have been adjusted and refined. A complete listing for all the known extrasolar planets would take up too much space and would lead to a degree of overlap with the previous results listed in Donnison (2010a). We will therefore only apply the approximation derived here to determine stability of only those transiting extrasolar planets with well determined orbits and masses that have been discovered since 2010. This does not include the recent Kepler data for which in general the planetary mass is not determined (http://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html).

Table 1 We show the data for the transiting extrasolar systems where the mass is determined (discovered since 2010) with the name, \(M_{p}\), semi-major axis \(a_{p}\), eccentricity \(e_{p}\), and the mass of the parent star \(M_{*}\), in solar masses listed in columns (1)–(5)
Full size table

Table 1 is a list of systems with data taken from the web sites http://exoplanet.org and http://exoplanet.eu/catalog.php. The planetary masses satisfy \(M_{p}<13\) Jupiter masses (M J ), which is below the critical lithium burning mass (Spiegel et al. 2011), while additional masses satisfy \(M_{p}<20\) M J . To determine the critical distance and hence the critical separation distance, Eq. (17) is applied to a system given that \(M_{p},a_{p},e_{p}\) and \(M_{*}\) are all available. If the eccentricity of the orbit of the extrasolar planet is not known, then it is assumed to move on a circular orbit. In columns (1–5) are the observed data for the extrasolar planet, with the name of the system, the mass of the planet, \(M_{p},\) in Jupiter masses, the semi-major axis \(a_{p}\) in au, the eccentricity \(e_{p}\) of the planet, and the mass of the parent star \(M_{*}\) in solar masses. The order of the listing is based on increasing period of the planet orbit, though an effort has been made to keep the data for most multiple systems together. In columns (6–8) are the derived critical distances \(a_{1}\) divided by the appropriate Hill radius \(a_{1}/R_{H}\), shown for planet mass ratios \(\lambda =1.0,10,100,1{,}000\). These mass ratios span the range from a binary planet down to an Earth mass planet orbiting a Jupiter mass planet.

It is clear from the results that as \(\lambda\) increases from \(\lambda =1.0\) to \(\lambda =1{,}000\), the critical separation also decreases so that the systems progressively becomes less stable. When the planet moves on a circular orbit relative to the central star, the changes in \(a_{1}\) with mass are relatively small. The effect is more pronounced when the eccentricity of the planet about the star, \(e_{p}\), is non-zero. With changes by a factor of 10 between \(\lambda =1.0\) and \(\lambda =10^{3}\) not uncommon. These results are broadly in line with those of Donnison (2010a). It should be noted that the number of systems overall for which all the required data is not available is relatively high, representing some 18 % of the newly discovered planets.

7.3 Changes in the Range of Binary Orbits

We will now apply the approximation obtained earlier generally to a binary composed of a planet and its companion moon moving on an inclined, eccentric orbit. Equation (17) has now to be solved to give critical \(\left( a_{2}/a_{1}\right)\) values for a range of \(e_{1}\) and \(i\) values for given values for \(x_{0},\lambda\) and \(e_{2}.\) Figure 4 is a plot of the critical \(\left( a_{2}/a_{1}\right)\) value against the binary eccentricity \(e_{1}\) for the inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) with \(e_{2}=0.0\). As before, the masses satisfy the condition \(x_{0}=\left( \left( M_{P}+M_{S}\right) /3M_{*}\right) ^{\frac{1}{3}}=0.1\), which is relevant to a Jupiter mass planet with an accompanying moon. The solid curves show the situation of a binary planet, that is the binary mass ratio is \(\lambda =1.0.\) The curves for \(\lambda =10\) are shown as dotted curves for the same inclinations. The dashed curves give the regions for \(\lambda =100\). The curves for \(\lambda =1{,}000\) are not shown as they cannot be clearly separated from those of \(\lambda =100.\) Any other values of \(\lambda\) in the range \(1.0\le \lambda \le 1{,}000\) are not shown to avoid over complicating the figure. As before, the systems which are Hill stable against exchange lie to the right of the curves. To the left of the curves, the surfaces open out and exchange or collision becomes a possibility but it is not an inevitable outcome. It is clear that the critical distances increase and the regions of stability decrease as the value of \(\lambda\) decreases, that is the larger the mass of the moon relative to the planet the more likely it is for an exchange of the masses to take place. The critical distance also increases and the stability decreases as the eccentricity of the binary \(e_{1}\) and the inclination of the orbit i increase in their value for a particular \(\lambda\). The results are in line with the previous work of Donnison (2009, 2010a) using the full three-body formulation, and Szenkovits and Makó (2008) using an elliptic restricted three-body criterion of stability for extrasolar planets in stellar binary systems. These results clearly give the general trends in stability for systems but we can now apply the theory more specifically to actual observed transiting extrasolar planetary systems.

Fig. 3
figure 3

In this figure the range of the moon–planet ratio is reduced to cover the smaller moons. The range of \(\lambda\) is \(10\le \lambda \le 200\), which extends the mass range down into the Earth and super-Earth mass range

Full size image
Fig. 4
figure 4

This figure is a plot of the critical \(\left( a_{2}/a_{1}\right)\) value against the binary eccentricity \(e_{1}\) for the inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) with \(e_{2}=0.0\). As before, the masses satisfy the condition \(x_{0}=\left( \left( M_{1}+M_{2}\right) /3M_{3}\right) ^{\frac{1}{3}}=0.1\), which is relevant to a Jupiter mass planet with an accompanying moon. The solid curves show the situation of a binary planet, that is the binary mass ratio is \(\lambda =1.0.\) The curves for \(\lambda =10\) are shown as dotted curves for the same inclinations. The dashed curves give the regions for \(\lambda =100\). The curves for \(\lambda =1{,}000\) are not shown as they cannot be clearly separated from those of \(\lambda =100.\)

Full size image

7.3.1 Application to Observed Systems

Here we will investigate more fully the variations in the actual planet–moon orbit for the actual systems when the moon is allowed to have non-zero eccentricity and the planet–moon orbital plane can be inclined to the central star. As previously the mass ratio, given by \(\lambda\), is allowed to vary from \(\lambda =1.0\) to \(\lambda =1{,}000\), with \(\lambda =1.0\) representing the possibility that there is a binary planet system orbiting the central star, while \(\lambda =1{,}000\) represents a small moon. It should be noted that the changes in \(a_{1}\) (and \(a_{1}/R_{H}\)) occurring for changes in \(e_{1}\) and i are much smaller than they are for variations in \(e_{2}.\) The theory, in particular Eq. (17), was applied to the  same known transiting extrasolar planetary systems as previously discussed. The results obtained for \(\lambda =1.0\) and \(\lambda =100\) are shown in Figs. 5 and 6, respectively where the known \(e_{2}\) for a system is plotted against the critical \(a_{1}/R_{H}\) for a range of different \(e_{1}\) values given by 0.0, 0.25, 0.5, 0.75. Here \(e_{1}=0.0\) (black solid circles), \(e_{1}=0.25\) (red squares), \(e_{1}=0.5\) (green diamonds), \(e_{1}=0.75\) (blue upward triangles). It was found that for these actual extrasolar planetary systems that when \(\lambda =1.0,\) then as the eccentricity of the moon, \(e_{1},\) was increased then the distance ratio \(\left( a_{2}/a_{1}\right)\) increased so that the critical separation \(a_{1}\)( and \(a_{1}/R_{H}\)) only decreased by small amounts. This is clearly shown in Fig. 5 where the distributions of values of the systems for the different values of \(e_{1}\) move to the left reducing the critical value of \(a_{1}/R_{H}\). Similarly for \(\lambda =100\) in Fig. 6, there was a corresponding decrease in \(a_{1}\) (and \(a_{1}/R_{H}\)) as \(e_{1}\) increased. The critical separation also decreased with \(\lambda\). This was further corroborated by the values for \(\lambda =10\) and \(\lambda =1{,}000\) not shown, so that in general there were small changes in \(a_{1}/R_{H}\) as \(\lambda\) increased. The effect of inclination of the planet–moon binary system on the stability of the binary orbit was also investigated. The critical separations were determined for actual systems for inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ },\) initially for circular moon orbits and subsequently for a full range values of \(e_{1}\). The results are shown for \(\lambda =1.0\) and \(\lambda =100\) with circular moon orbits in Figs. 7 and 8, respectively where \(e_{2}\) is plotted against \(a_{1}/R_{H}\) for different inclinations. Here \(i=0.0\) (black solid circles), \(i=30^{\circ }\) (red squares), \(i=45^{\circ }\) (green diamonds), \(i=60^{\circ }\) (blue upward triangles), \(i=75^{\circ }\) (yellow right side ward triangles), \(i=90^{\circ }\) (pink left side ward triangles). It was found that for a given \(\lambda\) value, that as \(i\) increased the critical separation \(a_{1}\) (and \(a_{1}/R_{H}\)) decreased. Though the changes were very small there was a significant trend. Similarly for the non-zero values of the eccentricity of the moon, the critical separation distance also decreased further as the eccentricity increased in value. When the orbital eccentricity of the systems was plotted against the critical \(a_{1}/R_{H}\) value for binary eccentricities of \(e_{1}=0.5\) for the same values of \(\lambda\) used previously in Fig. 1 (not shown) it was found the outer boundary for stability has moved closer to \(a_{1}/R_{H}=0.5\) for the higher eccentricity case.

Fig. 5
figure 5

In this figure \(e_{2}\) is plotted against \(a_{1}/R_{H}\) for \(\lambda =1.0\) with the different \(e_{1}\) values for all the currently known  transiting extrasolar planetary systems. Here \(e_{1}=0.0\) black solid circles, \(e_{1}=0.25\) red squares, \(e_{1}=0.5\) green diamonds, \(e_{1}=0.75\) blue upward triangles. (Color figure online)

Full size image
Fig. 6
figure 6

In this figure \(e_{2}\) is plotted against \(a_{1}/R_{H}\) for \(\lambda =100\) with the different \(e_{1}\) values for all the currently known transiting extrasolar planetary systems. The colour code is as in Fig. 5. (Color figure online)

Full size image

8 Rôche Limiting Distances

Fig. 7
figure 7

In this figure \(e_{2}\) is plotted against \(a_{1}/R_{H}\) for \(\lambda =1.0\) with the different inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) for all the currently known transiting extrasolar planetary systems. Here \(i=0.0\) black solid circles, \(i=30^{\circ }\) red squares, \(i=45^{\circ }\) green diamonds, \(i=60^{\circ }\) blue upward triangles, \(i=75^{\circ }\) yellow right side ward triangles, \(i=90^{\circ }\) pink left side ward triangles. (Color figure online)

Full size image
Fig. 8
figure 8

In this figure \(e_{2}\) is plotted against \(a_{1}/R_{H}\) for \(\lambda =100\) with the different inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) for all the currently known  transiting extrasolar planetary systems. The colour code is the same as in Fig. 7. (Color figure online)

Full size image
Fig. 9
figure 9

This shows a plot of the critical Hill separation distances \(a_{1}\), for \(\lambda =10\) and \(e_{1}=0.0\), in Jupiter radii estimated from the observed transiting extrasolar planets against the limiting Rôche distances in R J for the three densities. Results for a density of 1 g cm\(^{-3}\) are shown as solid black circles, 3 g \(\hbox {cm}^{-3}\) as red squares and 6 g \(\hbox {cm}^{-3}\) as green diamonds. (Color figure online)

Full size image

The Rôche limit of a satellite, as indicated earlier for possible moons, clearly depends on the internal structure of the satellite as shown by its inverse dependency on the satellite density. Following Weidner and Horne (2010), we consider typical moons with densities in the range 1–6 g cm\(^{-3},\) specifically \(\rho _{s}=1\), 3 and 6 g cm\(^{-3},\) representing everything from gaseous to rocky satellites. This represents a decrease respectively to 0.6934 and 0.5503 of the Rôche limiting distance at 1 g cm\(^{-3}\) as the density increases from 3 to 6 g cm\(^{-3}\). Figure 9 shows a plot of the critical Hill separation distances \(a_{1},\) for \(\lambda =10\) and \(e_{1}=0.0,\) measured in Jupiter radii R J estimated from the observed transiting extrasolar planets against the limiting Rôche distances in R J for the three densities. The results for a density of 1 g cm\(^{-3}\) are shown as solid black circles, 3 g cm\(^{-3}\) as red squares and 6 g cm\(^{-3}\) as green diamonds. Clearly any moons with Hill separations less than the limiting Rôche distance are not likely to have formed or have been destroyed. The lower the density the further out is the critical Rôche distance for a given system so that as far as the range of structurally stable regions is concerned the denser solid moons are favoured over the gaseous moons. Further graphs of \(a_{1}\) against the same limiting Rôche distances in R J for the same three densities were obtained for the other three values of \(\lambda\) already discussed. As the results are fairly obvious and the graphs fairly similar they have not been included. It is clear from them and our earlier results that as \(\lambda\) decreases the critical \(a_{1}\) values increase, so that the ratio \(a_{1}/R_{roche}\) increases for all the densities considered. Hence the difference between the outer Hill stability boundary \(a_{1}\) and the inner Rôche limit bound \(R_{roche}\) therefore decreases the larger the planet/moon ratio. Similarly the number of systems with Hill separations less than or close to the limiting Rôche distance is likely to increase as the planet/moon ratio increases. The number of possible stable systems having a large planet/moon ratio will therefore be reduced.

9 Conclusions

The stability of the orbits of possible moons orbiting extrasolar planets has been examined. Limits have been placed on the range of orbits and masses for these moons. The Rôche limiting radius determines how close the moon can approach its parent planet before it becomes tidally disrupted. This limit is applied to the currently known transiting extrasolar planets with well determined orbits and masses. The outer stability of the orbit of the moon against detachment from the planet by the central star is determined by the Hill stability of the star–planet–moon system. The Hill stability in this case was derived for a full three-body system with the binary composed of the planet and moon moving on an inclined, elliptical orbit relative to the central star, where the binary mass is very small compared to the mass of the star. The approximation derived here has not previously been applied to this particular Hill stability problem and gives expressions for the critical distance ratios \(a_{2}/a_{1}\) and \(q_{2}/a_{1}\) in a closed form. This Hill stability criterion was discussed generally for a wide range of planet/moon mass ratios \(\lambda\) of 1.0, 10, 100 and 1,000, for the full range of orbital eccentricities \(e_{2}\), assuming the moon moves on a circular orbit. It was also applied to all transiting extrasolar planetary systems which have follow up the radial velocity determinations, particularly listing those discovered since the last estimation of critical separations in 2010. It was evident that in those cases where the planet moves on a circular orbit about the central star, the critical separation of the moon from the planet does not change very significantly as the planet-moon mass ratio is increased. For eccentric orbits relative to the central star there can be large reductions in the critical separation as the mass ratio increases with the variation depending strongly on the size of the eccentricity of the planetary orbit.

The effects of eccentricity and inclination on the stability of the orbit of the extrasolar moon was discussed generally in terms of the Hill stability criterion and applied to a range of planet/moon mass ratios with \(\lambda\) of 1.0, 10, 100 and 1,000. Although this is a secondary effect compared to the orbital eccentricity around the central star, it is still significant. The Hill stability criterion was applied to all the transiting extrasolar planets, assuming the same planet-moon mass ratios but with the moon moving with a variety of eccentricities and inclinations. For the non-zero values of the eccentricity of the moon, the critical separation distance decreased further as the eccentricity increased in value. For inclinations \(i=0^{\circ },30^{\circ },45^{\circ },60^{\circ },75^{\circ }\) and \(90^{\circ }\) it was found that for a given \(\lambda\) value, that as \(i\) increased the critical separation \(a_{1}\) decreased. Though the changes were very small there was a significant trend. Combinations of increasing binary eccentricity and inclination clearly decreased the Hill stability of such systems.

From the work of Kipping (2009) and also more recently (Kipping et al. 2012, 2013), it is clear that the photometry available on the Kepler mission, which was specifically designed to detect Earth-sized transiting objects, is capable of detecting large moons similar to those we have discussed earlier. It is therefore likely that the first detection establishing the existence of extrasolar moons is not far away.