Skip to main content
SpringerLink
Log in

Closed-Form Solutions for Free Vibration Frequencies of Functionally Graded Euler-Bernoulli Beams

  • Published:
Mechanics of Composite Materials Aims and scope

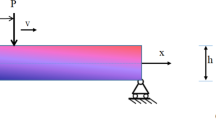
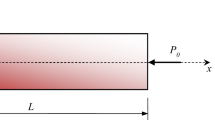
The bending vibration of a functionally graded Euler–Bernoulli beam is investigated by the transformed-section method. The material properties of the functionally graded beam (FGB) are assumed to vary across its thickness according to a simple power law. Closed-form solutions for free vibration frequencies of FGBs with classical boundary conditions are derived. Some analytical results are compared with numerical results found in the published literature to verify the accuracy of the model presented, and a good agreement between them is observed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. S. Suresh, “Modeling and design of multi-layered and graded materials,” Prog. Mater. Sci., 42, 243-251 (1997).

    Article  Google Scholar 

  2. Y. Miyamoto, W. A. Kaysser and B. H. Rabin, Functionally Graded Materials: Design, Processing and Applications, Dordrecht, Kluwer Academic Publishers (1999).

  3. V. Birman and L. W. Byrd, “Modeling and analysis of functionally graded materials and structures,” Appl. Mech. Rev., 60, 195-216 (2007).

    Article  Google Scholar 

  4. M. Aydogdu and V. Taskin, “Free vibration analysis of functionally graded beams with simply supported edges,” Mat. Des., 28, 1651-1656 (2007).

    Article  Google Scholar 

  5. X. F. Li, “A unified approach for analyzing static and dynamic behaviors of functionally graded Timoshenko and Euler-Bernoulli beams,” J. Sound Vib., 318, 1210-1229 (2008).

    Article  Google Scholar 

  6. S. Sina, H. M. Navazi and H. Haddadpour, “An analytical method for free vibration analysis of functionally graded beams,” Mat. Des., 30, 741-747 (2009).

    Article  Google Scholar 

  7. M. T. Piovan and R. Sampaio, “A study on the dynamics of rotating beams with functionally graded properties,” J. Sound Vib., 327, 134–143 (2009).

  8. M. Simsek, “Vibration analysis of a functionally graded beam under a moving mass by using different beam theories,” Compos. Struct., 92, 904-917 (2010).

    Article  Google Scholar 

  9. M. Simsek, “Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories,” Nucl. Eng. Des., 240, 697-705 (2010).

    Article  Google Scholar 

  10. A. E. Alshorbagy, M. A. Eltaher and F. F. Mahmoud, “Free vibration characteristics of a functionally graded beam by finite element method,” Appl. Math. Mod., 35, 412-425 (2011).

    Article  Google Scholar 

  11. S. C. Mohanty, R. R. Dash, and T. Rout, “Parametric instability of a functionally graded Timoshenko beam on Winkler’s foundation,” Nucl. Eng. Des., 241, 2698-2715 (2011).

    Article  Google Scholar 

  12. K. S. Anandrao, R. K. Gupta, P. Ramachandran, and G. V. Rao, “Free vibration analysis of functionally graded beams,” Def. Sci. J., 62, 139-146 (2012).

    Article  Google Scholar 

  13. H. T. Thai and T. P. Vo, “Bending and free vibration of functionally graded beams using various higher-order shear deformation beam theories,” Int. J. Mech. Sci., 62, 57–66 (2012).

  14. N. Wattanasakulpong and V. Ungbhakorn, “Free vibration analysis of functionally graded beams with general elastically end constraints by DTM,” World J. Mech., 2, 297-310 (2102).

  15. H. Su, J. R. Banerjee, and C. W. Cheung, “Dynamic stiffness formulation and free vibration analysis of functionally graded beams,” Compos. Struct., 106, 854–862 (2013).

    Article  Google Scholar 

  16. T. K. Nguyen, T. P. Vo, and H. T. Thai, “Static and free vibration of axially loaded functionally graded beams based on the first-order shear deformation theory,” Compos.: Part B, 55, 147–157 (2013).

  17. K. K. Pradhan and S. Chakraverty, “Free vibration of Euler and Timoshenko functionally graded beams by Rayleigh-Ritz method,” Compos.: Part B, 51, 175-184 (2013).

  18. K. K. Pradhan and S. Chakraverty, “Effects of different shear deformation theories on free vibration of functionally graded beams,” Int. J. Mech. Sci., 82, 149-160 (2014).

    Article  Google Scholar 

  19. M. Aydogdu, “Semi-inverse method for vibration and buckling of axially functionally graded beams,” J. Reinf. Plast. Compos., 27, 683-691 (2008).

    Article  Google Scholar 

  20. Y. Huang and X. F. Li, “Bending and vibration of circular cylindrical beams with arbitrary radial non-homogeneity,” Int. J. Mech. Sci., 52, 595-601 (2010).

    Article  Google Scholar 

  21. J. Murin, M. Aminbaghai, and V. Kutis, “Exact solution of the bending vibration problem of FGM beams with variation of material properties,” Eng. Struct., 32, 1631-1640 (2010).

    Article  Google Scholar 

  22. A. Shahba, R. Attarnejad, and M. T. Marvi, “Free vibration and stability analysis of axially functionally graded tapered Timoshenko beams with classic and non-classical boundary conditions,” Compos.: Part B, 42, 801-808 (2011).

  23. X. F. Li, Y. A. Kang, and J. X. Wu, “Exact frequency equations of free vibration of exponentially functionally graded beams,” Appl. Acoust., 74, 413–420 (2013).

    Article  Google Scholar 

  24. M. Aminbaghai, J. Murin, and V. Kutis, “Modal analysis of the FGM-beams with continuous transversal symmetric and longitudinal variation of material properties with effect of large axial force,” Eng. Struct., 34, 314-329 (2012).

    Article  Google Scholar 

  25. J. Murin, M. Aminbaghai, V. Kutis, and J. Hrabovsky, “Modal analysis of the FGM beams with effect of axial force under longitudinal variable elastic Winkler foundation,” Eng. Struct., 49, 234-247 (2013).

    Article  Google Scholar 

  26. J. Murin, M. Aminbaghai, J. Hrabovsky, V. Kutis, and St. Kugler, “Modal analysis of the FGM beams with effect of the shear correction function,” Compos.: Part B, 45, 1575–1582 (2013).

  27. J. Murin, M. Aminbaghai, J. Hrabovsky, V. Kutis, J. Paulech, and S. Kugler, “A new 3D FGM beam finite element for modal analysis,” Proceedings of the 11th world congress on computational mechanics (WCCM XI), 5th European conference on computational mechanics (ECCM V), 6th European conference on computational fluid dynamics (ECFD VI). Barcelona, Spain (2014).

  28. A. C. Ugural, Mechanical Design: An Integrated Approach, Singapore, McGrow-Hill Company (2004).

  29. W. Weaver, S. P. Timoshenko, and D. H. Young, Vibration Problems in Engineering, 5th ed., John Wiley & Sons, Inc. (1990).

  30. S. S. Rao, Mechanical Vibrations, 3rd ed., Addison-Wesley Publishing Company (1995).

  31. L. Meirovitch, Fundamentals of Vibrations, International Edition, McGraw-Hill (2001).

  32. S. B. Coşkun, M. T. Atay, and B. Öztürk, “Transverse vibration analysis of Euler-Bernoulli beams using analytical approximate techniques,” Advances in Vibration Analysis Research, Dr. Farzad Ebrahimi (Ed.), ISBN: 978-953-307-209-8, InTech (2011).

  33. M. Simsek and T. Kocatürk, “Free and forced vibration of a functionally graded beam subjected to a concentrated moving harmonic load,” Compos. Struct., 90, 465-473 (2009).

  34. S. Natarajan, P. M. Baiz, S. Bordas, T. Rabczuk, and P. Kerfriden, “Natural frequencies of cracked functionally graded material plates by the extended finite element method,” Compos. Struct., 93, 3082-3092 (2011).

    Article  Google Scholar 

  35. X. Zhao and K. M. Liew, “Free vibration analysis of functionally graded conical shell panels by a meshless method,” Compos. Struct., 93, 649-664 (2011).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Chinese Culture University, Taipei, Taiwan, R.O.C.

    W. R. Chen & H. Chang

Authors
  1. W. R. Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to W. R. Chen.

Additional information

Russian translation published in Mekhanika Kompozitnykh Materialov, Vol. 53, No. 1, pp. 119-142 , January-February, 2017.

Appendix A

Appendix A

Based on the transformed-section method, the effective second moment of area of the transformed cross section of beams about their neutral axis is given as

$$ {I}_{\mathrm{eff}}={I}_{y_1}={\displaystyle {\int}_{A_t}{z}_1^2dA.} $$
(A1)

Introducing z 1 = z − h o into Eq. (A1) yields

$$ {I}_{\mathrm{eff}}={\displaystyle {\int}_{A_t}{z}_1^2dA-{h}_o^2}{\displaystyle {\int}_{A_t}dA={I}_y-{h}_o^2{A}_t.} $$
(A2)

The quantities I y and A t are calculated as follows:

$$ {I}_y={\displaystyle {\int}_{\frac{-h}{2}}^{\frac{h}{2}}{\displaystyle {\int}_{\frac{-bn(z)}{2}}^{\frac{bn(z)}{2}}{z}^2 dydz}=}{\displaystyle {\int}_{\frac{-h}{2}}^{\frac{h}{2}}bn(z){z}^2dz}, $$
(A3)
$$ {A}_t={\displaystyle {\int}_{\frac{-h}{2}}^{\frac{h}{2}}{\displaystyle {\int}_{\frac{-bn(z)}{2}}^{\frac{bn(z)}{2}} dydz}=}{\displaystyle {\int}_{\frac{-h}{2}}^{\frac{h}{2}}bn(z){z}^2dz}. $$
(A4)

Inserting Eq. (5) into Eqs. (A3) and (A4) and performing integration, it is found that

$$ {I}_y=\frac{b{h}^3}{12}\left[\frac{E_b}{E_t}+12\left(1-\frac{E_b}{E_t}\right)\left(\frac{1}{k+3}-\frac{1}{k+2}+\frac{1}{4\left(k+1\right)}\right)\right], $$
(A5)
$$ {A}_t=bh\left[\frac{E_b}{E_t}+\left(1-\frac{E_b}{E_t}\right)\frac{1}{k+1}\right]. $$
(A6)

Using Eqs. (A5), (A6) and (6) in Eq. (A2), the effective second area moment about the neutral axis of the transformed cross section of a functionally graded beam is obtained in the form

$$ {I}_y=\frac{b{h}^3}{12}\left[\frac{E_b}{E_t}+12\left(1-\frac{E_b}{E_t}\right)\left(\frac{1}{k+3}-\frac{1}{k+2}+\frac{1}{4\left(k+1\right)}\right)-\frac{3{k}^2{\left(1-{E}_b/{E}_t\right)}^2}{\left(k+1\right){\left(k+2\right)}^2{\left(1+k\;{E}_b/{E}_t\right)}^2}\right]. $$
(A7)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chen, W.R., Chang, H. Closed-Form Solutions for Free Vibration Frequencies of Functionally Graded Euler-Bernoulli Beams. Mech Compos Mater 53, 79–98 (2017). https://doi.org/10.1007/s11029-017-9642-3

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11029-017-9642-3

Keywords

Search

Navigation