Fracture mechanics analysis of debond growth in a single-fiber composite under cyclic loading

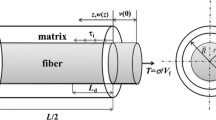
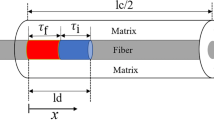
A model is developed to analyze the growth of a fiber/matrix debond along a broken fiber interface in a single-fiber composite subjected to tension-tension fatigue. The Paris law expressed in terms of debond growth and strain energy release rates is used. An analytical solution for the Mode II energy release rate G _II is obtained for long debonds, where the interface crack growth is self-similar. For short debonds, the interface crack interacts with the fiber break, and therefore a FEM modeling in combination with the virtual crack closure technique was performed to calculate the increase in G _II . Finally, the calculated G _II dependences are summarized in simple expressions that are used to simulate the debond growth in fatigue. A parametric study of the effect of Paris law parameters on the debond growth is performed.

Appendix

Distribution of stresses. The two cylinder model shown in Fig. 2 is subjected to a constant strain ε_z0 in the axial direction, resulting from the displacement u _z0/2 applied at both its ends, and to a temperature increment ΔT. In the bonded case, the axial strain in the fiber and matrix is the same, but in the debonded one, only the matrix is subjected to ε_z0. The expressions given below follow from Appendix 2 in [8] and are valid both for bonded and debonded cases. The procedure of their derivation is the same as in [14,15].

Both constituents of the composite are transversely isotropic and follow Hooke’s law, which for normal stresses here can be written in form

$$ {\sigma_i} = {C_{ij}}\left( {{\varepsilon_j} - {\alpha_j}\Delta T} \right), $$

where C _ij is the stiffness matrix and α _j are the thermal expansion coefficients. Here, 3 is the axial direction, and 1 and 2 are two orthogonal directions in the plane of isotropy. All shear stresses are zero.

The elastic solution valid for any transversely isotropic cylindrical phase under this type of loading can be written as

$$ \begin{array}{*{20}{c}} {{u_r} = {A_1}r + {A_2}{r^{ - 1}},} \\ {{\sigma_z} = {A_1}f + g{\varepsilon_{z0}} - {H_3}\Delta T,} \\ {{\sigma_r} = {A_1}\beta + {A_2}\gamma {r^{ - 2}} + \varphi {\varepsilon_{z0}} - {H_r}\Delta T,} \\ {{\sigma_\theta } = {A_1}\beta - {A_2}\gamma {r^{ - 2}} + \varphi {\varepsilon_{z0}} - {H_r}\Delta T.} \\ \end{array} $$

(A1)

Here, new constants have been introduced:

$$ g = {C_{33}},f = 2{C_{32}},\varphi\varphi = {C_{32}},\beta = {C_{22}} + {C_{12}},\gamma = {C_{12}} - {C_{22}},{H_3} = {C_{33}}{\alpha_z} + 2{C_{32}}{\alpha_r},{H_r} = {C_{32}}{\alpha_z} + \beta {\alpha_r} $$

An additional superscript k is also introduced, where k= 1 and 2 for the fiber and matrix, respectively, to mark the constants of the constituents.

The unknown constants $A_1^k$ and $A_2^k$, k= 1 and 2, have to be determined from the following conditions:

• the radial displacements are zero on the symmetry axis,

$$ u_r^1\left( {r = 0} \right) = 0; $$

(A2)

• the displacements and radial stresses are continuous at the interface,

$$ u_r^1\left( {{r_f}} \right) = u_r^2\left( {{r_f}} \right), $$

(A3)

$$ \sigma_r^1\left( {{r_f}} \right) = \sigma_r^2\left( {{r_f}} \right), $$

(A4)

• the radial stresses at the outer boundary r=R of the cylinder assembly are zero,

$$ \sigma_r^2(R) = 0. $$

(A5)

From Eq. (A2), we obtain that $A_2^1 = 0$. For given ε_z0 and ΔT, the system of three equations following from conditions (A3)-A(5) allows one to determine the three constants $A_1^1$, $A_1^2$, and $A_2^2$. Obviously, their values will depend on the strain ε_z0 and the temperature increment ΔT applied.