On the moving load problem in beam structures equipped with tuned mass dampers

Abstract

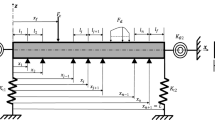
This paper proposes an original and efficient approach to the moving load problem on Euler–Bernoulli beams, with Kelvin–Voigt viscoelastic translational supports and rotational joints, and in addition, equipped with Kelvin–Voigt viscoelastic tuned mass dampers (TMDs). While supports are taken as representative of external devices such as grounded dampers or in-span supports with flexibility and damping, the rotational joints may model rotational dampers or connections with flexibility and damping arising from imperfections or damage. The theory of generalised functions is used to treat the discontinuities of the response variables, which involves deriving exact complex eigenvalues and eigenfunctions from a characteristic equation built as determinant of a 4 × 4 matrix. Based on built pertinent orthogonality conditions for the deflection eigenfunctions, a closed-form analytical response is established in the time domain. The proposed solution holds for any number of TMDs and along-axis supports/joints. To show its applicability, accuracy and efficiency, in a numerical application a beam with multiple supports/joints is considered, subjected to a moving concentrated force and a series of concentrated forces, respectively. In two different configurations, the beam is equipped with one TMD and three TMDs, respectively.

Appendix

This Appendix reports closed-form analytical expressions for all terms in Eqs. (10) and (11), as derived in Ref. [36].

Terms of matrix ${\varvec{\Omega}}\left( x \right)$ in Eq. (10) are given as

$$\begin{array}{*{20}l} {\Omega_{\psi 1} \left( x \right) = {\text{e}}^{ - \omega x} ;} \hfill & {\Omega_{\psi 2} \left( x \right) = {\text{e}}^{\omega x} ;} \hfill & {\Omega_{\psi 3} \left( x \right) = \cos \left( {\omega x} \right);} \hfill & {\Omega_{\psi 4} \left( x \right) = \sin \left( {\omega x} \right)} \hfill \\ {\Omega_{\vartheta 1} \left( x \right) = - \omega {\text{e}}^{ - \omega x} ;} \hfill & {\Omega_{\vartheta 2} \left( x \right) = \omega {\text{e}}^{\omega x} ;} \hfill & {\Omega_{\vartheta 3} \left( x \right) = - \omega \sin \left( {\omega x} \right);} \hfill & {\Omega_{\vartheta 4} \left( x \right) = \omega \cos \left( {\omega x} \right)} \hfill \\ {\Omega_{\mu 1} \left( x \right) = - \omega^{2} {\text{e}}^{ - \omega x} ;} \hfill & {\Omega_{\mu 2} \left( x \right) = - \omega^{2} {\text{e}}^{\omega x} ;} \hfill & {\Omega_{\mu 3} \left( x \right) = \omega^{2} \cos \left( {\omega x} \right);} \hfill & {\Omega_{\mu 4} \left( x \right) = \omega^{2} \sin \left( {\omega x} \right)} \hfill \\ {\Omega_{\chi 1} \left( x \right) = \omega^{3} {\text{e}}^{ - \omega x} ; \, } \hfill & {\Omega_{\chi 2} \left( x \right) = - \omega^{3} {\text{e}}^{\omega x} ; \, } \hfill & {\Omega_{\chi 3} \left( x \right) = - \omega^{3} \sin \left( {\omega x} \right); \, } \hfill & {\Omega_{\chi 4} \left( x \right) = \omega^{3} \cos \left( {\omega x} \right)} \hfill \\ \end{array}$$

(35a–p)

Particular integrals ${\mathbf{J}}^{\left( p \right)} \left( {x,x_{j} } \right)$ for a point force p = 1 at $x = x_{j}$

$$J_{\psi }^{\left( p \right)} \left( {x,x_{j} } \right) = 2^{ - 1} \omega^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0pt} 2}}} \left[ {\sinh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) - { \sin }\left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(36)

$$J_{\vartheta }^{\left( p \right)} \left( {x,x_{j} } \right) = 2^{ - 1} \omega^{ - 1} \left[ {\cosh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) - \cos \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(37)

$$J_{\mu }^{\left( p \right)} \left( {x,x_{j} } \right) = - 2^{ - 1} \omega^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} \left[ {\sinh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) + \sin \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(38)

$$J_{\chi }^{\left( p \right)} \left( {x,x_{j} } \right) = - 2^{ - 1} \left[ {\cosh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) + \cos \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(39)

Particular integrals ${\mathbf{J}}^{{\left( {\Delta\uptheta} \right)}} \left( {x,x_{j} } \right)$ for a relative rotation $\Delta\uptheta = 1$ at $x = x_{j}$

$$J_{\psi }^{{\left( {\Delta\uptheta} \right)}} \left( {x,x_{j} } \right) = 2^{ - 1} \omega^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-0pt} 2}}} \left[ {\sinh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) + \sin \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(40)

$$J_{\vartheta }^{{\left( {\Delta\uptheta} \right)}} \left( {x,x_{j} } \right) = 2^{ - 1} \left[ {\cosh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) + \cos \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(41)

$$J_{\mu }^{{\left( {\Delta\uptheta} \right)}} \left( {x,x_{j} } \right) = - 2^{ - 1} \omega^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left[ {\sinh \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right) - \sin \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(42)

$$J_{\chi }^{{\left( {\Delta\uptheta} \right)}} \left( {x,x_{j} } \right) = - 2^{ - 1} \omega \left[ {\cosh \left( {\sqrt \omega \left( {x - x_{0} } \right)} \right) - \cos \left( {\sqrt \omega \left( {x - x_{j} } \right)} \right)} \right]H\left( {x - x_{j} } \right)$$

(43)

The particular integrals are all continuous, except for $x = x_{0}$ where appropriate, i.e.:

$$\begin{array}{*{20}c} {J_{\chi }^{\left( p \right)} \left( {x_{0}^{ + } ,x_{0} } \right) - J_{\chi }^{\left( p \right)} \left( {x_{0}^{ - } ,x_{0} } \right) = - 1} \\ {J_{\vartheta }^{{\left( {\Delta\uptheta} \right)}} \left( {x_{0}^{ + } ,x_{0} } \right) - J_{\vartheta }^{{\left( {\Delta\uptheta} \right)}} \left( {x_{0}^{ - } ,x_{0} } \right) = 1} \\ \end{array}$$

(44a,b)