Nonlinear axisymmetric response of temperature-dependent FGM conical shells under rapid heating

Abstract

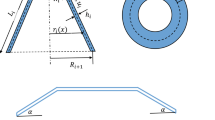
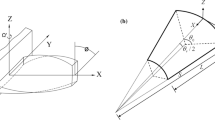
Considering the uncoupled thermoelasticity assumptions, a thermally induced vibration analysis for functionally graded material (FGM) conical shells is performed in this research. Thermo-mechanical properties of the conical shell are assumed to be temperature and position dependent. The conical shell is under rapid heating with various cases of thermal loads on the outer surface, whereas the opposite surface is kept at reference temperature or thermally insulated. Since the ratio of thickness to radius is much smaller than one, the transient heat conduction equation, for simplicity, may be established and solved for one-dimensional condition. Assuming temperature-dependent material properties, the heat conduction equation is nonlinear and should be solved using a numerical method. A hybrid generalized differential quadrature (GDQ) and Crank–Nicolson method is used to obtain the temperature distribution in thickness direction, respectively. Based on the first-order shear deformation theory and geometrically nonlinear assumptions, the equations of motion are obtained applying the Hamilton principle. Discretization of the equations of motion in the space domain and boundary conditions is performed by applying the GDQ method, and then, the system of highly nonlinear coupled ordinary differential equations is solved by the iterative Newmark time-marching scheme and well-known Newton–Raphson method. Since the thermally induced vibration of the conical shells is not reported in the literature, the results are compared with the case of a circular plate. Also, studies of the FGM conical shells for various types of boundary conditions, functionally graded patterns, and thermal loads are provided. The effects of temperature dependency, geometrical nonlinearity, semi-vertex angle, shell length, and shell thickness upon the deflections of the conical shells are investigated.

Appendix

The discretized equations of motion based on GDQ method may be written as

$$\begin{aligned}&A_{11}\left( \sum _{j=1}^{N_x}\bar{B}_{ij}u_{j} + \frac{\sin (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}u_{j}- \frac{\sin ^{2}(\beta _0)}{r^{2}(x_{i})}u_{i} - \frac{\sin (\beta _{0})\cos (\beta _{0})}{r^{2}(x_{i})}w_{i}+ \left( \sum _{j=1}^{N_x}\bar{B}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right. \nonumber \\&\quad +\left. \frac{\sin (\beta _{0})}{2r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right) +B_{11}\left( \sum _{j=1}^{N_x}\bar{B}_{ij}\varphi _{j} + \frac{\sin (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j}- \frac{\sin ^{2}(\beta _0)}{r^{2}(x_{i})}\varphi _{i} \right) \nonumber \\&\quad +A_{12}\left( \frac{\cos (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}- \frac{\sin (\beta _{0})}{2r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right) = I_1\ddot{u}_i+I_2\ddot{\varphi }_{i},\end{aligned}$$

(A.1)

$$\begin{aligned}&A_{11}\left( -\frac{\cos (\beta _{0})\sin (\beta _{0})}{r^{2}(x_{i})}u_{i} - \frac{\cos ^{2}(\beta _{0})}{r^{2}(x_{i})}w_{i} + \left( \sum _{j=1}^{N_x}\bar{B}_{ij}u_{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) + \left( \sum _{j=1}^{N_x}\bar{A}_{ij}u_{j} \right) \left( \sum _{k=1}^{N_x}\bar{B}_{ik}w_{k} \right) \right. \nonumber \\&\quad +\frac{\sin (\beta _{0})}{r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}u_{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) + \frac{3}{2}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) \left( \sum _{l=1}^{N_x}\bar{B}_{il}w_{l}\right) \nonumber \\&\quad +\left. \frac{\sin (\beta _{0})}{2r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) \left( \sum _{l=1}^{N_x}\bar{A}_{il}w_{l} \right) \right) +B_{11}\left( -\frac{\cos (\beta _{0})\sin (\beta _{0})}{r^{2}(x_{i})}\varphi _{i}\right. \nonumber \\&\quad \left. +\left( \sum _{j=1}^{N_x}\bar{B}_{ij}\varphi _{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) + \left( \sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j} \right) \left( \sum _{k=1}^{N_x}\bar{B}_{ik}w_{k} \right) + \frac{\sin (\beta _{0})}{r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j} \right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right) \nonumber \\&\quad +\frac{A_{12}}{r(x_{i})}\left( -\cos (\beta _{0})\sum _{j=1}^{N_x}\bar{A}_{ij}u_{j} + \sin (\beta _{0})\left( \sum _{j=1}^{N_x}\bar{A}_{ij}u_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) + \sin (\beta _0)u_{i}\sum _{j=1}^{N_x}\bar{B}_{ij}w_{j}\right. \nonumber \\&\quad +\left. \cos (\beta _{0})w_{i}\sum _{j=1}^{N_x}\bar{B}_{ij}w_{j} + \frac{\cos (\beta _{0})}{2}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k} \right) \right) +\frac{B_{12}}{r(x_{i})}\left( -\cos (\beta _{0})\sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j} \right. \nonumber \\&\quad \left. + \sin (\beta _{0})\left( \sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) +\sin (\beta _0)\varphi _{i}\sum _{j=1}^{N_x}\bar{B}_{ij}w_{j}\right) +A_{55}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j}+ \frac{\sin (\beta _{0})}{r(x_{i})}\varphi _{i}\right. \nonumber \\&\quad +\left. \sum _{j=1}^{N_x}\bar{B}_{ij}w_{j} +\frac{\sin (\beta _{0})}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) -N^\mathrm{T}\left( \sum _{j=1}^{N_x}\bar{B}_{ij}w_{j}+ \frac{\sin (\beta _{0})}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) + \frac{\cos (\beta _0)}{r(x_{i})}N^\mathrm{T} =I_1\ddot{w}_i,\end{aligned}$$

(A.2)

$$\begin{aligned}&B_{11}\left( \sum _{j=1}^{N_x}\bar{B}_{ij}u_{j} + \frac{\sin (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}u_{j}- \frac{\sin ^{2}(\beta _0)}{r^{2}(x_{i})}u_{i} - \frac{\sin (\beta _{0})\cos (\beta _{0})}{r^{2}(x_{i})}w_{i} +\left( \sum _{j=1}^{N_x}\bar{B}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right. \nonumber \\&\quad +\left. \frac{\sin (\beta _{0})}{2r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right) +D_{11}\left( \sum _{j=1}^{N_x}\bar{B}_{ij}\varphi _{j} + \frac{\sin (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}\varphi _{j}- \frac{\sin ^{2}(\beta _0)}{r^{2}(x_{i})}\varphi _{i} \right) \nonumber \\&\quad {+}B_{12}\left( \frac{\cos (\beta _0)}{r(x_{i})}\sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}{-} \frac{\sin (\beta _{0})}{2r(x_{i})}\left( \sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{ik}w_{k}\right) \right) {-}A_{55}\left( \varphi _{i}{+}\sum _{j=1}^{N_x}\bar{A}_{ij}w_{j}\right) {=} I_2\ddot{u}_i{+}I_3\ddot{\varphi }_{i} \end{aligned}$$

(A.3)

where $i=2,3,\ldots ,N_{x}-1$. Also, the boundary conditions should be discretized using GDQ method as follows:

$$\begin{aligned} u_{s}&=0 \qquad \mathrm {or} \qquad A_{11}\left( \sum _{j=1}^{N_x}\bar{A}_{sj}w_{j}+\frac{1}{2}\left( \sum _{j=1}^{N_x}\bar{A}_{sj}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{sk}w_{k}\right) \right) +A_{12}\left( \frac{\sin (\beta _{0}) }{r(x_s)}u_{s}+\frac{\cos (\beta _{0})}{r(x_s)}w_{s}\right) \nonumber \\&+B_{11}\sum _{j=1}^{N_x}\bar{A}_{sj}\varphi _{j}+B_{12}\frac{\sin (\beta _{0})}{r(x_s)} \varphi _{s} -N^T=0, \quad s=1,N_{x},\end{aligned}$$

(A.4)

$$\begin{aligned} w_{s}&=0 \qquad \mathrm {or} \qquad A_{55}\left( \sum _{j=1}^{N_x}\bar{A}_{sj} w_{j} + \varphi _{s}\right) + \left( \sum _{l=1}^{N_x}\bar{A}_{sl}w_{l}\right) \left\{ A_{11}\left( \sum _{j=1}^{N_x}\bar{A}_{sj} u_{j} + \frac{1}{2} \left( \sum _{j=1}^{N_x}\bar{A}_{sj}w_{j}\right) \right. \right. \nonumber \\&\left. \left( \sum _{k=1}^{N_x}\bar{A}_{sk}w_{k}\right) \right) +A_{12}\left( \frac{\sin (\beta _0)}{r(x_{s})}u_{s} + \frac{\cos (\beta _0)}{r(x_{s})}w_{s}\right) + B_{11} \sum _{j=1}^{N_x}\bar{A}_{sj} \varphi _{j}\nonumber \\&\left. +B_{12} \frac{\sin (\beta _0)}{r(x_{s})} \varphi _{s}-N^T\right\} =0, \quad s=1,N_{x},\end{aligned}$$

(A.5)

$$\begin{aligned} \varphi _{s}&=0 \qquad \mathrm {or} \qquad B_{11}\left( \sum _{j=1}^{N_x}\bar{A}_{sj}w_{j}+\frac{1}{2}\left( \sum _{j=1}^{N_x}\bar{A}_{sj}w_{j}\right) \left( \sum _{k=1}^{N_x}\bar{A}_{sk}w_{k}\right) \right) +B_{12}\left( \frac{\sin (\beta _{0}) }{r(x_s)}u_{s}+\frac{\cos (\beta _{0})}{r(x_s)}w_{s}\right) \nonumber \\&+D_{11} \sum _{j=1}^{N_x}\bar{A}_{sj}\varphi _{j} +D_{12} \frac{\sin (\beta _{0})}{r(x_s)} \varphi _{s} -M^T=0, \quad s=1,N_{x}, \end{aligned}$$

(A.6)

where $\bar{A}_{ij}$ and $\bar{B}_{ij}$ are weighting coefficients of the first- and second-order derivative, respectively, and are defined as follows:

$$\begin{aligned}&\bar{A}_{ij}= {\left\{ \begin{array}{ll} \frac{\Upsilon (x_i)}{(x_i-x_j)\Upsilon (x_j)}\quad &{}\hbox { when }\quad i\ne j\\ -\sum \limits _{k=1,k\ne i}^{N_{x}}\bar{A}_{ik} \qquad &{}\hbox { when }\quad i=j \end{array}\right. }\qquad i,j=1,2,\ldots ,N_{x} \end{aligned}$$

(A.7)

in which

$$\begin{aligned} \Upsilon (x_i)= \prod _{k=1,k\ne i}^{N_{x}} (x_i-x_k) \end{aligned}$$

(A.8)

and

$$\begin{aligned}&{\left\{ \begin{array}{ll} \bar{B}_{ij} = 2 \left( \bar{A}_{ii} \bar{A}_{ij} -\frac{\bar{A}_{ij}}{(x_i-x_j)}\right) \\ i,j=1,2,\ldots ,N_{x} \end{array}\right. }&\mathrm{when} \quad i\ne j, \nonumber \\&{\left\{ \begin{array}{ll} \bar{B}_{ii} = -\sum \limits _{k=1,k\ne i}^{N_{x}} \bar{B}_{ik} \\ i=1,2,\ldots ,N_{x} \end{array}\right. }&\mathrm{when} \quad i=j. \end{aligned}$$

(A.9)