Abstract
As is well known to physicists, the axial anomaly of the massless free fermion in Euclidean signature is given by the index of the corresponding Dirac operator. We use the Batalin–Vilkovisky (BV) formalism and the methods of equivariant quantization of Costello and Gwilliam to produce a new, mathematical derivation of this result. Using these methods, we formalize two conventional interpretations of the axial anomaly, the first as a violation of current conservation at the quantum level and the second as the obstruction to the existence of a well-defined fermionic partition function. Moreover, in the formalism of Costello and Gwilliam, anomalies are measured by cohomology classes in a certain obstruction–deformation complex. Our main result shows that—in the case of the axial symmetry—the relevant complex is quasi-isomorphic to the complex of de Rham forms of the space–time manifold and that the anomaly corresponds to a top-degree cohomology class which is trivial if and only if the index of the corresponding Dirac operator is zero.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
1.1 Background
The axial anomaly is the failure of a certain classical symmetry of the massless free fermion to persist after quantization (see [2] for an original reference on the topic). It is well known to physicists that the axial anomaly is measured precisely by the index of the Dirac operator (see, e.g., Chapter 22.2 of [18] or [16]); the aim of this paper is to prove this fact in a mathematically rigorous context for perturbative quantum field theory (QFT). Namely, we use the framework for the study of anomalies in Euclidean signature developed by Costello and Gwilliam [7].
Given a generalized Dirac operator D on a \(\mathbb {Z}/2\)-graded vector bundle \(V\rightarrow M\) over a Riemannian manifold M, the massless free fermion is described by the equation of motion
for \(\phi \) a section of V. Consider the operator \(\Gamma \) which is the identity on even sections of V and minus the identity on odd sections of V, i.e., \(\Gamma \) is the chirality involution. Then, \(\Gamma \) anti-commutes with D, since D is odd for the \(\mathbb {Z}/2\)-grading. It follows that if \(D\phi = 0\), then
In other words, the operator \(\Gamma \) preserves the equations of motion, so generates a U(1) symmetry of the classical theory. This symmetry is known as the axial symmetry. One can ask whether this symmetry persists after the massless free fermion is quantized. This is in general not the case; the axial anomaly measures the obstruction to the promotion of this classical symmetry to a quantum one. More generally, we say that a classical symmetry is anomalous if it does not persist after quantization. Anomalies in fermionic field theories have been an object of renewed recent interest [11, 20], in part because of their relevance to topological phases of matter.
The question of what it means mathematically to quantize a field theory is still an open one. However, the formalism of Costello and Gwilliam [6,7,8] is one approach to the perturbative quantization of field theories which has been able to reproduce many properties of quantum field theory—especially those pertaining to the observables of quantum field theories—that physicists have long studied. This formalism naturally includes a framework for studying symmetries, and it is within this framework that we prove our results.
From another (heuristic) vantage point, a fermionic anomaly is an obstruction to the existence of a well-defined fermionic partition function, in the following sense. To compute the partition function of a quantum field theory involving fermionic fields, one performs a path integral over the space of all quantum fields. To do this, one first fixes a number of pieces of geometric and topological data, such as a manifold M, a metric on M, a spin structure on M. Let  denote the “space” of all relevant pieces of geometric and topological data. The scare quotes are there because we might need a more abstract notion of space (such as a stack) to appropriately describe the situation. Given a point
denote the “space” of all relevant pieces of geometric and topological data. The scare quotes are there because we might need a more abstract notion of space (such as a stack) to appropriately describe the situation. Given a point  , we can form the space of fields, which is a product
, we can form the space of fields, which is a product  of the fermionic fields
of the fermionic fields  and the non-fermionic fields
and the non-fermionic fields  at x. The non-fermionic fields
at x. The non-fermionic fields  may include a gauge field or a scalar field with which the fermionic fields interact. As x varies, these spaces of fields fit together into something like a product
may include a gauge field or a scalar field with which the fermionic fields interact. As x varies, these spaces of fields fit together into something like a product  of fibrations over
of fibrations over  . In a given fiber
. In a given fiber  , one can choose to perform the path integral by first integrating over
, one can choose to perform the path integral by first integrating over  , choosing a fixed
, choosing a fixed  . Because the fermionic fields are coupled to the fields in
. Because the fermionic fields are coupled to the fields in  , the fermionic integration produces something which varies over
, the fermionic integration produces something which varies over  , i.e., depends both on the fixed non-fermionic field
, i.e., depends both on the fixed non-fermionic field  and on the point
and on the point  . However, the fermionic integration does not canonically produce a number in general; it produces an element of a (super-)line depending on the background data. In other words, there is a line bundle
. However, the fermionic integration does not canonically produce a number in general; it produces an element of a (super-)line depending on the background data. In other words, there is a line bundle

This is called the determinant line bundle, because its fiber over a point  is the natural home for the determinant of the Dirac operator corresponding to the massless free fermion theory with background data encoded in y. The fermionic path integral produces a section \(\sigma \) of this bundle, which deserves to be called “the partition function” only when L is endowed with a trivialization, for in that case, one can compare \(\sigma \) to this trivialization to get an honest function.
is the natural home for the determinant of the Dirac operator corresponding to the massless free fermion theory with background data encoded in y. The fermionic path integral produces a section \(\sigma \) of this bundle, which deserves to be called “the partition function” only when L is endowed with a trivialization, for in that case, one can compare \(\sigma \) to this trivialization to get an honest function.
There is a well-developed mathematical literature addressing many of the relevant issues in the case where one chooses  and restricts attention to a subspace of
and restricts attention to a subspace of  which is an actual space (see [4, 5, 10]). These ideas make maneuvers of physicists (e.g., zeta-function regularization) precise in the special context of families of massless free fermionic field theories. In the present article, we allow
which is an actual space (see [4, 5, 10]). These ideas make maneuvers of physicists (e.g., zeta-function regularization) precise in the special context of families of massless free fermionic field theories. In the present article, we allow  to be non-trivial, fix
to be non-trivial, fix  (and therefore a manifold M on which the theory lives), and study the dependence of L only over the fiber
(and therefore a manifold M on which the theory lives), and study the dependence of L only over the fiber  . In other words, we study the pullback
. In other words, we study the pullback

We will let  be a space of perturbative gauge fields, i.e.,
be a space of perturbative gauge fields, i.e.,  will be the space of background gauge fields for the axial symmetry.
will be the space of background gauge fields for the axial symmetry.
We note that the present work differs from the mathematical treatments in the vein of [10] in two ways. The first is that the “space”  is best understood as an object of formal derived deformation theory [14]. In [7], the authors explain how perturbative field theory can be described with the language of formal derived deformation theory; the essence of this relationship is that, for the purposes of quantum field theory, formal derived deformation theory provides a nice unification of perturbation theory and gauge theory. In the context of symmetries of quantum field theory, the approach of [7] amounts essentially to turning on a background gauge field for the symmetry in question and then studying the gauge invariance of the partition function as a function of this background gauge field. In the present work, we will mainly use formal derived deformation theory for the geometric intuition it provides. In particular, we will prove homological algebraic results about certain modules over a commutative differential graded algebra, and intuitions from formal derived deformation theory will allow us to interpret these results as related to the heuristic discussion above.
is best understood as an object of formal derived deformation theory [14]. In [7], the authors explain how perturbative field theory can be described with the language of formal derived deformation theory; the essence of this relationship is that, for the purposes of quantum field theory, formal derived deformation theory provides a nice unification of perturbation theory and gauge theory. In the context of symmetries of quantum field theory, the approach of [7] amounts essentially to turning on a background gauge field for the symmetry in question and then studying the gauge invariance of the partition function as a function of this background gauge field. In the present work, we will mainly use formal derived deformation theory for the geometric intuition it provides. In particular, we will prove homological algebraic results about certain modules over a commutative differential graded algebra, and intuitions from formal derived deformation theory will allow us to interpret these results as related to the heuristic discussion above.
The second way in which our work differs from existing treatments of anomalies is that we focus on a general approach to field theories and their quantization known as the Batalin–Vilkovisky (BV) formalism. In the work of Costello and Gwilliam, this formalism is used to perform the quantization of the observables of field theories and their symmetries. Our work shows that, simply by “turning the crank on the machine” of BV quantization, one naturally recovers the axial anomaly. In other words, we study the axial anomaly using a framework that was not handmade for the case of the massless free fermion.
We note also that we work entirely in Euclidean signature; for a mathematical discussion of the axial anomaly in Lorentzian signature, see [1], which also provides a historical survey of the topic.
1.2 Presentation of main results
This paper has two main results. First, we compute the equivariant quantum observables of a massless free fermion with a symmetry. Second, we compute the axial anomaly of the massless free fermion and show that it is given by the index of the associated Dirac operator.
Costello and Gwilliam provide definitions of the notions of free quantum field theory and of symmetries of such theories. In their formalism, a symmetry is effected by the action of a differential graded Lie algebra (dgla)  on the space of fields, and one can study the obstruction to the quantization of this symmetry, as well as the cochain complex of equivariant quantum observables, which forms a differential graded module for the commutative differential graded algebra
on the space of fields, and one can study the obstruction to the quantization of this symmetry, as well as the cochain complex of equivariant quantum observables, which forms a differential graded module for the commutative differential graded algebra  (the Chevalley–Eilenberg cochains of
(the Chevalley–Eilenberg cochains of  ). Our first main result is the following proposition:
). Our first main result is the following proposition:
Proposition
(Cf. Proposition 5.1, Lemma 5.9) Let  be a dgla acting on the massless free fermion by symmetries,
be a dgla acting on the massless free fermion by symmetries,  be the corresponding Chevalley–Eilenberg cochain complex, and
be the corresponding Chevalley–Eilenberg cochain complex, and  the underlying graded vector space of
the underlying graded vector space of  . The equivariant quantum observables of the massless free fermion with action of
. The equivariant quantum observables of the massless free fermion with action of  are quasi-isomorphic to a
are quasi-isomorphic to a  -module P whose underlying graded vector space is
-module P whose underlying graded vector space is  . This module is isomorphic to the trivial such module if and only if the obstruction is trivial.
. This module is isomorphic to the trivial such module if and only if the obstruction is trivial.
In Sect. 5, we will comment on the interpretation of this proposition as an instantiation of the heuristic discussion of the line bundle  in the previous subsection.
in the previous subsection.
In the framework of Costello and Gwilliam, there is an obstruction–deformation complex and the obstruction is a cohomology class \([\mathfrak {Obstr}]\) in this complex (see Definition-Lemma A.40 and Lemma A.44). The obstruction is what physicists would call an “anomaly,” and we will use the two terms more or less interchangeably.
and the obstruction is a cohomology class \([\mathfrak {Obstr}]\) in this complex (see Definition-Lemma A.40 and Lemma A.44). The obstruction is what physicists would call an “anomaly,” and we will use the two terms more or less interchangeably.
Our aim is to compute the anomaly, at least for certain actions of a dgla  on the massless free fermion. To accomplish this, one needs to understand the structure of
on the massless free fermion. To accomplish this, one needs to understand the structure of  . For the case of the axial symmetry, which corresponds to the dgla
. For the case of the axial symmetry, which corresponds to the dgla  , we show the following two results:
, we show the following two results:
Proposition
(Cf. Proposition 6.1) If M is oriented, there is a canonical quasi-isomorphism
of complexes of sheaves on M. Here \(\Omega ^\bullet _M\) is the abelian elliptic dgla encoding the axial symmetry of the massless free fermion theory.
The assumption of orientability is not necessary for a version of the above proposition to be true; see Remark 6.4.
Main Theorem
(Cf. Theorem 6.2) The cohomology class of \(\mathfrak {Obstr}\) is equal to the cohomology class of
where \(\Phi \) is the quasi-isomorphism of the Proposition and \(dVol_g\) is the Riemannian volume form on (M, g).
In fact, we will have very similar theorems in case a Lie algebra \({\mathfrak {g}}\) acts on the fermions in a way that commutes with the corresponding Dirac operator. We prove the corresponding generalizations of the above results in Sect. 7.
We note that the obstruction-theoretic approach to anomalies is known also to physicists: see, e.g., Chapter 22.6 of [18]. In the present work, we give a mathematically precise version of this approach; in particular, we use the renormalization techniques of [6].
Readers with a background in physics are likely to be more familiar with the perspective on anomalies as violations of current conservation at the quantum level. This perspective is essentially dual to the one we highlight here; in fact, the formalism of Costello and Gwilliam in Chapter 12 of [7] incorporates both perspectives—albeit at a very abstract level—and the authors freely move between the two. We comment on the current conservation perspective in Sect. 6.3.
Let us summarize. In this paper, we focus on two perspectives on anomalies in fermionic theories. In the first, anomalies are obstructions to the construction of a well-defined fermionic partition function, which perspective will be justified by Lemma 5.9. In the second perspective, anomalies are the obstruction to the persistence of a symmetry after quantization. This perspective is justified by the arguments of Sect. 6.3, using the obstruction-theoretic result of Main Theorem.
1.3 Future directions
In this subsection, we outline a few natural extensions of the present work.
One of the novel realizations of Costello and Gwilliam is that the observables of a quantum field theory fit together into a local-to-global (on the space–time manifold), cosheaf-like object known as a factorization algebra. In this paper, we use only the global observables on M. However, the factorization-algebraic structure of observables often reproduces familiar algebraic gadgets which mix geometry and algebra: locally constant factorization algebras, as shown by Lurie [15], are equivalent to \(E_n\)-algebras, and holomorphic factorization algebras produce vertex algebras (see chapter 5 of [8] for the general construction, and [12] for an example of the construction). It would be interesting to understand the analogous sort of structure in the case at hand.
Another interesting local-to-global aspect of field theories in the formalism of Costello and Gwilliam is that, given a theory on a manifold M, the formalism naturally produces a sheaf of theories on M. Moreover, the construction of the massless free fermion on M depends only a metric, a \(\mathbb {Z}/2\)-graded vector bundle on M, and a generalized Dirac operator D. All three objects are local in nature, so that it is to be expected that the massless free fermion can be extended to a sheaf of theories on an appropriate site of smooth manifolds (i.e., manifolds equipped with a metric, \(\mathbb {Z}/2\)-graded vector bundle, and Dirac operator). We would like to give sheaf-theoretic extensions of the main theorems of this paper.
In yet another direction, we would like to use the BV formalism to make analogous constructions to those in [10]. Namely, in the case where we have a family of Dirac operators parametrized by a manifold B, we expect the BV formalism to produce a line bundle over B just as we saw in the first subsection. We hope to give a BV-inspired construction of a metric and compatible connection, which can be used to probe the line bundle.
Finally, in the case that the anomaly does vanish, we would like to compute the partition function.
1.4 Plan of the paper
The plan for the rest of the paper is as follows. In the next section, we provide a lightning review of basic concepts from the theory of generalized Dirac operators sufficient to define the theory of massless free fermions in the BV formalism. In Sect. 3, we introduce the main example of the massless free fermion and its axial symmetry. This section relies heavily on the techniques of Costello and Gwilliam, the relevant background on which we review in “Appendix.” In Sect. 4, we discuss a few lemmas concerning BV quantization which appear implicitly in some form or other in the literature, but whose statements and proofs we make explicit in the present context. Next, in Sect. 5, we prove the first proposition from Sect. 1.2. In Sect. 6 (Sects. 6.1 and 6.2) , we show that the index of the Dirac operator completely characterizes the anomaly by proving more precise versions of the second Proposition above and Main Theorem. Also in Sect. 6 (Sect. 6.3), we bring our discussion closer to the physics literature by describing the relationship between the axial anomaly and the existence of conserved currents in the massless free fermion quantum field theory. Finally, in Sect. 7, we prove equivariant generalizations of the preceding results.
1.5 Notation and conventions
We assemble here many conventions and notations that we use throughout the remainder of the text. Some may be explained where they first appear, but we believe it to be useful to the reader to collect them in one place.
-
The references we cite are rarely the original or definitive treatments of the subject; they are merely those which most directly inspired and informed the work at hand. We have made every attempt to indicate which results are taken or modified from another source.
-
The free fermion theory will be formulated on a Riemannian manifold M. We will assume M to be connected for simplicity, though our results are easily extended to non-connected M.
-
If a Latin letter in standard formatting is used to denote a vector bundle, e.g., E, then that same letter in script formatting, e.g.,
 , is used to denote its sheaf of sections. Letters in script formatting, except
, is used to denote its sheaf of sections. Letters in script formatting, except  , will always denote sheaves of smooth sections of vector bundles.
, will always denote sheaves of smooth sections of vector bundles. -
We use the notation \(\cong \) for isomorphisms and \(\simeq \) for quasi-isomorphisms (weak equivalences).
-
We use the notation \(C^{\infty }_M\) and \(\Omega ^k_M\) for the sheaves of smooth functions and smooth k-forms, respectively, on M. We use the notation \(\underline{\mathbb R}\), \(\Lambda ^k T^*M\) for the corresponding vector bundles.
-
If V is a finite-dimensional vector space, \(V^\vee \) is the linear dual to V; if V is a topological vector space, then \(V^\vee \) is the continuous linear dual. If \(V\rightarrow M\) is a finite-rank vector bundle, then \(V^\vee \rightarrow M\) is the fiberwise dual to V.
-
If \(V_1\rightarrow M_1\) and \(V_2\rightarrow M_2\) are vector bundles and \(M_3\) is a manifold, then we denote by \(V_1\boxtimes V_2\) the bundle \(p_1^*(V_1)\otimes p_1^*(V_2)\rightarrow M_1\times M_2\times M_3\), where \(p_1: M_1\times M_2\times M_3 \rightarrow M_1\) and \(p_2: M_1\times M_2\times M_3\rightarrow M_2\) are the canonical projections. If \(M_3\) is not explicitly mentioned, it is assumed to be pt.
-
We will use \(\otimes \) to denote the completed projective tensor product of topological vector spaces as well as the algebraic tensor product of finite-dimensional vector spaces. The completed projective tensor product has the nice characterization that if
 and
and 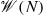 are vector spaces of global sections of vector bundles \(V\rightarrow M\) and \(W\rightarrow N\), then
are vector spaces of global sections of vector bundles \(V\rightarrow M\) and \(W\rightarrow N\), then  is the space of global sections of the bundle \(V\boxtimes W\) over \(M\times N\).
is the space of global sections of the bundle \(V\boxtimes W\) over \(M\times N\). -
If V is a \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector space and v is a homogeneous element of v, then |v| and \(\pi _v\) refer to the \(\mathbb {Z}\) and \(\mathbb {Z}/2\)-degrees of v, respectively. We will also call |v| the ghost number of v and \(\pi _v\) the statistics of v. This gives a convenient terminology for distinguishing between the various types of grading our objects will have; it is a terminology that conforms loosely to that of physics. We will sometimes also refer to ghost number as cohomological degree.
-
If \(V\rightarrow M\) is a vector bundle, then \(V^!\) is the bundle \(V^\vee \otimes Dens_M\), where \(Dens_M\) is the density bundle of M.
 will denote the sheaf of sections of \(V^!\).
will denote the sheaf of sections of \(V^!\). -
If V is a \(\mathbb {Z}\)-graded vector space, then V[k] is the \(\mathbb {Z}\)-graded vector space whose i-th homogeneous space is \(V_{i+k}\). In other words, V[k] is V shifted down by k “slots.”
-
If M is compact and Riemannian with metric g, then for a one-form \(\alpha \),
$$\begin{aligned} |\alpha |^2 : = g^{-1}(\alpha , \alpha )\in C^{\infty }(M). \end{aligned}$$Here, \(g^{-1}\) is the metric on \(T^*M\) induced from g. There is a similar definition if \(\alpha \) is a section of a vector bundle \(V\rightarrow M\) with metric \((\cdot , \cdot )\).
-
If V is a \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector space, then Bilin(V) is the \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector space of bilinear maps \(V\otimes V\rightarrow V\).
-
When dealing with \(\mathbb {Z}\times \mathbb {Z}/2\)-graded objects, we will always say “graded (anti)-symmetric” if we wish Koszul signs to be taken into account. If we simply say (anti)-symmetric, we mean that this notion is to be interpreted without taking Koszul signs into account.
-
If \(v\in {{\mathrm{Sym}}}(V)\) for some vector space V, then \(v^{(r)}\) denotes the component of v in \({{\mathrm{Sym}}}^r(V)\).
-
Let V be a (non-graded) vector space and \(\phi : V\rightarrow V\) a linear map. We denote by \(\phi _{0\rightarrow 1}\) the cohomological degree 1 operator
$$\begin{aligned} V \overset{\phi }{\longrightarrow } V[-1], \end{aligned}$$and similarly for \(\phi _{1\rightarrow 0}\). We denote by \(\phi _{0\rightarrow 0}\) the cohomological degree 0 operator on \(V\oplus V[-1]\) which acts by \(\phi \) on V and by 0 on \(V[-1]\); similarly, \(\phi _{1\rightarrow 1}\) is the operator on \(V\oplus V[-1]\) which acts by 0 on V and by \(\phi \) on \(V[-1]\).
-
If
 is an elliptic dgla, then we will use
is an elliptic dgla, then we will use  to denote the differential on the complex of Chevalley–Eilenberg cochains of
to denote the differential on the complex of Chevalley–Eilenberg cochains of 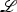 .
.
2 Generalized Laplacians, heat kernels, and Dirac operators
We present here a list of definitions and results relevant to our work, taking most of these from [3]. Throughout, (M, g) is a closed Riemannian manifold of dimension n with Riemannian volume form \(dVol_g\). We let \(V\rightarrow M\) be a \(\mathbb {Z}/2\)-graded vector bundle with \(V^+,V^-\) the even and odd bundles, respectively. We let  be the sheaf of smooth sections of V, and similarly
be the sheaf of smooth sections of V, and similarly  the sheaf of smooth sections of \(V^\pm \). We always use normal-font letters for vector bundles and script letters for the sheaves of sections of the corresponding vector bundles.
the sheaf of smooth sections of \(V^\pm \). We always use normal-font letters for vector bundles and script letters for the sheaves of sections of the corresponding vector bundles.
Definition 2.1
A \(\mathbb {Z}/2\)-graded metric bundle is a metric bundle \(V\rightarrow M\) with an orthogonal decomposition \(V=V^+\oplus V^-\).
Definition 2.2
(Proposition 2.3 of [3]). Let V be a \(\mathbb {Z}/2\)-graded metric bundle. A generalized Laplacian on V is a differential operator

such that
where we are thinking of smooth functions as operators which act on sections of V by pointwise scalar multiplication .
We say that H is formally self-adjoint if for all  ,
,
Remark 2.3
The equation defining a generalized Laplacian is a coordinate-free way of saying that H is a second-order differential operator on V whose principal symbol is just the metric, i.e., that in local coordinates, H looks like \(g^{ij} \partial _i \partial _j+\text {lower-order derivatives}\). \(\square \)
Remark 2.4
We did not strictly need V to be \(\mathbb {Z}/2\)-graded to define a generalized Laplacian, but since we only ever work in this case, we do not use this slightly different definition. \(\square \)
Definition 2.5
(Definition 3.36 of [3]) A Dirac operator on V is an odd differential operator

such that \(D^2\) is a generalized Laplacian. The definition of formal self-adjointness makes sense also for Dirac operators.
Example 2.6
Let \(V = \Lambda ^\bullet T^*M\), with the \(\mathbb {Z}/2\)-grading given by the form degree mod 2. Then, the operator \(d+d^*\) is a generalized Dirac operator since its square \((d+d^*)^2\) is the Laplace-Beltrami operator. Here, \(d^*\) is the formal adjoint of d, characterized by
It is clear from this description that \(d+d^*\) is formally self-adjoint, since it is the sum of an operator with its formal adjoint. Via Hodge theory, the kernel of \(d+d^*\) is canonically identified with the de Rham cohomology \(H^\bullet _{dR}(M)\). \(\square \)
There are numerous other examples of interest—for example, the traditional Dirac operator on an even-dimensional spin manifold and \(\sqrt{2}\left( {\bar{\partial }} +{\bar{\partial }}^*\right) \) on a Kähler manifold—and our formalism will work for these as well. We refer the reader to Section 3.6 of [3] for the details of the construction of these operators.
Definition-Lemma 2.7
(Proposition 3.38 of [3]) If V is a \(\mathbb {Z}/2\) graded bundle over (M, g) a Riemannian manifold and D a Dirac operator on V, then the Clifford action of 1-forms on V
is defined on exact forms by
and extended to all 1-forms by \(C^{\infty }\)-linearity. This action is well defined.
Theorem 2.8
(The heat Kernel; Section 8.2.3 of [7]) Let V be a \(\mathbb {Z}/2\)-graded metric bundle with metric \((\cdot , \cdot )\) and Dirac operator D. Write \(H:=D^2\) for the generalized Laplacian corresponding to D. Then, there is a unique heat kernel\(k \in \Gamma (M\times M,V\boxtimes V)\otimes C^{\infty }(\mathbb R_{>0})\) satisfying:
-
1.
$$\begin{aligned} \frac{d}{dt}k_t + (H\otimes 1)k_t = 0, \end{aligned}$$
where \(k_t\in \Gamma (M\times M,V\boxtimes V)\) is the image of k under the map
$$\begin{aligned}id\otimes ev_t:\Gamma (M\times M,V\boxtimes V)\otimes C^{\infty }(\mathbb R_{>0})\rightarrow \Gamma (M\times M,V\boxtimes V)\end{aligned}$$induced from the evaluation of functions at \(t\in \mathbb R_{>0}\).
-
2.
For
 , $$\begin{aligned} \lim _{t\rightarrow 0}\int _{y\in M} id\otimes (\cdot ,\cdot )(k_t(x,y)\otimes s(y)) dVol_g(y) = s(x), \end{aligned}$$
, $$\begin{aligned} \lim _{t\rightarrow 0}\int _{y\in M} id\otimes (\cdot ,\cdot )(k_t(x,y)\otimes s(y)) dVol_g(y) = s(x), \end{aligned}$$where the limit is uniform over M and is taken with respect to some norm on V.
The scale t heat kernel \(k_t\) is the integral kernel of the operator \(e^{-tH}\) in the sense that
Definition 2.9
(Proposition 3.48 of [3]) Let \(D^\pm \) denote  for D a formally self-adjoint Dirac operator D. The index\({\text {ind}}(D)\) of D is \(\dim (\ker (D^+))-\dim ({\text {coker}}(D^+))\). By the formal self-adjointness of D, we have also the alternative formula
for D a formally self-adjoint Dirac operator D. The index\({\text {ind}}(D)\) of D is \(\dim (\ker (D^+))-\dim ({\text {coker}}(D^+))\). By the formal self-adjointness of D, we have also the alternative formula
for the index of D.
Example 2.10
The index of the Dirac operator from Example 2.6 is
where \(\chi (M)\) is the Euler characteristic of M. \(\square \)
The following definition can be found in the discussion preceding Proposition 1.31 of [3]
Definition 2.11
If \(\phi : V\rightarrow V\) is a grading–preserving endomorphism of the super-vector space V, then the supertrace of \(\phi \) is
Let \(\Gamma : V\rightarrow V\) denote the operator which is the identity on \(V^+\) and minus the identity on \(V^-\). Then, \({\text {Str}}(\phi ) = {{\mathrm{Tr}}}(\phi \Gamma )\).
With these definitions in place, we can finally state the following
Theorem 2.12
(Theorem 3.50 of [3]) Let V be a Hermitian, \(\mathbb {Z}/2\)-graded vector bundle on a closed Riemannian manifold M, with \(dVol_g\) the Riemannian volume form on M. Let D be a formally self-adjoint Dirac operator on V, with \(k_t\) the heat kernel of \(D^2\). Then
where the last trace is an \(L^2\) trace of the bounded operator \(e^{-tD^2}\).
This is the McKean–Singer theorem.
We will also need a few technical results that will be useful, especially in Sect. 7. The first is
Lemma 2.13
(Proposition 3.48 of [3]) If D is a formally self-adjoint Dirac operator over a compact manifold, then

where the decomposition is orthogonal with respect to the metric on  induced from \((\cdot , \cdot )\).
induced from \((\cdot , \cdot )\).
Remark 2.14
This is a special case of a general Hodge decomposition that applies for any elliptic complex with a metric on the corresponding bundle of sections. \(\square \)
The second result is Proposition 2.37 of [3], as used in the proof of the McKean–Singer Theorem.
Lemma 2.15
If D is a formally self-adjoint Dirac operator, and if \(P_{\pm }\) is the orthogonal projection onto \(\ker (D^\pm )\), then for t large,

where \(\lambda _1\) is the smallest nonzero eigenvalue of \(D^2\) and C is a constant (i.e., independent of t).
Finally, we present useful analytic facts about the spectrum of a Laplacian on a compact manifold.
Lemma 2.16
(Cf. Proposition 2.36 of [3]) If H is a formally self-adjoint generalized Laplacian on a compact manifold, then H has a unique self-adjoint extension \({\bar{H}}\) with domain a subspace of \(L^2\) sections of V; \({\bar{H}}\) has discrete spectrum, bounded below, and each eigenspace is finite-dimensional, with smooth eigenvectors. Letting \(\phi _j\) be an eigenvector for \({\bar{H}}\) with eigenvalue \(\lambda _j\), we have
Moreover, \(e^{-t{\bar{H}}}\) is compact (and therefore bounded and trace class).
3 The massless free fermion and its axial symmetry
In this section, we introduce the main examples which will concern us in the rest of the paper, namely the example of the massless free fermion and its axial symmetry. We use the formalism of (equivariant) Batalin–Vilkovisky (BV) quantization and renormalization, as developed in [6,7,8]. “Appendix” consists of a self-contained summary of all the relevant background materials; we encourage the reader to peruse it as necessary. To the reader already familiar with this material, we note that in our work, we allow the space of fields of a free field theory and all objects built from this space of fields to possess an extra \(\mathbb {Z}/2\)-grading which tracks particle statistics—fermionic or bosonic, corresponding to odd or even \(\mathbb {Z}/2\)-grading, respectively. In this convention for the usage of the term “statistics,” ghosts, anti-fields, and anti-ghosts for fermionic fields have fermionic statistics. Of course, fermionic ghosts and anti-fields are each mutually commuting, so our usage of the term “statistics” differs from the conventional physics usage.
In the formalism of [6, 8], a free BV theory is specified by a triple  , where
, where  is an elliptic complex on a manifold N and \(\left\langle \cdot ,\cdot \right\rangle \) is a degree –1 pairing \(F\otimes F\rightarrow \text {Dens}_N\). The triple is required to satisfy some conditions elaborated in “Appendix.” It is also possible to define what is meant by a gauge-fixing of a free BV theory and an action of an elliptic differential graded Lie algebra (dgla)
is an elliptic complex on a manifold N and \(\left\langle \cdot ,\cdot \right\rangle \) is a degree –1 pairing \(F\otimes F\rightarrow \text {Dens}_N\). The triple is required to satisfy some conditions elaborated in “Appendix.” It is also possible to define what is meant by a gauge-fixing of a free BV theory and an action of an elliptic differential graded Lie algebra (dgla)  on a free BV theory
on a free BV theory  . Given such an action, one can define cochain complexes \( {\text {Obs}}^{cl} \) and \( {\text {Obs}}^{q} {}[t]\) of equivariant classical observables and equivariant scale-t quantum observables for the action. Moreover, there is a scale-t obstruction \(\mathfrak {Obstr}[t]\) and its \(t\rightarrow 0\) limit exists and is denoted \(\mathfrak {Obstr}\). The aim of this section is to present an example of a free BV theory with an action of an elliptic dgla, which we call the axial symmetry of the massless free fermion. The aim of the remainder of the paper will be to better understand the structure of \( {\text {Obs}}^{q} {}[t]\) and \(\mathfrak {Obstr}\).
. Given such an action, one can define cochain complexes \( {\text {Obs}}^{cl} \) and \( {\text {Obs}}^{q} {}[t]\) of equivariant classical observables and equivariant scale-t quantum observables for the action. Moreover, there is a scale-t obstruction \(\mathfrak {Obstr}[t]\) and its \(t\rightarrow 0\) limit exists and is denoted \(\mathfrak {Obstr}\). The aim of this section is to present an example of a free BV theory with an action of an elliptic dgla, which we call the axial symmetry of the massless free fermion. The aim of the remainder of the paper will be to better understand the structure of \( {\text {Obs}}^{q} {}[t]\) and \(\mathfrak {Obstr}\).
We will show that a formally self-adjoint Dirac operator defines a free BV theory; first, though, we need to establish some notation. Let (M, g) be, as in Sect. 2, a Riemannian manifold with Riemannian density \(dVol_g\), V a \(\mathbb {Z}/2\)-graded metric bundle on M with metric \((\cdot , \cdot )\), and D a formally self-adjoint Dirac operator. Define  to be
to be  . Let
. Let
with purely odd \(\mathbb {Z}/2\) grading (and let  denote the sheaf of sections of S), and
denote the sheaf of sections of S), and
when either \(|f_1|=0\) and \(|f_2|=1\) or vice versa. As described in Notation and Conventions subsection of Sect. 1, we let \(D_{0\rightarrow 1}\) denote the operator of degree 1 on  which is simply given by D, and similarly for \(D_{0\leftarrow 1}\), \(\Gamma _{0\rightarrow 0}\), etc. With all these notations in place, we can state and prove the following
which is simply given by D, and similarly for \(D_{0\leftarrow 1}\), \(\Gamma _{0\rightarrow 0}\), etc. With all these notations in place, we can state and prove the following
Lemma 3.1
 is a free BV theory, which we call the massless free fermion, and \(\Gamma _{0\rightarrow 0} D_{1\rightarrow 0}\) is a gauge-fixing for this theory.
is a free BV theory, which we call the massless free fermion, and \(\Gamma _{0\rightarrow 0} D_{1\rightarrow 0}\) is a gauge-fixing for this theory.
Proof
Let us first note the following facts: since D reverses the \(\mathbb {Z}/2\)-grading of  , \(D\Gamma = -\Gamma D\) (hence, \(D_{0\rightarrow 1}\Gamma _{0\rightarrow 0}=-\Gamma _{1\rightarrow 1}D_{0\rightarrow 1})\); moreover, \(\Gamma \) is self-adjoint for the pairing \((\cdot , \cdot )\).
, \(D\Gamma = -\Gamma D\) (hence, \(D_{0\rightarrow 1}\Gamma _{0\rightarrow 0}=-\Gamma _{1\rightarrow 1}D_{0\rightarrow 1})\); moreover, \(\Gamma \) is self-adjoint for the pairing \((\cdot , \cdot )\).
\(D_{0\rightarrow 1}\Gamma _{0\rightarrow 0}\) and \(\Gamma _{0\rightarrow 0} D_{1\rightarrow 0}\) can be checked directly to have the required symmetry properties with respect to \(\left\langle \cdot ,\cdot \right\rangle \) as a consequence of the above facts and the formal self-adjointness of D.
\(\left\langle \cdot ,\cdot \right\rangle \) is symmetric (in the brute, non-graded, sense) because of the symmetry of \((\cdot , \cdot )\); this is consistent with Eq. 16 since all fields have fermionic statistics, i.e., \(\left\langle \cdot ,\cdot \right\rangle \) is graded skew-symmetric.
It remains only to check that \([Q,Q^{GF}]\) is a generalized Laplacian. Using the first fact noted at the beginning of the proof, and the fact that \(\Gamma ^2=1\), it is a direct computation to show that \([Q,Q^{GF}]=D^2_{0\rightarrow 0}+D^2_{1\rightarrow 1}\), so is in fact a generalized Laplacian. \(\square \)
Remark 3.2
The metric on V can be used to identify V with \(V^\vee \), and the Riemannian density can be used to trivialize the bundle of densities on M, so that \(V^!\cong V\). As a result, it can be shown that the free fermion theory is isomorphic, under the obvious notion of isomorphism of free theories, to the cotangent theory to the elliptic complex

We will use this characterization in the sequel. \(\square \)
In “Appendix,” we define what it means for an elliptic dgla to act on a free BV theory. The next lemma provides an action of the elliptic dgla \(\Omega ^\bullet _M\) on the massless free fermion.
Lemma 3.3
Let  , equipped with the de Rham differential and trivial Lie bracket. If \(f\in C^{\infty }(M)\), we let
, equipped with the de Rham differential and trivial Lie bracket. If \(f\in C^{\infty }(M)\), we let
If \(\alpha \in \Omega ^1(M)\), let
where \(c(\alpha )\) is the Clifford action of forms on sections of V. For \(\beta \) a form of degree greater than 1, let \([\beta ,\cdot ]=0\). Then, these equations define an action of  on the massless free fermion. This action is known as the axial symmetry in physics.
on the massless free fermion. This action is known as the axial symmetry in physics.
Proof
Let us check the derivation property of a dgla:
Assuming that \(|\varphi |=0\) (otherwise both sides of the above equation are 0), we find that the right-hand side of the above equation is
which agrees with \(Q[f,\varphi ]\).
The remaining checks—namely of the Jacobi equation and the invariance of \(\left\langle \cdot ,\cdot \right\rangle \) under this action—are straightforward and direct computations along similar lines. \(\square \)
Remark 3.4
Note that the constant functions act by a multiple of \(\Gamma \) on the degree 0 fields in  . This is the sense in which the symmetry is axial: it acts by opposite factors on
. This is the sense in which the symmetry is axial: it acts by opposite factors on  and
and  . \(\square \)
. \(\square \)
4 A few lemmas on Batalin–Vilkovisky quantization
In this section, we prove three lemmas which will be useful in the sequel, and which are implicit in the literature, but which have not been directly proved there. For a more complete discussion of the BV formalism, see “Appendix,” which assembles results from the literature relevant to the discussion here.
In “Appendix,” we define the strong (equivariant) quantum master equation (sQME) for the action of an elliptic dgla  on a BV theory
on a BV theory  . For the reader familiar with the formalism of Costello and Gwilliam, a solution of the sQME is what those authors would call an inner action of
. For the reader familiar with the formalism of Costello and Gwilliam, a solution of the sQME is what those authors would call an inner action of  on the quantum theory
on the quantum theory  . The first of the three remaining lemmas in this section makes precise the idea that the sQME measures the failure of an
. The first of the three remaining lemmas in this section makes precise the idea that the sQME measures the failure of an  -equivariant quantization to be trivial over
-equivariant quantization to be trivial over  . Before we state it, we make the following
. Before we state it, we make the following
Definition 4.1
Assume given an action of an elliptic dgla  on a free theory
on a free theory  ; let \(I_{\hbar =1}[t]\) denote \(I_{tr}[t]+I_{wh}[t]\). Then, for any \(t\in \mathbb R_{>0}\), the scale t fundamentally quantum equivariant observables, denoted \({\text {Obs}}^q_{\hbar =1}[t]\), are
; let \(I_{\hbar =1}[t]\) denote \(I_{tr}[t]+I_{wh}[t]\). Then, for any \(t\in \mathbb R_{>0}\), the scale t fundamentally quantum equivariant observables, denoted \({\text {Obs}}^q_{\hbar =1}[t]\), are

in other words, \({\text {Obs}}^q_{\hbar =1}[t]\) is \( {\text {Obs}}^{q} {}[t]\) with \(\hbar \) set to 1. Similarly, let \({\text {Obs}}^q_{\hbar =1,0}\) denote the cochain complex whose underlying graded vector space agrees with that of \({\text {Obs}}^q_{\hbar =1}[t]\), but with differential  ; this is the analogous construction for the trivial action of
; this is the analogous construction for the trivial action of  on
on  .
.
Remark 4.2
It is worth noting here that the scale t plays the same role here as the heat kernel parameter (which is also denoted by the symbol t) in Theorem 2.8, since the BV Laplacian \(\Delta _t\) is defined in terms of this heat kernel. Physically, t carries units of inverse length squared. \(\square \)
Lemma 4.3
If I[t] satisfies the scale t sQME, then multiplication by \(e^{I_{\hbar =1}[t]}\) gives a cochain isomorphism \({\text {Obs}}^q_{\hbar =1}[t]\rightarrow {\text {Obs}}^q_{\hbar =1,0}[t]\). More generally, let \({\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[t]\) denote the cochain complex

where \(\mathfrak {Obstr}[t]\cdot \) denotes multiplication by the obstruction in the symmetric algebra  . Then, multiplication by \(e^{I_{\hbar =1}[t]}\) gives an isomorphism \({\text {Obs}}^q_{\hbar =1}[t]\rightarrow {\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[t]\).
. Then, multiplication by \(e^{I_{\hbar =1}[t]}\) gives an isomorphism \({\text {Obs}}^q_{\hbar =1}[t]\rightarrow {\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[t]\).
Proof
By direct computation,

Let J be an element of \( {\text {Obs}}^{q} _{\hbar ^{-1}}[t]\). Now, consider

Q and  are both graded derivations for the commutative product; \(\Delta _t\), however, is not, and the Poisson bracket is precisely the failure of this to be the case. In fact, direct computation reveals that
are both graded derivations for the commutative product; \(\Delta _t\), however, is not, and the Poisson bracket is precisely the failure of this to be the case. In fact, direct computation reveals that
It follows that

The above equation states precisely that multiplication by \(e^{I_{\hbar =1}[t]}\) intertwines the differentials of \({\text {Obs}}^q_{\hbar =1}[t]\) and \({\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[t]\). \(\square \)
Lemma 4.4
For a free theory with an action of the elliptic dgla  , the obstruction \(\mathfrak {Obstr}[t]\) is independent of t. Using Lemma A.44 in Appendix, this implies that \(\mathfrak {Obstr}[t]\) is local.
, the obstruction \(\mathfrak {Obstr}[t]\) is independent of t. Using Lemma A.44 in Appendix, this implies that \(\mathfrak {Obstr}[t]\) is local.
Proof
Let us rewrite Lemma A.43 as the following equation:
The right-hand side of the above equation is represented diagrammatically by a sum over connected Feynman trees where one of the vertices uses \(\mathfrak {Obstr}[t]\) and all the others use \(I_{tr}[t]\). At any scale, the Feynman diagram expansion of \(\mathfrak {Obstr}[t]\) for a free theory has only external edges corresponding to  . The elements of
. The elements of  are non-propagating fields in the sense that the propagators appearing in the Feynman diagrams of RG flow connect only
are non-propagating fields in the sense that the propagators appearing in the Feynman diagrams of RG flow connect only  edges and not
edges and not  edges. This means, in particular, that the only connected Feynman diagrams having a vertex labeled by a term from \(\mathfrak {Obstr}[t]\) are those with only that vertex. In other words, the right-hand side of the equation above is just \(\mathfrak {Obstr}[t]\), which completes the proof. \(\square \)
edges. This means, in particular, that the only connected Feynman diagrams having a vertex labeled by a term from \(\mathfrak {Obstr}[t]\) are those with only that vertex. In other words, the right-hand side of the equation above is just \(\mathfrak {Obstr}[t]\), which completes the proof. \(\square \)
Remark 4.5
This result is particular to the case that we are dealing with families of free theories. \(\square \)
Let us now examine what happens if \(\mathfrak {Obstr}[t]\) is exact in  :
:
Lemma 4.6
If  for some
for some  , then \(I[t]-\hbar J\) solves the scale t sQME. Conversely, if there exists J such that \(I[t]-\hbar J\) solves the scale t sQME, then
, then \(I[t]-\hbar J\) solves the scale t sQME. Conversely, if there exists J such that \(I[t]-\hbar J\) solves the scale t sQME, then  .
.
Proof
Let us start with the first assertion:

where we are using that J does not depend on  , so that \(QJ = \Delta _t J = \{J,\cdot \}_t=0\). Thus, \(I[t]-\hbar J\) solves the sQME. Conversely, the above equation shows that if there exists a
, so that \(QJ = \Delta _t J = \{J,\cdot \}_t=0\). Thus, \(I[t]-\hbar J\) solves the sQME. Conversely, the above equation shows that if there exists a  such that \(I[t]-\hbar J\) satisfies the scale t sQME, then \(\mathfrak {Obstr}[t]\) is exact. \(\square \)
such that \(I[t]-\hbar J\) satisfies the scale t sQME, then \(\mathfrak {Obstr}[t]\) is exact. \(\square \)
Remark 4.7
Combining the preceding lemma with Lemma A.39, we see that the obstruction is exact at one scale if and only if it is exact at all scales, since
by an analysis of the Feynman diagram expansion of
If one prefers not to use Feynman diagrams, one can use the explicit definition of the operator \(W(P(t',t),\cdot )\) and the fact that \(\partial _P J=0\). \(\square \)
5 The equivariant observables of the massless free fermion
In this section, we use the notations of Sect. 3 concerning the massless free fermion. We will assume that an elliptic dgla  acts on the free theory
acts on the free theory  . This could be the complex
. This could be the complex  from Lemma 3.3, but our results will hold in the more general case.
from Lemma 3.3, but our results will hold in the more general case.
The main goal of this section is to prove the following
Proposition 5.1
If an elliptic dgla  acts on the massless free fermion theory
acts on the massless free fermion theory  , then there is a deformation retraction of
, then there is a deformation retraction of  -modules
-modules

More precisely, \(\tilde{\eta }\) is a degree –1 map and the three maps satisfy
Here, \(\delta \) is a degree-one endomorphism such that  . We recall that
. We recall that  is the underlying graded vector space of
is the underlying graded vector space of  , and it is given the obvious
, and it is given the obvious  -module structure, namely the one where
-module structure, namely the one where  acts on
acts on  by multiplication.
by multiplication.
We will see that \(\delta \) is given by an explicit, if complicated, formula.
Remark 5.2
By a small modification of the arguments in [7], (infinitesimal) homotopical RG flow defines cochain isomorphisms \({\text {Obs}}^q_{\hbar =1}[t]\cong {\text {Obs}}^q_{\hbar =1}[t']\) for all \(t,t'\). It follows that \({\text {Obs}}^q_{\hbar =1}[t]\) also deformation retracts onto a rank-one  module for all t. \(\square \)
module for all t. \(\square \)
We note that because D is formally self-adjoint, we can use the characterization of the heat kernel from Lemma 2.16. This implies, in particular, that we can define the scale-infinity BV heat kernel \(K_\infty \) and propagator \(P(0,\infty )\), and therefore, the cochain complex of scale-infinity equivariant quantum observables \( {\text {Obs}}^{q} {}[\infty ]\) in the proposition is well defined.
Recall that the  symmetry has an obstruction \(\mathfrak {Obstr}\) to quantization. As a corollary of Proposition 5.1, we will find the following:
symmetry has an obstruction \(\mathfrak {Obstr}\) to quantization. As a corollary of Proposition 5.1, we will find the following:
Corollary A
Choose the same hypothesis as in Proposition 5.1, and recall the notation \({\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}\) from Lemma 4.3. There is a deformation retraction of  -modules
-modules

Here, \(\mathfrak {Obstr}[\infty ]\cdot \) denotes multiplication by \(\mathfrak {Obstr}[\infty ]\) in  .
.
Finally, in Lemma 5.9, we show that—as a consequence of the corollary—the rank-one module of the proposition is isomorphic to the trivial  -module if and only if \(\mathfrak {Obstr}\) is cohomologically trivial.
-module if and only if \(\mathfrak {Obstr}\) is cohomologically trivial.
Remark 5.3
The  -module
-module  with differential
with differential  can be thought of as the space of sections of a line bundle over the formal moduli problem
can be thought of as the space of sections of a line bundle over the formal moduli problem  . Lemma 5.9 then implies that this line bundle is trivial if and only if the obstruction is cohomologically trivial. In other words, Lemma 5.9 is an interpretation the statement “the anomaly is the obstruction to the existence of a well-defined and gauge-invariant partition function” discussed in the introduction. \(\square \)
. Lemma 5.9 then implies that this line bundle is trivial if and only if the obstruction is cohomologically trivial. In other words, Lemma 5.9 is an interpretation the statement “the anomaly is the obstruction to the existence of a well-defined and gauge-invariant partition function” discussed in the introduction. \(\square \)
5.1 The proof of Proposition 5.1
The proof of Proposition 5.1 is a minor modification of arguments in Chapters 2.5-2.6 of [13], and it uses the Hodge decomposition of Lemma 2.13 and properties of deformation retractions, including the homological perturbation lemma. Before we begin the proof itself, we spell out some details of the relevant background information.
The following is the main theorem discussed in [9]; it is a generalization of Theorem 2.5.3 of [13].
Lemma 5.4
(Homological perturbation lemma). Suppose that

is a deformation retraction, and suppose that \(\delta _V\) is a degree 1 operator such that \(d_V+\delta _V\) is a differential and \((1-\delta _V\eta )\) is invertible. Then,

is a deformation retraction, where
are the perturbed data of the deformation retraction.
Lemma 5.5
Given two deformation retractions

and

the composite

is also a deformation retraction.
Proof
Direct computation. \(\square \)
Armed with the preceding results on deformation retractions, we can proceed to the proof of Proposition 5.1. The main idea of the proof is repeated application of the homological perturbation lemma. We will break the proof up into small pieces.
Let us first establish some notation that we will use throughout the remainder of this section. Let  denote the underlying graded vector space of \({\text {Obs}}^q_{\hbar =1}\). Let us also abbreviate
denote the underlying graded vector space of \({\text {Obs}}^q_{\hbar =1}\). Let us also abbreviate  to W, letting \(W^{(j)}\) denote the \({{\mathrm{Sym}}}^j\) space of W. Similarly, let \(W_\perp \) denote
to W, letting \(W^{(j)}\) denote the \({{\mathrm{Sym}}}^j\) space of W. Similarly, let \(W_\perp \) denote  , with \(W_\perp ^{(j)}\) the \({{\mathrm{Sym}}}^j\) space of \(W_\perp \).
, with \(W_\perp ^{(j)}\) the \({{\mathrm{Sym}}}^j\) space of \(W_\perp \).
The Hodge decomposition of Lemma 2.13 tells us that the cokernel of D is isomorphic to its kernel. This allows us to decompose  as follows:
as follows:

It follows that  , and we denote by
, and we denote by  the cochain complex \({\text {Im}}D \overset{D\Gamma }{\longrightarrow }{\text {Im}}D\); this notation is appropriate because \({\text {Im}}D=\ker D^\perp \).
the cochain complex \({\text {Im}}D \overset{D\Gamma }{\longrightarrow }{\text {Im}}D\); this notation is appropriate because \({\text {Im}}D=\ker D^\perp \).
It follows that \(W={{\widehat{{{\mathrm{Sym}}}}}}\left( (\ker D)^\vee \oplus (\ker D)^\vee [1]\right) \) and similarly
Using Eq. 6,

Since  , we can endow
, we can endow  with a
with a  -module structure, which gives a dg-
-module structure, which gives a dg- -module structure when we endow
-module structure when we endow  with the differentials from either \({\text {Obs}}^q_{\hbar =1}[\infty ]\) or \({\text {Obs}}^q_{\hbar =1,0}[\infty ]\). Throughout the remainder of this section, any cochain complex whose underlying graded vector space is of the form
with the differentials from either \({\text {Obs}}^q_{\hbar =1}[\infty ]\) or \({\text {Obs}}^q_{\hbar =1,0}[\infty ]\). Throughout the remainder of this section, any cochain complex whose underlying graded vector space is of the form  , where U is a graded vector space, is given the dg-
, where U is a graded vector space, is given the dg- -module structure in an analogous way. In all cases, it will be manifest that the
-module structure in an analogous way. In all cases, it will be manifest that the  action on
action on  interacts as necessary with the differential on
interacts as necessary with the differential on  .
.
Recall that the differential on \({\text {Obs}}^q_{\hbar =1}[\infty ]\) can be written as a sum

We will treat the terms \(\Delta _\infty \) and \(\{I_{\hbar =1}[\infty ],\cdot \}_\infty \) as successive deformations of the differential  on
on  , starting from a homotopy equivalence of
, starting from a homotopy equivalence of  with a smaller subspace. The cochain complex
with a smaller subspace. The cochain complex  describes the classical observables of the massless free fermion with trivial
describes the classical observables of the massless free fermion with trivial action.
action.
Proposition 5.6
(Cf. Proposition 2.5.5 and Theorem 2.6.2 in [13]) There is a deformation retraction of  -modules
-modules

Proof
As described in Section 2.6 of [13], the Hodge decomposition leads to the desired homotopy equivalence, with maps \(\pi ,\iota ,\) and \(\eta \) defined as follows. \(\pi \) is just projection onto the subspace of  for which \(k=0\), and \(\iota \) is the inclusion of this subspace into
for which \(k=0\), and \(\iota \) is the inclusion of this subspace into  . On the other hand, \(\eta \) is a bit more subtle. We let P denote the degree –1 operator on
. On the other hand, \(\eta \) is a bit more subtle. We let P denote the degree –1 operator on  whose kernel is \(P(0,\infty )\) (see Definition A.27). On
whose kernel is \(P(0,\infty )\) (see Definition A.27). On  , P acts by 0 on \(\ker D\) and by \(D^{-1}\) on \({\text {Im}}D\). P also induces an operator on
, P acts by 0 on \(\ker D\) and by \(D^{-1}\) on \({\text {Im}}D\). P also induces an operator on  , and we can also extend it
, and we can also extend it  -linearly to
-linearly to  as a derivation for the multiplication in \(W_\perp \); we will abuse notation and call all three operators P. We define \(\eta \) to be 0 on the \(k=0\) component of
as a derivation for the multiplication in \(W_\perp \); we will abuse notation and call all three operators P. We define \(\eta \) to be 0 on the \(k=0\) component of  and P / k on the \(k\ne 0\) components of
and P / k on the \(k\ne 0\) components of  . Note that \(\eta \) acts only on the \(W_\perp \) part of
. Note that \(\eta \) acts only on the \(W_\perp \) part of  . The fact that this is a deformation retraction is verified in [13]. \(\square \)
. The fact that this is a deformation retraction is verified in [13]. \(\square \)
Now, we turn on the deformation \( \Delta _\infty \) to compute the quantum observables of the theory with trivial  action:
action:
Proposition 5.7
There is a deformation retraction of  -modules
-modules

In other words, the deformation \(\Delta _\infty \) of the differential on  induces the same deformation on
induces the same deformation on  .
.
Proof
We use the homological perturbation lemma, though we need to check that the hypotheses of that lemma apply. First, note that the operator  is a differential, since it is the differential on \({\text {Obs}}^q_{\hbar =1,0}\), i.e., it is the differential on
is a differential, since it is the differential on \({\text {Obs}}^q_{\hbar =1,0}\), i.e., it is the differential on  for the trivial action of
for the trivial action of  on
on  . Moreover, \((1-\Delta _\infty \eta )\) is invertible, as we now show. The operator \(\Delta _\infty \) is the operator of contraction with \(K_\infty \); based on the description of \(K_t\) in the proof of Lemma 6.5 in the next section, and using the characterization of the heat kernel immediately preceding Proposition 2.37 in [3], it follows that
. Moreover, \((1-\Delta _\infty \eta )\) is invertible, as we now show. The operator \(\Delta _\infty \) is the operator of contraction with \(K_\infty \); based on the description of \(K_t\) in the proof of Lemma 6.5 in the next section, and using the characterization of the heat kernel immediately preceding Proposition 2.37 in [3], it follows that
Here, \(\{\phi _i\}\) is an orthonormal basis for \(\ker D\) sitting in degree 0 and \(\xi _i\) is \(\phi _i\) as an element of  , but living in degree 1 in
, but living in degree 1 in  . Let \(\{\phi ^*_i\}\) and \(\{\xi ^*_i\}\) denote the dual bases for \(\ker D^\vee \).
. Let \(\{\phi ^*_i\}\) and \(\{\xi ^*_i\}\) denote the dual bases for \(\ker D^\vee \).
It follows that
So \(\Delta _\infty \) lowers \({{\mathrm{Sym}}}\)-degree in W by 2. On the other hand, \(\eta \) does not change \({{\mathrm{Sym}}}\)-degree in W. More important, no element of  can have a dependence of degree greater than \(\dim \ker D\) on the \(\phi _i\), since the \(\phi _i\) are of ghost number 0 and have fermionic statistics and so anti-commute with each other. It follows that \((\Delta _\infty \eta )^{\dim \ker D+1}=0\) so that
can have a dependence of degree greater than \(\dim \ker D\) on the \(\phi _i\), since the \(\phi _i\) are of ghost number 0 and have fermionic statistics and so anti-commute with each other. It follows that \((\Delta _\infty \eta )^{\dim \ker D+1}=0\) so that
and the homological perturbation lemma applies to our situation. Moreover, since \(\iota \), \(\pi \), and \(\eta \) were constructed to be  -linear, the explicit formulas of the homological perturbation lemma show that the perturbed data are also
-linear, the explicit formulas of the homological perturbation lemma show that the perturbed data are also  -linear.
-linear.
The perturbation \(\delta _{\Delta _\infty }\) of the differential on  is given by the formula
is given by the formula
however, since \(\eta \) acts trivially on elements of  and \(\Delta _\infty \) preserves
and \(\Delta _\infty \) preserves  , the formula for \(\delta _{\Delta _\infty }\) simplifies:
, the formula for \(\delta _{\Delta _\infty }\) simplifies:
The proposition follows. \(\square \)
Now, we would like to understand the cochain complex  a bit better. We continue to use the notation \(\xi ^*_i, \phi ^*_i\) from the proof of the previous proposition.
a bit better. We continue to use the notation \(\xi ^*_i, \phi ^*_i\) from the proof of the previous proposition.
Proposition 5.8
There is a deformation retraction of  -modules
-modules

The main consequence of this proposition, together with Proposition 5.7, is
Corollary B
\({\text {Obs}}^q_{\hbar =1,0}[\infty ]\) deformation retracts onto a free rank-one  -module.
-module.
Proof of Proposition 5.8
\(\iota ''\) and \(\pi ''\) will be, just like \(\iota \) and \(\pi \), inclusion and projection operators; we simply need to identify the relevant one-dimensional subspace of W onto which to project. To this end, let \(\{\tilde{\phi }^*_i\}_{i=1}^{\dim \ker D^+}\) be an orthonormal basis for \((\ker D^+)^\vee \) and \(\{\tilde{\tilde{\phi }}^*_i\}_{j=1}^{\dim \ker D^-}\) be an orthonormal basis for \((\ker D^-)^\vee \). The one-dimensional subspace of W we seek is spanned by
i.e., it is the subspace \(\Lambda ^{top} (\ker D^+)^\vee \otimes \Lambda ^{top} (\ker D^-)^\vee \). Now, \(\iota ''\) can be verified directly to be a cochain map, while to verify that \(\pi ''\) is a cochain map, note first that \(\pi ''\Delta _\infty =0\) since \(\Delta _\infty \) necessarily lowers the degree of dependence on the \(\phi _i\). Thus,

since \(\pi ''\) manifestly intertwines the  differential. Moreover, \(\pi ''\iota ''=id\), by construction.
differential. Moreover, \(\pi ''\iota ''=id\), by construction.
It remains to construct \(\eta ''\) and verify that \(\eta ''\) is a chain homotopy between \(\iota ''\pi ''\) and id. We can write
where the \(\phi ^*_i\) have ghost number 0 and have fermionic statistics, while the \(\xi ^*_i\) have ghost number –1 and have fermionic statistics as well. In other words, the \(\xi ^*_i\) commute with each other, while the \(\phi ^*_i\) anti-commute among themselves and with the \(\xi ^*_i\). Now, we let \(I=(i_1,\cdots , i_{\dim \ker D})\) be a multi-index, \(J\subset (1,\cdots , \dim \ker D)\), and  ; we consider J to be a multi-index with all indices zero or 1. Moreover, define
; we consider J to be a multi-index with all indices zero or 1. Moreover, define
and denote by |I| the total degree of I, that is
Let
Here, \(|J^c|\) is the cardinality of the complement of J in \(\{1,\cdots , \dim \ker D\}\). We let \(1/(|J^c|+\sigma _{I,J})=0\) when both summands in the denominator are zero. Note that
when \(i_k\ne 0\), where \(I\backslash \{k\}\) is I with \(i_k\) set to 0. We will use this fact tacitly below. Let us verify, using the notation \(\delta _{jk}\) for the Kronecker delta:

It follows that, unless \(|J^c|=\sigma _{I,J}=0\), i.e., unless \(\xi _I^*\phi ^*_J=\phi ^*_1\cdots \phi ^*_{\dim \ker D}\) (a spanning element of \(\det D^+\subset W\)),

And, if \(|J^c|=\sigma _{I,J}=0\), then

whence, the proposition follows, once we note that \(\eta ''\) is manifestly  -linear (once one takes into account the fact that \(\eta ''\) has odd cohomological degree and so acquires an extra sign when commuting past elements of
-linear (once one takes into account the fact that \(\eta ''\) has odd cohomological degree and so acquires an extra sign when commuting past elements of  ). \(\square \)
). \(\square \)
So far, we have shown that \({\text {Obs}}^q_{\hbar =1,0}[\infty ]\)—i.e., the cochain complex of equivariant observables for the trivial -action on
-action on  —deformation retracts onto a rank-one
—deformation retracts onto a rank-one  -module. To prove Proposition 5.1, we need to prove the analogous statement for the cochain complex of equivariant observables with non-trivial
-module. To prove Proposition 5.1, we need to prove the analogous statement for the cochain complex of equivariant observables with non-trivial  action. The differential on this latter chain complex is a perturbation of the differential on \({\text {Obs}}^q_{\hbar =1,0}[\infty ]\) by the term \(\{I_{\hbar =1}[\infty ],\cdot \}_\infty \), so to complete the proof of Proposition 5.1, we need to check that this perturbation satisfies the hypotheses of the homological perturbation lemma.
action. The differential on this latter chain complex is a perturbation of the differential on \({\text {Obs}}^q_{\hbar =1,0}[\infty ]\) by the term \(\{I_{\hbar =1}[\infty ],\cdot \}_\infty \), so to complete the proof of Proposition 5.1, we need to check that this perturbation satisfies the hypotheses of the homological perturbation lemma.
Proof of Proposition 5.1
The three preceding propositions, together with Proposition 5.5, can be combined to yield a deformation retraction

We need only to verify that the perturbation \(\{I_{\hbar =1}[\infty ], \cdot \}_{\infty }\) satisfies the hypotheses of the homological perturbation lemma. Then, the degree-one endomorphism \(\delta \) which appears in the statement of the proposition can be computed by applying the homological perturbation lemma with \((V,d_V)={\text {Obs}}^q_{\hbar =1}\),  , \(\delta _V=\{I_{\hbar =1}[\infty ],\cdot \}_\infty \):
, \(\delta _V=\{I_{\hbar =1}[\infty ],\cdot \}_\infty \):
We have seen that the operator

is a differential (satisfies the wQME), so it remains to show that \((1-\{I_{\hbar =1}[\infty ],\cdot \}_\infty \circ \eta ''')\) is invertible. To do this, we must understand \(\eta '''\) a bit better. In the notations of Propositions 5.7 and 5.8,
Let us explicitly compute \(\iota '\), \(\eta '\), and \(\pi '\). Let \(\iota , \eta , \) and \(\pi \) be as in Proposition 5.6. Then,
\(\iota '=\iota \) because \(\Delta _\infty \) preserves  , but \(\eta \) acts by 0 on this subspace. To show that \(\pi ' = \pi \), note that \( \Delta _\infty \eta \) commutes with \(\iota \pi \) because both \(\Delta _\infty \) and \(\eta \) preserve W. Moreover, \(\eta \iota \pi =0\); whence,
, but \(\eta \) acts by 0 on this subspace. To show that \(\pi ' = \pi \), note that \( \Delta _\infty \eta \) commutes with \(\iota \pi \) because both \(\Delta _\infty \) and \(\eta \) preserve W. Moreover, \(\eta \iota \pi =0\); whence,
Recall also that the sum in \(\eta '\) is finite, since \(\eta \) and \(\Delta _\infty \) commute and \(\Delta _\infty ^{\dim \ker D^++1}=0\).
We will need to understand the effect that various operators have on the \({{\mathrm{Sym}}}\)-grading in  . The results are depicted in Fig. 1. The table should be interpreted as follows: a “0” means that the operator preserves the corresponding degree, a “>” means the operator has only terms which increase the corresponding degree, a “\(\ge \)” means the operator has terms which increase the corresponding degree, but none that decrease it; “\(<'\)’ and “\(\le \)” have analogous meanings. In all cases except the “>”, the operators only have a finite number of terms increasing or decreasing the corresponding degree.
. The results are depicted in Fig. 1. The table should be interpreted as follows: a “0” means that the operator preserves the corresponding degree, a “>” means the operator has only terms which increase the corresponding degree, a “\(\ge \)” means the operator has terms which increase the corresponding degree, but none that decrease it; “\(<'\)’ and “\(\le \)” have analogous meanings. In all cases except the “>”, the operators only have a finite number of terms increasing or decreasing the corresponding degree.
To show that \((1- \{I_{\hbar =1}[\infty ],\cdot \}_\infty \circ \eta ''')\) is invertible, we will show that the sum
is well defined. Let \(\theta ^{(i,j,k)}\) denote the component of \(\theta \) in

and let \(\zeta \) denote the putative value of \((1-\{I_{\hbar =1}[\infty ],\cdot \}_\infty \circ \eta ''')^{-1}\theta \), with \(\zeta ^{(i,j,k)}\) defined similarly. The  column in Fig. 1 tells us that \(\zeta ^{(i,j,k)}\) contains only sums of terms like
column in Fig. 1 tells us that \(\zeta ^{(i,j,k)}\) contains only sums of terms like
for \(l+i'\le i\), i.e., only a finite number of \(i'\) contribute to \(\zeta ^{(i,j,k)}\). Moreover, since in all spaces, but the >, the corresponding operator has only a finite number of terms changing degree, at a fixed l and \(i'\), there is a maximum amount by which \(\left( \{I[\infty ,\cdot \}_\infty \eta '''\right) ^l\) can change \(j',k'\). Thus, \(\zeta ^{(i,j,k)}\) only has contributions from
when \(l+i'\le i\) and \(|j'-j|,|k'-k|\) are small enough for the given l and \(i'\). It follows that \((1-\{I_{\hbar =1}[\infty ],\cdot \}_\infty \eta ''')^{-1}\) is well defined, whence the proposition. \(\square \)
5.2 More results concerning the equivariant observables
In Sect. 4 and the previous subsection, we saw some indication that the obstruction \(\mathfrak {Obstr}\) is related to the triviality of the equivariant quantum observables \( {\text {Obs}}^{q} \) as a  -module (see, e.g., Lemma 4.3 and the Corollary to Proposition 5.1). In this subsection, we show that \(\mathfrak {Obstr}\) is precisely the measure of the non-triviality of the observables as a
-module (see, e.g., Lemma 4.3 and the Corollary to Proposition 5.1). In this subsection, we show that \(\mathfrak {Obstr}\) is precisely the measure of the non-triviality of the observables as a  -module. We begin by proving Corollary A:
-module. We begin by proving Corollary A:
Proof of Corollary A
From the proof of Proposition 5.1, we have a deformation retraction

The differential on \({\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[\infty ]\) is a perturbation of  by the operator \( \mathfrak {Obstr}[\infty ]\cdot \). For the same reasons as in the proof of Proposition 5.1, this perturbation satisfies the hypotheses of the homological perturbation lemma. Therefore, all we need to check is that the corresponding differential on
by the operator \( \mathfrak {Obstr}[\infty ]\cdot \). For the same reasons as in the proof of Proposition 5.1, this perturbation satisfies the hypotheses of the homological perturbation lemma. Therefore, all we need to check is that the corresponding differential on  is as specified. To see this, recall that the perturbation of the differential on
is as specified. To see this, recall that the perturbation of the differential on  is given by the formula
is given by the formula
Since  , multiplication by \(\mathfrak {Obstr}[\infty ]\) preserves the subspace
, multiplication by \(\mathfrak {Obstr}[\infty ]\) preserves the subspace

Moreover, by construction, \(\eta '''\) is 0 on this subspace. Also, tracing through the definitions of \(\iota '''\) and \(\pi '''\), one finds that they are simply the usual inclusion and projection maps for the subspace  with respect to the Hodge decomposition of
with respect to the Hodge decomposition of  . The Corollary follows. \(\square \)
. The Corollary follows. \(\square \)
Together with the isomorphism \({\text {Obs}}^q_{\hbar =1}[\infty ] \rightarrow {\text {Obs}}^q_{\hbar =1,\mathfrak {Obstr}}[\infty ]\), Corollary A gives us an explicit characterization of the differential on  from Proposition 5.1. Moreover, this differential is directly related to the obstruction. Finally, we can state and prove the following lemma.
from Proposition 5.1. Moreover, this differential is directly related to the obstruction. Finally, we can state and prove the following lemma.
Lemma 5.9
The dg  module
module

is isomorphic to the trivial  -module
-module  if and only if \(\mathfrak {Obstr}[\infty ]\) is exact in
if and only if \(\mathfrak {Obstr}[\infty ]\) is exact in  .
.
Proof
Suppose  for
for  . Then, multiplication by \(e^{ \alpha }\) gives a cochain isomorphism
. Then, multiplication by \(e^{ \alpha }\) gives a cochain isomorphism

On the other hand, suppose given a cochain isomorphism of  -modules
-modules

The statement that this map intertwines differentials and multiplication by elements of  implies, in particular, that
implies, in particular, that

Since \(\Phi \) is an isomorphism, \(\Phi (1)\) must be invertible in the symmetric algebra  , so that \(\log \Phi (1)\) is defined. It follows that
, so that \(\log \Phi (1)\) is defined. It follows that

so that \(\mathfrak {Obstr}[\infty ]\) is exact in  . \(\square \)
. \(\square \)
6 The obstruction and the obstruction complex
In this section, we study and characterize \(\mathfrak {Obstr}\) in its entirety for the case of the axial symmetry. In Sect. 6.1, we give an abstract characterization of the cohomology class of \(\mathfrak {Obstr}\) (Theorem 6.2). This is the main theorem of the paper. The proof of the theorem relies on a Feynman diagram computation which we defer to Sect. 6.2, where we also compute the obstruction as evaluated on one-forms. Finally, in Sect. 6.3, we connect our approach to the more traditional Fujikawa approach, as discussed in [18].
6.1 The main results
We continue to use the notations from Sect. 3 relating to the massless free fermion and its axial symmetry; in short, we continue to let  be the space of fields for the free fermion theory, with
be the space of fields for the free fermion theory, with  acting by the axial symmetry. The following nice characterization of the obstruction complex
acting by the axial symmetry. The following nice characterization of the obstruction complex  will allow us, in Theorem 6.2, to characterize the obstruction entirely.
will allow us, in Theorem 6.2, to characterize the obstruction entirely.
Proposition 6.1
(Obstruction Complex). If M is oriented, the map of complexes of sheaves
given by
is a quasi-isomorphism.
Having established a characterization of the obstruction complex, we can state the main theorem of this paper (cf. Main Theorem of the introduction):
Theorem 6.2
Let (M, g) be a Riemannian manifold of dimension n, \(V\rightarrow M\) a \(\mathbb {Z}/2\)-graded vector bundle with metric \((\cdot ,\cdot )\), and D a formally self-adjoint Dirac operator. Denote by  the dgla \(\Omega ^\bullet _M\). (These are the data of the massless free fermion and its axial symmetry, which has an obstruction \(\mathfrak {Obstr}\).) Under the quasi-isomorphism \(\Phi \) of Proposition 6.1, the cohomology class of \(\mathfrak {Obstr}[t]\) corresponds to
the dgla \(\Omega ^\bullet _M\). (These are the data of the massless free fermion and its axial symmetry, which has an obstruction \(\mathfrak {Obstr}\).) Under the quasi-isomorphism \(\Phi \) of Proposition 6.1, the cohomology class of \(\mathfrak {Obstr}[t]\) corresponds to
More precisely,
in cohomology. This statement is also true if M is not oriented.
Remark 6.3
Top-degree classes in de Rham cohomology on an oriented manifold are determined by their integral; the integral of \(\mathfrak {Obstr}\) is
Thus, the cohomology class of \(\mathfrak {Obstr}\) coincides with the class of
as stated in the Introduction. \(\square \)
Proof of Proposition 6.1
Our line of attack will be to first prove that the two complexes have the same cohomology and then to use the well-understood structure of the cohomology of the de Rham complex to show that \(\Phi \) is a quasi-isomorphism. This first step uses very similar techniques to those employed in Chapter 5.6 of [6], Proposition 8.10 of [12], and elsewhere; we adapt those techniques to the case at hand and fill in details missing in the references. The proof in the second step is, to the best of our knowledge, new.
We first invoke Lemma A.14, which provides a quasi-isomorphism

where the sheaf of jets \(J(\Omega ^\bullet _M)\) is defined in Definition A.13 and  is defined in Eq. 18. We will replace both terms in the derived tensor product above with quasi-isomorphic complexes. Let’s start with the map of bundles of dglas and of \(D_{M}\)-modules
is defined in Eq. 18. We will replace both terms in the derived tensor product above with quasi-isomorphic complexes. Let’s start with the map of bundles of dglas and of \(D_{M}\)-modules
which in the fiber over \(x\in M\) takes \(c\in \mathbb R\) to the jet at x of the constant zero-form c. Recall that \(D_M\) is the sheaf of differential operators on M. By definition, it acts on \(C^{\infty }_M\); \(J(\Omega ^\bullet _M)\) is a \(D_M\)-module, as discussed in Section 6.2 of Chapter 5 of [6]. The Poincaré lemma can be used to show that this is a quasi-isomorphism of \(D_{M}\) modules. Namely, since the differential arises from a fiberwise endomorphism of J, we can in each fiber use the Poincaré lemma to show that the fiber is quasi-isomorphic to \(\mathbb R\) in degree 0. More precisely, on a sufficiently small open set \(U\subset M\),
with \(dx_i\) in cohomological degree 1. Here, the \(x_i\) are formal coordinates on U, i.e., variables with respect to which the Taylor expansions of elements in the fibers of the jet bundle of \(\Lambda ^\bullet T^*M\) over U are computed. The “evaluation at 0” map \(\mathbb R[\![x_1,\cdots ,x_n]\!][dx_1,\cdots , dx_n]\rightarrow \mathbb R\) gives a map
which, as U varies over the open subsets of M, gives a sheaf map. Finally, the proof of the Poincaré Lemma furnishes a degree –1 map
which provides a chain homotopy in a deformation retraction of \(\mathbb R[\![x_1,\cdots ,x_n]\!][dx_1,\cdots , dx_n]\), equipped with the de Rham differential, onto \(\mathbb R\); we let
\(\eta (U)\) is manifestly \(C^{\infty }_M(U)\)-linear and intertwines with restriction maps. Moreover, \(\iota (U)\), \(\pi (U)\), and \(\eta (U)\) together form a deformation retraction of complexes of sheaves; it follows that \(\iota (U)\) is a quasi-isomorphism for all sufficiently small U, so that \(\iota \) is a quasi-isomorphism of complexes of sheaves.
Moreover, \(\iota \) induces a quasi-isomorphism of \(D_{M}\)-modules

We consider next the \(\text {Dens}_{M}\) factor in the local Chevalley–Eilenberg cochains. Since M is Riemannian, \(\text {Dens}_{M}\) is trivial as a bundle, and its (right) \(D_{M}\)-module structure is induced from viewing a density as a distribution. This \(D_M\)-module structure encodes the fact that total derivatives integrate to zero, and it has the following projective resolution:
where the differential \(\delta \) is given by the formula
where \(\nabla \) is the natural flat connection on \(D_M\) and the map \(\Omega ^n_{dR}\otimes D_M \rightarrow \text {Dens}_{M}\) is given by the action of \(D_{M}\) on densities, which happen to also be n forms because M is oriented. It is a direct computation to check that on a local coordinate patch U, this is a Koszul resolution of \(\text {Dens}_{M}(U)\) with respect to the regular sequence \(\{\partial _i\}_{i=1}^n\) of \(D_{M}\) and so gives a quasi-isomorphism \(\left( \Omega ^\bullet _M[n]\otimes _{C^{\infty }_M}D_M\right) \rightarrow \text {Dens}_{M}\).
As a result, we have the following equivalence

where here, the symbol \(\simeq \) means “has isomorphic cohomology to.” We now need to identify this last complex with \(\Omega ^\bullet _M\), but this simply follows from the associativity of the tensor product and variations on the fact that \(A\otimes _A M\cong M\) (isomorphism of left A-modules) for any left A-bimodule M. More precisely, by associativity we have
\(D_M\otimes _{D_M}C^{\infty }_M\) is isomorphic as a left \(D_M\)-module and hence as a \(C^{\infty }_M\)-module, to \(C^{\infty }_M\); it follows that

where, again, the symbol \(\simeq \) means “has isomorphic cohomology to.”
We need only to show that \(\Phi \) itself is a quasi-isomorphism, which can be checked on open balls. Suppose that U is homeomorphic to \(\mathbb R^n\); then by the Poincaré Lemma, the cohomology of \(\Omega ^\bullet _M(U)[n-1]\) is just \(\mathbb R\) concentrated in degree \(-n+1\) and spanned by the constant function 1. Thus, it suffices to check that the following ghost number \(-n+1\) element (which is precisely the image of \(1\in \Omega ^0_{dR}(U)\) under \(\Phi \)) of  is not exact:
is not exact:
where on the left-hand side we are thinking of \(\omega \) as a collection of jets of n forms on U and on the right-hand side we are thinking of \(\omega \) as a density on U. \(\Xi \) is linear in the jets of its input, and since we are dealing with an abelian dgla, the differential  preserves the \({{\mathrm{Sym}}}\) grading. Therefore, if \(\Xi \) were exact in
preserves the \({{\mathrm{Sym}}}\) grading. Therefore, if \(\Xi \) were exact in  , it would be
, it would be  for J some degree \(-n\) element of
for J some degree \(-n\) element of
but the degree \(-n\) elements of this latter space are zero, and \(\Xi \ne 0\), so \(\Xi \) is not exact. Thus, \(\Phi (U)\) is a quasi-isomorphism for all open \(\mathbb R^n\)’s U, which implies the statement of the proposition. \(\square \)
Remark 6.4
The assumption of orientability is not crucial: we can replace the de Rham complex in the domain of \(\Phi \) with the twisted de Rham complex, i.e., the space of de Rham forms with values in the orientation line bundle. The proof is essentially identical, except that since the densities are no longer to be identified with top forms, but rather with top twisted forms, we use \(D_M\otimes \Omega ^\bullet _{tw,dR}\) in the Koszul resolution of the sheaf of densities. \(\square \)
Proof of Theorem 6.2
\(\mathfrak {Obstr}\) represents a degree 1 cohomology class in  , so corresponds under \(\Phi \) to a top-degree cohomology class in \(H^\bullet _{dR,tw}(M)\). Whether or not M is oriented, its top-degree twisted de Rham cohomology is \(\mathbb R\), and the map \(ev_{dR}:\Omega ^{top,tw}_{dR}(M) \rightarrow \mathbb R\) given by integration is a surjection onto cohomology. In a similar vein, define a map
, so corresponds under \(\Phi \) to a top-degree cohomology class in \(H^\bullet _{dR,tw}(M)\). Whether or not M is oriented, its top-degree twisted de Rham cohomology is \(\mathbb R\), and the map \(ev_{dR}:\Omega ^{top,tw}_{dR}(M) \rightarrow \mathbb R\) given by integration is a surjection onto cohomology. In a similar vein, define a map  given by evaluation of the cochain at the constant function 1. These maps descend to cohomology, and we have the following commutative diagram:
given by evaluation of the cochain at the constant function 1. These maps descend to cohomology, and we have the following commutative diagram:

We claim that the map \(H^1\Phi \) is an isomorphism. This is because \(\Phi \) is a quasi-isomorphism, so induces a quasi-isomorphism on derived global sections. Both \(\Omega ^\bullet _{dR,tw}\) and  are complexes of c-soft sheaves since they are sheaves of sections of smooth vector bundles, so their spaces of global sections give a model for the derived global sections. The claim follows.
are complexes of c-soft sheaves since they are sheaves of sections of smooth vector bundles, so their spaces of global sections give a model for the derived global sections. The claim follows.
All but the arrow on the right side of the square have been shown to be isomorphisms, so that arrow is also an isomorphism. It follows that  corresponds to \(\beta \in H^{top}_{dR,tw}(M)\) under \(H^1\Phi \) if and only if \(ev_{dR}(\beta ) = (-1)^{n+1}ev_{loc}(\alpha )\). To complete the proof, we need to show that \(\mathfrak {Obstr}(1) = -2\int _M {\text {Str}}k_t(x,x)dVol_g(x)\). We will prove this claim in the next subsection using a Feynman diagram computation. \(\square \)
corresponds to \(\beta \in H^{top}_{dR,tw}(M)\) under \(H^1\Phi \) if and only if \(ev_{dR}(\beta ) = (-1)^{n+1}ev_{loc}(\alpha )\). To complete the proof, we need to show that \(\mathfrak {Obstr}(1) = -2\int _M {\text {Str}}k_t(x,x)dVol_g(x)\). We will prove this claim in the next subsection using a Feynman diagram computation. \(\square \)
6.2 Explicit computation of the obstruction
Our first main goal here is to prove the following
Lemma 6.5
Let (M, g) be a Riemannian manifold, \(V\rightarrow M\) a \(\mathbb {Z}/2\)-graded metric vector bundle with metric \((\cdot ,\cdot )\), and D a formally self-adjoint Dirac operator. Denote by  the dgla \(\Omega ^\bullet _M\). (These data define the massless free fermion theory
the dgla \(\Omega ^\bullet _M\). (These data define the massless free fermion theory  , together with an action of
, together with an action of  on the theory, which has an obstruction \(\mathfrak {Obstr}\).) Then, \(\mathfrak {Obstr}[t]\), when evaluated on a constant function \(\lambda \), satisfies,
on the theory, which has an obstruction \(\mathfrak {Obstr}\).) Then, \(\mathfrak {Obstr}[t]\), when evaluated on a constant function \(\lambda \), satisfies,
where \(k_t\) is the heat kernel for the generalized Laplacian \(D^2\).
Once this lemma is proved, Theorem 6.2 follows immediately.
Remark 6.6
Compare this formula to Equations 22.2.10 and 22.2.11 in [18], which provide an unregulated formula for the anomaly, i.e., the author computes the \(t\rightarrow 0\) limit of the above expression by computing the supertrace of the \(t\rightarrow 0\) limit of \(k_t\). This is ill-defined: since the \(t\rightarrow 0\) limit of \(k_t\) is the kernel of the identity operator, this limit is singular on the diagonal in \(M\times M\). In [18], the author regulates those expressions by introducing a mass scale and taking that scale to infinity. On the other hand, in the present work, we have used the heat kernel techniques of [6] to make sense of the ill-defined expressions. \(\square \)
The proof of Lemma 6.5 is not tremendously difficult; it simply requires a careful accounting of signs. One major component of this accounting consists of determining the precise relationship between the BV heat kernel \(K_t\) and the heat kernel \(k_t\) as defined in Theorem 2.8, and the next lemma is devoted to specifying this relationship.
Lemma 6.7
Let \(k_{t,1}\) denote the heat kernel for the generalized Laplacian \(D^2\), viewed as an element of  . Similarly, let \(k_{t,2}\) denote the heat kernel viewed as an element of
. Similarly, let \(k_{t,2}\) denote the heat kernel viewed as an element of  . Then, the BV heat kernel satisfies the following equation
. Then, the BV heat kernel satisfies the following equation
In particular, \(K_t\) is antisymmetric under interchange of its two factors.
Proof
Recall that, by Definition A.24,  satisfies
satisfies
where  . We need to make precise meaning of the expression on the left-hand side of Equation 8, keeping track of all the signs that arise from the Koszul sign rule. This is a slightly subtle issue, so we will first consider a simple example to illustrate why this subtlety arises.
. We need to make precise meaning of the expression on the left-hand side of Equation 8, keeping track of all the signs that arise from the Koszul sign rule. This is a slightly subtle issue, so we will first consider a simple example to illustrate why this subtlety arises.
Let us consider the symmetric monoidal category of \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector spaces where the braiding is given by
Given W in this category, we ask what the natural way to pair an element \(\omega _1\otimes \omega _2 \in W^\vee \otimes W^\vee \) with an element \(w_1\otimes w_2\in W\otimes W\) is, assuming that \(\omega _1\), \(\omega _2\), \(w_1\), and \(w_2\) are homogeneous. To do this, we compute the image of \(\omega _1\otimes \omega _2\otimes w_1 \otimes w_2\) under the following composition of maps:
where \(ev: W^\vee \otimes W\rightarrow \mathbb R\) is the natural pairing of a vector space with its dual and \(\mu \) is multiplication of real numbers. In short, by \((\omega _1\otimes \omega _2)(w_1\otimes w_2)\), we mean
Analogously, we understand the term on the left-hand side of Eq. 8 as the image of \(-id\otimes \langle \cdot , \cdot \rangle \otimes K_t\otimes s\) under the following chain of compositions:

where the first map uses the Koszul braiding on our symmetric monoidal category to move the first factor of  past
past  and the second map is a tensor product of evaluation maps
and the second map is a tensor product of evaluation maps

and

It follows that \(K_t = -k_{t,1}+k_{t,2}\), with the relative minus sign arising because the first factors of \(k_{t,1}\) and \(k_{t,2}\) have ghost numbers of opposite parity. \(\square \)
Proof of Lemma 6.5
Recall (Lemma A.41) that

We note that the term  is zero because it evaluates \(I_{wh}\) with \(d\lambda =0\) in one of the slots, so the only term we have to consider is \(\Delta _{t}I_{tr}[t](\lambda )\).
is zero because it evaluates \(I_{wh}\) with \(d\lambda =0\) in one of the slots, so the only term we have to consider is \(\Delta _{t}I_{tr}[t](\lambda )\).
Let us study the Feynman diagrams appearing in \(I_{tr}[t]\) with a \(\lambda \) input into each  leg, i.e., onto each “wavy” external edge. See Fig. 2 for a diagrammatic interpretation of \(I_{tr}[t]\). Let \(I_{tr}^{(r)}[t]\) denote the component of \(I_{tr}[t]\) in \({{\mathrm{Sym}}}\)-degree r with respect to
leg, i.e., onto each “wavy” external edge. See Fig. 2 for a diagrammatic interpretation of \(I_{tr}[t]\). Let \(I_{tr}^{(r)}[t]\) denote the component of \(I_{tr}[t]\) in \({{\mathrm{Sym}}}\)-degree r with respect to  inputs (\(I_{tr}^{(r)}[t]\) is represented by a tree diagram with r squiggly edges). Because of the shift by one in the definition of Chevalley–Eilenberg cochains, \(I^{(r)}\) must be antisymmetric with respect to zero-form inputs; in particular, \(I^{(r)}(\lambda ,\cdots ,\lambda )=0\) if \(r>1\). It follows that \(\mathfrak {Obstr}[t](\lambda ) =\Delta _t I_{tr}^{(1)}[t](\lambda )\), which has a diagrammatic interpretation as the tadpole in Fig. 3.
inputs (\(I_{tr}^{(r)}[t]\) is represented by a tree diagram with r squiggly edges). Because of the shift by one in the definition of Chevalley–Eilenberg cochains, \(I^{(r)}\) must be antisymmetric with respect to zero-form inputs; in particular, \(I^{(r)}(\lambda ,\cdots ,\lambda )=0\) if \(r>1\). It follows that \(\mathfrak {Obstr}[t](\lambda ) =\Delta _t I_{tr}^{(1)}[t](\lambda )\), which has a diagrammatic interpretation as the tadpole in Fig. 3.
The tadpole diagram, evaluated on \(\lambda \), gives
where \(\tau \) is the Koszul braiding on the symmetric monoidal category of \(\mathbb {Z}\times \mathbb {Z}/2\)-graded (topological) vector spaces. Relative to the corresponding notion without Koszul signs, \(\tau K_t\) has
-
1.
no sign arising from ghost number considerations, since \(K_t\) is of degree 1 and therefore belongs to
 , and
, and -
2.
a sign arising from the fact that all elements of
 have fermionic statistics.
have fermionic statistics.
The last equality in Eq. 9 then follows because by construction \(\langle \cdot , [\lambda , \cdot ]\rangle \) is antisymmetric in its two arguments.
We need to show that
which will complete the proof in light of Eq. 9. Heuristically, the term
should compute the trace of \(K_t\), since \(\lambda \) simply acts by multiplication by \(\pm \lambda \) and \(\left\langle \cdot ,\cdot \right\rangle (K_t)\) pairs the two tensor factors of \(K_t\) via \((\cdot ,\cdot )\).
To compute \(-\langle \cdot , [\lambda , \cdot ]\rangle (K_t)\), we take \(K_t(x,x)\) (which is an element of the fiber of \(V\otimes V\) over x), let \(\lambda \) act on the second factor, pair the two factors using \((\cdot ,\cdot )\), and integrate the resulting function over M against the Riemannian density. We also use the description of \(K_t\) from Lemma 6.7. Taking into account all of these comments, we have
which is precisely what we claimed; this completes the proof. \(\square \)
Remark 6.8
The proof of the McKean–Singer formula in [3] has two parts: one first shows that the supertrace of the heat kernel is independent of t; then one shows that the \(t\rightarrow \infty \) limit of the supertrace is \({\text {ind}}(D)\). Our work has given a physical, Feynman diagrammatic interpretation of the first part of that proof. Namely, Lemmas 4.4 and 6.5 together imply that
is independent of t. One can take the \(t\rightarrow \infty \) limit to get \({\text {ind}}(D)\). \(\square \)
We have so far only understood explicitly the obstruction \(\mathfrak {Obstr}\) evaluated on closed zero-forms \(\lambda \). What happens when we evaluate it on other closed forms? The following two results show that Lemma 6.5 already contains all of the difficult computations we need to do to answer this question. This subsection lies somewhat outside the main line of development of this paper, but we include it here for completeness.
Lemma 6.9
Let \(\mathfrak {Obstr}^{(r)}[t]\) be the component of \(\mathfrak {Obstr}[t]\) living in \({{\mathrm{Sym}}}\)-degree r in  . Then, for \(\alpha _1,\cdots , \alpha _r\in \Omega ^\bullet _M(M)\), \(\mathfrak {Obstr}^{(r)}[t](\alpha _1,\cdots , \alpha _r)\) is zero unless one of the \(\alpha _i\) is a function and the rest are one-forms.
. Then, for \(\alpha _1,\cdots , \alpha _r\in \Omega ^\bullet _M(M)\), \(\mathfrak {Obstr}^{(r)}[t](\alpha _1,\cdots , \alpha _r)\) is zero unless one of the \(\alpha _i\) is a function and the rest are one-forms.
Proof
Since \(\mathfrak {Obstr}[t]\) is a degree 1 Chevalley–Eilenberg cocycle, \(\mathfrak {Obstr}^{(r)}[t]\) is nonzero only when evaluated against arguments whose total ghost number in  is–1. However, if any of these forms has degree higher than 1 in
is–1. However, if any of these forms has degree higher than 1 in  , then \(\mathfrak {Obstr}\) will evaluate to zero because \(\mathfrak {Obstr}\) only uses forms through their action on
, then \(\mathfrak {Obstr}\) will evaluate to zero because \(\mathfrak {Obstr}\) only uses forms through their action on  and these higher forms act trivially on
and these higher forms act trivially on  . Thus, \(\mathfrak {Obstr}^{(r)}[t]\) is nonzero only when evaluated on a collection of one-forms and functions whose total ghost number in
. Thus, \(\mathfrak {Obstr}^{(r)}[t]\) is nonzero only when evaluated on a collection of one-forms and functions whose total ghost number in  is –1. This can only be accomplished if all but one of the forms is a one-form. \(\square \)
is –1. This can only be accomplished if all but one of the forms is a one-form. \(\square \)
Thus, to understand \(\mathfrak {Obstr}[t]\) explicitly, we need only to evaluate it on collections of de Rham forms of the sort described in the preceding lemma. In fact, because a symmetric function is determined by its value when all of its inputs are identical, it suffices to consider \(\mathfrak {Obstr}[t](\lambda +\alpha )\), where \(\alpha \) is a 1-form and \(\lambda \) is a function, and we are most interested in the case that \(\alpha \) and \(\lambda \) are closed. The following corollary then follows from Theorem 6.2 and suffices to characterize \(\mathfrak {Obstr}[t]\) evaluated on any collection of closed forms.
Corollary
Let \(\alpha \) be a closed 1-form and \(\lambda \) a closed 0-form. Then,
Together with Lemma 6.9, this characterizes the value of \(\mathfrak {Obstr}[t]\) on all closed forms.
Proof
First note that both \(\mathfrak {Obstr}[t]\) and \(\Delta _t I_{tr}^{(1)}\) are closed elements of  . For \(\mathfrak {Obstr}[t]\), this is contained in the statements of Definition-Lemma A.40 and Lemma 4.4. On the other hand, \(\Delta _t I_{tr}^{(1)}\) is local because by a small modification in the proof of Lemma 6.5, it satisfies
. For \(\mathfrak {Obstr}[t]\), this is contained in the statements of Definition-Lemma A.40 and Lemma 4.4. On the other hand, \(\Delta _t I_{tr}^{(1)}\) is local because by a small modification in the proof of Lemma 6.5, it satisfies
for \(f\in C^{\infty }(M)\). This is manifestly local. Furthermore, \(\Delta _t I_{tr}^{(1)}\) is closed because it is an element of  of top ghost number and
of top ghost number and  preserves \({{\mathrm{Sym}}}\)-degree. Thus,
preserves \({{\mathrm{Sym}}}\)-degree. Thus,  is of Sym-degree 1 and of ghost number one greater than \(\Delta _t I_{tr}^{(1)}\); hence, it is 0.
is of Sym-degree 1 and of ghost number one greater than \(\Delta _t I_{tr}^{(1)}\); hence, it is 0.
The crucial observation is that \(\mathfrak {Obstr}[t](\lambda )=\Delta _t I_{tr}^{(1)}(\lambda )\), as we saw in the proof of Lemma 6.5. Then, by the proof of Theorem 6.2, it follows that \(\mathfrak {Obstr}[t]\) and \(\Delta _t I_{tr}^{(1)}\) represent the same cohomology class in  . Since evaluation on cocycles in \(H^\bullet _{dR}\) is independent of the choice of representative of a class in
. Since evaluation on cocycles in \(H^\bullet _{dR}\) is independent of the choice of representative of a class in  , the two cocycles take the same value when evaluated on closed de Rham forms, so that
, the two cocycles take the same value when evaluated on closed de Rham forms, so that
where the last equality follows from the linearity of \(I_{tr}^{(1)}\) in its  arguments. But, by Lemma 6.9, \(\Delta _{t} I_{tr}^{(1)}(\alpha )=0\), so that
arguments. But, by Lemma 6.9, \(\Delta _{t} I_{tr}^{(1)}(\alpha )=0\), so that
as desired. \(\square \)
6.3 The anomaly as a violation of current conservation
In this subsection, we make contact with the traditional (and familiar to physicists) notion that an anomaly is the failure of a current which is conserved classically to be conserved at the quantum level. The discussion will be relatively informal, but we will secretly be using a very simplified version of the Noether formalism of Chapter 12 of [7].
Before we begin, we should establish some notation. So far, we have worked only with the equivariant observables. In this subsection, we will work also with the non-equivariant observables; that is, we will work with the observables of the theory defined by  , an object which is well defined without reference to any particular action of a dgla on
, an object which is well defined without reference to any particular action of a dgla on  . We let
. We let  denote the classical observables of
denote the classical observables of  , i.e., the Chevalley–Eilenberg cochains of the abelian dgla
, i.e., the Chevalley–Eilenberg cochains of the abelian dgla  , and
, and  denote the quantum observables of
denote the quantum observables of  , i.e., the graded vector space
, i.e., the graded vector space  together with the differential
together with the differential  .
.
We discuss the classical master equation (Eq. 21) in “Appendix.” In the case at hand, the classical master equation is equivalent to the statement that the map

given by
is a cochain map.
Remark 6.10
Recall that we defined I to be an element of  . We abuse notation and refer to the corresponding map
. We abuse notation and refer to the corresponding map  also as I. We will often use the notation \(I_X\) for the observable I(X). \(\square \)
also as I. We will often use the notation \(I_X\) for the observable I(X). \(\square \)
Remark 6.11
We should think of the above map as defining a conserved vector current because it (in particular) takes in a one-form and gives a degree zero observable. More precisely, let us “define” a vector current

by the equation
for all one-forms \(\alpha \). j is conserved in the following sense. The above Lemma tells us that if \(\alpha = df\), then
is an exact observable. Unpacking the definition of exactness in  , we discover that \(I_\alpha \) is zero when evaluated on fields \(\phi , \psi \) which satisfy the equation of motion \(Q\phi = Q\psi =0\). In other words, the following observable
, we discover that \(I_\alpha \) is zero when evaluated on fields \(\phi , \psi \) which satisfy the equation of motion \(Q\phi = Q\psi =0\). In other words, the following observable
is zero when evaluated on fields satisfying the equations of motion. This implies that \(\text {div}(j)=0\) when evaluated on the solutions of the equations of motion, which is the usual statement of current conservation. \(\square \)
Now, we would like to see whether we can define an analogous map  . We will see that this is obstructed precisely by the supertrace of the heat kernel. In particular, suppose we had a map
. We will see that this is obstructed precisely by the supertrace of the heat kernel. In particular, suppose we had a map

whose \(\hbar ^0\) component is I. Let us write
To say that \(I'\) is a cochain map, we need to show that

The \(\hbar ^0\) part of this equation is satisfied by the previous Lemma. However, the \(\hbar ^1\) coefficient is:

It follows after a bit of reflection that \(I^{(1)}\) satisfies this equation if and only if
for some linear map \(J: \Omega ^\bullet _M[1]\rightarrow \mathbb R\). But this last equality is equivalent to the cohomological triviality of \(\mathfrak {Obstr}\), since \([\mathfrak {Obstr}]=[\Delta _t I^{(1)}_{tr}[t]]\), as we have seen. Moreover, we can simply take \(I^{(j)} =0\) for \(j>1\). We have therefore shown the following Lemma:
Lemma 6.12
There exists a lift in the diagram

if and only if \(\mathfrak {Obstr}\) is cohomologically trivial in  .
.
Remark 6.13
In the proof of the previous lemma, we found that the lift was obstructed by the one-leg (i.e., \({{\mathrm{Sym}}}^1\)) term of \(\mathfrak {Obstr}\) (the one represented by the tadpole diagram in Fig. 3). However, \(\mathfrak {Obstr}\) has higher-leg contributions which made no appearance in the proof. Although these higher-leg terms are exact as a corollary of Theorem 6.2, it is still worth wondering why those terms did not appear in the proof of the lemma. The answer lies in the fact that we are only considering whether or not I can be lifted to a quantum observable, whereas our computation is a precise way of addressing the question of whether or not \(e^{I/\hbar }\) is a quantum observable. \(\square \)
The preceding Lemma still seems to make little point of contact with the notion of conserved quantum vector currents. The following remark closes the gap.
Remark 6.14
We have not proved or discussed this here, but the exactness of an observable in \( {\text {Obs}}^{q} \) implies that that observable has expectation value zero, if expectation values exist at all (see [8] for details on this point). Thus, the lift \( I'\) (when it exists) should be viewed as giving a current whose expectation value is conserved. More precisely, just as we should think of \(I_{dA}\) as the divergence of the conserved vector j, \( I'_{dA}\) is a quantization of the divergence of j. The fact that \(I'_{dA}\) is exact says that the quantum expectation value of div(j) vanishes. \(\square \)
7 Equivariant generalizations
In this section, we continue to study the massless free fermion theory  associated with a \(\mathbb {Z}/2\)-graded vector bundle V equipped with a Dirac operator; however, we would like to replace the Lie algebra
associated with a \(\mathbb {Z}/2\)-graded vector bundle V equipped with a Dirac operator; however, we would like to replace the Lie algebra  from Lemma 3.3 with a slightly more general algebra, in the following way. Suppose we have an ordinary Lie algebra \({\mathfrak {g}}\) acting on V and that this action commutes both with the \(C^{\infty }_M\) action and with D. In other words, we have a map of \(\mathbb {Z}/2\)-graded Lie algebras
from Lemma 3.3 with a slightly more general algebra, in the following way. Suppose we have an ordinary Lie algebra \({\mathfrak {g}}\) acting on V and that this action commutes both with the \(C^{\infty }_M\) action and with D. In other words, we have a map of \(\mathbb {Z}/2\)-graded Lie algebras
such that \(\rho (\gamma )(D\phi )=D\rho (\gamma )(\phi )\) for all  , \(f\in C^{\infty }(M)\), and \(\gamma \in {\mathfrak {g}}\). What we have performed so far is the special case that \({\mathfrak {g}}=\mathbb R\) acting by scalar multiplication, and in fact the general case proceeds very similarly, as we will see.
, \(f\in C^{\infty }(M)\), and \(\gamma \in {\mathfrak {g}}\). What we have performed so far is the special case that \({\mathfrak {g}}=\mathbb R\) acting by scalar multiplication, and in fact the general case proceeds very similarly, as we will see.
Remark 7.1
The physical interpretation of this \({\mathfrak {g}}\)-action is as symmetries of the massless free fermion: since elements of \({\mathfrak {g}}\) commute with D, they infinitesimally preserve the equation of motion \(D\phi = 0\). \(\square \)
We will usually just denote the action of an element \(\gamma \in {\mathfrak {g}}\) on a section  by \(\gamma \phi \). Since \(\gamma \) commutes with D, it preserves \(\ker D^+\) and \({\text {coker}}D^+\), so we are free to make the following
by \(\gamma \phi \). Since \(\gamma \) commutes with D, it preserves \(\ker D^+\) and \({\text {coker}}D^+\), so we are free to make the following
Definition 7.2
Let \({\mathfrak {g}}\) act on V as in the first paragraph of this section. Then, the equivariant index of D is the following linear function on \({\mathfrak {g}}\):
Remark 7.3
Note that \({\text {ind}}([\gamma ,\gamma '],D)=0\), since traces of commutators are always zero. In other words, the index defines an element of the Lie algebra cohomology of \({\mathfrak {g}}\). This will be important in the sequel, since the obstruction–deformation complex in this context will be related to the Lie algebra cohomology of \({\mathfrak {g}}\) in a way made precise by Proposition 7.6. \(\square \)
With this definition in hand, we can now state the equivariant McKean–Singer theorem:
Theorem 7.4
Let (M, g) be a Riemannian manifold, \(V\rightarrow M\) a \(\mathbb {Z}/2\)-graded metric vector bundle, and D a formally self-adjoint Dirac operator on V. Suppose given an action \(\rho \) of the Lie algebra \({\mathfrak {g}}\) on V which commutes with the Dirac operator. Then,
Here, \(dVol_g\) is the Riemannian density.
The version of the equivariant McKean–Singer theorem presented here is the infinitesimal version of Proposition 6.3 of [3]. Alternatively, one can prove Equation 10 using a slight modification of either of the proofs of that proposition.
Note that in the special case where \({\mathfrak {g}}= \mathbb R\) and the action is given by scalar multiplication, this theorem just reproduces the regular McKean–Singer formula.
The relevant elliptic dgla in this context is  . We will see that, assuming that \({\mathfrak {g}}\) acts as above,
. We will see that, assuming that \({\mathfrak {g}}\) acts as above,  acts on the free fermion theory. Let us first make the following notational choice. Recall that
acts on the free fermion theory. Let us first make the following notational choice. Recall that  . If \(\gamma \in {\mathfrak {g}}\), we denote by \(\gamma ^\ddagger \) the operator which acts by \(\gamma \) on
. If \(\gamma \in {\mathfrak {g}}\), we denote by \(\gamma ^\ddagger \) the operator which acts by \(\gamma \) on  and \(-\gamma ^T\) on
and \(-\gamma ^T\) on  . In other words, \(\gamma ^\ddagger \) acts on
. In other words, \(\gamma ^\ddagger \) acts on  by the given representation \(\rho \) of \({\mathfrak {g}}\) and on
by the given representation \(\rho \) of \({\mathfrak {g}}\) and on  by the dual representation. Now, we can construct the action of
by the dual representation. Now, we can construct the action of  on the theory
on the theory  .
.
Lemma 7.5
Let

be given by
for \(f\in C^{\infty }(M)\),
for \(\alpha \in \Omega ^1_{dR}(M)\), and
for \(\omega \in \Omega ^{>1}_{dR}(M)\). \(\sigma \) is an action of  on the massless free fermion theory. Here, \(c(\alpha )\) denotes the Clifford action of Definition-Lemma 2.7.
on the massless free fermion theory. Here, \(c(\alpha )\) denotes the Clifford action of Definition-Lemma 2.7.
Proof
As above, we will often use \([\cdot , \cdot ]\) to denote the bracket on  provided by \(\sigma \). We need to check that
provided by \(\sigma \). We need to check that
-
1.
\(Q[\alpha , \zeta ] = [d_{dR}\alpha ,\zeta ]+(-1)^{|\alpha |}[\alpha , Q\zeta ]\) for all forms \(\alpha \) and all
 , i.e., \(Q+d_{dR}\) is a derivation for \([\cdot , \cdot ]\),
, i.e., \(Q+d_{dR}\) is a derivation for \([\cdot , \cdot ]\), -
2.
\([\alpha , [\beta , \zeta ]]=[[\alpha , \beta ],\zeta ]+(-1)^{|\alpha ||\beta |}[\beta ,[\alpha ,\zeta ]]\) for all forms \(\alpha , \beta \) and all
 , i.e., the Jacobi identity is satisfied, and
, i.e., the Jacobi identity is satisfied, and -
3.
\(\left\langle {[\alpha ,\zeta ]},\eta \right\rangle +(-1)^{|\alpha ||\zeta |}\left\langle \zeta , {[\alpha ,\eta ]} \right\rangle =0\) for all forms \(\alpha \),
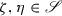 , i.e., \([\alpha , \cdot ]\) is a derivation for the pairing \(\left\langle \cdot ,\cdot \right\rangle \).
, i.e., \([\alpha , \cdot ]\) is a derivation for the pairing \(\left\langle \cdot ,\cdot \right\rangle \).
The terms in the first identity are nonzero only if \(\alpha \) has degree zero in  and \(\zeta \) has ghost number zero in
and \(\zeta \) has ghost number zero in  ; in that case, the identity reads
; in that case, the identity reads
Here, the question mark over the equals sign means that the equality does not necessarily hold, and is rather an equality whose truth we want to check.
We note the following identities
-
1.
\(\gamma ^\ddagger \Gamma _{i\rightarrow i}= \Gamma _{i\rightarrow i}\gamma ^\ddagger \)
-
2.
\(D_{0\rightarrow 1} \gamma ^\ddagger = \gamma ^\ddagger D_{0\rightarrow 1}\)
-
3.
\(\gamma ^\ddagger c(df)_{0\rightarrow 1} = c(df)_{0\rightarrow 1} \gamma ^\ddagger \).
The first holds because \(\gamma \) and \(\gamma ^T\) preserve  and
and  ; the second identity holds because by assumption \(\gamma \) commutes with D and so too does \(\gamma ^T\) by the formal self-adjointness of D; the third identity holds because c(df) is defined in terms of only D and f, both of which commute with \(\gamma \) and \(\gamma ^T\) by assumption. Using these identities, Eq. 11 becomes
; the second identity holds because by assumption \(\gamma \) commutes with D and so too does \(\gamma ^T\) by the formal self-adjointness of D; the third identity holds because c(df) is defined in terms of only D and f, both of which commute with \(\gamma \) and \(\gamma ^T\) by assumption. Using these identities, Eq. 11 becomes
which is true by the definition of c(df).
Now we turn to the verification of the Jacobi identity. If \(\alpha \) and \(\beta \) are both of nonzero cohomological degree, then both sides of the Jacobi identity are automatically zero. Hence, suppose \(\alpha = \gamma _1 \otimes f\) and \(\beta = \gamma _2\otimes g\) where \(f,g\in C^{\infty }\) and \(\gamma _1,\gamma _2 \in {\mathfrak {g}}\). We have
and we see that the Jacobi identity is satisfied because the actions of \(\gamma \) and \(-\gamma ^T\) are Lie algebra actions. In case \(f,\gamma _1,\gamma _2\) are as above and \(\alpha \) is a one-form, we have
Because \(c(\alpha )\) is defined using only the actions of D and \(C^{\infty }_M\) on  , \(c(\alpha )\) commutes with \(\gamma _1^\ddagger \), and so the last term in the above equation is \(\gamma _2\gamma _1(c(\alpha )\zeta )\). Just as for the first case, then, the Jacobi identity is satisfied.
, \(c(\alpha )\) commutes with \(\gamma _1^\ddagger \), and so the last term in the above equation is \(\gamma _2\gamma _1(c(\alpha )\zeta )\). Just as for the first case, then, the Jacobi identity is satisfied.
Finally, we must verify that the pairing is invariant under this action. To this end, let  have ghost numbers 0 and 1, respectively, and both be elements of
have ghost numbers 0 and 1, respectively, and both be elements of  , \(f\in C^{\infty }_M\), \(\gamma \in {\mathfrak {g}}\), and \(\alpha \in \Omega ^1_{dR}\). Then
, \(f\in C^{\infty }_M\), \(\gamma \in {\mathfrak {g}}\), and \(\alpha \in \Omega ^1_{dR}\). Then
the result holds analogously if  ; if \(\zeta , \eta \) have the same ghost number or live in opposite \(\mathbb {Z}/2\) components of
; if \(\zeta , \eta \) have the same ghost number or live in opposite \(\mathbb {Z}/2\) components of  , all terms in the above chain of equalities are zero. For \(\zeta , \eta \) now both of ghost number 0 and in
, all terms in the above chain of equalities are zero. For \(\zeta , \eta \) now both of ghost number 0 and in  , we have
, we have
just as for the case of zero-forms, the proof for  is entirely analogous, and if \(\zeta , \eta \) have differing ghost number or live in pieces of
is entirely analogous, and if \(\zeta , \eta \) have differing ghost number or live in pieces of  of opposite \(\mathbb {Z}/2\)-grading, all terms in the preceding chain of equalities are zero. \(\square \)
of opposite \(\mathbb {Z}/2\)-grading, all terms in the preceding chain of equalities are zero. \(\square \)
We also have results analogous to those of Sect. 6.
Proposition 7.6
Let M be a manifold, \({\mathfrak {g}}\) a Lie algebra, and  . If M is orientable, there is a map
. If M is orientable, there is a map

given by
and \(\Phi \) is a quasi-isomorphism. Here,  is the cochain complex of reduced, local Chevalley–Eilenberg cochains. There is an analogous statement if M is not orientable using twisted de Rham forms.
is the cochain complex of reduced, local Chevalley–Eilenberg cochains. There is an analogous statement if M is not orientable using twisted de Rham forms.
Proof
The proof is similar to that of Proposition 6.1. Letting \(J_{{\mathfrak {g}}}\) refer to the jet bundle of \(\Omega ^\bullet _M\otimes {\mathfrak {g}}\), we have a quasi-isomorphism of sheaves of dglas
and then, \(C^\bullet _{red}(J_{\mathfrak {g}})\) is quasi-isomorphic to \(C^\infty _M \otimes C^\bullet _{red}({\mathfrak {g}})\). Then, just as in Proposition 6.1, we can show that both the source and target of \(\Phi \) have the same cohomology groups.
It remains to show that the map specified above is a quasi-isomorphism. We show this by a spectral sequence argument. Both source and target of \(\Phi \) are filtered by \({{\mathrm{Sym}}}\) degree, and \(\Phi \) preserves the filtrations. Therefore, the cohomology of both can be computed by a spectral sequence and there is a map of spectral sequences between the two. The first page of the spectral sequence just computes the cohomology of both sides with respect to the differential induced by the de Rham differential; on both sides, this is \({{\mathrm{Sym}}}^{>0}({\mathfrak {g}}[1]^\vee )\otimes H^\bullet _{dR} \). This is obvious on the source side, while on the target side, this is a minor modification of the argument of Proposition 6.1. The induced map on \(E_1\) pages is induced from \(\Phi \), where we think of both source and target as having only the truncated, Sym-degree-preserving differential. A small modification of the argument from Proposition 6.1 can be used to show that the map on \(E_1\) pages is indeed an isomorphism. Namely, on a neighborhood U of M homeomorphic to \(\mathbb R^n\), the cohomology of \({{\mathrm{Sym}}}^{> 0}({\mathfrak {g}}[1]^\vee )\otimes \Omega ^\bullet _M(U)\) is \({{\mathrm{Sym}}}^{> 0}({\mathfrak {g}}[1]^\vee )\). To prove that the induced map on \(E_1\) pages is an isomorphism, we need to show that the images of elements of \({{\mathrm{Sym}}}^{> 0}({\mathfrak {g}}[1]^\vee )\) under \(\Phi \) are not exact in the cochain complex

(The differential on this complex is just the differential on the \(E_1\) page in the spectral sequence for  , since the differential induced from the Lie bracket changes \({{\mathrm{Sym}}}\)-filtration.) However, if \(\Phi (\omega )\) were exact in this truncated CE complex for some \(\omega \), then
, since the differential induced from the Lie bracket changes \({{\mathrm{Sym}}}\)-filtration.) However, if \(\Phi (\omega )\) were exact in this truncated CE complex for some \(\omega \), then
would be zero for any \(\gamma _1,\cdots , \gamma _r\) and any closed \(\alpha _1,\cdots , \alpha _r\) of total degree n, with at least 1 of the \(\alpha _i\) compactly supported. Take \(\gamma _1,\cdots ,\gamma _r\) such that \(\omega (\gamma _1,\cdots , \gamma _r)\ne 0\), set \(\alpha _1=\cdots = \alpha _{r-1}=1\), and choose a closed, but non-exact compactly supported top form \(\alpha _r\in \Omega ^n_{dR}\). Such a top form exists because the compactly-supported cohomology of \(\mathbb R^n\) is \(\mathbb R\) in degree n. Then,
This shows that the map induced on \(E_1\)-pages is locally an isomorphism, so it is an isomorphism of sheaves. It follows that the induced map on \(E_2\)-pages is an isomorphism. But the \(E_2\) page is also the \(E_\infty \) page, so we see that \(\Phi \) indeed induces an isomorphism on cohomology. \(\square \)
We also have an analogue to Theorem 6.2; however, this proof requires a slightly more sophisticated touch, since the appropriate generalization of the diagram in Eq. 7 is not immediately obvious.
Theorem 7.7
Let (M, g) be a Riemannian manifold, \(V\rightarrow M\) a \(\mathbb {Z}/2\)-graded vector bundle with metric \((\cdot ,\cdot )\), and D a formally self-adjoint Dirac operator. Let \({\mathfrak {g}}\) act on VD-equivariantly and denote by  the dgla \({\mathfrak {g}}\otimes \Omega ^\bullet _M\). (These are the data defining a free classical fermion theory
the dgla \({\mathfrak {g}}\otimes \Omega ^\bullet _M\). (These are the data defining a free classical fermion theory  , together with an action of
, together with an action of  on the theory, which has an obstruction \(\mathfrak {Obstr}\).) Under the quasi-isomorphism \(\Phi \) of Proposition 7.6, the cohomology class of \(\mathfrak {Obstr}\) as an element of
on the theory, which has an obstruction \(\mathfrak {Obstr}\).) Under the quasi-isomorphism \(\Phi \) of Proposition 7.6, the cohomology class of \(\mathfrak {Obstr}\) as an element of
coincides with the cohomology class of
in \(C^\bullet _{red}({\mathfrak {g}})\otimes \Omega ^\bullet _M(M)[n]\).
Proof
Consider the following diagram:

Only the downward pointing arrows have not yet been discussed. PD, whose letters stand for “Poincaré Duality,” is a composition given by first taking the projection of \(\Omega ^\bullet _M\) onto \(H^\bullet _{dR}\) given by Hodge theory and then taking the Poincaré duality map. The map res is a bit more involved. Let p be an element of \({{\mathrm{Sym}}}^k(({\mathfrak {g}}\otimes \Omega ^\bullet _M(M))^\vee )\). Then, res is defined by
where on the right-hand side we have used the harmonic representative for the cohomology class \(\beta \) to understand \(\beta \) as a de Rham form. We are also thinking of the right-hand side of the above expression as an element of the coinvariants with respect to the \(S_k\) action of permutation of the \(\gamma _i\)’s. It is a quick verification that the diagonal map is a chain map and that the diagram commutes.
Now, since the two maps out of \(C^\bullet _{red}({\mathfrak {g}})\otimes \Omega ^\bullet _M(M)\) are quasi-isomorphisms, it follows that the composite map
is a quasi-isomorphism as well. In particular, this tells us that the inclusion of local Chevalley–Eilenberg cochains into the full space of Chevalley–Eilenberg cochains is injective on cohomology, i.e., if two local cochains differ by an exact term in the full space, they also differ by an exact term in the local complex.
We claim that
in cohomology. Here, it is crucial to us that \(\eta \) factors through the full Chevalley–Eilenberg cochain complex, since this allows us to treat the  and \(\Delta _t I_{tr}[t]\) terms separately. (Recall that we know only that the sum
and \(\Delta _t I_{tr}[t]\) terms separately. (Recall that we know only that the sum  is local.) First of all, this allows us to note that the term
is local.) First of all, this allows us to note that the term  in the scale t obstruction is exact in \(C^\bullet _{red}({\mathfrak {g}}\otimes \Omega ^\bullet _M)\), so that it does not contribute to the class \([\eta (\mathfrak {Obstr}[t])]\).
in the scale t obstruction is exact in \(C^\bullet _{red}({\mathfrak {g}}\otimes \Omega ^\bullet _M)\), so that it does not contribute to the class \([\eta (\mathfrak {Obstr}[t])]\).
We are left with the task of showing that the cohomology class of \(\Delta _t I_{tr}[t]\) coincides with that of \(\Phi ({\mathfrak {T}})\). We claim first of all that the one-leg term \(\eta (\Delta _tI^{(1)}_{tr}[t])=id\otimes PD({\mathfrak {T}})\) To see this, note that \(id\otimes PD ({\mathfrak {T}})\in C^1_{red}({\mathfrak {g}})\otimes {{\mathrm{Hom}}}_\mathbb R(H^0_{dR}(M),\mathbb R)=C^1_{red}({\mathfrak {g}})\), so corresponds to a linear functional on \({\mathfrak {g}}\). In fact, we have
To prove the claim about the one-leg term, it suffices to show that
The single-leg contribution corresponds to the tadpole diagram in Fig. 3, and that diagram gives a contribution
In the last equality, we use the fact that \(k_t=k_t^T\) as a result of the formal self-adjointness of D, so that we have \({{\mathrm{Tr}}}_{V^-}(\gamma ^T k_t(x,x)) = {{\mathrm{Tr}}}_{V^{-}}((k_t(x,x)\gamma )^T)={{\mathrm{Tr}}}_{V^-}(\gamma k_t(x,x)) \). Equation 12 follows.
To complete the proof of the theorem, it now suffices to show that all higher-leg contributions to \(\Delta _t I_{tr}[t]\) go to something exact under res. To see this, note that—by Lemma 6.9, which applies equally well here—any term with r legs is nonzero only when it has one zero-form input and \(r-1\) one-form inputs. This implies, in particular, that \(\eta \) takes any term in \(\Delta _t I_{tr}[t]\) with more than two legs to zero. This is because such diagrams are zero when evaluated on anything with more than one zero-form input, and \(\eta \) evaluates a Sym-degree r element of \(C^\bullet _{loc,red}\) on \(r-1\) zero-forms.
We are left with just the task of showing that the two-leg term in \(\Delta _t I_{tr}[t]\) goes to something exact under \(\eta \). Under \(\eta \), the two-leg term gives a class in \(H^2({\mathfrak {g}}) \otimes {{\mathrm{Hom}}}_\mathbb R(H^1_{dR}(M),\mathbb R)\); however, for the special case of a simple Lie algebra \({\mathfrak {g}}\), \(H^2({\mathfrak {g}})=0\), so that the two-leg term is exact under \(\eta \) and therefore exact in \(C^\bullet _{loc,red}({\mathfrak {g}}\otimes \Omega ^\bullet _M(M))\).
We prove the general case in the \(t\rightarrow \infty \) limit, after first establishing some notation. Let

where \(P_t\) is the operator which appears in Definition A.27 for the propagator P(0, t). We will let P denote the \(t\rightarrow \infty \) limit of \(P_t\); P is characterized by the fact that it is 0 on  and \(D^{-1}\) on
and \(D^{-1}\) on  . Both \(P_t\) and P are distributional in nature, acting as operators on smooth sections of
. Both \(P_t\) and P are distributional in nature, acting as operators on smooth sections of  . We also allow t to take the value \(\infty \) in
. We also allow t to take the value \(\infty \) in  . Finally, let \(H:=[Q,Q^{GF}]\) be the generalized Laplacian of the gauge-fixed massless free fermion.
. Finally, let \(H:=[Q,Q^{GF}]\) be the generalized Laplacian of the gauge-fixed massless free fermion.
With all these notations in place, we note that the two-leg contribution to \(\eta (\Delta _t I_{tr}[t])\) comes from the diagram shown in Fig. 4, and its value, on a harmonic one-form \(\alpha \) and elements \(\gamma _1, \gamma _2\in {\mathfrak {g}}\), is

where  for any smooth kernel \(\ell \in C^{\infty }(M\times M;S\boxtimes S)\). We claim that the \(t\rightarrow \infty \) limit of the above quantity is given by
for any smooth kernel \(\ell \in C^{\infty }(M\times M;S\boxtimes S)\). We claim that the \(t\rightarrow \infty \) limit of the above quantity is given by

Here, for any operator Z on 
 , where \(\Pi \) is the orthogonal projection onto cohomology afforded to us by Lemma 2.13.
, where \(\Pi \) is the orthogonal projection onto cohomology afforded to us by Lemma 2.13.
Let us assume for the moment that the claim is proved; we wish to show that the quantity in Expression 14 is zero. To see this, suppose that  ; then, because \(\gamma _1^\ddagger \otimes \alpha \) changes degree by \(+1\), \(\gamma _2^\ddagger \otimes 1 \circ P \circ \gamma _1^\ddagger \otimes \alpha \varphi =0\); on the other hand, \(P\varphi =0\), since
; then, because \(\gamma _1^\ddagger \otimes \alpha \) changes degree by \(+1\), \(\gamma _2^\ddagger \otimes 1 \circ P \circ \gamma _1^\ddagger \otimes \alpha \varphi =0\); on the other hand, \(P\varphi =0\), since  and by construction P is zero on the cohomology of
and by construction P is zero on the cohomology of  . Moreover, \(\gamma _2^\ddagger \otimes 1\) preserves the cohomology of
. Moreover, \(\gamma _2^\ddagger \otimes 1\) preserves the cohomology of  , so
, so
Thus, \(Z_\infty \varphi =0\). Similarly, if  ,
,

This shows that Expression 14 is zero.
It remains only to show that Expression 13 has Expression 14 as its \(t\rightarrow \infty \) limit. The difference between the two expressions is

Let us note that  , so is the product of two operators
, so is the product of two operators  and \(e^{-tH/2}\) with smooth kernels, which therefore admit extensions to bounded operators acting on \(L^2\) sections of S. As operators on \(L^2(M;S)\), they are Hilbert–Schmidt and the trace
and \(e^{-tH/2}\) with smooth kernels, which therefore admit extensions to bounded operators acting on \(L^2\) sections of S. As operators on \(L^2(M;S)\), they are Hilbert–Schmidt and the trace  corresponds to the Hilbert space trace, using a modification of the arguments presented in the proof of Proposition 2.32 of [3]. Similar arguments apply for
corresponds to the Hilbert space trace, using a modification of the arguments presented in the proof of Proposition 2.32 of [3]. Similar arguments apply for  and
and  , using \(e^{-tH/2}\Pi =\Pi \). Thus, we are permitted to switch to the \(L^2\) context for the computation of traces; all appearances of the expression
, using \(e^{-tH/2}\Pi =\Pi \). Thus, we are permitted to switch to the \(L^2\) context for the computation of traces; all appearances of the expression  in the sequel will therefore refer to the trace in the Hilbert space sense. Now, on an eigenvector of D with eigenvalue \(\lambda \), \(P_t\) is zero if \(\lambda \) is zero and otherwise multiplies the eigenvector by \(\lambda ^{-1}(1-e^{-t\lambda ^2})\). This is bounded as a function of \(\lambda \), so that \(P_t\) is a bounded operator. Similarly, P acts by 0 on \(\ker D\) and by \(\lambda ^{-1}\) on nonzero eigenvectors of D with eigenvalue \(\lambda \). Since the spectrum of D is discrete (Lemma 2.16), it follows that P is bounded in norm. It also follows from the characterizations of \(P_t\) and P that \(P_t-P\) acts by zero on \(\ker D\) and by \(\lambda ^{-1}e^{-t\lambda ^2}\) on eigenvectors with nonzero eigenvalue. This last quantity is monotonically decreasing with \(\lambda \) and so
in the sequel will therefore refer to the trace in the Hilbert space sense. Now, on an eigenvector of D with eigenvalue \(\lambda \), \(P_t\) is zero if \(\lambda \) is zero and otherwise multiplies the eigenvector by \(\lambda ^{-1}(1-e^{-t\lambda ^2})\). This is bounded as a function of \(\lambda \), so that \(P_t\) is a bounded operator. Similarly, P acts by 0 on \(\ker D\) and by \(\lambda ^{-1}\) on nonzero eigenvectors of D with eigenvalue \(\lambda \). Since the spectrum of D is discrete (Lemma 2.16), it follows that P is bounded in norm. It also follows from the characterizations of \(P_t\) and P that \(P_t-P\) acts by zero on \(\ker D\) and by \(\lambda ^{-1}e^{-t\lambda ^2}\) on eigenvectors with nonzero eigenvalue. This last quantity is monotonically decreasing with \(\lambda \) and so

where \(\lambda _1\) is the smallest nonzero eigenvalue of D and C is some constant and \(||\cdot ||\) refers to the operator norm on bounded operators on \(L^2\). Again, we have used the fact that the spectrum of \(D^2\) is discrete. It follows that  in the operator norm. Thus,
in the operator norm. Thus,

where we have used the fact that for a bounded operator A and a trace class, formally self-adjoint, nonnegative operator B,
Now, since  in the operator norm and \(e^{-tH}\rightarrow \Pi \) in the trace norm (Lemma 2.15), this shows that
in the operator norm and \(e^{-tH}\rightarrow \Pi \) in the trace norm (Lemma 2.15), this shows that

as desired. \(\square \)
Remark 7.8
Just as in Sect. 6.2, the t-independence of the obstruction, together with the single-leg computation in the above proof, shows the t-invariance of the quantity appearing on the right-hand side of the equivariant McKean–Singer formula, Equation 10. Moreover, one can take the \(t\rightarrow \infty \) limit of this quantity (see [3]). As is to be expected, the result is \({\text {ind}}(\gamma ,D)\), the global quantity appearing in the equivariant McKean–Singer formula. \(\square \)
References
Bär, C., Strohmaier, A.: A rigorous geometric derivation of the chiral anomaly in curved backgrounds. Commun. Math. Phys. 347(3), 703–721 (2016). https://doi.org/10.1007/s00220-016-2664-1
Bell, J.S., Jackiw, R.: A PCAC puzzle: \(\pi _0\rightarrow \gamma \gamma \) in the \(\sigma \)-model. Nuovo Cimento A Serie 60, 47–61 (1969). https://doi.org/10.1007/BF02823296
Berline, N., Getzler, E., Vergne, M.: Heat Kernels and Dirac Operators. Grundlehren Text Editions. Springer, Berlin (2004). (Corrected reprint of the 1992 original)
Bismut, J.M., Freed, D.S.: The analysis of elliptic families. I. Metrics and connections on determinant bundles. Commun. Math. Phys. 106(1), 159–176 (1986). http://projecteuclid.org/euclid.cmp/1104115586
Bismut, J.M., Freed, D.S.: The analysis of elliptic families. II. Dirac operators, eta invariants, and the holonomy theorem. Commun. Math. Phys. 107(1), 103–163 (1986). http://projecteuclid.org/euclid.cmp/1104115934
Costello, K.: Renormalization and Effective Field Theory, Mathematical Surveys and Monographs, vol. 170. American Mathematical Society, Providence (2011). https://doi.org/10.1090/surv/170
Costello, K., Gwilliam, O.: Factorization Algebras in Quantum Field Theory, vol. 2. http://people.math.umass.edu/~gwilliam/vol2may8.pdf. Accessed 25 Nov 2018
Costello, K., Gwilliam, O.: Factorization Algebras in Quantum Field Theory. Vol. 1, New Mathematical Monographs, vol. 31. Cambridge University Press, Cambridge (2017). https://doi.org/10.1017/9781316678626
Crainic, M.: On the perturbation lemma, and deformations. ArXiv Mathematics e-prints (2004)
Freed, D.S.: Determinants, torsion, and strings. Commun. Math. Phys. 107(3), 483–513 (1986). http://projecteuclid.org/euclid.cmp/1104116145
Freed, D.S.: Anomalies and invertible field theories. In: String-Math 2013, Proceedings of Symposia in Pure Mathematics, vol. 88, pp. 25–45. American Mathematical Society, Providence (2014). https://doi.org/10.1090/pspum/088/01462
Gorbounov, V., Gwilliam, O., Williams, B.: Chiral differential operators via Batalin-Vilkovisky quantization. ArXiv e-prints (2016)
Gwilliam, O.: Factorization Algebras and Free Field Theories. ProQuest LLC, Ann Arbor, MI (2012). http://people.math.umass.edu/~gwilliam/thesis.pdf. Accessed 25 Nov 2018. Ph.D. Thesis, Northwestern University
Lurie, J.: Derived Algebraic Geometry X: formal Moduli Problems. http://www.math.harvard.edu/~lurie/papers/DAG-X.pdf. Accessed 25 Nov 2018
Lurie, J.: Higher Algebra. http://www.math.harvard.edu/~lurie/papers/HA.pdf. Accessed 25 Nov 2018
Nielsen, N.K., Römer, H., Schroer, B.: Anomalous currents in curved space. Nucl. Phys. B 136(3), 475–492 (1978). https://doi.org/10.1016/0550-3213(78)90271-7
Peskin, M.E., Schroeder, D.V.: An Introduction to Quantum Field Theory. Addison-Wesley Publishing Company, Advanced Book Program, Reading (1995). (Edited and with a foreword by David Pines)
Weinberg, S.: The Quantum Theory of Fields, vol. II. Cambridge University Press, Cambridge (2005). Modern applications
Wilson, K.G., Kogut, J.: The renormalization group and the \(\epsilon \) expansion. Phys. Rep. 12(2), 75–199 (1974). https://doi.org/10.1016/0370-1573(74)90023-4. http://www.sciencedirect.com/science/article/pii/0370157374900234
Witten, E.: Fermion path integrals and topological phases. Rev. Mod. Phys. 88(3), 035001 (2016). https://doi.org/10.1103/RevModPhys.88.035001
Acknowledgements
Open access funding provided by Max Planck Society. The author would like to thank Owen Gwilliam and Brian Williams for many incredibly helpful discussions and immeasurable guidance in this project. He has Owen Gwilliam to thank for pointing him in the direction of this work. He would also like to thank his advisor Peter Teichner for inviting him to the Max Planck Institut für Mathematik in Bonn, for encouraging the author to speak in his (Peter’s) student seminars, and for his comments on an earlier draft of this paper. Furthermore, he would like to thank Matthias Ludewig for many helpful comments on an earlier draft. Finally, thanks are due to the Max Planck Institut für Mathematik in Bonn for its hospitality while much of the work on this project was completed. This research was supported in part by Perimeter Institute for Theoretical Physics. Research at Perimeter Institute is supported by the Government of Canada through the Department of Innovation, Science and Economic Development and by the Province of Ontario through the Ministry of Research and Innovation. Some revisions of the present work resulted from the author’s stay at the Perimeter Institute, and the author is thankful to Ben Albert and Kevin Costello for helpful comments. The author would like to thank an anonymous referee for numerous and helpful suggestions. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE 1752814. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.
Author information
Authors and Affiliations
Corresponding author
A Background on equivariant BV quantization
A Background on equivariant BV quantization
1.1 A.1 Introduction
In this appendix, we set up the mathematical framework for studying what is in physics called an anomaly. Roughly speaking, an anomaly is the failure of a symmetry of a classical field theory to persist after quantization. Symmetries are usually encoded in actions of a Lie algebra—or more generally a dgla, or even more generally an \(L_\infty \)-algebra—on the space of fields of the theory. We develop this perspective below, following [7, 13], which provide a general framework for treating actions of an \(L_\infty \)-algebra on a quantum field theory. We will not need the full generality of that framework below—restricting ourselves to dgla actions on free field theories—though by illuminating the relationship of this special case to index theory, we hope to provide motivation for the study of the more general case.
Another perspective on symmetries is that they consist of an interaction term I representing a coupling of the physical fields to background gauge fields. I is required to satisfy a Maurer–Cartan equation which contains the content of the fact that \({\mathfrak {g}}\) acts on the corresponding theory. This equation is called the classical master equation. This perspective is equivalent to the perspective of the previous paragraph.
To summarize, there are two equivalent perspectives on the notion of a symmetry of a classical theory. We can view a symmetry as
-
1.
an action of a dgla \({\mathfrak {g}}\) on the space of fields of a field theory or
-
2.
a \({\mathfrak {g}}\)-dependent interaction term in the action of the field theory. The elements of \({\mathfrak {g}}\) are considered to be background fields.
There will be analogues of the classical master equation for I in the quantum case, called the weak and strong quantum master equations. The strong quantum master equation, in particular, is central to the discussion of anomalies.
1.2 A.2 Free Batalin–Vilkovisky theories
Free Batalin–Vilkovisky (BV) theories are the starting point for quantization, since in the perturbative formalism we think of interacting theories as perturbations of free ones. In this paper, we are mostly be concerned with families of free theories. However, the formalism for families of free theories requires us to consider interactions, even if the individual theories in the family are free; we will discuss the necessary formalism for interactions in Sect. A.4.
We will frequently deal with \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector spaces in the sequel. Recall from Sect. 1.5 that if v is a homogeneous element of a \(\mathbb {Z}\times \mathbb {Z}/2\)-graded vector space, we use the notation |v| to denote its \(\mathbb {Z}\) degree and \(\pi _v\) to denote its \(\mathbb {Z}/2\) degree.
The following is Definition 7.0.1 of Chapter 5 of [6], modified to allow an extra \(\mathbb {Z}/2\)-grading on the space of fields.
Definition A.1
A free classical BV theory on a compact manifold N consists of the following data:
- 1.:
-
A \(\mathbb {Z}\times \mathbb {Z}/2\)-graded \(\mathbb R-\)vector bundle F over N. We will call the sheaf of sections
 the space of fields of the theory.
the space of fields of the theory. - 2.:
-
A map of vector bundles
$$\begin{aligned} \left\langle \cdot ,\cdot \right\rangle _{loc}: F\otimes F \rightarrow \text {Dens}_N \end{aligned}$$of degree \((-1,0)\). We will denote by \(\left\langle \cdot ,\cdot \right\rangle \) the following pairing on the space of global sections
 : $$\begin{aligned} \left\langle f_1,f_2 \right\rangle = \int _N \left\langle f_1,f_2 \right\rangle _{loc}. \end{aligned}$$
: $$\begin{aligned} \left\langle f_1,f_2 \right\rangle = \int _N \left\langle f_1,f_2 \right\rangle _{loc}. \end{aligned}$$ - 3.:
-
A differential operator
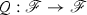 of degree (1,0).
of degree (1,0).
The above data are required to satisfy the following additional conditions:
- 1.:
-
\(\left\langle \cdot ,\cdot \right\rangle _{loc}\) is graded antisymmetric and non-degenerate on each fiber.
- 2.:
-
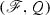 is a (\(\mathbb {Z}/2\)-graded) elliptic complex.
is a (\(\mathbb {Z}/2\)-graded) elliptic complex. - 3.:
-
Q is graded skew self-adjoint for \(\left\langle \cdot ,\cdot \right\rangle \).
Remark A.2
By graded anti-symmetry of \(\left\langle \cdot ,\cdot \right\rangle _{loc}\), we mean that if \(f_1,f_2\) are homogeneous elements of the fiber of F over \(x\in N\), then
All notions of graded symmetry and anti-symmetry should be analogously understood. We also note that since \(\left\langle \cdot ,\cdot \right\rangle \) is of degree –1, it is only nonzero on pairs \(f_1\) and \(f_2\) with \(|f_1|\) and \(|f_2|\) of opposite parity, so that we can rewrite the above equation as
\(\square \)
Remark A.3
The elliptic complex  encodes the information of the linear PDE
encodes the information of the linear PDE
The zeroth cohomology of  is the space of solutions to this PDE modulo the identification of solutions differing by an exact term; physically, the zeroth cohomology is the space of solutions of the equations of motion modulo the identification of physically indistinguishable (gauge-equivalent) configurations. \(\square \)
is the space of solutions to this PDE modulo the identification of solutions differing by an exact term; physically, the zeroth cohomology is the space of solutions of the equations of motion modulo the identification of physically indistinguishable (gauge-equivalent) configurations. \(\square \)
When we discuss the quantization of free BV theories in Sect. A.4, we will need to equip the free BV theory with one more piece of auxiliary data:
Definition A.4
(Definition 7.4.1 of Chapter 5 of [6]) A gauge-fixing\(Q^{GF}\) for a free BV theory is a degree \((-1,0)\) differential operator  , such that \([Q,Q^{GF}]\) is a generalized Laplacian for some metric on N and \(Q^{GF}\) is graded self-adjoint for the pairing \(\left\langle \cdot ,\cdot \right\rangle \).
, such that \([Q,Q^{GF}]\) is a generalized Laplacian for some metric on N and \(Q^{GF}\) is graded self-adjoint for the pairing \(\left\langle \cdot ,\cdot \right\rangle \).
Remark A.5
In physics, the (opposite of the) \(\mathbb {Z}\)-degree of an element of  is called the “ghost number,” while its \(\mathbb {Z}/2\)-degree is often called its “statistics;” we say that an element of
is called the “ghost number,” while its \(\mathbb {Z}/2\)-degree is often called its “statistics;” we say that an element of  has bosonic or fermionic statistics depending on whether it has grading 0 or 1, respectively. The extra \(\mathbb {Z}/2\)-grading has the effect of changing signs in commutation relations. \(\square \)
has bosonic or fermionic statistics depending on whether it has grading 0 or 1, respectively. The extra \(\mathbb {Z}/2\)-grading has the effect of changing signs in commutation relations. \(\square \)
As a very simple example of a free field theory, we have
Example A.6
Given an (ordinary, i.e., \(\mathbb {Z}\)-graded) elliptic complex  , the cotangent theory\(T^*[-1]\mathscr {E}\) to
, the cotangent theory\(T^*[-1]\mathscr {E}\) to  has space of fields
has space of fields  , with all fields having odd \(\mathbb {Z}/2\)-grading. We define \(\left\langle \cdot ,\cdot \right\rangle _{loc}\) to be the natural pairing on
, with all fields having odd \(\mathbb {Z}/2\)-grading. We define \(\left\langle \cdot ,\cdot \right\rangle _{loc}\) to be the natural pairing on  and Q to be \(P+P^!\). Here,
and Q to be \(P+P^!\). Here,  is the sheaf of sections of the bundle \(F^\vee \otimes \text {Dens}\). \(\square \)
is the sheaf of sections of the bundle \(F^\vee \otimes \text {Dens}\). \(\square \)
As another simple example, we have the massless scalar boson theory:
Example A.7
Let (N, h) be a Riemannian manifold with Riemannian density \(dVol_h\). The massless scalar boson is the free BV theory with space of fields \(C^{\infty }_N\oplus C^{\infty }_N[-1]\), Q the Laplacian on N, and with the pairing \(\left\langle \cdot ,\cdot \right\rangle _{loc}\) determined uniquely by
when \(|f_1|=0\) and \(|f_2|=1\). To satisfy the appropriate anti-symmetry conditions, we must take the opposite sign if \(|f_1|=1\) and \(|f_2|=0\). All fields have bosonic statistics. \(\square \)
1.3 A.3 Actions of an elliptic differential graded Lie algebra on a free theory
We would like to understand what it means for a dgla to act on a free theory. To begin with, we should specify the particular class of dglas suited to the analytic nature of quantum field theory and the associated notions of Chevalley–Eilenberg cochains.
1.3.1 A.3.1 Elliptic differential graded Lie algebras and their Chevalley–Eilenberg cochains
Definition A.8
(Definition 7.2.1 of [13]) An elliptic differential graded Lie algebra is a sheaf of sections of a \(\mathbb {Z}\)-graded vector bundle \(L\rightarrow N\) which is also a sheaf of dglas. The differential must give
is a sheaf of sections of a \(\mathbb {Z}\)-graded vector bundle \(L\rightarrow N\) which is also a sheaf of dglas. The differential must give  the structure of an elliptic complex, and the bracket must be given by a bidifferential operator.
the structure of an elliptic complex, and the bracket must be given by a bidifferential operator.
Example A.9
For a manifold M and a Lie algebra \({\mathfrak {g}}\), the sheaf \(\Omega ^\bullet _M\otimes {\mathfrak {g}}\) is an elliptic dgla with differential given by the de Rham differential and bracket given by the wedge product on the differential form factor and Lie bracket on the \({\mathfrak {g}}\) factor. \(\square \)
An elliptic dgla has the standard Chevalley–Eilenberg (CE) cochain complex, as well as a cochain complex of functionals that are more nicely behaved and are defined using the fact that  is a sheaf of smooth sections of a vector bundle.
is a sheaf of smooth sections of a vector bundle.
Definition A.10
Let  be an elliptic dgla. The Chevalley–Eilenberg cochain complex of
be an elliptic dgla. The Chevalley–Eilenberg cochain complex of  is the commutative differential graded algebra
is the commutative differential graded algebra

equipped with the Chevalley–Eilenberg differential defined as in the finite-dimensional case. Here, we use \(\vee \) to denote continuous linear dual, and the \({{\mathrm{Sym}}}\) is taken with respect to the projective tensor product of Nuclear spaces. Namely,

where the subscript \(S_n\) denotes coinvariants of the \(S_n\) action which permutes the tensor factors. See Appendix 2 in [6] and Appendix B.1 in [7] for more details. We will often use the notation  to describe the underlying graded vector space.
to describe the underlying graded vector space.
Definition A.11
(Definition 7.2.7 of [13]) The cochain complex  of local Chevalley–Eilenberg cochains of the dgla
of local Chevalley–Eilenberg cochains of the dgla  is the subcomplex of
is the subcomplex of  given by sums of functionals of the form
given by sums of functionals of the form
where each \(D_i\) is a differential operator from  to \(C^{\infty }_N\) and \(d\mu \) is a smooth density on N. We view \(F_n\) as a coinvariant of the \(S_n\) action. We can also study
to \(C^{\infty }_N\) and \(d\mu \) is a smooth density on N. We view \(F_n\) as a coinvariant of the \(S_n\) action. We can also study  , which is the quotient of
, which is the quotient of  by the subcomplex \(\mathbb R\) (which lives in \({{\mathrm{Sym}}}\)-degree 0). We also have
by the subcomplex \(\mathbb R\) (which lives in \({{\mathrm{Sym}}}\)-degree 0). We also have  , defined analogously.
, defined analogously.
Remark A.12
Here, we are using that N is compact to be able to integrate densities. However, to prove our main theorem, it is necessary to extend  to a sheaf on N. On open subsets of N, we would like to define
to a sheaf on N. On open subsets of N, we would like to define  to be the space of all Lagrangian densities (an idea made precise below). Densities cannot in general be integrated over non-compact U. Thus, in this case, we cannot think of local cochains on U as living inside the space of all CE cochains. \(\square \)
to be the space of all Lagrangian densities (an idea made precise below). Densities cannot in general be integrated over non-compact U. Thus, in this case, we cannot think of local cochains on U as living inside the space of all CE cochains. \(\square \)
In light of the previous remark, we would like to have an alternative characterization of the local Chevalley–Eilenberg cochain complex that is naturally sheaf-like. To do this, we introduce the language of jets:
Definition A.13
(Cf. Section 5.6.2 of [6]) The sheaf of jetsJ(L) of the elliptic dgla  is the sheaf of sections of the vector bundle of dglas over N whose fiber at a point \(x\in N\) is the space of formal germs at x of sections of L.
is the sheaf of sections of the vector bundle of dglas over N whose fiber at a point \(x\in N\) is the space of formal germs at x of sections of L.
The dgla structure on the fiber is induced from the same structure on L and the fact that the dgla operations of  are polydifferential operators. Moreover, as discussed in Section 6.2 of Chapter 5 of [6], J(L) has a natural (left) \(D_N\)-module structure, where \(D_N\) is the sheaf of differential operators on N. Furthermore, J(L) is an inverse limit of finite-dimensional \(C^{\infty }_N\)-modules; we can therefore endow it with the topology of the inverse limit.
are polydifferential operators. Moreover, as discussed in Section 6.2 of Chapter 5 of [6], J(L) has a natural (left) \(D_N\)-module structure, where \(D_N\) is the sheaf of differential operators on N. Furthermore, J(L) is an inverse limit of finite-dimensional \(C^{\infty }_N\)-modules; we can therefore endow it with the topology of the inverse limit.
Now, let \(J(L)^\vee \) denote the following \(C^{\infty }_N\)-module
where \({{\mathrm{Hom}}}_{C^{\infty }_N}\) means continuous homomorphisms of \(C^\infty _N\) modules (i.e., those that respect the inverse limit topology on J(L)). Let also

Note that  has a natural differential encoding the Chevalley–Eilenberg differential on
has a natural differential encoding the Chevalley–Eilenberg differential on  . Moreover,
. Moreover,  has the structure of a left \(D_N\)-module.
has the structure of a left \(D_N\)-module.
Lemma A.14
(Lemma 6.6.1 of Chapter 5 of [6]). For  an elliptic dgla, there is a canonical isomorphism of cochain complexes
an elliptic dgla, there is a canonical isomorphism of cochain complexes

Here, \(\text {Dens}_N\) is given the right \(D_N\)-module structure induced from considering densities as distributions.
Remark A.15
The object on the right-hand side of the isomorphism of Lemma A.14 is manifestly the space of global sections of the sheaf  . We therefore will, in the sequel, abuse notation and use
. We therefore will, in the sequel, abuse notation and use  to refer also to this sheaf. \(\square \)
to refer also to this sheaf. \(\square \)
Lemma A.16
(Lemma 6.6.2 of Chapter 5 of [6]). For  an elliptic dgla, there is a quasi-isomorphism
an elliptic dgla, there is a quasi-isomorphism

Putting this together with the previous lemma, we see that the actual tensor product is a model for the derived tensor product.
We use this Lemma in the proof of Proposition 6.1.
1.3.2 A.3.2 Actions of an elliptic dgla on a free theory
In this subsubsection, we review the main results concerning the action of an elliptic dgla on a free BV theory. However, most of what we do works in a far more general context of elliptic \(L_\infty \)-algebras acting on a general BV theory. We will point out the few instances in which results are specific to the case we consider.
Definition A.17
(Special case of Definition 11.1.2.1 of [7]) If  is an elliptic dgla, and \(\mathscr {E}\) is an elliptic complex, then an action of
is an elliptic dgla, and \(\mathscr {E}\) is an elliptic complex, then an action of  on \(\mathscr {E}\) is the structure of an elliptic dgla on
on \(\mathscr {E}\) is the structure of an elliptic dgla on  such that the maps in the linear exact sequence
such that the maps in the linear exact sequence

as well as the map  , are openwise dgla maps (i.e., they commute with brackets). We are thinking of \(\mathscr {E}[-1]\) as an elliptic abelian dgla.
, are openwise dgla maps (i.e., they commute with brackets). We are thinking of \(\mathscr {E}[-1]\) as an elliptic abelian dgla.
In other words, an action of  on \(\mathscr {E}\) is just a map
on \(\mathscr {E}\) is just a map

satisfying certain coherence relations encoding the fact that the differential on  is a derivation for \(\rho \) and that the bracket on
is a derivation for \(\rho \) and that the bracket on  satisfies the Jacobi identity. Equivalently, we require that
satisfies the Jacobi identity. Equivalently, we require that  be an
be an  -module. We will also use \([\cdot ,\cdot ]\) to denote \(\rho \) and
-module. We will also use \([\cdot ,\cdot ]\) to denote \(\rho \) and  to denote the resulting dgla.
to denote the resulting dgla.
Finally, we define what it means for an elliptic dgla to act on a free BV theory:
Definition A.18
(Definition 11.1.2.1 of [7]) Let  be a free BV theory and
be a free BV theory and  an elliptic dgla. An action of
an elliptic dgla. An action of  on
on  is an action of
is an action of  on the elliptic complex
on the elliptic complex  such that the map \(\rho \) leaves the pairing \(\left\langle \cdot ,\cdot \right\rangle \) invariant in the sense that \(\rho (\alpha , \cdot )\) is a graded derivation with respect to \(\left\langle \cdot ,\cdot \right\rangle \) for all
such that the map \(\rho \) leaves the pairing \(\left\langle \cdot ,\cdot \right\rangle \) invariant in the sense that \(\rho (\alpha , \cdot )\) is a graded derivation with respect to \(\left\langle \cdot ,\cdot \right\rangle \) for all  . This means that
. This means that
for all  . Moreover, we require the action of
. Moreover, we require the action of  on
on  to be even with respect to the \(\mathbb {Z}/2\) grading of
to be even with respect to the \(\mathbb {Z}/2\) grading of  in the sense that
in the sense that
for all  and
and  .
.
Remark A.19
The requirement that the differential on  act as a derivation for \([\cdot , \cdot ]\) implies that
act as a derivation for \([\cdot , \cdot ]\) implies that  acts on
acts on  . This is the sense in which we should think of a dgla action as a symmetry; since the cohomology of
. This is the sense in which we should think of a dgla action as a symmetry; since the cohomology of  is to be thought of as the moduli space of classical solutions, the fact that
is to be thought of as the moduli space of classical solutions, the fact that  acts on
acts on  is a precise way of saying that
is a precise way of saying that  acts on
acts on  in a way that (cohomologically) preserves the equations of motion. \(\square \)
in a way that (cohomologically) preserves the equations of motion. \(\square \)
Returning now to the general context of an elliptic dgla acting on a free theory  , we note that a free BV theory provides the quadratic action functional
, we note that a free BV theory provides the quadratic action functional
and the action of  on
on  provides the following cubic deformation of the action functional on
provides the following cubic deformation of the action functional on  :
:
The complex  has a degree +1 Poisson bracket \(\{\cdot , \cdot \}\) induced from \(\left\langle \cdot ,\cdot \right\rangle \), whose precise construction can be found in Section 5.3 of [6]. The bracket \(\{\cdot , \cdot \}\) can be extended to all of
has a degree +1 Poisson bracket \(\{\cdot , \cdot \}\) induced from \(\left\langle \cdot ,\cdot \right\rangle \), whose precise construction can be found in Section 5.3 of [6]. The bracket \(\{\cdot , \cdot \}\) can be extended to all of  by
by  -linearity. Moreover, as discussed in Section 11.1 of [7], we can equivalently think of an action of
-linearity. Moreover, as discussed in Section 11.1 of [7], we can equivalently think of an action of  on
on  as a degree-zero element
as a degree-zero element

satisfying the Maurer–Cartan Equation

which is also known as the classical master equation. In our special case, we require I to have \({{\mathrm{Sym}}}\)-degree 1 with respect to  and \({{\mathrm{Sym}}}\)-degree 2 with respect to
and \({{\mathrm{Sym}}}\)-degree 2 with respect to  . If I has the correct \({{\mathrm{Sym}}}\)-degrees and satisfies the classical master equation, then it determines the action of
. If I has the correct \({{\mathrm{Sym}}}\)-degrees and satisfies the classical master equation, then it determines the action of  on
on  and vice versa. Furthermore, we consider
and vice versa. Furthermore, we consider  to be the space of background fields because we have not demanded that
to be the space of background fields because we have not demanded that  be endowed with a pairing as
be endowed with a pairing as  is.
is.
Notice that the interaction \(I(X,\phi )\), though of cubic and higher order with respect to X and \(\phi \) together, is only quadratic in \(\phi \). This is particular to our case; if we were to use the full language of \(L_\infty \)-algebras, we would be able to describe deformations of  into non-free theories, in which case we would allow cubic and higher-order interactions in
into non-free theories, in which case we would allow cubic and higher-order interactions in  fields.
fields.
Graphically, the interaction I can be depicted by a vertex with two straight half-edges and one wavy half-edge. See Fig. 5. The perspective on I as such a vertex anticipates the formalism of Feynman diagrams. See also Remark A.29.
Remark A.20
If  is an elliptic complex, and
is an elliptic complex, and  acts on the cotangent theory to
acts on the cotangent theory to  as an extension of an action of
as an extension of an action of  on
on  , then the interaction I can be rewritten as
, then the interaction I can be rewritten as
where  and
and  are viewed as the base and fiber components of a general element of
are viewed as the base and fiber components of a general element of  . The factor of 1/2 has disappeared because of the symmetry properties of \([X,\cdot ]\). In this case, we can add arrows to the vertex to indicate that, with respect to the decomposition of
. The factor of 1/2 has disappeared because of the symmetry properties of \([X,\cdot ]\). In this case, we can add arrows to the vertex to indicate that, with respect to the decomposition of  into base and fiber, I is nonzero only when evaluated on a base field as one input and a fiber field as another. Figure 6 shows this modified graphical interpretation. \(\square \)
into base and fiber, I is nonzero only when evaluated on a base field as one input and a fiber field as another. Figure 6 shows this modified graphical interpretation. \(\square \)
Definition A.21
(Proof of Proposition 11.3.0.1 in [7]) If  acts on the free field theory
acts on the free field theory  , then the cochain complex of global equivariant classical observables\( {\text {Obs}}^{cl} \) is
, then the cochain complex of global equivariant classical observables\( {\text {Obs}}^{cl} \) is  , the (completed) differential graded commutative algebra of Chevalley–Eilenberg cochains on the dgla
, the (completed) differential graded commutative algebra of Chevalley–Eilenberg cochains on the dgla  . We will use
. We will use  to denote the underlying graded vector space.
to denote the underlying graded vector space.
Remark A.22
Recall that Chevalley–Eilenberg cochains of a dgla  are, as a vector space,
are, as a vector space,  ; since we let
; since we let  be \(\mathbb {Z}\times \mathbb {Z}/2\) graded, we view
be \(\mathbb {Z}\times \mathbb {Z}/2\) graded, we view  as a \(\mathbb {Z}\times \mathbb {Z}/2\) graded object and the symmetrization is with respect to the Koszul sign rules for \(\mathbb {Z}\times \mathbb {Z}/2\) graded objects. \(\square \)
as a \(\mathbb {Z}\times \mathbb {Z}/2\) graded object and the symmetrization is with respect to the Koszul sign rules for \(\mathbb {Z}\times \mathbb {Z}/2\) graded objects. \(\square \)
1.4 A.4 Equivariant quantization
In this subsection, we continue the notation of the previous subsection, letting  act on the free classical theory
act on the free classical theory  . Since \(\left\langle \cdot ,\cdot \right\rangle \) gives a sort of
. Since \(\left\langle \cdot ,\cdot \right\rangle \) gives a sort of  -equivariant symplectic structure on
-equivariant symplectic structure on  , we would hope that it induces a Poisson bracket and Laplacian \(\Delta \) on \( {\text {Obs}}^{cl} \), as can be performed in the finite-dimensional case. If this were the case, we could define \( {\text {Obs}}^{q} \) to be
, we would hope that it induces a Poisson bracket and Laplacian \(\Delta \) on \( {\text {Obs}}^{cl} \), as can be performed in the finite-dimensional case. If this were the case, we could define \( {\text {Obs}}^{q} \) to be  , but with the differential from \( {\text {Obs}}^{cl} \) deformed by the term \(\hbar \Delta \). This is what is considered BV quantization in the finite-dimensional case. However, the Poisson bracket is only defined if one of the arguments is local, and the Laplacian is undefined. This is because the naïve way to define these operations involves pairing distributions with each other, an operation which is ill-defined in general.
, but with the differential from \( {\text {Obs}}^{cl} \) deformed by the term \(\hbar \Delta \). This is what is considered BV quantization in the finite-dimensional case. However, the Poisson bracket is only defined if one of the arguments is local, and the Laplacian is undefined. This is because the naïve way to define these operations involves pairing distributions with each other, an operation which is ill-defined in general.
The solution to this problem is effective field theory, whose essence, as developed in [6] (especially Chapters 2 and 5), is to replace the interaction I with a family I[t], one for each \(t\in \mathbb R_{>0}\), and to correspondingly define a Poisson bracket \(\{\cdot , \cdot \}_t\) and BV Laplacian \(\Delta _t\) for every t (see also [19] and Chapter 12.1 of [17] for physical perspectives on some of these ideas.) We can then define \( {\text {Obs}}^{q} {}[t]\) as a graded vector space to be \( {\text {Obs}}^{cl} {}[\![\hbar ]\!]\), but with putative differential  . However, the putative differential may not square to zero. We will first address the procedure of renormalization, then the question of the existence of the desired differential.
. However, the putative differential may not square to zero. We will first address the procedure of renormalization, then the question of the existence of the desired differential.
1.4.1 A.4.1 Renormalization and the BV formalism
We assume that  has been equipped with a gauge-fixing \(Q^{GF}\); then, \(H:=[Q,Q^{GF}]\) is a generalized Laplacian, and so H has an integral heat kernel \(k_t\). We will actually use a heat kernel more suited to the study of BV theories:
has been equipped with a gauge-fixing \(Q^{GF}\); then, \(H:=[Q,Q^{GF}]\) is a generalized Laplacian, and so H has an integral heat kernel \(k_t\). We will actually use a heat kernel more suited to the study of BV theories:
Definition A.23
(Section 8.3 of Chapter 5 of [6]) Let \(t\in \mathbb R_{>0}\). The scale tBV heat kernel\(K_t\) is the unique degree 1 element of  satisfying
satisfying
for all  . The non-degeneracy property of the pairing \(\left\langle \cdot ,\cdot \right\rangle \), along with the existence of the heat kernel \(k_t\), guarantees that \(K_t\) exists.
. The non-degeneracy property of the pairing \(\left\langle \cdot ,\cdot \right\rangle \), along with the existence of the heat kernel \(k_t\), guarantees that \(K_t\) exists.
Definition A.24
(Section 9.1 of Chapter 5 of [6]) The scale tBV Laplacian \(\Delta _t\) is the operator  , where \(\partial _{K_t}\) is the unique order-2 differential operator on
, where \(\partial _{K_t}\) is the unique order-2 differential operator on  which is 0 on \({{\mathrm{Sym}}}^{<2}\) and which on \({{\mathrm{Sym}}}^2\) is just contraction with \(K_t\).
which is 0 on \({{\mathrm{Sym}}}^{<2}\) and which on \({{\mathrm{Sym}}}^2\) is just contraction with \(K_t\).
Definition A.25
(Section 9.2 of Chapter 5 of [6]) The scale tPoisson bracket \(\{\cdot ,\cdot \}_t\) is the map

given by
In other words, the Poisson bracket measures the failure of the BV Laplacian to be a derivation for the commutative algebra  . Figure 7 gives a schematic depiction of the Poisson bracket and BV Laplacian. Notice that, based on the diagrammatic depiction of \(\Delta _t\), \(\{J,J'\}_t\) is 0 if either J or \(J'\) has a dependence only on
. Figure 7 gives a schematic depiction of the Poisson bracket and BV Laplacian. Notice that, based on the diagrammatic depiction of \(\Delta _t\), \(\{J,J'\}_t\) is 0 if either J or \(J'\) has a dependence only on  and not on
and not on  . The same is true for \(\Delta _t J\). This is because \(K_t\) has components only in
. The same is true for \(\Delta _t J\). This is because \(K_t\) has components only in  as a consequence of the fact that we have not required
as a consequence of the fact that we have not required  to have a gauge-fixing or a pairing \(\left\langle \cdot ,\cdot \right\rangle \). These facts about \(\Delta _t\) and \(\{\cdot ,\cdot \}_t\) simplify our analysis dramatically.
to have a gauge-fixing or a pairing \(\left\langle \cdot ,\cdot \right\rangle \). These facts about \(\Delta _t\) and \(\{\cdot ,\cdot \}_t\) simplify our analysis dramatically.
Schemata of the Poisson bracket and BV Laplacian. a A diagrammatic depiction of a term in the Poisson bracket \(\{J,J'\}\). The Poisson bracket is the graded sum over all ways of contracting out one edge from J with one edge from \(J'\) with \(K_t\). b A diagrammatic depiction of a term in the BV Laplacian. It is a graded sum over all ways of contracting out pairs of edges in J with \(K_t\)
The following lemma is useful for computational reasons. It can be verified by explicit computation.
Lemma A.26
\(\Delta _t\) has the following two properties:
-
1.
\(\Delta _t\) squares to zero.
-
2.
\(\Delta _t\) is a derivation for the Poisson bracket \(\{\cdot ,\cdot \}_t\).
We have addressed two of the three scale-t objects that are needed for our purposes: we just need to explain how I gives rise to the family I[t]. This is by far the most subtle part of renormalization, and we refer the reader to [6] for the full treatment of this subject. We will content ourselves to present the results of the renormalization procedure as applied in the case of  acting on a free theory. To do this, we first need the following few definitions:
acting on a free theory. To do this, we first need the following few definitions:
Definition A.27
(Section 8.3 of Chapter 5 of [6]) Let \(t'>t>0\). The propagator from scale tto \(t'\) is denoted \(P(t,t')\) and is the unique element of  satisfying
satisfying
for  .
.
This tells us that, in particular, \(P(t,t')\) is smooth so long as both t and \(t'\) are positive. In the limit as \(t\rightarrow 0\), \(P(t,t')\) becomes distributional. On occasion, we need to consider P(0, t).
Definition A.28
(Section 13.4 of Chapter 2 of [6]) The RG flow operator from scale tto scale \(t'\) is the following operator on 
where P is the operator whose kernel is \(P(t,t')\). \(\partial _{P}\) is defined analogously to \(\partial _{K_t}\) (see Definition A.24).
Remark A.29
The RG flow operator has a natural interpretation in terms of Feynman diagrams, and we refer the reader to [6] Chapter 2.3 for details. We comment only that we use the word “leg” where [6] uses the word “tail” to describe external edges of Feynman diagrams, i.e., edges that end at a univalent vertex. \(\square \)
As mentioned above, we would like to replace I with a family of interactions \(\{I[t]\}\), one for each \(t>0\); however, we will do so in a way that the I[t] are related by the RG flow equation \(I[t'] = W(P(t,t'),I[t])\). This is the main purpose of the operator \(W(P(t,t'), \cdot )\), but we will have other uses for it in the sequel, e.g., the following
Definition A.30
(Definition 7.5.1 of [13]) The tree-level, scale-tinteraction is the element \(I_{tr}[t]\) of  given by
given by
where I is the interaction in Expression 19.
Remark A.31
The limit exists, though we do not prove it here. See section 5 of Chapter 2 of [6] for details. \(\square \)
Remark A.32
This is called the tree-level interaction because the Feynman diagrams which represent it are all trees. \(\square \)
Since the propagator \(P(t,t')\) connects only  edges, all of the trees contributing to \(I_{tr}\) have only two
edges, all of the trees contributing to \(I_{tr}\) have only two  legs. Thus, \(\Delta _t I_{tr}\) belongs to
legs. Thus, \(\Delta _t I_{tr}\) belongs to  .
.
If the limit as \(t\rightarrow 0\) of \(W(P(t,t'),I)\) (not just the \(\hbar ^0\) part) existed, we would not need renormalization; this is, however, not the case. So, we must take the renormalized limit of the operator W. The precise procedure for doing this in general is spelled out in Chapter 2 of [6], and the result of this procedure in the case at hand is discussed in [13]. We note only that in the case of an action of  on a free theory, this procedure produces a family \(I_{wh}[t]\) of interactions schematized in Fig. 8 (the subscript \(_{wh}\) stands for “wheel,” describing the corresponding Feynman diagrams). We do not need to know much about \(I_{wh}[t]\); it suffices for our purposes to know that it’s an element of
on a free theory, this procedure produces a family \(I_{wh}[t]\) of interactions schematized in Fig. 8 (the subscript \(_{wh}\) stands for “wheel,” describing the corresponding Feynman diagrams). We do not need to know much about \(I_{wh}[t]\); it suffices for our purposes to know that it’s an element of  . With these data in place, we can describe the promised family I[t].
. With these data in place, we can describe the promised family I[t].
Definition A.33
(Lemma 7.5.3 of [13]) The scale-trenormalized interaction for  acting on
acting on  is denoted I[t] and given by
is denoted I[t] and given by
Remark A.34
The renormalized interaction takes this form only in the context of an elliptic dgla (or more generally an elliptic \(L_\infty \)-algebra) deforming a free theory into a family of free theories. If the original theory is interacting, or if the \(L_\infty \)-algebra deforms free theories into interacting ones, the structure of I[t] becomes more complicated and in particular includes contributions at all powers of \(\hbar \). \(\square \)
1.4.2 A.4.2 The quantum master equation and the obstruction
The essence of BV quantization is the introduction of a deformation of the Chevalley–Eilenberg differential on  . Indeed, we would like to define the cochain complex \( {\text {Obs}}^{q} {}[t]\), which is, as a vector space
. Indeed, we would like to define the cochain complex \( {\text {Obs}}^{q} {}[t]\), which is, as a vector space  , but which has as differential
, but which has as differential  . The only issue is that this differential may not square to zero. In fact,
. The only issue is that this differential may not square to zero. In fact,
Lemma A.35
The square of the putative differential  on \( {\text {Obs}}^{q} {}[t]\) satisfies the equation
on \( {\text {Obs}}^{q} {}[t]\) satisfies the equation

Proof
Direct computation, using the fact that \(\Delta _t\) is a derivation for \(\{\cdot ,\cdot \}_t\). \(\square \)
Therefore, \(d_t^2=0\) if and only if

is in the \(\{\cdot , \cdot \}_t\)-center of \( {\text {Obs}}^{q} {}[t],\) or equivalently if O[t] lies in  .
.
We will see below that \(d_t^2\) will always be 0 for an action of  on a free theory. However, we would like to demand something stronger, which we codify in the second part of the following definition.
on a free theory. However, we would like to demand something stronger, which we codify in the second part of the following definition.
Definition A.36
The weak scale tquantum master equation (wQME) is

The strong scale tquantum master equation (sQME) is

Definition A.37
If I[t] satisfies the wQME, then the cochain complex of global equivariant quantum observables is

Multiplication by elements of  in the obvious way naturally endows \( {\text {Obs}}^{q} {}[t]\) with the structure of a
in the obvious way naturally endows \( {\text {Obs}}^{q} {}[t]\) with the structure of a  -module.
-module.
If the generalized Laplacian \([Q,Q^{GF}]\) is formally self-adjoint and positive for some metric on F, then we can also define scale \(\infty \) observables because the operator \(\exp \left( -t[Q,Q^{GF}]\right) \) is bounded and has a \(t\rightarrow \infty \) limit.
Remark A.38
In the language of [7], the wQME is the equation defining an action of  on the quantum field theory of
on the quantum field theory of  , and the sQME is the equation defining an inner action of
, and the sQME is the equation defining an inner action of  on
on  . \(\square \)
. \(\square \)
The following lemma tells us that the sQME interacts as we would like with the RG flow operator. It is Lemma 9.2.2 of Chapter 5 of [6].
Lemma A.39
If I satisfies the scale t sQME, then \(W(P(t',t),I)\) satisfies the scale \(t'\) sQME.
Let us examine the failure of the sQME to be satisfied in a bit more detail. Since I was required to satisfy  , the general machinery of renormalization implies that the \(\hbar ^0\) part of the sQME is satisfied (see, e.g., Lemma 9.4.1. of Chapter 5 of [6]). Thus, we make the following definition:
, the general machinery of renormalization implies that the \(\hbar ^0\) part of the sQME is satisfied (see, e.g., Lemma 9.4.1. of Chapter 5 of [6]). Thus, we make the following definition:
Definition-Lemma A.40
(Cf. Corollary 5.11.1.2 of [6]) The scale tobstruction to the -equivariant quantization of
-equivariant quantization of  is
is

The obstruction is a closed, cohomological degree 1 element of \( {\text {Obs}}^{q} {[t]}\).
The following is Lemma 7.5.4 of [13]. It gives us an explicit formula for the scale t obstruction.
Lemma A.41
For the action of an elliptic dgla on a free theory,

\(\mathfrak {Obstr}[t]\) depends only on  , i.e., is also a closed, ghost number 1 element of
, i.e., is also a closed, ghost number 1 element of  .
.
Proof
Recall that \(I[t] = I_{tr}[t]+\hbar I_{wh}[t]\), where  , so that \(QI_{wh}[t]=\{I_{wh}[t],\cdot \}_t=\Delta _t I_{wh}[t]=0\). Moreover, by the commentary preceding the definition of the obstruction,
, so that \(QI_{wh}[t]=\{I_{wh}[t],\cdot \}_t=\Delta _t I_{wh}[t]=0\). Moreover, by the commentary preceding the definition of the obstruction,  . The first statement of the lemma then follows by direct computation. To see that
. The first statement of the lemma then follows by direct computation. To see that  , recall that \(I_{tr}[t]\) has Sym-degree two with respect to
, recall that \(I_{tr}[t]\) has Sym-degree two with respect to  inputs, so that \(\Delta _tI_{tr}[t]\) has Sym-degree zero with respect to
inputs, so that \(\Delta _tI_{tr}[t]\) has Sym-degree zero with respect to  inputs, so that
inputs, so that  . Moreover, all terms in \(\Delta _tI_{tr}[t]\) and
. Moreover, all terms in \(\Delta _tI_{tr}[t]\) and  have at least linear dependence on
have at least linear dependence on  inputs, so that
inputs, so that  . \(\square \)
. \(\square \)
Remark A.42
This form for the obstruction is particular to families of free theories. \(\square \)
By Lemma A.41, I[t] satisfies the wQME, since  and all elements of
and all elements of  are in the \(\{\cdot , \cdot \}_t\)-center of \( {\text {Obs}}^{q} {}[t]\).
are in the \(\{\cdot , \cdot \}_t\)-center of \( {\text {Obs}}^{q} {}[t]\).
We have also the following lemma, which describes the relationship between the obstructions at various length scales. It is a modification of Lemma 11.1.1 from Chapter 5 of [6] to the case where the obstruction lives only at order \(\hbar \), which we know to be the case by the previous lemma.
Lemma A.43
(Lemma 11.1.1 of Chapter 5 of [6]). Let

be the map defined by
Then, if \(\varepsilon \) is a parameter of cohomological degree \(-1\) and square 0, we have
This lemma gives precise meaning to the idea that the collection \(\{\mathfrak {Obstr}[t]\}\) lies in the tangent space to the classical theory described by \(\{I_{tr}[t]\}\). Moreover, it is discussed in [6] that \(\lim _{t\rightarrow 0}W_{t,t'}(I_{tr}[t])\) exists and is local, so we have the following
Lemma A.44
(Corollary 11.1.2 of Chapter 5 of [6]). The limit
exists and is a closed, degree 1 element of  .
.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rabinovich, E. A mathematical analysis of the axial anomaly. Lett Math Phys 109, 1055–1117 (2019). https://doi.org/10.1007/s11005-018-1142-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11005-018-1142-4
Keywords
- Perturbative anomalies
- Batlin-Vilkovisky formalism
- Cohomological methods in quantum field theory
- Massless free fermion



 , is used to denote its sheaf of sections. Letters in script formatting, except
, is used to denote its sheaf of sections. Letters in script formatting, except  , will always denote sheaves of smooth sections of vector bundles.
, will always denote sheaves of smooth sections of vector bundles. and
and 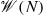 are vector spaces of global sections of vector bundles
are vector spaces of global sections of vector bundles  is the space of global sections of the bundle
is the space of global sections of the bundle  will denote the sheaf of sections of
will denote the sheaf of sections of  is an elliptic dgla, then we will use
is an elliptic dgla, then we will use  to denote the differential on the complex of Chevalley–Eilenberg cochains of
to denote the differential on the complex of Chevalley–Eilenberg cochains of  .
. ,
, 



 , and
, and have fermionic statistics.
have fermionic statistics. , i.e.,
, i.e.,  , i.e., the Jacobi identity is satisfied, and
, i.e., the Jacobi identity is satisfied, and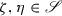 , i.e.,
, i.e., 
 the space of fields of the theory.
the space of fields of the theory. :
: 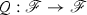 of degree (1,0).
of degree (1,0).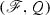 is a (
is a (


