1 Introduction

Sedimentary basins are large-scale systems characterized by significant planar extent where long term subsidence takes place, thus providing the possibility for sediments to be deposited and accumulated across geologic time scales (Allen and Allen 2013). Subsidence processes are associated with a variety of causes that can include, e.g., the thinning of the underlying crust as well as the effects of transport of sediment loadings. When considering a time frame of millions of years, changes of thickness or density of adjacent bodies, uplift movements, as well as space-time dynamics of underwater sea depth (bathymetry) and sea level (eustasy) can also contribute to the formation and evolution of these basins.

The study of sedimentary basins is often referred to as basin modeling or sedimentary basin analysis (Wangen 2010). Stratigraphic interpretation is traditionally grounded on geologic interpretation, where hypotheses on geologic history are qualitatively compared against available field data. In the last three decades, Stratigraphic Forward Models (SFMs) have been developed to assist interpretation of the evolutionary process of sedimentary basins. These are numerical, process-based computational tools that allow simulating sedimentary and tectonic processes that control a depositional architecture (Paola 2000; Burgess et al. 2012). These models are primarily used in petroleum geology for the assessment of the internal make-up of the subsurface, in terms of spatial distribution of facies and their geometrical features (Warrlich et al. 2008). For instance, three-dimensional visualizations reconstructed through modeling procedures allow quantifying the extent and geometry of sedimentary bodies.

SFMs typically include a large number of input parameters related to the physical/geochemical processes of interest and/or to the problem boundary conditions (Granjeon 1997; Blum et al. 2006), such as those describing accommodation, erosion, supply, production, transport, accumulation and compaction of basin sediments (Burgess et al. 2008; Csato et al. 2013). Estimation of these inputs is unavoidably fraught with uncertainty and rests on information regarding the geological history of the system considered. Such information content is typically collected through literature studies or may be inferred by field measurement campaigns. Outputs of SFMs are usually given in terms of a modeled stratigraphy and a set of paleoenvironmental conditions, such as the paleobathymetry associated with the considered geological domain. As these models involve a large number of input parameters, a key limitation is the validation process of the resulting modeled stratigraphy, which is one of the main outputs of SFMs (Falivene et al. 2014). Applications of SFMs are usually based on literature information to constrain model parameter values on a qualitative comparison between final modeling outputs and field data, parameter uncertainty being only considered by trial and error (Gervais et al. 2018). In this context, a significant amount of work and time resources need to be invested to manually calibrate stratigraphic models to somehow match available information. This significantly hampers the use of SFMs in industrial applications and the potential that these tools can offer has been only partially explored in industrially relevant scenarios.

Trial and error approaches often adopted in practice are time intensive and typically result in a single solution, i.e. actually, they correspond to a deterministic calibration. However, the nonlinearity of SFMs, the paucity of data and the ensuing uncertainties imply that the inverse problem should be set in a stochastic context. In this setting a single (deterministic) calibration is not informative of the uncertainties associated with the system behavior and their implications in terms of geological scenarios. A stochastic model calibration strategy is required to evaluate the risk tied to the uncertainty of SFMs (Charvin et al. 2009; Skauvold and Eidsvik 2018).

The impact of embedding uncertainty quantification within direct and inverse modeling of sediment deposition processes across geologic time scales through SFMs is only marginally addressed in the literature (Charvin et al. 2011; Sacchi et al. 2015; Wingate et al. 2016). During this last decade automatic parameter estimation for a SFM is playing a key role in the oil industry and as far as is known, Falivene et al. (2014) provide the only attempt for the Dionisos tool (Granjeon 1997). These authors show promising results regarding the applicability of an automatic model calibration procedure to SFMs. Given the typically large number of input parameters required in SFMs, the effectiveness and efficiency of model calibration may be largely improved by relying on the joint use of Sensitivity Analysis (SA) and reduced order models, as discussed by Gervais et al. (2018) in the context of forward uncertainty quantification for SFMs. Surrogate models may then be used to reduce the computational cost associated with uncertainty propagation of the most relevant inputs to a selected range of outputs (e.g., distribution of sand volumes, Gervais et al. 2018).

This study leverages on the above mentioned works and incorporates modern numerical tools, SA techniques, and stochastic inverse modeling approaches, providing major elements of methodological innovation. Given the large number of parameters required in stratigraphic simulations, the first objective is to diagnose the model behavior prior to model calibration. This enables us to assess the way parametric uncertainty contributes to target modeling goals, such as lithological sediment distribution at selected locations or the vertical thickness of stratigraphic units. Quantification of the degree of influence on each model parameter to the variability of the results of a model requires performing a SA, several techniques being available for this purpose (Saltelli et al. 2006; Borgonovo et al. 2017; Dell’Oca et al. 2017; Gupta and Razavi 2018). SA can also assist to uncertainty quantification, through identification and enhanced understanding of model inputs that cause significant or negligible variability in the output.

Here, the first step is employing a parameter screening procedure based on the evaluation of elementary effects and ensuing global sensitivity indices (see Morris 1991, and Campolongo et al. 2007). These indices are then combined with Principal Component Analysis (PCA) and allow identifying the parameters that are most influential on the behavior of the geological system considered. This screening analysis process is applied here in the context of geological models and is selected because of its simplicity and its reduced computational cost (a similar approach to SA is proposed in Ruffo et al. 2006). The step is propaedeutic to inverse modeling. The latter is performed in a probabilistic context, yielding estimates of the probability distribution of the identified influential model inputs conditional to available data. The goal is then to maximize the information content of data by providing alternative stratigraphic reconstructions, thus being able to evaluate uncertainty. To this end: (i) a reduced complexity (surrogate) model of the full SFM is formulated; and (ii) a stochastic inversion tool grounded on a machine learning approach to search the parameter space for optimal combinations of model parameters is proposed. Here, the surrogate system model is built on the Polynomial Chaos Expansion (PCE) technique (Xiu and Karniadakis 2003; Sudret 2008; Formaggia et al. 2013), while in the stochastic calibration phase a Particle Swarm Optimization (PSO) algorithm (Robinson and Rahmat-Samii 2004; Kennedy 2010) is used. PCE-based surrogate models are computationally efficient tools that have been used in a variety of engineering applications, including basin compaction modeling (Porta et al. 2014; Colombo et al. 2018). In the context of this study, the formulation of a surrogate model is key to obtain a large number of model realizations, which are required for stochastic model calibration through PSO. As far as is known, the application of PCE-based surrogate models and machine learning within stochastic inverse modeling of sedimentary basin formation across geologic time scales has not been explored in previous studies and is proposed here for the first time.

The modeling strategy is assessed through a realistic synthetic scenario. The selected testbed incorporates several sources of uncertainty, stemming from parameters related to clastic sediment supplies through lateral sources, carbonate sediment production within the domain, and transport of these sediments inside the sedimentary system.

2 Methods

2.1 Dionisos Model

Dionisos (DIffusive Oriented Normal and Inverse Simulation Of Sedimentation, Granjeon 1997) is a SFM designed for three-dimensional numerical simulations of sediment deposition processes across geologic time scales. It has been used to model various depositional environments, including deltaic (Burgess et al. 2008) and carbonate (Williams et al. 2011) systems, or complex geodynamic settings such as growth-faulted margins (Alzaga-Ruiz et al. 2009), as well as in the context of rifting/basin inversion processes (Csato et al. 2013).

Characterization of the sedimentary architecture is attained via three main components (Granjeon 1997; Blum et al. 2006): (i) assessment of the space available for sediment accumulation; (ii) quantification of sediment supply inflows and in situ production thereof; and (iii) dynamic redistribution of sediments within the depositional environment.

The temporal evolution of the space available for sediment accumulation chiefly depends on external geological processes (including, e.g., subsidence or uplift due to thermal or tectonic processes and eustatic fluctuations caused by climate phenomena), as well as on processes taking place within the system (such as, e.g., compaction, salt diapirism, and flexural isostatic adjustments). Parameters associated with mathematical representations of such processes constitute inputs to Dionisos and are typically assessed from expert knowledge about the time frame of the sedimentary system development combined with collections of available field data. Dionisos can consider siliciclastic and carbonate sediments (Granjeon 1997; Csato et al. 2013; Hawie et al. 2017). The former can derive from continental erosion and are fed to sedimentary basins through river discharge. Lateral supply is characterized upon specifying the number of sediment sources along the boundary, including their spatial extent, position, sediment supply rate, and type of sediments supplied by each source, as well as the associated fluvial discharge. All of these quantities may vary across the window of geologic ages considered. Production of carbonate sediments is quantified through empirical formulations upon relying on factors such as bathymetry and siliciclastic fluxes (Kolodka et al. 2016) at specific locations (termed production zones). Parameters describing carbonate production can be classified into two groups, i.e., (i) growth rates, which can vary with time and define the largest rate at which each type of carbonate sediments may be formed, and (ii) effectiveness of carbonate growth, to reflect also the influence of depth below sea level.

Sediment transport within the basin is modeled by relying on two key large-scale mechanisms (Csato et al. 2013), i.e., hillslope creeping and fluvial transport. These processes involve differing spatial and temporal scales, fluvial transport being considered to take place within time frames shorter than those associated with hillslope creeping. The transport process (Granjeon 1997; Granjeon et al. 2014) is driven by the diffusion equation coupled with mass conservation

$$\begin{aligned} \frac{\partial {h}}{\partial {t}}=-\frac{\partial {Q}_{sed}}{\partial {x}}, \end{aligned}$$
(1)

where \(Q_{sed}\) [km\(^2\)/ky] and h [km] represent sediment flux and ground elevation with respect to a fixed reference plane, respectively. Transport mechanisms are constrained by a maximum allowed erosion (Granjeon 1997; Csato et al. 2013) to enable a realistic large-scale sedimentary basin evolution.

Discharge \(Q_{sed}\) is evaluated by superimposition of several physical processes. In this study the analysis is limited to hillslope creeping and fluvial transport, i.e., it is considered that \(Q_{sed} = Q_{HS} + Q_{FT}\), where

$$\begin{aligned} Q_{HS}= & {} K_{s} \ S, \end{aligned}$$
(2)
$$\begin{aligned} Q_{FT}= & {} K_{w} \ (Q_{w})^{N_q}(S)^{N_s}. \end{aligned}$$
(3)

Here, \(K_{s}, K_{w}\) are the (constant) slope- and water-driven diffusion coefficients [km\(^2\)/ky], respectively; S is the local gradient of the basin slope; and \(Q_{w}\) is the dimensionless water flux, while \(N_q\) and \(N_s\) are two fixed coefficients. It should be noted that the linear behavior expressed by Eq. (2) can be considered as a reasonable approximation of the actual system behavior for gentle slopes, i.e., \(S < 25^{\circ }\) (Roering et al. 1999), and the model assumes that steeper slopes do not appear. Water-driven transport is governed by fluvial discharge. Fluid flow associated with sediment sources at a given cell in the domain is directed across the simulated system by apportioning water discharge amongst all lower (in terms of elevation) nearby cells according to slope ratios (Csato et al. 2013). Values of diffusion parameters in Eqs. (2)–(3) depend on sediment class, low average grain size corresponding to a high value of the diffusion coefficient. These parameters also depend on the environment where transport takes place, e.g., sediment transport in continental and submarine environments are associated with differing diffusion coefficients.

Seasonal variations of water discharge can also be included in the model (Granjeon and Joseph 1999; Alzaga-Ruiz et al. 2009). Dionisos allows modulating the ratio between high-energy phenomena such as flooding, which is typically associated with short term periods, and long term transport mechanisms, linked to low energy flows.

The mechanism of slope failure (Falivene et al. 2014) is also included in Dionisos, to simulate sediment instability in terms of debris flows or sediment slumps. In this context, deposited sediments start to move downward when the local slope is higher than a predefined critical threshold, whose value depends on sediment class (Alzaga-Ruiz et al. 2009). Critical angles are considered as time-invariant in this study.

2.2 Sensitivity Analysis

Setting up a model within the Dionisos computational framework requires specifying a remarkably high amount of input parameters. As such, the identification of the set of parameters which are most influential on a target model output is a critical element of interest. This study follows the approach proposed by Morris (1991), which is well-suited when the number of uncertain parameters is large and model simulations are highly demanding, in terms of computational cost. The technique relies on the evaluation of a set of local sensitivities, typically termed as Elementary Effects (EEs) (Campolongo et al. 2007) and defined as follows.

Considering \(y(\mathbf{p} _{N})\) (\(\mathbf{p} _{N}=[p_1,p_2,\dots , p_N]\) being a vector whose entries are N model input parameters) as a target output of the model, the Elementary Effect, \(EE_{i}\), of the i-th parameter onto output y is expressed as (Morris 1991)

$$\begin{aligned} EE_i(\mathbf{p} _{N})=\frac{\varDelta y (\mathbf{p} _{N})}{\varDelta }=\frac{y(p_1,p_2,\dots ,p_i+\varDelta ,\dots ,p_N)-y(\mathbf{p} _{N})}{\varDelta }, \end{aligned}$$
(4)

where \(\varDelta \) is a given increment in the parameter space.

A collection of EEs is evaluated for each input parameter by sampling random realizations of \(\mathbf{p} _{N}\) across the parameter space. Here, input parameters are considered to be independent and identically distributed (iid) random variables, each characterized by a uniform probability density function, whose support is assessed based on expert opinion or literature information.

The approach introduced by Morris (1991) requires the design of M trajectories randomly selected in the parameter space, M typically ranging between 10 and 50 which are here selected following Campolongo et al. (2007). The EEs are then evaluated upon running Dionisos for the selected parameter combinations. Then the following three indices (Morris 1991, and Campolongo et al. 2007) are considered

$$\begin{aligned} \mu (p_i,y)= & {} \frac{1}{M} \sum _{k=1}^{M} EE_{i,k}, \end{aligned}$$
(5)
$$\begin{aligned} \sigma (p_i,y)= & {} \sqrt{\frac{1}{M} \sum _{k=1}^{M} (EE_{i,k} - \mu (p_i,y))^2},\end{aligned}$$
(6)
$$\begin{aligned} \mu ^* (p_i,y)= & {} \frac{1}{M}\sum _{k=1}^{M} |EE_{i,k}| . \end{aligned}$$
(7)

These represent the mean, the standard deviation, and the mean of the absolute values of the EEs, respectively. Evaluation of these global sensitivity indices enables us to identify input parameters that have limited influence on given model outputs with modest computational efforts (e.g., Porta et al. 2018). This sets the basis for a subsequent step of the workflow which entails model complexity reduction through the formulation of a surrogate model (Sect. 2.3).

Various sets of indices are obtained depending on the model goal of interest (e.g., spatial distribution of sediments or layer thickness). A synthesis of the information content associated with R model outputs of interest is then obtained through PCA (Lawson and Hanson 1995). Morris indices \(\mu \) are considered to represent an approximation of the entries of the Jacobian matrix in the parameters’ space, which are then rendered by the mean of the derivatives of each of the R model outputs of interest with respect to N model parameters, i.e.

$$\begin{aligned} \mathbf{J} = \begin{bmatrix} \mu (p_1,y_1) &{} \dots &{} \mu (p_N,y_1) \\ \vdots &{} \ddots \\ \mu (p_1,y_R) &{} &{} \mu (p_N,y_R) \end{bmatrix}, \end{aligned}$$
(8)

where matrix \(\mathbf{J} \) has dimensions [\(R \times N\)]. Sensitivity indices are rescaled with respect to the corresponding maximum value for each variable and centered around the column mean, to circumvent issues related to combining several outputs. Note that parameter screening is here performed with a view to a subsequent inverse modeling (or model calibration) step, i.e., the R model outputs considered correspond to a set of available calibration data.

Then PCA is applied to matrix \(\mathbf{J} ^T\mathbf{J} \) through singular value decomposition

$$\begin{aligned} \mathbf{J} ^T\mathbf{J} =\mathbf{VBV} ^T, \end{aligned}$$
(9)

where B is a [\(N \times N\)] diagonal matrix whose entries are the N eigenvalues of \(\mathbf{J} ^T\mathbf{J} \) and the N columns of matrix V are the set of orthonormal eigenvectors of \(\mathbf{J} ^T\mathbf{J} \).

Matrix \(\mathbf{V} \) identifies the so called principal components, \(PC_i\), through a linear combination of the entries of \(\mathbf{J}\). The weight associated with the i-th principal component is expressed in terms of the corresponding eigenvalues (or singular values)

$$\begin{aligned} U(PC_i)=\frac{\lambda (PC_i)}{\sum _{{i}=1}^{N}\lambda (PC_i)}. \end{aligned}$$
(10)

While one could then proceed by replacing the set of model parameters with a selection of the principal components identified at this step, the original parameters are kept for the model calibration step, to preserve a direct link between the prior geologic knowledge and the mathematical formulation leading to model calibration. Thus, the importance of any given parameter \(p_i\) is calculated in terms of its contribution to the sum of the values \(\lambda (PC_i)\). Model parameters are then ranked through the following metric

$$\begin{aligned} Contribution(p_i)=\sum _{j=1}^{N_{PC}}V_{i,j}^2 U(PC_j)=\frac{\sum _{k=1}^{R}\mu ^2(p_i,y_k)}{{\sum _{{j}=1}^{N_{PC}}\lambda (PC_j)}}, \end{aligned}$$
(11)

where \(N_{PC}\) is the number of PCs (which coincides with N), \(V_{i,j}\) is the loading associated with parameter \(p_i\) within principal component \(PC_j\), the sum of all squared loadings being equal to 1. Contribution to all outputs normalized by the sum of eigenvalues yields the influence of each parameter with respect to principal components. This allows ranking parameters through a metric that takes into account their impact on various outputs at once. In this context, the joint use of sensitivity indices and PCA allows identifying a reduced number of parameters that are most influential on the output variables considered.

2.3 Model Reduction

A major issue limiting an effective routine industrial use of SFMs and their application in the context of an inverse modeling workflow is related to the computational cost required for numerical simulations of scenarios of interest. Here, this aspect is circumvented through the formulation of a surrogate model. The latter is intended to mimic selected outputs of Dionisos at a reduced computational effort. The PCE technique (Ghanem and Spanos 2003) is employed, where the surrogate model is expressed through a polynomial approximation formulated in terms of model input parameters. This technique has been adopted in a variety of studies in the earth sciences dealing with the characterization of subsurface systems (see Fajraoui et al. 2011; Zhang and Sahinidis 2012; Porta et al. 2014; Colombo et al. 2018 and references therein).

A limited number \(n_{rdc}\) (with \(n_{rdc}<N\)) of uncertain model parameters is selected via the procedure of Sect. 2.2 in a vector \(\mathbf{p} \) and approximates a given model output, \(y(\mathbf{p} _{N})\), as (Sudret 2008)

$$\begin{aligned} y(\mathbf{p} _{N})\approx y_{PC}(\mathbf{p} )=\sum _{j=1}^{O_P}\alpha _j\varPsi _j(\mathbf{p} ),\ \ \mathbf{p} \sim \mathbf{Unif} . \end{aligned}$$
(12)

Here, \(\varPsi _j\) are orthonormal multivariate Legendre polynomials, \(\mathbf{p} \) is a vector containing \(n_{rdc}\) random variables which are uniformly distributed onto the space \(\mathbf{Unif} \), and the number of polynomial terms \(O_P\) is defined as

$$\begin{aligned} O_P = \left( {\begin{array}{c}n_{rdc}+D\\ D\end{array}}\right) =\frac{\left( n_{rdc}+D\right) !}{n_{rdc}!D!}, \end{aligned}$$
(13)

where D indicates the maximum degree of the polynomial approximation with respect to a single parameter.

Evaluation of the PCE coefficients, \(\alpha _j\), entails solving the complete model to compute \(y(\mathbf{p} _{N})\) for several combinations of the uncertain parameters. Amongst the various strategies that can be used to sample the parameter space, here a sparse grid technique (see, e.g., Beck et al. 2012; Porta et al. 2014) is employed.

For each collocation point in the parameter space, a forward run of Dionisos is performed with the corresponding parameter combination. Coefficients \(\alpha _j\) are then computed through a least square minimization of the truncation error due to the use of a finite number, \(O_P\), of polynomial terms, i.e.

$$\begin{aligned} \hat{\alpha }_j= \arg \min \frac{1}{N_{coll}}\sum _{i=1}^{N_{coll}}\left\{ y(\mathbf{p} _{N})-\sum _{j=1}^{O_P }\alpha _j\varPsi _j(\mathbf{p} _i)\right\} ^2, \end{aligned}$$
(14)

where \(N_{coll}\) is the number of collocation points and the entries of vector \(\mathbf{p} _i\) correspond to the combination of parameters used for the i-th simulation. Consider that function \(\arg \min \) applies to vector \(\pmb {\alpha }\) containing \(\alpha _j\) entries (with \(j=1,\dots ,O_P\)).

Note that an additional advantage of employing a PCE representation is that Sobol global sensitivity indices (Sobol 2001) can be computed with simple algebraic operations from Eq. (12). These indices are variance-based global sensitivity metrics and can be employed to apportion the variance of a target model output amongst the uncertain parameters employed to describe the system behavior (see Gervais et al. 2018 for applications to SFMs).

According to Eq. (13), the number of coefficients to be estimated increases markedly with the number of model parameters and the highest degree set for the PCE. In this study, the construction of the surrogate model is further streamlined by following the approach of Fajraoui et al. (2012). This procedure allows reducing the number of coefficients to be estimated by setting a threshold value, \(v_{thr}\), and solely retaining coefficients associated with a relative contribution larger than \(v_{thr}\) to the normalized output variance.

For each model output considered, the order of the polynomial (and the above mentioned threshold value, when required) is then chosen so that the root mean squared error (RMSE) with respect to a sample of (randomly selected) 100 full model simulations is the lowest.

2.4 Stochastic Inverse Modeling

Data that are typically used to constrain/calibrate stratigraphic models include (i) thickness and sediment distributions along wellbores, and (ii) seismic information (Charvin et al. 2009; Bertoncello et al. 2013; Sacchi et al. 2015). The latter are interpreted to yield a reconstruction of the geometric features of the main layers forming the internal architecture of the subsurface system. A deterministic inverse modeling approach is geared towards finding a unique set of model parameters that minimizes a given objective function (Duan 2017). Here instead a stochastic calibration (or stochastic inverse modeling) is considered to estimate the probability density function of the (unknown) parameters conditioned to a set of available data (Tarantola 2005). Vectors \(\mathbf{y} _k^* = [y^*_{k,1} \ldots y^*_{k,N_k}]\), whose entries are \(N_k\) observations of a given model output k (e.g., sediment thicknesses or sediment fraction at wells) and \(\mathbf{y} _k(\mathbf{p} _j)\), which represents values of the corresponding quantity computed through the full (or surrogate) model at measurement locations for parameter combination \(\mathbf{p }_j\) are considered. This stochastic model calibration approach is grounded on the evaluation of the following objective function, \(OF(\mathbf{p} _j)\)

$$\begin{aligned} OF(\mathbf{p}_j)=\sum _{k=1}^{N_{out}}\frac{\sum _{i=1}^{N_{k}}(\mathbf{y} _{k,i}^*-\mathbf{y} _{k,i}{(\mathbf{p} _j)})^2}{N_k(\max (\mathbf{y} _{k}^*)-\min (\mathbf{y} _{k}^*))^2}, \end{aligned}$$
(15)

where the outer sum is performed across all model output variables, \(N_{out}\). Equation (15) is minimized through a machine learning technique termed PSO (see Eberhart and Kennedy 1995; Kiranyaz et al. 2014). At the initial step of the inversion, i.e., for \(t = t_0\), a number \(N_p\) of points \(\mathbf{p} _j(t_0)\) with \(j = 1, \ldots , N_p\) is randomly sampled from a uniform distribution within the \(n_{rdc}\)-dimensional parameter space together with a random value of the displacement \(\mathbf{v} _j(t_0)\). The latter is drawn from a uniform distribution within the support [0, 1]. Particle displacements are then updated during subsequent evolutionary steps of the algorithm to evaluate new particle locations. The optimal choice for \(N_p\) is problem-dependent, \(N_p\) being typically in the range 20-50 (Rahmat-Samii and Michielssen 1999). Each of the selected points is then displaced across the parameter space according to

$$\begin{aligned} \mathbf{p} _{j}(t+1)= \mathbf{p} _{j}(t) + \mathbf{v} _j(t). \end{aligned}$$
(16)

The objective function of Eq. (15) is evaluated for each parameter combination corresponding to a particle location \(\mathbf{p} _{j}(t+1)\). Due to the computational complexity associated with Dionisos, this step is tackled by relying on the surrogate model of the system constructed as described in Sect. 2.3.

At each step, t, of the calibration two reference locations in the parameter space are evaluated, i.e., \(\mathbf{p} _{best,j}\) and \(\mathbf{g} _{best}\), representing the location of maximum fitness (minimum distance to data) discovered by particle j and the location associated with the maximum fitness ever discovered by all particles, respectively (note that \(\mathbf{p} _{best}\) is evaluated at each step of the inversion for each particle j, while \(\mathbf{g} _{best}\) is the same for the entire particle set). Thus, the best estimate of the parameter set at step t is identified with \(\mathbf{g} _{best}\).

Following Eberhart and Kennedy (1995), displacement is then updated by considering \(v_j(t+1)\) as a linear function of the previous displacement (\(v_j(t)\)), the best position of the swarm (\(\mathbf{g} _{best}\)) and the best position of particle j (\(\mathbf{p} _{best,j}\)). In this analysis convergence of the algorithm (i.e., minimization of Eq. (15)) is attained when a minimum value of the objective function which is set proportional to the variance of measurement errors is reached or after 300 iterations of the PSO algorithm. While the latter criterion does not ensure convergence to a global minimum, such a number of iterations is considered as a good compromise between accuracy and computational cost.

Repeating this procedure for a variety of random initial parameter combinations and measurement errors (i.e., random perturbation of the entries of \(\mathbf{y} _k^*\)) allows exploring the parameter and solution spaces, thus yielding \(N_{calib}\) sets of model parameters satisfying the imposed convergence criterion. These are then analyzed through their empirical frequency distributions. As such, these results correspond to a frequentist analysis of a collection of model parameter estimates.

3 Application of the Workflow to a Showcase Scenario

3.1 Test Case

The robustness of this approach and operational workflow is assessed through a realistic synthetic showcase. The domain considered has a planar (in the xy-plane) extent of \(240\times 240 \ = 57{,}600 \ \mathrm{km}^2\). Its vertical extent (identified through coordinate z) is variable in time and depends on the initial subsidence map. The planar domain is discretized onto a mesh comprised of \(N_x\times N_y = 16\times 16 = 256\) cells of uniform size, a total number of \( N_z=146\) variable-thickness cells being employed to represent the vertical extent of the system (for a global number of \( N_x\times N_y\times N_z = 16 \times 16 \times 146= 37{,}376\) cells). Each computational cell is defined by the position of its centroid within the domain \((x_i,y_j,z_k)\), with \(i=1,2,..,N_x\), \(j=1,2,..,N_y\), \(k=1,2,..,N_z\).

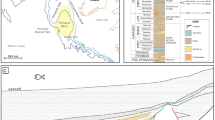
Here 3 lateral sources of sediment supply are considered, each with constant (in time) position and width. Figure 1 depicts a sketch of the planar domain considered and the spatial distribution of the lateral sources and wells. Figure 1 also reports the initial bathymetry map employed and related to 167 Mya. Such a bathymetry is obtained through interpretation of seismic data (following indication of downlap and onlap terminations), together with literature information and regional biostratigraphic studies.

Fig. 1
figure 1

Planar domain, location of the three sources and of the five wells (\(W_i\), \(i=1,..,5\)) and initial bathymetry map at 167 Mya employed in the synthetic scenario

Full size image

Depositional and production processes take place across 4 ages spanning the temporal window, covering the time intervals 167–164, 164–156, 156–120 and 120–94 Mya, respectively. Each variable-thickness cell corresponds to a constant time step equal to 0.5 My. The global depositional time is 73 My, spanning between the initial subsidence map of the model (related to 167 Mya) and the thickness attained at 94 Mya. The set of 94 model parameters are grouped according to three main categories, each corresponding to a given process, i.e., (i) boundary supply, (ii) carbonate production, and (iii) sediment transport. Uncertain model parameters are taken as independent and identically distributed random variables, each being uniformly distributed within the corresponding range of variability. This modeling choice rests on the idea of assigning equal weight to each value of the model parameter distribution. The focus is on the model outputs associated with (i) five volumetric fractions of sediments (i.e., sand, shale, compact carbonate, porous carbonate, and evaporite) and (ii) the thickness of cells (expressed in meters).

Information on the vertical distribution of these model outputs at the current depositional time is supposed to be available at the five observation wells and constitutes the reference data-set upon which stochastic model calibration is grounded. The objective function is built by averaging the above mentioned Dionisos outputs across sets of approximately 15 vertical cells. This yields 10 (vertically averaged) values of sediment fractions along each of the five wellbores. Each of these sub-levels corresponds to a depositional time of approximately 6.5 to 7.5 Ma. A similar concept is applied to quantify the vertical thickness of each of the above mentioned ten sub-levels, calculated as the sum of the thicknesses of about 15 variable-thickness cells.

An additional quantity considered in the model calibration is the total thickness of the system as a result of sediment accumulation between 167 and 94 Mya, corresponding to the total temporal window taken into account in this scenario. This quantity is evaluated at each of the 256 cells composing the planar domain. Table 1 lists these variables and the associated identifier.

Table 1 Target model outputs considered for the exemplary showcase
Full size table

For the purpose of model calibration, a synthetic dataset is obtained from a forward simulation performed with Dionisos upon fixing a randomly selected set of model parameters (hereinafter labeled as parameter reference values). This simulation is considered as the ground truth upon which the inverse modeling strategy implemented is assessed. As calibration data are considered, (i) the total thickness (\(dz_{256}\)) of the domain at each cell in the xy-plane, and (ii) the vertically varying volumetric fractions of sand, shale, porous carbonate and compact carbonate, obtained within each of the 10 sub-levels at the location of well \(W_2\), together with (iii) the thickness of each of these sub-levels.

3.2 Parameter Screening

Sensitivity indices are evaluated through Eqs. (5), (6) and (7) by relying on 1900 forward simulations of Dionisos, which are required to obtain a sample of 20 elementary effects for each of the 94 parameters and model outputs considered.

A first feature stemming from these results is that the sensitivity index \(\mu ^*\) is spatially heterogeneous. Figure 2 depicts examples of the spatial distribution of the values of \(\mu ^*\) associated with two selected model parameters and referred to the total sediment thickness (i.e., \(dz_{256}\) in Table 1) deposited between 167 and 94 Mya. The spatial distribution of the impact of parameter influence can be related to available volume of sedimentation evaluated by combining the strength of the subsidence process and bathymetry maps. Parameter #29 refers to the production of compact carbonate. Optimal conditions for the production of this lithology take place at the right boundary of the area, where bathymetry attains a value of approximately 50 m (Fig. 1) and where the subsidence map allows for carbonate accumulation. Moreover, it can be noted that carbonates in this area are sufficiently far away from siliciclastic sources. All these factors contribute to the dominant influence of parameter #29 on the result on the sedimentary process. Otherwise, parameter #92 (i.e., high energy versus low energy in the sediment transport regime) is related to transport processes. A variation of this parameter can cause significant increase/decrease of sediment thicknesses at relatively large distances from sediment sources, as shown in Fig. 2b.

Figure 3 synthesizes the SA results for \(dz_{256}\). In the figure, parameters along the horizontal axis are grouped by categories; symbols correspond to the average value of the Morris index \(\mu ^*\) evaluated across the set of 256 cells in the xy-plane, the length of the vertical bars being representative of the standard deviation of the associated population of (spatially variable) indices. These results evidence that some parameters (e.g., parameter #29 and #92) are markedly influential on the model output, while most of the parameters display negligible mean and standard deviation values for \(\mu ^*\).

Fig. 2
figure 2

Spatial distributions of the sensitivity index \(\mu ^*\) for parameter (a) #29, (b) #92 and referred to the total sediment thickness, \(dz_{256}\) deposited between 167 and 94 Mya

Full size image
Fig. 3
figure 3

Average values of \(\mu ^*\) (symbols) evaluated across the 256 x-y cells for all uncertain model parameters. Blue, green, and orange symbols correspond to parameters related to boundary supply (from #1 to #24), carbonate production (from #25 to #69), and transport (from #70 to # 94), respectively. Vertical bars represent the standard deviation of \(\mu ^*\) values computed over the whole domain

Full size image

Sensitivity is quantified through the same outputs by considering the sensitivity of sediment fractions and vertical distribution of properties at selected well locations. The relative importance of model parameters to the overall set of model outputs (sampled at selected locations) is quantified through a combination of PCA and the Morris indices evaluated via Eq. (5), as explained in Sect. 2.2. Figure 4 synthetizes the results of the analysis. For each parameter the contribution calculated through Eq. (11) which quantifies the relative impact on expected output variations is reported. Here the 20 parameters displaying the highest contributions are selected, note that the sum of the contributions of these selected parameters amounts to 70% of the sum of all \(\lambda (PC_j)\), as expressed in Eq. (10). This result is considered a good compromise between computational requirements in the stochastic inversion procedure and the degree of system complexity that can be included in the modeling effort.

Fig. 4
figure 4

Contribution of each of the 94 parameters following the analysis illustrated in Sect. 2.2. Blue, green, and orange bars correspond to parameters related to boundary supply (from #1 to #24), sediment production (from #25 to #69), and transport (from #70 to #94), respectively

Full size image

3.3 Surrogate Model

Table 2 lists the 20 parameters that are selected as most influential on model outputs on the basis of the analysis described in Sect. 3.2. These results are the ground for the formulation of the surrogate model (i.e., a model with reduced complexity) which will then be employed in the context of stochastic inverse modeling.

The training data set used to build the PCE surrogate models comprises 11,461 Dionisos runs and the PCE coefficients (see Sect. 2.3) are computed through regression according to Eq. (14) for differing values of the largest order of the ensuing polynomial. These are evaluated (i) at the 5 well locations (\(W_i, \ i = 1, ..., 5\)) and each of the 10 sub-levels where the target volumetric fractions and thickness (i.e., \(V_{ss}\), \(V_{sh}\), \(V_{ca}\), \(V_{cp}\), dz) are sampled, and (ii) at each cell in the horizontal plane, with reference to the total thickness, \(dz_{256}\).

The accuracy of the surrogate model is evaluated by comparison against full model results corresponding to \(N_{control}=100\) randomly selected parameter combinations (drawn for the same prior distributions) that are not used to construct the PCE. Figure 5 provides an appraisal of the quality of the surrogate model by depicting the root mean square error (RMSE)

$$\begin{aligned} RMSE = \sqrt{\frac{\sum _{i=1}^{N_{control}}[y(\mathbf{p} _i)^{DION}-y(\mathbf{p} _i, O_P)^{PCE}]^2}{N_{control}}}, \end{aligned}$$
(17)

where \(y(\mathbf{p} _i, O_P)^{PCE}\) and \(y(\mathbf{p} _i)^{DION}\) are the outputs of interest evaluated with the PCE and with the full Dionisos model, respectively, with combination i of model parameters. Note that \(y(\mathbf{p} _i, O_P)^{PCE}\) depends on the number of terms (i.e., \(O_P\)) included in the polynomial expansion. Here, results obtained by (i) setting the polynomial order to \(D = 1, 2, 3,\) and 4 including all possible combinations between parameters up to order D, and (ii) setting the polynomial order to \(D = 4\) (which includes 10,626 terms) and selecting only those who contribute to the output variance more than a given threshold, \(v_{thr}\), as explained in Sect. 2.3 are compared. As an example of the type of results obtained, the focus is on the fraction of shale and compact carbonate along well \(W_2\) depicted in Fig. 5. Values of the RMSE representing the quality of the PCE approximation are within the order of 0.01–0.025 with regard to sediment composition, while the average error for thickness ranges from 1 to 3 m appoximately. This result is considered as a good compromise between the robustness of the surrogate model and the computational cost that is required for stochastic inverse modeling. Obtaining a lower RMSE value would require increasing the polynomial order. As this would hamper the possibility to complete the stochastic inverse analysis due to a prohibitive computational demand, this avenue is not further pursued.

Fig. 5
figure 5

PCE results at well \(W_2\): RMSE (Eq. (17)) versus number of polynomial terms retained in the expansion for a shale and b compact carbonate. Blue curves correspond to given PCE orders (\(D = 1,..,4\), indicated by blue labels) whereas green curves represent results for the reduced polynomial of order \(D = 4\) with different selected threshold values (\(v_{thr}\), indicated by green labels)

Full size image

3.4 Stochastic Model Calibration

This stochastic model calibration is performed by relying on the constructed surrogate models and a collection of \(N_{calib} = 500\) realizations of perturbed observations. As stated in Sect. 2.4, data collected in the reference system realization are considered to be associated with a zero mean Gaussian error with standard deviation equal to 25 m for thicknesses and 0.05 for volumetric fractions of sediments, to mimic measurement errors. Thus, available data about sediment volumetric fractions and layer thicknesses are characterized by a coefficient of variation (CV) ranging between 0.07 and 5.4 or 0.004 and 0.2, respectively, which are considered as representative values of field settings. Since prior assessments of noisy data are not available, considering a range of CV values allows quantifying the influence of measurement error on output variables and the related uncertainty. Measurement errors are also introduced to consider uncertainty related to age definitions, which are implicitly associated with sediment composition and deposition thickness. The workflow presented is not constrained by these specific values, other measurement error assumptions being fully compatible with the stochastic calibration procedure. This enables us to obtain the empirical multivariate distribution of parameter estimates given the perturbed data. The total computational cost involves running \(\approx \) 4 million realizations of the surrogate model. Note that a single forward simulation of the full Dionisos model requires (on average) between 10 and 20 min, the surrogate model being associated with a computational cost of about 0.5 seconds. This leads to a remarkable saving of computational time (i.e., about 23 days of CPU time instead of 41,667 days = 114 years with an Intel® Core™ i7-6900K CPU@3.20GHz processor) .

Figure 6 depicts a boxplot representation of the marginal distributions associated with the parameter values obtained from the inverse modeling procedure together with lower and upper limits of the support of the prior distributions (red crosses, see Table 2). The parameter reference values (green circles) generally lie within the first and third quartile (and close to the median values) of the corresponding empirical distributions, an exception being noted for parameters #3, #28 and #32, whose corresponding reference values lie at the tails of the distributions. The reduction of uncertainty is quite remarkable for some parameters (e.g. parameters #5, #6, #21, #43 and #93) while being less evident for others. Figure 7 depicts the sample histograms representing the marginal distributions of 4 selected parameters. Note that all parameters are associated with distributions differing markedly from the uniform probability density function assumed a priori, i.e., in the absence of information. For instance, parameter #3 (Fig. 7a) displays a seemingly Gaussian marginal distribution, as a result of assimilating information through model calibration. Other parameters display skewed (e.g., parameter #8, #35) or bimodal (parameter #71) distributions. With reference to the latter feature, it might be an artifact related to random variation of the frequency values.

Fig. 6
figure 6

Boxplot representation of the marginal distributions of parameter values resulting from the inverse modeling procedure. Green circles indicate the reference value, red crosses lower and upper limits of the support of the prior distributions

Full size image

Then, parameter combinations obtained through inverse modeling are employed to simulate 500 Dionisos calibrated models. Figure 8 depicts the vertical distribution of the median values resulting from the \(N_{calib} = 500\) volumetric fractions \(V_{ss}\), \(V_{sh}\), \(V_{ca}\), and \(V_{cp}\) at well \(W_2\) obtained through the inversion procedure (blue solid curves). The corresponding reference values and measurement errors (red circles and horizontal bars) are depicted. Variability of results is illustrated in terms of the range of values comprised between the 5th and 95th percentile of the distribution (yellow shaded area). It is noted that (i) reference values always lie within the shaded area and (ii) the median values of the populations of estimated model outputs are very close to reference values, thus supporting the robustness of the model calibration procedure.

Table 2 Parameters used for the construction of surrogate models: parameter number, short description, units and range of variability considered for PCE approximations
Full size table
Fig. 7
figure 7

Histograms of 4 selected parameters: a #3, b #8, c #35, and d #71. Solid and dashed vertical red lines indicate median, first and third quartile of the distribution, respectively. Green dashed lines represent parameter reference values. Red crosses indicates lower and upper limits of the support of the prior distributions

Full size image
Fig. 8
figure 8

Vertical distributions of median values resulting from \(N_{calib} = 500\) volumetric fractions of a sand, b shale, c compact carbonate and d porous carbonate at well \(W_2\) (blue solid lines), their reference values and measurement errors (red points and horizontal bars). Uncertainty intervals between the 5th and 95th percentile are also shown (yellow shaded areas)

Full size image

3.5 Uncertainty Quantification Based on Stochastic Model Calibration

The probabilistic results obtained in Sect. 3.4 can be employed to yield an assessment of the uncertainty associated with target model outputs at unsampled locations, e.g., at well \(W_3\). This represents a common situation in field scenarios, where, for example, exploration campaigns may be supported by a risk assessment evaluation.

Figure 9 depicts vertical distributions of the median (blue solid curves) values of volumetric fractions of a sand, b shale, c compact carbonate and d porous carbonate obtained at well \(W_3\) by relying on the model parameter combinations obtained in Sect. 3.4, together with reference values and measurement errors (red circles and horizontal bars). As expected, the widths of the intervals associated with values comprised between the 5th and 95th percentile of the distribution are larger than their counterparts evaluated at the locations where (noisy) data are available (see Fig. 8). Hence, these latter results show that (i) propagation of uncertainty from model parameters to outputs can be significantly heterogeneous along the temporal window considered, and (ii) there is the possibility that multiple geological interpretations/settings be (statistically) compatible with the information content available. As such, a strength of this approach is its ability to inform geological interpretation about the likelihood of occurrence of multiple stratigraphic sequences, given an available dataset.

Fig. 9
figure 9

Vertical distributions of the median (blue solid curves) volumetric fractions of a sand, b shale, c compact carbonate and d porous carbonate obtained at well \(W_3\) by relying on the model parameter combinations obtained in Sect. 3.4. Red circles and horizontal bars correspond to reference values and measurement errors. The width of the yellow area corresponds to the range of values comprised between the 5th and 95th percentiles of the distribution

Full size image

4 Conclusions

The key objective of this study is the development of a methodological and operational framework for (i) diagnosis of stratigraphic models through quantification of the relative importance of uncertain model parameters on modeling goals of interest and (ii) stochastic inverse modeling in the context of the assessment of sediment deposition processes across geologic time scales. The focus is on the widely used Stratigraphic Forward Model (SFM) Dionisos (DIffusive Oriented Normal and Inverse Simulation Of Sedimentation, Granjeon 1997) that allows three-dimensional numerical simulations of the accumulation of siliciclastic and carbonate sediments within a given temporal window. This work leads to the following key conclusions.

  1. 1.

    While previous studies of stratigraphic modeling have often been tackled through local SA and qualitative comparisons of model results against available data, this strategy seamlessly integrates elements of local and global SA (Sect. 2.2) and model reduction techniques (Sect. 2.3), which are then used to assist stochastic inverse modeling (Sect. 2.4). This yields probability distributions of uncertain model parameters conditional on available information which can then be used to propagate residual (i.e., after calibration) parameter uncertainty to modeling goals. The ensuing probability distribution of the latter can then be used for uncertainty quantification and associated risk assessment protocols.

  2. 2.

    Starting from a considerable number (in this case 94) of uncertain parameters, the approach leads to the identification of a reduced parameter set (in this case 20 parameters) which explains a given amount (in this case about 70%) of system variability. Thus, this quantitative procedure for parameter screening can be employed to effectively complement qualitative choices based on expert opinion and literature studies to identify the parameters which are most influential to drive stratigraphic modeling results. Probability distributions of these model parameters conditional on available data can then be evaluated through stochastic inverse modeling.

  3. 3.

    It is shown that it is possible to reduce the complexity of the full Dionisos model. This is done by relying on a PCE approach. The latter enables us to formulate a surrogate model, according to which a given output variable is expressed as a polynomial approximation written in terms of the identified reduced set of input parameters. These results show that PCE-based surrogate models are well suited to approximate outputs of stratigraphic models and can be employed to markedly speed up the stochastic inverse modeling step, the general workflow proposed being otherwise fully compatible with other types of surrogate models.

  4. 4.

    Model calibration is performed in a stochastic context by relying on the PCE-based surrogate model and considering noisy data (i.e., sediment fractions and total thickness of the domain) to mimic measurement errors associated with data collected in a realistic synthetic showcase scenario and taken as the ground truth against which this modeling workflow can be assessed. Empirical frequency distributions of model parameters and spatial distributions of output variables conditional on available information are obtained. The results of the workflow (i) are consistent with the calibration data and (ii) can be used to quantify the uncertainty related to sediment distributions at unsampled locations, where data are not available. A key feature of the approach is that the frequency distribution of model parameters allows identifying a collection of possible model responses, fully conditional on a given set of observations. As such, this integrated approach markedly reduces computational efforts and yields a set of stratigraphic configurations which can then enrich the geological characterization of field scenarios at basin scale.