1 Introduction

Nearest neighbor classification (see, e.g., Cover and Hart 1967; Fix and Hodges 1989) is a simple and popular nonparametric method in the machine learning literature. For a fixed value of \(k\), the \(k\) nearest neighbor classifier assigns an unlabeled observation \(\mathbf{z}\) to the class having the maximum number of representatives in the set of \(k\) labeled observations closest to \(\mathbf{z}\). When the training sample size \(n\) (i.e., the number of labeled observations) is large compared to the data dimension \(d\), the \(k\) nearest neighbor classifier usually performs well. For an appropriate choice of \(k\) (which increases with \(n\)), its misclassification probability converges to the Bayes risk as \(n\) grows to infinity (see, e.g., Hall et al. 2008). However, like other nonparametric methods, the classic nearest neighbor (NN) classifier suffers from curse of dimensionality. So, it may yield poor performance for data in high dimensions. Radovanovic et al. (2010) discussed the presence of hubs and the violation of the cluster assumptions for such high-dimensional data. They further studied adverse effects of hubness on supervised, semi-supervised and unsupervised learning based on nearest neighbors.

For high-dimensional data, Francois et al. (2007) showed that pairwise distances between all observations in a class (after appropriate scaling) concentrate around a single value. Hall et al. (2005) also studied the geometry of a data cloud in high dimension, low sample size (HDLSS) situations and proved results related to the concentration of pairwise distances under appropriate conditions. Like Francois et al. (2007), their analysis showed that the observations in each class have a tendency to lie deterministically at the vertices of a regular simplex, and the randomness in the data appears only as a random rotation of that simplex. Further, Hall et al. (2005) used this high-dimensional geometry of the data to analyze the behavior of some popular classifiers including the classic NN classifier.

We now demonstrate adverse effects of concentration of pairwise distances on the performance of the classic NN classifier in high dimensions. Consider a classification problem between two \(d\)-dimensional normal distributions with mean vectors \(\mathbf{0}_d=(0,\ldots ,0)^{T}\) and \({{\varvec{\nu }}}_d=(\nu ,\ldots ,\nu )^{T}\), and dispersion matrices \(\sigma _1^2 \mathbf{I}_d\) and \(\sigma _2^2 \mathbf{I}_d\), respectively. Here, \(\sigma _1^2 \ne \sigma _2^2\), and \(\mathbf{I}_d\) denotes the \(d \times d\) identity matrix. Now, if \(\mathbf{X}=(X_1,\ldots ,X_d)^T\) and \(\mathbf{X}^{'}=(X_1^{'},\ldots ,X_d^{'})^T\) are two independent observations from class-1, \(\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ^2/2\sigma _1^2 \sim \chi ^2_d\), the chi-square distribution with \(d\) degrees of freedom (df). Here, \(\Vert \cdot \Vert \) denotes the usual Euclidean distance. Since \(E(\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ^2/d)=2\sigma _1^2\) and \(Var(\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ^2/d) =8\sigma _1^4/d \rightarrow 0\) as \(d \rightarrow \infty \), we have \(\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ^2/d \mathop {\rightarrow }\limits ^{P} 2\sigma _1^2\) as \(d \rightarrow \infty \). Similarly, if \(\mathbf{Y}\) and \(\mathbf{Y}^{'}\) are two independent observations from class-2, we have \(\Vert \mathbf{Y}-\mathbf{Y}^{'}\Vert ^2/d \mathop {\rightarrow }\limits ^{P} {2}\sigma _2^2 ~\hbox {as}~ d \rightarrow \infty \). Now, if \(\mathbf{X}\) is from class-1 and \(\mathbf{Y}\) is from class-2, \(\Vert \mathbf{X}- \mathbf{Y}\Vert ^2 / (\sigma _1^2+\sigma _2^2) \sim \chi ^2_d(\delta )\), the non-central chi-square distribution with \(d\) df and the non-centrality parameter \(\delta = \nu ^2 / (\sigma _1^2 + \sigma _2^2)\). One can show that \(\Vert \mathbf{X}-\mathbf{Y}\Vert ^2/d \mathop {\rightarrow }\limits ^{P}\sigma _1^2+\sigma _2^2+\nu ^2~\hbox {as}~d \rightarrow \infty \). Suppose that we have two sets of labeled observations \(\mathbf{x}_1,\ldots ,\mathbf{x}_{n_1}\) and \(\mathbf{y}_1,\ldots ,\mathbf{y}_{n_2}\) from class-1 and class-2, respectively. Now, for any future observation \(\mathbf{z}\) from class-1, \(\Vert \mathbf{z}-\mathbf{x}_i\Vert /\sqrt{d} \mathop {\rightarrow }\limits ^{P} \sigma _1 \sqrt{2}\) for all \(1 \le i \le n_1\), while \(\Vert \mathbf{z}-\mathbf{y}_j\Vert /\sqrt{d} \mathop {\rightarrow }\limits ^{P} \sqrt{\sigma _1^2+\sigma _2^2+\nu ^2}\) for all \(1 \le j \le n_2\) as \(d \rightarrow \infty \). So, \(\mathbf{z}\) is correctly classified by the NN classifier if \(\nu ^2>\sigma _1^2-\sigma _2^2\). Similarly, a future observation from class-2 is correctly classified if \(\nu ^2>\sigma _2^2-\sigma _1^2\). Therefore, the classic NN classifier correctly classifies all unlabeled observations if \(\nu ^2 > |\sigma ^2_1-\sigma _2^2|\) (also see Hall et al. (2005, p. 436)). Otherwise, irrespective of the choice of \(k\), it classifies all unlabeled observations to a single class. For instance, if two high-dimensional normal distributions differ only in their scales (i.e., \(\nu ^2=0\) and \(\sigma _1^2 \ne \sigma _2^2\)), the classic NN classifier classifies all observations to the class having smaller spread.

To illustrate this, we considered a classification problem involving \(N_d(\mathbf{0}_d, \mathbf{I}_d)\) and \(N_d(\mathbf{0}_d, 1/4\mathbf{I}_d)\). We generated 10 observations from each class to form the training sample, and they were used to classify 200 unlabeled observations (100 from each class). This procedure was repeated 250 times to compute the average misclassification rate of the NN classifier. Figure 1 shows these misclassification rates and the corresponding Bayes risks for various choices of \(d\). For large values of \(d\), while the Bayes risk was close to zero, the classic NN classifier failed to discriminate between the two classes and classified all unlabeled observations to class-2.

Fig. 1
figure 1

Misclassification rates for \(d=2,5,10,20,50,100,200\) and \(500\)

Full size image

Several attempts have been made in the literature to reduce dimension of the data, and use the NN classifier on the reduced subspace. The simplest method of dimension reduction is by projecting the data along some random directions (see, e.g., Fern and Brodley 2003). Another popular approach is to use projections based on principal component analysis (see, e.g., Deegalla and Bostrom 2006). Other approaches to NN classification for high-dimensional data include Goldberger et al. (2005), Weinberger et al. (2006), Tomasev et al. (2011). Chen and Hall (2009) proposed a robust version of the NN classifier for high-dimensional data, but it is applicable to a specific type of two-class location problem.

In this article, we propose some nonlinear transformations of the data that lead to substantial reduction in dimension for HDLSS data. These transformations are motivated from theoretical results on the high-dimensional geometry of a data cloud. They are based on inter-point distances, and enhance separability among the competing classes in the transformed space. As a result, when the NN classifier is used on the transformed data, it usually yields improved performance. We carry out a theoretical investigation on the misclassification probabilities of these classifiers, and show that concentration of pairwise distances can be used to develop a ‘perfect learning machine’ for HDLSS data.

2 Transformation based on averages of pairwise distances

Consider a two class problem with labeled observations \(\mathbf{x}_1, \ldots ,\mathbf{x}_{n_1}\) from class-1 and \(\mathbf{y}_1,\ldots ,\mathbf{y}_{n_2}\) from class-2. If the component variables in each class are independent and identically distributed (i.i.d.) Gaussian random variables, for any of these \(n=n_1+n_2\) labeled observations, its distances from the observations in each class (after dividing by \(\sqrt{d}\)) converge to a constant. These two constants (one for each class) depend on the class label of the observation. So, if we transform all labeled observations based on average distances, we expect to have two distinct clusters in the transformed two-dimensional space, one for each class. For \(n_1,n_2 \ge 2\), these transformed data points are given as follows

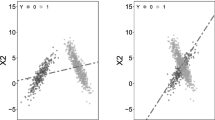
$$\begin{aligned} \mathbf{x}_i^{*}= & {} \left( \displaystyle \frac{1}{{n_1-1}} \displaystyle \sum _{j=1, j\ne i}^{n_1} \frac{\Vert \mathbf{x}_i-\mathbf{x}_j\Vert }{\sqrt{d}}, \frac{1}{n_2} \displaystyle \sum _{j=1}^{n_2} \frac{\Vert \mathbf{x}_i-\mathbf{y}_j\Vert }{\sqrt{d}} \right) ^T \quad \hbox {for} \quad 1\le i \le n_1\hbox { and}\nonumber \\ \mathbf{y}_{j}^{*}= & {} \left( \displaystyle \frac{1}{n_1} \displaystyle \sum _{i=1}^{n_1} \frac{\Vert \mathbf{y}_j-\mathbf{x}_i\Vert }{\sqrt{d}}, \frac{1}{n_2-1} \displaystyle \sum _{i=1, i\ne j}^{n_2} \frac{\Vert \mathbf{y}_j-\mathbf{y}_i\Vert }{\sqrt{d}} \right) ^T \quad \hbox {for} \quad 1 \le j \le n_2. \end{aligned}$$
(1)

Recall the two class classification problem involving the distributions \(N_d(\mathbf{0}_d, \mathbf{I}_d)\) and \(N_d(\mathbf{0}_d, 1/4\mathbf{I}_d)\) discussed in Sect. 1. In this example, for higher values of \(d\), the classic NN classifier could not discriminate between the two classes and led to an average misclassification rate of almost 50 % (see Fig. 1). Figure 2 shows the scatter plots of transformed training sample observations for \(d=50\) and \(500\), where the black dots and the gray dots represent observations from class-1 and class-2, respectively. Clearly, the transformation based on average distances not only reduces the data dimension, but enhances separability between the two classes. This separability becomes more prominent as the dimension increases.

Fig. 2
figure 2

Scatter plots of training data points after transformation based on average distances

Full size image

In a \(J\) class \((J > 2)\) problem, we project an observation to a \(J\)-dimensional space, where the \(i\)-th co-ordinate denotes its average distance from the observations in the \(i\)-th class \((1 \le i \le J)\). Here, we expect to have \(J\) distinct clusters, one for each class (assume that there are at least two labeled observations from each class). So, it is more meaningful to use the NN classifier on the transformed data. The NN classifier, which is used after this TRansformation based on Average Distances (henceforth referred to as NN-TRAD) possesses nice theoretical properties, and we state them in the following sub-sections.

2.1 Distributions with independent component variables

We have observed that if the components of \(\mathbf{X}\) and \(\mathbf{Y}\) are i.i.d. Gaussian variables, then the transformed labeled observations from the two classes converge to two points in \({\mathbb R}^2\) as the dimension increases. While the \(\mathbf{x}_i^{*}\)’s converge in probability to \(\mathbf{a}_1 = (\sigma _1\sqrt{2},\sqrt{\sigma _1^2+\sigma _2^2+\nu ^2})^T\), the \(\mathbf{y}_j^{*}\)’s converge to \(\mathbf{a}_2=(\sqrt{\sigma _1^2+\sigma _2^2+\nu ^2}, \sigma _2\sqrt{2})^T\) in probability. Here \(\sigma _1^2=Var(X_1), \sigma _2^2=Var(Y_1)\) and \(\nu ^2=E(X_1-Y_1)^2\). This result continues to hold if the the components of \(\mathbf{X}\) and \(\mathbf{Y}\) are not necessarily Gaussian, but they are i.i.d. with finite second moments. In such cases, the distance convergence results follow from the weak law of large numbers [WLLN] (see, e.g., Feller 1968). For instance, \({\Vert \mathbf{X}-\mathbf{Y}\Vert ^2}/d = \sum _{q=1}^{d}(X_q -Y_q)^2/d \mathop {\rightarrow }\limits ^{P} E(X_1-Y_1)^2 = (\sigma _1^2+\sigma _2^2+\nu ^2)\) as \(d \rightarrow \infty \). Now, \(\mathbf{a}_1\) and \(\mathbf{a}_2\) are indistinguishable if and only if \(\sigma _1^2=\sigma _2^2 ~\hbox {and}~ \nu ^2=0\). So, for high-dimensional data, unless we have \(\nu ^2=0\) and \(\sigma _{1}^2=\sigma _{2}^2\), the transformed observations \(\mathbf{x}_1^{*},\ldots ,\mathbf{x}_{n_1}^{*}\) and \(\mathbf{y}_1^{*},\ldots ,\mathbf{y}_{n_2}^{*}\) form two distinct clusters.

Using this transformation on an unlabeled observation \(\mathbf{z}\), we get

$$\begin{aligned} \mathbf{z}^{*}=\left( \frac{1}{{n_1}}\sum _{i=1}^{n_1}\frac{\Vert \mathbf{x}_i-\mathbf{z}\Vert }{\sqrt{d}}, \frac{1}{n_2} \sum _{j=1}^{n_2} \frac{\Vert \mathbf{y}_j-\mathbf{z}\Vert }{\sqrt{d}} \right) ^T. \end{aligned}$$
(2)

For any \(\mathbf{z}\) from class-1 (respectively, class-2), \(\Vert \mathbf{z}-\mathbf{x}_i\Vert /\sqrt{d}\) converges to \(\sigma _1\sqrt{2}\) (respectively, \(\sqrt{\sigma _1^2+\sigma _2^2+\nu ^2})\) for \(1 \le i \le n_1\), and \(\Vert \mathbf{z}-\mathbf{y}_j\Vert /\sqrt{d}\) converges to \(\sqrt{\sigma _1^2+\sigma _2^2+\nu ^2}\) (respectively, \(\sigma _2 \sqrt{2})\) for \(1 \le j \le n_2\). So, \(\mathbf{z}^{*}\) converges to \(\mathbf{a}_1\) (respectively, \(\mathbf{a}_2\)) if \(\mathbf{z}\) comes from class-1 (respectively, class-2). Therefore, \(\mathbf{z}\) is correctly classified by the NN-TRAD classifier with probability tending to one as \(d\) grows to infinity.

We can observe this concentration of pairwise distances and hence optimality of the misclassification rate of the NN-TRAD classifier even when the components of \(\mathbf{X}\) and \(\mathbf{Y}\) are independent, but not identically distributed. In such cases, one needs stronger assumptions. For instance, we have the convergence of the pairwise distances if the fourth moments of the component variables are uniformly bounded (see \((A1)\) in Sect. 2.2). In this case, \(\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ^2/d, \Vert \mathbf{Y}-\mathbf{Y}^{'}\Vert ^2/d\) and \(\Vert \mathbf{X}-\mathbf{Y}\Vert ^2/d\) converge in probability to \(2\sigma _1^2, 2\sigma _2^2\) and \((\sigma _1^2+\sigma _2^2+\nu ^2)\), respectively, where \(\sigma _{1}^2, \sigma _2^2\) and \(\nu ^2\) are defined as the limiting values (as \(d \rightarrow \infty \)) of \(\sigma _{1,d}^2 = \sum _{q=1}^{d} Var(X_q)/d, \sigma _{2,d}^2 = \sum _{q=1}^{d} Var(Y_q)/d\) and \(\nu _{12,d}^2= \sum _{q=1}^{d} \{E(X_q)-E(Y_q)\}^2/d\) (also see \((A2)\) in Sect. 2.2), respectively.

2.2 Distributions with dependent component variables

Under appropriate conditions (see \((A1)\) and \((A2)\) stated below), the distance convergence holds for uncorrelated measurement variables as well (follows from Lemma 1 in the “Appendix”). However, Francois et al. (2007) observed that for high-dimensional data with highly correlated or dependent measurement variables, pairwise distances are less concentrated than if all variables are independent. They claimed that the concentration phenomenon depends on the intrinsic dimension of the data, instead of the dimension of the embedding space. So, in order to have distance concentration in high dimensions, one needs high intrinsic dimensionality of the data or weak dependence among the measurement variables. Hall et al. (2005) assume such weak dependence (see \((A3)\) stated below) for investigating the distance concentration property in high dimensions. Motivated from Hall et al. (2005), we consider the following assumptions:

\((A1)\) :

In each of the \(J\) competing classes, fourth moments of the component variables are uniformly bounded.

\((A2)\) :

Let \(\varvec{\mu }_{i,d}\) and \(\varvec{\Sigma }_{i,d}\) be the \(d\)-dimensional mean vector and the \(d \times d\) dispersion matrix for the \(i\)-th class \(( 1\le i \le J)\). There exists constants \(\sigma _i^2>0\) for all \(1 \le i \le J\) and \(\nu _{ij}\) for all \(i \ne j (1 \le i,j \le J)\), such that \((i) d^{-1}trace(\varvec{\Sigma }_{i,d}) \rightarrow \sigma _{i}^2\) and \((ii) d^{-1}\Vert \varvec{\mu }_{i,d}-\varvec{\mu }_{j,d}\Vert ^2 \rightarrow \nu _{ij}^2\), as \(d \rightarrow \infty \).

\((A3)\) :

Let \(\mathbf{U}=(U_1,U_2,\ldots )^T\) and \(\mathbf{V}=(V_1,V_2,\ldots )^T\) be two independent observations either from the same class or from two different classes. Under some permutation of the components variables (which is same in all classes), the \(\rho \)- mixing property holds for the sequence \(\{(U_q-V_q)^2,{q\ge 1}\}\), i.e.,

$$\begin{aligned} sup_{1 \le q < q^{'} \le \infty ,~|q-q^{'}|>r} \left| Corr\left\{ (U_q-V_q)^2,(U_{q^{'}}-V_{q^{'}})^2\right\} \right| \le \rho (r), \end{aligned}$$

where \(\rho (r) \rightarrow 0\) as \(r \rightarrow \infty \).

Note that Jung and Marron (2009) assumed almost similar conditions to prove high-dimensional consistency of estimated principal component directions. Biswas and Ghosh (2014) and Biswas et al. (2014) used similar conditions to derive consistency of their two-sample tests for HDLSS data.

Conditions \((A1)\)–\((A3)\) are quite general. The first two are moment conditions that ensure some ‘regularity’ of the random variables. In classification problems, we usually get more information about class separation as the sample size increases. But, in HDLSS set up, we consider the sample size to be fixed, and under \((A2)\), we expect information about class separation to increase as \(d\) increases (unless \(\sigma _1^2=\sigma _2^2\) and \(\nu ^2=0\)). Assumption \((A3)\) implies a form of weak dependence among the measurement variables so that WLLN holds for the sequence of dependent random variables as well (see Lemma 1 in the “Appendix”). For time series data, this indicates that the lag correlation shrinks to zero as the length of the lag increases. In particular, for data generated from discrete ARMA processes, all these conditions are satisfied. Importantly, stationarity of the time series is not required here. These assumptions also hold for \(m\)-dependent processes and Markov processes over finite state spaces. Recall that if the measurement variables are i.i.d., \((A2)\) and \((A3)\) hold automatically, and instead of \((A1)\), we only need existence of second moments for the weak convergence of pairwise distances.

Under \((A1)\) and \((A3), \bigl |\sum _{q=1}^{d} (U_q-V_q)^2/d - \sum _{q=1}^{d}E(U_q-V_q)^2/d \bigr | \mathop {\rightarrow }\limits ^{P} 0\) as \(d \rightarrow \infty \) (see Lemma 1). Now, depending on the choice of \((\mathbf{U},\mathbf{V})=(\mathbf{X},\mathbf{X}^{'}), (\mathbf{Y},\mathbf{Y}^{'})\) or \((\mathbf{X},\mathbf{Y})\), under \((A2), \sum _{q=1}^{d}E(U_q-V_q)^2/d\) converges to \(2\sigma _1^2, 2\sigma _2^2\) or \((\nu ^2+\sigma _1^2+\sigma _2^2)\), respectively. Hence, we have

$$\begin{aligned}&(i)\Vert \mathbf{X}-\mathbf{X}^{'}\Vert /\sqrt{d} \mathop {\rightarrow }\limits ^{P} \sigma _1\sqrt{2},\,(ii) \Vert \mathbf{Y}-\mathbf{Y}^{'}\Vert /\sqrt{d} \mathop {\rightarrow }\limits ^{P} \sigma _2\sqrt{2}~~\hbox {and}\nonumber \\&\quad (iii)~ \Vert \mathbf{X}-\mathbf{Y}\Vert /\sqrt{d} \mathop {\rightarrow }\limits ^{P} \sqrt{\sigma _1^2+\sigma _2^2+\nu ^2} ~\hbox {as}~~ d \rightarrow \infty . \end{aligned}$$
(3)

So, depending on whether \(\mathbf{z}\) comes from class-1 or class-2, \(\mathbf{z}^{*}\) converges to \(\mathbf{a}_1\) or \(\mathbf{a}_2\) as before. For large values of \(d, \mathbf{z}^{*}\) is expected to lie closer to the cluster formed by the transformed observations from the same class as \(\mathbf{z}\). The same argument can be used for \(J\) class (with \(J > 2\)) problems as well. The following theorem shows the high-dimensional optimality of the misclassification probability for the NN-TRAD classifier.

Theorem 1

Suppose that the \(J\) competing classes satisfy assumptions (A1)–(A3). Also assume that \(\sigma _i^2 \ne \sigma _j^2\) or \(\nu _{ij}^2>0\) for every \(1 \le i < j \le J\). Then the misclassification probability of NN-TRAD classifier converges to \(0\) as \(d \rightarrow \infty \).

The proof of this theorem is given in the “Appendix”. Recall that under \((A1)\)–\((A3)\), the classic NN classifier fails to achieve the optimal misclassification rate when \(\nu _{ij}^2 < |\sigma _i^2-\sigma _j^2|\) for some \(1 \le i < j \le J\), but NN-TRAD works well even in such situations. Instead of \((A1)\)–\((A3)\), Andrews (1988) and de Jong (1995) considered another set of assumptions to derive weak and strong laws of large numbers for mixingales. One may also use those assumptions to prove the distance convergence in high dimensions. Note that Francois et al. (2007) assumed stronger conditions for almost sure convergence of the distances.

3 A new transformation based on inter-point distances

The transformation based on average distances (TRAD) may fail to extract meaningful discriminating features from the data if one or more of the competing populations have some hidden sub-populations (e.g., the class distribution is a mixture of two or more unimodal distributions). In such cases, it may happen that \((A1)\)–\((A3)\) do not hold for the whole class distribution, but they hold for each of the sub-class distributions. Consider an example where each class is an equal mixture of two \(d\)-dimensional (we used \(d=100\)) normal distributions, each having the same dispersion matrix \(\mathbf{I}_d\). For class-1, the location parameters of the two distributions were taken to be \(\mathbf{0}_d\) and \((\mathbf{10}_2^T, \mathbf{0}_{d-2}^{T})^{T}\), while in class-2 they were \((10,\mathbf{0}_{d-1}^{T})^{T}\) and \((0,10,\mathbf{0}_{d-2}^{T})^{T}\). Taking an equal number of observations from these two classes, we generated a training set of size 20 and a test set of size 200. When TRAD was applied to this data, all transformed data points overlapped with each other (see Fig. 3). As a result, NN-TRAD misclassified almost half of the test set observations.

Fig. 3
figure 3

Scatter plots of training (left) and test (right) data points after TRAD

Full size image

In order to overcome this limitation of TRAD and retain the discriminatory information contained in pairwise distances, we propose the following transformation of the training data:

$$\begin{aligned} \mathbf{x}_i^{**}= & {} \left( \frac{\Vert \mathbf{x}_i-\mathbf{x}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{x}_i-\mathbf{x}_{n_1}\Vert }{\sqrt{d}}, \frac{\Vert \mathbf{x}_i-\mathbf{y}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{x}_i-\mathbf{y}_{n_2}\Vert }{\sqrt{d}} \right) ^T~\hbox {and}\nonumber \\ \mathbf{y}_j^{**}= & {} \left( \frac{\Vert \mathbf{y}_j-\mathbf{x}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{y}_j-\mathbf{x}_{n_1}\Vert }{\sqrt{d}}, \frac{\Vert \mathbf{y}_j-\mathbf{y}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{y}_j-\mathbf{y}_{n_2}\Vert }{\sqrt{d}} \right) ^T \end{aligned}$$
(4)

for \(1 \le i \le n_1\) and \(1 \le j \le n_2\). Note that the \(i\)-th component in \(\mathbf{x}_i^{**}\) is \(0\), while the \((n_1+j)\)-th component in \(\mathbf{y}_j^{**}\) is \(0\). For any new observation \(\mathbf{z}\), using this transformation we get

$$\begin{aligned} \mathbf{z}^{**} = \left( \frac{\Vert \mathbf{z}-\mathbf{x}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{z}-\mathbf{x}_{n_1}\Vert }{\sqrt{d}}, \frac{\Vert \mathbf{z}-\mathbf{y}_1\Vert }{\sqrt{d}}, \ldots , \frac{\Vert \mathbf{z}-\mathbf{y}_{n_2}\Vert }{\sqrt{d}} \right) ^T. \end{aligned}$$
(5)

Here, we get a \((n_1+n_2)\)-dimensional projection. In a \(J\) class problem, we consider a \(n\)-dimensional projection, where \(n=n_1+\cdots +n_J\). In the HDLSS setup (where \(d\) is larger than \(n\)), this transformation leads to substantial reduction in data dimension.

The plots in the left panel of Fig. 4 show co-ordinates of the transformed observations. The training and the test set cases from the two classes are indicated using gray and black dots, respectively. In each plot, we can observe two clusters of either black or gray dots along each co-ordinate. This gives us an indication that discriminative information is contained in almost all co-ordinates. It is more transparent from the scatter plots of the 10th and the 11th co-ordinates of the transformed observations shown in the right panel of Fig. 4. When the NN classifier was used after TRansformation based on Inter-Point Distances (henceforth referred to as NN-TRIPD), it correctly classified almost all test set observations.

Good performance of NN-TRIPD for classification among such high-dimensional mixture populations is asserted by Theorem 2(a) under assumption \((A4)\) stated below.

Fig. 4
figure 4

The left panel shows different co-ordinates of the training (top row) and the test (bottom row) data points after TRIPD. The right panel shows the joint structure of the 10-th and the 11-th co-ordinate of the transformed observations

Full size image
\((A4)\) :

Suppose that the distribution of the \(i\)-th \((1 \le i \le J)\) class is a mixture of \(R_i ~(R_i \ge 1)\) many sub-class distributions, where each of these sub-class distributions satisfy \((A1)\)–\((A3)\). If \(\mathbf{X}\) is from the \(s\) -th sub-class of the \(i\)-th class, and \(\mathbf{Y}\) is from the \(t\)- th sub-class of the \(j\)- th class \((1 \le i \ne j \le J, 1 \le s \le R_i, 1 \le t \le R_j) \sum _{q=1}^{d} Var(X_q)/d, \sum _{q=1}^{d} Var(Y_q)/d\) and \(\sum _{q=1}^d \{E(X_q)-E(Y_q)\}^2/d\) converge to \(2\sigma _{i_s}^2, 2\sigma _{j_t}^2\) and \(\nu _{i_sj_t}^2,\) respectively, as \(d \rightarrow \infty \).

If the competing classes satisfy \((A1)\)–\((A3), (A4)\) holds automatically. But, \((A4)\) holds in many other cases including the example involving mixture distributions discussed above, where \((A1)\)–\((A3)\) fail to hold. The following theorem gives an idea about the asymptotic (as \(d \rightarrow \infty \)) behavior of the misclassification probability of the NN-TRIPD classifier under this assumption. Throughout this article, we will assume that there are at least two labeled observations from each of the sub-classes.

Theorem 2(a)

Suppose that the \(J\) competing classes satisfy assumption (A4). Further assume that for every \(i, j, s\) and \(t\) with \(1 \le s \le R_i, 1 \le t \le R_j, 1 \le i \ne j \le J\), we either have \(\nu _{i_sj_t}^2>|\sigma _{i_s}^2-\sigma _{j_t}^2|\) or \(0 < \nu _{i_sj_t}^2 < |\sigma _{i_s}^2-\sigma _{j_t}^2|-8(n_{i_sj_t}-1)\max \{\sigma _{i_s}^2,\sigma _{j_t}^2\}/n_{i_sj_t}^2\), where \(n_{i_sj_t}\) is the total training sample size of these two sub-classes. Then the misclassification probability of NN-TRIPD classifier based on the \(l_2\) norm converges to \(0\) as \(d \rightarrow \infty \).

The proof of the theorem is given in the “Appendix”. Let us now consider the case when \(J=2\) and \(R_1=R_2=1\). Recall that NN-TRAD is optimal here in the sense that it only requires \(\sigma _1^2 \ne \sigma _2^2\) or \(\nu _{12}^2>0\) for the misclassification probability to go to zero. But, NN-TRIPD possess this asymptotic optimality if \(0 < \nu _{12}^2<|\sigma _{1}^2-\sigma _{2}^2|-8(n-1) \max \{\sigma _{1}^2,\sigma _{2}^2\}/n^2 ~\hbox {or}~ \nu _{12}^2 > |\sigma _{1}^2-\sigma _{2}^2|\). For \(n>2\), we have a wide variety of examples (see, e.g., Example-1 in Sect. 5) where \(\nu _{12}^2 < |\sigma _{1}^2-\sigma _{2}^2|-8(n-1) \max \{\sigma _{1}^2,\sigma _{2}^2\}/n^2 < |\sigma _{1}^2-\sigma _{2}^2|\). In such cases, the classic NN classifier fails, but NN-TRIPD works well. NN-TRIPD has better theoretical properties if one uses the \(l_1\) norm or the \(l_p\) norm with fractional \(p (0 < p < 1)\) instead of the usual \(l_2\) norm for NN classification in the transformed space. Like NN-TRAD, such a classifier requires only \(\sigma _1^2 \ne \sigma _2^2\) or \(\nu _{12}^2>0\) to achieve asymptotic optimality. One should note that both versions of NN-TRIPD usually outperform the NN-TRAD classifier if the competing populations are mixtures of several sub-populations.

Theorem 2(b)

Suppose that the \(J\) competing classes satisfy assumption (A4). Further assume that either \(\sigma ^2_{i_s} \ne \sigma _{j_t}^2\) or \(\nu _{i_sj_t}^2>0\) for every \(1 \le s \le R_i, 1 \le t \le R_j\) and \(1 \le i \ne j \le J\). Then, for any \(p \in (0,1]\), the misclassification probability of NN-TRIPD classifier based on the \(l_p\) norm converges to \(0\) as \(d \rightarrow \infty \).

The proof of the theorem is given in the “Appendix”. Aggarwal et al. (2001) carried out an investigation on the performance of the \(l_p\) norms for high-dimensional data with varying choices of \(p\). They observed that the \(l_p\) norm is more relevant for \(p=1\) and \(p=2\) than value of \(p \ge 3\), while fractional values of \(p (0<p<1)\) are quite effective in measuring proximity of data points. The relevance of the Euclidean distance has also been questioned in the past, and fractional norms were introduced to fight the concentration phenomenon (see, e.g., Francois et al. 2007).

4 Some discussions on NN-TRAD and NN-TRIPD

Although TRAD and TRIPD are motivated from theoretical results on concentration of pairwise distances, such transformations are not new in the machine learning literature (see, e.g., Cazzanti et al. 2008 for more details). For transformations based on principal component directions (see, e.g., Deegalla and Bostrom 2006) or multi-dimensional scaling (see, e.g., Young and Hoseholder 1938), one needs to compute pairwise distances among training sample observations. Like these methods, the proposed transformations also embed observations in a lower-dimensional subspace. Embedding of observations in Euclidean and pseudo-Euclidean space was also considered by Goldfarb (1985) and Pekalska et al. (2001).

In similarity based classification (see, e.g., Cazzanti et al. 2008; Chen et al. 2009), an index is defined to measure similarity of an observation with respect to training sample observations, and those similarity measures are used as features to develop a classifier. For instance, a nonlinear support vector machine (SVM) (see, e.g., Vapnik 1998) can be viewed as a similarity based classifier, where a kernel function is used to measure similarity/dissimilarity between two observations. Graepel et al. (1999) and Pekalska et al. (2001) used several standard learning techniques on these similarity based features. A discussion on similarity based classifiers including SVM, kernel Fisher discriminant analysis and those based on entropy can be found in Cazzanti et al. (2008). It has been observed in the literature that NN classifiers on similarity measures usually yield low misclassification rates (see, e.g., Cost and Salzberg 1993; Pekalska et al. 2001). One main goal of this paper is to provide a theoretical foundation for these two similarity based NN classifiers, namely, NN-TRAD and NN-TRIPD in the context of HDLSS data.

We now discuss the computational complexity of our methods. For transformation of \(n\) labeled observations, both NN-TRAD and NN-TRIPD require \(O(n^2d)\) computations to calculate all pairwise distances. For the classic NN classifier, one need not compute these distances unless a cross-validation type method is used to choose a value of \(k\). However, this is an off-line calculation. Given a test case \(\mathbf{z}\), all these methods need \(O(nd)\) computations to calculate \(n\) distances. After the distance computation, the classic NN classifier with a fixed \(k\) requires \(O(n)\) computations to find the \(k\) neighbors of \(\mathbf{z}\) (see Aho et al. 1974). So, classification of \(\mathbf{z}\) requires \(O(nd)\) calculations. NN-TRAD performs NN classification in the transformed \(J\)-dimensional space. So, re-computation of \(n\) distances in that space and finding the \(k\) neighbors require \(O(n)\) calculations. Therefore, its computational complexity for a test case is also \(O(nd)\). In the case of NN-TRIPD, since the transformed space is \(n\)-dimensional, re-computation of distances and finding neighbors require \(O(n^2)\) calculations. We deal with HDLSS data (where \(d \gg n\)) where \(O(nd)\) dominates \(O(n^2)\). In such situations, NN-TRIPD also requires \(O(nd)\) computations to classify \(\mathbf{z}\).

5 Results from the analysis of simulated data sets

We analyzed some high-dimensional simulated data sets to compare the performance of the classic NN, NN-TRAD and NN-TRIPD classifiers. For NN-TRIPD, we used \(l_p\) norms for several choices of \(p\) to compute the distance in the transformed space. The overall performance of NN-TRIPD classifiers for \(p>2\) was inferior compared with \(p=2\). The performance for fractional values of \(p\) was quite similar to \(p=1\). So, we have reported results for \(p=1\) and \(p=2\) only. These two classifiers are referred to as \(\hbox {NN-TRIPD}_1\) and \(\hbox {NN-TRIPD}_2\), respectively. In each example, we generated 10 observations from each of the two classes to form the training sample, while a test set of size 200 (100 from each class) was used. This procedure was repeated 250 times to compute the average test set misclassification rates of different classifiers. Average misclassification rates were computed for a set of increasing values of \(d\) (namely, \(2,5,10,20,50,100,200\) and \(500\)).

Recall that the classic NN classifier needs the value of \(k\) to be specified. Existing theoretical results (see, e.g., Hall et al. 2008) give us an idea about the optimal order of \(k\) when the sample size \(n\) is large. But these results are not applicable to HDLSS data. In such situations (with low sample sizes), Chen and Hall (2009) suggested the use of \(k=1\). Hall et al. (2008) reported the optimal order of \(k\) to be \(n^{4/(d+4)}\), which also tends to \(1\) as \(d\) grows to infinity. In practice, when we deal with a fixed sample size, we often use the cross-validation technique on the training data (see, e.g., Duda et al. 2000; Hastie et al. 2009) to choose the optimum value of \(k\). However, there is high variability in the cross-validation estimate of the misclassification rate, and this method often fails to choose \(k\) appropriately (see, e.g., Hall et al. 2008; Ghosh and Hall 2008). In most of our experiments with simulated and real data sets, cross-validation led to inferior results compared to those obtained using \(k=1\). So, throughout this article, we used \(k=1\) for the classic NN classifier. To keep our comparisons fair, we used the same value of \(k\) for NN-TRAD, and for both versions of NN-TRIPD as well.

Let us begin with the following examples involving some normal distributions, and their mixtures.

figure a

In Examples-1, 2, and 4, assumptions \((A1)\)–\((A3)\) hold for each of the competing classes. In Example-3, all competing classes satisfy \((A4)\) (i.e., \((A1)\)–\((A3)\) hold for each sub-class). Average misclassification rates of different classifiers for varying values of \(d\) are shown in Fig. 5.

Fig. 5
figure 5

Misclassification rates of classic NN, NN-TRAD, \(\hbox {NN-TRIPD}_1\) and \(\hbox {NN-TRIPD}_2\) for different values of \(d\)

Full size image

For the location problem in Example-1, the two competing classes are widely separated, and the Bayes risk is almost zero for any value of \(d\). In this example, we have information about class separability only in the first co-ordinate and accumulate noise as the value of \(d\) increases. Surprisingly, the presence of noise did not have any significant effect on the performance of any of these classifiers (see Fig. 5a). Except for \(d=500\), all the classifiers correctly classified almost all test set observations. But, the picture changed completely for the scale problem in Example-2. Since, all the co-ordinates have discriminatory information, one should expect the misclassification rates of all classifiers to converge to zero as \(d\) increases. However, the misclassification rate of the classic NN classifier dived a bit when we moved from \(d=2\) to \(d=5\), but thereafter it gradually increased with \(d\). In fact, it performed as worse as a random classifier for values of \(d\) greater than \(50\). On the other hand, the misclassification rates of NN-TRAD and both versions of NN-TRIPD decreased steadily as \(d\) increased. For \(d \ge 100\), almost all test set observations were classified correctly. Recall that for large \(d\), the classic NN classifier correctly classifies all unlabeled observations if \(\nu _{12,d}^2 > |\sigma _{1,d}^2 - \sigma _{2,d}^2|\). In Example-1, we have \(\sigma _{1,d}^2=\sigma _{2,d}^{2}=1\) and \(\nu _{12,d}^2 = 100/d\) for all \(d\), and hence \(\nu _{12,d}^2 > |\sigma _{1,d}^2 - \sigma _{2,d}^2|\). So, the classic NN classifier worked well. For high values of \(d\), since the difference was smaller, it misclassified some observations. In Example-2, we have \(|\sigma _{1,d}^2 - \sigma _{2,d}^2|=3/4\) but \(\nu _{12,d}^2\) is \(0\) for all \(d\). So, the classic NN classifier yielded almost 50 % misclassification rate even for moderately high values of \(d\). In both these examples, NN-TRAD had a slight edge over NN-TRIPD as none of the competing classes had any further sub-classes.

In the presence of sub-populations in Example-3, NN-TRAD yielded almost 50 % misclassification rate for all values of \(d\), but NN-TRIPD led to substantial improvement (see Fig. 5c). In fact, it correctly classified almost all the test set observations for any value of \(d\). The classic NN classifier performed perfectly up to \(d=50\), but its misclassification rate increased thereafter. The misclassification rate was 4.05 % for \(d=100\), but it increased sharply to 42.26 % for \(d=200\). To explain this behavior, let us consider the first sub-class in class-1 and the second sub-class in class-2. We have \(\sigma _{1_1,d}^2=1, \sigma _{2_2,d}^{2}=1/4\) and \(\nu _{1_12_2,d}^2 = 100/d\) for all \(d\). Note that \(\nu _{1_12_2,d}^2\) is larger than \(|\sigma _{1_1,d}^2 - \sigma _{2_2,d}^2|\) for \(d \le 100\), but it is smaller than \(|\sigma _{1_1,d}^2 - \sigma _{2_2,d}^2|\) for \(d \ge 200\). The same holds for the second sub-class of class-1 and the first sub-class of class-2. This led to sharp increase in the misclassification rate when we moved from \(d=100\) to \(d=200\). Example-4 shows the superiority of \(\hbox {NN-TRIPD}_1\) over \(\hbox {NN-TRIPD}_2\). Unlike Example-1, the condition given in Theorem 2(a) (with \(R_1=R_2=1\)) fails to hold in this scale problem. NN-TRAD had good performance in this example because of unimodality of the class distributions.

We now consider some examples where the competing classes differ neither in their locations nor in their scales (i.e., \(\sigma _{1,d}^2=\sigma _{2,d}^{2}\) and \(\nu _{12,d}^2 = 0\) for all \(d\)).

figure b

Figure 6 shows the performance of different classifiers for varying choices of \(d\). In Examples-5 and 6, the two competing classes differ in their correlation structure. They have the same scatter matrix but differ in their shapes in Example-7. For Example-5, the classic NN classifier failed to discriminate between the two classes. For higher values of \(d\), it misclassified almost half of the unlabeled observations. Performances of \(\hbox {NN-TRIPD}_1\) and \(\hbox {NN-TRIPD}_2\) were comparable, and both of them had lower misclassification rates than NN-TRAD. In Example-6, NN-TRAD performed very poorly, but the performance of NN-TRIPD was much better. In this example, \(\hbox {NN-TRIPD}_2\) outperformed all its competitors. For \(d=500\), while \(\hbox {NN-TRIPD}_1\) had an average misclassification rate of 36 %, \(\hbox {NN-TRIPD}_2\) yielded an average misclassification rate close to 26 %. However, in Example-7 \(\hbox {NN-TRIPD}_1\) had the best performance closely followed by NN-TRAD. For \(d=500\), the average misclassification rate of \(\hbox {NN-TRIPD}_1\) was almost half of \(\hbox {NN-TRIPD}_2\). We now consider an example from Chen and Hall (2009).

figure c
Fig. 6
figure 6

Misclassification rates of classical NN, NN-TRAD, \(\hbox {NN-TRIPD}_1\) and \(\hbox {NN-TRIPD}_2\) for different values of \(d\)

Full size image

In this example, the robust NN classifier of Chen and Hall (2009) failed to improve upon the performance of the classic NN classifier (see (Chen and Hall (2009), p. 3201)), but NN-TRAD and both versions of NN-TRIPD outperformed the classic NN classifier for large values of \(d\).

From the analysis of these simulated data sets, it is evident that both \(\hbox {NN-TRIPD}_1\) and \(\hbox {NN-TRIPD}_2\) have a clear edge over NN-TRAD for classifying HDLSS data. But, there is no clear winner among the first two. In practice, one needs to decide upon one of these two classifiers. We use the training sample to compute the leave-one-out cross-validation estimates of misclassification rates for both classifiers. The one with the lower misclassification rate is chosen, and it is used to classify all the tests cases. For further data analysis, this classifier will be referred to as the proposed classifier.

6 Comparison with other popular classifiers

We now compare the performance of our proposed classifier with some popular classifiers available in the literature. Here, we consider the examples studied in Sect. 5 for the case \(d=500\). As before, we use training sets and test sets of sizes 20 and 200, respectively, and each experiment is carried out 250 times. Table 1 shows the average test set misclassification rates of the classic NN classifier and our proposed NN classifier along with their corresponding standard errors reported within parentheses. Results are also reported for NN classifiers based on random projection (see, e.g., Fern and Brodley 2003) and principal component analysis [PCA] (see, e.g., Deegalla and Bostrom 2006). These two classifiers will be referred to as NN-RAND and NN-PCA, respectively. Misclassification rates are reported for linear and nonlinear (with radial basis function (RBF) kernel \(K_{\gamma }(\mathbf{x},\mathbf{y}) = \exp \{-\gamma \Vert \mathbf{x}- \mathbf{y}\Vert ^2 \}\)) support vector machines [SVM] (see, e.g., Vapnik 1998) as well. In the case of SVM-RBF, the results are reported for the default value of the regularization parameter \(\gamma =1/d\) as used in http://www.csie.ntu.edu.tw/~cjlin/libsvm/. We also used the value of \(\gamma \) chosen by tenfold cross-validation method, but that did not yield any significant improvement in the performance of the resulting classifier. In fact, in more than half of the cases, \(\gamma =1/d\) led to lower misclassification rates than those obtained using the cross-validated choice of \(\lambda \). In view of high statistical instability of cross-validation estimates, this is expected in HDLSS situations, GLMNET, a method of logistic regression that uses convex combination of lasso and ridge penalties for dimension reduction (see, e.g., Simon et al. 2011), and a boosted version of classification tree known as random forest [RF] (see, e.g., Breiman 2001; Liaw and Wiener 2002) have also been used. For all these methods, we used available R codes with default tuning parameters.

Table 1 Misclassification rates (in %) of different classifiers on simulated data sets for \(d=500\) with the minimum indicated in bold
Full size table

Our proposed classifier had the best overall performance among the classification methods considered here. It yielded the best performance in five out of these eight data sets. In other cases, its misclassification rates were quite close to the minimum. The NN classifiers based on dimension reduction techniques (i.e., NN-RAND and NN-PCA) had substantially higher misclassification rates than the classic NN classifier in Examples-1, 6 and 8. Only in Example-3, they yielded much lower misclassification rates compared to the classic NN classifier. Among other competitors, GLMNET yielded the best misclassification rate in three data sets, but it had very poor performance in five other data. In Examples-1, 3 and 8, we have discriminatory information only in a few components. GLMNET is a classification method developed specifically for this type of sparse data, and hence it performed well in these examples. The linear SVM classifier is expected to perform well when the population distributions differ in their locations. However, in the presence of small training samples, it failed to extract sufficient discriminating information. It yielded high misclassification rates even for the location problem in Example-1. Its nonlinear version, SVM-RBF had better performance. It led to the lowest misclassification rate in Example-2. RF had competitive performance in Example-8, but in all other examples, its performance was not comparable to our method.

6.1 Comparison based on the analysis of benchmark data sets

We further analyzed twenty benchmark data sets for assessment of our proposed method. The first fourteen data sets listed in the UCR Time Series Classification/Clustering Page (http://www.cs.ucr.edu/~eamonn/time_series_data/) are considered. The Madelon data set is from the UCI machine learning repository (http://archive.ics.uci.edu/ml/datasets.html). We also considered the first five data sets listed in the Kent Ridge Bio-medical Data Set Repository (http://levis.tongji.edu.cn/gzali/data/mirror-ketridge.html). All these data sets have specific training and test sets. However, instead of using those single training and test samples, we used random partitioning of the whole data to form 250 training and test sets. The sizes of the training and the test sets in each partition are reported in Table 2. Average misclassification rates of different classifiers were computed over these 250 partitions, and they are reported in Table 3 along with their corresponding standard errors inside parentheses.

The overall performance of the proposed method was fairly competitive. In six out of these twenty data sets, our proposed classifier yielded the lowest misclassification rate. It was either in second or in third position in six other data sets. One should also notice that in twelve out of these twenty data sets, the proposed method outperformed the classic NN classifier. In majority of the cases, it had lower misclassification rates than NN-RAND and NN-PCA as well. Among other classifiers, the overall performance of RF turned out to be very competitive, and it outperformed our proposed classifier in seven out of sixteen data sets. However, the R code for RF was computationally infeasible on four data sets with dimension greater than \(7000\). NN-PCA had similar problems with memory as the data dimension was high. For such high-dimensional data sets, GLMNET and linear SVM had competitive performance. In many of these high-dimensional benchmark data sets, the measurement variables were highly correlated. The intrinsic dimension of the data was low, and the pairwise distances failed to concentrate. As a consequence, although our proposed method had competitive performance, its superiority over other classifiers was not as prominent as it was in the simulated examples.

Table 2 Brief description of benchmark data sets
Full size table
Table 3 Misclassification rates (in %) of different classifiers on benchmark data sets with the minimum indicated in bold
Full size table

7 Kernelized versions of NN-TRAD and NN-TRIPD

Observe that NN-TRAD and NN-TRIPD transform the data based on pairwise distances, and use the NN classifier on the transformed data. Classifiers like nonlinear SVM (see, e.g., Vapnik 1998) also adopt a similar idea. Using a function \(\varPhi : {\mathbb {R}}^{d} \rightarrow {\mathcal {H}}\), it projects multivariate observations to the reproducing kernel Hilbert space \({\mathcal {H}}\), and then constructs a linear classifier on the transformed data. Inner product between any two observations \(\varPhi (\mathbf{x})\) and \(\varPhi (\mathbf{y})\) in \({\mathcal {H}}\) is given by \(\langle \varPhi (\mathbf{x}),\varPhi (\mathbf{y}) \rangle = K_{\gamma }(\mathbf{x},\mathbf{y})\), where \(K_{\gamma }\) is a positive definite (reproducing) kernel, and \(\gamma \) is the associated regularization parameter. Kernel Fisher discriminant analysis (see, e.g., Hofmann et al. 2008) is also based on this idea. The performance of these classifiers depends on the choice of \(K_{\gamma }\) and \(\gamma \). Although RBF kernel is quite popular in the literature, it works well if \(\gamma \) is chosen appropriately. Unlike these methods, NN-TRAD and NN-TRIPD does not involve any tuning parameter.

Now, let us investigate the performance of the classic NN classifier on the transformed data in \({\mathcal {H}}\). Assume the kernel \(K_{\gamma }\) to be isotropic, i.e., \(K_{\gamma }(\mathbf{x},\mathbf{y}) = g(\gamma ^{1/2}\Vert \mathbf{x}-\mathbf{y}\Vert )\), where \(g(t)>0\) for \(t \ne 0\) (see, e.g., Genton 2001). The squared distance between \(\varPhi (\mathbf{x})\) and \(\varPhi (\mathbf{y})\) in \({\mathcal {H}}\) is given by \(\Vert \varPhi (\mathbf{x}) - \varPhi (\mathbf{y})\Vert ^2 = K_{\gamma }(\mathbf{x},\mathbf{x}) + K_{\gamma }(\mathbf{y},\mathbf{y}) - 2K_{\gamma }(\mathbf{x},\mathbf{y})= 2g({0})-2g(\gamma ^{1/2}\Vert \mathbf{x}- \mathbf{y}\Vert )\). Clearly, if \(g\) is monotonically decreasing in \([0, \infty )\) (for the RBF kernel, we have \(g(t)=e^{- t^2}\)), the ordering of pairwise distances in \({\mathcal {H}}\) remains the same. So, the NN classifier in \({\mathcal {H}}\) will inherit the same problems as the classic NN classifier in \({\mathbb {R}}^{d}\).

To understand this better, assume \((A1)\)–\((A3)\) and let \(g\) be continuous with \(g(t) \rightarrow 0\) as \(t \rightarrow \infty \). Suppose \(\mathbf{X}, \mathbf{X}^{'}\) are two independent observations from class-1 and \(\mathbf{Y}, \mathbf{Y}^{'}\) are two independent observations from class-2. If \(\gamma \) remains fixed as \(d\) increases (or, \(\gamma \) decreases slowly such that \(\gamma d \rightarrow \infty \) as \(d \rightarrow \infty \)), then \(g(\gamma ^{1/2}\Vert \mathbf{X}-\mathbf{Y}\Vert )=g((\gamma d)^{1/2}d^{-1/2}\Vert \mathbf{X}-\mathbf{Y}\Vert ) \mathop {\rightarrow }\limits ^{P} 0\) as \(d \rightarrow \infty \). So, separability among the competing classes decreases in high dimensions. Similarly, if \(\gamma d \rightarrow 0\) as \(d \rightarrow \infty , g(\gamma ^{1/2}\Vert \mathbf{X}-\mathbf{X}^{'}\Vert ), g(\gamma ^{1/2}\Vert \mathbf{Y}-\mathbf{Y}^{'}\Vert )\) and \(g(\gamma ^{1/2}\Vert \mathbf{X}-\mathbf{Y}\Vert )\) all converge in probability to \(g(0)\). The kernel transformation becomes non-discriminative in both cases. Therefore, \(\gamma =O(1/d)\) seems to be the optimal choice, and this justifies the use of \(\gamma =1/d\) as a default value in http://www.csie.ntu.edu.tw/~cjlin/libsvm/. Henceforth, we will assume that \(\gamma d \rightarrow a_0\) as \(d \rightarrow \infty \). Using (3), it can now be shown that

$$\begin{aligned}&(i)~ \Vert \varPhi (\mathbf{X})-\varPhi (\mathbf{X}^{'})\Vert ^2 \mathop {\rightarrow }\limits ^{P} 2g(0)-2g\left( \sigma _1\sqrt{2a_0}\right) ,\nonumber \\&(ii)~ \Vert \varPhi (\mathbf{Y})-\varPhi (\mathbf{Y}^{'})\Vert ^2 \mathop {\rightarrow }\limits ^{P} 2g(0)-2g\left( \sigma _2\sqrt{2a_0}\right) \hbox { and}\nonumber \\&(iii)~ \Vert \varPhi (\mathbf{X})-\varPhi (\mathbf{Y})\Vert ^2 \mathop {\rightarrow }\limits ^{P} 2g(0)-2g\left( \sqrt{a_0(\sigma _1^2+\sigma _2^2+\nu _{12}^2)}\right) \end{aligned}$$
(6)

as \(d \rightarrow \infty \). Since \(g\) is monotone, the NN classifier on the transformed observations in \({\mathcal {H}}\) classifies all observations to a single class if \(\nu _{12}^2<|\sigma _1^2-\sigma _2^2|\) (like the classic NN classifier in \({\mathbb {R}}^{d}\)).

The nonlinear SVM classifier constructs a linear classifier in the transformed space \({\mathcal {H}}\). Under \((A1)\)–\((A3)\), Hall et al. (2005, p. 434) showed that in a high-dimensional two class problem, the linear SVM classifier classifies all observations to a single class if \(|\sigma _1^2/n_1-\sigma _2^2/n_2|\) exceeds \(\nu _{12}^2\). Following their argument and replacing \(\sigma _1^2, \sigma _2^2\) and \(\nu _{12}^2\) by \(g(0) - g(\sigma _{1}\sqrt{2a_0}), g(0) - g(\sigma _{2}\sqrt{2a_0})\) and \(g(\sigma _{1}\sqrt{2a_0}) + g(\sigma _{2}\sqrt{2a_0}) - 2g(\sqrt{a_0(\sigma _{1}^2+\sigma _{2}^2+\nu _{12}^2)})\), respectively (compare Eq. (3) from p. 7 and Eq. (6)), one can derive a similar condition when the nonlinear SVM classifier based on RBF classifies all observations to a single class. However, NN-TRAD and NN-TRIPD can work well on the transformed observations, and one can derive results analogous to Theorems 1, 2(a) and 2(b). The results are summarized below.

Theorem 3

Assume that the reproducing kernel of the Hilbert space \({\mathcal {H}}\) is of the form \(K_{\gamma }=g(\gamma ^{1/2}\Vert \mathbf{x}-\mathbf{y}\Vert )\), where \((i)\, g:[0,\infty ) \rightarrow (0,\infty )\) is continuous and monotonically decreasing, and \((ii)\, \gamma d \rightarrow a_0 (>0)\) as \(d \rightarrow \infty \).

  1. (a)

    Under the conditions of Theorem 1, the misclassification probability of the kernelized version of NN-TRAD classifier converges to \(0\) as \(d \rightarrow \infty \).

  2. (b)

    Suppose that the \(J\) competing classes satisfy (A4). Also assume the inequality in Theorem 2(a) with \(\sigma _{i_s}^2, \sigma _{j_t}^2\) and \(\nu _{i_sj_t}^2\) replaced by \(g(0) -g(\sigma _{i_s}\sqrt{2a_0}), g(0) -g(\sigma _{j_t}\sqrt{2a_0})\) and \(g(\sigma _{i_s}\sqrt{2a_0})+g(\sigma _{j_t}\sqrt{2a_0}) -2g(\sqrt{a_0(\sigma _{i_s}^2+\sigma _{j_t}^2+\nu _{i_sj_t}^2)})\), respectively. Then, the misclassification probability of the kernelized version of NN-TRIPD classifier based on the \(l_2\) norm converges to \(0\) as \(d \rightarrow \infty \).

  3. (c)

    Under the conditions of Theorem 2(b), for any \(p \in (0, 1]\), the misclassification probability of the kernelized version of NN-TRIPD classifier based on the \(l_p\) norm converges to \(0\) as \(d \rightarrow \infty \).

We have used kernelized versions of NN-TRAD and NN-TRIPD classifiers on all the simulated and benchmark datasets from Sect. 6. The overall performance of the latter turned out to be better. Tables 4 and 5 present average misclassification rates of the kernelized NN-TRIPD classifier along with their corresponding standard errors. Misclassification rates of the usual NN-TRIPD classifier are also shown alongside to facilitate comparison.

Table 4 Misclassification rates (in %) of usual and kernelized version of proposed classifiers on simulated data sets with the minimum indicated in bold
Full size table
Table 5 Misclassification rates (in %) of usual and kernelized version of proposed classifiers on benchmark data sets with the minimum indicated in bold
Full size table

For the kernelized version, we have used \(\gamma =1/d\) for the first fourteen data sets. In the other six cases, we used \(\gamma =10^{-t}/d\) (i.e., \(a_0=10^{-t}\)), where the non-negative integer \(t\) was chosen based on a small pilot survey. The overall performance of the kernelized version was fairly competitive. In three out of eight simulated data sets, it had lower misclassification rates than the usual version. The usual version had better performance in four out of eight examples. In Example-2, both versions correctly classified all test set observations. The kernelized version performed better than the usual version in twelve out of twenty benchmark data sets as well.

8 Concluding remarks

In this article, we have proposed some nonlinear transformations of the data for nearest neighbor classification in the HDLSS setup. While the classic NN classifier suffers due to distance concentration in high dimensions, these transformations use this property to their advantage and enhance class separability in the transformed space. When the NN classifier is used on the transformed data, the resulting classifiers usually lead to improved performance. Using several simulated and real data sets, we have amply demonstrated this. We have derived asymptotic optimality of the misclassification probabilities for the resulting classifiers in the HDLSS asymptotic regime, where the sample size remains fixed and the dimension of the data grows to infinity. Similar optimality results have been derived for kernelized versions of these classifiers as well. As future work, it would be interesting to study the behavior of these classifiers in situations where the sample size increases simultaneously with the data dimension.

Throughout this article, we have used \(k=1\) for all nearest neighbor classifiers. However, NN-TRAD and NN-TRIPD classifiers with other values of \(k\) had better performance in some data sets. Due to high stochastic variation, the cross-validation method often failed to select those values of \(k\). Other re-sampling techniques could be helpful in such cases. Similarly, other resampling methods can be used to choose between \(p=1\) and \(p=2\) in our proposed classifier. Recall that NN-TRAD often performs poorly in the presence of sub-classes. So, if we can identify these hidden sub-classes using an appropriate clustering algorithm, the performance of NN-TRAD can be improved. Similarity based clustering methods (see, e.g., Ding et al. 2005; Arora et al. 2013) can be used for this purpose. In this article, a theoretical investigation has been carried out on the good properties of the proposed transformations in the case of the nearest neighbor classification. A study for other well-known classifiers remains to be investigated.