Learning policies for battery usage optimization in electric vehicles

Abstract

The high cost, limited capacity, and long recharge time of batteries pose a number of obstacles for the widespread adoption of electric vehicles. Multi-battery systems that combine a standard battery with supercapacitors are currently one of the most promising ways to increase battery lifespan and reduce operating costs. However, their performance crucially depends on how they are designed and operated.

In this paper, we formalize the problem of optimizing real-time energy management of multi-battery systems as a stochastic planning problem, and we propose a novel solution based on a combination of optimization, machine learning and data-mining techniques. We evaluate the performance of our intelligent energy management system on various large datasets of commuter trips crowdsourced in the United States. We show that our policy significantly outperforms the leading algorithms that were previously proposed as part of an open algorithmic challenge. Further, we show how to extend our approach to an incremental learning setting, where the policy is capable of improving and adapting as new data is being collected over time.

1 Introduction

Electric vehicles, partially or fully powered by batteries, are one of the most promising directions towards a more sustainable transportation system. However, the high costs, limited capacities, and long recharge times of batteries pose a number of obstacles for their widespread adoption. Several researchers in the field of Computational Sustainability (Gomes 2009) have addressed aspects of this problem. In particular, there is an active line of research focusing on improving navigation systems with novel routing algorithms, both by taking into account specific features of electric vehicles (Sachenbacher et al. 2011), and by considering new aspects such as real-time information about road conditions and traffic lights (Apple et al. 2011).

In this paper, we focus on a complementary aspect of the problem that is optimizing the energy efficiency of batteries in electric vehicles. There are two main sources of inefficiencies in batteries. The first one is that due to internal resistance, battery energy is partially wasted as heat when it is charged and discharged. The second one is that due to Peukert’s Law, the actual delivered capacity of a battery depends on the rate at which it is discharged. Furthermore, current battery technology imposes rather severe limits on the number of charge/recharge cycles a battery can handle, thus reducing their lifespan and increasing operating costs.

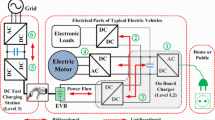
One promising direction towards addressing these issues are multi-battery systems, such as the ones proposed in Dille et al. (2010) and Kötz et al. (2001), which integrate a standard battery with one or more supercapacitors, as depicted in Fig. 1. Intuitively, the idea is that while the battery is good at holding the charge for long times, the supercapacitor is efficient for rapid cycles of charge and discharge. Using the capacitor as an energy buffer, one can significantly increase the battery’s lifespan by reducing its duty. In fact, although supercapacitors have low energy densities, they behave like an ideal battery that can efficiently handle millions of full charge/discharge cycles. The performance of these systems is heavily dependent on how they are managed. In this direction, there has been recent work in the automated planning community on the optimal scheduling of multi-battery systems (Fox et al. 2011; Jongerden et al. 2009). However, previous work assumes full knowledge of an underlying probabilistic model describing the system, which is not available for electric vehicles. Since it would be very difficult to construct such a model using a priori information, in Ermon et al. (2012) we present a data driven approach to the problem. In particular, we leverage a large dataset of commuter trips collected across the United States by Chargecar (CreateLab 2012), a crowdsourcing project open to the public, and we construct an efficient management scheme using a sample-based optimization approach. Specifically, after defining a suitable set of features, we learn an empirical Markov Decision Process (MDP) model from the available data, and we compute a policy that optimizes the average performance. This policy is represented as a large table of state-action pairs, and is only defined for states that were previously observed in the dataset, while we wish to construct a more general management scheme that applies to a wider range of scenarios. We therefore use this policy as a training set, and we use supervised learning techniques to learn a new policy that compactly represents the information available and generalizes to situations previously unseen in the training set. This policy is shown to outperform the leading algorithms that were previously proposed as part of an open algorithmic challenge.

Fig. 1

Architecture of the battery system and sign convention used (a positive number indicates current flowing in the direction of the arrow)

One limitation of this approach (Ermon et al. 2012) is that only considers a batch learning scenario, where the energy management strategy is computed offline, assuming the entire training data is available upfront. The resulting policy is then deployed and used as it is, without the possibility of changing it over time. In this paper, we show how to extend our previous approach (Ermon et al. 2012) so that the resulting policy is capable of improving and adapting as new data is being collected over time. Rather than retraining a new policy from scratch as soon as new data is available, we use an incremental approach that significantly reduces the computational cost. At the same time, we show empirically that the policy learned incrementally achieves a level of performance (in terms of energy savings) comparable with a policy learned in batch on the same training data.

2 Sampling-based optimization

We will formulate the battery management problem as a Markov Decision Process (MDP), a general framework to study probabilistic planning problems. An MDP is a tuple (S,A,P,c) where S is a set of states, A is a set of actions, P is a set of transition probabilities and $c:S \times A \times S \mapsto\mathbb{R}$ is an (immediate) cost function. If an agent executes an action a∈A while in a state s∈S, then it incurs in an immediate cost c(s,a,s′) and it transitions to a new state s′∈S with probability P(s′|s,a). We denote by $\mathcal{A}(s) \subseteq A$ the set of actions available while the agent is in state s. Further, there exists a finite set of goal states G⊆S, where the agent stops to execute actions, and no longer incurs in any cost.

In this paper, we consider a class of factored MDPs where S=X×Y so that any state s∈S has two components s=(x,y) with x∈X and y∈Y. We assume the dynamics of the two components are independent, i.e. the transition probabilities can be factored as follows

$$P\bigl(\bigl(x',y'\bigr)|(x,y), a\bigr) = P_x\bigl(x'|x\bigr) P_y \bigl(y'|y,a\bigr). $$

Notice that x′ does not depend on the action a, which only affects the component y′. The two components of the state are however coupled by the immediate cost function c((x,y),a,(x′,y′)), which can depend on both x and y. We assume that P _y (⋅) and the immediate cost function c(⋅) are known but P _x (⋅) is unknown. However, we are given a set of K i.i.d. sample trajectories $\mathcal{T}_{1}, \ldots, \mathcal{T}_{K}$ of the x component of the state space, where

$$\mathcal{T}_i = \bigl(x_0^i, x_1^i, \ldots, x_{T_i-1}^i\bigr) $$

is sampled according to P _x (x′|x) and $x_{T_{i}-1}^{i} \in G_{x}$ is a goal state. For example, in our battery management application, each trajectory corresponds to one commuter trip, x corresponds to the state of the vehicle, y to the state of the batteries and actions a to the energy allocation to meet the power demand from the motor. Given this information, our objective is to find an admissible policy that minimizes the expected cost for this partially unknown MDP.

Given x,x′∈X, let f(x,x′) be the empirical transition probability from x to x′ according to the available samples (the number of times x′ appears immediately after x over the number of times x appears). We can define DP equations based on the sampled transition probabilities as follows

$$V(x,y) = \min_{a \in\mathcal{A}(x,y)} \biggl( \sum_{x' \in X} \sum_{y' \in Y} f\bigl(x,x'\bigr) P_y\bigl(y'|y,a\bigr) \bigl(c\bigl((x,y),a, \bigl(x',y'\bigr)\bigr) + V\bigl(x',y' \bigr) \bigr) \biggr) $$

for all observed states $x \in\bigcup\mathcal{T}_{i}$. Solving the DP equations, we can compute the “optimal posterior action” a ^∗(s)=a ^∗(x,y) for all $x \in\mathcal{T}_{i}$ and for all y∈Y, that is the action minimizing the total expected cost according to our maximum-likelihood estimate of the underlying MDP model. Notice that the “optimal posterior action” a ^∗(s) converges to the true optimal action for the MDP as K→∞ because f(x,x′)→P _x (x′|x) (assuming the initial states $x_{0}^{i}$ are uniformly sampled).

Although the number of distinct states $x \in\bigcup\mathcal{T}_{i} \subseteq X$ can be very large, the samples $\mathcal{T}_{1}, \ldots, \mathcal{T}_{K}$ do not necessarily cover the entire state space X. We therefore wish to obtain a compact representation of the policy a ^∗(⋅), that hopefully will be able to generalize to states x∈X such that $x \notin\bigcup\mathcal{T}_{i}$, i.e. states previously unseen in the set of available samples. We therefore generate a labeled training set of state-action pairs

$$\bigcup_i \bigl\{\bigl((x,y),a^\ast(s) \bigr), x \in\mathcal{T}_i, y \in Y\bigr\} $$

and we use supervised learning to learn a policy π:S→A. Notice that the particular structure of the problem, with independent dynamics and partially known transition probabilities, allows us to artificially generate |Y| times more training examples than what we originally started with. This aspect leads to significant improvements in our battery management application problem.

2.1 Related work

Sampling-based solutions, where a finite number of sampled trajectories is used to optimize performance, are a popular technique in the fields of approximate dynamic programming (Powell 2007) and reinforcement learning (Sutton and Barto 1998), especially for complicated systems for which a model is not known or only available through simulation. However, unlike Reinforcement Learning we are dealing with a non-interactive learning scenario, where we cannot choose how to interact with the system while samples are collected. Specifically, the learning process occurs offline and in batch. Further, since we have partial knowledge about the MDP (e.g., the immediate cost function), we use a model-based method (Kaelbling et al. 1996) similar to the certainty equivalence method (Kumar and Varaiya 1986) where we estimate the most likely transition probabilities for the unknown part of the model. Unlike the dominant approach that uses function approximations to represent the value function (or Q-values) (Bertsekas and Tsitsiklis 1996; Tsitsiklis and Van Roy 1997; Gordon 1995) and selects the action based on the greedy policy with respect to the estimated values, we directly represent a policy mapping states to actions. Specifically, we use supervised learning to train a policy using a dataset of “posterior optimal” actions computed according to the learned MDP model. The policy compactly represents the available information and, in our application, empirically performs better than models fitted to the Q-values. Further, in this way we can directly analyze the structure of policy being used, thus simplifying the deployment on a vehicle.

Our approach is similar to a line of research in the planning community (Fox et al. 2011; Khardon 1999a, 1999b; Yoon et al. 2007), where researchers have tried to learn strategies to solve planning problems in a fixed domain by learning from particular solutions to training problems sampled from the same domain. Specifically, our work is most closely related to Fox et al. (2011), where they use a sample-based approach to learn a policy for a multiple-battery system modeled as an MDP. However, since we are dealing with electric vehicles we need to optimize charge/discharge cycles while they focus on the discharge aspect only. Consequently, we use a quadratic objecting function, while they optimize for the plan length. Further, their work is based on synthetic data generated from a known model, while we face the problem of learning a probabilistic model from real-world crowdsourced data, which creates additional challenges such as feature selection. Furthermore, in Fox et al. (2011) they use as training examples sequences of state-action pairs where the actions are obtained optimizing in hindsight for a single sample realization of the randomness, i.e. the training set is generated using an optimal omniscient policy that knows the future ahead of time. Although the method is shown to perform well in practice, it doesn’t provide any theoretical guarantee. As a counterexample, consider a simple MDP modeling a lottery with an expected negative return, where the actions are either bet on a number or not to play at all. Given any realization of the randomness, the optimal omniscient policy would always suggest to bet (since it knows the future), but the optimal risk-neutral strategy is not to play the lottery, and therefore it cannot be learned from such training examples. In contrast, we also use a form of hindsight optimization, but we jointly consider all the samples, using a sample-based approximation for the expectation that provably converges to the true optimal value as the number of samples grows.

In the remainder of the paper, we will describe how we apply this general approach to the battery management application.

3 Problem description

There are two main sources of inefficiencies in batteries. The first one is that batteries have an internal resistance R _int , and therefore they dissipate power as heat as R _int i ² when charged or discharged with a current i. Secondly, the capacity of a battery is related to the rate at which it is discharged by Peukert’s Law. In particular, the faster a battery is discharged with respect to the nominal rate (by pulling out a higher current), the smaller the actual delivered capacity is. The effect depends on the chemical properties of the battery and is exponential in the size of the current. Therefore, substantial savings can be obtained by reducing the current output from the battery used to achieve a certain desired power. Although in the remainder we will mainly focus on the internal resistance part (by reducing the squared current i ²), by keeping the battery output more stable we will also indirectly reduce energy waste due to Peukert’s Law.

One promising direction towards improving battery efficiency are multiple-battery systems such as the ones proposed in Dille et al. (2010) and Kötz et al. (2001), which integrate a standard battery with one or more supercapacitors, as depicted in Fig. 1. Intuitively, the idea is that the battery is good at holding the charge for long times, while the supercapacitor is efficient for rapid cycles of charge and discharge. Using the supercapacitor as a buffer, high peaks in the battery’s charge and discharge currents can be reduced, thus reducing the losses due to Peukert’s Law and the internal resistance. In fact, supercapacitors are not affected by Peukert’s Law and behave like an ideal battery. Furthermore, this can substantially increase the lifespan of batteries because of the reduced number of full charge-discharge cycles the battery must handle (supercapacitors on the other hand can handle millions of full charge/discharge cycles). Improvements in battery efficiency lead to reduced costs, increased range, and therefore more practical electric vehicles.

While the savings obtained with multi-battery systems can be substantial, they heavily depend on how the system is managed, i.e. on the strategy used to charge and discharge the capacitor. Managing such systems is non-trivial because there is a mix of vehicle acceleration and regenerative braking (when power can be stored in the battery system) over time, and there is a constraint on the maximal charge the capacitor can hold. For instance, keeping the capacitor close to full capacity would allow the system to be ready for sudden accelerations, but it might not be optimal because there might not be enough space left to hold regenerative braking energy. Intelligent management algorithms therefore need to analyze driving behavior and vehicle conditions (speed, acceleration, road conditions, …) in order to make informed decisions on how to allocate the power demand. Intuitively, the system needs to be able to predict future high-current events, preparing the supercapacitor to handle them and thus reducing the energy losses on the battery. The results can be quite impressive. In Fig. 2 we show the battery output over a 2 minutes window of a real world trip, when no capacitor is used, when it is managed with a naive buffer policy (charging the capacitor only from regenerative braking, and utilizing the capacitor whenever there is demand and energy available), and when it is managed by our novel system DPDecTree. While the total power output is the same in all 3 cases, when the system is managed by DPDecTree the output tends to be more constant over time, thus reducing the energy wasted due to battery inefficiencies (leading to an estimated 10 % increased range for a typical vehicle, compared to about 5 % with simple buffer policy).

Fig. 2

Battery power output over time. A smoother more constant-like curve means reduced losses due to battery inefficiencies

4 Modeling

To formalize the battery management problem described earlier, we consider a discrete time problem where decisions need to be taken every δ _t seconds. A decision is a choice for the variables (i _bc ,i _bm ,i _cm ) in Fig. 1, where i _bc is the current flowing from the battery to the capacitor, i _bm and i _cm are the currents from the battery and capacitor to the motor, respectively. These variables must satisfy certain constraints, namely the capacitor cannot be overcharged or overdrawn and the energy balance must be preserved. As a performance metric, we consider the i ²-score proposed in Dille et al. (2010) and used in the Chargecar contest (CreateLab 2012), where the objective is to minimize the sum of the squared battery output current (i _bc +i _bm )² over time. Intuitively, reducing the i ²-score means reducing the energy wasted as heat and due to Peukert’s Law, as well as increasing battery lifespan (Peterson et al. 2010).

We first consider a simplified setting where we assume to know the future energy demand of the motor (positive when energy is required for accelerations, negative when energy is recovered from regenerative braking) ahead of time. This translates into a deterministic planning problem because we assume there is no more randomness involved. By computing the optimal sequence of actions (since the problem is deterministic, we don’t need a policy), we obtain a lower bound on the i ²-score that is achievable in real-world problems where the future demand is not known.

4.1 A quadratic programming formulation

Consider a single trip, where T is the number of discrete time steps (of size δ _t ) in the control horizon. Let C _max be the maximum charge the capacitor can hold. As previously noted in Wong (2011), the problem can be formalized as a Quadratic Program. Specifically, we wish to minimize

$$\min\sum_{t=0}^{T-1} \bigl(i_{bc}(t)+i_{bm}(t) \bigr)^2 $$

subject to

(1)

(2)

where d(t) is the motor demand at time step t. The first set of constraints (1) requires that the demand d(t) is met at every time step t=0,…,T−1. The second set of constraints (2) ensures that the capacitor is never overcharged or overdrawn (the capacitor is assumed to be empty at the beginning of the trip, and not to lose charge over time). Notice that the battery charge level over time is completely determined by the decision variables, and does not affect the i ²-score.

4.1.1 Reducing the dimensionality

We introduce a new set of variables

$$\Delta(t) = i_{bc}(t)-i_{cm}(t),\quad t=0, \ldots, T-1 $$

and using (1) we can rewrite the objective function as

Further, the constraints (2) can be rewritten in terms of Δ(t) as

$$ 0 \leq\sum_{k=0}^t{\Delta(k)} \leq C_{max}/\delta_t,\quad \forall t=0, \ldots, T-1 $$

(3)

In this way we have simplified the problem from 3T variables {(i _bc (t),i _bm (t),i _cm (t)),t=0,…,T−1} to T variables {Δ(t),t=0,…,T−1}.

The resulting Quadratic Programs can be solved to optimality using standard convex optimization packages, but long trips can take a significant amount of time (see comparison below). Since we will later consider the stochastic version of the planning problem, we consider an alternative approximate solution technique that takes into account the sequential nature of the problem and generalizes to the stochastic setting.

4.2 A dynamic programming solution

A faster but approximate solution can be obtained via Dynamic Programming by discretizing the capacity levels of the supercapacitor with a step δ _C and then recursively solving the Bellman equation

$$J(t,C) = \min_{ 0 \leq C' < N} \bigl\{ \bigl(d(t)+\delta_C \bigl(C'-C\bigr)/\delta_t \bigr)^2+J \bigl(t+1,C'\bigr) \bigr\} $$

for t=0,…,T−1, with boundary condition

$$J(T,C) = 0 \quad \forall C $$

Note the term δ _C (C′−C)/δ _t corresponds to the current Δ required for changing the capacity level from C to C′. If the maximum capacity C _max is discretized with N steps, the complexity is O(N ² T) for a trip of length T. This method is faster than solving the previous Quadratic Program directly, even though the solution is suboptimal because of the discretization. Furthermore, the DP solution does not just provide a sequence of “optimal” actions, but an actual policy that gives the action as a function of the current capacity level (for a fixed load profile).

4.2.1 Choosing the discretization step

There is a tradeoff involved in the choice of the discretization step δ _C of the capacity level. The smaller δ _C is, the better is our approximation to the original QP, but the running time also grows quadratically with 1/δ _C .

In order to choose the proper value of δ _C , we solved a representative subset of 54 trips (see below for the dataset description) using the QP solver in the package CVXOPT (Dahl et al. 2006). We obtained a total i ²-score of 3.070⋅10⁸ in about 11 minutes. Using our DP solver with N=90 steps, we obtained a score of 3.103⋅10⁸ in 15 seconds; with N=45 steps we obtained 3.197⋅10⁸ in about 3 seconds. This experiment empirically shows that our DP based solver is about 2 orders of magnitude faster than solving the quadratic program directly, and provides solutions that are close to optimal. These experiments will guide the choice of the discretization step also for the original stochastic setting where the demand is not known ahead of time.

4.2.2 Robustness

Since we will later use supervised learning techniques to learn a policy from a training set, we are interested in measuring how robust is the policy to implementation errors on the actions. The sensitivity plot in Fig. 3 is obtained by artificially adding i.i.d. Gaussian noise with variance σ ² to the optimal action given by the optimal omniscient policy. The plot is averaged over a subset of trips and shows that the performance degrades smoothly as a function of the variance of the implementation error.

Fig. 3

Performance with noise in the implementation of the optimal policy. On the y-axis is the percentage reduction in the i ²-score with respect to baseline (no capacitor)

4.2.3 Rolling horizon

In order to compute the optimal omniscient policy, we need to know the entire future demand {d(t),t=0,…,T−1} ahead of time. Relaxing this assumption, we now assume to know the future demand only for a window of M steps. We then use a rolling horizon policy, where at every step t we replan computing the optimal sequence of actions for the next M steps, taking the first one. In Fig. 4 we show how the performance improves as the length of the rolling horizon window M increases. In particular, notice that if we were able to predict (exactly) the future demand for the next 30 steps (corresponding to 30 seconds), on average we would lose less than 5 % over the optimal omniscent policy (that knows the entire future demand ahead of time). This experiment suggests than even a fairly limited probabilistic model that can predict the future demand for a few seconds could provide substantial energy savings, and motivates our search for an MDP model.

Fig. 4

Performance improvement as the length of the rolling horizon window increases

5 Probabilistic planning

5.1 An MDP model

In general, we cannot know in advance what will be the future demand (load profile), but we can assume the existence of an underlying stochastic model, from which the trips and driving behaviors we observe are sampled from. Specifically, we consider a state space $S = \mathcal{F} \times [0,C_{max}]$, where $\mathcal{F}$ is a feature space. The idea is to use a set of features $\mathbf{f} = (f^{1}, \ldots, f^{K}) \in\mathcal{F}$ and a capacity level 0≤c≤C _max to represent the state of the electric vehicle at any given time. The features we use are driver ID (and type of vehicle), GPS latitude and longitude, direction, speed, acceleration, altitude, instantaneous demand d, past average demand, time of the day. According to the problem definition, for any state $s = (\mathbf{f},c) \in\mathcal{S}$, there exists a set of admissible actions $\mathcal {A}(s)=\{\Delta, -c \leq\Delta\leq C_{max}- c \}$, i.e. the admissible changes of the capacitor level that satisfy the constraints of the problem.

Our underlying assumption is that there exist a probabilistic model describing the evolution of the state P(s _t+1|s ₀,…,s _t ,Δ₀,…,Δ _t ) as a function of the previous history and the sequence of action Δ₀,…,Δ _k taken. Further, we assume that

$$ P (s_{t+1}|s_0,\ldots,s_t, \Delta_0,\ldots,\Delta_t ) =P (\mathbf{f}_{t+1}|\mathbf{f}_0,\ldots, \mathbf{f}_t ) P(c_{t+1}|c_t, \Delta_t) $$

(4)

that is the evolution of f _t is independent of c _t and the actions Δ _t taken (equivalently, we assume the driving behavior and road conditions do not depend on the capacitor charge levels). On the other hand, according to the problem description c _t+1 depends deterministically on the past, specifically c _t+1=c _t +Δ _t . In this way, P(c _t+1|c _t ,Δ _t )=1 if and only if c _t+1=c _t +Δ _t .

In this MDP framework, an energy management system is a function mapping histories to a feasible action, i.e. a history-dependent feasible policy (Puterman 1994). Upon defining an immediate cost c(Δ,s,s′)=(d+Δ)² for transitioning from state s to state s′ when taking action Δ (equal to the squared current output from the battery), an optimal energy management system can be defined as one minimizing the total expected cost.

5.2 A sample-based approach

Since the probabilistic model P(f _t+1|f ₀,…,f _t ) is unknown, we use a sample-based approach where we leverage a large dataset of commuter trips crowdsourced in the United States and available online (CreateLab 2012) in order to learn it from the data. Specifically, we assume that each trip in the dataset corresponds to one particular realization of the underlying stochastic process, e.g. a sampled trajectory of length T _i in the feature space $\mathcal{F}$. In particular, we project the trip data on the feature space $\mathcal{F}$ , generating a trajectory $\mathcal{T}_{i}=(\mathbf{f}_{0}, \mathbf{f}_{1}, \ldots, \mathbf{f}_{T_{i}-1})$ where for each time step $\mathbf{f}_{t} \in \mathcal{F}$. Then, for any sequence of actions $(\Delta_{0},\ldots,\Delta _{T_{i}-1})$ and initial capacity level c ₀, we can generate the corresponding trajectories in the state space ((f ₀,c ₀),(f ₁,c ₁),…,(f _T−1,c _T−1)) according to (4).

Let $\mathcal{T}_{1}, \ldots, \mathcal{T}_{K}$ be the sample trajectories available. For any state s=(f,c)∈S we define the multiset

$$\mathcal{N}(\mathbf{f})=\bigcup_{i=1}^K \bigl\{ \mathbf{f}_{t+1} | \mathbf{f}_{t} \in\mathcal{T}_i, \|\mathbf{f}_{t}-\mathbf{f}\|_{\infty}<\epsilon\bigr\} \subseteq \mathcal{F} $$

that when ϵ=0 corresponds to the set of feature vectors that we have observed occurring immediately after f in the sample trajectories. In practice, since our feature space is continuous we choose ϵ>0 to discretize the space, so that two feature vectors are considered to be the same if they are close enough (e.g., when a driver comes to an intersection with approximately the same speed, acceleration, etc.). We use k-d trees (Bentley 1975) to speed up the computation of $\mathcal{N}(\mathbf{f})$ for all observed feature vectors $\mathbf{f} \in\bigcup\mathcal{T}_{i}$, and in our experiments ϵ is set to one thousandth of the average distance between consecutive feature vectors in the available trajectories. Similarly, we can define a multiset of possible successors in the state space as

$$\mathcal{S}(s)=\mathcal{S}(\mathbf{f},c) = \bigcup_{c'=0}^{C_{max}} \bigl\{ \bigl(\mathbf{h},c'\bigr) | \mathbf{h} \in\mathcal{N}( \mathbf{f}) \bigr\} $$

5.2.1 Posterior optimal actions

We can then define sample-based Dynamic Programming equations as follows

$$V(s) = \min_{\Delta\in\mathcal{A}(s)} \biggl( \frac{1}{|\mathcal {S}(s)|} \sum _{s' \in\mathcal{S}(s)} V\bigl(s'\bigr) + c\bigl( \Delta,s,s'\bigr) \biggr) $$

and solve for the “posterior optimal action”

$$\Delta^\ast(s) = \arg\min_{\Delta\in\mathcal{A}(s)} \biggl( \frac{1}{|\mathcal{S}(s)|} \sum_{s' \in\mathcal{S}(s)} V\bigl(s' \bigr) +c\bigl(\Delta,s,s'\bigr) \biggr) $$

This approach has the nice theoretical property that the sample-based approximation converges to the true DP equations (for the discretized MDP) in the limit of infinite samples. Similarly, Δ^∗(s) converges to the optimal action as more samples are collected. In contrast, separately optimizing for the single realizations as in Fox et al. (2011) (which corresponds to choosing $\mathcal{N}(\mathbf {f}_{t})=\mathbf{f}_{t+1}$) doesn’t necessarily converge to the true optimal action as K→∞, although it has been shown to work well in practice.

5.3 Regressing the optimal policy

Using the available sample trajectories $\mathcal{T}_{1}, \ldots, \mathcal {T}_{K}$, we generate a labeled training set¹ of (state, optimal action) pairs by solving the corresponding sample-based DP equations using value iteration (notice that the “empirical” MDP can have loops, so we cannot solve it in one pass). Specifically, we compute Δ^∗(f,c) for every $\mathbf{f} \in\mathcal{T}_{i}$ and for every capacity level c∈[0,C _max ]. We then use supervised learning to learn the relationship between a state s=(f,c)=(f ¹,…,f ^K,c)∈S and the corresponding optimal action Δ. Notice that the particular structure of the problem allows us to artificially generate N times more data points than what we originally started with. Experimentally, we have seen this to be a crucial improvement in order for the supervised learning algorithm to correctly understand the role of the capacity level c. In particular, we found that generating a dataset just using the optimal sequence of actions a ^∗ for each trajectory (f ₀,f ₁,…,f _T−1) is not sufficient to achieve state-of-the-art performance (about 10 % performance drop when evaluated on the ChargeCar dataset described below). Further, we have observed that the performance increases monotonically as a function of the number of training examples used.

The quadratic nature of the cost function gives us further insights on the performance of the supervised learning method used. In particular, the mean-squared error (MSE) is an important error metric in this case, because by reverse triangular inequality

$$\bigl\|\bigl(\mathbf{a}^\ast+\mathbf{d}\bigr)-(\widehat{\mathbf{a}}+ \mathbf{d})\bigr\|_2= \bigl\|\mathbf{a}^\ast-\widehat{\mathbf{a}}\bigr\|_2 \geq \|\widehat{\mathbf{a}}+\mathbf{d}\|_2 -\bigl\|\mathbf{a}^\ast+\mathbf{d}\bigr\|_2 $$

where $\mathbf{a}^{\ast}= (\Delta_{0}^{\ast},\ldots,\Delta_{T-1}^{\ast})$ is the optimal sequence of actions, $\widehat{\mathbf{a}}$ is the sequence of actions given by regression, and d=(d(0),…,d(T−1)) is the demand vector. This gives

$$\|\widehat{\mathbf{a}}+\mathbf{d}\|_2 \leq\bigl\|\mathbf{a}^\ast- \widehat{\mathbf{a}}\bigr\|_2 + \bigl\|\mathbf{a}^\ast+ \mathbf{d}\bigr\|_2 $$

so that $\|\mathbf{a}^{\ast}-\widehat{\mathbf{a}}\|_{2}$ bounds the difference in terms of i ²-score between the optimal sequence of actions a ^∗ and $\widehat{\mathbf{a}}$.

6 Evaluation: the Chargecar competition

As previously mentioned, we evaluate our method on the publicly available dataset provided by Chargecar (CreateLab 2012), a crowdsourcing project open to the public with the goal of making electric vehicles more practical and affordable. Along with the dataset, the Chargecar project provides a simulator to evaluate the performance of power management policies on the trips contained in the dataset. Furthermore, they set up an open algorithmic challenge where the goal of the contest is to design policies that optimize the energy performance of electric vehicles, as measured in terms of the i ²-score. All the parameters of the model are set as in the competition. In particular, the supercapacitor and the battery provide 50 Watt-hour and 50000 Watt-hour, respectively. Among many other factors, the energy efficiency of multi-battery schemes depends crucially on these parameters. Understanding their interplay with smart energy management policies is one of the goals of the competition, because it would allow us to design better, more efficient electric vehicles.

6.1 Dataset

The dataset (CreateLab 2012) contains a total of 1984 trips (with an average length of 15 minutes), subdivided into 6 separate datasets according to the driver ID. Each one of these dataset is further separated into two subsets: a training and judging set. There are 168 trips in the judging set, accounting for about 8 % of the total. Using the trips contained in the training set, we generate a dataset of labeled (state, optimal action) example pairs with the method explained in the previous section. The maximum capacity level is discretized into N=45 discrete steps, and the time step is δ _t =1 s, such that the resulting training dataset contains 75827205 examples. Since the complete training dataset generated with the previously described approach is too big to fit into memory, we divide it according to the driver ID, generating separate training sets for each driver. When these datasets are still too big, we divide them again according to the capacity level feature (selecting entries corresponding to one or more rows of the DP tables). We then learn separate models for each one of these smaller datasets, as shown in Fig. 5.²

Fig. 5

An overview of our intelligent energy management system

6.2 Supervised learning

We used non-parametric exploratory models as there is little or no prior knowledge and possibly highly non-linear interactions. In particular, we use bagged decision trees, with the REPTree algorithm as implemented in the Weka package (Hall et al. 2009) as the base learner. REPTree is a fast regression tree learner that uses information gain as the splitting criterion and reduced-error pruning (with backfitting). Following standard practice, the parameters were set by 5-fold crossvalidation, selecting the model with the best MSE score. We call the resulting policy DPDecTree. Using decision trees, we can represent and evaluate the policy efficiently in order to compute the optimal action. In contrast, it can be impractical to compute an action solving an optimization problem based on a estimated future demand, because in a real-world setting it might not be feasible to solve such problems with a high frequency on a car.

6.3 Evaluation

We evaluate the performance of DPDecTree on the separate judging set of trips using the simulator. If the action suggested by DPDecTree would overcharge the capacitor, we charge it to full capacity; if it overdraws, we discharge it completely. However, this situation is rare and DPDecTree gives feasible actions 99.8 % of the time when evaluated on the judging set. We compare our solution against MPL (CreateLab 2012), the current winning algorithm in the competition at the moment of this paper submission, and to a simple buffer policy. The MPL policy is based on a large table of thresholds for the battery output i _bc +i _bm , chosen according to driver ID, speed, demand and GPS coordinates. If the current location (GPS coordinates) has not been seen before, then it switches to another table based on driver ID, speed, and demand. The naive buffer policy charges the capacitor only from regenerative braking (i.e., when the demand is negative) and when there is a positive energy demand, it tries to meet it utilizing the capacitor first. If there is not enough energy stored, then it utilizes the battery for the remaining part. We also provide the i ²-score when the supercapacitor is not used (or is not available) as a baseline.

As can be seen from Table 1, DPDecTree leads to significant energy savings with respect to the simple buffer policy. Although is it often far from the upper bound represented by the optimal Omniscient policy (except on the mike dataset where they differ only by 5 %), the good performance of DPDecTree suggests that it is very effective at predicting future energy demands, and that the policy learned from the training examples generalizes to new, previously unseen scenarios. In general, the rather broad spectrum of energy savings (optimal and achieved by DPDecTree) we see on the different datasets is due to their different geographic locations (e.g., hilly vs. flat) and driving patterns (e.g., highway vs. city driving). Further, DPDecTree improves over MPL in 5 out of 6 datasets (each one corresponding to a different driver). We believe the problem with the arnold dataset is the presence of different driving behaviors in the same dataset that the learning algorithm was not able to separate using the available covariates.

Table 1 Results on driver specific judging datasets. i ²-scores are in 10⁸⋅A ² s

In the bottom row of Table 1 we provide the resulting scores for the entire judging dataset. On average, DPDecTree leads to a 2.5 % improvement on the i ²-score with respect to MPL. According to a one-sided paired t-test, the difference is statistically significant (with P-value 0.0058). The result is significant also according to a Wilcoxon signed-rank test (with P-value 0.00028) (Wilcoxon 1945). While there is still a significant 20 % gap with respect to the optimal omniscent policy, it is not clear how much can still be achieved in the real online setting where the future demand is not known ahead of time. These results suggest that there is a great potential for including routing information (e.g., from a car navigation system) into the problem, since they would bring the policies closer to the omniscient case. However, in this paper we assume that routing information is not available, as in the competition.

7 An adaptive policy

The approach outlined in the previous sections considered a batch learning scenario, where the entire training data is available upfront, the battery management policy is computed offline and then deployed and used as it is, without the possibility of changing it over time. From an engineering perspective, this approach is quite robust, because the policy can be thoroughly tested and evaluated by a domain experts before being deployed on a vehicle, so that unexpected or unsafe behaviors can be ruled out. However, it is easy to see that the offline batch learning approach is suboptimal in terms of energy savings, in the sense that it does not leverage new data that can be collected after deployment, nor does it adapt to changing driving behaviors or road conditions.

In this section, we investigate the feasibility of an incremental learning approach, presenting an extension of our sample-based learning scheme that allows the policy to adapt and improve as new data is being collected. Clearly, a simple approach would be to retrain a new policy from scratch as new samples are being collected, using the same batch learning procedure outlined before. For example, as soon as a new trip ends, we could retrain a new policy on a new dataset that includes all the previous training data and the trip that just ended. This approach would be very effective in terms of i ²-score, but it would be impractical for two reasons. First, we completely lose control on the structure of the new policy, which could be in principle very different from the one learned in batch. Second, and perhaps more importantly, the batch learning procedure is computationally expensive and although it can be done offline as a preprocessing step, it might not be possible to carry out these computations at relatively high frequencies with limited hardware resources. We therefore present some approaches that allow some level of control on the behavior of the new policy, which, while significantly reducing the computational cost, empirically provide very good performance in terms of energy savings.

7.1 Incremental learning

Let π ₀ be the base policy learned in the batch learning preprocessing phase, which consists of a bag of decision trees. The idea is to collect a small number of samples T ₁,…,T _L (corresponding to, e.g., L=5 trips), and then generate a new (rather small) dataset of (state,action) pairs based only on these new set of trips T ₁,…,T _L . We then learn a new single decision tree D based on this dataset, and we add it to our bag of trees, i.e. we construct a new policy π _k+1 which is a weighted average of the current policy π _k and the newly learned tree D:

$$\pi_{k+1} = (1-\lambda_k) \pi_k + \lambda_k D $$

where the parameter λ _k controls the level of adaptivity of the solution, and π ₀ is the base policy learned in the batch learning phase. This approach is clearly suboptimal because it does not consider the joint information provided by both the original training set and the newly collected one, but it is computationally efficient in terms of memory and CPU time usage because the new dataset is rather small.

7.2 Evaluation

First, we investigate how much we could improve DPDecTree by leveraging the new information that is being collected during the evaluation phase. Using the incremental learning approach, we can further improve the performance of DPDecTree in terms of the i ²-score on the judging set which was reported in Table 1. For instance, the i ²-score for alik further improves by 1.1 %, achieving a score of 4.18510⁸⋅A ² s, for thor it improves by 1.2 % to a score of 1.64410⁸⋅A ² s, and for gary it also improves by 1 % to 1.9810⁸⋅A ² s. The performance for illah and mike does not change significantly because their judging set is too small. For all these experiments, the parameter λ _k is set to 1/(N _k +1) where N _k is the number of decision trees in the bag of the current policy π _k .

Encouraged by the previous results, we investigate the performance of a policy constructed in a purely incremental way, without using any batch learning preprocessing phase. In order to do this, we use the entire dataset available (not just the small judging part) so that we can evaluate the performance on a larger dataset. In this case, we use the same incremental learning approach proposed in the previous section, but we start with a simple base policy π ₀ called SpeedPolicy. This policy maintains a threshold for the battery usage based on the current vehicle speed. Again we add a new decision tree every L=5 trips, and the base policy is weighted as one decision tree. The results are reported in Table 2, for several possible values of λ _k . We see that the adaptive policy significantly improves over the base policy in all datasets, with improvements ranging from 13 % to 22 %. However, for this experiment we cannot compare with DPDecTree and MPL because they have been trained on a large part of the dataset we are using for evaluation. Further, we see that the performance is quite robust to the choice of the parameter λ _k , although the choice λ _k =1/(N _k +1) is the best performing one across all datasets. Intuitively, this more adaptive way of choosing λ _k =1/(N _k +1) increases the weight of the current policy as more decision trees are added to the bag (i.e., the policy has been trained on more examples and thus we are more confident about it). More sophisticated techniques that weight the policies based on the number of training examples used or their statistical performance (in terms of regression error) could also be employed.

Table 2 Incremental learning results. i ²-scores are in 10⁹⋅A ² s

While so far we have considered a method that keeps adding decision trees as more data is being collected, it is natural to consider an extension where only the most recent K trees are kept in the bag, discarding the older ones. In Table 3 we evaluate the performance of this approach for several values of K. We see that there is no significant drop in performance, even if we keep a rather small number of trees K=5. In some cases, this more adaptive policy (that is more tailored to recent driving behavior) can even slightly improve the performance, e.g. in the case of the gary dataset (indeed, the gary dataset benefited from larger values of λ _k , i.e. a more adaptive policy, also in the experiment reported in Table 2).

Table 3 Incremental learning with fixed bag size. i ²-scores are in 10⁹⋅A ² s

In order to compare the performance of the incremental learning scheme with DPDecTree and MPL, we first simulate the incremental learning process using part of the training set (but not the separate judging set). Then we freeze the model, and test its performance on the separate judging set, comparing it with DPDecTree that was trained in batch on the entire training dataset. Specifically, the base model π ₀ is first trained in batch using only the first 5 % of trips in the training set. We then simulate the incremental learning process using up to 20 %, 40 %, 60 % and 100 % of the trips in the training set, adding a decision tree incrementally every L=10 trips (we use L=2 for the alik dataset which has a rather small number of long trips). After that, we freeze the model, and test its performance on the same judging set as used in Sect. 6.3. Results are reported in Table 4. As shown in Table 4, performance improves as more data is being used in the training phase, and the energy savings of incremental learning are comparable with batch learning (DPDecTree) even when using only slightly over half of the available training data (60 % of the trips available). We see that in general the incremental learning procedure can capture the data properties almost as well as batch learning. We believe this is because the training data is generally fairly uniform and homogeneous, so that policies learned on different subsets of the data are not drastically different and can be effectively averaged.

Table 4 Comparison between batch and incremental learning. i ²-score are in 10⁸⋅A ² s

8 Conclusions

In this paper we have presented an effective solution to the problem of managing multi-battery systems in electric vehicles. Our novel intelligent energy management system is evaluated on a large dataset of commuter trips crowdsourced in the United States. Our approach is completely data-driven and can be expected to improve as more data is being collected and becomes available.

Our method combines several existing approaches to solve a problem that we model as an MDP with unknown transition probabilities. We use a sample-based approach, where samples are not generated from an analytic model or from a simulator but given as part of a dataset. By observing the empirical transition probabilities of a discretized problem, we solve sample-based dynamic programming equations using value iteration. Thanks to the special structure of the problem and its independent dynamics assumption, we can generate more artificial data points from the samples by exploiting the information contained in the dynamic programming tables. The optimal posterior actions given the observed samples are then combined to form a policy for the original problem. In order to do this, we use supervised machine learning techniques to build a regression model that gives the action as a function of the state of the system. The obtained policy is evaluated on a separate set of real world trips, where it is shown to generalize to situations that were previously unseen in the training set. Our novel system is shown to outperform the leading algorithms that were previously proposed as part of an open algorithmic challenge. Further, we showed how to extend our learning approach to an incremental setting where the policy is capable of improving and adapting as new data is being collected, considerably reducing the computational cost while preserving a good level of performance in terms of energy savings.