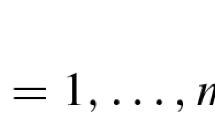Unified Robust Necessary Optimality Conditions for Nonconvex Nonsmooth Uncertain Multiobjective Optimization

Abstract

This paper is concerned with nonconvex nonsmooth uncertain multiobjective optimization problems, in which the decision variable of both objective and constraint functions is defined on Banach space while uncertain parameters are defined on arbitrary nonempty (may not be compact) sets. We employ the Stone–C̆ech compactification of uncertainty sets and the upper semicontinuous regularization of original functions with respect to uncertain parameters, giving rise to unified robust necessary optimality conditions for the local robust weakly efficient solution of the considered problem. Moreover, we derive weak and strong KKT robust necessary conditions via the constraint qualification and the regularity condition, respectively. Several examples are provided to illustrate the validity of our results.

1 Introduction

In the last decades, robust multiobjective optimization and its broad range of applications have been an active study area in mathematical programming. More and more complex optimization problems are addressed in contemporary society. These problems are characterized by multiple conflicting objectives and almost inevitably contain the uncertainty because of measurement errors, imprecise data, future developments, fluctuations, and disturbances (e.g., COVID-19). We apply a deterministic approach to deal with the uncertainty that is integrated with the multiobjective optimization. The deterministic approach is mainly based on robust optimization [1, 2] in this paper. Establishing robust necessary optimality conditions for uncertain multiobjective optimization problems has been an attractive issue recently [6,7,8,9, 15,16,17, 21, 31]. There are three types of robust necessary optimality conditions for uncertain multiobjective optimization problems. The first one is called Fritz John (FJ) robust necessary conditions when not all Lagrange multipliers of objective and constraint functions are zero. The second one is weak Karush–Kuhn–Tucker (WKKT) robust necessary conditions when at least one of Lagrange multipliers corresponding to objective functions is positive. The third one is strong Karush–Kuhn–Tucker (SKKT) robust necessary conditions when all Lagrange multipliers of objective functions are positive.

Recent references [19, 23, 29] presented necessary and sufficient conditions for robust solutions of uncertain optimization problems under the convex-concave assumption by various methods. These lead to the corresponding question of how to weaken the convex-concave assumption. Wei et al. [32] investigated the robust necessary optimality for uncertain optimization problems without any convexity or concavity assumptions but merely considered finite uncertainty sets. Meanwhile, the problem models in [19, 23, 29, 32] were only scalar cases. Robust necessary optimality conditions formulated by nondifferentiable and nonconvex functions were established in [4, 6, 8, 15,16,17, 21, 22, 27, 31], while uncertainty sets were compact. Moreover, Chuong [9] provided robust optimality conditions for nonconvex nonsmooth uncertain multiobjective optimization problems with uncertain parameters ranging in compact perturbed sets of active indices. A natural question arises: Is it possible to eliminate those assumptions? Namely, whether or not we can obtain robust optimality conditions for uncertain multiobjective optimization problems under nonconvex, nonsmooth and noncompact assumptions.

It is worth mentioning that Correa et al. [12, 13] perfectly removed the compactness of the index set and the continuity of the indicator parameter by using the compactification of the index set and an appropriate enlargement of the original family of data functions, and proposed general formulas for the subdifferential of the supremum of convex functions. Inspired by the work of [12, 13], a more precise question is: By virtue of the compactification of uncertainty sets and the appropriate enlargement of original functions, is there any chance for getting rid of the aforementioned assumptions (convexity-concavity of functions, compactness and continuity of uncertain parameters), but keeping alive the possibility of still applying robust optimality conditions developed under them?

In this paper, we employ the Stone–C̆ech compactification approach [11, 26] to drop out the standard assumption of the compactness of uncertainty sets. Moreover, we use the upper semicontinuous regularization to remove the continuity of uncertain parameters. Then, we formulate new descriptions of robust optimality conditions of uncertain multiobjective optimization problems for uniformly locally Lipschitz functions defined on Banach spaces (see Sect. 2) taken over arbitrary nonempty uncertainty sets. Compared with the ones developed in the previous literature [6, 8,9,10, 15, 16, 21, 22, 27, 31], we present weaker assumptions to obtain robust optimality conditions. Additionally, taking into account the constraint qualification and the regularity condition, we arrive at WKKT and SKKT robust necessary optimality conditions, respectively. Our results are new and extend or cover several corresponding known ones in the literature.

The rest of this paper is organized as follows. Section 2 provides some preliminary materials from variational analysis and generalized differentiation widely applied in formulations and proofs of the main results below. The major goal of Sect. 3 is to constructively establish unified robust necessary optimality conditions for uncertain multiobjective optimization problems by enlarged compactification sets and upper semicontinuous regularized functions. Based on these crucial developments, we derive some corollaries as some special cases of the main results. Section 4 continues the study of WKKT and SKKT robust necessary optimality conditions for uncertain multiobjective optimization problems by means of the constraint qualification and the regularity condition, respectively. Section 5 contains a brief summary of this paper.

2 Preliminaries

Our notation and terminology are basically standard and conventional in the area of variational analysis and generalized differentiation [10, 24, 25]. Unless otherwise stated in this paper, ${\mathbb {R}}^{l}$ signifies the l-dimensional Euclidean space and ${\mathbb {R}}^{l}_{+}$ denotes the nonnegative orthant in ${\mathbb {R}}^{l}$. Let X be a Banach space with the topological dual denoted by $X^{*}$, which is endowed with the weak$^{*}$ topology. The canonical pairing between X and $X^{*}$ is denoted by $\langle \cdot ,\cdot \rangle$. $\Vert \zeta \Vert _{*}$ denotes the norm in $X^{*}$ by $\Vert \zeta \Vert _{*}:=\sup \{\langle \zeta , d\rangle : d\in X, \Vert d\Vert \le 1\}$. The symbol ${\mathop {\longrightarrow }\limits ^{w^{*}}}$ denotes the convergence in the weak$^{*}$ topology of $X^{*}$. Moreover, the notations intS, clS and coS denote the interior, the closure hull and the convex hull of $S\subseteq X$, respectively, while cl$^{*}$ $A$ signifies the weak$^{*}$ topological closure of $A\subseteq X^{*}$. The symbol B(x, r) denotes the open ball with center $x\in X$ and radius $r>0$, and $B_{X}$ stands for the closed unit ball.

Let $\phi : X\rightarrow {\mathbb {R}}$ be a given function. The regular/Fréchet subdifferential of $\phi$ at ${\bar{x}}\in X$ is defined by

$$\begin{aligned} {\widehat{\partial }}\phi ({\bar{x}}):=\left\{ x^{*}\in X^{*}:\,\liminf _{x\rightarrow {\bar{x}}}\frac{\phi (x)-\phi ({\bar{x}})-\langle x^{*}, x-{\bar{x}}\rangle }{\Vert x-{\bar{x}}\Vert } \ge 0\right\} . \end{aligned}$$

Further, if the function $\phi$ is locally Lipschitz at ${\bar{x}}\in X$, then the generalized Clarke directional derivative of $\phi$ at ${\bar{x}}$ in the direction $d\in X$ is defined by

$$\begin{aligned} \phi ^{\circ }({\bar{x}}; d):=\limsup \limits _{\begin{array}{c} x\rightarrow {\bar{x}}\\ \tau \downarrow 0 \end{array}}\frac{\phi (x+\tau d)-\phi (x)}{\tau }. \end{aligned}$$

Then the Clarke subdifferential, or Clarke generalized gradient of $\phi$ at ${\bar{x}}$ is defined as

$$\begin{aligned} \partial \phi ({\bar{x}}):=\{x^{*}\in X^{*}:\,\langle x^{*}, d\rangle \le \phi ^{\circ }({\bar{x}}; d),\;\forall \;d\in X \}. \end{aligned}$$

The relationship between above subdifferentials of $\phi$ at ${\bar{x}}\in X$ is ${\widehat{\partial }}\phi ({\bar{x}})\subseteq \partial \phi ({\bar{x}})$; see [24]. If $\phi$ is convex, $\partial \phi ({\bar{x}})$ coincides with the subdifferential in the sense of convex analysis, that is,

$$\partial \phi ({\bar{x}})=\{x^{*}\in X^{*}: \langle x^{*}, x-{\bar{x}}\rangle \le \phi (x)-\phi ({\bar{x}}),\;\forall \, x\in X\}.$$

The following summarizes some basic properties of the Clarke subdifferential; see [10] for more details on those constructions.

Proposition 2.1

[10] Let $\phi$ be locally Lipschitz at ${\bar{x}}\in X$ with rank L. Then

• (a) $\partial \phi (\bar{x})$ is a nonempty, convex, weak$^{*}$-compact subset of $X^{*}$.

• (b) $\Vert \zeta \Vert _{*}\le L$ for every $\zeta$ in $\partial \phi (\bar{x})$.

• (c) For every $d\in X$, one has $\phi ^{\circ }(\bar{x}; d)=\max \{\langle x^{*}, d\rangle :\,x^{*}\in \partial \phi (\bar{x})\}$.

• (d) Let $x_{j}$ and $x_{j}^{*}$ be sequences in X and $X^{*}$ such that $x_{j}^{*}\in \partial \phi (x_{j})$. Suppose that $x_{j}$ converges to $\bar{x}$, and that $x^{*}$ is a cluster point of $x_{j}^{*}$ in the weak$^{*}$ topology. Then one has $x^{*}\in \partial \phi (\bar{x})$. (That is, the multifunction $\partial \phi$ is weak$^{*}$ closed.)

The mean value theorem for the Clarke subdifferential of Lipschitz functions is used later in the proof of the main results.

Lemma 2.1

[10] Let x and y be points in X, and suppose that $\phi$ is Lipschitz on an open set containing the line segment [x, y]. Then there exist a point $u\in (x, y)$ and $u^{*}\in \partial \phi (u)$ such that

$$\begin{aligned} \phi (y)-\phi (x)=\langle u^{*}, y-x\rangle , \end{aligned}$$

where $[x, y]:=co \{x, y\}$, and $(x, y):=co \{x, y\}\backslash \{x, y\}$.

The nonsmooth version of Fermat’s rule in the sense of the Clarke subdifferential is stated as follows.

Lemma 2.2

[10] If $\phi$ attains a local minimum or maximum at ${\bar{x}}$, then $0\in \partial \phi ({\bar{x}})$.

The following lemma is known as the Clarke subdifferential rule of the finite indexed family of functions.

Lemma 2.3

[10] Suppose that $\psi _{i}$ is a finite collection of functions $(i=1,2,\ldots ,l)$ each of which is locally Lipschitz at ${\bar{x}}$. The function $\varPsi$ defined by $\varPsi ({\bar{x}})=\max \{\psi _{i}({\bar{x}}): i=1,2,\ldots ,l\}$. Then, $\varPsi$ is locally Lipschitz at ${\bar{x}}$, and

$$\partial \varPsi ({\bar{x}})\subseteq co \left\{ \partial \psi _{i}({\bar{x}}): i\in I({\bar{x}})\right\} ,$$

where $I({\bar{x}})=\{i\in \{1,2,\ldots ,l\}: \psi _{i}({\bar{x}})=\varPsi ({\bar{x}})\}$.

Recall that the function $\phi$ is upper semicontinuous (u.s.c) [24] at ${\bar{x}}$ if

$$\begin{aligned} \limsup _{x\rightarrow {\bar{x}}}\phi (x)\le \phi ({\bar{x}}),\quad or equivalently \;\;\limsup _{x\rightarrow {\bar{x}}}\phi (x)= \phi ({\bar{x}}), \end{aligned}$$

and upper semicontinuous on X if this holds for every ${\bar{x}}\in X$. Moreover, the sequential Painlevé-Kuratowski upper/outer limit [24] of F with respect to the norm topology of X and the weak$^{*}$ topology of $X^{*}$ is defined as

$$\begin{aligned} \mathop {Limsup }\limits _{\mathop {x\rightarrow {\bar{x}}}}F(x):=\left\{ x^{*}\in X^{*}: \exists \,x_{n}\rightarrow {\bar{x}}, \exists \, x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} x^{*} \;with \; x_{n}^{*}\in F( x_{n}),\;\;n\in {\mathbb {N}}\right\} , \end{aligned}$$

where $F: X\rightrightarrows X^{*}$ is a set-valued mapping (multifunction).

Let $\varphi : X\times Y\rightarrow {\mathbb {R}}$ be functions decided on X parametrized by $y\in Y$. Assume that for some decision point x in X, $\varphi (\cdot , y)$ is locally Lipschitz at x. As usual, the symbol $\partial _{1}\varphi (\cdot , {\bar{y}})$ (resp., ${\widehat{\partial }}_{1}\varphi (\cdot , {\bar{y}})$) signifies the Clarke (resp., Fréchet) subdifferential operation with respect to the first variable of the function $\varphi$ at a given ${\bar{y}}\in Y$. Clarke [10] introduced a new kind of the partial generalized gradient, which takes account of variations in parameters rather than just the decision one. The subdifferential construction ${\overline{\partial }}_{1}\varphi ({\bar{x}}, {\bar{y}})\subseteq X^{*}$ from [10] is defined by

$$\begin{aligned} {\overline{\partial }}_{1}\varphi ({\bar{x}}, {\bar{y}}):=cl ^{*}co \left[ \mathop {Limsup }\limits _{\begin{array}{c} x\rightarrow {\bar{x}}\\ y\rightarrow {\bar{y}}, y\in Y \end{array}}\partial _{1}\varphi (x, y)\right] , \end{aligned}$$

(1)

where

$$\begin{aligned} \begin{aligned}&\mathop {Limsup }\limits _{\begin{array}{c} x\rightarrow {\bar{x}}\\ y\rightarrow {\bar{y}}, y\in Y \end{array}}\partial _{1}\varphi (x, y)\\&:=\left\{ x^{*}\in X^{*}: \exists \,x_{n}\rightarrow {\bar{x}},\, y_{n}\in Y,\,y_{n}\rightarrow {\bar{y}}, \,x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} x^{*} \;with \; \,x_{n}^{*}\in \partial _{1}\varphi (x_{n}, y_{n}),\;\;n\in {\mathbb {N}} \right\} .\\ \end{aligned} \end{aligned}$$

Let us now present the weak$^{*}$ closed concept for a multifunction by using the above generalized subdifferential construction for the case of locally Lipschitz functions from [10, Definition 2.8.1].

Definition 2.1

[10] The multifunction $(x, y)\rightrightarrows \partial _{1}\varphi (x, y)\subseteq X^{*}$ is said to be weak$^{*}$ closed at $({\bar{x}}, {\bar{y}})$ provided ${\overline{\partial }}_{1}\varphi ({\bar{x}}, {\bar{y}})= \partial _{1}\varphi ({\bar{x}}, {\bar{y}}).$

Note that this condition certainly holds if y is isolated in Y because of Proposition 2.1(d).

Throughout this paper, given a Banach space X, we consider the following uncertain constrained multiobjective optimization problem:

$$\begin{aligned} \begin{aligned} (UMP)\qquad&\min _{x\in X} \left( f_{1}(x, u_{1}),\ldots , f_{l}(x, u_{l})\right) \\&s.t. \;\;g_{i}(x,v_{i})\le 0, \;i=1,\ldots , m, \end{aligned} \end{aligned}$$

where $f_{k}: X\times U_{k}\rightarrow {\mathbb {R}}$, $k\in K:=\{1,\ldots , l\}$, $g_{i}: X\times V_{i}\rightarrow {\mathbb {R}}$, $i\in I:=\{1,\ldots , m\}$, and $U_{k}, k\in K$, $V_{i}, i\in I$ are nonempty uncertainty sets that are assumed to be arbitrary (equipped with a completely regular topology). $x\in X$ is called the decision variable and $u_{k}\in U_{k}$, $k\in K$, $v_{i}\in V_{i}$, $i\in I$ are called uncertain parameters. For any $x\in X$, $k\in K$ and $i\in I$, we always assume that functions $f_{k}(\cdot , u_{k})$, $u_{k}\in U_{k}$, and $g_{i}(\cdot , v_{i})$, $v_{i}\in V_{i}$ are uniformly locally Lipschitz at x with some given ranks $L_{k}>0$ and $\mathrm {L}_{i}>0$, respectively. This means the existence of some positive numbers $\delta _{k}$ and $\eta _{i}$ such that

$$\begin{aligned} |f_{k}(x_{1},u_{k})-f_{k}(x_{2},u_{k})|\le & {} L_{k}\Vert x_{1}-x_{2}\Vert ,\;\forall \, x_{1}, x_{2}\in B(x,\delta _{k}),\;\;\forall \, u_{k}\in U_{k}, \end{aligned}$$

(2)

$$\begin{aligned} |g_{i}(x_{1}, v_{i})-g_{i}(x_{2},v_{i})|\le & {} \mathrm {L}_{i}\Vert x_{1}-x_{2}\Vert ,\;\forall \, x_{1}, x_{2}\in B(x,\eta _{i}),\;\;\forall \, v_{i}\in V_{i}. \end{aligned}$$

(3)

To deal with the problem (UMP), the vast literature mainly considered the deterministic robust counterpart to the problem (UMP) as usual, which is described as follows:

$$\begin{aligned} \begin{aligned} (RMP)\qquad&\min _{x\in X} \left( \sup _{u_{1}\in U_{1}}f_{1}(x, u_{1}),\ldots , \sup _{u_{l}\in U_{l}}f_{l}(x, u_{l})\right) \\&s.t. \;\;g_{i}(x,v_{i})\le 0,\; \forall \, v_{i}\in V_{i}, \;i\in I. \end{aligned} \end{aligned}$$

We denote the feasible region of the problem (RMP) as follows:

$$\begin{aligned} C:=\{x\in X:\; g_{i}(x,v_{i})\le 0,\,\forall \,v_{i}\in V_{i},\;i\in I\}. \end{aligned}$$

Many concepts of robustness deal with uncertain multiobjective optimization problems, for instance, minmax robustness, highly robustness, optimistic robustness, regret robustness, adjustable robustness, and some new concepts for handling the uncertainty; see [3, 14, 18, 20]. However, the most common one applied in robust multiobjective optimization is minmax robustness; see [14]. We address this paper mainly to apply the notion of the local robust weakly efficient solution in the sense of minmax robustness, in which the optimization is conditioned on the worst-case realization of the uncertainty. For $x\in X$, we define and assume that $F_{k}(x):=\sup _{u_{k}\in U_{k}}f_{k}(x, u_{k})\in {\mathbb {R}}$, $k\in K$, $G_{i}(x):=\sup _{v_{i}\in V_{i}}g_{i}(x,v_{i})\in {\mathbb {R}}$, $i\in I$ and denote $F(x):=(F_{1}(x),\ldots , F_{l}(x))\in {\mathbb {R}}^{l}$, $G(x):=(G_{1}(x),\ldots , G_{m}(x))\in {\mathbb {R}}^{m}$ unless otherwise stated.

Definition 2.2

A vector ${\bar{x}}\in C$ is called a local robust weakly efficient solution of the problem (UMP) and is denoted by ${\bar{x}}\in loc S^{w}(RMP)$, if ${\bar{x}}\in C$ is a local weakly efficient solution of the problem (RMP), that is, there exists a neighborhood O of ${\bar{x}}$ such that

$$\begin{aligned}F(x)-F({\bar{x}})\notin -int {\mathbb {R}}_{+}^{l},\qquad \forall \,x\in C\cap O. \end{aligned}$$

When $O=X$, the definition is represented as the concept of the robust weakly efficient solution for the problem (UMP).

3 A Unified Study of Optimality Conditions

The main goal of this section is to establish new robust necessary optimality conditions for the nonconvex and nonsmooth problem (UMP) without the compactness of uncertainty sets and the continuity of uncertain parameters. Our approach is mainly based on the compactification of the sets and the u.s.c regularization of the functions, which have been proposed in [12, 13].

For any given set $U_{k}$, which is equipped with a completely regular topology, we first consider the Stone–C̆ech compactification [11, 26] of $U_{k}$. We denote by $C(U_{k},[0,1])$ the set of continuous functions from $U_{k}$ to [0, 1] and consider the product space $[0, 1]^{C(U_{k},[0,1])}$, which is compact for the product topology (by Tychonoff theorem). By this we assume without loss of generality that $U_{k}\subseteq [0, 1]^{C(U_{k},[0,1])}$. If $u\in U_{k}$, let $\mu _{u}: C(U_{k},[0,1])\rightarrow [0,1]$ be defined by $\mu _{u}(\varphi ):=\varphi (u)$ for every $\varphi \in C(U_{k},[0,1])$. It is easy to see that $\mu _{u}\in [0, 1]^{C(U_{k},[0,1])}$ and $\Vert \mu _{u}\Vert =1$. Let $\varDelta : U_{k}\rightarrow [0, 1]^{C(U_{k},[0,1])}$ be defined by $\varDelta (u):= \mu _{u}$. If $(u_{\gamma })_{\gamma }$ is a net in $U_{k}$ and $u_{\gamma }\rightarrow u$, then $\varphi (u_{\gamma })\rightarrow \varphi (u)$ for every $\varphi \in C(U_{k},[0,1])$. This says that $\mu _{u_{\gamma }}\rightarrow \mu _{u}$ in $[0, 1]^{C(U_{k},[0,1])}$. According to the compactification process, the closure of $\varDelta (U_{k})$ in $[0, 1]^{C(U_{k},[0,1])}$ for the product topology is the compact set

$$\begin{aligned}{\mathfrak {U}}_{k}:=cl (\varDelta (U_{k})). \end{aligned}$$

The convergence in ${\mathfrak {U}}_{k}$ is the pointwise convergence, that is, for $\mu \in {\mathfrak {U}}_{k}$ and a net $(\mu _{\gamma })_{\gamma }\subseteq {\mathfrak {U}}_{k}$ we have $\mu _{\gamma }\rightarrow \mu$ if and only if $\mu _{\gamma }(\varphi )\rightarrow \mu (\varphi )$ for all $\varphi \in C(U_{k},[0,1])$.

Proposition 3.1

[11] The map $\varDelta : U_{k}\rightarrow (\varDelta (U_{k}), \,weak^{*})$ is a homeomorphism if and only if $U_{k}$ is completely regular.

If $U_{k}$ has a compactification ${\mathfrak {U}}_{k}$, then $U_{k}$ must be completely regular, being a subspace of the completely regular space ${\mathfrak {U}}_{k}$. Conversely, if $U_{k}$ is completely regular, then $U_{k}$ has a compactification; see [26] for more discussions. We proceed similarly to the above compactification process for the sets $V_{i}\subseteq [0, 1]^{C(V_{i},[0,1])}$, $i\in I$. The closure of $\varDelta (V_{i})$ for the product topology is the compact set ${\mathfrak {V}}_{i}:=cl (\varDelta (V_{i}))$.

Next, we introduce new appropriate functions ${\hat{f}}_{k}: X\times {\mathfrak {U}}_{k}\rightarrow {\mathbb {R}}$, $k\in K$, defined by

$$\begin{aligned} {\hat{f}}_{k}(x, \mu ):=\limsup _{\mu _{u}\rightarrow \mu , u\in U_{k}}f_{k}(x, u), \end{aligned}$$

(4)

in other words,

$$\begin{aligned} {\hat{f}}_{k}(x, \mu )=\sup \left\{ \limsup _{\gamma }f_{k}(x, u_{\gamma }):\,(u_{\gamma })_{\gamma }\subseteq U_{k},\, \varphi (u_{\gamma })\rightarrow \mu (\varphi ),\, \forall \, \varphi \in C(U_{k},[0,1])\right\} . \end{aligned}$$

Moreover, the function (4) involves the following form:

$$\begin{aligned} {\hat{f}}_{k}(x, \mu _{u})=\limsup _{\mu _{s}\rightarrow \mu _{u}, s\in U_{k}}f_{k}(x, s). \end{aligned}$$

Thus, for any $u\in U_{k}$ and $x\in X$, we obtain

$$\begin{aligned} \begin{aligned} {\hat{f}}_{k}(x, \mu _{u})&=\sup \left\{ \limsup \limits _{\gamma }f_{k}(x, u_{\gamma }):\mu _{u_{\gamma }}\rightarrow \mu _{u}\right\} \\&\ge \sup \left\{ \limsup \limits _{\gamma }f_{k}(x, u_{\gamma }):u_{\gamma }\rightarrow u\right\} \ge f_{k}(x, u). \end{aligned} \end{aligned}$$

(5)

Similarly, we also introduce functions ${\hat{g}}_{i}: X\times {\mathfrak {V}}_{i}\rightarrow {\mathbb {R}}$, $i\in I$, defined by

$$\begin{aligned} {\hat{g}}_{i}(x, \nu ):=\limsup _{\nu _{v}\rightarrow \nu , v\in V_{i}}g_{i}(x, v). \end{aligned}$$

(6)

For any $k\in K$ and $i\in I$, one can see that new functions ${\hat{f}}_{k}(x, \mu )$ and ${\hat{g}}_{i}(x, \nu )$ are the u.s.c regularization of the original ones $f_{k}(x, u)$ and $g_{i}(x, v)$ with respect to uncertain parameters, respectively. The function ${\hat{f}}_{k}(x, \mu )$ provides the same supremum $F_{k}(x)$ as the original $f_{k}(x, u)$ with respect to uncertain parameters, as well as characterizations for the function ${\hat{g}}_{i}(x, \nu )$.

Lemma 3.1

For any $x\in X$, $k\in K$ and $i\in I$, we have

$$\begin{aligned}&\sup \limits _{\mu \in {\mathfrak {U}}_{k}}{\hat{f}}_{k}(x, \mu )=F_{k}(x)=\sup \limits _{u\in U_{k}}f_{k}(x, u);\end{aligned}$$

(7)

$$\begin{aligned}&\sup \limits _{\nu \in {\mathfrak {V}}_{i}}{\hat{g}}_{i}(x, \nu )=G_{i}(x)=\sup \limits _{v\in V_{i}}g_{i}(x, v). \end{aligned}$$

(8)

Proof

For each $\mu \in {\mathfrak {U}}_{k}$ and $x\in X$, we yield

$$\begin{aligned}{\hat{f}}_{k}(x, \mu )=\limsup _{\mu _{u}\rightarrow \mu , u\in U_{k}}f_{k}(x, u)\le F_{k}(x), \end{aligned}$$

which means that $\sup _{\mu \in {\mathfrak {U}}_{k}}{\hat{f}}_{k}(x, \mu )\le F_{k}(x)$. Moreover, since $F_{k}(x)=\sup _{u\in U_{k}}f_{k}(x, u)\in {\mathbb {R}}$, then there exists a net $(u_{n})_{n}\subseteq U_{k}$ such that $F_{k}(x)=\lim _{n}f_{k}(x, u_{n})$ for $x\in X$. Further, there exists a subnet $(u_{\gamma })_{\gamma }$ of $(u_{n})_{n}$ and $\mu \in {\mathfrak {U}}_{k}$ such that $\mu _{u_{\gamma }}\rightarrow \mu$, and thus

$$\begin{aligned} {\hat{f}}_{k}(x, \mu )\ge \limsup _{\gamma } f_{k}(x, u_{\gamma })=\lim _{\gamma }f_{k}(x, u_{\gamma })=\lim _{n}f_{k}(x, u_{n})=F_{k}(x), \end{aligned}$$

which implies that $\sup _{\mu \in {\mathfrak {U}}_{k}}{\hat{f}}_{k}(x, \mu )\ge F_{k}(x)$. Therefore, the equality (7) holds. One has analogs of (8) from the proof of (7). The proof is complete. $\square$

For given $x\in X$, $k\in K$ and $i\in I$. We provide the perturbed sets of active indices in $U_{k}, V_{i}, {\mathfrak {U}}_{k}$, and ${\mathfrak {V}}_{i}$, respectively.

$$\begin{aligned}&U_{k}^{\varepsilon _{k}}(x):=\{u\in U_{k}: f_{k}(x, u)\ge F_{k}(x)-\varepsilon _{k}\},\;\; \varepsilon _{k}\ge 0,\\&{\mathfrak {U}}_{k}^{\varepsilon _{k}}(x):=\{\mu \in {\mathfrak {U}}_{k}: {\hat{f}}_{k}(x, \mu )\ge F_{k}(x)-\varepsilon _{k}\},\;\; \varepsilon _{k}\ge 0,\\&V_{i}^{\epsilon _{i}}(x):=\{v\in V_{i}: g_{i}(x, v)\ge G_{i}(x)-\epsilon _{i}\},\;\; \epsilon _{i}\ge 0,\\&{\mathfrak {V}}_{i}^{\epsilon _{i}}(x):=\{\nu \in {\mathfrak {V}}_{i}: {\hat{g}}_{i}(x, \nu )\ge G_{i}(x)-\epsilon _{i}\},\;\; \epsilon _{i}\ge 0. \end{aligned}$$

Especially, $U_{k}(x):=U_{k}^{0}(x)=\{u\in U_{k}: f_{k}(x, u)= F_{k}(x)\}$. One has analogs of the sets ${\mathfrak {U}}_{k}(x)$, $V_{i}(x)$ and ${\mathfrak {V}}_{i}(x)$, which are exactly sets of active indices in ${\mathfrak {U}}_{k}$, $V_{i}$ and ${\mathfrak {V}}_{i}$ at x, respectively.

Remark 3.1

• (i) For any $\varepsilon _{k}>0$ and $\epsilon _{i}>0$, the sets $U_{k}^{\varepsilon _{k}}(x)$, ${\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$, $V_{i}^{\epsilon _{i}}(x)$ and ${\mathfrak {V}}_{i}^{\epsilon _{i}}(x)$ are always nonempty, and $U_{k}(x)\subseteq U_{k}^{\varepsilon _{k}}(x)$, ${\mathfrak {U}}_{k}(x)\subseteq {\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$, $V_{i}(x)\subseteq V_{i}^{\epsilon _{i}}(x)$ and ${\mathfrak {V}}_{i}(x) \subseteq {\mathfrak {V}}_{i}^{\epsilon _{i}}(x)$ by the definitions.

• (ii) If $u\in U_{k}^{\varepsilon _{k}}(x)$ for $\varepsilon _{k}\ge 0$, then $\mu _{u}\in {\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$. In fact, for every $u\in U_{k}^{\varepsilon _{k}}(x)$ we obtain that ${\hat{f}}_{k}(x, \mu _{u})\ge f_{k}(x, u)\ge F_{k}(x)-\varepsilon _{k}$ for $\varepsilon _{k}\ge 0$ by (5), which means that $\mu _{u}\in {\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$. In other words, $\varDelta (U_{k}^{\varepsilon _{k}}(x))\subseteq {\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$ for $\varepsilon _{k}\ge 0$ when $U_{k}^{\varepsilon _{k}}(x)\ne \emptyset$.

• (iii) The sets ${\mathfrak {U}}_{k}(x)$, $k\in K$ are always nonempty, whereas $U_{k}(x)$, $k\in K$ might be empty sets.

The following lemma shows that the compactness of the sets ${\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$ and ${\mathfrak {V}}_{i}^{\epsilon _{i}}(x)$ as well as the u.s.c property of functions ${\hat{f}}_{k}(x, \cdot )$ and ${\hat{g}}_{i}(x, \cdot )$ are preserved under the above consideration.

Lemma 3.2

For any $x\in X$, $k\in K$ and $i\in I$, one has the following assertions:

• (i) The sets ${\mathfrak {U}}_{k}^{\varepsilon _{k}}(x)$, $\varepsilon _{k}\ge 0$, and ${\mathfrak {V}}_{i}^{\epsilon _{i}}(x)$, $\epsilon _{i}\ge 0$ are nonempty and compact.

• (ii) For every net $(\mu _{\gamma })_{\gamma }\subseteq {\mathfrak {U}}_{k}$ converging to $\mu \in {\mathfrak {U}}_{k}$, one has

  $$\begin{aligned} \limsup \limits _{\gamma }{\hat{f}}_{k}(x, \mu _{\gamma })\le {\hat{f}}_{k}(x, \mu ). \end{aligned}$$

• (iii) For every net $(\nu _{\gamma })_{\gamma }\subseteq {\mathfrak {V}}_{i}$ converging to $\nu \in {\mathfrak {V}}_{i}$, one has

  $$\begin{aligned} \limsup \limits _{\gamma }{\hat{g}}_{i}(x, \nu _{\gamma })\le {\hat{g}}_{i}(x, \nu ). \end{aligned}$$

Proof

(i) We verify that the sets ${\mathfrak {U}}_{k}(x)$ and ${\mathfrak {V}}_{i}(x)$ are nonempty and compact, and the cases of $\varepsilon _{k}>0$ and $\epsilon _{i}>0$ are trivial. In fact, fix $k\in K$ and $x\in X$. Since $F_{k}(x)=\sup _{u\in U_{k}}f_{k}(x, u)\in {\mathbb {R}}$, then there exists a net $(u_{n})_{n}\subseteq U_{k}$ such that $F_{k}(x)=\lim _{n}f_{k}(x, u_{n})$. According to the compactness of ${\mathfrak {U}}_{k}$, there exists a subnet $(u_{\gamma })_{\gamma }$ of $(u_{n})_{n}$ such that $\mu _{u_{\gamma }}\rightarrow \mu \in {\mathfrak {U}}_{k}$. Together with (5), we have

$$\begin{aligned} \begin{aligned} F_{k}(x)&=\lim _{n}f_{k}(x, u_{n})=\lim _{\gamma }f_{k}(x, u_{\gamma })\le \lim _{\gamma }{\hat{f}}_{k}(x, \mu _{u_{\gamma }})\\&\le \limsup _{\mu _{u}\rightarrow \mu , u\in U_{k}}f_{k}(x, u)={\hat{f}}_{k}(x, \mu )\le F_{k}(x), \end{aligned} \end{aligned}$$

which implies $\mu \in {\mathfrak {U}}_{k}(x)$. Thus, ${\mathfrak {U}}_{k}(x)$ is nonempty.

Furthermore, we just prove that ${\mathfrak {U}}_{k}(x)$ is a closed subset of ${\mathfrak {U}}_{k}$, which is compact Hausdorff. Take an arbitrary net $(\mu _{\gamma })_{\gamma }\subseteq {\mathfrak {U}}_{k}(x)$ that converges to $\mu$ ($\in {\mathfrak {U}}_{k}$). Thus, for each $\gamma$, by the definition of the function ${\hat{f}}$, we can find a net $(u_{\gamma j})_{j}\subseteq U_{k}$ such that $\mu _{u_{\gamma j}}\rightarrow _{j}\mu _{\gamma }$ and

$$\begin{aligned}F_{k}(x)={\hat{f}}_{k}(x, \mu _{\gamma })=\lim _{j}f_{k}(x, u_{\gamma j}). \end{aligned}$$

Thus, there exists a diagonal net $\big (u_{\gamma j_{\gamma }}, f_{k}(x, u_{\gamma j_{\gamma }})\big )_{\gamma }\subseteq {\mathfrak {U}}_{k}\times {\mathbb {R}}$ such that $u_{\gamma j_{\gamma }}\rightarrow _{\gamma } \mu$ and $f_{k}(x, u_{\gamma j_{\gamma }})\rightarrow _{\gamma } F_{k}(x)$, in other words, ${\hat{f}}_{k}(x, \mu )\ge \limsup _{\gamma }f_{k}(x, u_{\gamma j_{\gamma }})=\lim _{\gamma }f_{k}(x, u_{\gamma j_{\gamma }})=F_{k}(x)$. Hence, $\mu \in {\mathfrak {U}}_{k}(x)$. Similarly, we can justify that ${\mathfrak {V}}_{i}(x)$ is nonempty and compact.

(ii) Since $U_{k}$ is completely regular, then ${\mathfrak {U}}_{k}$ is compact Hausdorff. Let a net $(\mu _{\gamma })_{\gamma }\subseteq {\mathfrak {U}}_{k}$ such that $\mu _{\gamma }\rightarrow \mu \in {\mathfrak {U}}_{k}$, where $\mu$ is the unique convergent point. Due to $F_{k}(x)\in {\mathbb {R}}$, we assume without loss of generality that $\mu _{\gamma }\rightarrow \mu$ and $\limsup _{\gamma }{\hat{f}}_{k}(x, \mu _{\gamma })=\lim _{\gamma }{\hat{f}}_{k}(x, \mu _{\gamma })=a\in {\mathbb {R}}$. Further, for each $\gamma$ there exists a net $(u_{\gamma j})_{j}\subseteq U_{k}$ such that $\mu _{u_{\gamma j}}\rightarrow _{j}\mu _{\gamma }$ and ${\hat{f}}_{k}(x, \mu _{\gamma })=\lim _{j}f_{k}(x, u_{\gamma j}),$ that is,

$$\begin{aligned}(\mu _{u_{\gamma j}}, f_{k}(x, u_{\gamma j}))\rightarrow _{j} (\mu _{\gamma }, {\hat{f}}_{k}(x, \mu _{\gamma }))\quad and \quad (\mu _{\gamma }, {\hat{f}}_{k}(x, \mu _{\gamma }))\rightarrow _{\gamma } (\mu , a). \end{aligned}$$

Thus, we can find a diagonal net $(u_{\gamma j_{\gamma }})_{\gamma }$ such that $(\mu _{u_{\gamma j_{\gamma }}}, f_{k}(x, u_{\gamma j_{\gamma }}))\rightarrow _{\gamma } (\mu , a)$. Then we have

$$\begin{aligned} {\hat{f}}_{k}(x, \mu )\ge \limsup _{\gamma }{\hat{f}}_{k}(x, u_{\gamma j_{\gamma }}) =a=\limsup _{\gamma }{\hat{f}}_{k}(x, \mu _{\gamma }). \end{aligned}$$

(iii) It is similar to the proof of (ii). The proof is complete. $\square$

Note that the proof of Lemmas 3.1 and 3.2 is similarly based on those in [12, 13]. Moreover, the Lipschitz property of the functions ${\hat{f}}_{k}(\cdot , \mu )$ and $F_{k}$ given in Proposition 3.2 plays a crucial role in establishing the main results. One has similar results for the Lipschitz property of ${\hat{g}}_{i}(\cdot , \nu )$ due to a similar construction (6).

Proposition 3.2

Let $x\in X$ and $k\in K$. If $f_{k}(\cdot , u_{k})$, $u_{k}\in U_{k}$ is uniformly locally Lipschitz at x with some given rank $L_{k}>0$, then

$$\begin{aligned}&|F_{k}(x_{1})-F_{k}(x_{2})|\le L_{k}\Vert x_{1}-x_{2}\Vert ,\;\forall \, x_{1}, x_{2}\in B(x,\delta _{k}). \end{aligned}$$

(9)

$$\begin{aligned}&|{\hat{f}}_{k}(x_{1},\mu )-{\hat{f}}_{k}(x_{2},\mu )|\le L_{k}\Vert x_{1}-x_{2}\Vert ,\;\forall \, x_{1}, x_{2}\in B(x,\delta _{k}),\;\;\forall \, \mu \in {\mathfrak {U}}_{k}. \end{aligned}$$

(10)

Proof

It follows from (2) that (9) holds as shown in [10]. Next let us derive (10).

$$\begin{aligned}&\left| {\hat{f}}_{k}(x_{1},\mu )-{\hat{f}}_{k}(x_{2},\mu )\right| \\&\quad =\left| \limsup _{\mu _{u}\rightarrow \mu , u\in U_{k}}f_{k}(x_{1}, u)-\limsup _{\mu _{u}\rightarrow \mu , u\in U_{k}}f_{k}(x_{2}, u)\right| \\&\quad =\Big |\sup \Big \{\limsup \limits _{\gamma }f_{k}(x_{1}, u_{\gamma }):\, (u_{\gamma })_{\gamma }\subseteq U_{k},\,\mu _{u_{\gamma }}\rightarrow \mu \Big \}\\&\qquad -\sup \Big \{\limsup \limits _{\gamma }f_{k}(x_{2}, u_{\gamma }):\, (u_{\gamma })_{\gamma }\subseteq U_{k},\,\mu _{u_{\gamma }}\rightarrow \mu \Big \}\Big |\\&\quad \le \sup \limsup \limits _{\gamma }|\{f_{k}(x_{1}, u_{\gamma })-f_{k}(x_{2}, u_{\gamma }): \, (u_{\gamma })_{\gamma }\subseteq U_{k},\,\mu _{u_{\gamma }}\rightarrow \mu \}|\\&\quad \le L_{k}\Vert x_{1}-x_{2}\Vert ,\;\forall \, x_{1}, x_{2}\in B(x,\delta _{k}),\;\;\forall \, \mu \in {\mathfrak {U}}_{k}. \end{aligned}$$

The last inequality assertion follows from (2) and the compactification process of the set $U_{k}$. The proof is complete. $\square$

Let us now present robust necessary conditions for the local robust weakly efficient solution of the problem (UMP), which is the main result of this paper.

Theorem 3.1

Let ${\bar{x}}\in loc S^{w}(RMP)$. Then there exist $\theta _{k}\ge 0$, $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that

$$\begin{aligned}&0\in \sum _{k\in K}\theta _{k}\,cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}})\Big \}+\sum _{i\in I}\lambda _{i}\,cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\Big \}, \end{aligned}$$

(11)

$$\begin{aligned}&\lambda _{i}\sup _{\nu ^{i}\in {\mathfrak {V}}_{i}}{\hat{g}}_{i}({\bar{x}}, \nu ^{i})=0, \;\;i\in I. \end{aligned}$$

(12)

Proof

Given arbitrary $k\in K$, we first prove the inclusion

$$\begin{aligned} \partial F_{k}({\bar{x}})\subseteq cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ): \mu \in {\mathfrak {U}}_{k}({\bar{x}})\Big \}. \end{aligned}$$

(13)

Assume by contradiction that there exists

$$\begin{aligned} x_{0}^{*}\in \partial F_{k}({\bar{x}})\setminus cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ): \mu \in {\mathfrak {U}}_{k}({\bar{x}})\Big \}. \end{aligned}$$

We deduce from Lemma 3.2 and Proposition 3.2 that ${\mathfrak {U}}_{k}(x)$ is nonempty compact and ${\hat{f}}_{k}(\cdot , \mu )$ is uniformly locally Lipschitz for $x\in X$. Thus $\partial _{1} {\hat{f}}_{k}(x, \mu )\ne \emptyset$ for $\mu \in {\mathfrak {U}}_{k}(x)$ and $x\in X$. So that $cl ^{*}co \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ): \mu \in {\mathfrak {U}}_{k}({\bar{x}})\}\ne \emptyset$ by the definition of ${\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu )$. According to the strong separation theorem, there exists $y\in X\setminus \{0\}$ such that

$$\begin{aligned} \langle x_{0}^{*}, y\rangle >\sup \left\{ \langle x^{*},y \rangle : x^{*}\in \bigcup _{\mu \in {\mathfrak {U}}_{k}({\bar{x}})}{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu )\right\} . \end{aligned}$$

(14)

Taking into account that $F_{k}$ is locally Lipschitz at ${\bar{x}}$ due to Proposition 3.2, there are sequences $(x_{n},\tau _{n})_{n}\subseteq X\times (0,+\infty )$ such that $x_{n}\rightarrow {\bar{x}}$, $\tau _{n}\rightarrow 0$ and

$$\begin{aligned} F_{k}^{\circ }({\bar{x}}, y)=\lim _{n}\frac{F_{k}(x_{n}+\tau _{n}y)-F_{k}(x_{n})}{\tau _{n}}. \end{aligned}$$

It follows from $x_{0}^{*}\in \partial F_{k}({\bar{x}})$ that $\langle x_{0}^{*}, y\rangle \le F_{k}^{\circ }({\bar{x}}, y)$, and then

$$\begin{aligned} \langle x_{0}^{*}, y\rangle \le \lim _{n}\frac{F_{k}(x_{n}+\tau _{n}y)-F_{k}(x_{n})}{\tau _{n}}. \end{aligned}$$

(15)

Since $x_{n}\rightarrow {\bar{x}}$, $\tau _{n}\downarrow 0$ as $n\rightarrow \infty$, we assume without loss of generality that $x_{n}, x_{n}+\tau _{n}y\in B({\bar{x}},\delta _{k})$. For each $n\in {\mathbb {N}}$, take a net $(\mu _{n\gamma })_{\gamma }\subseteq {\mathfrak {U}}_{k}(x_{n}+\tau _{n}y)$. By the nonempty and compact property of the set ${\mathfrak {U}}_{k}(x_{n}+\tau _{n}y)$, we deduce $\mu _{n\gamma }\rightarrow _{\gamma } \mu _{n}$ and $\mu _{n}\in {\mathfrak {U}}_{k}(x_{n}+\tau _{n}y)$, entailing that ${\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})= F_{k}(x_{n}+\tau _{n}y)$. Together with Lemma 3.1, we have

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})-{\hat{f}}_{k}(x_{n}, \mu _{n})\ge F_{k}(x_{n}+\tau _{n}y)-F_{k}(x_{n}). \end{aligned}$$

(16)

Invoking the mean value inequality for the function ${\hat{f}}_{k}(\cdot , \mu _{n})$ by Proposition 3.2 and Lemma 2.1, there exist $\theta _{n}\in (0,1)$ and $x_{n}^{*}\in \partial _{1} {\hat{f}}_{k}(x_{n}+\theta _{n}\tau _{n}y, \mu _{n})$ such that

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})-{\hat{f}}_{k}(x_{n},\mu _{n})=\langle x_{n}^{*}, \tau _{n}y\rangle , \end{aligned}$$

and $\Vert x_{n}^{*}\Vert _{*}\le L_{k}$. Since $B_{X^{*}}$ is compact with respect to the weak$^{*}$ topology, we suppose that $x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} z^{*}\in X^{*}$ (passing to a generalized subsequence if necessary). Therefore,

$$\begin{aligned} \limsup _{n}\frac{{\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})-{\hat{f}}_{k}(x_{n}, \mu _{n})}{\tau _{n}}=\langle z^{*}, y\rangle . \end{aligned}$$

Combining (15) and (16), we have

$$\begin{aligned} \langle x_{0}^{*}, y\rangle \le \langle z^{*}, y\rangle . \end{aligned}$$

(17)

Moreover, due to $\mu _{n}\in {\mathfrak {U}}_{k}(x_{n}+\tau _{n}y)$ and the compactness of ${\mathfrak {U}}_{k}$, without loss of generality we suppose that $\mu _{n}\rightarrow {\bar{\mu }}\in {\mathfrak {U}}_{k}$. It follows from Proposition 3.2 that

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})\le {\hat{f}}_{k}({\bar{x}}, \mu _{n})+L_{k}\Vert x_{n}+\tau _{n}y-{\bar{x}}\Vert . \end{aligned}$$

(18)

On the other hand, based on deriving in Lemma 3.1 we have

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu )\le F_{k}(x_{n}+\tau _{n}y),\quad \forall \,\mu \in {\mathfrak {U}}_{k}. \end{aligned}$$

(19)

Therefore, the following statement is derived from the combination of (18), (19) and ${\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu _{n})= F_{k}(x_{n}+\tau _{n}y)$.

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+\tau _{n}y, \mu )\le {\hat{f}}_{k}({\bar{x}}, \mu _{n})+L_{k}\Vert x_{n}+\tau _{n}y-{\bar{x}}\Vert ,\quad \forall \,\mu \in {\mathfrak {U}}_{k}. \end{aligned}$$

(20)

We conclude from assertion (ii) of Lemma 3.2 that ${\hat{f}}_{k}$ is u.s.c for uncertain parameters. Passing (20) to the superior limit as $n\rightarrow \infty$, we deduce that ${\hat{f}}_{k}({\bar{x}}, \mu )\le {\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})$ for all $\mu \in {\mathfrak {U}}_{k}$. Further, one can easily obtain that $F_{k}({\bar{x}})\le {\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})$, showing that ${\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$. Thus the above process provides that $x_{n}+\theta _{n}\tau _{n}y\rightarrow {\bar{x}}$, $\mu _{n}\in {\mathfrak {U}}_{k}(x_{n}+\tau _{n}y)$ with $\mu _{n}\rightarrow {\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$, and $x_{n}^{*}\in \partial _{1} {\hat{f}}_{k}(x_{n}+\theta _{n}\tau _{n}y, \mu _{n})$ with $x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} z^{*}$. This implies $z^{*}\in {\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})$ with ${\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$, contradicting (14) and (17). Therefore, we complete the proof of the inclusion (13). Given arbitrary $i\in I$, we proceed similarly to the proof of the following inclusion

$$\begin{aligned} \partial G_{i}({\bar{x}})\subseteq cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ): \nu \in {\mathfrak {V}}_{i}({\bar{x}})\Big \}. \end{aligned}$$

(21)

Furthermore, according to ${\bar{x}}\in loc S^{w}(RMP)$, it follows that there exists a neighborhood O of ${\bar{x}}$ such that

$$\begin{aligned} F(x)-F({\bar{x}})\notin -int {\mathbb {R}}_{+}^{l},\qquad \forall \,x\in C\cap O. \end{aligned}$$

(22)

We define $\psi (x):=\max \limits _{k\in K, i\in I}\{F_{k}(x)-F_{k}({\bar{x}}), G_{i}(x)\}$. Since ${\bar{x}}\in loc S^{w}(RMP)$, then it is a local minimizer of the unconstrained problem

$$\begin{aligned} \min \psi (x)\quad s.t. \quad x\in X. \end{aligned}$$

(23)

In fact, let us prove $\psi (x)\ge \psi ({\bar{x}})=0$ for all $x\in O$ arguing by contradiction. Assume that there is a point ${\hat{x}}\in O$ such that $\psi ({\hat{x}})<0$. If ${\hat{x}}\in C\cap O$ such that $\psi ({\hat{x}})<0$, then $F_{k}({\hat{x}})<F_{k}({\bar{x}})$ for all $k\in K$, which contradicts (22). If ${\hat{x}}\in O\backslash C$, then there is $i_{0}\in I$ such that $G_{i_{0}}({\hat{x}})>0$, which contradicts the initial assumption that $\psi ({\hat{x}})<0$. Invoking the generalized Fermat’s rule (Lemma 2.2) to the problem (23), one has $0\in \partial \psi ({\bar{x}})$. Applying Lemma 2.3 to the function $\psi$, we have

$$\begin{aligned}\partial \psi ({\bar{x}})\subseteq co \left\{ \partial F_{k}({\bar{x}}), \partial G_{i}({\bar{x}}):\,k\in K,\, G_{i}({\bar{x}})=0,\, i\in I \right\} . \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} \begin{aligned} 0\in \Bigg \{&\sum _{k\in K}\theta _{k}\partial F_{k}({\bar{x}})+ \sum _{i\in I}\lambda _{i}\partial G_{i}({\bar{x}}):\theta _{k}\ge 0,\,k\in K,\,\lambda _{i}\ge 0,\, \lambda _{i}G_{i}({\bar{x}})=0,\, i\in I,\\&\sum _{k\in K}\theta _{k}+ \sum _{i\in I}\lambda _{i}=1 \Bigg \}. \end{aligned} \end{aligned}$$

Combining this with (13) and (21), we conclude that (11) and (12) hold. The proof is complete. $\square$

Compared with the existing results in [6, 8,9,10, 15, 16, 21, 22, 27, 31], the assumptions of Theorem 3.1 are weaker. In addition, Theorem 3.1 provides a unified framework of robust necessary optimality conditions for the problem (UMP). Now we present some corollaries of Theorem 3.1, which can be unified and generalized by using Theorem 3.1.

Corollary 3.1

Let ${\bar{x}}\in loc S^{w}(RMP)$. Suppose that the following assumptions hold for any $k\in K$ and $i\in I$.

• (i) $U_{k}$ and $V_{i}$ are compact Hausdorff;

• (ii) $u_{k}\in U_{k}\mapsto f_{k}(x,u_{k})$ and $v_{i}\in V_{i}\mapsto g_{i}(x,v_{i})$ are u.s.c for each $x \in B({\bar{x}},\delta _{k})$ and $x \in B({\bar{x}},\eta _{i})$, respectively;

• (iii) $(x, u_{k})\in B({\bar{x}},\delta _{k})\times U_{k}\rightrightarrows \partial _{1} f_{k}(x, u_{k})$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{u}}_{k})$ for each ${\bar{u}}_{k}\in U_{k}({\bar{x}})$, and $(x, v_{i})\in B({\bar{x}},\eta _{i})\times V_{i}\rightrightarrows \partial _{1} g_{i}(x, v_{i})$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{v}}_{i})$ for each ${\bar{v}}_{i}\in V_{i}({\bar{x}})$.

Then there exist $\theta _{k}\ge 0$, $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that

$$\begin{aligned}&0\in \sum _{k\in K}\theta _{k}\,cl ^{*}co \Big \{\partial _{1} f_{k}({\bar{x}}, u_{k}): u_{k}\in U_{k}({\bar{x}})\Big \}+\sum _{i\in I}\lambda _{i}\,cl ^{*}co \Big \{\partial _{1} g_{i}({\bar{x}}, v_{i}): v_{i}\in V_{i}({\bar{x}})\Big \}, \end{aligned}$$

(24)

$$\begin{aligned}&\lambda _{i}\sup _{v_{i}\in V_{i}}g_{i}({\bar{x}}, v_{i})=0, \;\;i\in I. \end{aligned}$$

(25)

Proof

Since $U_{k}$, $k\in K$, and $V_{i}$, $i\in I$ are compact Hausdorff; thus, completely regular, we obtain that $U_{k}\equiv {\mathfrak {U}}_{k}$, $k\in K$, and $V_{i}\equiv {\mathfrak {V}}_{i}$, $i\in I$. On the one hand, for any $x\in X$, $k\in K$ and $u\in U_{k}$,

$$\begin{aligned} {\hat{f}}_{k}(x, \mu _{u})=\limsup _{\mu _{s}\rightarrow \mu _{u}, s\in U_{k}}f_{k}(x, s)=\limsup _{s\rightarrow u, s\in U_{k}}f_{k}(x, s)\le f_{k}(x, u), \end{aligned}$$

where the validity of the last inequality from assertion (ii). On the other hand, ${\hat{f}}_{k}(x, \mu _{u})\ge f_{k}(x, u)$ by (5). Thus the functions ${\hat{f}}_{k}$ and $f_{k}$ coincide, and a similar result of ${\hat{g}}_{i}$ and $g_{i}$ follows. Consequently, it follows from Theorem 3.1, Definition 2.1 and assertion (iii) that (24) and (25) hold. The proof is complete. $\square$

Zheng and Ng [33] derived that the closedness of the partial subdifferential operation is valid for subsmooth functions. Therefore, we further get the following corollary.

Corollary 3.2

Let ${\bar{x}}\in loc S^{w}(RMP)$. Suppose that the following assumptions hold for any $k\in K$ and $i\in I$.

• (i) $U_{k}$ and $V_{i}$ are compact Hausdorff;

• (ii) $u_{k}\in U_{k}\mapsto f_{k}(x,u_{k})$ and $v_{i}\in V_{i}\mapsto g_{i}(x,v_{i})$ are u.s.c for each $x \in B({\bar{x}},\delta _{k})$ and $x \in B({\bar{x}},\eta _{i})$, respectively;

• (iii) $f_{k}(x,u_{k})$, $u_{k}\in U_{k}$ and $g_{i}(x,v_{i})$, $v_{i}\in V_{i}$ are uniformly subsmooth at ${\bar{x}}$, that is, for any $\alpha _{k}>0$ and $\beta _{i}>0$ there are $\delta _{k}>0$ and $\eta _{i}>0$ such that

  $$\begin{aligned} f_{k}(y,u_{k})-f_{k}(x,u_{k})\ge \langle x^{*}, y-x\rangle -\alpha _{k}\Vert y-x\Vert ,\quad \forall y, x\in B({\bar{x}}, \delta _{k}),\;\;x^{*}\in \partial _{1} f_{k}(x, u_{k}); \end{aligned}$$
  $$\begin{aligned} g_{i}(y,v_{i})-g_{i}(x,v_{i})\ge \langle x^{*}, y-x\rangle -\beta _{i}\Vert y-x\Vert ,\quad \forall y, x\in B({\bar{x}}, \eta _{i}),\;\;x^{*}\in \partial _{1} g_{i}(x,v_{i}). \end{aligned}$$

Then there exist $\theta _{k}\ge 0$, $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that (24) and (25) hold.

Proof

According to Theorem 3.1 and Corollary 3.1, it remains to prove that $(x, u_{k})\in B({\bar{x}},\delta _{k})\times U_{k}\rightrightarrows \partial _{1} f_{k}(x, u_{k})$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{u}}_{k})$ for each ${\bar{u}}_{k}\in U_{k}({\bar{x}})$, and $(x, v_{i})\in B({\bar{x}},\eta _{i})\times V_{i}\rightrightarrows \partial _{1} g_{i}(x, v_{i})$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{v}}_{i})$ for each ${\bar{v}}_{i}\in V_{i}({\bar{x}})$. Invoking Definition 2.1, we need claim that $x_{n}^{*}\in \partial _{1}f_{k}(x_{n}, u_{n})$ with $x_{n}\rightarrow {\bar{x}}$, $u_{n}\in U_{k}(x_{n})$, $u_{n}\rightarrow {\bar{u}}$, $x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} x^{*}$, implies that $x^{*}\in \partial _{1} f_{k}({\bar{x}}, {\bar{u}})$ with ${\bar{u}}\in U_{k}({\bar{x}})$. Assume without loss of generality that $f_{k}({\bar{x}},u_{n})\rightarrow f_{k}({\bar{x}},{\bar{u}})$ due to assertion (ii). In fact, by the uniformly locally Lipschitz property of $f_{k}$ at ${\bar{x}}\in X$, we get $f_{k}(x_{n}, u_{n})\le f_{k}({\bar{x}}, u_{n})+L_{k}\Vert x_{n}-{\bar{x}}\Vert .$ On the other hand, we have $f_{k}(x_{n}, u)\le F_{k}(x_{n})$, for all $u\in U_{k}.$ Together with $u_{n}\in U_{k}(x_{n})$, one has

$$\begin{aligned} f_{k}(x_{n}, u)\le f_{k}({\bar{x}}, u_{n})+L_{k}\Vert x_{n}-{\bar{x}}\Vert ,\quad \forall u\in U_{k}. \end{aligned}$$

(26)

Therefore, $f_{k}({\bar{x}}, u)\le f_{k}({\bar{x}}, {\bar{u}})$ for all $u\in U_{k}$ follows from (26) due to assertion (ii) and the uniformly locally Lipschitz property of $f_{k}$ by passing to the superior limit as $n\rightarrow \infty$. Further, one can obtain that $F_{k}({\bar{x}})\le f_{k}({\bar{x}}, {\bar{u}})$, which gives ${\bar{u}}\in U_{k}({\bar{x}})$. Moreover, we derive from assertions (ii) and (iii) that

$$\begin{aligned} \begin{aligned}&f_{k}(x,{\bar{u}})-f_{k}({\bar{x}},{\bar{u}})\\&\quad \ge \limsup _{n}(f_{k}(x,u_{n})-f_{k}({\bar{x}},u_{n})+L_{k}\Vert x_{n}-{\bar{x}}\Vert )\\&\quad \ge \limsup _{n}(f_{k}(x,u_{n})-f_{k}(x_{n},u_{n}))\\&\quad \ge \limsup _{n}(\langle x_{n}^{*}, x-x_{n}\rangle -\alpha _{k}\Vert x-x_{n}\Vert )\\&\quad \ge \langle x^{*}, x-{\bar{x}}\rangle -\alpha _{k}\Vert x-{\bar{x}}\Vert \\ \end{aligned} \end{aligned}$$

whenever $x\in B({\bar{x}}, \delta _{k})$. Since the number $\alpha _{k}>0$ was chosen arbitrarily, then we have $x^{*}\in {\widehat{\partial }}_{1} f_{k}({\bar{x}}, {\bar{u}})\subseteq \partial _{1} f_{k}({\bar{x}}, {\bar{u}})$. Therefore, we obtain ${\overline{\partial }}_{1}f_{k}({\bar{x}}, {\bar{u}})= \partial _{1}f_{k}({\bar{x}}, {\bar{u}})$ with ${\bar{u}}\in U_{k}({\bar{x}})$. The case of the weak$^{*}$ closed property for $\partial _{1} g_{i}(x, v_{i})$ can be proved similarly. The proof is complete. $\square$

Remark 3.2

Compared with the previous literature, one has some notes as follows:

• (i) Theorem 3.1 provides robust necessary optimality conditions of the problem (UMP) not only in the nonconvex and nonsmooth setting but also in noncompact frameworks, dropping out the standard assumptions of the compactness of uncertainty sets and the continuity of the functions with respect to uncertain parameters. Obviously hypotheses required in Theorem 3.1 are weaker than those in Corollaries 3.1 and 3.2, and [6, 8,9,10, 15, 16, 21, 22, 27, 31]. In other words, Theorem 3.1 can be applied to a wide range of the problem (UMP).

• (ii) It is worth mentioning that Chuong [9] did not directly add the compactness requirement to $U_{k}$ and $V_{i}$ and imposed the compactness assumptions on $U_{k}^{\varepsilon _{k}}({\bar{x}})$ and $V_{i}^{\epsilon _{i}}({\bar{x}})$. No matter what the case, the assumptions imposed in Corollaries 3.1 and 3.2, and [6, 8,9,10, 15, 16, 21, 22, 27, 31] ensure that $U_{k}(x)$ and $V_{i}(x)$ are nonempty for $x\in B({\bar{x}}, \delta _{k})$. In contrast to this, $U_{k}(x)$ and $V_{i}(x)$ may be empty sets in situations of Theorem 3.1.

• (iii) Corollary 3.1 is a generalization of [8], in which objective functions do not contain uncertain parameters, and all of the sets were considered in finite-dimensional spaces. Corollaries 3.1 and 3.2 suitably extend the results of [6, 15, 21, 22] both for the hypotheses and the space of the sets as well.

• (iv) Corollaries 3.1 and 3.2 can be viewed as appropriate extensions of Theorem 3.1. As shown in [9], robust necessary optimality conditions were formulated when $U_{k}$ and $V_{i}$ were replaced all by $U_{k}^{\varepsilon _{k}}({\bar{x}})$ and $V_{i}^{\epsilon _{i}}({\bar{x}})$ in Corollary 3.1. This clearly implies that the results still hold when we replace all $U_{k}$ and $V_{i}$ with $U_{k}^{\varepsilon _{k}}({\bar{x}})$ and $V_{i}^{\epsilon _{i}}({\bar{x}})$ in Corollary 3.2.

The following simple example illustrates the application of Theorem 3.1 for the problem (UMP), to which Corollaries 3.1 and 3.2, and [6, 8,9,10, 15, 16, 21, 22, 27, 31] do not apply.

Example 3.1

Consider the problem (UMP). Take $f_{1}(x, n)=\max \left\{ \frac{n x}{n+1}, 0\right\}$, $f_{2}(x, n)=\max \left\{ -\frac{n x}{n+1}, 0\right\}$, and $g(x, n)=x-\frac{1}{n+1}$, where $X={\mathbb {R}}$, $U_{1}=U_{2}=V={\mathbb {N}}$. For the illustration let us consider a point ${\bar{x}}=0$.

It is easy to verify that $f_{1}(\cdot , n)$, $f_{2}(\cdot , n)$, and $g(\cdot , n)$, $n\in {\mathbb {N}}$ satisfy uniformly locally Lipschitzian for all $x\in X$. One can check directly from the definitions that $F_{1}(x)=\max \{x, 0\}$, $F_{2}(x)=\max \{-x, 0\}$, and $G(x)=x$, and so that ${\bar{x}}=0\in loc S^{w}(RMP)$.

Step 1: We calculate that $U_{1}=U_{1}^{\varepsilon _{1}}(0)=U_{1}(0)={\mathbb {N}}$, $U_{2}=U_{2}^{\varepsilon _{2}}(0)=U_{2}(0)={\mathbb {N}}$, and $V^{\epsilon }(0)=\left\{ n\in {\mathbb {N}}: \frac{1}{n+1}\le \epsilon \right\}$, $V(0)=\emptyset$. Observe that the results from Corollaries 3.1 and 3.2, [9, Theorem 3.10], and [6, 8, 10, 15, 16, 21, 22, 27, 31] are not applicable in this setting, because ${\mathbb {N}}$ is not compact and $V(0)=\emptyset$.

Step 2: Since ${\mathbb {N}}$ is closed set, then for any nets $(n_{\gamma })_{\gamma }\subseteq {\mathbb {N}}$, $n_{\gamma }\rightarrow n\in {\mathbb {N}}$. Thus $\varphi (n_{\gamma })\rightarrow \varphi (n)$ for every $\varphi \in C({\mathbb {N}},[0,1])$. This says that $\mu _{n_{\gamma }}\rightarrow \mu _{n}$ in $[0, 1]^{C({\mathbb {N}},[0,1])}$. Thus, ${\mathbb {N}}\subseteq {\mathfrak {U}}_{1}={\mathfrak {U}}_{2}={\mathfrak {V}}$. The Stone–C̆ech compactification of ${\mathbb {N}}$ can be formulated as follows.

$$\begin{aligned} \begin{aligned} {\mathfrak {U}}_{1}={\mathfrak {U}}_{2}&= {\mathbb {N}}\cup \left\{ \lim _{\gamma }\mu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq {\mathbb {N}},\,n_{\gamma }\rightarrow +\infty \right\} \\&={\mathbb {N}}\cup \left\{ \lim _{\gamma }\nu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq {\mathbb {N}},\,n_{\gamma }\rightarrow +\infty \right\} ={\mathfrak {V}}.\\ \end{aligned} \end{aligned}$$

For simplicity, we denote

$$\begin{aligned} S:=\left\{ \lim _{\gamma }\mu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq {\mathbb {N}},\,n_{\gamma }\rightarrow +\infty \right\} =\left\{ \lim _{\gamma }\nu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq {\mathbb {N}},\,n_{\gamma }\rightarrow +\infty \right\} . \end{aligned}$$

Next, we present the u.s.c regularized functions by (4). One has ${\hat{f}}_{1}(x, \mu )= f_{1}(x, n)$ when $\mu \equiv n\in {\mathbb {N}}$, and ${\hat{f}}_{1}(x, \mu )= \limsup \limits _{\mu _{n}\rightarrow \mu }f_{1}(x, n)=\max \{x, 0\}$ when $\mu \in S$. Similarly, we obtain that ${\hat{f}}_{2}(x, \mu )= f_{2}(x, n)$ when $\mu \equiv n\in {\mathbb {N}}$, and ${\hat{f}}_{2}(x, \mu )= \limsup \limits _{\mu _{n}\rightarrow \mu }f_{2}(x, n)=\max \{-x, 0\}$ when $\mu \in S$, as well as, ${\hat{g}}(x, \nu )= g(x, n)$ when $\nu \equiv n\in {\mathbb {N}}$, and ${\hat{g}}(x, \nu )= \limsup \limits _{\nu _{n}\rightarrow \nu }g(x, n)=x$ when $\nu \in S$. Moreover, we deduce ${\mathfrak {U}}_{1}(0)= {\mathfrak {U}}_{1}$, ${\mathfrak {U}}_{2}(0)= {\mathfrak {U}}_{2}$, and ${\mathfrak {V}}(0)=S$.

Step 3: We compute the corresponding Clarke subdifferential of the above functions.

$$\begin{aligned} \partial _{1}f_{1}(x, n)=\left\{ \begin{aligned}&\left\{ \frac{n}{n+1}\right\}&\quad x>0; \\&\left[ 0, \frac{n}{n+1}\right]&\quad x=0;\\&\{0\}&\quad x<0. \end{aligned} \right. \end{aligned}$$

$$\begin{aligned} \partial \left( \max \{x, 0\}\right) =\left\{ \begin{aligned}&\{1\}&\quad x>0; \\&[0, 1]&\quad x=0;\\&\{0\}&\quad x<0. \end{aligned} \right. \end{aligned}$$

Therefore, we obtain $\left\{ {\overline{\partial }}_{1}{\hat{f}}_{1}(0, \mu ): \mu \in {\mathfrak {U}}_{1}(0)\right\} =[0, 1]$ by (1). Similarly, we have

$$\begin{aligned}\left\{ {\overline{\partial }}_{1}{\hat{f}}_{2}(0, \mu ): \mu \in {\mathfrak {U}}_{2}(0)\right\} =[-1, 0]\;\; and \;\; \left\{ {\overline{\partial }}_{1}{\hat{g}}(0, \nu ): \nu \in {\mathfrak {V}}(0)\right\} =\{1\}. \end{aligned}$$

Thus there exist $\theta _{1}=\frac{1}{4}$, $\theta _{2}=\frac{1}{2}$ and $\lambda =\frac{1}{4}$ such that Theorem 3.1 holds.

As shown by Clarke [10], if $U_{k}$ is compact Hausdorff and the function $f_{k}$ is convex with respect to the decision variable x and continuous with respect to the uncertain parameter u, then $(x, u)\in B({\bar{x}},\delta )\times U_{k}\rightrightarrows \partial _{1} f_{k}(x, u)$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{u}})$ for any given $k\in K$. Moreover, the subdifferential $\partial _{1} f_{k}(x, u)$ coincides with the subdifferential in the sense of convex analysis. Now we remove the compactness of uncertainty sets and the continuity of uncertain parameters for the convex functions, which are able to achieve more general results.

Corollary 3.3

Let ${\bar{x}}\in loc S^{w}(RMP)$. If $f_{k}(\cdot , u_{k})$, $g_{i}(\cdot , v_{i})$ are convex on X for each $u_{k}\in U_{k}$, $k\in K$ and $v_{i}\in V_{i}$, $i\in I$ respectively, then there exist $\theta _{k}\ge 0$, $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that

$$\begin{aligned}&0\in \sum _{k\in K}\theta _{k}\,cl ^{*}co \Big \{\partial _{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}})\Big \}+\sum _{i\in I}\lambda _{i}\,cl ^{*}co \Big \{\partial _{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\Big \}, \\&\lambda _{i}\sup _{\nu ^{i}\in {\mathfrak {V}}_{i}}{\hat{g}}_{i}({\bar{x}}, \nu ^{i})=0, \;\;i\in I. \end{aligned}$$

Proof

Since $f_{k}(\cdot , u_{k})$, $g_{i}(\cdot ,v_{i})$ are convex on X for each $u_{k}\in U_{k}$, $k\in K$ and $v_{i}\in V_{i}$, $i\in I$, then ${\hat{f}}_{k}(\cdot , \mu )$, ${\hat{g}}_{i}(\cdot , \nu )$ are convex on X for each $\mu \in {\mathfrak {U}}_{k}$, $k\in K$ and $\nu \in {\mathfrak {V}}_{i}$, $i\in I$. This corollary follows immediately from Theorem 3.1 once one establishes that the multifunction $(x, \mu )\in B({\bar{x}},\delta _{k})\times {\mathfrak {U}}_{k}\rightrightarrows \partial _{1} {\hat{f}}_{k}(x, \mu )$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{\mu }})$ for each ${\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$, and $(x, \nu )\in B({\bar{x}},\eta _{i})\times {\mathfrak {V}}_{i}\rightrightarrows \partial _{1} {\hat{g}}_{i}(x, \nu )$ is weak$^{*}$ closed at $({\bar{x}}, {\bar{\nu }})$ for each ${\bar{\nu }}\in {\mathfrak {V}}_{i}({\bar{x}})$. To see this, let $x_{n}^{*}\in \partial _{1}{\hat{f}}_{k}(x_{n}, \mu _{n})$, where $x_{n}\rightarrow {\bar{x}},\, \mu _{n}\in {\mathfrak {U}}_{k}(x_{n}),\,\mu _{n}\rightarrow {\bar{\mu }},$ and $x_{n}^{*}{\mathop {\longrightarrow }\limits ^{w^{*}}} x^{*}$. It remains to prove that $x^{*}\in \partial _{1}{\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})$ with ${\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$. Assume without loss of generality that ${\hat{f}}_{k}({\bar{x}},\mu _{n})\rightarrow {\hat{f}}_{k}({\bar{x}},{\bar{\mu }})$ by Lemma 3.2. As follows from the proof of Theorem 3.1, one has ${\bar{\mu }}\in {\mathfrak {U}}_{k}({\bar{x}})$ by $\mu _{n}\in {\mathfrak {U}}_{k}(x_{n})$, $x_{n}\rightarrow {\bar{x}}$ and $\mu _{n}\rightarrow {\bar{\mu }}$. Now for any d sufficiently small,

$$\begin{aligned} {\hat{f}}_{k}(x_{n}+d, \mu _{n})-{\hat{f}}_{k}(x_{n}, \mu _{n})\ge \langle x_{n}^{*}, d\rangle , \end{aligned}$$

because ${\hat{f}}_{k}(\cdot , \mu _{n})$ is convex on X. Together with (10), one has

$$\begin{aligned} {\hat{f}}_{k}({\bar{x}}+d, \mu _{n})-{\hat{f}}_{k}({\bar{x}}, \mu _{n})\ge \langle x_{n}^{*}, d\rangle -2L_{k}\Vert x_{n}-{\bar{x}}\Vert . \end{aligned}$$

By Lemma 3.2, taking the superior limit as $n\rightarrow \infty$ yields

$$\begin{aligned} {\hat{f}}_{k}({\bar{x}}+d, {\bar{\mu }})-{\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})\ge \langle x^{*}, d\rangle . \end{aligned}$$

This implies $x^{*}\in \partial _{1}{\hat{f}}_{k}({\bar{x}}, {\bar{\mu }})$. The proof is complete. $\square$

As mentioned in [8], the hypothesis associated with the closeness of the partial subdifferential operation with respect to the first variable x is a relaxed property of the subdifferential of the convex functions. This property holds for a more general class of subsmooth functions under assertions (i) and (ii) of Corollary 3.2 as well.

4 Constraint Qualification and Regularity Condition

The results of Sect. 3 merely arrive at FJ type robust necessary optimality conditions for the problem (UMP). Note that the multipliers rule of the FJ type implies that the multipliers $\theta _{k}$, $k\in K$ corresponding to objective functions may be all zero. Obviously, if $\theta _{k}$ are all zero for $k\in K$, then objective functions no longer work in optimality conditions. To overcome the drawback, some hypotheses need to be imposed, which ensure the multipliers of objective functions not all zero. To proceed, we add the constraint qualification (resp. regularity condition) to obtain the WKKT (resp. SKKT) robust necessary optimality results.

The following constraint qualification is a very general assumption for the study of the problem (UMP).

Definition 4.1

The robust Mangasarian-Fromovitz constraint qualification (RMFCQ) holds at ${\bar{x}}\in C$ if

$$\begin{aligned} 0\notin cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}}), \,i\in I\right\} . \end{aligned}$$

(27)

Based on the obtained result in Theorem 3.1 together with the new concept of the RMFCQ, we establish WKKT robust necessary optimality conditions of the problem (UMP) for the local robust weakly efficient solution as follows.

Theorem 4.1

Let ${\bar{x}}\in loc S^{w}(RMP)$ and the RMFCQ hold at ${\bar{x}}$. Then there exist $\theta _{k}\ge 0$, $k\in K$ not all zero and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that (11) and (12) hold.

Proof

Based on Theorem 3.1, we continue to show that the multipliers of objective functions are not all zero. Assume by contradiction that $\theta _{k}=0$, for all $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$ with $\sum _{i\in I}\lambda _{i}=1$. Thus, we derive from (11) and (12) that

$$\begin{aligned}0\in \sum _{i\in I}\lambda _{i}\,cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\right\} . \end{aligned}$$

Therefore, $0\in cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}}), \,i\in I\right\}$, which contradicts (27). The proof is complete. $\square$

Remark 4.1

Employing Example 3.1 again, the RMFCQ holds at ${\bar{x}}=0$. Thus, Example 3.1 also illustrates the validity of WKKT robust necessary conditions in Theorem 4.1. Moreover, the formula (27) in Definition 4.1 reduces to $0\notin cl ^{*}co \left\{ \partial _{1} g_{i}({\bar{x}}, v_{i}): v_{i}\in V_{i}({\bar{x}}),\,i\in I\right\}$ under the assumptions made in Corollaries 3.1 and 3.2, which coincides with that in [8, 9]. We also obtain the multipliers of objective functions not all zero when we add the RMFCQ to Corollaries 3.1, 3.2 and 3.3.

Many papers [6,7,8,9, 15, 16, 21] obtained WKKT robust necessary optimality conditions for the problem (UMP). However, to the best knowledge of us, few papers address SKKT robust necessary optimality conditions for the problem (UMP). Every Lagrange multiplier associated with the objectives is active in SKKT robust necessary optimality conditions. It is therefore significant to develop SKKT conditions for the problem (UMP). Thus, we introduce a regularity condition and study SKKT robust necessary optimality conditions of the problem (UMP) for the local robust weakly efficient solution.

Definition 4.2

The robust Mangasarian-Fromovitz regularity condition (RMFRC) holds at ${\bar{x}}\in C$ if for each $j\in K$,

$$\begin{aligned} 0\notin cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k})\bigcup {\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}}),\,k\in K\setminus \{j\},\;\nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}}), \,i\in I\right\} . \end{aligned}$$

(28)

Theorem 4.2

Let ${\bar{x}}\in loc S^{w}(RMP)$ and the RMFRC hold at ${\bar{x}}$. Then there exist $\theta _{k}>0$, for all $k\in K$ and $\lambda _{i}\ge 0$, $i\in I$ such that (11) and (12) hold.

Proof

Based on Theorem 3.1, we fix an arbitrary $j\in K$ and first prove that $\theta _{j}>0$, $\theta _{k}\ge 0$, $k\in K\setminus \{j\}$ and $\lambda _{i}\ge 0$, $i\in I$, with $\sum _{k\in K}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$, such that (11) and (12) hold. Otherwise, one has $\theta _{j}=0$, $\theta _{k}\ge 0$, $k\in K\setminus \{j\}$, $\lambda _{i}\ge 0$, $i\in I$ and $\sum _{k\in K\setminus \{j\}}\theta _{k}+\sum _{i\in I}\lambda _{i}=1$ such that $0\in \sum _{k\in K\setminus \{j\}}\theta _{k}\,cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}})\right\} +\sum _{i\in I}\lambda _{i}\,cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\Big \}$ by Theorem 3.1. Therefore, one has

$$\begin{aligned}0\in cl ^{*}co \left\{ {\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k})\bigcup {\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}}),\,k\in K\setminus \{j\},\;\nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}}), \,i\in I\right\} ,\end{aligned}$$

which contradicts (28). Thus, for each $j\in K$, we have $\theta _{j}^{(j)}>0$, $\theta _{k}^{(j)}\ge 0$, $k\in K\setminus \{j\}$ and $\lambda _{i}^{(j)}\ge 0$, $i\in I$, such that

$$\begin{aligned} \begin{aligned} 0&\in \,\theta _{j}^{(j)}cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{j}({\bar{x}}, \mu ^{j}): \mu ^{j}\in {\mathfrak {U}}_{j}({\bar{x}})\Big \}\\&\quad +\sum _{k\in K\setminus \{j\}} \theta _{k}^{(j)}cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}})\Big \}\\&\quad +\sum _{i\in I}\lambda _{i}^{(j)}cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\Big \}. \end{aligned} \end{aligned}$$

(29)

Summing (29) over all j and rearranging conveniently the coefficients, we get

$$\begin{aligned} 0\in \sum _{k\in K}{\hat{\theta }}_{k}\,cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{f}}_{k}({\bar{x}}, \mu ^{k}): \mu ^{k}\in {\mathfrak {U}}_{k}({\bar{x}})\Big \}+\sum _{i\in I}{\hat{\lambda }}_{i}\,cl ^{*}co \Big \{{\overline{\partial }}_{1} {\hat{g}}_{i}({\bar{x}}, \nu ^{i}): \nu ^{i}\in {\mathfrak {V}}_{i}({\bar{x}})\Big \}, \end{aligned}$$

in which ${\hat{\theta }}_{k}=\theta _{k}^{(k)}+\sum _{j=1,j\ne k}^{l}\theta _{k}^{(j)}>0$, for all $k\in K$ and ${\hat{\lambda }}_{i}=\sum _{j=1}^{l}\lambda _{i}^{(j)}\ge 0$, $i\in I$. The proof is complete. $\square$

Remark 4.2

The formula (28) in Definition 4.2 reduces to

$$\begin{aligned}0\notin cl ^{*}co \{\partial _{1} f_{k}({\bar{x}}, u_{k})\bigcup \partial _{1} g_{i}({\bar{x}}, v_{i}): u_{k}\in U_{k}({\bar{x}}),\, k\in K\setminus \{j\},\,v_{i}\in V_{i}({\bar{x}}),\,i\in I\} \end{aligned}$$

under assumptions made in Corollaries 3.1 and 3.2. Adding the RMFRC to Corollaries 3.1, 3.2 and 3.3, we arrive at $\theta _{k}>0$ for all $k\in K$.

The following example illustrates SKKT robust necessary conditions in Theorem 4.2.

Example 4.1

Consider the problem (UMP). Take $f_{1}(x, n)=\max \left\{ -\frac{n x_{1}}{n+1}, 0\right\} +x_{2}$,

$f_{2}(x, u_{2})=x_{1}+|x_{2}|-u_{2}$, and $g(x, v)=x_{1}-\frac{1}{v}$, where $X={\mathbb {R}}^{2}$, $U_{1}={\mathbb {N}}$, $U_{2}=(0, 1)$ and $V={\mathbb {Z}}_{+}$. For the illustration let us consider a point $\bar{x}=(0, 0)^{T}$.

It is easy to verify that $f_{1}(\cdot , n)$, $n\in \mathbb {N}$, $f_{2}(\cdot , u_{2})$, $u_{2}\in (0, 1)$ and $g(\cdot , v)$, $v\in \mathbb {Z}_{+}$ satisfy uniformly locally Lipschitzian for all $x\in X$. One can derive directly from the definitions that $F_{1}(x)=\max \{-x_{1}, 0\}+x_{2}$, $F_{2}(x)=x_{1}+|x_{2}|$, $G(x)=x_{1}$, and $\bar{x}=(0, 0)^{T}\in loc S^{w}(RMP)$. Now we deduce the Stone–C̆ech compactification of uncertainty sets.

$$\begin{aligned} \begin{aligned}&\mathfrak {U}_{1}= \mathbb {N}\cup \left\{ \lim _{\gamma }\mu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq \mathbb {N},\,n_{\gamma }\rightarrow +\infty \right\} , \\&\mathfrak {U}_{2}=[0, 1],\\&\mathfrak {V}=\mathbb {Z}_{+}\cup \left\{ \lim _{\gamma }\nu _{v_{\gamma }}:\, (v_{\gamma })_{\gamma }\subseteq \mathbb {Z}_{+},\,v_{\gamma }\rightarrow +\infty \right\} . \end{aligned} \end{aligned}$$

For simplicity, we denote

$$\begin{aligned} A:= & {} \left\{ \lim _{\gamma }\mu _{n_{\gamma }}:\, (n_{\gamma })_{\gamma }\subseteq \mathbb {N},\,n_{\gamma }\rightarrow +\infty \right\} \;\;and \\ B:= & {} \left\{ \lim _{\gamma }\nu _{v_{\gamma }}:\, (v_{\gamma })_{\gamma }\subseteq \mathbb {Z}_{+},\,v_{\gamma }\rightarrow +\infty \right\} . \end{aligned}$$

Next, we derive u.s.c regularized functions by (4). One has $\hat{f}_{1}(x, \mu ^{1})= f_{1}(x, n)$ when $\mu ^{1}\equiv n\in \mathbb {N}$, and $\hat{f}_{1}(x, \mu ^{1})= \limsup \limits _{\mu _{n}\rightarrow \mu ^{1}}f_{1}(x, n)=\max \{-x_{1}, 0\}+x_{2}$ when $\mu ^{1}\in A$. $\hat{f}_{2}(x, \mu ^{2})= x_{1}+|x_{2}|-\mu ^{2}$, $\mu ^{2}\in [0, 1]$. $\hat{g}(x, \nu )= g(x, v)$ when $\nu \in \mathbb {Z}_{+}$, and $\hat{g}(x, \nu )= \limsup \limits _{\nu _{v}\rightarrow \nu }g(x, v)=x_{1}$ when $\nu \in B$. Moreover, we have $\mathfrak {U}_{1}(\bar{x})= \mathfrak {U}_{1}$, $\mathfrak {U}_{2}(\bar{x})= \{0\}$, and $\mathfrak {V}(\bar{x})=B$. Further, we compute the corresponding subdifferential (1) for the above functions. $\left\{ \overline{\partial }_{1}\hat{f}_{1}(\bar{x}, \mu ^{1}): \mu ^{1}\in \mathfrak {U}_{1}(\bar{x})\right\} =[-1, 0]\times \{1\},$ $\left\{ \overline{\partial }_{1}\hat{f}_{2}(\bar{x}, \mu ^{2}): \mu ^{2}\in \mathfrak {U}_{2}(\bar{x})\right\} =\{1\}\times [-1, 1],$ and $\left\{ \overline{\partial }_{1}\hat{g}(\bar{x}, \nu ): \nu \in \mathfrak {V}(\bar{x})\right\} =\{(1,0)^{T}\}.$ Then we verify that the RMFRC holds at $\bar{x}$. Thus, there exist $\theta _{1}=\frac{1}{2}$, $\theta _{2}=\frac{1}{2}$ and $\lambda =0$ such that Theorem 4.2 holds.

5 Conclusions

The compactification of uncertainty sets and u.s.c regularized functions allow us to remove the compact and continuous setting. This paper focuses on developing a unified theory of robust necessary optimality conditions for the problem (UMP), free of assumptions on uncertainty sets and uncertain parameters of original functions. Compared with the existing ones [6,7,8,9,10, 15, 16, 21, 22, 27, 31], Theorem 3.1 imposes weaker assumptions and has a wider range of applications, especially for the nonconvex, nonsmooth and noncompact robust multiobjective optimization. Simultaneously, the RMFCQ and the RMFRC are proposed to ensure WKKT and SKKT robust necessary optimality conditions for the problem (UMP), respectively. In future research, it is interesting to study the robust sufficient optimality conditions, duality, algorithm, radius and others for the problem (UMP) via robust necessary optimality conditions provided in this paper, similar to [5, 9, 28, 30].