Decomposition and Mean-Field Approach to Mixed Integer Optimal Compensation Problems

Abstract

Mixed integer optimal compensation deals with optimization problems with integer- and real-valued control variables to compensate disturbances in dynamic systems. The mixed integer nature of controls could lead to intractability in problems of large dimensions. To address this challenge, we introduce a decomposition method which turns the original n-dimensional optimization problem into n independent scalar problems of lot sizing form. Each of these problems can be viewed as a two-player zero-sum game, which introduces some element of conservatism. Each scalar problem is then reformulated as a shortest path one and solved through linear programming over a receding horizon, a step that mirrors a standard procedure in mixed integer programming. We apply the decomposition method to a mean-field coupled multi-agent system problem, where each agent seeks to compensate a combination of an exogenous signal and the local state average. We discuss a large population mean-field type of approximation and extend our study to opinion dynamics in social networks as a special case of interest.

1 Introduction

Mixed integer optimal compensation arises when optimizing a mix of integer- and real-valued control variables in order to compensate for disturbances in dynamic systems. Mixed integer control can be viewed as a specific subfield of optimal hybrid control [1], addressed recently also in a receding horizon framework [2]. Optimal integer control problems have been receiving growing attention and are often categorized under different names (e.g., alphabet control [3, 4]). Handling integer control requires more than standard convex optimization techniques. It is known that new structural properties of the problem play important roles in mixed integer control; as an example, see multimodularity presented as the counterpart of convexity in discrete action spaces [5]. We should note that there is vast literature on mixed integer programming [6], and it is in this context that we cast the problem addressed in this paper. For a survey of solution methods for mixed integer lot sizing models circa early 1990s, we refer the reader to [7]. Mixed integer optimal control has been dealt with in [8–11].

1.1 Highlights of the Main Results and Relationship with the Relevant Literature

We build on existing results in the lot sizing literature that convert lot sizing problems into shortest path problems. More details on this conversion can be found in [12, p. 98] and [13, 14]. The underlying idea is summarized in Fig. 1, which depicts a qualitative time plot of the stock versus time (right column) for different reordering policies and associated paths (dashed arcs in figures on the left). One can use a graph where nodes correspond to periods and (solid) arcs to regeneration intervals (time intervals between consecutive orders). For a 4-period demand, the just in time policy consisting of reordering at every period in order to fulfill the expected daily demand corresponds to the path (ordered sequence of nodes) traversing all the nodes, i.e., $\{0,1,2,3,4\}$ (top). The other extreme case is the one shot reordering policy where one reorders only once and at the beginning of the interval in order to fulfill the 4-period demand. The corresponding path is the single arc from node 0 to node 4, i.e., $\{0,4\}$ (middle). An intermediate policy would be to reorder at periods 0 and 2 in order to fulfill the 2-period demand. The corresponding path traverses nodes 0, 2, and 4, i.e., $\{0,2,4\}$ (bottom). In the paper, we extend this scheme to more general systems.

Fig. 1

Lot sizing problem turned into a shortest path problem: (top) just in time policy; (middle) one shot production policy; (bottom) two period production policy

Specifically, the paper makes three main contributions. First, we formulate the mixed integer optimal compensation problem. Second, we provide a performance analysis of the decomposition method that reformulates the n-dimensional mixed integer problem as n independent uncertain lot sizing systems. Each of these problems can be viewed as a two-player zero-sum game, which introduces some element of conservatism. Third, we view each decomposed mixed integer problem as a shortest path problem and solve the latter through linear programming.

The conservatism arising from the robust decomposition and approximation can be reduced if we operate in accordance with the predictive control technique: (i) optimize controls for each independent system based on the prediction of other states, (ii) apply the first control, (iii) provide measurement updates of other states and re-iterate.

There are several differences between the problem treated and the approach adopted in this paper and those in the related literature. The difference from [2], for example, is that here we focus on a smaller class of problems that can be solved exactly by simply relaxing the integer constraints. In that respect, the lot sizing like model used in this paper has much to do with the inventory example briefly mentioned in [1]. There, the authors simply include the example in a large list of hybrid optimal control problems but do not address the issue of how to fit general methods to this specific problem. Here, however, we emphasize the computational benefits that can be derived from the “nice structure” of the lot sizing constraints matrix. Binary variables, used to model impulses, match linear programming in [15]. There, the linear reformulation is a straightforward derivation of the (inverse) dwell time conditions that have first appeared in [16]. Similarity with [15] is the use of total uni-modularity to prove the exactness of the linear programming reformulation. Differences are in the procedure itself upon which the linear program is built. The shortest path model is an additional new element which distinguishes the present approach from that of [15].

We also provide in the paper a discussion on a special case of interest where each agent seeks to compensate a combination of the exogenous signal and the local state average. Here, the model is suitable to capture opinion fluctuations (sawtooth waves) in social networks [17]. We assume that the opinion dynamics are influenced by three different factors: the media, whose influence is modeled as an exogenous signal; the presence of a stubborn agent who is able to reset other agent’s opinions; and the interactions among the agents (the endogenous factor). An underlying assumption here is that a reset for a particular agent occurs whenever that agent chooses to meet with the stubborn agent, in which case the binary control is set to one. Also, the interactions among the agents are captured by an averaging process.

In the sense above, our decomposition idea is similar to mean-field methods in large population consensus. The mean-field theory of dynamical games with large but finite populations of asymptotically negligible agents (as the population size grows to infinity) originated in the work of Huang et al. [18–20] and independently in that of Lasry and Lions [21–23], where the now standard terminology of mean-field games (MFG) was introduced. In addition to this, the closely related notion of Oblivious Equilibria for large population dynamic games was introduced by Weintraub et al. [24] in the framework of Markov decision processes. This theory is very versatile and is attracting an ever-increasing interest with several applications in economics, physics and biology (see [25–27]). From a mathematical point of view, the mean-field approach leads to the study of a system of partial differential equations (PDEs), where the classical Hamilton–Jacobi–Bellman equation is coupled with a Fokker–Planck equation for the density of the players, in a forward–backward fashion. The decomposition method proposed here requires that each agent i computes in advance the time evolution of the local average (see, e.g., the Fokker–Planck–Kolmogorov equation in [23, 28–33]). However, since this is practically impossible, we use here the predictive control method to approximate the computation of the solution.

The main contributions of this work can therefore be summarized as follows: First, we draw a connection between game theory and a class of mixed integer control problems by decomposing an n-dimensional optimization problem into n two-player zero-sum games. Second, by reformulating decomposed problems as shortest path problems, we show that mixed integer optimal compensation problems are tractable under certain assumptions. Third, we leverage this connection to develop a mean-field game approach to study the large-scale optimization problem using a large population game framework.

A preliminary version of this paper was presented at the 2012 American Control Conference [34]. In addition to what was presented in [34], the current paper includes a detailed analysis of the case where a large number of agents interact and this interaction is described through a state averaging process. For this case, we provide a macroscopic description of the system in terms of consensus to the average mass distribution. This part of the paper includes an additional example (Example 6.3) that illustrates possible population evolutions. A further element, which is not present in [34], is an experimentally driven discussion on performance and complexity of the method provided in Example 6.2.

The paper is organized as follows. We present the problem statement in Sect. 2. We then move to present the decomposition method in Sect. 3. In Sect. 4, we turn to introducing the shortest path reformulation and the linear program. In Sect. 5, we discuss the case where the local state average appears in the dynamics. In Sect. 6, we present three numerical examples to illustrate the results in the paper. We conclude the paper with the recap of Sect. 7.

2 Mixed Integer Optimal Compensation (MIPC)

In mixed integer optimal compensation problems, we have continuous states $x(k) \in {\mathbb {R}}^n$, continuous controls $u(k) \in {\mathbb {R}}^n$, discrete controls $y(k) \in \{0,1\}^n$, and continuous disturbances $w(k)\in {\mathbb {R}}^n$, where $k=0,1,\ldots$ is the time index. Evolution of the state over a finite horizon of length N is described by a linear discrete-time (difference) equation in the general form (1) below, where A and E are matrices of compatible dimensions and $x(0)=\xi _0 \ge 0$ is a given initial state. Continuous and discrete controls are linked through the general capacity constraints (2), where the (scalar) parameter c is an upper bound on control, with the inequalities in (1) and (2) to be interpreted component wise.

$$\begin{aligned} x(k+1)&=A x(k) + E w(k) + u(k) \ge 0, \quad x(N)=0, \end{aligned}$$

(1)

$$\begin{aligned} 0&\le u(k) \le cy(k), \quad y(k)\in \{0,1\}^n. \end{aligned}$$

(2)

The above dynamics are characterized by one discrete and one continuous control variable per each state. Starting from nonnegative initial states, we force the state to remain confined to the positive orthant, which may describe a safety region in engineering applications or reflect the desire to prevent shortfalls in inventory applications. The final state, x(N), is forced to be equal to zero, which corresponds to saying that the control u(k) has to “compensate” the cumulative effects of the disturbances E w(k) and term Ax(k) over the given horizon.

The following assumption serves to describe the common situation where the disturbance seeks to push the state out of the desired region. Its value is given at the beginning and fixed that way. Each column of matrix E establishes how each disturbance component influences the evolution of the state vector.

Assumption 1

(Unstabilizing disturbance effects)

$$\begin{aligned} Ew(k) < 0, \end{aligned}$$

(3)

where the inequality is to be interpreted component wise.

Actually, the control actions push the state away from the boundaries into the positive orthant, thus counteracting the destabilizing effects of the disturbances. However, controlling the system has a cost and “over acting” on it is penalized, which is quantified through a cost/objective function. This function, to be minimized with respect to y(k) and u(k), is a linear one including proportional, holding, and fixed cost terms expressed by parameters $p^k$, $h^k$, and $f^k$, respectively:

$$\begin{aligned} \sum _{k=0}^{N-1} \left( \left\langle p^k,u(k) \right\rangle + \left\langle h^k,x(k) \right\rangle + \left\langle f^k,y(k) \right\rangle \right) , \end{aligned}$$

(4)

where $\langle \cdot ,\cdot \rangle$ denotes the Euclidean inner product. The problem of interest is thus completely characterized by (1)–(4). This hybrid minimization problem can be turned into a mixed integer linear program by using the standard method discussed next. Henceforth we refer to (1)–(4) as (MIPC).

2.1 Introducing Some Structure on A

With regard to (1), we can isolate the dependence of one component state on the other ones and rewrite (1) in a way that establishes similarity with standard lot sizing models [7]:

$$\begin{aligned} x(k+1)=x(k) + B x(k) + E w(k) + u(k) \ge 0. \end{aligned}$$

(5)

Equation (5) is a straightforward representation of (1) where

$$\begin{aligned} B:= A-I =: \{b_{ij}\},\quad b_{ij} = a_{ij} - \delta _{ij},\quad \delta _{ij}:=\left\{ \begin{array}{ll}1, &{}\quad \text {if }i=j,\\ 0, &{} \quad \text {otherwise}. \end{array}\right. \end{aligned}$$

(6)

To preserve the nature of the problem, which has stabilizing control actions playing against unstabilizing disturbances, we assume that the influence of other states on state i is relatively “weak.” In other words, we assume that the influence of B x(k) is small if compared with the unstabilizing effects of disturbances captured by the term E w(k).

Assumption 2

(Weak coupling)

$$\begin{aligned} B x(k) + E w(k) < 0, \end{aligned}$$

(7)

where inequality is again component wise.

Essentially, the states’ mutual dependence expressed by B x(k) only emphasizes or reduces “weakly” the destabilizing effects of the disturbances. In the next section, we present a decomposition approach that translates dynamics (5) into n scalar dynamics in “lot sizing” form [7].

3 Robust Decomposition

With the term “robust decomposition,” we mean a transformation through which dynamics (5) are replaced by n independent uncertain lot sizing models of the form (8) where $x_i(k)$ is the inventory, $d_i(k)$ the demand, $u_i(k)$ the reordered quantity and ${\mathcal {D}}_i^k \subset {\mathbb {R}}$ denotes the uncertainty set:

$$\begin{aligned} x_i(k+1)= x_i(k) - d_i(k) + u_i(k) \ge 0, \quad d_i(k) \in {\mathcal {D}}_i^k. \end{aligned}$$

(8)

Recall that in (5) the disturbance is given at the beginning and fixed that way. We use those values of the disturbance to determine set ${\mathcal {D}}_i^k$ in (8), as explained in the following. Replacing (5) with (8) is possible once we relate the demand $d_i(k)$ to the current values of all other state components and disturbances as expressed below:

$$\begin{aligned} \begin{array}{lll} d_i(k) &{} = &{} -\left[ \sum \limits _{j=1}^n b_{ij} x_j(k) + \sum \limits _{j=1}^n E_{ij} w_j(k) \right] \\ &{} = &{} - \left[ \left\langle B_{i \bullet } x(k) \right\rangle + \left\langle E_{i \bullet } w(k) \right\rangle \right] , \end{array} \end{aligned}$$

(9)

where we denote by $B_{i \bullet }$ the $i\hbox {th}$ row of the matrix B, with the same convention applying to $E_{i \bullet }$. Following the decomposition, each lot sizing model is controlled by an agent i (whose state is $x_i$) who plays against a virtual opponent which selects a worst-case demand, which can be viewed as a two-player game.

Our next step is to make the n dynamics in the form (8) mutually independent. Toward that end, we introduce $X^k$ as the set of x(k) and observe that this set is bounded for bounded $d_i(k)$. The set $X^k$ can be defined in two steps. First, we assume that the states never leave a given region, and then we compute the worst-case vector x(k) in the region, namely the vector x(k) that, once substituted in (9), has the effect of pushing the $i\hbox {th}$ state out of the safe region. Then, we check whether the trajectory still lies within the region.

Boundedness of $X^k$ means that there exists a scalar $\phi >0$ such that $\Vert x\Vert _{\infty }\le \phi$ for all $x\in X^k$. In view of this, it is possible to decompose the system by replacing the current demand $d_i(k)$ by the maximal or minimal demand as computed below:

$$\begin{aligned} d_i^+(k)= & {} \max _{\xi \in X^k} \left\{ - \langle B_{i \bullet } \xi \rangle - \langle E_{i \bullet } w(k) \rangle \right\} = \sum _{j}[B_{ij}]_- \phi - \langle E_{i \bullet } w(k) \rangle ,\end{aligned}$$

(10)

$$\begin{aligned} d_i^-(k)= & {} \min _{\xi \in X^k} \left\{ - \langle B_{i \bullet } \xi \rangle - \langle E_{i \bullet } w(k) \rangle \right\} = \sum _{j}[B_{ij}]_+ \phi - \langle E_{i \bullet } w(k) \rangle , \end{aligned}$$

(11)

where $[B_{ij}]_+$ denotes the positive part of $B_{ij}$, i.e., $\max \{B_{ij},0\}$ and $[B_{ij}]_-$ the negative part. In the following, we will write compactly $d_i^e(k)$, $e\in \{+,-,nil\}$ to generically address the maximal demand (10) when $e=+$, the minimal demand (11) when $e=-$, and the exact demand (9) when $e=\mathrm{nil}$. From the above preamble, we derive the uncertainty set as

$$\begin{aligned} {\mathcal {D}}_i^k = \{\eta \in {\mathbb {R}}: \, d_i^-(k)\le \eta \le d_i^+(k)\}. \end{aligned}$$

Likewise, (11) describes the demand that would push the state out of the positive orthant in the longest time. To complete the decomposition, it remains to transform the objective function (4) into n independent ones:

$$\begin{aligned} J_i(u_i,y_i)=\sum _{k=0}^{N-1} \left( p_i^k u_i(k) + h_i^k x_i(k) + f_i^k y_i(k)\right) . \end{aligned}$$

Note that because of the linear structure of J(u, y) in (4), we have

$$\begin{aligned} J(u,y)=\sum _{i=1}^{n} J_i(u_i,y_i). \end{aligned}$$

Thus, we have transformed the original problem into n independent mixed integer minimization problems of the form (12)–(14) below.

In the spirit of predictive control, we solve, for $\tau =0,\ldots ,N-1$, and $e(\tau )=\mathrm{nil}$, $e(k)=e$, for $k > \tau$, $e\in \{\mathrm{nil}, +, -\}$, and with $\xi _i^\tau$ being the measured state at time $\tau$:

$$\begin{aligned} \left( \mathrm{MIPC}_i\right) ^e \qquad \qquad&\min _{u_i,y_i} \quad \sum _{k=\tau }^{N-1} \left( p_i^k u_i(k) + h_i^k x_i(k) + f_i^k y_i(k)\right) \end{aligned}$$

(12)

$$\begin{aligned}&x_i(k+1)= x_i(k) - d_i^{e(k)}(k) + u_i(k) \ge 0, \end{aligned}$$

(13)

$$\begin{aligned}&x_i(\tau )=\xi _i^\tau , \, x_i(N)=0,\nonumber \\&0 \le u_i(k) \le c y_i(k), \, y_i(k)\in \{0,1\}. \end{aligned}$$

(14)

Note that when the superscript $e=\mathrm{nil}$, we simply write $\left( \mathrm{MIPC}_i \right)$. Denote by $(\mathrm{MIPC})^r$ the relaxation of $\left( \mathrm{MIPC}_i \right)$ where $0 \le y \le 1$.

Lemma 3.1

The following relations hold:

$$\begin{aligned} \left( \mathrm{MIPC}_i\right) ^-,\,(\mathrm{MIPC})^r \le \left( \mathrm{MIPC}_i\right) \le (\mathrm{MIPC}_i)^+. \end{aligned}$$

Proof

The conditions $\left( \mathrm{MIPC}_i\right) ^- \le \left( \mathrm{MIPC}_i\right) \le \left( \mathrm{MIPC}_i\right) ^+$ are true as $d_i^-(k) \le d_i(k) \le d_i^+(k)$ for all $k=0,\ldots ,N-1$, and the cost (12) is increasing in the demand. The inequality $\left( \mathrm{MIPC} \right) ^r \le \left( \mathrm{MIPC}_i\right)$ follows from observing that in $\left( \mathrm{MIPC} \right) ^r$ we relax the integer restrictions on y and therefore the cost cannot be higher than that in $\left( \mathrm{MIPC}_i \right)$. $\square$

4 Shortest Path and Linear Programming

What we will establish here is that, for the problem at hand, relaxing and massaging the problem in a certain manner leads to a shortest path reformulation of the original problem. Shortest path formulations are based on the notion of regeneration interval as discussed next.

Let us borrow from [7] the concept of regeneration interval and adapt it to the generic minimization problem i defined by (12)–(14).

Definition 4.1

(Pochet and Wolsey [7]) An interval $[\alpha , \beta ]$ forms a regeneration interval for $(x_i,u_i,y_i)$ if $x_i(\alpha -1) = x_i(\beta )=0$ and $x_i(k)>0$ for $k=\alpha ,\alpha +1, \ldots ,\beta -1$.

Given a regeneration interval $[\alpha ,\beta ]$, we can define the accumulated demand over the interval $d_i^{\alpha \beta }$, and the residual demand $r_i^{\alpha \beta }$, as

$$\begin{aligned} d_i^{\alpha \beta }= \sum _{k=\alpha }^{\beta } d_i^{e(k)}(k),\quad r_i^{\alpha \beta }= d_i^{\alpha \beta } - \left\lfloor \frac{d_i^{\alpha \beta }}{C}\right\rfloor C. \end{aligned}$$

(15)

The path we take now is to reformulate problem (12)–(14) in terms of some new variables. More formally, let us consider variables $y_i^{\alpha \beta } (k)$ and $\epsilon _i^{\alpha \beta } (k)$ defined below with the following interpretation. Variable $y_i^{\alpha \beta } (k)$ is equal to 1 in the presence of a saturated control at time k, and 0 otherwise. Similarly, variable $\epsilon _i^{\alpha \beta } (k)$ is equal to 1 in the presence of a non-saturated control at time k, and 0 otherwise:

$$\begin{aligned} y_i^{\alpha \beta } (k)=\left\{ \begin{array}{ll}1 &{} \quad u_i(k)=c,\\ 0 &{} \quad \text {otherwise},\end{array}\right. \quad \epsilon _i^{\alpha \beta } (k)=\left\{ \begin{array}{ll}1, &{} \quad 0 < u_i(k)< c,\\ 0,&{}\quad \text {otherwise}.\end{array}\right. \end{aligned}$$

Variables $y_i^{\alpha \beta } (k)$ and $\epsilon _i^{\alpha \beta } (k)$ tell us on which period full or partial batches are ordered. Then, we can use some well-known results from the lot sizing literature to convert the original mixed integer problem (12)–(14) into a number of linear programs $\left( \mathrm{LP}_i^{\alpha \beta } \right)$, each one corresponding to a specific regeneration interval $[\alpha ,\beta ]$.

Letting $e_i^k:=p_i^k + \sum _{j=k+1}^{N-1} h_i^j$, after some standard manipulations, the linear program $\left( \mathrm{LP}_i^{\alpha \beta } \right)$ for fixed regeneration interval $[\alpha ,\beta ]$ can be expressed as:

$$\begin{aligned}&\min _{y_i^{\alpha ,\beta },u_i^{\alpha ,\beta } } \, \sum _{k=\alpha }^{\beta } \left( ce_i^k + f_i^k \right) y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{\beta } \left( r^{\alpha \beta } e_i^k + f_i^k \right) \epsilon _i^{\alpha \beta } (k) \end{aligned}$$

(16)

$$\begin{aligned}&\sum _{k=\alpha }^{\beta } y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{\beta } \epsilon _i^{\alpha \beta } (k) = \left\lceil \frac{d_i^{\alpha \beta }}{c} \right\rceil , \end{aligned}$$

(17)

$$\begin{aligned}&\sum _{k=\alpha }^{t} y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{t} \epsilon _i^{\alpha \beta } (k) \ge \left\lceil \frac{d_i^{\alpha t}}{c} \right\rceil , \quad t=\alpha ,\ldots ,\beta -1, \end{aligned}$$

(18)

$$\begin{aligned}&\sum _{k=\alpha }^{\beta } y_i^{\alpha \beta } (k) = \left\lceil \frac{d_i^{\alpha \beta }- r_i^{\alpha \beta }}{c} \right\rceil , \end{aligned}$$

(19)

$$\begin{aligned}&\sum _{k=\alpha }^{t} y_i^{\alpha \beta } (k) \ge \left\lceil \frac{d_i^{\alpha t} - r_i^{\alpha t}}{c} \right\rceil , \quad t=\alpha ,\ldots ,\beta -1, \end{aligned}$$

(20)

$$\begin{aligned}&y_i^{\alpha \beta } (k), \, \epsilon _i^{\alpha \beta } (k) \ge 0, \quad k=\alpha ,\ldots ,\beta . \end{aligned}$$

(21)

The above model has been extensively used in the lot sizing context.

Equality constraints (17) and (19) tell us that the ordered quantity over the interval has to be equal to the accumulated demand over the same interval. This makes sense as the initial and final states of a regeneration interval are null by definition. The inequality constraints (18) and (20) impose that the accumulated demand in any subinterval may not exceed the ordered quantity over the same subinterval. Again, this is due to the condition that the states are nonnegative in any period of a regeneration interval. Finally, the objective function (16) is simply a rearrangement of (12) induced by the variable transformation seen above and specialized to the regeneration interval $[\alpha ,\beta ]$ rather than being on the entire horizon [0, N].

The solutions of $(\mathrm{LP}_i^{\alpha \beta })$ that are binary are called “feasible.” We are now in a position to recall the following “nice property” of $(\mathrm{LP}_i^{\alpha \beta })$ presented first by Pochet and Wolsey [7].

Theorem 4.1

(Total Uni-modularity) The optimal solution of $(\mathrm{LP}_i^{\alpha \beta })$ is feasible.

Proof

Note that the constraint matrix of $\left( \mathrm{LP}_i^{\alpha \beta }\right)$ is a 0–1 matrix. We can reorder the constraints in a certain manner, so that the matrix has the consecutive 1’s property on each column and turns out to be totally uni-modular. It then follows that $y_i^{\alpha ,\beta }$ and $\epsilon _i^{\alpha ,\beta }$ are 0–1 in any extreme solution. $\square$

4.1 Shortest Path

We now resort to well-known results on lot sizing to arrive at a shortest path model which links together the linear programming problems of all possible regeneration intervals.

Toward that end, let us define variables $z_i^{\alpha \beta } \in \{0,1\}$, which yield 1 when a regeneration interval $[\alpha ,\beta ]$ appears in the solution of (12)–(14), and 0 otherwise. The linear programming problem $\left( \mathrm{LP}_i\right)$ solving (12)–(14) takes on the form below. For $\tau =0,\ldots ,N-1$, solve

$$\begin{aligned} \min _{y_i^{\alpha \beta },u_i^{\alpha \beta }, z_i^{\alpha \beta }} \sum _{\alpha =\tau +1}^{N-1} \sum _{\beta =\alpha }^{N-1} \sum _{k=\alpha }^{\beta } \left[ \left( ce_i^k + f_i^k \right) y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{\beta } \left( r^{\alpha \beta } e_i^k + f_i^k \right) \epsilon _i^{\alpha \beta } (k) \right] \end{aligned}$$

$$\begin{aligned} \sum _{\beta =\tau +1}^N z_i^{\tau +1,\beta }=1\\ \sum _{\alpha =\tau +1}^{t-1} z_i^{\alpha ,t-1} - \sum _{\beta =t}^N z_i^{t\beta }=0&\quad t=\tau +2,\ldots ,N, \\ {}&\quad \tau +1 \le \alpha \le \beta \le N\\ \sum _{k=\alpha }^{\beta } y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{\beta } \epsilon _i^{\alpha \beta } (k) = \left\lceil \frac{d_i^{\alpha \beta }}{c} \right\rceil z_i^{\alpha \beta },&\quad \tau +1 \le \alpha \le \beta \le N\\ \sum _{k=\alpha }^{t} y_i^{\alpha \beta } (k) + \sum _{k=\alpha }^{t} \epsilon _i^{\alpha \beta } (k) \ge \left\lceil \frac{d_i^{\alpha t}}{c} \right\rceil z_i^{\alpha \beta },&\quad t=\alpha ,\ldots ,\beta -1, \\&\quad \tau +1 \le \alpha \le \beta \le N\\ \sum _{k=\alpha }^{\beta } y_i^{\alpha \beta } (k) = \left\lceil \frac{d_i^{\alpha \beta }- r_i^{\alpha \beta }}{c} \right\rceil z_i^{\alpha \beta }&\quad \tau +1 \le \alpha \le \beta \le N\\ \sum _{k=\alpha }^{t} y_i^{\alpha \beta } (k) \ge \left\lceil \frac{d_i^{\alpha t} - r_i^{\alpha t}}{c} \right\rceil z_i^{\alpha \beta },&\quad t=\alpha ,\ldots ,\beta -1, \\&\quad \tau +1 \le \alpha \le \beta \le N\\ y_i^{\alpha \beta } (k), \, \epsilon _i^{\alpha \beta } (k),\, z_i^{\alpha \beta } \ge 0,&\quad k=\alpha ,\ldots ,\beta . \end{aligned}$$

The above constraints have already appeared in $\left( \mathrm{LP}_i^{\alpha \beta } \right)$. The only difference here is that, now, because of the presence of $z_i^{\alpha \beta }$ in the right-hand term, the constraints referring to a given regeneration interval come into play only if that interval is chosen as part of the solution, that is, whenever $z_i^{\alpha \beta }$ is set equal to one. Furthermore, a new class of constraints appear in the first line of the constraints. These constraints are typical of shortest path problems and in this specific case help us force the variables $z_i^{\alpha \beta } (k)$ to describe a path from 0 to N. Finally, note that for $\tau =0$, the linear program $(\mathrm{LP}_i)$ coincides with the linear program presented by Pochet and Wolsey [7].

At this point, we are in a position to recall the important result established by Pochet and Wolsey [7] and adapt it to $(\mathrm{MIPC}_i)$ within the assumption of null final state (high values of $h_i^N$).

Theorem 4.2

The linear program (LP$_i)$ solves (MIPC$_i)$ with null final state.

Proof

It turns out that the linear program $(\mathrm{LP}_i)$ is a shortest path problem on variables $z_i^{\alpha ,\beta }$. Arcs are all associated with a different regeneration interval $[\alpha ,\beta ]$, and the respective costs are the optimal values of the objective functions of the corresponding linear programs $\left( \mathrm{LP}_i^{\alpha ,\beta }\right)$ (cf. [7]). $\square$

4.2 Receding Horizon Implementation of $(\mathrm{LP}_i)$

The main difference between the lot sizing model [7] and the $(\mathrm{LP}_i)$ arrived at here is that in the $(\mathrm{LP}_i)$ the initial state is non null. Actually, successive linear programs $(\mathrm{LP}_i)$ are linked together by the initial state condition expressed in (13), which we rewrite below

$$\begin{aligned} x_i(\tau )=\xi _i^\tau . \end{aligned}$$

To address this issue, we need to elaborate more on how to compute the accumulated demand in (15). Take for $[\tau ,t]$ any interval with $x(\tau )=\xi _i^\tau > 0$. Then, condition (15) needs to be revised as

$$\begin{aligned} d_i^{\tau t}= \max \left\{ \sum _{k=\tau }^{t} d_i^{e(k)}(k)- \xi _i^\tau ,0\right\} . \end{aligned}$$

(22)

The effective demand over an interval is the accumulated demand reduced by the inventory stored and initially available at the warehouse. From a computational standpoint, the revised expression (22) has a different effect depending on whether the accumulated demand exceeds the initial state or not, as discussed next.

• 1. $\sum _{k=\alpha }^{\beta } d_i^{e(k)}(k) \ge \xi _i^\tau$: the mixed linear program $(\mathrm{MIPC}_i)$ with initial state $x(\tau )=\xi _i^\tau > 0$ and accumulated demand $\sum _{k=\alpha }^{\beta } d_i^{e(k)}(k)$ is converted into an $(\mathrm{LP}_i)$ characterized by null initial state $x(\alpha -1)=0$ and effective demand $d_i^{\alpha \beta }=\sum _{k=\alpha }^{\beta } d_i^{e(k)}(k) - \xi _i^\tau$ as in the example below:

  $$\begin{aligned} (\mathrm{MIPC}_i) \quad \sum _{k=\alpha }^{\beta } d_i^{e(k)}(k)=12, \quad x(\tau )=\xi _i^\tau =10 \\ \Longrightarrow (\mathrm{LP}_i) \quad x(\alpha -1)=0, \quad d_i^{\alpha \beta }=2. \end{aligned}$$

• 2. $\sum _{k=\alpha }^{\beta } d_i^{e(k)}(k) < \xi _i^\tau$: the mixed linear program $(\mathrm{MIPC}_i)$ with initial state $x(\tau )=\xi _i^\tau > 0$ and accumulated demand $\sum _{k=\alpha }^{\beta } d_i^{e(k)}(k)$ is infeasible. The solution obtained at the previous period $\tau -1$ applies. The example below shows unfeasibility:

  $$\begin{aligned} (\mathrm{MIPC}_i) \quad \sum _{k=\alpha }^{\beta } d_i^{e(k)}(k)=7, \quad x(\tau )=\xi _i^\tau =10 \\ \Longrightarrow (\mathrm{LP}_i) \text { unfeasible}. \end{aligned}$$

5 Mean-Field Coupling

In this section, we discuss a special case of interest where each agent seeks to compensate a combination of the exogenous signal and the local state average. We assume that the worst-case demand introduced earlier takes into account also of the mean-field influence of the population behavior on the $i\hbox {th}$ dynamics. Thus, each agent plays his best-response against the population behavior. The resulting model is a mean-field game, which is suitable to describe fluctuations (sawtooth waves) in opinion dynamics. Indeed, we can interpret the state of each agent as her opinion on a certain issue, the exogenous signal as the media influence, and the control as an instantaneous reset on the opinion subsequent to a meeting with a stubborn agent [17]. In addition, the dependence on endogenous factors, represented by the averaging process, is the result of the interactions among the agents. In this case, our decomposition methodology becomes similar to mean-field methods in large population consensus [20, 33, 35]. We discuss below the mean-field approximations as well as the application of predictive control methods to approximate the computation.

5.1 Multi-Agent System Model

Consider a graph $G=(V,E)$ with a set of vertices $V=\{1,\ldots , n\}$ and a set of edges $E\subseteq V \times V$. Denote by $N_i$ the neighborhood of agent i, i.e., $N_i=\{j \in V: (i,j) \in E\}$. We can associate with the graph G the normalized graph Laplacian matrix $L \in {\mathbb {R}}^{n\times n}$ whose ij-th entry is

$$\begin{aligned} l_{ij}=\left\{ \begin{array}{ll} \frac{-1}{|N_i|}, &{} \quad j \in N_i,\\ 1, &{} \quad j=i.\end{array}\right. \end{aligned}$$

Now, a special case of interest is when B in (5) is $B=- \epsilon L$ for some sufficiently small scalar $\epsilon >0$. In this case, dynamics (5) become:

$$\begin{aligned} x(k+1) = x(k) - \epsilon Lx(k) + Ew(k) + u(k) \ge 0. \end{aligned}$$

(23)

Essentially, the above dynamics together with the constraint $x(N)=0$ arise in all those situations where each agent $i=1,\ldots , n$ tries to compensate a combination of the exogenous signal w(k) and the local state average given by

$$\begin{aligned} \bar{m}_i(k)= \frac{1}{|N_i|} \sum _{j\in N_i} x_j(k). \end{aligned}$$

Elaborating along the line of the robust decomposition (8), we can then compute the disturbance taking into account the influence of the local average on the exogenous signal as follows:

$$\begin{aligned} \begin{array}{lll} d_i(k)&= -\left[ \epsilon (\bar{m}_i(k) -x_i(k)) + \langle E_{i \bullet },w(k) \rangle \right] . \end{array} \end{aligned}$$

Note that Assumption 2 in this case says that the exogenous signal is dominant if compared to the weak influence from neighbors.

In principle, for the decomposition method to be exact, each agent i should know in advance the time evolution of the local average $\bar{m}_i(k)$, for $k=0,\ldots ,N$. However, this may not be feasible. One way to approximate the local average $\bar{m}_i(k)$ is through mean-field methods. Under the further assumption that the number of agents is large and the agent dynamics are symmetric, the local average can be characterized through the finite-difference approximation of the continuity or advection equation that describes the transport of a conserved quantity [35]. Another way to deal with the problem is to use the predictive control method to approximate the computation. More specifically, when we solve the problem over the horizon from $\tilde{k} \ge 0$ to N, we assume that neighbor agents communicate their state and so at least the first sample $\bar{m}_i(\tilde{k})$ is exact. In the later stages of the horizon, each agent approximates the local average by specializing (10)–(11) to our case. Note that maximal and minimal demand can be obtained by assuming that all agents $j \not = i$ are in 0 or $\phi$, respectively, and thus we have for agent i:

$$\begin{aligned} d_i^+(k) = \epsilon x_i - \langle E_{i \bullet },w(k)&\rangle , \quad d_i^-(k) = -\left[ \epsilon (\phi - x_i) + \langle E_{i \bullet },w(k) \rangle \right] . \end{aligned}$$

Alternatively, this also corresponds to assuming for the uncertain set ${\mathcal {D}}_i^k$ the following expression:

$$\begin{aligned} {\mathcal {D}}_i^k = \{\eta \in {\mathbb {R}}: \,- \epsilon (\phi - x_i) - \langle E_{i \bullet },w(k) \rangle \le \eta \le \epsilon x_i - \langle E_{i \bullet },w(k) \rangle \}. \end{aligned}$$

The above set up includes the case where agents are homogeneous as explained next.

5.2 Homogeneous Agents

Within the realm of mean-field coupling, a particularly interesting case is the one where agents are homogeneous in the sense that they behave similarly when at the same state. For these problems, a main question is the asymptotic population behavior, i.e., the behavior of the population when the number of agents is large.

Suppose that all agents face the same disturbance comprised of a constant value plus a random walk, i.e., $\omega _i(k):=E_{i\bullet } w(k)= const. + \sigma _i \gamma _i(k)$ where $\gamma _i(k)$ is the random walk, and $\sigma _i$ is the random walk coefficient, for all agents i.

Denoting the saturation function by

$$\begin{aligned} sat[x]= \left\{ \begin{array}{ll} x^+, &{} \quad \text {if }x>x^+, \\ x^-, &{} \quad \text {if }x<x^-,\\ x, &{} \quad \text {if }x^- \le x \le x^+, \end{array}\right. \end{aligned}$$

(24)

the system dynamics takes the form

$$\begin{aligned} x_i(k+1)= & {} x_i(k) - d_i(k) + u_i(k),\nonumber \\ d_i(k)= & {} -[sat[\epsilon (\bar{m}_i(k)-x_i(k))] + \omega _i(k)], \end{aligned}$$

(25)

where $u_i(k)$ is an (s, S) strategy (see, e.g., [36]) of the type

$$\begin{aligned} u_i(k)= \left\{ \begin{array}{ll} S-x_i(k) &{} \quad \text {if }x_i(k) \pm \varepsilon \le s,\\ 0 &{} \quad \text {otherwise}. \end{array}\right. \end{aligned}$$

(26)

Essentially, the control restores the original upper threshold S anytime when the stocked inventory (the state) goes below a lower threshold s. Such a policy has been proven to be optimal in the presence of fixed costs in a number of inventory applications. Note that the saturation function is used here only to avoid state oscillations when the agents are far enough from the local average.

Our goal is now to provide a macroscopic description of the system and analyze the corresponding behavior. To do this, we borrow from [37] a modeling approach based on stochastic matrices. Let $W=I-\epsilon L$ be a row stochastic matrix, i.e., $W {\mathbf {1}}={\mathbf {1}}$. The system Eq. (23) can be rewritten as

$$\begin{aligned} x(k+1) = W x(k) + \omega _i(k) + u(k). \end{aligned}$$

Given the distribution m(k) followed by x(k), denote the corresponding average distribution as $\bar{m}(k)=\frac{1}{n} \langle {\mathbf {1}}, x(k)\rangle$. Using the property ${\mathbf {1}}^T W ={\mathbf {1}}^T$, we can derive for the average the following recursive equation:

$$\begin{aligned} \bar{m}(k+1)= & {} \frac{1}{n}\langle {\mathbf {1}}, x(k+1)\rangle = \frac{1}{n}\langle {\mathbf {1}}, W x(k)+ \omega (k) + u(k)\rangle \nonumber \\= & {} \bar{m}(k) + \frac{1}{n}\langle {\mathbf {1}}, \omega (k) + u(k)\rangle , \end{aligned}$$

(27)

where $\omega (k)$ is the vector whose $i\hbox {th}$ component is $\omega _i(k)$.

The above is a stochastic process whose first-order moment is generated by

$$\begin{aligned} {\mathbb {E}} \bar{m}(k+1)= & {} {\mathbb {E}} \bar{m}(k) + const. + \frac{1}{n}\langle {\mathbf {1}}, u(k)\rangle ,\nonumber \\ {\mathbb {E}} \bar{m}(0)= & {} {\sum }_{i=1}^n x_i(0). \end{aligned}$$

(28)

Now, our aim is to analyze the convergence of the agents’ opinions to their average. Toward that end, define ${\mathcal {M}}= \frac{1}{n} {\mathbf {1}} \otimes {\mathbf {1}}$. Then for a given vector x(k), we have ${\mathcal {M}} x(k)=(\frac{1}{n} {\mathbf {1}} \otimes {\mathbf {1}}) x(k)= \bar{m}(k) {\mathbf {1}}$. With the above in mind, the deviation of each agent state $x_i(k)$ from the average $\bar{m}(k)$ is captured by the vector

$$\begin{aligned} z(k) := x(k) - {\mathcal {M}} x(k) = (I - {\mathcal {M}} ) x(k). \end{aligned}$$

If agents reach average-consensus, i.e., their opinions all converge to the average, then the variable z(k) goes to zero. After some transformations, we obtain for z(k) the following iteration:

$$\begin{aligned} z(k+1)= & {} (I - {\mathcal {M}} ) (W x(k)+ \omega (k) + u(k))\\= & {} (W - {\mathcal {M}} ) (I - {\mathcal {M}} ) x(k) + (I - {\mathcal {M}} ) (\omega (k) + u(k))\\= & {} (W - {\mathcal {M}} ) z(k) + (I - {\mathcal {M}} ) (\omega (k) + u(k)). \end{aligned}$$

Following a few recursions, we can relate z(k) to the initial discrepancy value z(0) and to the sequence of inputs $\omega (k)$ and u(k) as follows:

$$\begin{aligned} z(k) = (W - {\mathcal {M}})^k z(0) + \sum _{t=0}^{k-t-1} (I - {\mathcal {M}}) (\omega (k) + u(k)). \end{aligned}$$

Now, $z(k) = (W - {\mathcal {M}})^k z(0)$ is a typical averaging rule and we know that it converges to the average if $\Vert W - {\mathcal {M}}\Vert <1$, where we denote by $\Vert W - {\mathcal {M}}\Vert$ the spectral or maximum singular value norm of the matrix $W - {\mathcal {M}}$ [37]. In the absence of Brownian motions, the agents can still reach consensus or at least $\varepsilon$-consensus ($\varepsilon$ is convergence tolerance) as established in the following result.

Theorem 5.1

(Controlled invariance) Let $\sigma _i=0$ for all i and $\Vert W - {\mathcal {M}}\Vert <1$. If there exists a $\tau >0$ such that $\Vert z(\tau )\Vert \le \varepsilon$ for a sufficiently small positive $\varepsilon$, then $\Vert z(k)\Vert \le \varepsilon$ for all $k\ge \tau$.

Proof

First, note that from $\sigma _i=0$ for all i and homogeneity it follows that $(I - {\mathcal {M}}) \omega (k) = 0$ for all k. Now, observe that if $\Vert z(\tau )\Vert \le \varepsilon$ then $(I - {\mathcal {M}}) u(k)\approx 0$. This also means that

$$\begin{aligned} \sum _{k=0}^\infty \Vert (I - {\mathcal {M}}) u(k)\Vert ^2 = \sum _{k=0}^{\tau -1} \Vert (I - {\mathcal {M}}) u(k)\Vert ^2 < \infty , \quad \lim _{k\rightarrow \infty } \Vert (I - {\mathcal {M}}) u(k)\Vert ^2=0. \end{aligned}$$

The above uses the fact that $\Vert (I - {\mathcal {M}}) u(k)\Vert ^2$ is bounded for all k and implies that the sequence $\{z(k)\}$ is convergent. Now, let us consider the subsequence $\{\zeta (k)\}$ where $\zeta (k)=z(\tau + k)$. We know that $\{\zeta (k)\}$ follows the equation $\zeta (k) = (W - {\mathcal {M}})^k \zeta (0)$ and from $\Vert W - {\mathcal {M}}\Vert <1$ it converges to zero. Since $\{z(k)\}$ is convergent and the subsequence $\{\zeta (k)\}$ converges to zero, we can conclude that $\{z(k)\}$ converges to zero as well. $\square$

Example 5.1

For a given x(0) we can compute the first time that a control $u_i$ is set to 1. Let us denote this time by $\tilde{t}$. We can also compute $\tau = \min \{k >0 | \, \Vert (W - {\mathcal {M}})^k z(0) \Vert \le \varepsilon \}$ and check that $\tau \le \tilde{t}$. If the latter condition holds true, then the above theorem applies and opinions of all agents evolve according to the periodic law (27) of $\bar{m}(k)$ and reach consensus to the average.

6 Numerical Examples

In this section, we present three numerical examples to illustrate the findings in the paper.

6.1 Second-Order Dynamics

Example 6.1

In this specific example, dynamics (1) take the form given below in (29). Such dynamics are particularly significant as they reproduce the typical interaction between position and velocity in a sampled second-order system. Initial and final states are null, $x(0)=x(N)=0$, and state values must remain in the positive quadrant for all time. More specifically, denoting by $x_1(k)$ the position and $x_2(k)$ an opposite in sign velocity, the dynamics appear as:

$$\begin{aligned} \left[ \begin{array}{ll} x_1(k+1)\\ x_2(k+1)\end{array}\right] =\left[ \begin{array}{lc} 1 &{} - \kappa \\ \kappa &{} 1\end{array}\right] \left[ \begin{array}{ll} x_1(k)\\ x_2(k)\end{array}\right] - \left[ \begin{array}{ll} w_1(k)\\ w_2(k)\end{array}\right] +\left[ \begin{array}{ll} u_1(k)\\ u_2(k)\end{array}\right] \ge 0. \end{aligned}$$

(29)

A closer look at the first equation reveals that a higher velocity $x_2(k)$ leads to a faster decrease of position $x_1(k+1)$. Similarly, the second equation tells us that a higher position $x_1(k)$ induces a faster increase of velocity $x_2(k+1)$ because of some elastic reaction. In both equations, the positive disturbances, $w_i(k) > 0$ seek to push the states $x_i(k+1)$ out of the positive quadrant. Their effect is counterbalanced by positive control actions $u_i$. Also, acting on parameter $\kappa$ we can easily guarantee the “weakly coupling” condition given in Assumption 2.

Turning to the capacity constraints (2), for this two-dimensional example, these constraints can be rewritten as:

$$\begin{aligned} 0 \le \left[ \begin{array}{ll} u_1(k)\\ u_2(k)\end{array}\right] \le C \left[ \begin{array}{ll} y_1(k)\\ y_2(k)\end{array}\right] , \quad \left[ \begin{array}{ll} y_1(k)\\ y_2(k)\end{array}\right] \in \{0,1\}^2. \end{aligned}$$

Regarding the objective function (4), we consider the case where fixed costs are much more relevant than the proportional and holding ones. This results in choosing a high value for $f^k$ in comparison with values of parameters $p^k$, $h^k$ as shown in the next linear objective function where ${\mathbf {1}}^n$ indicates the n-dimensional row vector on 1’s:

$$\begin{aligned} J(u,y)= \sum _{k=0}^{N-1} \left( \langle {\mathbf {1}}^n,u(k) \rangle + \langle {\mathbf {1}}^n,x(k) \rangle + 100 \langle {\mathbf {1}}^n,y(k) \rangle \right) . \end{aligned}$$

(30)

This choice makes sense for two reasons. First, all the work is centered around issues deriving from the integer nature of y(k). So, high values of $f^k$ emphasize the role of integer variables in the objective function. Second, high fixed costs lead to solutions with the fewest number of control actions and this facilitates the validation and interpretation of the simulated results.

Next, we decompose dynamics (29) in scalar lot sizing form (13) which we rewrite below:

$$\begin{aligned} x_i(k+1)=x_i(k) - d_i^{e(k)}(k) + u_i(k). \end{aligned}$$

As regards the estimated demand $d_i^+$, a natural choice is to set $d_i^+$ as below, where we have denoted by $\tilde{x}_1(k)$ (respectively, $\tilde{x}_2(k)$) the estimated value of state $x_1(k)$ (respectively, $x_2(k)$) in the dynamics of $x_2(k)$ (respectively, $x_1(k)$):

$$\begin{aligned} \left[ \begin{array}{ll} d_1^+(k)\\ d_2^+(k) \end{array}\right] =\left[ \begin{array}{cc} 0 &{} \kappa \\ -\kappa &{} 0 \end{array}\right] \left[ \begin{array}{ll} \tilde{x}_1(k)\\ \tilde{x}_2(k)\end{array}\right] + \left[ \begin{array}{ll} w_1(k)\\ w_2(k)\end{array}\right] . \end{aligned}$$

(31)

Now, the question is: Which expression should be used to represent the set of admissible state vectors, $X^k$, appearing in equation (10)? A possible answer is given next:

$$\begin{aligned} \left[ \begin{array}{ll} \tilde{x}_1(k+1)\\ \tilde{x}_2(k+1)\end{array}\right] =&\left[ \begin{array}{ll} \tilde{x}_1(k)\\ \tilde{x}_2(k)\end{array}\right] +\left[ \begin{array}{ll} 0 \\ \kappa \bar{x}_1\end{array}\right] - \left[ \begin{array}{ll} 0 \\ w_2(k) \end{array}\right] \nonumber \\&+ \left[ \begin{array}{ll} 0 \\ C \end{array}\right] , \quad \left[ \begin{array}{ll} \tilde{x}_1(0)\\ \tilde{x}_2(0)\end{array}\right] = \left[ \begin{array}{ll} x_1(0)\\ \tilde{x}_2(0)\end{array}\right] . \end{aligned}$$

(32)

Let us elaborate more on the above equations. Regarding variable $\tilde{x}_2(k)$, this is used in the evolution of $d_1^+(k)$ as in the first equation of (31). Because of the positive contribution of the term $\kappa \tilde{x}_2(k)$ on $d_1^+(k)$, a conservative approach would suggest to take for $\tilde{x}_2(k)$ a possible upper bound of $x_2(k)$ and this is exactly the spirit behind the evolution of $\tilde{x}_2(k)$ as expressed in the second equation of (32). Here, $\bar{x}_1$ is an average value for $x_1$. A similar reasoning applies to $\tilde{x}_1(k)$, used in the evolution of $d_2^+(k)$ as in the second equation of (31). We now observe a negative contribution of the term $-\kappa \tilde{x}_1(k)$ on $d_2^+(k)$ and therefore take for $\tilde{x}_1(k)$ a possible lower bound of $x_1(k)$ as shown in the first equation of (32).

We can now move to show and comment on our simulated results.

We have carried out two different sets of experiments. In the line of the weakly coupling assumption (see Assumption 2), we have set $\kappa$ small enough and in the range from 0.01 to 0.225. Such a range works well as we will see that $|\kappa x_i|$ is always less than $w_i$, which also means $B x(k) + E w(k) < 0$. For the sake of simplicity and without loss of generality, we take capacity $C=3$, disturbances $w_i=1$ and $\bar{x}_1=1$. Unitary disturbances facilitate the validation and interpretation of the results as the accumulated demand over the horizon turns to be very close to the horizon length. The two experiments differ also in the horizon length N for reasons to be clarified next. All simulations were carried out with MATLAB on an Intel(R) Core(TM)2 Duo CPU P8400 at 2.27 GHz and a 3 GB of RAM.

The first set of experiments aims at analyzing the computational benefits of the decomposition and relaxation upon which our solution method is based. So, we consider $\kappa =0.1$ and horizon lengths $N=1, \ldots , 10$. We do not need to consider larger values of N as even in this small range of values, the differences in the computational times are already sufficiently evident as clearly illustrated in Fig. 2. Here, we plot the average computational time versus the horizon lengths N of the mixed integer predictive control problem (solid diamonds), of the decomposed problem $(\mathrm{MIPC}_i)$ (dashed squares) and of the linear program $(\mathrm{LP}_i)$ (dotted circles). Average computational time means the average time one agent takes to make a single decision (the total time is about 2N times the average one). As it can be seen, the computational time of the linear program $(\mathrm{LP}_i)$ is a fraction either of the one required by the (MIPC) or of the one required by the $(\mathrm{MIPC}_i)$.

Fig. 2

Average computational time versus horizon length N of the mixed integer predictive control problem (solid diamonds), of the decomposed problem $(\mathrm{MIPC}_i)$ (dashed squares), and of the linear program $(\mathrm{LP}_i)$ (dotted circles)

Fig. 3

Percentage error $\epsilon ~\%$ for different values of the elastic coefficient $\kappa$

In a second set of simulations, for a horizon length $N=6$, we have studied how the percentage error below varies with different values of the elastic coefficient $\kappa =\{0.01, \;0.2, \,0.225\}$:

$$\begin{aligned} \epsilon ~\%=\frac{\text {optimal cost of }(\mathrm{MIPC}_i)- \text {optimal cost of (MIPC)}}{\text {optimal cost of (MIPC)}}~\%. \end{aligned}$$

The role of $\kappa$ is crucial as we recall that $\kappa$ describes the effective tightness and coupling between different states $x_1(k)$ and $x_2(k)$. We do expect that small values for coefficient $\kappa$, which means weak coupling of state components, may lead to small errors $\epsilon ~\%$. Differently, high values of $\kappa$, describing a strong coupling between state components, are supposed to induce higher values of $\epsilon ~\%$.

This is in line with what we can observe in Fig. 3 where we plot the error $\epsilon ~\%$ as a function of coefficient $\kappa$. For relatively small values of $\kappa$ in the range from 0 to 0.2, we observe a percentage error not exceeding 1 %, $\epsilon ~\% \le 1$. A discontinuity at around $\kappa =0.2$ causes the error $\epsilon ~\%$ to go from about 1–$20~\%$.

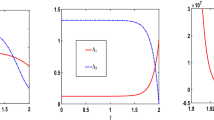
In Fig. 4, for a horizon length $N=6$ and for a value of $\kappa =0.225$, we depict the exact solution (dashed squares) and approximate solution (solid triangles) returned by the (MIPC) and by the $(\mathrm{LP}_i)$, respectively. Dotted lines represent predicted trajectories in earlier periods of the receding horizon. We note that controls $u_i(k)$ never exceed the capacity and are always associated with unitary control actions $y_i(k)$. Also, we observe four control actions (four peaks at 1) in the approximate solution and three in the exact solution. So we have an increase in the percentage error, of $20 \%$. A last observation concerning the exact plot of $y_i(k)$ is that the number of control actions is as minimal as possible, i.e., 3 for $y_1(k)$ and 2 for $y_2(k)$, as seen by dividing the accumulated demand (about 6) by the capacity $C=3$ and rounding the fractional result up to the next integer.

Fig. 4

Elastic coefficient $\kappa =0.225$. Exact solution (dashed squares) and approximate solution (solid triangles) returned by the mixed integer linear program (MIPC) and by the linear program $(\mathrm{LP}_i)$, respectively. Horizon length is $N=6$. Time plot of states $x_i(k)$, continuous controls $u_i(k)$ and discrete controls $y_i(k)$

We also compared exact and approximate solutions for a smaller value of $\kappa =0.2$ and observed that we still have notable differences in the plot of continuous controls $u_1(k)$ which cause a reduced percentage error $\epsilon ~\%=1$. We have concluded our simulations by noticing that the percentage error $\epsilon ~\%$ is around zero when we reduce further the value of $\kappa$ to 0.01.

6.2 Numerical Examples on the Mean-Field

In this subsection, we present two numerical examples on the mean-field approximation.

Example 6.2

Consider a complete network of $n=10$ agents. The local state average is the same for all i and also is equal to the global average, i.e., for all i it holds that $\bar{m}_i(k)= \frac{1}{n} \sum _{j\in V, j\not = i} (x_j(k) - x_i(k))$. The horizon length is $N=15$, the scalar $\epsilon =0.1$, the initial state is $x(0)=[4\ldots 13]$, and the disturbance is $E_{i\bullet } w(k)=1$ if k is odd and $E_{i\bullet } w(k)=2$ otherwise for all agents i. The bound on input is $C=3$, and the objective function is given below where ${\mathbf {1}}^n$ indicates the n-dimensional row vector on 1’s:

$$\begin{aligned} J(u,y)= \sum _{k=0}^{N-1} \left( \left\langle {\mathbf {1}}^n,u(k) \right\rangle + \left\langle {\mathbf {1}}^n,x(k) \right\rangle + 100 \left\langle {\mathbf {1}}^n,y(k) \right\rangle \right) . \end{aligned}$$

(33)

We also take $\phi =13$. We plot in Fig. 5 the time evolution of the state x(k). As expected, the state is nonnegative for all k. Also, the state x(k) converges to a neighborhood of zero of size $c - \min _k \{d_i^-(k)\} = 2$.

Fig. 5

Time evolution of state x(k)

Fig. 6

Population evolution for values of the averaging parameter $\epsilon =10^{-4},10^{-1},1$ and initial sparsity std $=~10^{-1}, 5, 10$ (from top to bottom): (left) time plot of state x(k); (right) average distribution and standard deviation

Fig. 7

Distribution for increasing values of the averaging parameter $\epsilon =10^{-4},10^{-1},1$ and initial sparsity std $=~10^{-1},5,10$ (from top to bottom)

Example 6.3

Consider a complete network of $n=1000$ homogeneous agents. As in the previous example, the local state average is the same for all i and also equal to the global average, i.e., for all i it holds that $\bar{m}_i(k)= \frac{1}{n} \sum _{j\in V, j\not = i} (x_j(k) - x_i(k))$. The horizon length is $N=60$, the scalar $\epsilon =10^{-4},10^{-1},1$, and the initial state x(0) is extracted from a Gaussian distribution with mean 70 and standard deviation $std=10^{-1},5,10$. The disturbance is $E_{i\bullet } w(k)=10 + 2 \gamma _i(k)$ where $\gamma _i(k)$ is a random walk, for all agents i. Thus, the system dynamics take the form

$$\begin{aligned} x_i(k+1)= & {} x_i(k) - d_i(k) + u_i(k),\nonumber \\ d_i(k)= & {} -[sat[\epsilon (\bar{m}_i(k)-x_i(k))] + 10 + 2 \gamma _i(k)] , \end{aligned}$$

(34)

where $u_i(k)$ is an (s, S) strategy of the type

$$\begin{aligned} u_i(k)= \left\{ \begin{array}{ll} 100, &{}\quad \text {if }x_i(k) \pm \varepsilon \le 20,\\ 0, &{} \quad \text {otherwise}. \end{array}\right. \end{aligned}$$

(35)

Results are shown in Figs. 6 and 7. In particular, Fig. 6 shows the population evolution for increasing averaging parameter $\epsilon =10^{-4},10^{-1},1$ and initial sparsity std $=~10^{-1}, 5, 10$ (from top to bottom). On the left column, we observe the time plot of state x(k); on the right column, we have the mean distribution and standard deviation. Clearly, a higher averaging parameter $\epsilon$ leads the agents to converge (with reduced standard deviation) in accordance with a consensus-type dynamics.

Figure 7 shows the population distribution for each one of the above simulations (from top to bottom). Thick lines highlight initial and final distributions.

7 Conclusions

In a nutshell, we have proposed a robust decomposition method which brings an n-dimensional hybrid optimization problem into n independent tractable scalar problems of lot sizing form. Through examples, we have illustrated the mean-field coupling in a multi-agent system problem, where each agent seeks to compensate a combination of an exogenous signal and the local state average. We have discussed a large population mean-field type of approximation as well as the application of predictive control methods.

There are at least three possibilities for future developments. First, one needs to study connections between regeneration intervals and reverse dwell time conditions developed in hybrid/impulsive control. Second, we intend to zoom in on the exploitation of cutting plane methods to increase the efficiency of linear relaxation approximations. Third, it would be of interest to investigate the mean-field large population approximations that arise from the decomposition of the mixed integer optimal compensation problem.