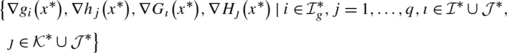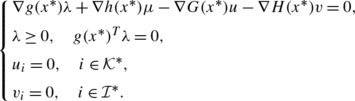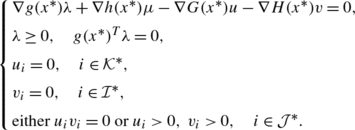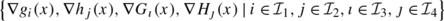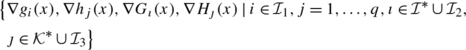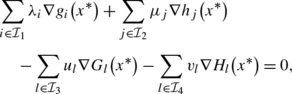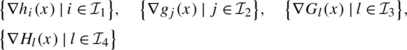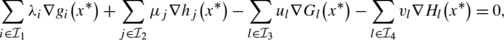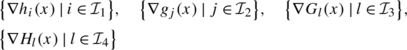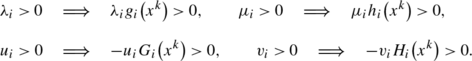Abstract
We study the constraint qualifications for mathematical programs with equilibrium constraints (MPEC). Firstly, we investigate the weakest constraint qualifications for the Bouligand and Mordukhovich stationarities for MPEC. Then, we show that the MPEC relaxed constant positive linear dependence condition can ensure any locally optimal solution to be Mordukhovich stationary. Finally, we give the relations among the existing MPEC constraint qualifications.

Similar content being viewed by others
References
Ye, J.J., Zhu, D.L., Zhu, Q.J.: Exact penalization and necessary optimality conditions for generalized bilevel programming problems. SIAM J. Optim. 7, 481–507 (1997)
Luo, Z.Q., Pang, J.S., Ralph, D.: Mathematical Programs with Equilibrium Constraints. Cambridge University Press, Cambridge (1996)
Outrata, J.V., Kocvara, M., Zowe, J.: Nonsmooth Approach to Optimization Problems with Equilibrium Constraints: Theory, Applications and Numerical Results. Kluwer Academic Publishers, Boston (1998)
Fukushima, M., Lin, G.H.: Smoothing methods for mathematical programs with equilibrium constraints. In: Proceedings of the ICKS’04, pp. 206–213. IEEE Comput. Soc., Los Alamitos (2004)
Flegel, M.L., Kanzow, C.: A direct proof for M-stationarity under MPEC-GCQ for mathematical programs with equilibrium constraints. In: Dempe, S., Kalashnikov, V. (eds.) Optimization with Multivalued Mappings, vol. 2, pp. 111–122. Springer, New York (2006)
Kanzow, C., Schwartz, A.: Mathematical programs with equilibrium constraints: enhanced fritz john conditions, new constraint qualifications and improved exact penalty results. SIAM J. Optim. 20, 2730–2753 (2010)
Scheel, H.S., Scholtes, S.: Mathematical programs with complementarity constraints: stationarity, optimality, and sensitivity. Math. Oper. Res. 25, 1–22 (2000)
Ye, J.J.: Constraint qualifications and necessary optimality conditions for optimization problems with variational inequality constraints. SIAM J. Optim. 10, 943–962 (2000)
Ye, J.J.: Necessary and sufficient optimality conditions for mathematical programs with equilibrium constraints. J. Math. Anal. Appl. 307, 350–369 (2005)
Ye, J.J., Ye, X.Y.: Necessary optimality conditions for optimization problems with variational inequality constraints. Math. Oper. Res. 22, 977–997 (1997)
Fletcher, R., Leyffer, S., Ralph, D., Scholtes, S.: Local convergence of SQP methods for mathematical programs with equilibrium constraints. SIAM J. Optim. 17, 259–286 (2006)
Lin, G.H., Guo, L., Ye, J.J.: Solving mathematical programs with equilibrium constraints as constrained equations (submitted)
Hu, X., Ralph, D.: Convergence of a penalty method for mathematical programming with equilibrium constraints. J. Optim. Theory Appl. 123, 365–390 (2004)
Scholtes, S.: Convergence properties of a regularization scheme for mathematical programs with complementarity constraints. SIAM J. Optim. 11, 918–936 (2001)
Guo, L., Lin, G.H., Ye, J.J.: Second order optimality conditions for mathematical programs with equilibrium constraint (submitted)
Mordukhovich, B.S.: Variational Analysis and Generalized Differentiation. I. Basic Theory. Grundlehren der Mathematischen Wissenschaften, vol. 330. Springer, Berlin (2006)
Rockafellar, R.T., Wets, R.J.-B.: Variational Analysis. Springer, Berlin (1998)
Flegel, M.L., Kanzow, C.: On M-stationary points for mathematical programs with equilibrium constraints. J. Math. Anal. Appl. 310, 286–302 (2005)
Ioffe, A.D., Outrata, J.V.: On metric and calmness qualification conditions in subdifferential calculus. Set-Valued Anal. 16, 199–227 (2008)
Andreani, R., Haeser, G., Schuverdt, M.L., Siliva, J.S.: A relaxed constant positive linear dependence constraint qualification and applications. Math. Program. (2011). doi:10.1007/s10107-011-0456-0
Ye, J.J., Zhang, J.: Enhanced Karush–Kuhn–Tucker condition for mathematical programs with equilibrium constraints (submmited)
Flegel, M.L., Kanzow, C.: On the guignard constraint qualification for mathematical programs with equilibrium constraints. Optimization 54, 517–534 (2005)
Moldovan, A., Pellegrini, L.: On regularity for constrained extremum problems. Part 2. Necessary optimality conditions. J. Optim. Theory Appl. 142, 165–183 (2009)
Hoheisel, T., Kanzow, C., Schwartz, A.: Theoretical and numerical comparison of relaxation methods for mathematical programs with complementarity constraints. Math. Program. (2011). doi:10.1007/s10107-011-0488-5
Kanzow, C., Schwartz, A.: A new regularization method for mathematical programs with complementarity constraints with strong convergence properties (submitted)
Minchenko, L., Stakhovski, S.: Parametric nonlinear programming problems under the relaxed constant rank condition. SIAM J. Optim. 21, 314–332 (2011)
Acknowledgements
The authors are grateful to two anonymous referees and Professor Franco Giannessi for their helpful suggestions and comments.
This work was supported in part by NSFC Grant #11071028.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Nobuo Yamashita.
Appendices
Appendix A: Existing Constraint Qualifications for MPEC
The constraint qualifications given for MPEC in the literature include the following ones: Let x ∗∈X.
- (a):
-
[7] We say that the MPEC linear independence constraint qualification (MPEC-LICQ) holds at x ∗ iff the family of gradients
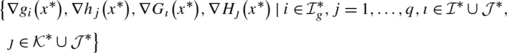
is linearly independent.
- (b):
-
[9, 15] We say that the MPEC linear constraint qualification (MPEC Linear CQ) holds iff all functions {g,h,G,H} in the constraints are affine.
- (c):
-
[6, 7] We say that the MPEC Mangasarian–Fromovitz constraint qualification (MPEC-MFCQ) holds at x ∗ iff there is no nonzero multipliers {λ,μ,u,v} such that
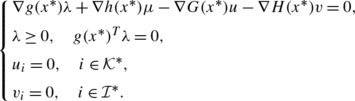
- (d):
-
[1, 6, 9] We say that the MPEC no nonzero abnormal multiplier constraint qualification (MPEC-NNAMCQ) holds at x ∗ iff there is no nonzero multipliers {λ,μ,u,v} such that
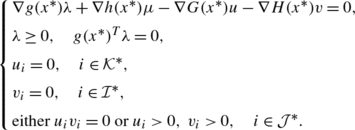
- (e):
-
[15, 24] We say that the MPEC constant rank constraint qualification (MPEC-CRCQ) holds at x ∗ iff there exists δ>0 such that, for any \(\mathcal{I}_{1}\subseteq \mathcal{I}_{g}^{*}, \mathcal{I}_{2}\subseteq\{1,\ldots, q\}\), \(\mathcal{I}_{3}\subseteq\mathcal{I}^{*}\cup\mathcal{J}^{*}\), and \(\mathcal{I}_{4} \subseteq \mathcal{K}^{*}\cup\mathcal{J}^{*}\), the family of gradients
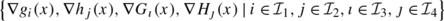
has the same rank for each \(x\in\mathcal{B}_{\delta}(x^{*})\).
- (f):
-
[15] We say that the MPEC relaxed constant rank constraint qualification (MPEC-RCRCQ) holds at x ∗ iff there exists δ>0 such that, for any \(\mathcal{I}_{1}\subseteq \mathcal{I}_{g}^{*}\) and \(\mathcal{I}_{2}, \mathcal{I}_{3}\subseteq \mathcal{J}^{*} \), the family of gradients
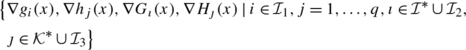
has the same rank for each \(x\in\mathcal{B}_{\delta}(x^{*})\).
- (g):
-
[24, 25] we say that the MPEC constant positive linear dependent condition (MPEC-CPLD) holds at x ∗∈X iff, for any \(\mathcal{I}_{1}\subseteq\mathcal{I}_{g}^{*}\), \(\mathcal{I}_{2}\subseteq\{1,\ldots, q\}\), \(\mathcal{I}_{3}\subseteq\mathcal{I}^{*}\cup\mathcal{J}^{*}\), and \(\mathcal{I}_{4} \subseteq\mathcal{K}^{*}\cup\mathcal{J}^{*}\), whenever there exist multipliers {λ,μ,u,v}, not all zero, with λ i ≥0 for each \(i\in\mathcal{I}_{1}\), such that
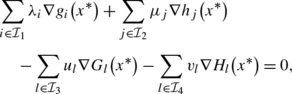
there exists a neighborhood B(x ∗) of x ∗ such that, for any x∈B(x ∗), the vectors
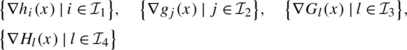
are linearly dependent.
- (g′):
-
[15, 21] We say that the MPEC constant positive linear dependent condition (MPEC-CPLD) holds at x ∗∈X iff, for any \(\mathcal{I}_{1}\subseteq\mathcal{I}_{g}^{*}\), \(\mathcal{I}_{2}\subseteq\{1,\ldots, q\}\), \(\mathcal{I}_{3}\subseteq\mathcal{I}^{*}\cup\mathcal{J}^{*}\), and \(\mathcal{I}_{4} \subseteq\mathcal{K}^{*}\cup\mathcal{J}^{*}\), whenever there exist multipliers {λ,μ,u,v}, not all zero, with λ i ≥0 for each \(i\in\mathcal{I}_{1}\), either u l v l =0 or u l >0,v l >0 for each \(l \in\mathcal{J}^{*}\), such that
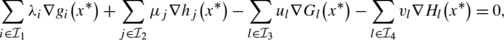
there exists a neighborhood B(x ∗) of x ∗ such that, for any x∈B(x ∗), the vectors
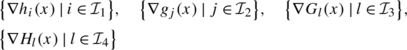
are linearly dependent.
- (h):
-
[6] We say that the MPEC pseudonormality holds at x ∗ iff there is no multipliers {λ,μ,u,v} such that
-
∇g(x ∗)λ+∇h(x ∗)μ−∇G(x ∗)u−∇H(x ∗)v=0;
-
\(\lambda\geq0,g(x^{*})^{T}\lambda= 0, u_{i}=0\ \mathrm{for}\ i\in\mathcal{K}^{*}, v_{i}=0\ \mathrm{for}\ i\in\mathcal{I}^{*},\ \mathrm{either}\ u_{i}v_{i}=0 \mathrm{or} \ u_{i}> 0, v_{i}> 0\ \mathrm{for}\ i\in\mathcal{J}^{*}\);
-
there exists a sequence {x k}→x ∗ such that, for each k,
$$\sum_{i=1}^p \lambda_i \nabla g_i\bigl(x^k\bigr) + \sum _{j=1}^q\mu_j \nabla h_j \bigl(x^k\bigr) - \sum_{i=1}^m u_\imath\nabla G_\imath\bigl(x^k\bigr) - \sum _{i=1}^m v_\jmath\nabla H_\jmath\bigl(x^k\bigr)>0. $$
-
- (i):
-
[6] We say that the MPEC quasinormality holds at x ∗ iff there is no nonzero multipliers {λ,μ,u,v} such that
-
∇g(x ∗)λ+∇h(x ∗)μ−∇G(x ∗)u−∇H(x ∗)v=0;
-
\(\lambda\geq0, g(x^{*})^{T}\lambda= 0, u_{i}=0\ \mathrm{for}\ i\in\mathcal{K}^{*}, v_{i}=0\ \mathrm{for} \ i\in\mathcal{I}^{*},\ \mathrm{either}\ u_{i}v_{i}=0 \mathrm{or} \ u_{i}> 0, v_{i}> 0 \ \mathrm{for}\ i\in\mathcal{J}^{*}\);
-
there exists a sequence {x k}→x ∗ such that, for each k,
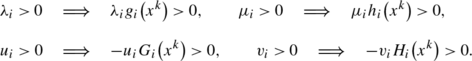
-
- (j):
-
[9, 18] We say that the MPEC Abadie constraint qualification (MPEC Abadie CQ) holds at x ∗ iff \(\mathcal{T}_{X}(x^{*})=\mathcal{L}_{\mathit{MPEC}}(x^{*})\).
- (k):
-
[5] We say that the MPEC Guignard constraint qualification (MPEC Guignard CQ) holds at x ∗ iff \(\mathcal{T}_{X}(x^{*})^{o}=\mathcal{L}_{\mathit{MPEC}}(x^{*})^{o}\).
It is easy to see that the MPEC-CPLD given in [15, 21] is weaker than the one given in [24, 25]. Note that the MPEC-CPLD in Fig. 1 is understood in the sense of [24, 25].
Appendix B: Proof of “MPEC-RCRCQ ⟹ MPEC Abadie CQ”
Suppose that the MPEC-RCRCQ holds at x ∗∈X. Let
For each partition \((\mathcal{J}^{*}_{1},\mathcal{J}^{*}_{2})\in\mathcal{P}(\mathcal{J}^{*})\), we consider the following restricted problem associated with (1):

Denote by \(X(\mathcal{J}^{*}_{1},\mathcal{J}^{*}_{2})\) the feasible region of (13). It is not difficult to see that

where \(\mathcal{L}_{X(\mathcal{J}^{*}_{1},\mathcal{J}^{*}_{2})}(x^{*})\) is the linearized cone of \(X(\mathcal{J}^{*}_{1},\mathcal{J}^{*}_{2})\) at x ∗.
Since x ∗ satisfies the MPEC-RCRCQ, the RCRCQ holds at x ∗ for each partition \((\mathcal{J}^{*}_{1},\mathcal{J}^{*}_{2})\in\mathcal{P}(\mathcal{J}^{*})\). It follows from Lemma 6 in [26] that

This, together with (14), indicates that \(\mathcal{T}_{X}(x^{*})=\mathcal{L}_{\mathit{MPEC}}(x^{*})\) and hence the MPEC Abadie CQ holds at x ∗.
Rights and permissions
About this article
Cite this article
Guo, L., Lin, GH. Notes on Some Constraint Qualifications for Mathematical Programs with Equilibrium Constraints. J Optim Theory Appl 156, 600–616 (2013). https://doi.org/10.1007/s10957-012-0084-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10957-012-0084-8