Numerical Optimization of Low Eigenvalues of the Dirichlet and Neumann Laplacians

Antunes, Pedro R. S.; Freitas, Pedro

doi:10.1007/s10957-011-9983-3

Numerical Optimization of Low Eigenvalues of the Dirichlet and Neumann Laplacians

Published: 10 January 2012

Volume 154, pages 235–257, (2012)
Cite this article

Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Pedro R. S. Antunes^1,2 &
Pedro Freitas^2,3

772 Accesses
60 Citations
Explore all metrics

Abstract

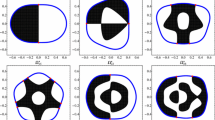
We perform a numerical optimization of the first ten nontrivial eigenvalues of the Neumann Laplacian for planar Euclidean domains. The optimization procedure is done via a gradient method, while the computation of the eigenvalues themselves is done by means of an efficient meshless numerical method which allows for the computation of the eigenvalues for large numbers of domains within a reasonable time frame. The Dirichlet problem, previously studied by Oudet using a different numerical method, is also studied and we obtain similar (but improved) results for a larger number of eigenvalues. These results reveal an underlying structure to the optimizers regarding symmetry and connectedness, for instance, but also show that there are exceptions to these preventing general results from holding.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Optimisation of Eigenvalues of the Dirichlet Laplacian with a Surface Area Restriction

Article 23 June 2015

The eigenvalues of the Laplacian with Dirichlet boundary condition in $$\mathbb {R}^2$$ are almost never minimized by disks

Article 25 November 2014

Optimization of the First Dirichlet Laplacian Eigenvalue with Respect to a Union of Balls

Article 04 April 2023

References

Antunes, P., Freitas, P.: New bounds for the principal Dirichlet eigenvalue of planar regions. Exp. Math. 15, 333–342 (2006)
Article MathSciNet MATH Google Scholar
Antunes, P., Freitas, P.: A numerical study of the spectral gap. J. Phys. A 5(055201) (2008) 19 pp.
Google Scholar
Henrot, A., Oudet, E.: Minimizing the second eigenvalue of the Laplace operator with Dirichlet boundary conditions. Arch. Ration. Mech. Anal. 169, 73–87 (2003)
Article MathSciNet MATH Google Scholar
Oudet, E.: Numerical minimization of eigenmodes of a membrane with respect to the domain. ESAIM Control Optim. Calc. Var. 10, 315–330 (2004)
Article MathSciNet MATH Google Scholar
Courant, R., Hilbert, D.: Methods of Mathematical Physics, vol. I. Interscience, New York (1953)
Google Scholar
Henrot, A.: Extremum Problems for Eigenvalues of Elliptic Operators. Frontiers in Mathematics. Birkhäuser, Basel (2006)
MATH Google Scholar
Faber, G.: Beweis, dass unter allen homogenen membranen von gleicher flüche und gleicher spannung die kreisfürmige den tiefsten grundton gibt. Sitz. ber. bayer. Akad. Wiss., 169–172 (1923)
Krahn, E.: Über eine von Rayleigh formulierte minimaleigenschaft des kreises. Math. Ann. 94, 97–100 (1924)
Article MathSciNet Google Scholar
Pólya, G.: On the characteristic frequencies of a symmetric membrane. Math. Z. 63, 331–337 (1955)
Article MathSciNet MATH Google Scholar
Krahn, E.: Über Minimaleigenshaften der Kugel in drei und mehr Dimensionen. Acta Comm. Univ. Dorpat. A9, 1–44 (1926)
Google Scholar
Kornhauser, E.T., Stakgold, I.: A variational theorem for ∇² u+λu=0 and its applications. J. Math. Phys. 31, 45–54 (1952)
MathSciNet MATH Google Scholar
Szegö, G.: Inequalities for certain eigenvalues of a membrane of given area. Arch. Ration. Mech. Anal. 3, 343–356 (1954)
MATH Google Scholar
Weinberger, H.F.: An isoperimetric inequality for the N-dimensional free membrane problem. Arch. Ration. Mech. Anal. 5, 633–636 (1956)
MathSciNet MATH Google Scholar
Girouard, A., Nadirashvili, N., Polterovich, I.: Maximization of the second positive Neumann eigenvalue for planar domains. J. Differ. Geom. 83(3), 637–662 (2009)
MathSciNet MATH Google Scholar
Bucur, D., Henrot, A.: Minimization of the third eigenvalue of the Dirichlet Laplacian. Proc. R. Soc. Lond. 456, 985–996 (2000)
Article MathSciNet MATH Google Scholar
Wolf, S.A., Keller, J.B.: Range of the first two eigenvalues of the Laplacian. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 447, 397–412 (1994)
Article MathSciNet MATH Google Scholar
Buttazzo, G., Dal Maso, G.: An existence result for a class of shape optimization problems. Arch. Ration. Mech. Anal. 122, 183–195 (1993)
Article MathSciNet MATH Google Scholar
Cox, S.J.: Extremal eigenvalue problems for starlike planar domains. J. Differ. Equ. 120(1), 174–197 (1995)
Article MATH Google Scholar
Poliquin, G., Roy-Fortin, G.: Wolf-Keller theorem for Neumann eigenvalues. Ann. Sci. Math. Québec (to appear)
Colbois, B., El Soufi, A.: Extremal eigenvalues of the Laplacian on Euclidean domains and Riemannian manifolds (preprint)
Bogomolny, A.: Fundamental solutions method for elliptic boundary value problems. SIAM J. Numer. Anal. 22(4), 644–669 (1985)
Article MathSciNet MATH Google Scholar
Alves, C.J.S., Antunes, P.R.S.: The method of fundamental solutions applied to the calculation of eigenfrequencies and eigenmodes of 2D simply connected shapes. Comput. Mater. Continua 2(4), 251–266 (2005)
Google Scholar
Goldberg, D.: Genetic Algorithms. Addison Wesley, Reading (1988)
Google Scholar
Nocedal, J., Wright, S.J.: Numerical Optimization. Springer, Berlin (1999)
Book MATH Google Scholar
Snyman, J.A.: Practical Mathematical Optimization: An Introduction to Basic Optimization Theory and Classical and New Gradient-Based Algorithms. Springer, Berlin (2005)
MATH Google Scholar
Sokolowski, J., Zolesio, J.P.: Introduction to Shape Optimization: Shape Sensitivity Analysis. Springer Series in Computational Mathematics, vol. 10. Springer, Berlin (1992)
MATH Google Scholar
Barnett, A.H., Betcke, T.: Stability and convergence of the method of fundamental solutions for Helmholtz problems on analytic domains. J. Comput. Phys. 227, 7003–7026 (2008)
Article MathSciNet MATH Google Scholar
Moler, C.B., Payne, L.E.: Bounds for eigenvalues and eigenfunctions of symmetric operators. SIAM J. Numer. Anal. 5, 64–70 (1968)
Article MathSciNet MATH Google Scholar
Pólya, G.: On the eigenvalues of vibrating membranes. Proc. Lond. Math. Soc. 11, 419–433 (1961)
Article MATH Google Scholar
Chen, J.T., Chen, I.L., Lee, Y.T.: Eigensolutions of multiply connected membranes using the method of fundamental solutions. Eng. Anal. Bound. Elem. 29, 166–174 (2005)
Article MATH Google Scholar
Antunes, P.R.S.: Numerical calculation of eigensolutions of 3D shapes using the method of fundamental solutions. Numer. Methods Partial Differ. Equ. 27(6), 1525–1550 (2011)
Article MathSciNet MATH Google Scholar

Download references

Acknowledgements

P.R.S.A. was partially supported by FCT, Portugal, through the scholarship SFRH/BPD/47595/2008 and the project PTDC/MAT/105475/2008 and by Fundação Calouste Gulbenkian through program Estímulo à Investigação 2009. Both authors were partially supported by FCT’s project PTDC/MAT/101007/2008.

Author information

Authors and Affiliations

Department of Mathematics, Universidade Lusófona de Humanidades e Tecnologias, Av. do Campo Grande, 376, 1749-024, Lisbon, Portugal
Pedro R. S. Antunes
Group of Mathematical Physics of the University of Lisbon, Complexo Interdisciplinar, Av. Prof. Gama Pinto 2, 1649-003, Lisbon, Portugal
Pedro R. S. Antunes & Pedro Freitas
Department of Mathematics, Faculdade de Motricidade Humana, TU Lisbon, Lisbon, Portugal
Pedro Freitas

Authors

Pedro R. S. Antunes
View author publications
You can also search for this author in PubMed Google Scholar
Pedro Freitas
View author publications
You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Pedro Freitas.

Additional information

Communicated by Enrique Zuazua.

Appendix

i	λ ₅		λ ₆		λ ₇		λ ₈
i	a _i	b _i	a _i	b _i	a _i	b _i	a _i	b _i
0	0.55438079		0.540969934		0.555917408		0.52402981
1	0.013238729	0.0057015487	−0.0254618108	0.20040578	−0.0396571523	0.0142910591	−0.133073983	−0.237327033
2	−0.077358408	0.092876235	−0.0441431399	−0.0456353393	−0.0378443687	−0.069786321	0.0524340446	0.0850167772
3	−0.0051545105	−0.0024247559	−0.0573759273	0.023490155	−0.0159573574	0.059561064	−0.0123987019	−0.0376173185
4	0.014513074	0.080309088	−0.0106613347	−0.0482010972	−0.0563539206	0.0490047495	−0.0260590608	0.00874912734
5	−0.0060402322	0.0077267846	0.0138861761	0.000120165574	−0.00279806649	−0.00185896562	−0.00308877567	−0.00973987438
6	0.0080050385	0.0023040320	0.000823401662	−0.00116176266	0.028061714	0.00907415168	−0.00634415879	0.014659245
7	−0.00041462756	0.0055027319	0.000493117601	0.000994308524	−0.00621703077	0.00398846543	−0.00742943607	0.00144421808
8	0.011735634	−0.0056190380	0.00160548125	−0.00108261442	0.00163688539	0.00365127087	0.0144983946	0.00753703381
9	0.0039973580	0.0034615840	−0.0000526885146	0.000351429203	0.00321047409	−0.00372583508	−0.00642345426	−0.013566282
10	−0.00022151852	−0.0026638205	0.000112772803	−0.0000539188865	0.0066201419	−0.00279887602	−0.00391602052	0.0101569665
11	0.0027374112	0.00075580032	−0.000110774901	0.000119156464	−0.00362005727	0.000298194234	0.00186757844	−0.00127916948
12	−0.0017708460	−0.0030278106	−0.000109752183	−0.000168572897	−0.00258236878	−0.00312578819	0.0024586174	0.00171021319
13	0.00096320890	−0.0020044397	7.12030548×10⁻⁶	−0.0000117806279	0.00193116396	0.0000971958322	−0.00172422653	−0.00153156433
14	−0.000035727810	0.00044155670	7.24155168×10⁻⁶	−3.84022077×10⁻⁶	−0.00131702223	−0.000360018056	0.00181204829	0.00094827332
15	−0.00053585540	−0.0017723963	−4.96715037×10⁻⁶	−3.61610015×10⁻⁶	−0.00172076406	0.000688255022	−0.00166054256	−0.00127832356
16	−0.00012345948	0.00096474668	3.08139935×10⁻⁷	−2.03467268×10⁻⁷	−0.00115709151	0.000109810932	0.000431561493	0.00130351922
17	−0.0013188383	−0.00070898727	1.33654316×10⁻⁷	1.43346737×10⁻⁷	0.00149459761	0.000610453469	0.0000346589834	0.000803396577
18	0.00022774519	0.000042899804	−1.13982504×10⁻⁷	5.93369227×10⁻⁸	−0.000305459945	0.00101611823	0.00188952975	−0.00135359719
19	−0.00050075176	0.000026338167			−0.000427708258	−0.000303869144	−0.00221559806	−0.000232152954
20	−0.00016570749	0.00018779596			0.000678645943	0.000276590019	0.00103793066	0.000830350291
21					0.000569909436	−0.000046937353	−0.000313475612	−0.000209535319
22					0.0000654203457	0.0000144614045	0.000450916946	−0.000139709455
23					−0.000351309674	−0.000371289997	−0.000211391115	0.0001928562
24					0.000351733859	−0.000136480239	0.000217311751	−0.000318264501

i	λ ₉		λ ₁₀		λ ₁₁		λ ₁₂
i	a _i	b _i	a _i	b _i	a _i	b _i	a _i	b _i
0	0.550655939		0.5595999481423		0.556134818		0.560041023
1	−0.0998751448	0.0773421852	0.0138865410279	−0.008909759517606	−0.0368731391	0.0239315354	−0.0379604707	0.0121487257
2	0.0550157453	−0.0430957094	0.002833319704712	0.002227574982416	−0.0182053322	0.0378034906	0.0387729478	0.0507913179
3	0.0399594874	0.0593875966	−0.008349328761967	0.0957550910192	−0.00715126258	−0.101591534	−0.0015923326	0.00266165893
4	0.00142349384	0.0425900486	0.005723472594822	−0.002967862015974	−0.0297483526	−0.0418656294	−0.0146793258	0.0490107094
5	−0.0139749255	−0.0408617143	0.002652563387632	0.002447234406475	0.0241573412	0.011609453	0.00402780473	−0.0090959291
6	−0.00367223638	0.0134695479	−0.004599950115557	0.02627159459515	0.0164630521	−0.00243660354	0.0172020883	−0.00377988974
7	0.0082532258	0.00455014924	−0.002226983087317	0.000837603292585	−0.00634085209	0.00454033198	0.000684280074	0.00988820653
8	−0.00895830418	0.00176185763	0.00158099064617	0.00129569319721	−0.00412733089	0.0136032862	0.0176838961	0.0101877652
9	0.00783739536	0.00272856592	0.000470007408465	−0.00146767096302	−0.00119221343	−0.00583869131	−0.00650954246	−0.00231789514
10	0.00224548719	−0.00470960161	−0.00032089848269	−0.0000433152786976	−0.000348634021	0.0023618601	0.00215815089	0.000591548356
11	−0.00333457231	0.00120461234	−0.000417096748991	−0.000549411311543	−0.00458553797	−0.000155987857	0.00268858702	−0.000746677809
12	0.00200923924	0.00134340334	0.00118106640714	−0.00326484110276	0.00156859838	−0.00100931829	0.00277871992	−0.00316449624
13	−0.00128480877	−0.00273791879	0.0000474565496931	0.0000106513746558	0.00246569204	−0.000345244088	−0.00204072395	0.00161161335
14	0.000462592585	0.00386907619	−0.000325293746937	−0.000447970381423	−0.000674880003	−0.00290011162	−0.0000851755712	−0.00180079941
15	0.00220397703	−0.00328595287	−0.0000233520418177	−2.21572997176×10⁻⁶	0.000577306217	0.0013066555	0.000479952574	−0.00218761547
16	−0.00159326685	0.000960521718	0.000145484964248	0.0000270002808451	−0.000130890779	−0.000367319041	−0.00119840099	−0.00172733708
17	0.000330803919	0.000303830978	0.0000346822452809	0.0000929323504196	−0.00153045766	−0.0000950422371	0.00130704997	0.00124434852
18	−0.000225563872	−0.00129473302	−0.000323698743562	0.000580384511426	0.000111369245	0.0000164522889	−0.00102042771	−0.00100033718
19	−0.000189994632	0.000379332968	5.83949533850×10⁻⁶	−3.49905606658×10⁻⁶	0.000181076275	−0.000228614786	−0.000755371705	0.0000336785202
20	0.00114449161	0.000603512001	0.0000728114477851	0.000158698077368	0.0000332405057	−0.00075412169	−0.000423177546	0.000174586669
21	−0.00107566805	−0.000685698552	−6.75766392730×10⁻⁹	8.82905652608×10⁻⁹	0.0000453530838	0.000211630126	0.000529771728	−0.000195846058
22			−4.71286357457×10⁻⁹	−1.34781200234×10⁻⁹	0.000790026567	0.00042327352	−0.000711361356	0.000555750456
23			4.91209220912×10⁻⁹	−1.56660058965×10⁻⁹	−0.000395412526	−0.0000237025238	−0.000200059087	0.000361447102
24			1.34638456165×10⁻⁸	−1.42615694109×10⁻⁸	−0.000221380759	0.000184318601	6.73027374×10⁻⁶	0.000121028574
25			−2.01122360346×10⁻⁹	−3.63972837821×10⁻¹⁰
26			−5.44330996748×10⁻⁹	−6.68514460573×10⁻⁹
27			1.73465493720×10⁻⁹	−1.98827703541×10⁻⁹
28			1.26990184897×10⁻⁹	6.02497710742×10⁻¹⁰
29			−6.50409422882×10⁻¹⁰	5.20844861007×10⁻¹⁰
30			−4.33794173095×10⁻⁹	2.75350252810×10⁻⁹

i	λ ₁₃		λ ₁₄		λ ₁₅
i	a _i	b _i	a _i	b _i	a _i	b _i
0	0.551503971		0.557612527		0.559420408
1	−0.0338396841	−0.114953381	0.0207678515	−0.0631536572	6.04658369×10⁻⁶	0.0000124733917
2	0.0303279427	−0.0574495473	0.058792891	−0.00649772139	−0.0000161762498	5.76792466×10⁻⁶
3	−0.0130257251	−0.0745641579	0.00531111557	0.0725253769	−0.00258516561	0.098348305
4	0.00554729211	0.0470925562	−0.0238412727	0.00370821936	0.0000123512599	−0.000190815291
5	−0.000623410989	0.0156226091	−0.00423481014	0.0177123045	−0.000180152753	−0.000020711265
6	0.017655584	0.0236085722	0.0103355869	0.00370104625	−0.0272911266	−0.00107299012
7	0.0157809243	0.0041362414	0.00304837882	−0.014888849	0.0000811807213	0.000119491243
8	−0.0102727122	0.00626879621	−0.00901708416	−0.00469316105	0.0000417425306	−0.000256107706
9	0.00478087159	0.0101645762	−0.00164226506	0.0112119165	0.00153912059	−0.0158989451
10	−0.00238858367	−0.00266695979	0.00355556561	0.00270396021	−0.0000614558942	−0.000447492308
11	−0.00105832356	−0.00408004353	0.000321931966	−0.00139053897	0.000866001007	0.00027348823
12	−0.000322435582	−0.00132277381	0.000904139462	−0.000968101304	−0.00316306275	−0.000317748954
13	−0.000213314175	−0.00418096453	−0.000540135261	0.00109132915	−0.000144984378	−0.0000655946379
14	0.00272342258	0.000515668982	0.00225122256	0.00138225898	0.0000138295682	0.0000408821376
15	0.00227560059	−0.00387180384	0.00168277384	−0.00245914572	0.000674764382	−0.00440846194
16	−0.00134117822	0.000421056294	−0.0020040944	−0.00149449634	0.000187045993	−0.0000389099159
17	0.00206300976	0.00168123748	−0.00133504032	0.00121246955	0.000295365946	0.000120717313
18	−0.000134937278	−0.000594329311	0.000932926429	0.000698600595	0.00201216141	0.000363000545
19	−0.000198444012	0.000832646684	0.000619420867	−0.000348513148	0.0000688156095	−0.0000196772322
20	−0.00102360784	0.0000520444273	−0.000149699453	−0.000278429144	−0.0000745226863	0.00023283672
21	−0.001672364	0.000149383067	−0.0000699271742	−5.4335581×10⁻⁶	0.000139260778	−0.000810604043
22	−0.0000358586874	0.000530041321	0.0000435046984	0.0000790199395	0.0000853310383	−0.0000589423176
23	−0.000396920563	−0.00174332362	0.000122963842	−0.0000894017094	−9.68881282×10⁻⁶	−0.0000137876809
24	−0.000877487074	0.000231158959	−0.000096357168	−0.000130817975	0.000859421574	0.000254606817
25	0.00081526229	−0.0000801225237			0.000192873826	0.00041027021
26	−0.0000126186682	−0.000184605499			−0.0000242683214	0.000159546939
27	0.000719525244	0.00045645044			−0.0000380641833	0.0000291315401
28	0.0000402334404	0.0000752523567
29	−0.000231434094	0.000612933714
30	0.000248027728	0.000375568407

i	μ ₃		μ ₄		μ ₅
i	a _i	b _i	a _i	b _i	a _i	b _i
0	0.549954737		0.554098864		0.560519732
1	−0.000578925467	0.122335927	0.00784197933	0.00418017833	2.70058702×10⁻⁶	−7.43462854×10⁻⁷
2	0.0268566607	0.000218577103	−0.0567066976	−0.085617596	−2.82208992×10⁻⁶	0.0891304954
3	0.000496273706	−0.119430145	0.0000940623335	0.00223713046	−2.99864606×10⁻⁶	3.78746736×10⁻⁶
4	0.0393289299	0.000347273779	−0.0418915905	0.1008615	0.0176267143	−1.07708404×10⁻⁶
5	0.000137109558	0.0106100598	−0.00119189439	0.000890469706	2.41171388×10⁻⁶	2.88093629×10⁻⁶
6	0.00283111302	−0.000494884753	−0.000628688812	−0.000171550392	−3.02951992×10⁻⁷	0.000287510816
7	0.000178562726	0.00858917695	0.000993259124	0.000551021581	−1.89820251×10⁻⁶	1.35592844×10⁻⁶
8	−0.0044258337	−0.000117746227	0.00172088603	0.00189395041	−0.0000537048883	−3.03014709×10⁻⁷
9	−0.000153351823	−0.00245969402	0.0000211410532	0.000121738707	1.11865906×10⁻⁸	1.5845649×10⁻⁸
10	0.000262693154	0.00011309051	0.0000861800292	−0.000464999058	−7.95639895×10⁻¹⁰	1.16121376×10⁻⁸
11	0.0000273742248	−0.000637837391	−2.92218066×10⁻⁶	3.16893374×10⁻⁶	−9.58692935×10⁻⁹	7.27334368×10⁻⁹
12	0.000277665815	0.000118370769	0.000038215104	−1.87411565×10⁻⁶	−1.01220124×10⁻⁸	−2.3451735×10⁻¹⁰
13	4.89182689×10⁻⁷	−1.22498345×10⁻⁶	5.19443562×10⁻⁷	−6.26013908×10⁻⁶	−8.39746687×10⁻¹⁰	−1.23147374×10⁻⁹
14	−7.17958187×10⁻⁷	−5.83425372×10⁻⁷	−2.72365156×10⁻⁸	4.12250759×10⁻⁸
15	9.84379966×10⁻⁷	−1.28371466×10⁻⁶	−3.8438191×10⁻⁷	1.2958845×10⁻⁷
16	1.0499127×10⁻⁶	3.93269146×10⁻⁷	−1.20147834×10⁻⁷	−8.02744085×10⁻⁸
17	−5.21573808×10⁻⁸	1.3948447×10⁻⁷
18	4.29340708×10⁻⁷	−7.32876443×10⁻⁸

i	μ ₆		μ ₇		μ ₈
i	a _i	b _i	a _i	b _i	a _i	b _i
0	0.544423006		0.561303447		0.563472327
1	0.154549722	0.074592044	−0.0296105015	0.00929288081	−0.0135281387	−0.0125695822
2	−0.0238297433	−0.0134221544	0.00292713876	0.000461527094	−0.00100221576	0.000360922605
3	0.0465889872	0.0735117289	−0.00581168985	0.00629595371	−0.000758596993	−0.00183183995
4	0.00798942924	0.0640407746	0.000521812939	0.000923350669	0.0108989574	−0.00829182165
5	−0.00631739792	−0.018003381	−0.00154983934	0.0094039286	−0.000820543007	−0.000308128932
6	−0.0137357316	0.0204107763	−0.00501494717	0.0700259021	0.000874631017	−0.00117284521
7	−0.0216354835	0.0151204116	−0.00243458512	−0.012367072	−0.00888157387	−0.00150292924
8	−0.00906075347	0.00115927695	0.00113180953	0.000671399157	0.000674798064	0.000729850385
9	−0.008733436	0.000345375567	0.00256031464	0.00298770473	−0.0000147809707	0.000267662456
10	0.00229280469	−0.00114925445	0.00279992286	−0.000175531225	−0.00054844287	−0.000335737527
11	0.00315240014	0.00284257911	0.00354013286	0.00287589877	0.00119052948	−0.000881687946
12	−0.00163249012	0.00100770067	0.0137409909	0.000577609805	0.000195303616	0.0000981460855
13	−0.0000192004444	0.00315093287	−0.0052461102	0.00145050804	0.000174689747	0.000173203814
14	−0.00187726514	0.0026655375	0.00146193752	−0.0000610893421	−0.00126202335	−0.000458787859
15	−0.00216069733	0.00147185804	0.00022791128	−0.0021485341	0.0000822630097	0.000478005166
16	−0.00226807794	0.00129214283	−0.0000970608746	0.000143359763	1.09927346×10⁻⁶	0.0000300340072
17	−0.00096819417	−0.000488799805	0.000144426536	−0.00032671668	−9.92661542×10⁻⁶	−2.66527939×10⁻⁶
18	−0.000118656413	−0.00018293087	0.0000407362083	−0.000176673501	0.0000515695341	−9.26540504×10⁻⁶
19	−0.000192492127	0.0000493303754	−0.0000273822824	0.000171666015	−7.89252523×10⁻⁶	−6.26345568×10⁻⁶
20	0.000263760246	0.000350170164	0.0000432423872	−0.000127265244	2.41000428×10⁻⁶	−2.3749484×10⁻⁶
21	1.16558991×10⁻⁶	4.96712883×10⁻⁶			−5.85227252×10⁻⁶	−6.79087762×10⁻⁶
22	−1.63244689×10⁻⁶	6.47331955×10⁻⁶			−3.33045158×10⁻⁶	7.49271783×10⁻⁶
23	−3.4729084×10⁻⁶	5.95322586×10⁻⁶			1.88193258×10⁻⁶	−3.98305519×10⁻⁷
24	−4.96630548×10⁻⁶	1.72968518×10⁻⁶			−2.36175431×10⁻¹⁸	2.51061885×10⁻⁷
25	5.12755036×10⁻⁸	2.14945715×10⁻⁷
26	−3.07397112×10⁻⁸	2.19743806×10⁻⁷
27	−6.99669598×10⁻⁸	1.77349366×10⁻⁷

i	μ ₉		μ ₁₀
i	a _i	b _i	a _i	b _i
0	0.546107642		0.557982648
1	0.132184562	0.0832860664	−0.0107226947	−0.00560550488
2	−0.0422564242	−0.081406976	−0.00243459937	0.00272185071
3	−0.00288494405	0.0494657212	−0.106247514	−0.0216645017
4	−0.00990364257	0.0141660798	0.00371146609	−0.00230659129
5	0.044032033	−0.02072678	0.0000381990189	0.00245899729
6	0.0162253823	0.00284538146	0.0299771487	0.017040206
7	−0.00684008357	−0.00453911102	−0.0033437228	0.00348204544
8	0.0113448501	0.0332865286	0.000299992113	−0.00319195161
9	−0.00329408749	0.0181081652	−0.0217413819	−0.0152507074
10	−0.001807493	0.000642929037	0.000428329649	0.00273289835
11	−0.00649512127	0.00171952483	0.000587136389	−0.0000355914864
12	0.00379245547	0.00021410323	0.0000998793688	−0.000710946153
13	−0.000881363531	−0.00148150927	0.00168461816	−0.00141128391
14	−0.00288415573	−0.0106440172	−0.000916519918	0.000996942438
15	0.000669513161	−0.0000464470469	0.00151666691	0.00459881141
16	0.00163822411	−0.000542216743	−0.00150433091	0.000444760945
17	0.0087891035	−0.00109922112	0.00109118785	−0.000873399337
18	0.000888529246	0.000976724264	−0.00103745245	−0.00391413716
19	0.000561401536	0.00191176013	0.000136745573	0.000451314701
20	0.000172718181	0.00178646218	−0.000328686271	0.0000923832995
21	−0.0000607718052	−0.00115913985	0.0000607676685	0.000247990695
22	−0.00224226772	0.000812563001	0.000109497006	−0.0000372289029
23	−0.0026768554	0.0000114857432	−0.0000756102401	0.0000118837984
24	0.00107005965	−0.000253133326	−0.000067632927	0.000143418041

Rights and permissions

Reprints and permissions

About this article

Cite this article

Antunes, P.R.S., Freitas, P. Numerical Optimization of Low Eigenvalues of the Dirichlet and Neumann Laplacians. J Optim Theory Appl 154, 235–257 (2012). https://doi.org/10.1007/s10957-011-9983-3

Download citation

Received: 21 September 2011
Accepted: 20 December 2011
Published: 10 January 2012
Issue Date: July 2012
DOI: https://doi.org/10.1007/s10957-011-9983-3

Keywords

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Numerical Optimization of Low Eigenvalues of the Dirichlet and Neumann Laplacians

Abstract

Access this article

Similar content being viewed by others

Optimisation of Eigenvalues of the Dirichlet Laplacian with a Surface Area Restriction

The eigenvalues of the Laplacian with Dirichlet boundary condition in $$\mathbb {R}^2$$ are almost never minimized by disks

Optimization of the First Dirichlet Laplacian Eigenvalue with Respect to a Union of Balls

References

Acknowledgements

Author information

Authors and Affiliations

Corresponding author

Additional information

Appendix

Rights and permissions

About this article

Cite this article

Keywords

Navigation

Numerical Optimization of Low Eigenvalues of the Dirichlet and Neumann Laplacians

Abstract

Access this article

Similar content being viewed by others

Optimisation of Eigenvalues of the Dirichlet Laplacian with a Surface Area Restriction

The eigenvalues of the Laplacian with Dirichlet boundary condition in $$\mathbb {R}^2$$ are almost never minimized by disks

Optimization of the First Dirichlet Laplacian Eigenvalue with Respect to a Union of Balls

References

Acknowledgements

Author information

Authors and Affiliations

Corresponding author

Additional information

Appendix

Appendix

Rights and permissions

About this article

Cite this article

Share this article

Keywords

Search

Navigation