Abstract
A monomer-dimer model with a short-range attractive interaction favoring collinear dimers is considered on the lattice \(\mathbb Z^2\). Although our choice of the chemical potentials results in more horizontal than vertical dimers, the horizontal dimers have no long-range translational order—in agreement with the Heilmann–Lieb conjecture (Heilmann and Lieb in J Stat Phys 20(6):679–693, 1979).



Similar content being viewed by others
Notes
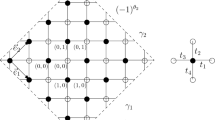
Two sites \(x=(x_{\mathrm{h}},{x_\mathrm{v}}),\,y=({y_{\mathrm{h}}},{y_\mathrm{v}})\in \mathbb Z^2\) are neighbors (\(x\sim y\)) if \(|x_{\mathrm{h}}-{y_{\mathrm{h}}}|+|{x_\mathrm{v}}-{y_\mathrm{v}}|=1\). A pair of sites (x, y) is a bond if x, y are neighbors. \(B(\mathbb Z^2)\) denotes the set of bonds.
Two sites \(x=(x_{\mathrm{h}},{x_\mathrm{v}}),\,y=({y_{\mathrm{h}}},{y_\mathrm{v}})\in \mathbb Z^2\) are h-neighbors if \({x_\mathrm{v}}={y_\mathrm{v}}\) and \(|x_{\mathrm{h}}-{y_{\mathrm{h}}}|=1\), they are v-neighbors if \(x_{\mathrm{h}}={y_{\mathrm{h}}}\) and \(|{x_\mathrm{v}}-{y_\mathrm{v}}|=1\). A bond \((x,y)\in B(\mathbb Z^2)\) is horizontal if x, y are h-neighbors, it is vertical if x, y are v-neighbors.
Theexternal boundary of \(\Lambda \) is \(\partial ^{\mathrm{ext}} \Lambda :=\{x\in \mathbb Z^2\setminus \Lambda \,|\,x\text { neighbor of }y\in \Lambda \}\). The internal boundary of \(\Lambda \) is instead \(\partial \Lambda \equiv \partial ^{\mathrm{int}} \Lambda :=\{x\in \Lambda \,|\,x\text { neighbor of }y\in \mathbb Z^2\setminus \Lambda \}\). We set \({\bar{\Lambda }}:=\Lambda \cup \partial ^{\mathrm{ext}} \Lambda \).
Namely we allow dimers having one endpoint in \(\Lambda \) and one in \(\mathbb Z^2\setminus \Lambda \).
Also fixed positions work, provided that the positions of the two h-dimers at the endpoints of each horizontal line of \(\Lambda \) allow a pure dimer configuration on that line.
\(\partial _\mathrm{v},\,\partial _{\mathrm{h}}\) denote respectively the vertical, horizontal component of the boundary; e.g. \(\partial _\mathrm{v}\Lambda :=\{x\in \Lambda \,|\,x \mathrm{h}\text {-}\mathrm{neighbor\,of} y\in \mathbb Z^2\setminus \Lambda \}\) and \(\partial _{\mathrm{h}}\Lambda :=\{x\in \Lambda \,|\,x \mathrm{v}\text {-}\mathrm{neighbor\,of }y\in \mathbb Z^2\setminus \Lambda \}\).
When the expectation of the order parameter is zero but the variance is not, a small perturbation can lead to a spontaneous order of the system.
We say that the site x has a left-dimer if there is a dimer on the bond \(\big (x,x-(1,0)\big )\), a right-dimer if there is a dimer on the bond \(\big (x,x+(1,0)\big )\).
On any graph the distance between two objects is defined as the length of the shortest path connecting them. In particular \({{\mathrm{dist}}}_{\mathbb Z^2}(S,S'):=\inf _{x\in S,\,y\in S'}{{\mathrm{dist}}}_{\mathbb Z^2}(x,y)\) for all \(S,S'\subset \mathbb Z^2\) and \({{\mathrm{dist}}}_{\mathbb Z^2}(x,y):=|x_{\mathrm{h}}-{y_{\mathrm{h}}}|+|{x_\mathrm{v}}-{y_\mathrm{v}}|\) for all \(x=(x_{\mathrm{h}},{x_\mathrm{v}}),\,y=({y_{\mathrm{h}}},{y_\mathrm{v}})\in \mathbb Z^2\).
\(\partial _\mathrm{l},\,\partial _\mathrm{r}\) denote respectively the left, right component of the vertical boundary; e.g. \(\partial _\mathrm{l}\Lambda :=\{x\in \Lambda \,|\,x-(1,0)\in \mathbb Z^2\setminus \Lambda \}\) and \(\partial _\mathrm{r}\Lambda :=\{x\in \Lambda \,|\,x+(1,0)\in \mathbb Z^2\setminus \Lambda \}\).
The possible states of a site \(x\in L\) are three: “l”=left-dimer namely a dimer on the bond \(\big (x,x-(1,0)\big )\), “r” \(=\) right-dimer namely a dimer on the bond \(\big (x,x+(1,0)\big )\), “m”=monomer. Here we think \(I_{\mathrm{l},x_\mathrm{l}},\,I_{\mathrm{r},x_\mathrm{r}}\) as vectors: \(I_{\mathrm{l},x_\mathrm{l}}=\begin{pmatrix} I_{\mathrm{l},x_\mathrm{l}}(l)&I_{\mathrm{l},x_\mathrm{l}}(r)&I_{\mathrm{l},x_\mathrm{l}}(m) \end{pmatrix}\) and \(I_{\mathrm{r},x_\mathrm{r}}=\begin{pmatrix} I_{\mathrm{r},x_\mathrm{r}}(l)&I_{\mathrm{r},x_\mathrm{r}}(r)&I_{\mathrm{r},x_\mathrm{r}}(m) \end{pmatrix}\).
In the first product on the r.h.s. of (3.10) the shorten notation \(b_{\mathrm{l}/\mathrm{r},x}\) means: take \(b_{\mathrm{l},x}\) if \(x\in \partial _\mathrm{l}\Lambda \), take \(b_{\mathrm{r},x}\) if \(x\in \partial _\mathrm{r}\Lambda \); notice that \(\partial _\mathrm{l}\Lambda \) and \(\partial _\mathrm{r}\Lambda \) are disjoint for \(N>1\). In the last product instead the shorten notation \(b_{\mathrm{r}/\mathrm{l},x}\) means: take \(b_{\mathrm{r},x}\) if \(x\in \partial _\mathrm{l}^{\mathrm{ext}} S_i\) only, take \(b_{\mathrm{l},x}\) if \(x\in \partial _\mathrm{r}^{\mathrm{ext}} S_i\) only, and take the product \(b_{\mathrm{r},x}\,b_{\mathrm{l},x}\) in the case that x belongs to both \(\partial _\mathrm{l}^{\mathrm{ext}} S_i\) and \(\partial _\mathrm{r}^{\mathrm{ext}} S_j\).
As explained in the Appendix B, using the definition (3.18) for \(\delta \), a family of polymers \((P_1,\dots ,P_q)\) is a cluster iff \(\cup _{t=1}^q{{\mathrm{supp}}}P_t\) is connected in \({\widetilde{\mathbb Z}}^2\).
This can be easily proven by induction on the number of edges.
The families of regions \((S_i)_{i=1}^n\) such that \({{{\mathrm{dist}}}_{\mathrm{h}}}(S_i,S_j)=\infty \) for at least one edge \((i,j)\in \mathcal {T}\) give zero contribution to the sum, therefore we do not need to worry about them.
This is an improvement of the well-known Cayley’s formula.
\(N_0=\frac{2}{m}\log \frac{32}{m}\).
The condition \({{{\mathrm{dist}}}_{\mathrm{h}}}({{\mathrm{supp}}}P,x)>1\) guarantees that \({{\mathrm{supp}}}P\subseteq \Lambda \setminus x\) and that the polymer P does not include any line \(L_k\) having one endpoint on \(x\pm (1,0)\), nor any region \(S_i\) containing these points.
The first possibility, namely P polymer only of the lattices that contain x, happens when \({{\mathrm{supp}}}P\ni x\) or P includes a region \(S_i\) containing \(x-(1,0)\). The second possibility, namely P polymer only of the lattices that do not contain x, happens when P includes a line \(L_k\) with one endpoint on \(x\pm (1,0)\). The last possibility happens when P includes a region \(S_i\) containing \(x+(1,0)\) (and does not verify the other conditions).
The transfer energy of a monomer is half the energy of a monomer because it appears during two “transfers”.
The discriminant of the cubic is \(\Delta =18a(1-b)+4a^2(1-b)+a^2+4-27a^2(1-b)\), which is strictly positive for all \(0\le a,b\le 1\), \((a,b)\ne (1,0)\).
References
Bovier, A., Zahradnik, M.: A simple inductive approach to the problem of convergence of cluster expansions of polymer models. J. Stat. Phys. 100(3–4), 765–778 (2000)
Contucci, P.: An analyticity bound for two-dimensional Ising model at low temperature. J. Stat. Phys. 82(5–6), 1647–1657 (1993)
Disertori, M., Giuliani, A.: The nematic phase of a system of long hard rods. Commun. Math. Phys. 323(1), 143–175 (2013)
Dobrushin, R.L.: Estimates of semi-invariants for the ising model at low temperatures. In: Dobrushin, R.L., Minlos, R.A., Shubin, M.A., Vershik, A.M. (eds.) Topics in Statistical and Theoretical Physics. F.A. Berezin Memorial Volume, pp. 59–81. American Mathematical Society, Providence, RI (1995)
Fernández, R., Procacci, A.: Cluster expansion for abstract polymer models. New bounds from an old approach. Commun. Math. Phys. 274(1), 123–140 (2007)
Gallavotti, G., Martin-Löf, A., Miracle-Solé, S.: Some Problems Connected with the Description of Coexisting Phases at Low Temperatures in the Ising Model. Lecture Notes in Physics, vol. 20, pp. 162–204. Springer, Heidelberg (1973)
Gruber, C., Kunz, H.: General properties of polymer systems. Commun. Math. Phys. 22, 133–161 (1971)
Heilmann, O.J., Lieb, E.H.: Monomers and dimers. Phys. Rev. Lett. 24(25), 1412–1414 (1970)
Heilmann, O.J., Lieb, E.H.: Theory of monomer-dimer systems. Commun. Math. Phys. 25(3), 190–232 (1972)
Heilmann, O.J., Lieb, E.H.: Lattice models for liquid crystals. J. Stat. Phys. 20(6), 679–693 (1979)
Kotecky, R., Preiss, D.: Cluster expansion for abstract polymer models. Commun. Math. Phys. 103(3), 491–498 (1986)
Letawe, I.: Le Modèle de Cristaux Liquides de Heilmann et Lieb, thesis in Physics at Université Catholique de Louvain, supervisor J. Bricmont (1994)
Miracle-Solé, S.: On the convergence of cluster expansions. Physica A 279, 244–249 (2000)
Onsager, L.: The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 51, 627–659 (1949)
Papanikolaou, S., Charrier, D., Fradkin, E.: Ising nematic fluid phase of hard-core dimers on the square lattice. (2014). arXiv:1310.4173
Ruelle, D.: Statistical Mechanics: Rigorous Results, vol. 4. W.A. Benjamin Inc., New York (1969)
Ueltschi, D.: Cluster expansion & correlation functions. Mosc. Math. J. 4, 511522 (2004)
Acknowledgments
I thank Prof. Elliott H. Lieb for his invitation at Princeton University, for having proposed me to work on his conjecture and for many useful discussions. I thank Prof. Pierluigi Contucci, Emanuele Mingione and Lukas Schimmer for interesting discussions. Financial support from UniBo Department of Mathematics, from FIRB Grant RBFR10N90W and from PRIN Grant 2010HXAW77 is acknowledged.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: 1D Systems
Consider a finite line L, that is a finite connected sub-lattice of \(\mathbb Z\). Consider a monomer-dimer model on L given by the following partition function:
\(\mathscr {D}_L\) denotes the set of monomer-dimer configurations on L (allowing also external dimers at the endpoints of L); the Hamiltonian is defined as

\(x_\mathrm{l},x_\mathrm{r}\) denote the left and the right endpoint of L respectively; \(I_\mathrm{l},I_\mathrm{r}\) represent the interaction among the configuration on L and the boundary condition outside its endpoints.
This one-dimensional system can be described by a transfer matrix T over the three possible states of a site, \(l\equiv \)“left-dimer”, \(r\equiv \)“right-dimer”, \(m\equiv \)“monomer”:
where to shorten the notation we set \(\sqrt{a}:=e^{-\beta \frac{\mu _{\mathrm{h}}+J}{4}}\) the transfer contribution of a monomerFootnote 20, \(\sqrt{b}:=e^{-\beta \frac{J}{2}}\) the transfer contribution of a site with a dimer but neighbor to a monomer. Two vectors are also needed to encode the boundary conditions:
Proposition 5.1
The partition function of the system rewrites as a bilinear form:
Proof
According to the previous definitions it is clear that for every configuration \(\alpha \in \{l,r,m\}^{|L|}\)
Therefore
\(\square \)
Assume for the moment that the transfer matrix T is diagonalizable. Denote by \(\lambda _1,\lambda _2,\lambda _3\) its eigenvalues and by \(E_\mathrm{r}^{(1)},E_\mathrm{r}^{(2)},E_\mathrm{r}^{(3)}\), \(E_\mathrm{l}^{(1)},E_\mathrm{l}^{(2)},E_\mathrm{l}^{(3)}\) the corresponding right (column) eigenvectors and left (row) eigenvectors, normalized so that \(E_\mathrm{l}^{(i)} E_\mathrm{r}^{(i)} = 1\) for \(i=1,2,3\).
Corollary 5.2
Proof
Since we are assuming that T is diagonalizable, it holds \(T=P\,D\,P^{-1}\) where D is the diagonal matrix of eigenvalues, P is the matrix with the right eigenvectors on the columns, \(P^{-1}\) has the left eigenvectors on the rows. Then \(T^{|L|-1}=P\,D^{|L|-1}\,P^{-1}\) and
\(\square \)
Now our purpose is to diagonalise the transfer matrix T when \(\beta \) is large.
Proposition 5.3
For all \(\beta >0\) the transfer matrix T is diagonalizable over \(\mathbb R\). Its eigenvalues are
as \(\beta \rightarrow \infty \).
Proof
The eigenvalues \(\lambda _1,\lambda _2,\lambda _3\) are the (complex) roots of the characteristic polynomial of T, that is
For all \(\beta >0\) it turns out that p has 3 distinct real rootsFootnote 21 , hence T is diagonalizable over the reals.
As \(\beta \rightarrow \infty \), \(p(\lambda )\rightarrow \lambda (\lambda ^2-1)\) hence \(\lambda _1\rightarrow 1\), \(\lambda _2\rightarrow -1\), \(\lambda _3\rightarrow 0\). Thus it is convenient to write \(\lambda _1=1+\varepsilon _1\), \(\lambda _2=-1+\varepsilon _2\), \(\lambda _3=a+\varepsilon _3\) with \(\varepsilon _i\rightarrow 0\) as \(\beta \rightarrow \infty \) for \(i=1,2,3\). Now expand the polynomial p in powers of \(\varepsilon _i\) and truncate it at the first order:
In order to find the following order of \(\lambda _3\), now one can write \(\lambda _3=a-ab\,(1+\varepsilon _3')\) with \(\varepsilon _3'\rightarrow 0\) as \(\beta \rightarrow \infty \) and repeat the procedure:
\(\square \)
Proposition 5.4
The right eigenvectors of the transfer matrix T are
and moreover
as \(\beta \rightarrow \infty \). The left eigenvectors are obtained by a simple transformation: \(E_\mathrm{l}^{(i)} = \sigma \big (E_\mathrm{r}^{(i)}\big )\) for \(i=1,2,3\), where
Proof
The right eigenvectors \(E_\mathrm{r}\) associated to the eigenvalue \(\lambda \) are the non-zero solutions of the linear system
And the left eigenvectors \(E_\mathrm{l}\) associated to the same eigenvalue \(\lambda \) are the non-zero solutions of the linear system
The desired normalization \(E_\mathrm{l}\,E_\mathrm{r}= 1\) can be obtained by choosing
in both cases. Now to conclude the proof it is sufficient to exploit the estimates of the eigenvalues given by the proposition 5.3. \(\square \)
The formula (5.10) together with the estimates of propositions 5.3, 5.4 give us a complete control on the one-dimensional system on L at low temperature, for every choice of the boundary conditions.
We concentrate on providing an estimation of the quantity \(R_L\) defined by (3.9), since it is needed in the Sect. 3. We have to distinguish three cases, according to where the endpoints of L lie.
Lemma 5.5
The ratios of the eigenvalues of the transfer matrix T are
as \(\beta \rightarrow \infty \). In particular setting \(m:=-\log |\lambda _2/\lambda _1|\) it holds
Proof
It follows immediately from the proposition 5.3. \(\square \)
Lemma 5.6
If \(x_\mathrm{l}\in \partial ^{\mathrm{ext}} _\mathrm{r}S_j\), then as \(\beta \rightarrow \infty \)
If \(x_\mathrm{r}\in \partial ^{\mathrm{ext}} _\mathrm{l}S_j\), then the same estimates hold for \(E_\mathrm{l}^{(1)}B_\mathrm{r}\), \(E_\mathrm{l}^{(2)}B_\mathrm{r}\), \(E_\mathrm{l}^{(3)}B_\mathrm{r}\) respectively.
Proof
If \(x_\mathrm{l}\in \partial ^{\mathrm{ext}} _\mathrm{r}S_j\) then by (3.7) and (5.8) the vector describing the boundary condition on the left side of the line L is \(B_\mathrm{l}= \begin{pmatrix} 0&\sqrt{b}&\sqrt{a} \end{pmatrix}\). Then the estimates for \(B_\mathrm{l}\,E_\mathrm{r}^{(i)}\), \(i=1,2,3\), are computed using the proposition 5.4. \(\square \)
Lemma 5.7
If \(x_\mathrm{l}\in \partial _\mathrm{l}\Lambda \), then as \(\beta \rightarrow \infty \)

If \(x_\mathrm{r}\in \partial _\mathrm{r}\Lambda \), then the same estimates hold respectively for \(E_\mathrm{l}^{(1)}B_\mathrm{r}\), \(E_\mathrm{l}^{(2)}B_\mathrm{r}\), \(E_\mathrm{l}^{(3)}B_\mathrm{r}\) after substituting: \(x_\mathrm{l}-(1,0)\) by \(x_\mathrm{r}+(1,0)\), “left” by “right” and “right” by “left”.
Proof
If \(x_\mathrm{l}\in \partial _\mathrm{l}\Lambda \) then by (3.7) and (5.8) the vector describing the boundary condition on the left side of the line L is: \(B_\mathrm{l}= \begin{pmatrix} 0&1&\sqrt{ab} \end{pmatrix}\) if a left-dimer is fixed on \(x_\mathrm{l}\!-\!(1,0)\); \(B_\mathrm{l}= \begin{pmatrix} 1&0&0 \end{pmatrix}\) if a right-dimer is fixed on \(x_\mathrm{l}\!-\!(1,0)\); \(B_\mathrm{l}= \begin{pmatrix} 1&1&\sqrt{ab} \end{pmatrix}\) if on \(x_\mathrm{l}\!-\!(1,0)\) there is a h-dimer with free position. Then the estimates for \(B_\mathrm{l}\,E_\mathrm{r}^{(i)}\), \(i=1,2,3\), are computed using the proposition 5.4. \(\square \)
Proposition 5.8
Denote by o(1) any function \(\omega (\beta ,\mu _{\mathrm{h}},J)\) that goes to zero as \(\beta \rightarrow \infty \) and does not depend on the choice of the line L nor on \(\Lambda \). Then for every line \(L\in {\mathscr {L}}_{\Lambda }(\cup _jS_j)\), \(S_j\in \mathscr {S}_\Lambda \) pairwise disconnected, \(\Lambda \subset \mathbb Z^2\) finite, it holds
where the quantity \(\gamma _L\) can be chosen as follows:
Proof
-
Suppose \(x_\mathrm{l}\in \partial ^{\mathrm{ext}} _\mathrm{r}S_i\) and \(x_\mathrm{r}\in \partial ^{\mathrm{ext}} _\mathrm{l}S_j\). The definition (3.9) and the corollary 5.2 give
$$\begin{aligned} \begin{array}{ll} \lambda _1\,R_L \,&{}=\, \frac{Z_L}{\lambda _1^{|L|-1}} \,-\, B_\mathrm{l}E_\mathrm{r}^{(1)}E_\mathrm{l}^{(1)}B_\mathrm{r}\\ &{}=\, \left( \frac{\lambda _2}{\lambda _1}\right) ^{\!|L|-1}\!B_\mathrm{l}E_\mathrm{r}^{(2)}E_\mathrm{l}^{(2)}B_\mathrm{r}\,+\, \left( \frac{\lambda _3}{\lambda _1}\right) ^{\!|L|-1}\!B_\mathrm{l}E_\mathrm{r}^{(3)}E_\mathrm{l}^{(3)}B_\mathrm{r}. \end{array} \end{aligned}$$By the lemma 5.5 \(|\lambda _3/\lambda _1|\le a\,|\lambda _2/\lambda _1|\) when \(\beta \) is sufficiently large. Therefore, using also the estimates of lemma 5.6, one finds
$$\begin{aligned} |R_L| \,\le \, \left| \frac{\lambda _2}{\lambda _1}\right| ^{|L|-1} \left( \frac{b}{2} + a^{|L|} \right) (1+o(1)) . \end{aligned}$$ -
Suppose now \(x_\mathrm{l}\in \partial ^{\mathrm{ext}} _\mathrm{r}S_j\) and \(x_\mathrm{r}\in \partial _\mathrm{r}\Lambda \). The definition (3.9) and the corollary 5.2 give
$$\begin{aligned} \begin{array}{ll} \lambda _1^{1/2}\,R_L \,&{}=\, \frac{Z_L}{\lambda _1^{|L|-1}E_\mathrm{l}^{(1)}B_\mathrm{r}} \,-\, B_\mathrm{l}E_\mathrm{r}^{(1)}\\ &{}=\, \left( \frac{\lambda _2}{\lambda _1}\right) ^{\!|L|-1} \frac{B_\mathrm{l}E_\mathrm{r}^{(2)}E_\mathrm{l}^{(2)}B_\mathrm{r}}{E_\mathrm{l}^{(1)}B_\mathrm{r}} \,+\, \left( \frac{\lambda _3}{\lambda _1}\right) ^{\!|L|-1} \frac{B_\mathrm{l}E_\mathrm{r}^{(3)}E_\mathrm{l}^{(3)}B_\mathrm{r}}{E_\mathrm{l}^{(1)}B_\mathrm{r}} . \end{array} \end{aligned}$$By the lemma 5.5 \(|\lambda _3/\lambda _1|\le a\,|\lambda _2/\lambda _1|\) when \(\beta \) is sufficiently large. Therefore, using also the estimates of lemmas 5.6, 5.7, one finds
$$\begin{aligned} |R_L| \,\le \, \left| \frac{\lambda _2}{\lambda _1}\right| ^{|L|-1}\, \frac{\sqrt{b}}{\sqrt{2}}\,(1+o(1)) . \end{aligned}$$ -
Suppose now \(x_\mathrm{l}\in \partial _\mathrm{l}\Lambda \) and \(x_\mathrm{r}\in \partial _\mathrm{r}\Lambda \). The definition (3.9) and the corollary 5.2 give
$$\begin{aligned} \begin{array}{ll} R_L \,&{}=\, \frac{Z_L}{\lambda _1^{|L|-1}B_\mathrm{l}E_\mathrm{r}^{(1)}E_\mathrm{l}^{(1)}B_\mathrm{r}} \,-\, 1 \\ &{}=\, \left( \frac{\lambda _2}{\lambda _1}\right) ^{\!|L|-1} \frac{B_\mathrm{l}E_\mathrm{r}^{(2)}E_\mathrm{l}^{(2)}B_\mathrm{r}}{B_\mathrm{l}E_\mathrm{r}^{(1)}E_\mathrm{l}^{(1)}B_\mathrm{r}} \,+\, \left( \frac{\lambda _3}{\lambda _1}\right) ^{\!|L|-1} \frac{B_\mathrm{l}E_\mathrm{r}^{(3)}E_\mathrm{l}^{(3)}B_\mathrm{r}}{B_\mathrm{l}E_\mathrm{r}^{(1)}E_\mathrm{l}^{(1)}B_\mathrm{r}} . \end{array} \end{aligned}$$By the lemma 5.5 \(|\lambda _3/\lambda _1|\le a\,|\lambda _2/\lambda _1|\) when \(\beta \) is sufficiently large. Therefore, using also the estimates of lemma 5.7, one finds
$$\begin{aligned} |R_L| \,\le \, \left| \frac{\lambda _2}{\lambda _1}\right| ^{|L|-1}\,(1+o(1)) . \end{aligned}$$
\(\square \)
Appendix B: Cluster Expansion
In this Appendix we state the main results about the general theory of cluster expansion used in this paper. The condition that we adopt to guarantee the convergence of the expansion is due to Kotecky–Preiss [11]. For a modern proof we refer to [17].
Let \(\mathscr {P}\) be a finite set, called the set of polymers. Let \(\varrho :\mathscr {P}\rightarrow \mathbb C\), called the polymer activity, and \(\delta :\mathscr {P}\times \mathscr {P}\rightarrow \{0,1\}\), called the polymer hard-core interaction, such that \(\delta (P,P)=0\) and \(\delta (P,P')=\delta (P',P)\) for all \(P,P'\in \mathscr {P}\). Consider the polymer partition function:
A family of polymers \((P_1,\dots ,P_q)\) is called compatible if \(\delta (P_t,P_s)=1\) for all \(t\ne s\); otherwise it is called incompatible. Observe that in the partition function \(\mathcal {Z}\) only the compatible families of polymers give non-zero contributions.
A family of polymers \((P_1,\dots ,P_q)\) is called a cluster if the graph with vertex set \(\{1,\dots ,q\}\) and edge set \(\{(t,s)\,|\,\delta (P_t,P_s)=0\}\) is connected.
Theorem 5.9
Suppose that there exists \(a\!:\mathscr {P}\rightarrow [0,\infty [\), called size function, such that the Kotecky–Preiss condition is satisfied, namely:
Then:
where the series on the r.h.s. is absolutely convergent and
Moreover, for all \(\mathscr {E}\subseteq \mathscr {P}\)
It is worth to observe that if \((P_1,\dots ,P_q)\) is not a cluster then \(u(P_1,\dots ,P_q)=0\). Therefore only the clusters of polymers (that are infinitely many) give non-zero contributions to the expansion (5.18) of \(\log \mathcal {Z}\).
Rights and permissions
About this article
Cite this article
Alberici, D. A Cluster Expansion Approach to the Heilmann–Lieb Liquid Crystal Model. J Stat Phys 162, 761–791 (2016). https://doi.org/10.1007/s10955-015-1421-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-015-1421-8