Operator Formalism for Topology-Conserving Crossing Dynamics in Planar Knot Diagrams

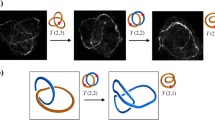
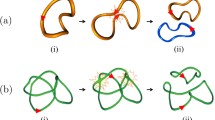
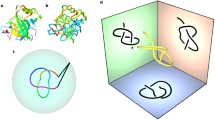
Abstract

We address here the topological equivalence of knots through the so-called Reidemeister moves. These topology-conserving manipulations are recast into dynamical rules on the crossings of knot diagrams. This is presented in terms of a simple graphical representation related to the Gauss code of knots. Drawing on techniques for reaction–diffusion systems, we then develop didactically an operator formalism wherein these rules for crossing dynamics are encoded. The aim is to develop new tools for studying dynamical behaviour and regimes in the presence of topology conservation. This necessitates the introduction of composite paulionic operators. The formalism is applied to calculate some differential equations for the time evolution of densities and correlators of crossings, subject to topology-conserving stochastic dynamics. We consider here the simplified situation of two-dimensional knot projections. However, we hope that this is a first valuable step towards addressing a number of important questions regarding the role of topological constraints and specifically of topology conservation in dynamics through a variety of solution and approximation schemes. Further applicability arises in the context of the simulated annealing of knots. The methods presented here depart significantly from the invariant-based path integral descriptions often applied in polymer systems, and, in our view, offer a fresh perspective on the conservation of topological states and topological equivalence in knots.

Appendix A: Thoughts Towards Simulated Annealing of Knots

It is interesting to ask how one may reduce or simplify a given knot to its “simplest form”. For instance, some complex knotted structure could perhaps be untangled and simplified to yield the underlying topologically equivalent prime knot. Indeed, analytical approaches to knot and braid reduction, based on algebraic techniques for reduction of words, have been considered (e.g. [18, 45]). How then does one quantify complexity of a knot? The crossing number has featured extensively here, for instance in the study of topological effects in polymer dynamics [46], the estimation of the number of knots with $n$ crossings through path integral techniques [47] and for analysing complexity of polygonal lattice knots [48]. The crossing number is also used in computer simulations addressing the relation of knot complexity and knotting probability [49]. Other measures of knot complexity include powers of some algebraic invariants, applied in studying knot entropies in the setting of braids and locally free groups [18].

A very physical approach to finding a “simplest configuration” of a knot is through minimisation of suitably defined knot energies. Indeed, energy spectra for knots have been defined through fluid mechanical techniques [50], and knot simplification has been studied in terms of electrostatic repulsion of equidistantly spaced charges along knots [51]. Extensions to this include bending energies [52] and Möbius knot energies defined in terms of integrals of curves [53]. It is even possible to obtain a minimal configuration of knots that is an invariant of knot type through global minimisation of knot energies based on the total curvature and electrostatic-type interactions [54].

Another physical idea is to “inflate” a knot to drive its geometric simplification [55]. Various definitions of knot thickness [56] and rope length of knots [57] have been applied to knot classification and simplification, and the relation of knot thickness to crossing number has been studied [58].

Since many of the above-mentioned ideas are very difficult to deal with analytically, the simplification of knots has also been studied extensively through computational/algorithmic techniques. Indeed, it is this question which we address below. Such procedures require two ingredients, namely a measure of knot complexity (e.g., the crossing number), and a driving process for the simplification / reduction (e.g., minimisation of knot energy). We briefly outline here how these concepts have been employed in simulations. Thereafter we suggest how our labelling scheme and dynamical rules could be employed to yield a simple algorithm for knot simplifications.

1.1 A1 Algorithmic Untangling of Knots: A Brief Overview

One key motivation for finding algorithmic prescriptions to simplify knots is the study of probability distributions of randomly generated knots [49] and to test for the equivalence of given knots. The latter question is particularly challenging, since it would otherwise involve testing for the existence of some sequence of Reidemeister moves that relates two knots (computationally an open problem), or calculating some knot invariant (an incomplete test for knot equivalence) [17].

Knot simplification simulations typically involve the improvement of some cost function related to the knot complexity. It has, for instance, been suggested to evolve knots iteratively along the gradient of some chosen energy function deterministically (e.g. [51]) or stochastically (e.g. [59]) through the introduction of small perturbations that are accepted if they affect the cost function favourably. Such techniques, however, are sensitive to getting stuck in local stationary states [17]. To avoid this issue, the problem has been tackled through simulated annealing [17, 60]. This approach involves the occasional acceptance of configurational changes that evolve the system against the gradient of the cost function. The acceptance of such “uphill” perturbations is often related to a temperature parameter, so that initially they are more likely to occur. The system is then gradually “cooled off” with time, and uphill perturbations become less likely. (The applicability of such Metropolis-type algorithms to annealing and optimisation problems in statistical physics has been demonstrated extensively; see, for instance, the highly-cited article of Kirkpatrick et al. [61].) Various uphill perturbation methods have been used, including placing point charges near the (charged) knot and allowing it to evolve under electrostatic forces, tightening or loosening various parts of the knot [17], and perturbing the vertices of a piecewise linear curve representation of the knot [60]. More recently, a considerable improvement in computation times has been achieved through algorithms that combine energy minimisation and tree-based probabilistic planning [62].

Several of the techniques addressed above are computationally intensive. We shall therefore outline here some ideas for a simple annealing algorithm contingent on our dynamical rules.

1.2 A2 Simulated Annealing: Suggestions Based on Arc Diagrams or the Gauss Code

The steps of a suggested algorithm for simulated annealing of knots are discussed below.3

A. Generation of a random knot

If this step is required, a random knot can be generated using pivot-type algorithms [63] or closures of random walks (see [64] and references therein).

B. Projection of the knot

The random knot can now be projected to yield an arc diagram according to Sect. 2. Alternatively, existing tools for finding the Gauss code of the random knot could be augmented to further record distances between consecutive crossings in the projection. (A possible point of departure is the Mathematica package +KnotTheory+ [65, 66].)

C. Cost function

For the purpose of driving the evolution of the annealing algorithm, we suggested a cost function with two core attributes. Firstly, a large crossing number should be penalised so that simplification (i.e., reduction of the crossing number) is favoured. Secondly, free loops should be penalised. Free loops on the random knot are any simple loops that could be removed through R1 annihilation; see Fig. 13. This aspect of the cost function would depend on the arc-length of such a loop (obtainable from the arc diagram), so that small loops are heavily penalised.

The total cost function for the complete knot is then the sum of contributions of all trivial loops together with the part that depends on the crossing number.

D. Simulated annealing

We split the simulation processes into several classes.

D1. Random stochastic evolution of the knot

This is done according to the Reidemeister moves R0 and R3 (these govern “diffusion-type” processes), and annihilation moves R1 and R2 (these govern “simplification-type” processes that reduce the crossing number). Begin by selecting an occupied site on the arc diagram and allowing that arc-foot to diffuse under the following provisos.

• R0 allows the segments of the knot to “diffuse” relative to each other. Diffusion may only occur to empty nearest-neighbouring sites.

• If the selected arc foot is part of a primitive loop, then there is a probability of removing this loop through an R1 annihilation step, related to the net reduction of the cost function.

• Should the selected arc foot be adjacent to an occupied site, test for the following:

  • If a valid R3 configuration is present, allow execution of R3. If not, the particle may not diffuse.

  • If the configuration allows for an annihilation move of the R2-type, allow this move with a certain probability (depending on the improvement of the cost function through reduction of the crossing number).

Every diffusion step should be such that it either reduces the cost function or leaves it unaltered.

D2. Perturbations

The second class of simulation processes involves the introduction of new crossings at empty sites on the arc diagram. This can be done in two ways.

• Introduce new primitive loops into the arc diagram through an R1 creation step. This is an “uphill” perturbation: both the crossing number aspect and the primitive loop aspect of the cost function are affected against the simplification gradient. Likelihood of such an uphill perturbation is then related to a temperature parameter in the system (see D3). If a new primitive loop has been introduced into the arc diagram, there is a chance of it “diffusing” into the rest of the knot through the stochastic evolution; see D1.

• Introduce crossing pairs through an through an R2 creation step. The cost function is affected through the resulting increase in crossing number, again against the simplification gradient. These crossings, too, may diffuse into the rest of the knot through the stochastic evolution; see D1.

D3. Cooling

The temperature parameter (i.e., the likelihood of uphill perturbations) is then reduced as simulation time progresses, inducing the system to settle to a minimal configuration.

The core ingredient to our algorithm is therefore a cost function that penalises trivial loops of the knot and favours smaller crossing numbers. Stochastic evolution and perturbations of the knot may were suggested, based on the Reidemeister moves. The introduction of uphill perturbations implies that our algorithm should be less sensitive to local minima of the cost function. The manipulations are on a quasi-one-dimensional representation of the knot, and therefore the computational cost of the algorithm would be minimal. Such an algorithm could be particularly useful in investigating the importance of the individual Reidemeister moves in a purely topological dynamical setting, for instance through relative weighting of rates that govern the different processes. In this way one could study rate-limiting effects in our topological dynamics, possibly as an indicator of topologically-induced glassy behaviour. The relevance and usefulness of our algorithm remains to be tested. It is not clear whether the projection procedure is necessarily easy, or whether sufficiently much information about the real-space configuration of the knot is maintained after the projection. Consequently other types of cost functions could be considered.