Minimal unlinking pathways as geodesics in knot polynomial space

Abstract

Physical knots observed in various contexts – from DNA biology to vortex dynamics and condensed matter physics – are found to undergo topological simplification through iterated recombination of knot strands following a common, qualitative pattern that bears remarkable similarities across fields. Here, by interpreting evolutionary processes as geodesic flows in a suitably defined knot polynomial space, we show that a new measure of topological complexity allows accurate quantification of the probability of decay pathways by selecting the optimal unlinking pathways. We also show that these optimal pathways are captured by a logarithmic best-fit curve related to the distribution of minimum energy states of tight knots. This preliminary approach shows great potential for establishing new relations between topological simplification pathways and energy cascade processes in nature.

Introduction

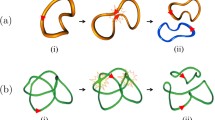
Physical knots observed in various contexts, such as DNA biology^1,2, vortex dynamics³, and condensed matter physics^4,5 are found to undergo topological simplification by following a common, qualitative pattern that brings complex structures to gradually degenerate to form simpler configurations till final production of small, unlinked, unknotted loops (see the trefoil knot evolution of Fig. 1a and the Hopf link cascade of Fig. 1b). The generic feature that characterizes the cascade process originates in the iterated recombination of knot strands through reconnection events that bear remarkable similarities across fields. The process of topological simplification that brings complex knots to simpler ones in a step-wise manner was first observed¹ in the analysis of site-specific recombination action on DNA catenanes (see Fig. 2a). Surprisingly, similar unlinking patterns were then observed also in classical vortex dynamics, superfluids, and condensates^6,7.

Fig. 1: Topological decay of fluid knots.

a Time evolution of reconnecting trefoil vortex in water (snapshots taken, with permission, from Supplementary movies 5 and 6 in ref. ³). b Time frame simulations of Hopf link defects in condensate⁵. Each stage is characterized by the topology of a torus knot or link represented pictorially by the corresponding minimal diagram presentation shown aside. Each torus knot/link T(p,q) is identified by the numbers p and q, denoting, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus. Red arrows denote vector field orientation (in this case vorticity), long black arrows topological transitions due to a single reconnection event.

Fig. 2: Topological transition by reconnection event.

a Minimal unlinking sequence representing iterated site-specific recombination action on DNA catenanes (taken from ref. ¹). Each torus knot/link T(p,q) is identified by the numbers p and q, denoting, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus; RH stands for right-hand knot/link and c-cat denotes catenanes with topological crossing number c_min. Long black arrows denote topological transitions due to a single recombination event. b Schematic representation of topological transition due to a single, anti-parallel reconnection of knot strands. Red arrows denote strand orientation and long arrow topological transition.

The universality of this process is rooted in the identical geometric mechanism that governs the change of topology of physical filaments^8,9,10,11,12, that through an iterated sequence of single, anti-parallel reconnection events¹³ (schematically represented in Fig. 2b) governs the topological cascade pattern of Fig. 2a. Topological changes were quantified by adapted HOMFLYPT polynomials derived from helicity by Liu and Ricca¹⁴ analyzing a family of torus knots and links (denoted by {T(p,q)}) given by knots/links wrapped on a mathematical torus p times in the longitudinal direction and q times in the meridian direction. It was found that the unlinking sequence of Fig. 2a can be described by a monotonic decreasing sequence of numerical values that matches the observed decrease in topological complexity. The untying sequence of Fig. 2a, however, is not unique. A given knot type, for instance the torus link with six minimum number of crossings denoted by T(2,6) in that sequence, can gradually unlink to the same final end-state, say the unknot T(2,1) (with topological crossing number zero), following pathways different from the one shown in Fig. 2a. So, what makes a given pathway a privileged route towards topological decay has yet to be understood, and even though this may well depend on the particular physical process, a general guiding principle is still lacking.

In order to make progress an extensive search on all possible routes that reduce topologically a given knot to the unknot under certain assumptions has been carried out by Stolz et al.² by analyzing hundreds of cases. A summary of the last, most probable stages starting from the torus link T(2,6) is shown in the diagram of Fig. 3, where knot types are pictorially represented by standard minimal presentations^15,16. In terms of possible transitions the diagram is by no means exhaustive, but it gives an idea of the most probable, alternative routes that T(2,6) can follow by a sequence of single reconnection events towards the unknot T(2,1). Note that the lowest branch of this diagram corresponds to the sequence of Fig. 2a, but what makes this very sequence special is not quite clear. The values computed by Liu and Ricca’s adapted polynomial are not so helpful either, since all the numerical sequences obtained from the other alternative routes are equally monotonic decreasing. Some sort of selective principle has been devised by Stolz et al. by computing a probability value for each topological transition given by a single reconnection event represented in Fig. 3 by a long, black arrow. Computation of these values, however, relies on a rather sophisticated machinery based on various assumptions and a combined use of topological analysis and simulations data.

Fig. 3: Alternative unlinking pathways.

Paths from torus link T(2,6) to the unknot T(2,1) (diagram adapted from ref. ²). Each torus knot/link is denoted by T(p,q), where the numbers p and q denote, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus. Knot/link representatives denoted by A–D correspond to the Thistlethwaite link notation L6a1 (mirror), 5₂, L4a1 (anti-parallel), and T(2,3)#L2a1 in the Rolfsen table; Lc_mina1 stands for link with topological crossing number c_min in table position 1, 5₂ denotes knot with topological crossing number c_min = 5 in table position 2, and T(2,3)#L2a1 the connected sum of trefoil knot (the first torus knot) T(2,3) and Hopf link (the first torus link) L2a1, also denoted by T(2,2); 31#31 denotes the composite knot made of two trefoil knots T(2,3) (see ref. ²⁸ for standard knot table and notations). The bottom branch of the diagram represents the minimal unlinking sequence representing iterated site-specific recombination action on DNA catenanes. Green arrows denote strand orientation, long black arrows topological transitions due to single recombination event.

This has prompted us to propose a far simpler, and intriguingly new scenario based on the interpretation of the sequences of Fig. 3 as geodesic flows in a knot polynomial space. By relying on Arnold’s original idea¹⁷ of interpreting evolutionary processes as geodesic flows in appropriate metric spaces we propose to identify decaying patterns of topological simplification with geodesic flows in a knot polynomial space. In general this knot space can be viewed as a manifold defined by knot types, whose points are determined by the relative knot polynomials. Since we refer to physical knots, we make use of the adapted polynomials introduced by Liu and Ricca^18,19 to quantify the topology of fluid knots.This is done by taking standard Legendre polynomials to construct a basis and an appropriate metric to compute distance using knot polynomials. This allows to measure and compare geodesic distances between knot types, define and compute relative probabilities, and relate minimal pathways to lower bounds given by minimum energy states^20,21,22.

In the next section we introduce this space, define an appropriate metric by means of Legendre polynomials, identify the knots by adapted Jones polynomials, compute relative deviation and probability, and provide a comparative analysis between our results and the results obtained by Stolz et al.². We find that the data obtained by our approach match very well the data obtained by the other method, suggesting that the alternative method based on use of geodesics in knot polynomial space has great potential for probability computation of decaying processes of physical systems, even far more complex than the one considered here. By using a new measure of topological complexity based on distances in the knot space we also show that the decaying patterns observed are captured by a logarithmic best-fit curve that is functionally related, and bounded from below, by the logarithmic distribution of minimum energy states of tight physical knots^21,22.

Results

Knot polynomial space

Since all prime knots with nine or fewer crossings have distinct Jones polynomials, for the purpose we have in mind the Jones polynomial V_K(x) (x polynomial variable) provides a sufficiently robust knot identifier. So let us consider the Liu and Ricca adapted Jones polynomial for fluid knots¹⁸, and restrict ourselves to the single variable polynomial with positive exponents of highest degree n. Let us introduce the knot polynomial space ${{\mathcal{V}}}_{n}^{+}$ according to the following

Definition 1 (Knot polynomial space). The knot polynomial space ${{\mathcal{V}}}_{n}^{+}$ is an n-dimensional, discrete, Euclidean space endowed by Euclidean metric (to be defined below), whose isolated points (singletons) are the Jones polynomial of knot and link types.

Each singleton in ${{\mathcal{V}}}_{n}^{+}$ represents a specific knot or link K through its Jones polynomial V_K(x). Let us take the unknot T(2,1) as the origin of ${{\mathcal{V}}}_{n}^{+}$ given by V_T(2,1) = 1 (the Jones polynomial value of the unknot). Topological complexity is thus graded by the discrete topology given by iso-complexity level sets ${\chi }_{{c}_{\min }}$ given by the topological crossing number ${c}_{\min }$, so that knots/links of same ${c}_{\min }$ lie on the same ${\chi }_{{c}_{\min }}$-set. Optimal unlinking paths, such as that represented by Fig. 2 (top row), can be interpreted by piece-wise linear geodesic flows in ${{\mathcal{V}}}_{n}^{+}$ through the level sets ${\chi }_{{c}_{\min }}=$ constant.

Metric by Legendre polynomials

In order to determine optimal pathways we must make use of an appropriate orthonormal metric. Since the discrete set of points in ${{\mathcal{V}}}_{n}^{+}$ are given by knot polynomials, for such a metric we must consider the inner product of polynomials P_n = P_n(x) and P_m = P_m(x) in the real variable x. In general this is given by

$$\langle {P}_{n},{P}_{m}\rangle =\int_{a}^{b}{P}_{n}(x){P}_{m}(x)\rho (x)\ {\mathrm{{d}}}x,$$

(1)

where a and b are finite, real values, with ρ(x) density function. Orthogonality (together with other mathematical properties) is ensured by a class of standard hyper-geometric polynomials (Jacobi polynomials), widely used in mathematical physics to construct solutions to second-order linear, ordinary differential equations²³. These, defined through the hyper-geometric function, are given by

$${P}_{n}^{(\alpha ,\beta )}(x) = \, \frac{\Gamma (\alpha +n+1)}{n!\Gamma (\alpha +\beta +n+1)}\mathop{\sum }\limits_{m = 0}^{n}\left({{n}\atop {m}}\right)\\ \quad \, \frac{\Gamma (\alpha +\beta +n+m+1)}{\Gamma (\alpha +m+1)}{\left(\frac{x-1}{2}\right)}^{m},$$

(2)

where Γ(n) = (n − 1)! for any positive integer n. Orthogonality condition of Jacobi polynomials is given by

$${\langle {P}_{n},{P}_{m}\rangle }_{J} = \, \int_{-1}^{1}{\left(1-x\right)}^{\alpha }{\left(1+x\right)}^{\beta }{P}_{n}^{(\alpha ,\beta )}(x){P}_{m}^{(\alpha ,\beta )}(x)\ {\mathrm{{d}}}x\\ = \, \frac{{2}^{\alpha +\beta +1}}{2n+\alpha +\beta +1}\frac{\Gamma (\alpha +n+1)\Gamma (\beta +n+1)}{\Gamma (\alpha +\beta +n+1)n!}{\delta }_{nm},\\ \,\,\, (\alpha\,> \,-\!1 ,\,\beta \, > \,-\!1),$$

(3)

where δ_nm denotes the standard Kronecker delta. The simplest case is given by taking the density function ρ(x) = 1, so that one recovers the special family of Legendre polynomials, with

$${\left\langle {P}_{n},{P}_{m}\right\rangle }_{L}=\int_{-1}^{1}{P}_{n}(x){P}_{m}(x)\ {\mathrm{{d}}}x=\frac{2}{2n+1}{\delta }_{nm},$$

(4)

which determines a complete set of polynomials up to a scale factor. In order to have a unit norm, we must then set

$${L}_{n}(x)=\sqrt{\frac{2n+1}{2}}{P}_{n}(x),$$

(5)

so that

$$\int_{-1}^{1}{L}_{n}(x){L}_{m}(x)\ {\mathrm{{d}}}x={\delta }_{nm}\,.$$

(6)

From linear algebra²⁴, we have

Theorem 1 (Legendre basis). A polynomial given by

$${V}_{n}(x)={c}_{0}+{c}_{1}x+{c}_{2}{x}^{2}+\ldots +{c}_{n}{x}^{n}$$

can be expanded into the first n + 1 Legendre polynomials L₀(x), …, L_n(x), which provide a complete basis for the knot polynomial space ${{\mathcal{V}}}_{n}^{+}$.

Let us identify the adapted Jones polynomial V_K(x) with V_n(x), and apply Theorem 1; we have

$${V}_{K}(x)={V}_{n}(x)={c}_{0}{L}_{0}(x)+{c}_{1}{L}_{1}(x)+{c}_{2}{L}_{2}(x)+\ldots +{c}_{n}{L}_{n}(x),$$

(7)

with

$${c}_{i}=\int_{-1}^{1}{V}_{n}(x){L}_{i}(x)\ {\mathrm{{d}}}x\qquad (i=0,1,2,\ldots ,n),$$

(8)

and c_i = 0 for all i > n. The coordinates of a point in ${{\mathcal{V}}}_{n}^{+}$ are thus given by V_K(x) = (c₀, c₁, c₂, …, c_n). Since from ref. ¹⁸ we have that x ∈ [1, e], we must perform a change of variable to transform the interval [1, e] → [ − 1, 1]; this is done by taking

$$x\to {x}^{\prime}=\frac{2}{e-1}x-\frac{1+e}{e-1},$$

(9)

that gives

$$\int_{1}^{e}f[{V}_{n}(x)]\ {\mathrm{{d}}}x=\frac{2}{e-1}\mathop{\int}\nolimits_{-1}^{1}f[{V}_{n}({x}^{\prime})]\ {\mathrm{{d}}}{x}^{\prime}\,.$$

(10)

Definition 2 (Metric). The distance ${d}_{ij}({V}_{{K}_{i}},{V}_{{K}_{j}})$ in ${{\mathcal{V}}}_{n}^{+}$ between two points ${V}_{{K}_{i}}$ and ${V}_{{K}_{j}}$ determined by Eq. (7), is given by the Euclidean distance

$${d}_{ij}=\;\parallel {V}_{{K}_{i}}-{V}_{{K}_{j}}\parallel \;=\sqrt{\frac{2}{e-1}}\sqrt{\mathop{\int}\nolimits_{-1}^{1}{\left[{V}_{{K}_{i}}({x}^{\prime})-{V}_{{K}_{j}}({x}^{\prime})\right]}^{2}{\mathrm{{d}}}{x}^{\prime}}\,.$$

(11)

Application to unlinking pathways

Let us apply Eq. (11) to the knot types of Fig. 3 to compute data for all possible unlinking pathways. For this we must compute the Legendre coordinates of all knots and links of Fig. 3 using Eq. (8). Numerical values are shown in Table 1, where actual values are computed with five precision digits. We identify 17 possible pathways shown in Fig. 4, including pathways through topological transitions A → T(2,5) and B → T(2,4) (denoted by long, dashed arrows in Fig. 4) that are not reported in the diagram of Fig. 3. The 17 possible pathways from T(2,6) to the unknot T(2,1) are described in Table 2.

Table 1 Legendre coordinates of knots and links in the decay from T(2,6) to T(2,1).

Fig. 4: Comparison between different decaying pathways.

Possible routes of decaying pathways from T(2,6) to T(2,1), color coded according to the legends. Each torus knot/link is denoted by T(p,q), where the numbers p and q denote, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus. Knot/link representatives denoted by A–D correspond to the Thistlethwaite link notation L6a1 (mirror), 5₂, L4a1 (anti-parallel), and T(2,3)#L2a1 in the Rolfsen table; Lc_mina1 stands for link with topological crossing number ${c}_{\min }$ in table position 1, 5₂ denotes knot with topological crossing number ${c}_{\min }=5$ in table position 2, and T(2,3)#L2a1 the connected sum of trefoil knot (the first torus knot) T(2,3) and Hopf link (the first torus link) L2a1, also denoted by T(2,2); 31#31 denotes the composite knot made of two trefoil knots T(2,3) (see ref. ²⁸ for standard knot table and notations). Green arrows denote strand orientation, long black arrows topological transitions due to single reconnection events. Long, dashed arrows indicate topological transitions due to single reconnection events not reported in ref. ².

Table 2 Possible routes to decaying pathways in the decay from T(2,6) to T(2,1).

The distance between the farthest knot T(2,6) and the unknot T(2,1) is measured by the length d₀ = d(Π₀) that determines the direct path Π₀ from T(2,6) to T(2,1), i.e.

$${d}_{0}=d({V}_{T(2,6)}-{V}_{T(2,1)})=d({V}_{T(2,6)}-1)\,.$$

(12)

From Table 1, we have d₀ = 6.35193 × 10⁶. The length d_i = d(Π_i) of each route Π_i (i = 1, … ,17) is given by the sum of the direct distances between knot pairs present in each route Π_i. In order to compare pathway lengths it is useful to introduce a non-dimensional measure given by the relative deviation σ_i of each Π_i from the direct route Π₀. This is given by σ_i = (d_i − d₀)/d₀.

We want to compute the probability associated with each route and compare the results with those of Stolz et al.². Keeping in mind the cascade scenarios discussed in the Introduction, we may simply relate pathway length to probability by identifying shortest paths with most probable routes. An elementary definition of probability p_i = p(Π_i) is thus given by taking p_i inversely proportional to σ_i; we have

$${p}_{i}=\frac{{\sigma }_{i}^{-1}}{\mathop{\sum }\nolimits_{k = 1}^{17}{\sigma }_{k}^{-1}},\qquad \mathop{\sum }\limits_{i = 1}^{17}{p}_{i}=1.$$

(13)

Numerical values of total length d_i, deviation σ_i and relative probability p_i are given in Table 3.

Table 3 Length, deviation and probability of the 17 routes considered in the decay from T(2,6) to T(2,1).

For the sake of example let’s compute the probability associated with the transition T(2,6) → T(2,5): this is part of five routes, Π₁, Π₂, Π₃, Π₄, and Π₅ (see Fig. 4). Taking data from Table 3, we have

$${{P}_{T(2,6)\to T(2,5)}}= \, {P{\left.({{\it{\Pi }}_{1}}\cup {\it{\Pi }_{2}}\cup {\it{\Pi }_{3}}\cup {\it{\Pi }_{4}}\cup {\it{\Pi }_{5}})\right|}_{T(2,6)\to T(2,5)}}\\ = \, 97.6203 \% +0.622067 \% +0.454444 \%\\ \, +0.45440 \% +0.454399 \% \\ \approx \, 99.6 \% .$$

Similarly for the computation of other probabilities associated with each transition. The results, shown in red in Fig. 5, are juxtaposed with those (in black) obtained by Stolz et al. As we see the comparison is very satisfactory, especially if we take into account the rate of change of each single transition (not shown).

Fig. 5: Comparative analysis of transition probability values.

Probability values obtained by Stolz et al.² (in black) juxtaposed with the ones in red obtained by the present method. Each torus knot/link is denoted by T(p,q), where the numbers p and q denote, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus. Knot/link representatives denoted by A–D correspond to the Thistlethwaite link notation L6a1 (mirror), 5₂, L4a1 (anti-parallel), and T(2,3)#L2a1 in the Rolfsen table; $L{c}_{\min }a1$ stands for link with topological crossing number ${c}_{\min }$ in table position 1, 5₂ denotes knot with topological crossing number ${c}_{\min }=5$ in table position 2, and T(2,3)#L2a1 the connected sum of trefoil knot (the first torus knot) T(2,3) and Hopf link (the first torus link) L2a1, also denoted by T(2,2); 31#31 denotes the composite knot made of two trefoil knots T(2,3) (see ref. ²⁸ for standard knot table and notations). Green arrows denote strand orientation, long black arrows topological transitions due to single reconnection event. The additional transitions A → T(2,5) and B → T(2,4) denoted by dashed arrows represent also topological transitions due single reconnection events and are not reported by Stolz et al. ²; these additional transitions determine some small corrections in the overall assessment of transition probabilities.

It is interesting to compare deviations, relative probabilities, and topological complexity of the routes examined. In Fig. 6 we show (panel a) the plot of deviations and (panel b) the relative probabilities against Π_i. As we see, deviations cluster into four, well separated sets identified by encircled regions. This clustering reflects the group of pathways shown in the diagrams of Fig. 4. Note that the deviation of Π₁ from Π₀ is as small as 0.0268%, two orders of magnitude smaller than σ₂; the probability of Π₁ is p₁ = 97.6% (Fig. 6b), proving to be by far the most probable route among all possible routes.

Fig. 6: Deviation and relative probability of the 17 routes examined.

a Relative deviation σ_i (i = 1, … ,17 denotes pathway number); σ_i values cluster into four, well separate sets identified by the encircled regions. b Probability p_i of each route Π_i. The first route Π₁ has probability p₁ = 97%, which is several orders of magnitude larger than the probability of all other pathways.

As far as topological complexity is concerned, we introduce a new complexity measure in terms of distance between points in ${{\mathcal{V}}}_{n}^{+}$ and the unknot making use of Eq. (11). Since the unknot has V_T(2,1) = 1 and knot complexity tends to increase exponentially with the topological crossing number ${c}_{\min }$, it is useful to provide a new definition of topological complexity in terms of natural logarithm.

Definition 3 (Complexity degree). The topological complexity of a knot K is defined by the complexity degree χ(K) given by

$$\chi (K)=\mathrm{ln}\,[1+d({V}_{K},{V}_{T(2,1)})]\,.$$

(14)

The plot χ = χ(K) for data extracted from Table 1 is shown in Fig. 7. The superposed dashed line is a best-fit curve given by $\chi =6.3\,{\mathrm{ln}}\,K-0.13$, where K denotes the knot/link present in Fig. 3. Since for increasing complexity we have a logarithmic growth in terms of ${c}_{\min }$, this is consistent with the usual assumption that the number of knot/link types must increase exponentially with ${c}_{\min }$.

Fig. 7: Complexity degree of knots and links.

Complexity degree χ (defined by Eq. (14)) plotted against knots and links K in pathways Π₁, … ,Π₁₇. Each torus knot/link is denoted by T(p,q), where the numbers p and q denote, respectively, the number of longitudinal and meridian wraps of the knot/link type on the mathematical torus. Knot/link representatives denoted by A–D correspond to the Thistlethwaite link notation L6a1 (mirror), 5₂, L4a1 (anti-parallel), and T(2,3)#L2a1 in the Rolfsen table; $L{c}_{\min }a1$ stands for link with topological crossing number ${c}_{\min }$ in table position 1, 5₂ denotes knot with topological crossing number ${c}_{\min }=5$ in table position 2, and T(2,3)#L2a1 the connected sum of trefoil knot (the first torus knot) T(2,3) and Hopf link (the first torus link) L2a1, also denoted by T(2,2); 31#31 denotes the composite knot made of two trefoil knots T(2,3) (see ref. ²⁸ for standard knot table and notations). Best-fit curve (dashed) is given by $\chi =6.3\,{\mathrm{ln}}\,K-0.13$; encircled regions identify knots and links of same topological crossing number ${c}_{\min }$.

Discussion

It is natural to ask whether the topological simplification analyzed here can be put in any relation with typical energy cascade processes observed in nature. The logarithmic best-fit curve of Fig. 7 is extrapolated from purely topological data, without any reference to physical or biological processes. A physical justification of this logarithmic growth, however, can be given by comparing these results with data obtained from the analysis of minimum energy states of magnetic knots and links²¹ and, to some extent, of elastic systems²². By examining the numerical values of the groundstate spectra determined there we can see that energy minima grow with topological complexity as $a\,\mathrm{ln}\,{\#}_{{\mathrm{{K}}}}+b$, with a and b constants (and independent of knot types), and #_K denoting knot tabulation according to increasing ropelength λ. Note that $\lambda ({\#}_{{\mathrm{{K}}}})\propto {c}_{\min }^{3/4}$^(ref. 21, Eq. (19)). This comparison shows a remarkable similarity between logarithmic growths. Since magnetic minima are magneto-hydrodynamic configurations that represent also steady states of Euler flows^25,26,27, one can interpret those minima as energy lower bound representatives of any pathway cascade associated with energy reduction, be it due to elastic relaxation, viscous dissipation, or quantum effects. Hence, it is not so surprising to observe that any of the 17 routes considered above fits into the logarithmic decay of Fig. 7. It is also worth noticing that the best-fit curve of the optimal geodesic given by the most probable sequence Π₁ is arguably the closest match to the best-fit behavior obtained in ref. ²¹.

In summary, a new way to analyze and interpret optimal pathways attained through topological simplification of physical knots and links by step-wise sequence of unlinking events, such as those studied by Stolz et al.², is introduced and tested. This is done by relying on Arnold’s original idea of interpreting an evolutionary process as geodesic in an appropriate metric space. For this we introduce a discrete knot polynomial space whose points are defined by knot polynomials. Here we consider the adapted Jones polynomials introduced by Liu and Ricca¹⁸, identifying knot coordinates by Legendre polynomials. By defining an appropriate orthonormal metric, we apply this method to analyze the last stages of the unlinking pathways studied by Stolz et al.² in terms of discrete geodesic flows, and for each topological transition we compute the relative probability. The results obtained match very well the data obtained in ref. ² without using any extra assumption other than complexity reduction by stepwise unlinking. Moreover, by introducing a new measure of topological complexity based on distances in the knot space, we show that optimal decaying pathways observed in various physical systems in nature are well captured by a logarithmic best-fit curve that is functionally related, and bounded from below, by the logarithmic distribution of minimum energy states of tight physical knots^21,22.

All in all this new approach proves to be rather powerful and flexible. The use of a knot polynomial space through the computation of point coordinates by direct application of Eq. (8) allows one to explore topological unlinking pathways more complex than the ones analyzed here. Moreover, the new measure of complexity degree (a scalar quantity) defined by Eq. (14) can be straightforwardly applied to sample and predict admissible pathways before any detailed evaluation of probability routes using this measure as an exclusion principle, by exploiting the fact that any admissible pathway generates a monotonically decreasing sequence of χ-values. Finally, a conjecture about energy-complexity relations: since the considerations above are independent from any specific physical process, it would seem plausible to assume that any minimal simplification process could yield structural simplification governed by a logarithmic decrease proportional to topological complexity. If so, this would suggest an intriguing connection between topological simplification and energy cascade and entropy production. In this regard the novel approach proposed here seem to have great potential for future investigations.