Skip to main content
SpringerLink
Log in

Entropic Fluctuations of Quantum Dynamical Semigroups

  • Published:
Journal of Statistical Physics Aims and scope Submit manuscript

Abstract

We study a class of finite dimensional quantum dynamical semigroups \(\{\mathrm {e}^{t\mathcal{L}}\}_{t\geq0}\) whose generators \(\mathcal{L}\) are sums of Lindbladians satisfying the detailed balance condition. Such semigroups arise in the weak coupling (van Hove) limit of Hamiltonian dynamical systems describing open quantum systems out of equilibrium. We prove a general entropic fluctuation theorem for this class of semigroups by relating the cumulant generating function of entropy transport to the spectrum of a family of deformations of the generator \({\mathcal{L}}\). We show that, besides the celebrated Evans-Searles symmetry, this cumulant generating function also satisfies the translation symmetry recently discovered by Andrieux et al., and that in the linear regime near equilibrium these two symmetries yield Kubo’s and Onsager’s linear response relations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. The name quantum Markov semigroup is also used in the literature.

  2. Alternative definitions of detailed balance can be found in [1, 3].

  3. The level sets of I are {ς | I(ς)≤l} where l∈[0,∞[.

  4. The derivative exists for all \(\rho\in \mathfrak{S}\), see Theorem 3 in [60].

  5. This does not imply that L jk =L kj .

  6. Here, we could also consider conserved charges and introduce associated chemical potentials. We refrain to do so in order to keep notation as simple as possible.

  7. In some models (like the spin-boson system) the operators \(R^{(k)}_{j}\) are unbounded and only affiliated to the W ∗-algebra \(\mathcal{O}_{j}\). With some additional technicalities the discussions of this and the next three section easily extend to such cases, see any of the references [15, 17, 19, 41, 48].

  8. The same conditions ensure that the terms \(\rho_{\beta_{0}}(D_{j}(H_{\mathcal{S}}, H_{\mathcal{S}}))\) in Theorem 3.5(1) are strictly positive, providing of course that .

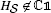  9. At the current level of generality, the verification of Hypothesis (RE) requires supplementing Davies’ conditions with additional regularity assumptions which we shall not discuss for reasons of space. In practice, i.e. in the context of concrete models, the verification of (RE) is typically an easy exercise.

References

  1. Agarwal, G.S.: Open quantum markovian systems and the microreversibility. Z. Physik 258, 409–422 (1973)

    Article  ADS  MathSciNet  Google Scholar 

  2. Andrieux, D., Gaspard, P., Monnai, T., Tasaki, S.: The fluctuation theorem for currents in open quantum systems. New J. Phys. 11, 043014 (2009)

    Article  ADS  Google Scholar 

  3. Alicki, R.: On the detailed balance condition for non-Hamiltonian systems. Rep. Math. Phys. 10, 249–258 (1976)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  4. Alicki, R., Lendi, K.: Quantum Dynamical Semigroups and Applications. Springer, Berlin (2007)

    MATH  Google Scholar 

  5. Aschbacher, W., Spohn, H.: A remark on the strict positivity of the entropy production. Lett. Math. Phys. 75, 17–23 (2006)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  6. Bryc, W.: A remark on the connection between the large deviation principle and the central limit theorem. Stat. Prob. Lett. 18, 253–256 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  7. Christensen, E., Evans, D.E.: Cohomology of operator algebras and quantum dynamical semigroups. J. London Math. Soc. 20, 358–368 (1979)

    Article  MATH  MathSciNet  Google Scholar 

  8. Chetrite, R., Mallick, K.: Quantum fluctuation relations for the Lindblad master equation. J. Stat. Phys. 148, 480–501 (2012)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  9. Davies, E.B.: Quantum stochastic processes II. Commun. Math. Phys. 19, 83–105 (1970)

    Article  ADS  MATH  Google Scholar 

  10. Davies, E.B.: Markovian master equations. Commun. Math. Phys. 39, 91–110 (1974)

    Article  ADS  MATH  Google Scholar 

  11. Davies, E.B.: Markovian master equations. II. Math. Ann. 219, 147–158 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  12. Davies, E.B.: Markovian master equations. III. Ann. Inst. H. Poincaré, section B 11, 265–273 (1975)

    MATH  Google Scholar 

  13. Davies, E.B.: Quantum Theory of Open Systems. Academic Press, London (1976)

    MATH  Google Scholar 

  14. Dereziński, J., de Roeck, W., Maes, C.: Fluctuations of quantum currents and unravelings of master equations. J. Stat. Phys. 131, 341–356 (2008)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  15. Dereziński, J., Früboes, R.: Fermi golden rule and open quantum systems. In: Attal, S., Joye, A., Pillet, C.-A. (eds.) Open Quantum Systems III. The Markovian Approach. Lecture Notes in Mathematics, vol. 1882. Springer, Berlin (2006)

    Google Scholar 

  16. Dereziński, J., Jakšić, V.: On the nature of Fermi Golden Rule for open quantum systems. J. Stat. Phys. 116, 411–423 (2004)

    Article  ADS  MATH  Google Scholar 

  17. Dereziński, J., Jakšić, V., Pillet, C.-A.: Perturbation theory of W ∗-dynamics, Liouvilleans and KMS-states. Rev. Math. Phys. 15, 447–489 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  18. de Roeck, W.: Quantum fluctuation theorem: Can we go from micro to meso? Comptes Rendus Phys. 8, 674–683 (2007)

    Article  ADS  Google Scholar 

  19. de Roeck, W.: Large deviation generating function for currents in the Pauli-Fierz model. Rev. Math. Phys. 21, 549–585 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  20. de Roeck, W., Kupianien, A.: ‘Return to Equilibrium’ for weakly coupled quantum systems: a simple polymer expansion. Commun. Math. Phys. 305, 797–826 (2011)

    Article  ADS  MATH  Google Scholar 

  21. de Roeck, W., Kupianien, A.: Approach to ground state and time-independent photon bound for massless spin-boson models. Ann. H. Poincaré 14, 253–311 (2013)

    Article  MATH  Google Scholar 

  22. de Roeck, W., Maes, C.: Steady state fluctuations of the dissipated heat for a quantum stochastic model. Rev. Math. Phys. 18, 619–653 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  23. Davies, E.B., Spohn, H.: Open quantum systems with time-dependent Hamiltonians and their linear response. J. Stat. Phys. 19, 511–523 (1978)

    Article  ADS  MathSciNet  Google Scholar 

  24. Dümcke, R., Spohn, H.: The proper form of the generator in the weak coupling limit. Z. Physik B 34, 419–422 (1979)

    Article  ADS  Google Scholar 

  25. Dembo, A., Zeitouni, O.: Large Deviations Techniques and Applications, 2nd edn. Applications of Mathematics, vol. 38. Springer, New York (1998)

    Book  MATH  Google Scholar 

  26. Evans, D.J., Cohen, E.G.D., Morriss, G.P.: Probability of second law violation in shearing steady flows. Phys. Rev. Lett. 71, 2401–2404 (1993)

    Article  ADS  MATH  Google Scholar 

  27. Esposito, M., Harbola, U., Mukamel, S.: Nonequilibrium fluctuations, fluctuation theorems, and counting statistics in quantum systems. Rev. Mod. Phys. 81, 1665–1702 (2009)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  28. Evans, D.E., Høegh-Krohn, R.: Spectral properties of positive maps on C ∗-algebras. J. London. Math. Soc. 17, 345–355 (1978)

    Article  MATH  MathSciNet  Google Scholar 

  29. Ellis, R.S.: Entropy, Large Deviations, and Statistical Mechanics. Classics of Mathematics. Springer, Berlin (1985). Reprinted in the series, 2006

    Book  MATH  Google Scholar 

  30. Evans, D.J., Searles, D.J.: Equilibrium microstates which generate second law violating steady states. Phys Rev. E 50, 1645–1648 (1994)

    Article  ADS  Google Scholar 

  31. Fagnola, F., Umanità, V.: Detailed balance, time reversal, and generators of quantum Markov semigroups. Mathematical Notes 84, 108–115 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  32. Gallavotti, G.: Extension of Onsager’s reciprocity to large fields and the chaotic hypothesis. Phys. Rev. Lett. 77, 4334–4337 (1996)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  33. Gallavotti, G., Cohen, E.G.D.: Dynamical ensembles in nonequilibrium statistical mechanics. Phys. Rev. Lett. 74, 2694–2697 (1995)

    Article  ADS  Google Scholar 

  34. Gallavotti, G., Cohen, E.G.D.: Dynamical ensembles in stationary states. J. Stat. Phys. 80, 931–970 (1995)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  35. Gorini, V., Kossakowski, A., Sudarshan, E.C.G.: Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 17, 821–825 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  36. Jakšić, V., Ogata, Y., Pautrat, Y., Pillet, C.-A.: Entropic fluctuations in quantum statistical mechanics—an introduction. In: Fröhlich, J., Salmhofer, M., de Roeck, W., Mastropietro, V., Cugliandolo, L.F. (eds.) Quantum Theory from Small to Large Scales. Oxford University Press, Oxford (2012)

    Google Scholar 

  37. Jakšić, V., Ogata, Y., Pillet, C.-A., Seiringer, R.: Quantum hypothesis testing and non-equilibrium statistical mechanics. Rev. Math. Phys. 24, 1230002 (2012)

    Article  MathSciNet  Google Scholar 

  38. Jakšić, V., Pillet, C.-A.: Non-equilibrium steady states of finite quantum systems coupled to thermal reservoirs. Commun. Math. Phys. 226, 131–162 (2002)

    Article  ADS  MATH  Google Scholar 

  39. Jakšić, V., Pillet, C.-A.: Entropic functionals in quantum statistical mechanics. In: Proceedings of the XVIIth International Congress of Mathematical Physics. Aalborg, Denmark (2012), to appear

    Google Scholar 

  40. Jakšić, V., Pillet, C.-A., Rey-Bellet, L.: Entropic fluctuations in statistical mechanics I. Classical dynamical systems. Nonlinearity 24, 699 (2011)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  41. Jakšić, V., Panati, A., Pillet, C.-A., Westrich, M.: Non-equilibrium statistical mechanics of Pauli-Fierz systems. In preparation

  42. Kossakowski, A., Frigerio, A., Gorini, V., Verri, M.: Quantum detailed balance and KMS condition. Commun. Math. Phys. 57, 91–110 (1977)

    Article  ADS  MathSciNet  Google Scholar 

  43. Kurchan, J.: Fluctuation theorem for stochastic dynamics. J. Phys. A 31, 3719–3729 (1998)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  44. Kurchan, J.: 2000, A quantum fluctuation theorem. Preprint. arXiv:cond-mat/0007360

  45. Lieb, E.H.: Convex trace functions and the Wigner-Yanase-Dyson conjecture. Adv. in Math. 11, 267–288 (1973)

    Article  MATH  MathSciNet  Google Scholar 

  46. Lindblad, G.: On the generators of quantum dynamical semigroups. Commun. Math. Phys. 48, 119–130 (1976)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  47. Lindblad, G.: Dissipative operators and cohomology of operator algebras. Lett. Math. Phys. 1, 219–224 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  48. Lebowitz, J.L., Spohn, H.: Irreversible thermodynamics for quantum systems weakly coupled to thermal reservoirs. Adv. Chem. Phys. 38, 109–142 (1978)

    Google Scholar 

  49. Lebowitz, J.L., Spohn, H.: A Gallavotti-Cohen-type symmetry in the large deviation functional for stochastic dynamics. J. Stat. Phys. 95, 333–365 (1999)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  50. Maes, C.: The fluctuation theorem as a Gibbs property. J. Stat. Phys. 95, 367–392 (1999)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  51. Majewski, W.A.: The detailed balance condition in quantum statistical mechanics. J. Math. Phys. 25, 614–616 (1984)

    Article  ADS  MathSciNet  Google Scholar 

  52. Maes, C., Redig, F., Verschuere, M.: From global to local fluctuation theorems. Mosc. Math. J. 1, 421–438 (2001)

    MATH  MathSciNet  Google Scholar 

  53. Matsui, T., Tasaki, S.: Fluctuation theorem, nonequilibrium steady states and MacLennan-Zubarev ensembles of a class of large quantum systems. In: Accardi, L., Tasaki, S. (eds.) Fundamental Aspects of Quantum Physics. World Scientific, Singapore (2003)

    Google Scholar 

  54. Ohya, M., Petz, D.: Quantum Entropy and its Use, 2nd edn. Springer, Berlin (2004)

    Google Scholar 

  55. Rebolledo, R.: Complete positivity and the Markov structure of open quantum systems. In: Attal, S., Joye, A., Pillet, C.-A. (eds.) Open Quantum Systems II. The Markovian Approach. Lecture Notes in Mathematics, vol. 1882. Springer, Berlin (2006)

    Google Scholar 

  56. Rondoni, L., Mejía-Monasterio, C.: Fluctuations in non-equilibrium statistical mechanics: models, mathematical theory, physical mechanisms. Nonlinearity 20, 1–37 (2007)

    Article  ADS  Google Scholar 

  57. Schrader, R.: Perron-Frobenius theory for positive maps on trazce ideals. In: Mathematical Physics in Mathematics and Physics, Siena, 2000. Fields Inst. Commun., vol. 30, pp. 361–378. AMS, Providence (2001)

    Google Scholar 

  58. Spohn, H.: Approach to equilibrium for completely positive dynamical semigroups of N-level systems. Rep. Math. Phys. 10, 189–194 (1976)

    Article  ADS  MathSciNet  Google Scholar 

  59. Spohn, H.: An algebraic condition for the approach to equilibrium of an open N-level system. Lett. Math. Phys. 2, 33–38 (1977)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  60. Spohn, H.: Entropy production for quantum dynamical semigroups. J. Math. Phys. 19, 1227–1230 (1978)

    Article  ADS  MATH  MathSciNet  Google Scholar 

  61. Stinespring, W.F.: Positive functions on C ∗-algebras. Proceedings of the American Mathematical Society 6, 211–216 (1955)

    MATH  MathSciNet  Google Scholar 

  62. Uhlmann, A.: Relative entropy and the Wigner-Yanase-Dyson-Lieb concavity in an interpolation theory. Comm. Math. Phys. 54, 21–32 (1977)

    Article  ADS  MATH  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montreal, QC, H3A 2K6, Canada

    V. Jakšić, C.-A. Pillet & M. Westrich

  2. Aix-Marseille Université, CNRS, CPT, UMR 7332, Case 907, 13288, Marseille, France

    C.-A. Pillet

  3. Université de Toulon, CNRS, CPT, UMR 7332, 83957, La Garde, France

    C.-A. Pillet

  4. FRUMAM, Marseille, France

    C.-A. Pillet

Authors
  1. V. Jakšić
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. C.-A. Pillet
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. Westrich
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to C.-A. Pillet.

Additional information

Dedicated to Herbert Spohn on the occasion of his 65th birthday.

The research of V.J. was partly supported by NSERC. The research of C.-A.P. was partly supported by ANR (grant 09-BLAN-0098). C.-A.P. is also grateful to the Department of Mathematics and Statistics at McGill University and to CRM (CNRS–UMI 3457) for hospitality and generous support during his stay in Montreal where most of this work was done. We are grateful to J. Dereziński, B. Landon, and A. Panati for useful comments. We also thank C. Maes and W. de Roeck for interesting related discussions.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Jakšić, V., Pillet, CA. & Westrich, M. Entropic Fluctuations of Quantum Dynamical Semigroups. J Stat Phys 154, 153–187 (2014). https://doi.org/10.1007/s10955-013-0826-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10955-013-0826-5

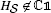Keywords

Search

Navigation