Zeros of Riemann’s Zeta Functions in the Line z=1/2+it₀

Abstract

It was found that, in addition to trivial zeros in points (z =  − 2N, N = 1, 2…, natural numbers), the Riemann’s zeta function ζ(z) has zeros only on the line {$z=\frac{1}{2}+\mathrm{i}{\mathrm{t}}_0$, t₀ is real}. All zeros are numerated, and for each number, N, the positions of the non-overlap intervals with one zero inside are found. The simple equation for the determination of centers of intervals is obtained. The analytical function η(z), leading to the possibility fix the zeros of the zeta function ζ(z), was estimated. To perform the analysis, the well-known phenomenon, phase-slip events, is used. This phenomenon is the key ingredient for the investigation of dynamical processes in solid-state physics, for example, if we are trying to solve the TDGLE (time-dependent Ginzburg-Landau equation).

1 Introduction

Investigations of Josephson effect, current flow in narrow superconducting strips [1], and dynamical states [2] in superconductors with use of TDGLE (time-dependent Ginzburg-Landau equation) lead to the necessity to deal with an important phenomenon: phase slip events. It is interesting that the study of the distribution of zeros for Riemann’s ζ function (see below Eqs. (15–17)) also requires an analysis of the same phenomenon. It means that there exists a deep internal connection between all these problems. It turns out that the Euler Γ function is also the essential ingredient of the scenario.

Riemann’s ζ function and Euler Γ function appear in many physical problems. For example, the study of the spin-orbit interaction in inhomogeneous superconductors state reveals the existence of the infinite set of nontrivial exact relations for Euler {ψ} function [3]; these relations are essential for the evaluation of the critical temperature. These equations contain the Bernoulli numbers B_n. In general, these problems appear as the consequence of mentioned internal ties and arise while the temperature technique and analytical continuation are used in the theory of superconductivity. We are trying to analyze these ties. We hope that the investigation of phase-slip events with the use of the distribution of zeros for Riemann’s ζ function will lead to new results, which are important not only in mathematics. They will provide a deep understanding of the phenomena mentioned above, especially for the case of strong suppression of superconductivity by an external field.

In order to investigate the zeros of ζ(z)_, it is more convenient to use the function Ξ(z), which can be presented in the symmetrical form as follows:

$$ \Xi (z)=\frac{z\left(z-1\right)}{4}\left[\zeta (z)\Gamma \left(z/2\right){\pi}^{-z/2}+\zeta \left(1-z\right)\Gamma \left(\left(1-z\right)/2\right){\pi}^{-\left(1-z\right)/2}\right] $$

(1)

where Γ(z) is Euler gamma function. The function Ξ(z) is the entire function of z. As for the zeros of ζ(z) and Ξ(z), they coincide on the stripe. If we put z = 1/2 + it, than Ξ(z) is even a function of t with real coefficients in its Taylor expansion in powers of t² [4]. The function of Ξ is real on the lines {$z=\frac{1}{2}+\mathrm{i}{\mathrm{t}}_0$; t₀ is real; z = ν; ν is real}. The line {z = 1/2 + it₀} is Stock’s line for Ξ function.

2 Main Equations

Each analytical function f(z) can be presented in the form as follows:

$$ f(x)=\mid f(x)\mid \exp \left( i\chi \right) $$

(2)

If f(x) ≠ 0 on some close counter C, then we are dealing with the following quantization rule:

$$ \underset{C}{\oint}\frac{\partial \chi }{\partial \mathbf{r}d\mathbf{r}}=2\pi \left({N}_z-{N}_p\right) $$

(3)

where N_z is a number of zeros, N_p is a number of poles inside the counter.

For z = 1/2 + ν + it₀ and ν ≫ 1, we have the following:

$$ \zeta (z)=1+\frac{1}{\sqrt{2}\cdot {2}^{\nu }}\Big(\cos \left({t}_0\ln 2\right)-i\sin \left({t}_0\ln 2\right) $$

(4)

From Eqs. (1, 4), we obtain that the integral of type (3) (see Fig. 1) for Ξ function is equal to two integrals type (3) on the counter {DABD₁}. Points {A, F} and {B, E} are symmetrically relative to the reflection over the {D, D₁} axis. The pair of zeros of zeta function placed in point $\left({t}_0^{(k)},\nu; {t}_0^{(k)},-\nu \right)$ is not giving any contribution to the phase change during the integration over the line {L, L₁}; the asymptotics (4) is canceling such a contribution by integration over the line {A, B}. Both these circumstances make impossible an appearance of pair zeros $\left({t}_0^{(k)},\nu; {t}_0^{(k)},-\nu \right)$ with ν ≠ 0. As a result, the total number of zeros of function Ξ inside counters C₁ and C₀ coincides. As for the interval {B, D₁}, the essential corrections to the phase change appear only for the regional order of one near D₁ point. Below, we will use the following expression for the ζ(z) function as follows:

$$ \zeta (z)=\frac{1}{1-{2}^{1-z}}\left\{{D}_1+{\mathrm{iD}}_2\right\},\kern1em z=1/2+\nu +{\mathrm{it}}_0 $$

(5)

where

$$ {\displaystyle \begin{array}{l}{D}_1=\left(1-{2}^{-1/2-\nu}\cos \left({t}_0\ln 2\right)\right)+\sum \limits_{k=2}^{\infty}\left(\frac{\cos \left({t}_0\ln \left(2k-1\right)\right)}{{\left(2k-1\right)}^{1/2+\nu }}-\frac{\cos \left({t}_0\ln (2k)\right)}{(2k)^{1/2+\nu }}\right)\\ {}{D}_2={2}^{-1/2-\nu}\sin \left({t}_0\ln 2\right)-\sum \limits_{k=2}^{\infty}\left(\frac{\sin \left({t}_0\ln \left(2k-1\right)\right)}{{\left(2k-1\right)}^{1/2+\nu }}-\frac{\sin \left({t}_0\ln (2k)\right)}{(2k)^{1/2+\nu }}\right)\end{array}} $$

(6)

Fig. 1

A single asterisk indicates a first zero of ζ function, counter C₀ (L, L₁, L₂, L₃), counter C₁ (F, D, A, B, D₁, E)

Note that in the points {t₀ ln 2 = 2πN, N ≠ 0, ν = 1/2}, we have D₁ = D₂ = 0 [5].

Let us consider the region t₀ ≫ 1 for the calculation of the distribution of zeros of the Ξ function. In this region, we obtain the following:

$$ \Xi (z)=\frac{\left({t}^2+1/4\right){\pi}^{1/4}{2}^{3/4}{e}^{-\pi t/4}}{4{t}^{1/4}}\left\{\zeta (z)\exp \left( i\phi (t)\right)+\zeta \left(1-z\right)\exp \left(- i\phi (t)\right)\right\} $$

(7)

where z = 1/2 + it = 1/2 + ν + it₀, ϕ is an analytical function with the following asymptotic expansion:

$$ \phi (t)=\frac{t}{2}\left(\ln \left(\frac{t}{2}\right)-\ln \pi -1\right)-\frac{\pi }{8}+\frac{1}{48t}+\dots $$

(8)

All zeros of function Ξcoincide with zeros of expression in brackets of Eq. (7). Here we use the ideas from the consideration of phase-slip events in solid-state physics [6]. More specifically, we define an analytical function η(t₀, ν) as follows:

$$ \eta \left({t}_0,\nu \right)={\eta}_1\left({t}_0,\nu \right)+i{\eta}_2\left({t}_0,\nu \right);\kern1em \eta \left({t}_0,\nu \right)=-{\eta}_1\left(-{t}_0,\nu \right)+i{\eta}_2\left(-{t}_0,\nu \right) $$

(9)

Then on the Stock’s line, we obtain the following:

$$ {\displaystyle \begin{array}{l}2{e}^{-{\eta}_2\left({t}_0\right)}\cos \left(\phi \left({t}_0\right)+{\eta}_1\left({t}_0\right)\right)={e}^{i\phi \left({t}_0\right)}\frac{D_1+{\mathrm{iD}}_2}{1-\sqrt{2}\cos \left({t}_0\ln 2\right)+i\sqrt{2}\sin \left({t}_0\ln 2\right)}+\\ {}{e}^{- i\phi \left({t}_0\right)}\frac{D_1-{i D}_2}{1-\sqrt{2}\cos \left({t}_0\ln 2\right)-i\sqrt{2}\left({t}_0\ln 2\right)}\end{array}} $$

(10)

On the Stock’s line, the function η₁(t₀, ν) satisfies the condition as follows:

$$ \mid {\eta}_1\mid <\pi /2 $$

(11)

Inside the range ν ≫ 1, we obtain the following equations for {η₁, η₂}:

$$ {\eta}_1=-\sin \left({t}_0\ln 2\right)/{2}^{1/2+\nu },\kern1em {\eta}_2=-\cos \left({t}_0\ln 2\right)/{2}^{1/2+\nu } $$

(12)

In addition, at the zero point with number N, we have two equations on the Stock’s line as follows:

$$ \frac{1}{\pi}\left(\phi \left({t}_0^{(N)}\right)+{\eta}_1\left({t}_0^{(N)}\right)\right)=N-3/2, $$

(13)

$$ {\left.\frac{\partial {\eta}_1\left({t}_0\right)}{\partial {t}_0}\right|}_{t_0^{(N)}}=0 $$

(14)

Equations (8, 11, 13, 14) allow us to estimate the location of the interval, where the zero point with number N is placed.

Note that there exists a large parameter t₀ ≫ 1 in the limit ln(t₀). It leads to the drastic increase of the first term in Eq. (10) relative the second term with an increase in ν; as a result, the existence of a pair of zeros (ν, −ν) with ν ≠ 0 is impossible. The ratio of these two terms is exp(ν ln(t₀/2π)). Equations (6, 13) allow us get the exact expression for the zeros of the Ξ function with a given number N and an asymptotic exact expression for ${\eta}_1\left({t}_0^{(N)}\right)$ and ${\eta}_2\left({t}_0^{(N)}\right)$ on a Stock’s line.

The Table contains the values of 29 first zeros of the zeta function from Ref. [7] and additional seven points with numbers 30, 40, 41, 42, 269, 270, and 271, which follow from Eqs. (10, 13, 14). For all these points, we added the values of functions ${\eta}_1\left({t}_0^{(N)}\right)$ and ${\eta}_2\left({t}_0^{(N)}\right)$.

The existence of the large parameter, lnt₀, allows to analyze Eqs. (10, 13, 14) with the use of the perturbation theory and estimate the functions {${\eta}_1\left({t}_0^{(N)}\right),{\eta}_2\left({t}_0^{(N)}\right)$}.

To perform this estimation, we present Eq. (10) in the form of the following:

$$ {e}^{-{\eta}_2\left({t}_0\right)}\cos \left(\phi \left({t}_0\right)+{\eta}_1\left({t}_0\right)\right)=\mu \left({t}_0\right) $$

(15)

where μ(t₀) is given by equation as follows:

$$ {\displaystyle \begin{array}{l}\mu \left({t}_0\right)=\frac{1}{2}\Big\{{e}^{i\phi \left({t}_0\right)}\frac{D_1+{i D}_2}{1-\sqrt{2}\cos \left({t}_0\ln 2\right)+i\sqrt{2}\sin \left({t}_0\ln 2\right)}+\\ {}{e}^{- i\phi \left({t}_0\right)}\frac{D_1-{i D}_2}{1-\sqrt{2}\cos \left({t}_0\ln 2\right)-i\sqrt{2}\left({t}_0\ln 2\right)}\Big\}\end{array}} $$

(16)

The value of functions ${\left.\left({\eta}_1,{\eta}_2\right)\right|}_{t_0\ne {t}_0^{(N)}}$ can be estimated from the equations as follows:

$$ {\displaystyle \begin{array}{l}\kern0.1em tg\kern0.1em \left(\phi \left({t}_0\right)+{\eta}_1\left({t}_0\right)\right)=-\frac{\mu^{\prime}\left({t}_0\right)}{\phi^{\prime}\left({t}_0\right)\mu \left({t}_0\right)}-\\ {}\frac{1}{\phi^{\prime}\left({t}_0\right)}\left[{\eta}_2^{\prime}\left({t}_0\right)+{\eta}_1^{\prime}\left({t}_0\right)\exp \left(-{\eta}_2\left({t}_0\right)\right)\frac{\sin \left(\phi \left({t}_0\right)+{\eta}_1\left({t}_0\right)\right)}{\mu \left({t}_0\right)}\right]\end{array}} $$

(17)

with the use of the perturbation theory relative to the second term on the right side of Eq. (17) and Eq. (15). Here f^′(t₀) = ∂f(t₀)/∂t₀.

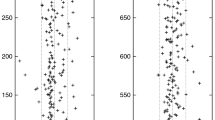
As an example, we made this procedure in the first order of the perturbation theory for three intervals 76.8 ≤ t₀ ≤ 83.2, 112.4 ≤ t₀ ≤ 127.9, and 498 ≤ t₀ ≤ 502. Inside these intervals, the zeros {N : 20,21,22}, {N : 40,41,42}, and {N : 269,270,271}are placed. Results are presented in Figs. 2, 3, 4, and 5 and in the Table 1.

Fig. 2

Functions {η₁, η₂} in the interval 76.8 < t₀ < 84.2; point with a single asterisk indicates zeros of ζ function with {N = 20,21,22; t₀ = 77.1448,79.3373,82.9104}

Fig. 3

Functions {η₁, η₂} in the interval 122.4 < t₀ < 127.9; point with a single asterisk indicates zeros of ζ function with {N = 40,41,42; t₀ = 122.94674,124.2568,127.5167}

Fig. 4

Functions {η₁, η₂} in the interval 122.4 < t₀ < 123.3; point with a single asterisk indicates zeros of ζ function with {N = 40; t₀ = 122.94674}

Fig. 5

Functions {η₁, η₂} in the interval 498 < t₀ < 502; point with a single asterisk indicates zeros of ζ function with {N = 269,270,271; t₀ = 498.5809,500.30905,501.6045}

Table 1 Column 1, number of zeros; column 2, table data (ref. [7]), value of zero N; column 3, calculated value of zero N with help of Eqs. (5, 6); columns 4–5, value of functions {η₁, η₂} in the point $\left({t}_0={t}_0^{(N)}\right)$

There is a very interesting interval {122.4 ≤ t₀ ≤ 123.3} with very small values of both functions {η₁, η₂}. Inside this interval, a zeta function zero with number N = 40 is located at the point {t₀ = 122.9467}. The value of functions {η₁, η₂} at this point is η₁(122.9467) = 3.154 ⋅ 10⁻³; η₂(122.9467) =  −  4.618 ⋅ 10⁻².

The values of the function {η₁, η₂} in the interval 122.4 ≤ t₀ ≤ 123.3 are presented in Fig. 4 on a large scale.

The similar situation takes place in the third interval in the vicinity of a zero of the zeta function with the number {N = 269, t₀ = 498.5809} 498.2 < t < 499.2. Functions {η₁, η₂} display fast oscillations with small amplitude in this interval near the values {− 0.31; − 1.28}. It looks as some special “zeros” are “attractive resonant centers.” Definitely, there exists the final concentration of such “centers.”

3 Conclusions

The key results of the paper are presented by the equations (10), (13), and (14). Equation (13) represents a strong improvement of the well-known result described in the book [5]. Equation (10) is the proof of the Riemann’s hypothesis. We introduce two analytical functions {ϕ and η}. The exact asymptotical expression for function ϕ on the stripe 0 < Re z < 1 for t₀ ≫ 1 is obtained. With the use of the functions {ϕ, η}, one can create additional relation between the functions {Γ(z), ζ(z)}, and this allows us to produce a numeration of zeros of the Riemann’s ζ function. Equation (10) was solved for the large values of the parameter $\ln \left(\frac{t_0}{2\pi}\right)$ for functions {η₁,η₂; η = η₁ + iη₂}. We also obtained the solution (in the first order of the perturbation theory) for three intervals 76.8 ≤ t₀ ≤ 83.2, 122.4 ≤ t₀ ≤ 127.9, and 498 ≤ t₀ ≤ 502.

The condition (14) connected with symmetry of the Riemann’s zeta function and corresponding simultaneous equality to zero of both terms in Eq. (7) appears to be very essential.

The study of the phase-slip events is connected with the zeros, which are discussed above. Unlike all previous studies based on the use of the perturbation theory, the present analysis allows us to obtain an exact solution, without invoking any small parameter.

The connection between the numbers N of zeros of the Riemann’s ζ function inside of the abovementioned “resonant centers” and the primes is rather obvious.