Stable and Accurate Filtering Procedures

Abstract

High frequency errors are always present in numerical simulations since no difference stencil is accurate in the vicinity of the $\pi$-mode. To remove the defective high wave number information from the solution, artificial dissipation operators or filter operators may be applied. Since stability is our main concern, we are interested in schemes on summation-by-parts (SBP) form with weak imposition of boundary conditions. Artificial dissipation operators preserving the accuracy and energy stability of SBP schemes are available. However, for filtering procedures it was recently shown that stability problems may occur, even for originally energy stable (in the absence of filtering) SBP based schemes. More precisely, it was shown that even the sharpest possible energy bound becomes very weak as the number of filtrations grow. This suggest that successful filtering include a delicate balance between the need to remove high frequency oscillations (filter often) and the need to avoid possible growth (filter seldom). We will discuss this problem and propose a remedy.

1 Introduction

For reliable solutions to initial boundary value problems (IBVP), stability is required. This can be achieved by using schemes on SBP form together with weak imposition of boundary conditions. A central feature with these schemes is that the discrete spatial operator is associated with a corresponding integration procedure (inner product). Stable and high order accurate discretizations of SBP type have been known for a long time [10].

High frequency errors are always present in numerical simulations since no difference stencil is accurate in the vicinity of the $\pi$-mode. To remove the defective high wave number information from the solution, artificial dissipation operators or filter operators may be applied. Artificial dissipation operators preserving the accuracy and energy stability of SBP schemes are available [6, 9]. However, for filtering procedures it was recently shown that stability problems may occur, even for originally energy stable (in the absence of filtering) SBP based schemes [7].

The application of an oscillation-reducing filter during a numerical simulation can be seen as one particular type of so-called transmission problems recently studied in [7]. It was shown that in order to preserve stability of the underlying numerical scheme, the transmission problem must be contractive with respect to the same inner product for which the discrete spatial operator is semi-bounded. Unfortunately, the boundary closures for explicit filters available in the previous literature do not satisfy this contractive property even in the most simple low order case. On the other hand, for transmission problems involving adaptive mesh refinement, so-called SBP preserving interpolation operators sometimes satisfy the required contractive property [5]. In this paper we will demonstrate that the SBP preserving concept (which we will denote inner product preserving (IPP) in the rest of the paper) is central also for the problem of constructing stable filters. In particular we will show that an IPP property is necessary but not sufficient for an explicit filter to be contractive. Sufficiency will be indicated by a set of separate criteria for filters of finite difference type. If the same filter operators are implemented in an implicit way, we prove that the IPP property is in itself also sufficient for stability.

This paper is organized as follows. The filter transmission problem is introduced in Sect. 2, together with the stability condition for explicit filters derived in [7]. Explicit finite difference stencils and a previous method for constructing boundary closures are reviewed in Sect. 3. A necessary IPP condition for stability is then formulated in Sect. 4, which explains the boundary instabilities previously observed. A solution to the stability problem is proposed in the form of a new filter construction formula with the IPP property. The new stable filters are extended to curved multi-dimensional geometries in Sect. 5. In Sect. 6 we investigate the numerical properties of the new explicit and implicit filter implementations, demonstrating the stability and excellent oscillation-reducing properties for a boundary layer problem. Finally in Sect. 7, we draw conclusions.

2 The Transmission Problem

In this section we briefly revisit the setting in [7] and introduce the necessary notation.

2.1 Continuous Model Problem

Consider a possibly nonlinear partial differential equation governing the evolution of a solution field u(t, x) on the domain $\varOmega \in \mathbb {R}^d$. We write,

$$\begin{aligned} \begin{aligned} u_t+D(u)&= 0, \quad x\in \varOmega , \quad t\ge 0 \\ L(u)&= g(t), \quad x\in \partial \varOmega \\ u(0,x)&= f(x), \end{aligned} \end{aligned}$$

(1)

where D is a differential operator, and L is a boundary operator. We assume that the problem is semi-bounded, i.e.

$$\begin{aligned} \int _{\varOmega } \phi D(\phi ) \ge 0, \end{aligned}$$

for smooth functions $\phi$ satisfying the homogenous version ($g=0$) of the boundary conditions in (1). Next, we semi-discretize the problem with homogeneous boundary conditions, and obtain,

$$\begin{aligned} \begin{aligned} U_t+\mathcal {D}(U)&= 0,\quad t \ge 0 \\ U(0)&= f(\mathbf {x}), \end{aligned} \end{aligned}$$

where $\mathbf {x}$ is a vector containing the grid points. The operator $\mathcal {D}$ approximates D and includes the weakly imposed boundary conditions.

Further, we assume that the discrete operator is also semi-bounded, i.e. that

$$\begin{aligned} (U,\mathcal {D}(U))_\mathcal {P} =U^T\mathcal {P}\mathcal {D}(U) \ge 0, \end{aligned}$$

(2)

where $\mathcal {P}$ is a diagonal operator (inner product and norm) containing the quadrature weights associated with $\mathcal {D}$. Stability then follows, since,

$$\begin{aligned} \Vert U(t)\Vert _\mathcal {P}\le \Vert f(\mathbf {x})\Vert _\mathcal {P} \end{aligned}$$

(3)

holds.

Next, we consider the problem of applying an oscillation-reducing filter to the solution at some arbitrary point $t_1$ in time. This operation can be seen as a so-called transmission problem [7]. Building directly on the semi-discretized form of the equations, we consider the problem,

$$\begin{aligned} \begin{aligned} U_t+\mathcal {D}(U)&= 0,\quad 0 \le t \le t_1 \\ V_t+\mathcal {D}(V)&= 0,\quad t \ge t_1 \\ U(0)&= f(\mathbf {x}) \\ V(t_1)&= \varPsi \left[ U(t_1),V(t_1)\right] , \end{aligned} \end{aligned}$$

(4)

where $\varPsi$ is a general filter function which can be either implicit or explicit ($\varPsi =\varPsi \left[ U(t_1)\right]$).

For stability we require the contractive property,

$$\begin{aligned} \Vert V(t_1)\Vert _\mathcal {P} \le \Vert U(t_1)\Vert _\mathcal {P}. \end{aligned}$$

(5)

which by (3) yields the desired result,

$$\begin{aligned} \Vert V(t)\Vert _\mathcal {P}\le \Vert f(\mathbf {x})\Vert _\mathcal {P}. \end{aligned}$$

(6)

The estimate (6) shows that (4) is estimated in the initial data of the problem (1). We say that schemes that satisfy (6) are time-stable. It was shown in [7] that schemes that are not time-stable can lead to erroneous energy growth.

We conclude this section by considering the special case of a linear explicit filter,

$$\begin{aligned} V(t_1) = \varPsi \left[ U(t_1)\right] =\mathcal {F} U(t_1), \end{aligned}$$

where $\mathcal {F}$ is a matrix (see Fig. 1). For such filters, (5) implies that the contractive property of $\mathcal {F}$ first identified in [7],

$$\begin{aligned} \mathcal {F}^T\mathcal {P}\mathcal {F} - \mathcal {P} \le 0, \end{aligned}$$

(7)

must hold. Note that in (7) there is no distinction made between explicit filters on constant coefficient or semi-linear (i.e. $\mathcal {F}= \mathcal {F}(U)$) form. In both cases, (7) leads directly to time-stability.

Fig. 1

Schematic of semi-discrete filter problem

3 Explicit Finite Difference Filters

We specify $\mathbf {x}=(0,\varDelta x, 2\varDelta x,\ldots ,1)$ to be a uniformly spaced grid vector in 1D with $N+1$ grid points, i.e. $\varDelta x =1/N$, and let $\mathcal {D}$ be a high order SBP finite difference operator with the inner product $\mathcal {P}$. The highest solution frequency which can be resolved on the grid is the so-called $\pi$-mode,

$$\begin{aligned} f_\pi = cos(N\pi \mathbf {x})=\begin{pmatrix} \ldots&1&-1&1&-1&\ldots \end{pmatrix}^T. \end{aligned}$$

(8)

The central feature of most oscillation-reducing explicit filters is to remove the $\pi$-mode from a numerical solution through the application of a dissipative high order derivative approximation.

It is well known that, down to a scaling factor, compact stencil approximations of even order derivatives leave the $\pi$-mode intact. For example, a symmetric second order accurate stencil approximating the 2n:th order derivative satisfies,

$$\begin{aligned} D_{2n} f_\pi = (-1)^n \frac{2^{(2n)}}{\varDelta x^{(2n)}} f_\pi , \end{aligned}$$

see e.g. [2]. Since $D_{2n}$ is itself scaled with a factor of $1/\varDelta x^{(2n)}$, second order accuracy means that polynomials up to order $2n+1$ are evaluated exactly. In particular, polynomials up to order $2n-1$ are then differentiated exactly to zero,

$$\begin{aligned} D_{2n} \mathbf {x}^{j} = 0 \quad j=0,1,\ldots , 2n-1, \end{aligned}$$

(9)

where the power j should be interpreted as an element-wise operation on $\mathbf {x}$. It follows that a filter defined by $F = I - \alpha (-1)^{n} D_{2n}$, where $\alpha =\varDelta x^{(2n)}/2^{(2n)}$, simultaneously cancels the $\pi$-mode while leaving low order frequency modes unaltered to within 2n:th order of accuracy,

$$\begin{aligned} F f_\pi&=0 \end{aligned}$$

(10)

$$\begin{aligned} F\mathbf {x}^j&= \mathbf {x}^j , \quad j=0,1,\ldots , 2n-1 . \end{aligned}$$

(11)

These filter properties only apply in the interior of the domain. In [2], boundary closures were constructed for stencils up to sixteenth order ($n=8$), leading to operators $\mathcal {D}_{2n}$ for a bounded domain satisfying the symmetry and accuracy conditions,

$$\begin{aligned} \mathcal {D}_{2n}&=\mathcal {D}_{2n}^T, \quad (-1)^{n} D_{2n} \ge 0 \end{aligned}$$

(12)

$$\begin{aligned} \mathcal {D}_{2n} \mathbf {x}^{j}&= 0 \quad j=0,1,\ldots , n-1. \end{aligned}$$

(13)

Based on these operators, an explicit filter defined by $\mathcal {F} = I - \alpha (-1)^{n} \mathcal {D}_{2n}$ then satisfies,

$$\begin{aligned} \mathcal {F}&=\mathcal {F}^T, \quad \lambda (\mathcal {F}) \le 1 \end{aligned}$$

(14)

$$\begin{aligned} \mathcal {F} \mathbf {x}^{j}&= \mathbf {x}^{j} \quad j=0,1,\ldots , n-1. \end{aligned}$$

(15)

where in addition (10) and (11) applies to the interior stencil of $\mathcal {F}$.

The fact that the spectral radius of $\mathcal {F}$ is smaller than unity implies that the contractive property (7) holds if $\mathcal {P}$ is proportional to the unit matrix, i.e. if $\mathcal {P}=\varDelta x I$. Unfortunately, this is typically not the inner product for which semi-boundedness (2) can be proven. For other $\mathcal {P}$:s, (7) can not be guaranteed based on the design requirements in (12) and (13). As observed in [7], even in the most simple and lowest order case, the operators in [2] fail to satisfy (7). Consider for example a second order accurate SBP norm with $N=3$ and $\varDelta x=1/3$,

$$\begin{aligned} \mathcal {P} = \frac{1}{3} \begin{pmatrix} 1/2 \\ &{} 1 \\ &{}&{} 1 \\ &{}&{}&{} 1/2 \end{pmatrix}. \end{aligned}$$

(16)

A symmetric filter of the form (14) and (15) for $n=1$ is given by,

$$\begin{aligned} \mathcal {D}_{2n} = 3^2\begin{pmatrix} -1 &{} 1 \\ 1 &{} -2 &{} 1 \\ &{} 1 &{} -2 &{} 1 \\ &{}&{} 1 &{} -1 \end{pmatrix} \quad \Rightarrow \quad \mathcal {F} = \frac{1}{4} \begin{pmatrix} 3 &{} 1 \\ 1 &{} 2 &{} 1 \\ &{} 1 &{} 2 &{} 1 \\ &{}&{} 1 &{} 3 \end{pmatrix}. \end{aligned}$$

The eigenvalues of $\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}$ become $[-\,0.9375, -\,0.5890, -\,0.1250, 0.0265]$. The positive eigenvalue indicates that the numerical scheme is not time-stable, which can lead to unwanted energy growth.

4 Stable Filters: Theory and a New Operator Definition

Even though in this paper we focus on filters to be used in conjunction with finite difference schemes, we stress that the formulation of the transmission problem in Sect. 2 is general and applies to all types of semi-bounded schemes. In this section we will derive stability results for general filters on both explicit and implicit form. We will then apply this theory to propose a new and improved finite difference filter definition.

4.1 A Necessary Stability Condition for Explicit Filters

The contractivity condition (7) implies that the construction of filter boundary closures must relate to the inner product $\mathcal {P}$. In Proposition 1 below we will show that the only way to achieve (7) is to let $\mathcal {F}$ be associated with another operator $\tilde{\mathcal {F}}$ of the same accuracy, such that they form a so-called IPP pair, defined by,

$$\begin{aligned} \tilde{\mathcal {F}}=\mathcal {P}^{-1}\mathcal {F}^T\mathcal {P} \quad \Rightarrow \quad (U,\mathcal {F}V)_\mathcal {P} =(\tilde{\mathcal {F}}U,V)_\mathcal {P}. \end{aligned}$$

(17)

This might seem like a counter-intuitive statement. The operator $\tilde{\mathcal {F}}$ does not appear in the scheme (4), but somewhat surprisingly, its existence is necessary for the transmission problem to be stable. To prove this, we need the following lemma.

Lemma 1

Let M be a symmetric matrix such that for some vector $\mathbf {v}$ we have both $\mathbf {v}^TM\mathbf {v}=0$ and $M\mathbf {v}\ne 0$. Then M is indefinite.

Proof

See Lemma 14 in [8]. $\square$

We can now prove

Proposition 1

Let the operator $\mathcal {F}$ in (4) be n:th order accurate, i.e. it satisfies (15). In order for the contractivity condition (7) to hold with respect to the inner product $\mathcal {P}$, it is necessary that also the operator $\tilde{\mathcal {F}}$ in (17) is n:th order accurate.

Proof

Assume that (15) holds, and consider the quadratic form,

$$\begin{aligned} \begin{aligned} (\mathbf {x}^{j})^T(\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P})\mathbf {x}^{j}&= (\mathcal {F}\mathbf {x}^{j})^T\mathcal {P}(\mathcal {F}\mathbf {x}^{j})-(\mathbf {x}^{j})^T\mathcal {P}\mathbf {x}^{j} \\&=(\mathbf {x}^{j})^T\mathcal {P}\mathbf {x}^{j}-(\mathbf {x}^{j})^T\mathcal {P}\mathbf {x}^{j}=0, \end{aligned} \end{aligned}$$

(18)

for $j=0,1,\ldots ,n-1$. It now follows from Lemma 1 that $\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}$ must be an indefinite matrix unless we also have,

$$\begin{aligned} (\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P})\mathbf {x}^{j} = 0, \quad j=0,1,\ldots , n-1. \end{aligned}$$

Inserting (15) again and then multiplying with $\mathcal {P}^{-1}$, this yields,

$$\begin{aligned} \tilde{\mathcal {F}}\mathbf {x}^{j} =\mathbf {x}^{j}, \quad j=0,1,\ldots , n-1, \end{aligned}$$

(19)

i.e. $\tilde{\mathcal {F}}$ is also n:th order accurate. $\square$

For a filter defined as before by $\mathcal {F} = I - \alpha (-1)^{n} \mathcal {D}_{2n}$, (19) does by no means follow from the properties (12) and (13). In fact one can easily verify numerically that (19) in general does not hold, thus showing that the filter definition $\mathcal {F} = I - \alpha (-1)^{n} \mathcal {D}_{2n}$ together with (12) and (13) is inadequate. With Proposition 1 in place, we are now equipped to reconsider the problem of constructing stable filter boundary closures. Indeed, we can rule out all cases where $\tilde{\mathcal {F}}$ as defined in (17) does not satisfy (19).

4.2 A Modified Finite Difference Filter Definition

By taking advantage of the fact that high order derivative operators $\mathcal {D}_{2n}$ satisfying (12) and (13) are already available, we consider the new filter definition,

$$\begin{aligned} \mathcal {F} = I - \alpha (-1)^{n} \mathcal {H}^{-1}\mathcal {D}_{2n}, \quad \alpha =\varDelta x^{(2n)}/2^{(2n)}, \end{aligned}$$

(20)

where $\mathcal {P}=\varDelta x \mathcal {H}$.

Remark 1

This modification is similar to the one proposed in [6] for artificial dissipation.

Note that the new definition (20) satisfies the same accuracy conditions (15) as before. Indeed, (13) implies that $\mathcal {F}$ reduces to an identity operator when applied to polynomials of order $n-1$. Moreover, from the symmetry of $\mathcal {D}_{2n}$ we have,

$$\begin{aligned} \mathcal {P}\mathcal {F}=\mathcal {P} - \alpha (-1)^{n} \varDelta x \mathcal {D}_{2n}\mathcal {P}^{-1}\mathcal {P}=(I - \alpha (-1)^{n} \mathcal {D}_{2n}\mathcal {H}^{-1})\mathcal {P} =\mathcal {F}^T\mathcal {P}, \end{aligned}$$

i.e. the matrix $\mathcal {P}\mathcal {F}$ is also symmetric. In the IPP definition (17), this leads to

$$\begin{aligned} \tilde{\mathcal {F}}=\mathcal {P}^{-1}\mathcal {F}^T\mathcal {P} = \mathcal {P}^{-1}\mathcal {P}\mathcal {F}=\mathcal {F}, \end{aligned}$$

(21)

i.e. $\mathcal {F}$ forms an IPP pair together with itself. The condition (19) necessary for stability hence follows directly by construction from the accuracy of $\mathcal {F}$ itself in (15). Note that while (19) is not sufficient in order to prove that contractivity (7) is satisfied, it is straightforward to verify numerically if this is the case or not, for a given combination of $\mathcal {F}$ and $\mathcal {P}$.

For example, $n=1$ together with the second order accurate norm (16) yields,

$$\begin{aligned} \mathcal {D}_{2n} =3^2\begin{pmatrix} -1 &{} 1 \\ 1 &{} -2 &{} 1 \\ &{} 1 &{} -2 &{} 1 \\ &{}&{} 1 &{} -1 \end{pmatrix} \quad \Rightarrow \quad \mathcal {F} = \frac{1}{4}\begin{pmatrix} 2 &{} 2 \\ 1 &{} 2 &{} 1 \\ &{} 1 &{} 2 &{} 1 \\ &{}&{} 2 &{} 2 \end{pmatrix}. \end{aligned}$$

The eigenvalues of $\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}$ are $[-\,0.875, -\,0.625, -\,0.25,0]$, implying time-stability of the numerical scheme. One can also easily construct examples where (19) is satisfied but where (7) is not, for example by adjusting the quadrature weights in (16). To make the theory complete, we have developed a set of sufficiency criteria to test whether a given filter of the type (20) is contractive or not. These criteria are independent of the grid size N, see “Appendix A”. Using these criteria we can prove that no eigenvalue of $\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}$ is positive for standard SBP finite difference norms up to eighth order accuracy.

To summarize this section, Proposition 1 was applied to propose a plausible candidate for a new filter definition (20). Furthermore, for each combination of operators $\mathcal {P}$ and $\mathcal {D}_{2n}$, the contractivity condition in (7) can be verified using the criteria for sufficiency given in “Appendix A”.

4.3 A Provably Stable Implicit Implementation

As we have seen, the IPP property (17) for explicit filters defines a new operator $\tilde{\mathcal {F}}$ which is not present in the original transmission problem (4). However, using an implicit formulation we can use this operator to design a provably contractive scheme. In (4), consider the previous explicit filter with an added implicit correction term,

$$\begin{aligned} \varPsi \left[ U(t_1),V(t_1)\right] = \mathcal {F}U(t_1)- \mathcal {F}\left( \tilde{\mathcal {F}}V(t_1)-U(t_1)\right) , \end{aligned}$$

leading to

$$\begin{aligned} \left( I+\mathcal {F}\tilde{\mathcal {F}}\right) V(t_1) = 2\mathcal {F} U(t_1), \end{aligned}$$

(22)

where $\tilde{\mathcal {F}}$ is defined as in (17). Note that if (19) holds, then the accuracy of this condition is of the same order as the operator $\mathcal {F}$ itself. As we shall now prove, (17) in combination with (22) is both necessary and sufficient for contractivity.

Proposition 2

Consider the implicit filter implementation (22). By defining $\tilde{\mathcal {F}}$ as in (17), the estimate

$$\begin{aligned} \Vert V(t_1)\Vert _{\mathcal {P}}^2=\Vert U(t_1)\Vert _{\mathcal {P}}^2 -\Vert U(t_1)-\tilde{\mathcal {F}}V(t_1)\Vert _{\mathcal {P}}^2 \end{aligned}$$

holds, i.e. the filter is contractive (5).

Proof

Multiplying (22) with $V(t_1)^T\mathcal {P}$ from the left yields,

$$\begin{aligned} \Vert V(t_1)\Vert _{\mathcal {P}}^2+(V(t_1),\mathcal {F}\tilde{\mathcal {F}}V(t_1))_\mathcal {P}= 2( V(t_1),\mathcal {F} U(t_1))_\mathcal {P} . \end{aligned}$$

From (17), this becomes,

$$\begin{aligned} \Vert V(t_1)\Vert _{\mathcal {P}}^2+\Vert \tilde{\mathcal {F}}V(t_1)\Vert _{\mathcal {P}}^2= 2(\tilde{\mathcal {F}} V(t_1), U(t_1))_\mathcal {P}. \end{aligned}$$

After adding and subtracting $\Vert U(t_1)\Vert _{\mathcal {P}}^2$ on the right hand side, we finally get,

$$\begin{aligned} \begin{aligned} \Vert V(t_1)\Vert _{\mathcal {P}}^2&=\Vert U(t_1)\Vert _{\mathcal {P}}^2-\Vert U(t_1)\Vert _{\mathcal {P}}^2 -\Vert \tilde{\mathcal {F}}V(t_1)\Vert _{\mathcal {P}}^2+ 2(\tilde{\mathcal {F}}V(t_1), U(t_1))_\mathcal {P} \\&=\Vert U(t_1)\Vert _{\mathcal {P}}^2- \Vert U(t_1)-\tilde{\mathcal {F}}V(t_1)\Vert _{\mathcal {P}}^2, \end{aligned} \end{aligned}$$

which concludes the proof. $\square$

We recall that the contractivity property (5) together with the estimate (3) of U leads to time-stability (6) of the transmission problem.

5 Extensions

To accommodate for non-Cartesian geometries in multiple dimensions, SBP finite difference discretizations of IBVPs can be extended through a combination of tensor products and curvilinear transformations in such a way that semi-boundedness (2) is preserved. In this section we will discuss how such extensions relate to filters.

5.1 Multiple Dimensions

Finite difference formulations in 1D can be extended to multi-dimensional Cartesian grids by the application of tensor products. For example, in the 2D case, let

$$\begin{aligned} \mathcal {P}=\mathcal {P}_x\otimes \mathcal {P}_y,\quad \mathcal {F}=\mathcal {F}_x\otimes \mathcal {F}_y, \end{aligned}$$

where $\otimes$ denotes the Kronecker (or tensor) product, and where $\mathcal {P}_x$, $\mathcal {P}_y$, $\mathcal {F}_x$ and $\mathcal {F}_y$ are integration and filter operators in the two coordinate directions, respectively. The IPP property (17) immediately extends from 1D to 2D operators, since

$$\begin{aligned} \tilde{\mathcal {F}}=\tilde{\mathcal {F}}_x \otimes \tilde{\mathcal {F}}_y= \left( \mathcal {P}_x^{-1}\mathcal {F}_x^T\mathcal {P}_x\right) \otimes \left( \mathcal {P}_y^{-1}\mathcal {F}_y^T\mathcal {P}_y\right) =\mathcal {P}^{-1}\mathcal {F}^T\mathcal {P}, \end{aligned}$$

following elementary rules of the Kronecker product. This means that the implicit filter implementation (22) extends directly to multiple dimensions in a stable and accurate way.

As for the contractive property (7), consider

$$\begin{aligned} \begin{aligned} \mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}&=(\mathcal {F}_x \otimes \mathcal {F}_y)^T(\mathcal {P}_x\otimes \mathcal {P}_y)(\mathcal {F}_x \otimes \mathcal {F}_y)-\mathcal {P}_x\otimes \mathcal {P}_y \\&=(\mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x)\otimes (\mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y)- \mathcal {P}_x\otimes \mathcal {P}_y. \end{aligned} \end{aligned}$$

By adding and subtracting $\frac{1}{2}\left[ \mathcal {P}_x\otimes (\mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y)+ (\mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x)\otimes \mathcal {P}_y\right]$, we find,

$$\begin{aligned} \begin{aligned} \mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}&=\frac{1}{2} \left[ (\mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x-\mathcal {P}_x)\otimes (\mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y+\mathcal {P}_y) \right. \\&\quad + \left. (\mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x+\mathcal {P}_x)\otimes (\mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y-\mathcal {P}_y) \right] . \end{aligned} \end{aligned}$$

Since $\mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x+\mathcal {P}_x$ and $\mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y+\mathcal {P}_y$ only have positive eigenvalues, it follows that (7) is satisfied provided that it is satisfied for the 1D operators, i.e.

$$\begin{aligned} \mathcal {F}_x^T\mathcal {P}_x\mathcal {F}_x-\mathcal {P}_x \le 0, \quad \mathcal {F}_y^T\mathcal {P}_y\mathcal {F}_y-\mathcal {P}_y \le 0. \end{aligned}$$

We have thus shown that stability is preserved for both the explicit and implicit implementations in 2D. By induction, these arguments can be extended to any number of dimensions.

5.2 Curvilinear Coordinates

Let $\hat{\mathbf {x}}$ denote a Cartesian grid in any number of space dimensions, and let $x=x(\hat{x})$ denote a curvilinear transformation such that we obtain a new grid vector $\mathbf {x}$. Moreover, let $\mathcal {J}$ be the diagonal matrix obtained by inserting values from the Jacobian determinant of this transformation at the grid points. From a discrete inner product $\hat{P}$ defined on the Cartesian grid, we can define a new operator $\mathcal {P}=\mathcal {J}\hat{P}$ containing the positive quadrature weights on $\mathbf {x}$.

We define the new filter operator on $\mathbf {x}$ as,

$$\begin{aligned} \mathcal {F}=\mathcal {J}^{-1/2}\hat{\mathcal {F}}\mathcal {J}^{1/2}, \end{aligned}$$

(23)

where $\hat{\mathcal {F}}$ is constructed with respect to the Cartesian grid exactly as in the previous section. An IPP pair is now obtained by analogously defining $\tilde{\mathcal {F}}$ as,

$$\begin{aligned} \tilde{\mathcal {F}} = \mathcal {J}^{-1/2} \tilde{\hat{\mathcal {F}}}\mathcal {J}^{1/2} = \mathcal {J}^{-1/2} \left( \hat{P}^{-1}\hat{\mathcal {F}}^T \hat{P}\right) \mathcal {J}^{1/2} = \hat{P}^{-1}\mathcal {J}^{-1}\mathcal {F}^T\mathcal {J} \hat{P}= \mathcal {P}^{-1}\mathcal {F}^T \mathcal {P} , \end{aligned}$$

showing that the implicit implementation (22) of $\mathcal {F}$ in (23) is stable and accurate.

Also the contractivity condition (7) extends to the curvilinear case, and we can prove

Lemma 2

If $\hat{\mathcal {F}}^T\hat{\mathcal {P}}\hat{\mathcal {F}}-\hat{\mathcal {P}}\le 0$, then $\mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}\le 0$, where $\mathcal {F}$ is defined in (23).

Proof

Consider,

$$\begin{aligned} \mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P} = \left( \mathcal {J}^{1/2}\hat{\mathcal {F}}^T\mathcal {J}^{-1/2} \right) \mathcal {J}\hat{\mathcal {P}} \left( \mathcal {J}^{-1/2}\hat{\mathcal {F}}\mathcal {J}^{1/2}\right) -\mathcal {J}\hat{\mathcal {P}}. \end{aligned}$$

Since both $\hat{\mathcal {P}}$ and $\mathcal {J}$ are diagonal, they commute, leading to,

$$\begin{aligned} \mathcal {F}^T\mathcal {P}\mathcal {F}-\mathcal {P}=\mathcal {J}^{1/2}\left( \hat{\mathcal {F}}^T\hat{\mathcal {P}}\hat{\mathcal {F}}\right) \mathcal {J}^{1/2}-\mathcal {J}\hat{\mathcal {P}}=\mathcal {J}^{1/2}\left( \hat{\mathcal {F}}^T\hat{\mathcal {P}}\hat{\mathcal {F}}-\hat{\mathcal {P}}\right) \mathcal {J}^{1/2}, \end{aligned}$$

and the result follows. $\square$

6 Numerical Calculations

We test the numerical properties of the filter definition in (20), henceforth referred to as the new filters, and compare to the previous version with $\mathcal {F} = I - \alpha (-1)^{n} \mathcal {D}_{2n}$, which we refer to as the old filters. In both cases, the high order derivative operators $\mathcal {D}_{2n}$ are taken from [2]. If filtering is carried out repeatedly after each or every few time steps in a simulation, the errors will accumulate over time. To avoid a reduction in convergence rate, the filter accuracy should be at least one order higher than that of the numerical scheme itself. To limit the number of cases considered, we shall for each value of n associate $\mathcal {F}$ with a finite difference operator of order $2(n-1)$ in the interior, and order $n-1$ in the boundary closure. The lower order accuracy in the boundary closure is a theoretical upper limit for the type of operators considered, see [3, 4].

6.1 Filter Properties

First we investigate the effect of the explicit (4) and implicit (22) filter implementations to functions with various frequencies. Consider the test function,

$$\begin{aligned} u = cos(\xi N x), \end{aligned}$$

(24)

where $0\le \xi \le \pi$ is the so-called wave number. Note that $\xi =\pi$ yields the $\pi$-mode $f_\pi$ in (8), i.e. the highest frequency that can be resolved on the grid.

Fig. 2

The old and new filters applied to functions of various frequencies

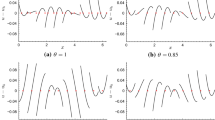
Consider the uniform grid $\mathbf {x}$ in 1D with $N+1$ grid points, and define the vector U such that $U_i=u(x_i)$. In Fig. 2 we plot U for a few different frequencies before and after filtering. Here we have used $N=32$ and $n=2$, i.e. a fourth order derivative $D_{2n}$ together with a norm $\mathcal {P}$ associated with an SBP finite difference operator of order 2 in the interior. As expected, filtering results in a cancellation of the $\pi$-mode in the interior of the domain, while the damping of low frequencies is small. In order to compare the different methods to one another, it is convenient to first separate the action in the interior of the domain from that of the boundary closures.

Fig. 3

Amplification factor of interior stencil as a function of wave number

In Fig. 3 we plot the interior damping as a function of the wave number, using $n=2,3,4$ and 5. Notice that the new and old explicit filter operators are identical in the interior, which is why no there is distinction between them here. We observe that all filters succeed in canceling the $\pi$-mode, and that higher order filters are less dissipative than lower order ones for all wave numbers smaller than $\pi$. For the same value of n, the implicit implementation is less dissipative than the explicit one.

Fig. 4

New and old filters applied to the $\pi$-mode close to one boundary

Finally, in Fig. 4 we take a closer look at the results from filtering the $\pi$-mode close to a domain boundary. The cases considered here do not differ significantly from each other, with the new filters showing slightly better damping for lower values of n, but slightly worse for $n=5$.

6.2 Boundary Layer Calculation

One possible source for unwanted oscillations in a numerical solution is when a second order derivative is approximated by applying a central first derivative operator twice, leading to a non-compact stencil. See e.g. [1] for an analysis of such oscillatory error modes. Since central difference approximations of odd order derivatives by themselves cancel out the $\pi$-mode, there is no natural mechanism in such schemes to damp out oscillations once they start appearing.

As a model problem, we consider the advection-diffusion equation with well-posed boundary conditions,

$$\begin{aligned} \begin{aligned} u_t+u_x&= \epsilon u_{xx}, \quad 0\le x\le 1, \quad t > 0 \\ u(0,t)-\epsilon u_x(0,t)&= 1 \\ \epsilon u_x(1,t)&= -1 \\ u(x,0)&= f(x) . \end{aligned} \end{aligned}$$

An exact steady-state solution with a steep boundary layer at $x=1$ is given by,

$$\begin{aligned} u_e(x)=1-exp\left( \frac{x-1}{\epsilon }\right) . \end{aligned}$$

Fig. 5

Error distribution at $t=10$ for boundary layer calculations on a Cartesian grid

Fig. 6

Maximum error as a function of time for the case $N=32$

Fig. 7

Convergence of maximum error with and without filtering. The dotted line indicates third order convergence

We let $\epsilon =0.1$, and use first derivative finite difference SBP operators to approximate both $u_x$ and $u_{xx}$. More details about this discretization technique can be found in [1]. In Fig. 5 we show examples of error distributions $e=U-u_e(\mathbf {x})$, where U is the numerical solution obtained either with or without filtering. We have used finite difference SBP operators of fourth order in the interior (and hence $n=3$), and compute the steady-state solution using the classical RK4 method in time. As initial solution we use f(x)=0. The time step size is chosen to be $\varDelta t = \varDelta x^2/4\epsilon$, and filters are applied after each time step. In Fig. 6 we plot the error in maximum norm (with respect to space) as a function of time, showing that steady-state is reached at around $t=5$ in all cases.

The positive effect of filtering is apparent. Dominated by oscillations, the errors are almost eliminated outside the boundary layer. For the new time-stable techniques, the oscillations close to $x=1$ are also reduced significantly. The old method on the other hand is showing clear problems, and even fails to converge with the same rate as the unfiltered scheme, see Fig. 7 for convergence plots of the error in maximum norm. Since the formal order of accuracy is the same in all cases, we conclude that this convergence issue is due to an instability caused by the old filter.

Fig. 8

Error distribution at $t=10$ for boundary layer calculations on a stretched grid

Fig. 9

Convergence of maximum error with and without filtering for the stretched grid calculation. The dotted line indicates third order convergence

Since the steepest gradients are found within the boundary layer close to $x=1$, it makes sense to reduce the grid spacing in this region. In the final test, we apply the smooth grid transformation,

$$\begin{aligned} x_i=\frac{tanh(d\hat{x_i})}{tanh(d)}, \end{aligned}$$

where $d=3/2$, and $\hat{\mathbf {x}}$ is a uniform grid with $N+1$ grid points. The filter operators are modified according to Sect. 5.2, and results are shown in Figs. 8 and 9. The error levels are significantly reduced compared to the Cartesian grid calculations, and the new filters are again superior to the old ones. Close to $x=1$, the errors from the explicit and implicit implementation are comparable. In the interior however, the implicit method is more accurate.

7 Conclusions

A new inner product preserving (IPP) filter definition for finite difference schemes was proposed. The IPP property was shown to be necessary for the stability of explicit filters in general, while sufficiency was verified for each operator individually. An implicit implementation of the same operators was also proposed, for which the IPP property was shown to be sufficient for stability. These theoretical results extend to filters used in conjunction with other types of schemes as well, and even to nonlinear filters.

The new filters can easily be extended to multiple dimensions and complex geometries in such a way that stability and accuracy is preserved. The advantage compared to a previous unstable filter definition was demonstrated by numerical calculations for an advection-diffusion boundary layer problem, using non-compact stencil second order derivative approximations.

Sufficient Conditions for Contractivity

In this section we derive sufficient conditions for explicit finite difference filters of the form (20) to be contractive (7). Due to symmetry, it is sufficient to consider the problem on a half-line. Thus we denote the diagonal elements in $\mathcal {H}$ with $h_j>0$, $j=0,1,\ldots ,\infty$. Recall that the inner product $\mathcal {H}$ has been scaled such that $h_j$ is independent of $\varDelta x$.

Let $\mathcal {D}_1$ denote the undivided forward difference operator,

$$\begin{aligned} \mathcal {D}_1=\begin{pmatrix} -1 &{} 1 \\ &{} -1 &{} 1\\ &{}&{} \ddots &{} \ddots \end{pmatrix}. \end{aligned}$$

(25)

The symmetric operators $\mathcal {D}_{2n}$ utilized to construct the filters in [2] can all be written on the following form,

$$\begin{aligned} \mathcal {D}_{2n} = (-1)^n (1/\varDelta x)(\mathcal {D}_1^n)^T\mathcal {D}_1^n. \end{aligned}$$

(26)

Thus, we can write (20) as

$$\begin{aligned} \mathcal {F}=I-\frac{1}{2^{(2n)}}\mathcal {H}^{-1}(\mathcal {D}_1^n)^T\mathcal {D}_1^n, \end{aligned}$$

which leads to

$$\begin{aligned} \mathcal {F}^T\mathcal {H}\mathcal {F}-\mathcal {H} =\frac{1}{2^{(2n)}} (\mathcal {D}_1^{n})^T\left[ -2I+\frac{1}{2^{(2n)}}\mathcal {D}_1^n\mathcal {H}^{-1}(\mathcal {D}_1^n)^T\right] \mathcal {D}_1^{n} . \end{aligned}$$

For contractivity, it is thus sufficient to consider the following matrix associated with each filter,

$$\begin{aligned} \mathcal {M}=-2I+\frac{1}{2^{(2n)}}\mathcal {D}_1^n\mathcal {H}^{-1}(\mathcal {D}_1^n)^T. \end{aligned}$$

(27)

Now, let $e_j$ be a vector with a single non-zero value of 1 in the j : th position, and 0 everywhere else,

$$\begin{aligned} e_j = \begin{pmatrix} 0 \\ {\vdots } \\ 0 \\ 1 \\ 0 \\ {\vdots } \end{pmatrix} \quad \Rightarrow \quad e_je_j^T = \begin{pmatrix} 0 \\ &{} {\ddots } \\ &{}&{} 0 \\ &{}&{}&{} 1 \\ &{}&{}&{}&{} 0 \\ &{}&{}&{}&{}&{} {\ddots } \end{pmatrix} \end{aligned}$$

We can now write,

$$\begin{aligned} \mathcal {H}^{-1} = \sum _0^\infty \frac{1}{h_j} e_je_j^T, \end{aligned}$$

The second term on the right hand side of (27) can thus be expanded into the sum of outer products,

$$\begin{aligned} \begin{aligned} \mathcal {D}_1^n\mathcal {H}^{-1}(\mathcal {D}_1^n)^T&= \mathcal {D}_1^n \left( \sum _{j=0}^{\infty }\frac{1}{h_j}e_je_j^T\right) (\mathcal {D}_1^n)^T= \sum _{j=0}^{\infty }\frac{1}{h_j}\mathcal {D}_1^n \left( e_je_j^T\right) (\mathcal {D}_1^n)^T \\&=\sum _{j=0}^{\infty } \frac{1}{h_j} (\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T. \end{aligned} \end{aligned}$$

Next, we will expand the unit matrix in (27) in a similar way, so that each term matches the non-zero structure of the corresponding term $(\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T$ above. From the definition of $e_j$, it is clear that the vector $\mathcal {D}_1^n e_j$ is given by the j : th column of the matrix $\mathcal {D}_1^n$, and the structure of $\mathcal {D}_1^n$ is illustrated in “Appendix A.1” through A.5. To accomplish the stated goal, we expand I as,

$$\begin{aligned} I = \frac{1}{n+1}\sum _{j=0}^\infty I_j, \end{aligned}$$

where,

and,

We can now write (27) as,

$$\begin{aligned} \mathcal {M} = \sum _{j=0}^{\infty } \left[ -\frac{2}{n+1}I_j + \frac{1}{h_j 2^{2n}} (\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T \right] , \end{aligned}$$

where both terms inside the summation have a non-zero part with the same position and dimension. Moreover, the only eigenvector with a non-zero eigenvalue to the outer product $(\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T$ is $\mathcal {D}_1^n e_j$ itself,

$$\begin{aligned} \left[ (\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T\right] \mathcal {D}_1^n e_j = \left[ \mathcal {D}_1^n e_j)^T(\mathcal {D}_1^n e_j)\right] \mathcal {D}_1^n e_j, \end{aligned}$$

since all other eigenvectors are given by the orthogonal set to $\mathcal {D}_1^n e_j$,

$$\begin{aligned} \varPhi ^T(\mathcal {D}_1^n e_j) \quad \Rightarrow \quad \left[ (\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T \right] \varPhi = 0. \end{aligned}$$

The single non-zero eigenvalue $\lambda$ is thus given by

$$\begin{aligned} \lambda = (\mathcal {D}_1^n e_j)^T(\mathcal {D}_1^n e_j)= \Vert \mathcal {D}_1^n e_j\Vert ^2, \end{aligned}$$

where $\Vert \cdot \Vert$ denotes the standard euclidean vector norm. Hence, a sufficient condition for $\mathcal {M}$ to be negative semi-definite is

$$\begin{aligned} -\frac{2}{n+1}+\frac{1}{h_j 2^{2n}}\Vert \mathcal {D}_1^n e_j\Vert ^2 \le 0, \quad \forall \ j\ge 0. \end{aligned}$$

In terms of the quadrature weights, we have thus derived the following simple test for contractivity.

Proposition 3

The finite difference filter (20) together with (26) is contractive in the sense of (7) if the quadrature weights in $\mathcal {H}$ satisfy the following set of inequalities,

$$\begin{aligned} h_j \ge \frac{(n+1) \Vert \mathcal {D}_1^n e_j\Vert ^2}{2^{2n+1}}, \end{aligned}$$

where $\mathcal {D}_1$ is the undivided forward difference operator in (25), and $\mathcal {D}_1^n e_j$ is given by the j : th column of $\mathcal {D}_1^n$.

Note that Proposition 3 provides a condition for contractivity which is sufficient but not necessary, i.e. the opposite of the situation in Proposition 1. In other words, a filter might still be contractive even if this condition is not satisfied. For example, in the interior of $\mathcal {D}_1^n$, each column contains the binomial coefficients with respect to n (with positive or negative sign, see the examples in “Appendix A.1” through A.5), and the euclidean norm is given by Vandermonde’s identity as,

$$\begin{aligned} \Vert \mathcal {D}_1^n e_{n+1}\Vert ^2=\Vert \mathcal {D}_1^n e_{n+2}\Vert ^2= \sum _{k=0}^n \begin{pmatrix} n \\ k \end{pmatrix}^2= \begin{pmatrix} 2n \\ n \end{pmatrix}. \end{aligned}$$

For sufficiently large values of j (i.e. such that both $j>n$ and $h_j=1$), the condition in Proposition 3 thus reduces to,

$$\begin{aligned} 1 \ge \frac{(n+1)}{2^{2n+1}}\begin{pmatrix} 2n \\ n \end{pmatrix}, \end{aligned}$$

and by inspection this inequality only holds for values of n between one and ten (i.e. for filters up to order 20). Hence, $n=10$ constitutes a hard upper limit above which Proposition 3 is no longer applicable.

As we shall see, the condition in Proposition 3 will be sufficient to prove contractivity in the large majority of cases with classical finite difference SBP operators (provided that $n\le 10$). However, there are some cases where it becomes insufficient due to some quadrature weights in the boundary part of $\mathcal {H}$ being much smaller than unity. A more powerful test can be obtained by considering the complete boundary part of $\mathcal {M}$ as a single matrix, which is given below.

Proposition 4

Let $\mathcal {H}=\mathrm {Diag}(h_0,h_1,\ldots ,h_r,1,1\ldots )$ be a given quadrature with $r+1$ non-unit weights. Then the associated filter (20) and (26) is contractive in the sense of (7) if $n\le 10$ (for the interior part), and

$$\begin{aligned} \sum _{j=0}^{\mathrm {max}(r,n)} \left[ -\frac{2}{n+1}I_j + \frac{1}{h_j 2^{2n}} (\mathcal {D}_1^n e_j)(\mathcal {D}_1^n e_j)^T \right] \le 0 , \end{aligned}$$

for the boundary part.

The principal difference between Propositions 3 and 4 is that the latter is less restrictive. The reason for this is that a single eigenvalue problem is considered for the whole boundary contribution in the energy method, whereas in Proposition 3 the contribution is split between each $h_j$ individually. The advantage of Proposition 3 is that it is much easier to apply, providing a clearly defined interval for each quadrature weight. In most cases this is enough to verify contractivity. In some cases however, the more powerful test of Proposition 4 is required.

1.1 Second Order Case

Using the second order derivative $\mathcal {D}_2$, i.e. $n=1$, we have,

$$\begin{aligned} \mathcal {D}_1^n = \mathcal {D}_1=\begin{pmatrix} -1 &{} 1 \\ &{} -1 &{} 1\\ &{}&{} \ddots &{} \ddots \end{pmatrix}. \end{aligned}$$

The conditions given in Proposition 3 are,

$$\begin{aligned} \begin{aligned} h_0&\ge 2\cdot 1/8 =1/4 \\ h_j&\ge 2\cdot 2/8 = 1/2, \quad j\ge 1. \end{aligned} \end{aligned}$$

1.2 Fourth Order Case

In the fourth order case ($n=2$), we have,

$$\begin{aligned} \mathcal {D}_1^n = \begin{pmatrix} 1 &{} -2 &{} 1 \\ &{}1 &{} -2 &{} 1\\ &{}&{} 1 &{} -2 &{} 1 \\ &{}&{}&{} \ddots &{} \ddots &{} \ddots \end{pmatrix}, \end{aligned}$$

and Proposition 3 yields the conditions,

$$\begin{aligned} \begin{aligned} h_0&\ge 3\cdot 1/32 = 3/32 \\ h_1&\ge 3\cdot 5/32=15/32 \\ h_j&\ge 3\cdot 6 /32=9/16, \quad j\ge 2. \end{aligned} \end{aligned}$$

1.3 Sixth Order Case

The sixth order operator ($n=3$) uses,

$$\begin{aligned} \mathcal {D}_1^n = \begin{pmatrix} -1 &{} 3 &{} -3 &{} 1 \\ &{}-1 &{} 3 &{} -3 &{} 1\\ &{}&{} -1 &{} 3 &{} -3 &{} 1 \\ &{}&{}&{} -1 &{} 3 &{} -3 &{} 1 \\ &{}&{}&{}&{} \ddots &{} \ddots &{} \ddots &{} \ddots \end{pmatrix}, \end{aligned}$$

and from Proposition 3 we have the conditions,

$$\begin{aligned} \begin{aligned} h_0&\ge 4\cdot 1/128 \ = 1/32 \\ h_1&\ge 4\cdot 10/128 = 5/16 \\ h_2&\ge 4\cdot 19/128 = 19/32 \\ h_j&\ge 4\cdot 20/128 = 5/8, \quad j\ge 3. \end{aligned} \end{aligned}$$

1.4 Eighth Order Case

The eighth order case ($n=4$) is given by,

$$\begin{aligned} \mathcal {D}_1^n = \begin{pmatrix} 1 &{} -4 &{} 6 &{} -4 &{} 1 \\ &{} 1 &{} -4 &{} 6 &{} -4 &{} 1\\ &{}&{} 1 &{} -4 &{} 6 &{} -4 &{} 1 \\ &{}&{}&{} 1 &{} -4 &{} 6 &{} -4 &{} 1\\ &{}&{}&{}&{} 1 &{} -4 &{} 6 &{} -4 &{} 1\\ &{}&{}&{}&{}&{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \end{pmatrix}, \end{aligned}$$

with the conditions, from Proposition 3,

$$\begin{aligned} \begin{aligned} h_0&\ge 5\cdot 1/512 \ = 1/512 \\ h_1&\ge 5\cdot 17/512 = 85/512 \\ h_2&\ge 5\cdot 53/512 = 265/512 \\ h_3&\ge 5\cdot 69/512 = 345/512 \\ h_j&\ge 5\cdot 70/512 = 175/256, \quad j\ge 4. \end{aligned} \end{aligned}$$

1.5 Tenth Order Case

In the tenth order case ($n=5$) we have,

$$\begin{aligned} \mathcal {D}_1^n = \left( \begin{array}{cccccccccccc} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1 \\ {}&{} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1\\ {}&{}&{} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1 \\ {}&{}&{}&{} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1\\ {}&{}&{}&{}&{} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1 \\ {}&{}&{}&{}&{}&{} -1 &{} 5 &{}-10 &{} 10 &{} -5 &{} 1 \\ {}&{}&{}&{}&{}&{}&{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots &{} \ddots \\ \end{array}\right) , \end{aligned}$$

and Proposition 3 yields,

$$\begin{aligned} \begin{aligned} h_0&\ge 6\cdot 1/2048 \ \ = 3/1024 \\ h_1&\ge 6\cdot 26/2048 \ = 39/512 \\ h_2&\ge 6\cdot 126/2048 = 189/512 \\ h_3&\ge 6\cdot 226/2048 = 339/512 \\ h_4&\ge 6\cdot 251/2048 = 753/1024 \\ h_j&\ge 6\cdot 252/2048 = 189/256, \quad j\ge 5. \end{aligned} \end{aligned}$$

1.6 High Order Quadrature Rules

The non-unit quadrature weights associated with classical finite difference SBP operators of minimal boundary closure dimension are given by,

$$\begin{aligned} \begin{aligned} h_0&= 1/2 \\ \left[ h_0, h_1,h_2,h_3\right]&=\left[ \frac{17}{48},\frac{59}{48},\frac{43}{48},\frac{49}{48}\right] \\ \left[ h_0, h_1,h_2,h_3,h_4,h_5\right]&= \left[ \frac{521}{1649},\frac{1129}{812},\frac{647}{1031},\frac{5359}{4320},\frac{1435}{1574},\frac{583}{575}\right] \\ \left[ h_0, h_1,h_2,h_3,h_4,h_5,h_6,h_7\right]&=\left[ \frac{202}{685},\frac{1483}{972},\frac{2349}{9124},\frac{953}{530},\frac{669}{1621},\frac{4522}{3537}, \frac{325}{352},\frac{757}{750} \right] , \end{aligned} \end{aligned}$$

for the second, fourth, sixth and eighth order accurate interior cases, respectively. In the tenth order case and above, some of the quadrature weights are negative and hence do not constitute a norm. In fact, already in the eighth order case some of the quadrature weights are quite small (in particular, $h_2$ and $h_4$). Due to this fact, we have found that Proposition 3 can only be used to prove contractivity using filters of order 18 and 20 (it.e. $n=9$ and $n=10$). On the other hand, Proposition 4 can be applied to prove that contractivity holds even with this quadrature for all filters down to second order ($n=1$).

For the first three quadratures listed above, we have found that Proposition 3 is sufficient to prove contractivity of all filters of order 20 (i.e. $n=10$) or less.