Higher Order Cut Finite Elements for the Wave Equation

Abstract

The scalar wave equation is solved using higher order immersed finite elements. We demonstrate that higher order convergence can be obtained. Small cuts with the background mesh are stabilized by adding penalty terms to the weak formulation. This ensures that the condition numbers of the mass and stiffness matrix are independent of how the boundary cuts the mesh. The penalties consist of jumps in higher order derivatives integrated over the interior faces of the elements cut by the boundary. The dependence on the polynomial degree of the condition number of the stabilized mass matrix is estimated. We conclude that the condition number grows extremely fast when increasing the polynomial degree of the finite element space. The time step restriction of the resulting system is investigated numerically and is concluded not to be worse than for a standard (non-immersed) finite element method.

1 Introduction

The cut finite element method [3] is an immersed method. For a domain immersed in a background mesh, one solves for the degrees of freedom of the smallest set of elements covering the domain. The inner products in the weak form are taken over the immersed domain. That is, on each element one integrates over the part of the element that is inside the domain. As a result of this, some elements will have a very small intersection with the immersed domain. This will make some eigenvalues of the discrete system very small and in turn, result in poorly conditioned matrices. A suggested way to remedy this is by adding stabilizing terms to the weak formulation. A jump-stabilization was suggested in [4] for the case of piecewise linear elements, where the jump in the normal derivative is integrated over the faces of the elements intersected by the boundary. This stabilization makes it possible to prove that the condition numbers of the involved matrices are bounded independently of how the boundary cuts the elements. This form of stabilization has been used with good results in several recent papers, see for example [3, 7, 15, 21], and has also been used for PDEs posed on surfaces in [5, 9].

Thus, a lot of attention has been directed to the use of lower order elements. Higher order cut elements have received less attention so far. These are interesting in wave propagation problems. The reason for this is that the amount of work per dispersion error typically increases slower for higher order methods for this type of problems. In [2] it was suggested to stabilize higher order elements by integrating also jumps in higher derivatives over the faces. This generalization of the jump-stabilization was further analyzed in [15].

In this paper, we consider solving the scalar wave equation using higher order cut elements. Both the mass and stiffness matrix are stabilized using the higher order jump-stabilization. We present numerical results showing that the method obtains a high order of accuracy. The time-step restriction of the resulting system is computed numerically and is concluded to be of the same size as for standard finite elements with aligned boundaries. Furthermore, we estimate how the condition number of the stabilized mass matrix depends on the polynomial degree of the basis functions. The estimate suggests that the condition number grows extremely fast with respect to the polynomial degree, which is supported by the numerical experiments. All numerical experiments are performed in two dimensions, but the generalization to three dimensions is immediate.

One reason why the considered stabilization is attractive is because it is quite easy to implement. Integrals over internal faces occur also in discontinuous Galerkin methods, thus making the implementation similar to what is already supported in many existing libraries.

The suggested jump-stabilization is one but not the only possibility for stabilizing an immersed method. In [10] a higher order discontinuous Galerkin method was suggested and proved to give optimal order of convergence. Here the problem of ill-conditioning was solved by associating elements that had small intersections with neighboring elements. Similar approaches has been used with higher order elements in for example [12, 16], where elements with small intersection take their basis functions from an element inside the domain. One problem with these approaches is that it is not obvious how to choose which elements should merge with or associate to one another. A related alternative to these is the approach in [18], where individual basis functions were removed if they have a small support inside the domain. A different approach was used in [11] where streamline diffusion stabilization was added to the elements intersected by the boundary. This was proved to give up to fourth order convergence. However, this approach is restricted to interface problems. Another alternative is to use preconditioners to try to overcome problems with ill-conditioning, such as in [13]. However, only preconditioning does not solve the problem of severe time-step restrictions when using explicit time-stepping. For this reason preconditioning alone is not sufficient in the context of wave-propagation.

This paper is organized in the following way. Notation and some basic problem setup are explained in Sect. 2.1, the stabilized weak formulation is described in Sect. 2.2, and the stability of the method is discussed in Sect. 2.3. Analysis of how fast the condition number increases when increasing the polynomial degree is presented in Sect. 2.4, and numerical experiments are presented in Sect. 3.

2 Problem Statement and Theoretical Considerations

2.1 Notation and Setting

Consider the wave equation

$$\begin{aligned} \ddot{u}&= \nabla ^2 u+f(x,t) \,&x\in \varOmega , \quad&t\in (0,t_f ), \end{aligned}$$

(1)

$$\begin{aligned} u&= g_D(x,t) \,&x\in \Gamma _D, \quad&t\in [0,t_f ], \end{aligned}$$

(2)

$$\begin{aligned} \frac{\partial u}{\partial n}&= g_N(x,t) \,&x\in \Gamma _N, \quad&t\in [0,t_f ],\end{aligned}$$

(3)

$$\begin{aligned} u&=u_0(x) \,&x\in \varOmega , \quad&t=0, \end{aligned}$$

(4)

$$\begin{aligned} \dot{u}&=v_0(x) \,&x\in \varOmega , \quad&t=0, \end{aligned}$$

(5)

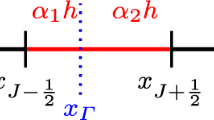
posed on a given domain $\varOmega$, with a smooth boundary $\partial \varOmega =\Gamma _D\cup \Gamma _N$. Let $\varOmega \subset \mathbb {R}^d$ be immersed in a mesh, $\mathcal {T}$, as in Fig. 1. We assume that each element $T\in \mathcal {T}$ has some part which is inside $\varOmega$, that is: $T\cap \varOmega \ne \emptyset$. Furthermore, let $\varOmega _\mathcal {T}$ be the domain that corresponds to $\mathcal {T}$, that is

$$\begin{aligned} \varOmega _\mathcal {T}=\bigcup _{T\in \mathcal {T}} T. \end{aligned}$$

(6)

Let $\mathcal {T}_\Gamma$ denote the set of elements intersected by $\partial \varOmega$:

$$\begin{aligned} \mathcal {T}_\Gamma =\{T\in \mathcal {T}: T \cap \partial \varOmega \ne \emptyset \}, \end{aligned}$$

(7)

as in Fig. 2. Let $\mathcal {F}_\Gamma$ denote the faces seen in Fig. 3. That is, the faces of the elements in $\mathcal {T}_\Gamma$, excluding the faces that make up $\partial \varOmega _\mathcal {T}$. To be precise, $\mathcal {F}_\Gamma$ is defined as

$$\begin{aligned} \mathcal {F}_\Gamma =\{F=\bar{T}_1 \cap \bar{T}_2 \; : \; T_1 \in \mathcal {T}_\Gamma \;\text { or }\; T_2 \in \mathcal {T}_\Gamma , \quad T_1,T_2\in \mathcal {T}\}. \end{aligned}$$

(8)

Fig. 1

$\varOmega$ immersed in a mesh $\mathcal {T}$, covering $\varOmega _\mathcal {T}$

We assume that our background mesh is sufficiently fine, so that the immersed geometry is well resolved by the mesh. Furthermore, we shall restrict ourselves to meshes as the one in Fig. 1, where we have a mesh consisting of hypercubes and our coordinate axes are aligned with the mesh faces. That is, the face normals have a nonzero component only in one of the coordinate directions. Denote the element side length by h.

Consider the situation in Fig. 4, where two neighboring elements, $T_1$ and $T_2$, are sharing a common face F. Denote by $\partial _n^k v$ the kth directional derivative in the direction of the face normal. That is, fix $j\in \{1,\ldots ,d\}$ and let the normal of the face, n, be such that

$$\begin{aligned} n_i= {\left\{ \begin{array}{ll} \pm 1 &{} i=j \\ 0 &{} i\ne j, \end{array}\right. } \end{aligned}$$

(9)

then define

$$\begin{aligned} \partial _{n}^{k}v = n_j^k \frac{\partial ^{k} v}{\partial x_j^{k}}. \end{aligned}$$

(10)

Fig. 2

Intersected elements $\mathcal {T}_\Gamma$

Fig. 3

Faces $\mathcal {F}_\Gamma$

Fig. 4

Two elements sharing a common face

In the following, we shall use the following inner products

$$\begin{aligned} (u,v)_{\varOmega }&=\int _{\varOmega } u v d\varOmega , \end{aligned}$$

(11)

$$\begin{aligned} \left\langle u,v\right\rangle _{\Gamma }&=\int _{\Gamma } u v d\Gamma , \end{aligned}$$

(12)

where the subscript indicates over which region we integrate. Note that (11) is used when we integrate over a d-dimensional subset of $\mathbb {R}^d$, while (12) is used when we integrate over a $d-1$ dimensional region. The $L_2$-norm over some part of the domain, Z, we will denote as $\Vert \cdot \Vert _Z$, or in some places as $\Vert \cdot \Vert _{L_2(Z)}$ if we want to particularly clear. Let $\Vert \cdot \Vert _{H^s(Z)}$ and $|\cdot |_{H^s(Z)}$ denote the $H^s(Z)$-norm and semi-norm. By [v] we shall denote a jump over a face, F:

$$\begin{aligned}{}[v]=v|_{F_+}-v|_{F_-}. \end{aligned}$$

(13)

We shall assume that our basis functions are tensor products of one-dimensional polynomials of order p. In particular, we shall use Lagrange elements with Gauss-Lobatto nodes, in the following referred to as $Q_p$-elements, $p\in \{1,2,\ldots \}$. Let $V_h^p$ denote a continuous finite element space, consisting of $Q_p$-elements on the mesh $\mathcal {T}$:

$$\begin{aligned} V_h^p=\left\{ v\in C^0(\varOmega _\mathcal {T}): \left. v\right| _{T}\in Q_p(T), \, T \in \mathcal {T}\right\} . \end{aligned}$$

(14)

Define also the following semi-norm

$$\begin{aligned} | v |_{\star }^2 = \Vert \nabla v \Vert _{\varOmega _\mathcal {T}}^2 + \frac{1}{h} \Vert v \Vert _{\Gamma _D}^2, \end{aligned}$$

(15)

which is a norm on $V_h^p$ in the case that $\Gamma _D\ne \emptyset$.

Fig. 5

An element having a small intersection (in gray) with the domain

2.2 The Stabilized Weak Formulation

Multiplying (1) by a test-function, integrating by parts, and applying boundary conditions by Nitsche’s method [17] leads to a weak formulation of the following form: find $u_h$ such that for each fix $t\in (0,t_f ]$, $u_h\in V_h^p$ and

$$\begin{aligned} (\ddot{u}_h,v)_\varOmega +a(u_h,v)=L(v), \quad \forall v\in V_h^p, \end{aligned}$$

(16)

where

$$\begin{aligned} a(u_h,v)= & {} (\nabla u_h, \nabla v)_\varOmega -\left\langle \frac{\partial u_h}{\partial n},v\right\rangle _{\Gamma _D} -\left\langle u_h,\frac{\partial v}{\partial n}\right\rangle _{\Gamma _D}+\frac{\gamma _{D}}{h} \left\langle u_h,v\right\rangle _{\Gamma _D}, \end{aligned}$$

(17)

$$\begin{aligned} L(v)= & {} (f,v)_\varOmega +\left\langle g_{D},\frac{\gamma _{D}}{h} v-\frac{\partial v}{\partial n}\right\rangle _{\Gamma _D} +\left\langle g_{N},v\right\rangle _{\Gamma _{N}}. \end{aligned}$$

(18)

What makes this different from standard finite elements is that the integration on each element needs to be adapted to the part of the element that is inside the domain. As illustrated in Fig. 5, some elements will have a very small intersection with the domain. Consider the mass-matrix from the method in (16):

$$\begin{aligned} \tilde{\mathcal {M}}_{ij}=(\phi _i,\phi _j)_\varOmega . \end{aligned}$$

(19)

Note that its smallest eigenvalue is smaller than each diagonal entry:

$$\begin{aligned} \lambda _{\min } =\min _{ z \in \mathbb {R}^N \, : \, z \ne 0 } \frac{z^T \tilde{\mathcal {M}} z}{z^T z}\le \tilde{\mathcal {M}}_{ii}, \quad i=1,\ldots ,N. \end{aligned}$$

(20)

Depending on the size of the cut with the background mesh some diagonal entries can become arbitrarily close to zero. Thus, both the mass and stiffness matrix can now be arbitrarily ill-conditioned depending on how the cut occurs. Because of this, one can not guarantee that the method is stable.

One way to remedy this is by adding stabilizing terms, j, to the two bilinear forms

$$\begin{aligned} M(\ddot{u}_h,v)&= (\ddot{u}_h,v)_\varOmega +\gamma _M j(\ddot{u}_h,v), \end{aligned}$$

(21)

$$\begin{aligned} A(u_h,v)&= a(u_h,v)+\gamma _A h^{-2} j(u_h,v), \end{aligned}$$

(22)

where $\gamma _M,\gamma _A>0$ are penalty parameters. This gives us the following weak formulation: find $u_h$ such that for each fix $t\in (0,t_f ]$, $u_h\in V_h^p$ and

$$\begin{aligned} M(\ddot{u}_h,v)+A(u_h,v)=L(v), \quad \forall v\in V_h^p. \end{aligned}$$

(23)

In [2] the following stabilization term was suggested

$$\begin{aligned} j(u,v)=\sum _{F\in \mathcal {F}_\Gamma } \sum _{k=1}^p h^{2k+1}\left\langle [\partial _n^k u],[\partial _n^k v]\right\rangle _F. \end{aligned}$$

(24)

This stabilization was analyzed and tested numerically for piecewise linear elements in [4]. The stabilization in (24) was further analyzed for higher order elements in [15]. The bilinear form (21) can be shown to define a scalar product which is norm equivalent to the $L_2$-norm on the whole background mesh:

$$\begin{aligned} C_L\Vert v \Vert _{\varOmega _\mathcal {T}}^2\le M(v,v)\le C_U \Vert v \Vert _{\varOmega _\mathcal {T}}^2, \quad \forall v\in V_h^p, \end{aligned}$$

(25)

and a corresponding equivalence holds for the gradient:

$$\begin{aligned} \tilde{C}_L\Vert \nabla v \Vert _{\varOmega _\mathcal {T}}^2\le \Vert \nabla v \Vert _\varOmega ^2 + \gamma _A h^{-2} j(v,v) \le \tilde{C}_U \Vert \nabla v \Vert _{\varOmega _\mathcal {T}}^2, \quad \forall v\in V_h^p. \end{aligned}$$

(26)

The constants in (25) and (26) depend on the polynomial degree of our basis functions, but not on how the boundary cuts through the mesh. Let $\mathcal {M}$ denote the mass matrix with respect to the bilinear form M, and $\mathcal {M}_\mathcal {T}$ with respect to the scalar product on the background mesh, that is:

$$\begin{aligned} \mathcal {M}_{ij}&=M(\phi _i,\phi _j), \end{aligned}$$

(27)

$$\begin{aligned} (\mathcal {M}_\mathcal {T})_{ij}&=(\phi _i,\phi _j)_{\varOmega _\mathcal {T}}. \end{aligned}$$

(28)

Now, (25) implies that the condition number, $\kappa (\mathcal {M})$, of $\mathcal {M}$ is bounded by the condition number of $\mathcal {M}_\mathcal {T}$:

$$\begin{aligned} \kappa (\mathcal {M})\le \frac{C_U}{C_L} \kappa (\mathcal {M}_\mathcal {T}). \end{aligned}$$

(29)

The property (26) is necessary in order to show that $A(\cdot ,\cdot )$ is coercive in $V_h^p$ with respect to the $| \cdot |_\star$-semi-norm on the background mesh:

$$\begin{aligned} \exists C_c > 0 \, \text {:} \quad C_c | v |_\star ^2 \le A(v,v), \quad \forall v\in V_h^p. \end{aligned}$$

(30)

As we shall see in Sect. 2.3 this is needed in order to show that the method is stable with respect to time. The result in (30) follows by the same procedure as in [15], assuming that the following inverse inequality holds

$$\begin{aligned} h^{1/2} \left\| \frac{\partial v}{\partial n} \right\| _{\Gamma \cap T} \le C p \Vert \nabla v \Vert _{T}, \quad \forall v\in V_h^p. \end{aligned}$$

(31)

For piecewise linear basis functions, this inequality follows in the same way as the proof of Lemma 4 in [6]. Related inverse inequalities were proved for planar cuts for higher order elements in [14]. The inequality (31) follows the same scaling with respect to h and p as the corresponding standard inverse inequality, which relates the norm over a face to the norm over the whole element. See for example [22].

The stabilization in (24) is the basic form of stabilization that we shall consider. However, each time we differentiate we will introduce some dependence on the polynomial degree. It therefore seems reasonable that each term in the sum should be scaled in some way. Because of this, we consider a stabilization of the following form:

$$\begin{aligned} j(u,v)=\sum _{F\in \mathcal {F}_\Gamma } \sum _{k=1}^p w_k\frac{h^{2k+1}}{(2k+1)(k!)^2}\left\langle [\partial _n^k u],[\partial _n^k v]\right\rangle _F, \end{aligned}$$

(32)

where $w_j\in \mathbb {R}^+$ are some weights, which we are free to choose as we wish. The choice of weights will determine how large our constants $C_U$, $C_L$ in (29) are, and in turn influence how well conditioned the mass matrix is. Given how the stabilization is derived from a Taylor expansion (see [15] or Sect. 2.4), it is perhaps most natural to use $w_k=1$. However, several papers [2, 8, 15] discussing high order cut finite elements state the stabilization as in (24). This would be equivalent to choosing $w_k=(k!)^2 (2k+1)$ in (32). We think it makes sense to introduce the weights in (32) to make it possible to analyze what effect different choices of weights have.

If the solution and the boundary are sufficiently smooth, a standard non-immersed finite element method with the same type of elements is expected to yield errors which converge as follows

$$\begin{aligned} \Vert u_h - u \Vert _{L_{2}(\varOmega )}&\le C h^{p+1}, \end{aligned}$$

(33)

$$\begin{aligned} \Vert u_h - u \Vert _{H^1(\varOmega )}&\le C h^{p}, \end{aligned}$$

(34)

$$\begin{aligned} \Vert u_h - u \Vert _{L_2(\Gamma _D)}&\le C h^{p+1}, \end{aligned}$$

(35)

$$\begin{aligned} \Vert \partial _n u_h - \partial _n u \Vert _{L_2(\Gamma _N)}&\le C h^{p}. \end{aligned}$$

(36)

This is also what we expect for the considered immersed method.

2.3 Stability

The bilinear forms in (23) are symmetric. This is a quite important property, since this in the end will guarantee stability of the system. In order to show stability we want a bound over time on $\Vert u \Vert _{\varOmega _\mathcal {T}}$. Define an energy, E, of the form

$$\begin{aligned} E(t):=\frac{1}{2} \left( M(\dot{u}_h,\dot{u}_h) + A(u_h,u_h) \right) . \end{aligned}$$

(37)

Since both bilinear forms are at least positive semi-definite, this energy has the property $E \ge 0$. The symmetry now allows us to show that for a homogeneous system,

$$\begin{aligned} f(x)=0, \quad g_D(x)=0, \quad g_N(x)=0, \end{aligned}$$

(38)

the energy is conserved:

$$\begin{aligned} \frac{\mathrm {d}E}{\mathrm {d}t}=M(\ddot{u}_h,\dot{u}_h)+A(u_h,\dot{u}_h)\overset{(23)}{=}0, \end{aligned}$$

(39)

so that

$$\begin{aligned} E(t)=E(0). \end{aligned}$$

(40)

By the definition of the energy together with (25) and (30) this immediately implies that $\Vert \dot{u}_h\Vert _{\varOmega _\mathcal {T}}$ and $\Vert \nabla u_h \Vert _{\varOmega _\mathcal {T}}$ are both bounded. For the case $\Gamma _D\ne \emptyset$ the semi-norm $| \cdot |_\star$ is a norm for the space $V_h^p$ and (30) implies that $\Vert u_h \Vert _{{\varOmega _\mathcal {T}}}$ is also bounded. When $\Gamma _D = \emptyset$ we can use that

$$\begin{aligned} 2 \Vert u_h \Vert _{\varOmega _\mathcal {T}} \frac{\mathrm {d}}{\mathrm {d}t} \Vert u_h \Vert _{\varOmega _\mathcal {T}}= \frac{\mathrm {d}}{\mathrm {d}t} \Vert u_h\Vert _{\varOmega _\mathcal {T}}^2 =2(u_h,\dot{u}_h)_{\varOmega _\mathcal {T}} \le 2 \Vert u_h\Vert _{\varOmega _\mathcal {T}} \Vert \dot{u}_h\Vert _{\varOmega _\mathcal {T}}, \end{aligned}$$

(41)

which gives us

$$\begin{aligned} \frac{\mathrm {d}}{\mathrm {d}t} \Vert u_h \Vert _{\varOmega _\mathcal {T}} \le \Vert \dot{u}_h \Vert _{{\varOmega _\mathcal {T}}}. \end{aligned}$$

(42)

By integrating we obtain that $\Vert u_h \Vert _{{\varOmega _\mathcal {T}}}$ is bounded since $\Vert \dot{u}_h \Vert _{{\varOmega _\mathcal {T}}}$ is bounded:

$$\begin{aligned} \Vert u_h (t) \Vert _{\varOmega _\mathcal {T}} \le \Vert u_h(0) \Vert _{\varOmega _\mathcal {T}} + \int _0^{t_f }\Vert \dot{u}_h \Vert _{{\varOmega _\mathcal {T}}} dt. \end{aligned}$$

(43)

Thus the system is stable.

In total the method (23) discretizes to a system of the form

$$\begin{aligned} \mathcal {M}\frac{\mathrm {d}^{2} \xi }{\mathrm {d}t^{2}}+\mathcal {A}\xi =\mathcal {L}(t), \end{aligned}$$

(44)

with $\mathcal {M},\mathcal {A}\in \mathbb {R}^{N \times N}$, $\xi \in \mathbb {R}^N$ and $\mathcal {L}: \mathbb {R}\rightarrow \mathbb {R}^N$, and where

$$\begin{aligned} \mathcal {A}_{ij}=A(\phi _i,\phi _j). \end{aligned}$$

(45)

When solving this system in time we will have a restriction on the time-step, $\tau$, of the form

$$\begin{aligned} \tau \le \alpha \beta _{cfl} h, \end{aligned}$$

(46)

where $\alpha$ is a constant which depends on the time-stepping algorithm. If we for example use a classical 4th-order explicit Runge–Kutta $\alpha =2\sqrt{2}$. The CFL-number, $\beta _{cfl}$, is given by

$$\begin{aligned} \beta _{cfl} =\frac{h^{-1}}{\sqrt{\lambda _{\max }}}, \end{aligned}$$

(47)

where $\lambda _{\max }$ is the largest eigenvalue of the generalized eigenvalue problem: find $(x,\lambda )$ such that

$$\begin{aligned} \mathcal {A} x -\lambda \mathcal {M}x=0, \quad x\in \mathbb {R}^N. \end{aligned}$$

(48)

One would expect that the added stabilization has some effect on the CFL-number. Because of this, we will investigate this constant experimentally in Sect. 3. It turns out that the CFL-number is not worse than for a standard non-immersed method.

2.4 Analysis of the Condition Number of the Mass Matrix

We would like to choose the weights in (32) in order to minimize the condition number of the mass matrix. This is particularly important when it comes to wave-propagation problems. For this application one typically uses an explicit time-stepping method. When this is the case we need to solve a system involving the mass matrix in each time-step.

In order to choose the weights we need to know how the condition number depends on the weights and the polynomial degree. To determine this, we follow essentially the same path as in [15] and keep track of the weights and the polynomial dependence of the involved inequalities. In the following, we denote by C various constants which do not depend on h or p, unless explicitly stated otherwise. We shall also by w denote the vector $w=(w_1,\ldots ,w_p)$, where $w_j$ are the weights in the stabilization term (32). We can now derive the following inequality, which is a weighted version of Lemma 5.1 in [15].

Lemma 1

Given two neighboring elements, $T_1$ and $T_2$, sharing a face F (as in Fig. 4), and $v\in V_h^p$, we have that:

$$\begin{aligned} \Vert v \Vert _{T_1}^2 \le {L(w)} \left( \Vert v \Vert _{T_2}^2 + \sum _{k=1}^p w_k \frac{h^{2k+1}}{(2k+1)(k!)^2} \Vert [\partial _n^k v] \Vert _{F}^2 \right) , \end{aligned}$$

(49)

where

$$\begin{aligned} {L(w)}=C_1(p) + \sum _{k=1}^p \frac{1}{w_k}. \end{aligned}$$

(50)

Proof

Denote by $v_i$ the restriction of v to $T_i$ and then extended by expression to the whole of $T_1 \cup T_2$. As in Fig. 4, let $x\in T_1$ and denote by $x_F(x)$ the projection of x onto the face. Let n be the normal pointing towards $T_1$ and let j denote the only nonzero component, as in (9). We may now Taylor expand from the face:

$$\begin{aligned} v_i(x)= \sum _{k=0}^p \frac{1}{k!} \partial _j^k v_i(x_F(x)) (x_j-x_{F,j})^k. \end{aligned}$$

(51)

Using that

$$\begin{aligned} x_j-x_{F,j}=n_j|x-x_F| \end{aligned}$$

(52)

gives us

$$\begin{aligned} v_i(x)= \sum _{k=0}^p \frac{1}{k!} \partial _n^k v_i(x_F(x)) |x-x_F(x)|^k, \end{aligned}$$

(53)

by definition of $\partial _n^k v$ from (10). Consequently we have that

$$\begin{aligned} v_1(x)=v_2(x)+\sum _{k=1}^p \frac{1}{k!} [\partial _n^k v(x_F)] |x-x_F|^k. \end{aligned}$$

(54)

Now introduce the following weighted $l^2(\mathbb {R}^{p+1})$-norm:

$$\begin{aligned} \Vert z \Vert _\alpha ^2 :=\sum _{k=0}^p \alpha _k z_k^2, \end{aligned}$$

(55)

where $\alpha _k>0$ and $z\in \mathbb {R}^{p+1}$. If $\Vert \cdot \Vert _1$ denotes the usual $l^1(\mathbb {R}^{p+1})$-norm we have that:

$$\begin{aligned} \Vert z \Vert _1^2:=\left( \sum _{k=0}^p |z_k|\right) ^2\le C_\alpha \Vert z\Vert _\alpha ^2, \end{aligned}$$

(56)

where

$$\begin{aligned} C_\alpha =\sum _{k=0}^p \frac{1}{\alpha _k}. \end{aligned}$$

(57)

Taking the $L_2(T_1)$-norm of (54) and using (56) now results in:

$$\begin{aligned} \Vert v_1 \Vert _{T_1}^2 \le C_\alpha \left( \alpha _{0} \Vert v_2 \Vert _{T_1}^2 + \sum _{k=1}^p \alpha _k \frac{h^{2k+1}}{(2k+1)(k!)^2} \Vert [\partial _n^k v] \Vert _{F}^2 \right) . \end{aligned}$$

(58)

Since $v_2$ lies in a finite dimensional polynomial space on $T_1 \cup T_2$ the norms on $T_1$ and $T_2$ are equivalent:

$$\begin{aligned} \Vert v_2 \Vert _{T_1}^2 \le C_1 \Vert v_2 \Vert _{T_2}^2, \end{aligned}$$

(59)

where $C_1=C_1(p)$. Using this in (58) and choosing

$$\begin{aligned} \alpha _{0}&=1/C_1, \end{aligned}$$

(60)

$$\begin{aligned} \alpha _{k}&=w_k, \quad k=1,\ldots ,p \end{aligned}$$

(61)

gives us (49). $\square$

Remark 1

The constant $C_1(p)$ will grow rapidly with the polynomial order. By only considering the highest order term in the polynomial a lower bound on the constant is achieved. We get an exponential dependence

$$\begin{aligned} C_1 (p) \ge \sqrt{ \frac{\int _h^{2h} x^{2p}dx}{\int _0^hx^{2p}dx}}\approx 2^{p+1/2}. \end{aligned}$$

(62)

This is however far from sharp. The constant can straightforwardly be computed numerically for a given p by considering how polynomials, which are orthonormal in one element, extend to a neighbouring element and are projected to the orthonormal polynomials of the neighbouring element. The constant equals the norm of the projection matrix. From such computations we see that $C_1(p) \sim e^{1.75p}$.

Lemma 1 will now allow us to give a lower bound on the bilinear form M, which was defined in (21).

Lemma 2

A lower bound for M(v, v) is:

$$\begin{aligned} \Vert v \Vert _{\varOmega _\mathcal {T}}^2 \le C_l {L(w)}^{N_J} M(v,v), \end{aligned}$$

(63)

where L(w) is given by (50), $N_J$ is some sufficiently large integer and $C_l$ is a constant independent of h and p.

Proof

Let $T_0\in \mathcal {T}_\Gamma$ and let $\{T_i\}_{i=1}^{N-1}$ (with $T_i\in \mathcal {T}_\Gamma$) be a sequence of elements that need to be crossed in order to get to an element $T_N\in \mathcal {T}\setminus \mathcal {T}_\Gamma$, as in Fig. 6, and let $F_i=T_{i-1}\cap T_i$. By using (49) we get

$$\begin{aligned} \Vert v \Vert _{T_0}^2 \le {L(w)}^N \left( \Vert v \Vert _{T_N}^2+ \sum _{i=1}^N \sum _{k=1}^p w_k \frac{h^{2k+1}}{(2k+1)(k!)^2} \Vert [\partial _n^k v] \Vert _{F_i}^2\right) , \end{aligned}$$

(64)

where we have used that ${L(w)}\ge 1$ (since at least $C_1\ge 1)$. Let now $N_J\ge 1$ denote some upper bound on the maximum number of jumps that needs to be made in the mesh. If our geometry is well resolved by our background mesh $N_J$ is a small integer. This gives us

$$\begin{aligned} \Vert v\Vert _{\varOmega _\mathcal {T}}^2= \sum _{T\in \mathcal {T}_\Gamma } \Vert v\Vert _{T}^2+\sum _{T\in \mathcal {T}\setminus \mathcal {T}_\Gamma } \Vert v\Vert _{T}^2 \le C {L(w)}^{N_J} \left( \sum _{T\in \mathcal {T}\setminus \mathcal {T}_\Gamma } \Vert v\Vert _{T}^2 + j(v,v) \right) , \end{aligned}$$

(65)

from which (63) follows. $\square$

Fig. 6

A sequence of jumps from a boundary element $T_0\in \mathcal {T}_\Gamma$ to an inside element $T_N$

We proceed by estimating how a bound on the jumps depends on the polynomial degree.

Lemma 3

For the jumps in the normal derivative we have that:

$$\begin{aligned} \Vert [\partial _n^k v] \Vert _F^2 \le C_k \frac{p^{4k+2}}{h^{2k+1}} \left( \Vert v \Vert _{T_F^+}^2+\Vert v \Vert _{T_F^-}^2 \right) , \quad \text {for} \quad k=1,2,\ldots ,p \end{aligned}$$

(66)

where $T_F^+$ and $T_F^-$ denotes the two elements sharing the face F.

Proof

Note first that

$$\begin{aligned} \Vert [\partial _n^k v] \Vert _F^2 \le 2 \left( \Vert \partial _n^k v_1 \Vert _{F}^2+\Vert \partial _n^k v_2 \Vert _{F}^2 \right) . \end{aligned}$$

(67)

We shall need the following inequalities:

$$\begin{aligned} \Vert v \Vert _F\le & {} C\frac{p}{\sqrt{h}} \Vert v \Vert _T, \end{aligned}$$

(68)

$$\begin{aligned} | v |_{H^s(T)}\le & {} C^s\frac{p^{2s}}{h^{s}} \Vert v \Vert _T, \quad s\in \mathbb {N}_0, \end{aligned}$$

(69)

which were discussed¹ in [20]. Although (69) holds for a whole element we shall use the corresponding inequality applied to a face:

$$\begin{aligned} | v |_{H^s(F)} \le C^s\frac{p^{2s}}{h^{s}} \Vert v \Vert _F. \end{aligned}$$

(70)

This is valid since a function v in the tensor product space over T will have a restriction $\left. v\right| _{F}$ in the tensor product space over the face F. Note that the constants, C, in (69) and (70) are not necessarily the same. By combining (67), (68) and (70) we obtain (66). $\square$

Using Lemma 3 we can now bound the bilinear form $M(\cdot ,\cdot )$ from above.

Lemma 4

An upper bound for M(v, v) is:

$$\begin{aligned} M(v,v)\le ( 1+C_g G(w) )\Vert v \Vert _{\varOmega _\mathcal {T}}^2, \end{aligned}$$

(71)

where

$$\begin{aligned} G(w)=\sum _{k=1}^p w_k\frac{p^{4k+2}}{(2k+1)(k!)^2}, \end{aligned}$$

(72)

and $C_g$ is a constant independent of h and p.

Proof

Using the definition of $j(\cdot ,\cdot )$ and applying Lemma 3 on each order of derivatives in the sum individually we have

$$\begin{aligned} j(v,v)\le C G(w)\sum _{F\in \mathcal {F}_\Gamma } \left( \Vert v \Vert _{T_F^-}^2 + \Vert v \Vert _{T_F^+}^2 \right) . \end{aligned}$$

(73)

Let $n_F$ denote the number of faces that an element has in $\mathbb {R}^d$. We now have

$$\begin{aligned} \sum _{F\in \mathcal {F}_\Gamma } \left( \Vert v \Vert _{T_F^+}^2 + \Vert v \Vert _{T_F^-}^2 \right) \le 2n_F \sum _{T\in \mathcal {T}} \Vert v \Vert _{T_F}^2 \le 2n_F \Vert v \Vert _{\varOmega _\mathcal {T}}^2, \end{aligned}$$

(74)

so we finally obtain:

$$\begin{aligned} j(v,v)\le C_g G(w)\Vert v \Vert _{\varOmega _\mathcal {T}}^2, \end{aligned}$$

(75)

which gives us (71). $\square$

By using Lemmas 2 and 4 we now have the following bound on the condition number.

Lemma 5

An upper bound for the condition number of the mass matrix is

$$\begin{aligned} \kappa (\mathcal {M})\le C_M(w) \kappa (\mathcal {M^*}), \end{aligned}$$

(76)

where

$$\begin{aligned} C_M=C_l {L(w)}^{N_J} (1+C_g G(w)) \kappa (\mathcal {M}^*). \end{aligned}$$

(77)

Proof

Denote eigenvalues by $\lambda$. From Lemmas 2 and 4 we obtain

$$\begin{aligned} \frac{\lambda _{\min } (\mathcal {M}^*)}{{C_l L(w)}^{N_J}}\le & {} \lambda _{\min }(\mathcal {M}), \end{aligned}$$

(78)

$$\begin{aligned} \lambda _{\max }(\mathcal {M})\le & {} (1+C_g G(w)) \lambda _{\max } (\mathcal {M}^*), \end{aligned}$$

(79)

which gives us (76). $\square$

Here, we would like to choose the weights in order to minimize the constant $C_M$. However, we have the following unsatisfying result, which shows that no matter how we choose the weights our bound on the condition number increases extremely fast with p.

Lemma 6

The constant $C_M(w)$ in Lemma 5 fulfills $C_M(w)\ge C_0 P(p)$, where $C_0$ does not depend on p or w. Here P(p) is the function

$$\begin{aligned} P(p)=\sum _{k=1}^p \frac{p^{4k+2}}{(k!)^2(2k+1)}, \end{aligned}$$

(80)

which is independent of the choice of weights w.

Proof

First note that

$$\begin{aligned} C_l {L(w)}^{N_J} (1+C_g G(w))\ge C_l C_g G(w) {L(w)}^{N_J}\ge C_l C_g L(w) G(w) . \end{aligned}$$

(81)

Now we have

$$\begin{aligned} {L(w)} G(w)\ge & {} \sum _{k=1}^p \left( w_k \frac{p^{4k+2}}{(2k+1)(k!)^2} \right) \sum _{k=1}^p \left( \frac{1}{w_k} \right) \nonumber \\\ge & {} \sqrt{\sum _{k=1}^p \left( w_k^2 \left( \frac{p^{4k+2}}{(2k+1)(k!)^2}\right) ^2 \right) } \sqrt{\sum _{k=1}^p \left( \frac{1}{w_k} \right) ^2}\ge P(p), \end{aligned}$$

(82)

where we first used that the $l^1(\mathbb {R}^{p})$-norm is greater than the $l^2(\mathbb {R}^{p})$-norm and finally Cauchy-Schwartz. From this the result follows. $\square$

The function P(p) increases incredibly fast when increasing the polynomial degree. This result could reflect either:

• 1. The analysis leading to Lemma 5 is not sharp. The bound $C_M$ is too generous, and a better bound exists.

• 2. The bound in Lemma 5 is not unnecessarily generous, so that the constant $C_M$ is in some sense “tight”. This means that the condition number of the stabilized mass matrix (27) will grow faster than the function P(p), regardless of the choice of weights.

Alternative 2 is rather devastating from a time-stepping perspective, since in order to time-step (44) an inverse of the mass matrix needs to be available in each time-step. If this inversion is done with an iterative method the number of required iterations until convergence is going to be large.

A combination of these two alternatives is, of course, possible. The estimate in Lemma 5 could be too pessimistic, but even the optimal bound increases incredibly fast. Given the results in Sect. 3 this appears to be the most plausible alternative.

2.5 Choosing Weights in the Jump-Stabilization

In order to do a computation, we are forced to make some choice of the weights $w_i$. The essence of Lemma 6 is that we can bound L(w)G(w) from below. So in order to choose weights let us assume that:

$$\begin{aligned} \kappa (\mathcal {M})\propto L(w)G(w). \end{aligned}$$

(83)

From Lemma 4 it is seen that choosing $w_i\gg 1$ makes G(w) very large. In the same way, Lemma 2 tells us that choosing $w_i \ll 1$ for some i makes L(w) very large. From this observation it seems reasonable to try to enforce both bounds to be of about the same magnitude. In this way, we minimize L(w)G(w) with respect to w and enforce $G(w)=L(w)$. This leaves us with

$$\begin{aligned} \nabla _w L+\nabla _w G=0, \end{aligned}$$

(84)

where $\nabla _w$ denotes the gradient with respect to w. This now gives us the following choice of weights

$$\begin{aligned} w_k=k!\frac{\sqrt{2k+1}}{p^{2k+1}}. \end{aligned}$$

(85)

Given the analysis here, we find that this is the choice of weights that is easiest to motivate. Although, this choice is not necessarily optimal. Numerical tests (not reported here) indicate that the conditioning is not very sensitive to the choice of weights.

3 Numerical Experiments

In the following, we shall solve both an inner problem and an outer problem using finite element spaces of different orders. In the inner problem we consider a simple bounded domain, while in the outer problem, the domain is bounded but exterior to a simple domain, see for example Figs. 1 and 10, respectively.

The weights from (85) are used. In addition, the following parameters are used

$$\begin{aligned} \gamma _M&=0.25\sqrt{3}, \end{aligned}$$

(86)

$$\begin{aligned} \gamma _A&=0.5\sqrt{3},\end{aligned}$$

(87)

$$\begin{aligned} \gamma _D&=5p^2. \end{aligned}$$

(88)

The scaling of $\gamma _D$ with respect to p follows from the inequality (31). When ${p=1}$ these parameters coincide with the parameters used in [21]. There the effect of $\gamma _M$ on the condition number of the mass matrix was investigated numerically. For $p=1$ this choice of $\gamma _A$ and $\gamma _D$ also coincides with the one in [4], where $\gamma _A$ was investigated numerically.

The geometry of $\varOmega$ is approximated as the zero level set of a function, $\psi _h$. This level set function, $\psi _h$, is an element in the space

$$\begin{aligned} W_h^p=\{v \in C_0(\varOmega _{\mathcal {T}_B}) : \left. v\right| _{T}=Q_p(T) \}, \end{aligned}$$

(89)

where

$$\begin{aligned} \varOmega _{\mathcal {T}_B}=\bigcup _{T\in \mathcal {T}_B} T, \end{aligned}$$

(90)

and where $\mathcal {T}_B$ is the larger background mesh from which $\mathcal {T}$ is created. In the experiments $\psi _h$ is the $L_2$-projection of an analytic level set function onto the space $W_h^p$. Which elements in $\mathcal {T}_B$ that should belong to $\mathcal {T}$ is determined by checking the sign of $\psi _h$ at the nodes on each element in $\mathcal {T}_B$. In order to approximate integrals on elements intersected by the boundary, we have used the algorithm in [19]. On each element, T, this algorithm generates quadrature rules for integration over $\varOmega \cap T$ and $\partial \varOmega \cap T$. This is done using the level set function, $\psi _h$. It is worth noting that also the errors of the solution are calculated with respect to this approximation of the geometry. That is, the $L_2$-norms are approximated as

$$\begin{aligned}&\Vert \cdot \Vert _\varOmega \approx \Vert \cdot \Vert _{\{x:\, \psi _h(x)<0 \}}, \end{aligned}$$

(91)

$$\begin{aligned}&\Vert \cdot \Vert _{\partial \varOmega } \approx \Vert \cdot \Vert _{\{x: \, \psi _h(x)=0 \}}. \end{aligned}$$

(92)

Order of accuracy is estimated as

$$\begin{aligned} \frac{\log (e_{i} / e_{i+1})}{\log (h_{i} / h_{i+1})}, \end{aligned}$$

(93)

where $e_i$ denotes an error corresponding to mesh size $h_i$.

Time-stepping is performed with a classical fourth order explicit Runge–Kutta, after rewriting the system (44) as a first order system in time. A time step, $\tau$, of size

$$\begin{aligned} \tau = \frac{0.4}{p^2} h \end{aligned}$$

(94)

is used. During the time-stepping we need to solve a system involving the mass matrix. When using higher order elements the condition number of the mass matrix is large, so an iterative method would require many iterations. However, we can approximate the integrals in the mass matrix using Gauss-Lobatto quadrature. This choice of reduced integration has the benefit that the mass matrix becomes almost diagonal. All off-diagonal entries in the mass matrix are related to degrees of freedom close to the immersed boundary. Since these are relatively few, it is feasible to use a direct solver.

The library deal.II [1] was used to implement the method.

3.1 Standard Reference Problem with Aligned Boundary

It is relevant to compare some of the properties of the mass and stiffness matrices with standard (non-immersed) finite elements. The unstabilized mass and stiffness matrices were computed on a rectangular grid with size $[-1.5,1.5] \times [-1.5,1.5]$, with Neumann boundary conditions. As for the immersed case, quadrilateral Lagrange elements with Gauss-Lobatto nodes were used. The computed CFL-number is shown in Table 1. The CFL-number was found by computing the largest eigenvalue of (48) and using this in (47). For a given p the value in Table 1 is the mean value when calculating the CFL-number over a number of grid sizes. The condition number of the mass matrix is shown in Fig. 7 and the minimal and maximal eigenvalues of the mass matrix is shown in Fig. 8. Since all eigenvalues should be proportional to $h^2$, the eigenvalues have been scaled by $h^{-2}$ for easier comparison.

Table 1 Computed CFL-numbers for the non-immersed case in Sect. 3.1 and the immersed inner problem in Sect. 3.2

Fig. 7

Condition number of the mass matrix for the non-immersed (N.I.) problem in Sect. 3.1 and the immersed inner problem in Sect. 3.2. For different h and p. The dashed lines denotes estimates according to the function P(p)

Fig. 8

Minimal/maximal eigenvalues (scaled by $h^{-2}$) of the mass matrix, for the non-immersed (N.I.) problem in Sect. 3.1 and the immersed inner problem in Sect. 3.2. For different h and p.

3.2 An Immersed Inner Problem

Let $\varOmega$ be a disk domain, centered at origo, with radius $R=1$, and enforce homogeneous Dirichlet boundary condition along the boundary

$$\begin{aligned} \left. u\right| _{\partial \varOmega }=0. \end{aligned}$$

(95)

Let $J_0$ denote the 0th order Bessel-function and let $\alpha _n$ denote its nth zero. By starting from initial conditions:

$$\begin{aligned} \left. u\right| _{t=0}&=J_0\left( \alpha _n \frac{\Vert x \Vert }{R}\right) , \end{aligned}$$

(96)

$$\begin{aligned} \left. \frac{\partial u}{\partial t}\right| _{t=0}&=0, \end{aligned}$$

(97)

we can calculate the error in our numerical solution with respect to the analytic solution:

$$\begin{aligned} u(x,t)= J_{0} \left( \alpha _{n} \frac{\Vert x \Vert }{R} \right) \cos (\omega _{n}t), \quad \omega _{n}=\frac{\alpha _{n}}{R}. \end{aligned}$$

(98)

Let $n = 3$. A few snapshots of the numerical solution are shown in Fig. 9. The problem was solved with the given method until an end-time, $t_f$, corresponding to a three periods:

$$\begin{aligned} t_f =3 T_p, \quad T_p=\frac{2 \pi }{\omega _n}. \end{aligned}$$

(99)

At the end-time the errors were computed.

Fig. 9

Snapshots of the vibrating membrane problem

The calculated errors and estimated orders of accuracy for the different element orders are shown in Tables 2, 3 and 4. The order of accuracy for each error agrees quite well with what is expected from (33)–(35).

Computed CFL-numbers for different element orders are shown in Table 1. The values were computed according to (47). We see that the CFL-number is essentially the same as for the non-immersed case. In the same way as for the non-immersed case, the values in Table 1 are the mean values over a number of grid sizes. However, the CFL-number only varied slightly when varying the grid size. By inserting the values in Table 1 into (46) one can see that it would have been possible to use a larger time-step than the one in (94).

How the condition number of the mass matrix depend on the grid size is shown in Fig. 7, for the different orders of p. We see that the condition numbers are essentially constant when refining h, in agreement with (25). We also see that the condition numbers increase extremely rapidly when increasing the polynomial degree, as predicted by Lemma 6. It is also clear from Fig. 7 that the condition number increase much faster than in the non-immersed case. The dashed lines in Fig. 7 denote the function CP(p), where P is the function from (80). The constant C was chosen so that CP(1) agreed with the mean (with respect to h) of the condition numbers for $V_h^1$. The estimate from Lemma 6 is fairly reasonable for the tested polynomial orders. It does, however, appear to be slightly too pessimistic.

Table 2 Errors and orders of accuracy for the inner problem when using the space $V_h^{1}$

Table 3 Errors and orders of accuracy for the inner problem when using the space $V_h^{2}$

Table 4 Errors and orders of accuracy for the inner problem when using the space $V_h^{3}$

The minimal and maximal eigenvalues for the different polynomial orders and refinements are seen in Fig. 8. As can be seen, the scaled eigenvalues are essentially constant with respect to h. Thus the dependence on h is in agreement with the theoretical considerations in Sect, 2.4. We see that the minimal eigenvalues decrease quite fast when increasing the polynomial degree, and that they are substantially smaller than in the non-immersed case. The maximal eigenvalues also decrease but much slower than in the non-immersed case.

Fig. 10

Geometry used for the outer problem

3.3 An Immersed Outer Problem

Consider instead an outer problem with the geometry depicted in Fig. 10. The star shaped geometry is the zero contour of the following level set function

$$\begin{aligned} \phi (r,\theta )= R+R_0 \sin (n\theta )-r \end{aligned}$$

(100)

where $(r,\theta )$ are the polar coordinates, and $R=0.5$, $R_0=0.1$, $n=5$. So our domain $\varOmega$ is given by

$$\begin{aligned} \varOmega = \{(x,y)\in \mathbb {R}^2 : x,y\in (-3/2,3/2) : \phi (x,y)<0 \}. \end{aligned}$$

(101)

Starting from zero initial conditions

$$\begin{aligned} \left. u\right| _{t=0}=0, \end{aligned}$$

(102)

$$\begin{aligned} \left. \frac{\partial u}{\partial t}\right| _{t=0}=0, \end{aligned}$$

(103)

we prescribe homogeneous Neumann boundary condition on the internal boundary

$$\begin{aligned} \left. \frac{\partial u}{\partial n}\right| _{\Gamma _I}=0, \end{aligned}$$

(104)

and Dirichlet boundary conditions on the external boundaries

$$\begin{aligned} u= {\left\{ \begin{array}{ll} g_D(x,t) &{}\quad x\in \Gamma _B \\ 0 &{}\quad x\in \Gamma _L \cup \Gamma _R \cup \Gamma _U. \end{array}\right. } \end{aligned}$$

(105)

Here, $g_D$ is the function

$$\begin{aligned} g_D(x,t)= \cos \left( \frac{\pi }{3} x \right) e^{-(t-t_c)^2/\sigma ^2}, \end{aligned}$$

(106)

where we have chosen $\sigma =0.25$, $t_c=3$. A few snapshots of the numerical solution are seen in Fig. 11.

Fig. 11

Snapshots of the numerical solution for the outer problem

Here, we don’t have an expression for the analytic solution. So when computing the errors we compare against a reference solution, $u_{\text {ref}}$. The reference solution was computed on a grid twice as fine as the finest grid that we present errors for.

The computed errors after solving to the end time $t_f =4$ are shown in Tables 5, 6 and 7. We see that the convergence is at least $h^{p+1}$ for the $L_2(\varOmega )$-error and $h^{p}$ for the $H^1(\varOmega )$-error. The last column shows the error in the Neumann boundary condition, which converges close to what is expected: $h^p$.

Table 5 Errors and orders of accuracy for the outer problem when using the space $V_h^{1}$

Table 6 Errors and orders of accuracy for the outer problem when using the space $V_h^{2}$

Table 7 Errors and orders of accuracy for the outer problem when using the space $V_h^{3}$

4 Discussion

The results in Sects. 3.2 and 3.3 show that it is possible to solve the wave equation and obtain up to 4th order convergence. In particular, it is also promising that the CFL-condition is not stricter than for the non-immersed case. However, both the theoretical results in Lemma 6 and the results in Sect. 3.2 show that there are problems with the conditioning of the mass matrix. It should be emphasized that even if the added stabilization creates some new problems it is by far better than using no stabilization at all. With the added stabilization the method can be proved to be stable, which is essential.

It would, of course, be advantageous if one would be able to create a stabilization which does not lead to conditioning problems. However, the prospects for creating a good preconditioner for the mass matrix is rather good, since the stabilization maintains the symmetry of the mass matrix and since one obtains bounds on its spectrum from the analysis.

The choice of the weights in (85) were based on hand-waving arguments and can, therefore, be criticized. We have tried other choices of weights but have not presented the results here. This is mainly because they give similar results and we have no reason to believe that there exists a choice which makes the condition number significantly better.