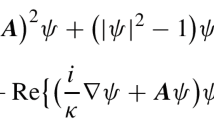Abstract
In this paper, we propose and analyze a stabilized semi-implicit Euler gauge-invariant method for numerical solution of the time-dependent Ginzburg–Landau (TDGL) equations in the two-dimensional space. The proposed method uses the well-known gauge-invariant finite difference approximations with staggered variables in a rectangular mesh, and a stabilized semi-implicit Euler discretization for time integration. The resulted fully discrete system leads to two decoupled linear systems at each time step, thus can be efficiently solved. We prove that the proposed method unconditionally preserves the point-wise boundedness of the solution and is also energy-stable. Moreover, the proposed method under the zero-electric potential gauge is shown to be equivalent to a mass-lumped version of the lowest order rectangular Nédélec edge element approximation and the Lorentz gauge scheme to a mass-lumped mixed finite element method. These indicate the method is also effective in solving the TDGL problems in non-convex domains although the solutions are often of low-regularity in such situation. Various numerical experiments are also presented to demonstrate effectiveness and robustness of the proposed method.






















Similar content being viewed by others
References
Alstrom, T., Sorensen, M., Pedersen, N., Madsen, S.: Magnetic flux lines in complex geometry type-II superconductors studied by the time dependent Ginzburg–Landau equation. Acta Appl. Math. 115, 63–74 (2011)
Arnold, D., Falk, R., Winther, R.: Finite element exterior calculus: from Hodge theory to numerical stability. Bull. Am. Math. Soc. (N.S.) 47, 281–354 (2010)
Buscaglia, G., Bolech, C., Lopez, A.: On the numerical solution of the time-dependent Ginzburg–Landau equations in multiply connected domains. In: Berger, J., Rubinstein, J. (eds.) Connectivity and superconductivity. LNP m62, pp. 200–214. Springer, Berlin (2000)
Carey, G., Knezevic, D.: Multiscale and hysteresis effects in vortex pattern simulations for Ginzburg–Landau problems. Int. J. Numer. Meth. Eng. 81, 866–891 (2010)
Chapman, S.J., Howison, S.D., Ockendon, J.R.: Macroscopic models for superconductivity. SIAM Rev. 34, 529–560 (1992)
Chen, Z.: Mixed finite element methods for a dynamical Ginzburg–Landau model in superconductivity. Numer. Math. 76, 323–353 (1997)
Chen, Z., Hoffmann, K.: Numerical studies of a non-stationary Ginzburg–Landau model for superconductivity. Adv. Math. Sci. Appl. 5, 363–389 (1995)
Christiansen, S., Halvorsen, T.: A Gauge invariant discretization on simplicial grids of the Schrödinger eigenvalue problem in an electromagnetic field. SIAM J. Numer. Anal. 49, 331–345 (2011)
Coskun, E., Kwong, M.: Simulating vortex motion in superconducting films with the time-dependent Ginzburg–Landau equations. Nonlinearity 10, 579–593 (1997)
Du, Q.: Finite element methods for the time-dependent Ginzburg–Landau model of superconductivity. Comput. Math. Appl. 27, 119–133 (1994)
Du, Q.: Discrete gauge-invariant approximations of a time dependent Ginzburg–Landau model of superconductivity. Math. Comput. 67, 965–986 (1998)
Du, Q., Gunzburger, M.D., Peterson, J.S.: Analysis and approximation of the Ginzburg–Landau model of superconductivity. SIAM Rev. 34, 54–81 (1992)
Du, Q., Ju, L., Li, X., Qiao, Z.: Stabilized linear semi-implicit schemes for the nonlocal Cahn–Hilliard equation. J. Comput. Phys. 363, 39–54 (2018)
Du, Q., Nicolaides, R., Wu, X.: Analysis and convergence of a covolume approximation of the Ginzburg–Landau model of superconductivity. SIAM J. Numer. Anal. 35, 1049–1072 (1998)
Frahm, H., Ullah, S., Dorsey, A.: Flux dynamics and the growth of the superconducting phase. Phys. Rev. Lett. 66, 3067–3070 (1991)
Gao, H., Li, B., Sun, W.: Optimal error estimates of linearized Crank–Nicolson Galerkin FEMs for the time-dependent Ginzburg–Landau equations in superconductivity. SIAM J. Numer. Anal. 52, 1183–1202 (2014)
Gao, H., Sun, W.: An efficient fully linearized semi-implicit Galerkin-mixed FEM for the dynamical Ginzburg–Landau equations of superconductivity. J. Comput. Phys. 294, 329–345 (2015)
Gao, H., Sun, W.: A new mixed formulation and efficient numerical solution of Ginzburg–Landau equations under the temporal gauge. SIAM J. Sci. Comput. 38, A1339–A1357 (2016)
Gao, H., Sun, W.: Analysis of linearized Galerkin—mixed FEMs for the time-dependent Ginzburg–Landau equations of superconductivity. Adv. Comput. Math. 44, 923–949 (2018)
Gor’kov, L.P., Eliashberg, G.M.: Generalization of the Ginzburg–Landau equations for non-stationary problems in the case of alloys with paramagnetic impurities. Sov. Phys. JETP 27, 328–334 (1968)
Gropp, W., Kaper, H., Leaf, G., Levine, D., Palumbo, M., Vinokur, V.: Numerical simulation of vortex dynamics in type-II superconductors. J. Comput. Phys. 123, 254–266 (1996)
Gunter, D., Kaper, H., Leaf, G.: Implicit integration of the time-dependent Ginzburg–Landau equations of superconductivity. SIAM J. Sci. Comput. 23, 1943–1958 (2002)
Kato, R., Enomoto, Y., Maekawa, S.: Computer simulations of dynamics of flux lines in type-II superconductors. Phys. Rev. B 47, 8016–8024 (1993)
Kaper, H., Kwong, M.: Vortex configurations in type-II superconducting films. J. Comput. Phys. 119, 120–131 (1995)
Kim, S., Burkardt, J., Gunzburger, M., Peterson, J., Hu, C.: Effects of sample geometry on the dynamics and configurations of vortices in mesoscopic superconductors. Phys. Rev. B 76, 024509 (2007)
Li, B.: Convergence of a decoupled mixed FEM for the dynamic Ginzburg-Landau equations in nonsmooth domains with incompatible initial data. Calcolo 54, 1441–1480 (2017)
Li, B., Zhang, Z.: Mathematical and numerical analysis of time-dependent Ginzburg–Landau equations in non-convex polygons based on Hodge decomposition. Math. Comput. 86, 1579–1608 (2017)
Li, B., Zhang, Z.: A new approach for numerical simulation of the time-dependent Ginzburg–Landau equations. J. Comput. Phys. 303, 238–250 (2015)
Liao, H., Zhou, S., Shi, X.: Simulating the time-dependent Ginzburg–Landau equations for type-II superconductors by finite-difference method. Chin. Phys. 13, 0737-09 (2004)
Monk, P.: Finite Element Methods for Maxwell’s Equations. Oxford University Press, New York (2003)
Mu, M.: A linearized Crank–Nicolson–Galerkin method for the Ginzburg–Landau model. SIAM J. Sci. Comput. 18, 1028–1039 (1997)
Mu, M., Huang, Y.: An alternating Crank–Nicolson method for decoupling the Ginzburg–Landau equations. SIAM J. Numer. Anal. 35, 1740–1761 (1998)
Raza, N., Sial, S., Siddiqi, S.: Approximating time evolution related to Ginzburg–Landau functionals via Sobolev gradient methods in a finite-element setting. J. Comput. Phys. 229, 1621–1625 (2010)
Richardson, W., Pardhanani, A., Carey, G., Ardelea, A.: Numerical effects in the simulation of Ginzburg–Landau models for superconductivity. Int. J. Numer. Meth. Eng. 59, 1251–1272 (2004)
Stosic, Darko, Stosic, Dusan, Ludermir, T., Stosic, B., Milosevic, M.: GPU-advanced 3D electromagnetic simulations of superconductors in the Ginzburg–Landau formalism. J. Comput. Phys. 322, 183–198 (2016)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer, Berlin (1997)
Tinkham, M.: Introduction to Superconductivity. McGraw-Hill, New York (1975)
Xu, C., Tang, T.: Stability analysis of large time-stepping methods for epitaxial growth models. SIAM J. Numer. Anal. 44, 1759–1779 (2006)
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
H. Gao’s research is partially supported by National Natural Science Foundation of China under Grant Number 11871234 and Fundamental Research Funds for the Central Universities (HUST) under Grant Number 2017KFYXJJ089. L. Ju’s research is partially supported by US National Science Foundation under Grant Number DMS-1818438.
Appendices
Appendix
An Example with Explicit Coefficient Matrices
In this appendix, we provide an example on a \(2\times 2\) mesh to show the equivalence of the gauge invariant finite difference approximation and the mass-lumped mixed finite element method. To this end, we shall only consider the Lorentz gauge scheme for \({\mathbf {A}}\) (2.34) and the mixed FEM (4.8)–(4.9). For simplicity, we take \(\Omega = (0,1)^2\) and set \(h= \frac{1}{2}\). There are 9 degrees of freedom (DOFs) for \(\Phi \) and 12 DOFs for \({\mathbf {A}}\), see Fig. 23.
The Lorentz gauge scheme (2.33)–(2.34) can be written as
where \(\nabla _h\) is a \(12 \times 9\) gradient matrix and \(D_h\) is a \(9 \times 12\) divergence matrix defined respectively by
and \({\mathbf {K}}_1\) is the coefficient matrix defined by
Let us recall that the mixed FEM introduces \(\Phi = -\mathrm {div}\, {\mathbf {A}}\) as an extra variable. Based on the lowest order bilinear element space \(S_h\) and lowest order rectangular Nédélec edge element space \(V_h\), we look for \((\Phi _h^n, {\mathbf {A}}_h^n) \, \in \, S_h \times V_h\) such that
which further can be represented by the following matrix equations
On the \(2 \times 2\) mesh, the above mass matrix \({\mathbf {M}}_{\text {bilinear}}\) generated by the lowest order bilinear Lagrange element space and the matrix \(\mathbf {\varvec{D}}_h\) are defined by
and the mass matrix \({\mathbf {M}}\) and stiffness matrix \({\mathbf {K}}_2\) generated by the lowest order rectangular Nédélec edge element space are defined respectively by
If the mass-lumping is used, then it holds
and we can obtain the following matrix equations
where \(\widetilde{{\mathbf {M}}}_{\text {bilinear}}\) and \(\widetilde{\mathbf {\varvec{M}}}\) are diagonal matrices as
and
By taking matrices \(\widetilde{{\mathbf {M}}}_{\text {bilinear}}\), \(\widetilde{\mathbf {\varvec{M}}}\) and \(\widetilde{{\mathbf {D}}}_h\) into (A.9), we can deduce that
It is easy to verify the following matrix qualities
which confirm our observation. Finally, we shall point out that similar equivalences also hold for L-shape and multi-connected domains.
Rights and permissions
About this article
Cite this article
Gao, H., Ju, L. & Xie, W. A Stabilized Semi-Implicit Euler Gauge-Invariant Method for the Time-Dependent Ginzburg–Landau Equations. J Sci Comput 80, 1083–1115 (2019). https://doi.org/10.1007/s10915-019-00968-5
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10915-019-00968-5