Derivative NMR Spectroscopy for J-Coupled Multiplet Resonances using Short Time Signals (0.5KB) Encoded at Low Magnetic Field Strengths (1.5T). Part II: Water Unsuppressed

Abstract

The topic of this work is on reliable resolving of J-coupled resonances in spectral envelopes from proton nuclear magnetic resonance (NMR) spectroscopy. These resonances appear as multiplets that none of the conventional nonderivative shape estimators can disentangle. However, the recently formulated nonconventional shape estimator, the derivative fast Padé transform (dFPT), has a chance to meet this challenge. In the preceding article with a polyethylene phantom, using the time signals encoded with water suppressed, the nonparametric dFPT was shown to be able to split apart the compound resonances that contain the known J-coupled multiplets. In the present work, we address the same proton NMR theme, but with sharply different initial conditions from encodings. The goal within the nonparametric dFPT is again to accurately resolve the J-coupled resonances with the same polyethylene phantom, but using raw time signals encoded without water suppression. The parallel work on the same problem employing two startlingly unequal time signals, encoded with and without water suppression in the preceding and the current articles, respectively, can offer an answer to a question of utmost practical significance. How much does water suppression during encoding time signals actually perturb the resonances near and farther away from the dominant water peak? This is why it is important to apply the same dFPT estimator to the time signals encoded without water suppression to complement the findings with water suppression. A notable practical side of this inquiry is in challenging the common wisdom, which invariably takes for granted that it is absolutely necessary to subtract water from the encoded time signals in order to extract meaningful information by way of NMR spectroscopy.

1 Introduction

In the accompanying article [1], we laid the ground for the specific problem under study by focusing on resolving J-coupled resonances in spectral envelopes corresponding to a polyethylene phantom [2, 3]. Therein, we used short time signals (0.5KB) encoded at a low magnetic field (1.5T) with water suppression during the course of measurements. As a prelude to this particular problem, we went beyond its immediate framework, by revisiting the background of chemical shift as one of key milestones in nuclear magnetic resonance (NMR) spectroscopy from a historical perspective.

This and some other related aspects of the NMR problem under study need not be reiterated in the present article. Such an opportunity leaves the space for concentrating here on the new information from reconstructions with time signals encoded without water suppression. Importantly, such time signals are not merely an alternative set of the acquired data. They raise a fundamental question which requires a proper answer: how much can the reconstructed information be impacted by partially removing the giant water peak in the process of encoding time signals?

Partially suppressing water when encoding time signals evidently amounts to modifying the content of the acquired information. Why would then this be not only the usual practice, but also the standard in NMR spectroscopy? The reason is an ever present dependence of measurements on theory for interpretation of the acquired information. The said modifications of encoded time signals are dictated only by the inability of all the conventional nonderivative signal processing (parametric and nonparametric alike) to extract enough interpretable spectral information in the presence of the original giant water resonance.

Could this disadvantageous situation be overturned into a more favorable prospect using derivative signal processing, particularly by means of the derivative fast Padé transform (dFPT) as a shape estimator alone? This is what we are here set to investigate.

In a broader context of biomedical time signals, particularly for NMR spectroscopy on humans, modifying the encoded information is the least desirable procedure in measurements. This occurs because one can never be sure whether the nature of the outcomes from the subsequent data analysis is due to suppressing water or to some pathological conditions in the patient (or both, which is the worst scenario, because of the lack of differentiation between the two effects).

The only way to rule out the influence of water suppression during measurements is to process the time signals having the unmodified water content. Thus, the repercussions of potentially favorable results from the nonparametric dFPT for a polyethylene phantom in the case of time signals encoded without water suppression would be invaluable, especially in the context that matters most for medical diagnostics, i.e. for in vivo NMR spectroscopy, which is alternatively called magnetic resonance spectroscopy (MRS).

2 Theory

A brief recapitulation of Padé and Fourier nonderivative and derivative estimations is given in Ref. [1]. This need not be reiterated here. Only certain aspects will be illuminated in this Section and the formulae complementary to Ref. [1] will be given. The same Padé nonderivative and derivative versions (theoretically and computationally) will be used in the present study as in Ref. [1]. This is very important to make sure that potential discrepancies in the reconstruction results obtained by using encoded time signals with and without water suppression are not partially due to algorithmic differences in computations with the applied signal processing procedures.

The total shape spectrum or envelope in the nonderivative diagonal fast Padé transform (FPT) is given by the quotient of two polynomials $P_K/Q_K$ [4,5,6]. The expansion coefficients $\{p_r,q_s\}\, (1\le r,s\le K)$ of polynomials $P_K$ and $Q_K$ are determined uniquely from two systems of linear equations, one for $P_K$ and the other for $Q_K.$ As detailed in Ref. [1], one actually needs to solve only a single system of linear equations which gives the expansion coefficients $\{q_s\}\, (1\le s\le K)$ of $Q_K.$ In contrast, the other system of linear equations for the expansion coefficients $\{p_r\}\, (1\le r\le K)$ of $P_K$ need not be solved at all. The reason is that $p_r$ is, in fact, an analytical expression (a straightforward convolution) in terms of the time signal points $\{c_n\}$ and the already found set $\{q_s\}$ associated with $Q_K.$

In any parameter estimator, the system of linear equations is necessarily overdetermined (more equations than the unknown parameters). Overdetermination implies prediction of some spurious (unphysical) information which, as such, is not present in the input time signal, or equivalently, free induction decay (FID). Therefore, there must be a guard against reconstructing unphysical resonances. Moreover, one must also be assured that no genuine (physical) information from the time signal is missing in the results of data analysis.

Such a guard is non-existent in fitting techniques, where over-fitting and under-fitting are a common occurrence with the appearance of spurious resonances and the absence of some of the genuine resonances, respectively. The FPT also produces spurious resonances. However, this estimator has a guard against unphysical resonances as these can unmistakably be identified and removed by the mechanism of pole-zero cancellations.

In a Padé spectral envelope $P_K/Q_K,$ the same spurious resonance appears in both the numerator $(P_K)$ and denominator $(Q_K),$ thus forming a doublet (called Froissart doublet) [7, 8]. This doublet annihilates itself in the spectral quotient $P_K/Q_K,$ where a spurious zero of $P_K$ cancels the corresponding spurious pole stemming from the root of $Q_K$ (pole-zero cancellation). This is how the FPT automatically eliminates every spurious resonance. In other words, the FPT has its inherently built-in self-correction mechanism against spoiling the predicted spectrum by spurious resonances [1].

Such an annulling of Froissart doublets is readily seen to occur in the canonical representation of $P_K/Q_K.$ In the alternative Heaviside partial decomposition of $P_K/Q_K,$ Froissart doublets vanish on account of their negligibly small intensities for encoded FIDs. This latter statement is easily understood by reference to the relationship between time signals and spectral lineshapes. Namely, every FID datum, $c_n,$ from the set $\{c_n\}\, (0\le n\le N-1)$ is described by a sum of K complex harmonics (complex exponentials) each having its complex amplitude $d_k\, (1\le k\le K).$ The peak height of an absorptive component Lorentzian lineshape is proportional to the quotient $|d_k|/\mathrm{Im}(\omega _k)$ [1], where $\omega _k$ is the angular fundamental frequency.

The intensity of an absorptive Lorentzian resonance is proportional to the peak height of the given lineshape profile. Spurious resonances have $d_k=0$ (noise-free synthesized FIDs) or $d_k\approx 0$ (noise-corrupted encoded FIDs). The Heaviside representation is a sum of complex Lorentzian components each containing $d_k$ as a multiplying term. Therefore, every summand in the Heaviside linear combination of partial fractions for spurious resonance will drop out because of negligibly small values of the signal amplitude $d_k$ (a weak resonance intensity) [1].

Pole-zero cancellation is also a way to achieve a dimensionality reduction of a large system. By pole-zero elimination of every spurious frequency from a total number K of the reconstructed frequencies (genuine G, plus spurious S, namely $K=K_{\mathrm{G}}+K_{\mathrm{S}}, \, K_{\mathrm{G}}\ll K_{\mathrm{S}}$), the previously larger dimension ($K\times K$) of the system is reduced to a smaller size ($K_{\mathrm{G}}\times K_{\mathrm{G}}$). In general, not knowing the number $K_{\mathrm{G}}$ of true resonances prior to estimations, one keeps on augmenting an initial estimate $K_{\mathrm{in}}$ of $K_{\mathrm{G}}.$

After a while, due to disappearance of all Froissart doublets, the parametrically generated Padé spectrum $P_K/Q_K,$ as a function of the running model order K,  stabilizes by reaching the final, equilibrium value $P_{K_{\mathrm{G}}}/Q_{K_{\mathrm{G}}},$ which contains only the genuine resonances. This stabilizing $K_{\mathrm{G}}$ represents the exact number of true, physical resonances. All the other parametric processors rely on guessing $K_{\mathrm{G}}.$ By contrast, in the parametric FPT, the number of true resonances is not surmised. Rather, $K_{\mathrm{G}}$ is treated as yet another unknown parameter to be reconstructed, together with the peak parameters for each genuine resonance [1, 4, 5].

Moreover, the described stabilization in the parametric FPT is also present in the shape estimation by the FPT. In the nonparametric FPT (shape estimations alone), pole-zero cancellations and Froissart doublets do not appear explicitly because neither zeros nor poles are reconstructed. Nevertheless, the nonparametrically computed envelope $P_K/Q_K$ stabilizes at the same model order $K_{\mathrm{G}}$ as does the total shape spectrum in the parametric FPT. This implies that in the Padé envelope, obtained by a sole shape estimation, poles and zeros are, in fact, implicitly present. Among these hidden poles, those that coincide with the hidden zeros do undergo pole-zero cancellations to lead to the stabilized nonparametrically predicted envelope $P_{K_{\mathrm{G}}}/Q_{K_{\mathrm{G}}}$ [1].

Stable and unstable resonances are classified as physical and unphysical, respectively. Both are identifiable by the FPT. Once the true number $K_{\mathrm{G}}$ of genuine resonances is reconstructed by either the shape or parameter estimations in the FPT, we can be sure that no spurious resonances can survive in the final results. Disentangling genuine from spurious resonances is known as the powerful concept of signal-noise separation (SNS) [8], unique to the FPT due to its rational polynomial $P_K/Q_K$ in the role of the Padé spectral envelope.

As outlined in Ref. [1], the derivative FPT, i.e. the dFPT, is obtained by applying the derivative operator $\mathrm{D}_m=(\text {d}/\text {d}\nu )^m$ to the stabilized Padé envelope (converged with respect to K). Here, $v$ is the sweep linear frequency. The latter envelope can be used from either the shape or parameter estimation, such that the corresponding processing will be referred to as the nonparametric and parametric dFPT, respectively. Both the parametric and nonparametric dFPT are also rational polynomials, albeit more complicated than $P_K/Q_K$ in the nonderivative FPT. The resonance parameters can be extracted from either the nonparametric or parametric dFPT. In principle, these two derivative estimators should give the same peak parameters for all physical resonances.

To obtain the derivative parameters, the rational polynomials in the nonparametric and parametric dFPT are not rooted, i.e. the quantification problems are not solved in the derivative signal processings. Instead, the derivative order m is monitored to find the value $m_{\mathrm{min}}$ for which the envelopes in the nonparametric and parametric dFPT become comprised solely of isolated Lorentzian lineshapes in the magnitude mode. This reduces the derivative envelope to the derivative components in the dFPT. From this point, it is trivial to extract the derivative peak parameters (position, width, height). Finally, the existing connection formulae are used to convert the derivative magnitude mode peak parameters (from the magnitude envelope) to the nonderivative peak parameters (from the absorptive envelope).

In the case of the parametric dFPT, this conversion recovers exactly the nonderivative absorption mode peak parameters that have already been reconstructed by the parametric FPT. Of course, the latter reconstruction set from the parametric FPT is all that is needed and, thus, one may wonder why the parametric dFPT would be necessary? In general, it would not be necessary, but it is needed to benchmark the entire procedure, i.e. to verify whether indeed the parametric dFPT could reproduce the peak signatures due to the parametric FPT (gold standard). After benchmarking this procedure for the parametric dFPT, we can confidently use it also for the nonparametric dFPT whose peak parameters are to be judged by their counterparts from the parametric dFPT. It is this most stringent testing which has been followed through in the companion work [1] and shall be performed here, as well.

The optimal mode for derivative spectra is the magnitude lineshape profile. The reason is in the fact that the magnitude mode is positive-definite, phase-insensitive and free from side lobes that plague extraction of peak parameters from derivative absorptive and dispersive lineshapes. In the magnitude mode, interference of absorptive and dispersive parts obliterates all side lobes. Resonances interact by way of interference, which itself is governed by resonance phases. Interference causes resonances to overlap. Thus, to arrive at isolated peaks, that would be more amenable to quantification, it would be necessary to weaken the phases. Weakened phases would reduce interference and as a result, the overlapped resonances would be separated.

One may wonder why NMR spectra abound with overlapping resonances in the first place? This is explained by the customary form of a complex Lorentzian lineshape, $L_k(\nu )\sim d_k/(\nu -\nu _k+i\varGamma _k),$ as a function of sweep linear frequency $\nu ,$ where $\varGamma _k=2\pi \mathrm{Im}(\nu _k).$ Away from the resonance linear frequency $\nu _k=\omega_{k}/(2\pi),$ it is seen that $L_k(\nu )$ varies slowly with $\nu ,$ according to the behavior $1/(\nu -\nu _k).$ Such a slow decline of $L_k(\nu )$ with increasing $\nu$ generates a long tail of this resonance lineshape which, therefore, can cause its notable overlaps not only with an adjacent, but also with distant Lorentzians.

Therefore, to split apart the overlapped resonances, their tails should be confined to a narrow frequency band around $\nu _k.$ This is reminiscent of turning a plane wave into a wave packet. In other words, farther from $\nu _k,$ the required modification of the lineshape should cut off the tail, e.g. by having the behavior $1/(\nu -\nu _k)^{m+1},$ where m is a positive integer. For $m\ge 1,$ it is clear that function $1/(\nu -\nu _k)^{m+1}$ falls off much faster with augmented $\nu$ than $1/(\nu -\nu _k).$ This sought behavior is achieved precisely by the $m\,$th order derivative operator $\mathrm{D}_m$ with the result in a simple form $(\text {d}/\text {d}\nu )^mL_k(\nu )=(-1)^mm!d_k/(\nu -\nu _k+i\varGamma _k)^{m+1}.$ We see then how asking the right question about the origin of overlapped resonances in NMR led naturally straight to derivative NMR.

Rather than repeating any of the working formulae from Ref. [1], we shall complement them by giving the explicit expressions for the nonparametric and parametric dFPT in the case of an arbitrary derivative order m. These expressions are obtained by applying the derivative operator $\mathrm{D}_m$ to the envelope $P_K/Q_K$ in the nonderivative FPT, which is:

$$\begin{aligned} R(u)\equiv \frac{f(u)}{g(u)}\,,\quad f(u)=P_K(u)\,,\quad g(u)=Q_K(u), \end{aligned}$$

(2.1)

where $u=\mathrm{e}^{\gamma \nu },$ $\gamma =-2\pi i\tau$ and $\tau$ is the sampling time for the encoded time signal. First, it is necessary to introduce two derivative operators, $\mathcal{D}_u$ and $\mathcal{D}_\nu ,$ relative to the variables u and $\nu ,$ respectively:

$$\begin{aligned} \mathcal{D}_u=\frac{\text {d}}{\text {d}u}\,,\quad \mathcal{D}_\nu =\frac{\text {d}}{\text {d}\nu }. \end{aligned}$$

(2.2)

The $m\,$th order of these two operators are connected by the following relationship:

$$\begin{aligned} \mathcal{D}^m_\nu =\gamma ^m\sum _{j=1}^mS(m,j)u^j\mathcal{D}^j_u. \end{aligned}$$

(2.3)

Here, $S(m,j )$ is the Stirling number of the second kind [9, 10]:

$$\begin{aligned} S(m,j)=\frac{1}{j!}\sum _{\lambda =0}^j(-1)^{j-\lambda }\left( {\begin{array}{c}j\\ \lambda \end{array}}\right) \lambda ^m, \end{aligned}$$

(2.4)

where $\left( {\begin{array}{c}j\\ \lambda \end{array}}\right)$ is the standard binomial coefficient. The results of the application of the $m\,$th order derivative operators $\mathcal{D}^m_u$ and $\begin{aligned} \mathcal{D}^m_\nu =\gamma ^m\sum _{j=1}^mS(m,j)u^j\mathcal{D}^j_u. \end{aligned}$ on functions $\{R(u),f(u),g(u)\}$ are denoted by $\{R^{(m)}_u(u),f^{(m)}_u(u),g^{(m)}_u(u)\}$ and $\{R^{(m)}_\nu (u),f^{(m)}_\nu (u),g^{(m)}_\nu (u)\},$ respectively:

$$\begin{aligned} \left. \begin{array}{c} R^{(m)}_u(u)=\mathcal{D}^m_uR(u)\,,\quad R^{(m)}_\nu (u)=\mathcal{D}^m_\nu R(u)\\ f^{(m)}_u(u)=\mathcal{D}^m_uf(u)\,,\quad f^{(m)}_\nu (u)=\mathcal{D}^m_\nu f(u)\\ g^{(m)}_u(u)=\mathcal{D}^m_ug(u)\,,\quad g^{(m)}_\nu (u)=\mathcal{D}^m_\nu g(u) \end{array}\right\} \quad (m=1,2,3,...). \end{aligned}$$

(2.5)

Then, the general $m\,$th order derivative envelope in the nonparametric dFPT can be cast into the form:

$$\begin{aligned} R^{(m)}_\nu (u)=\gamma ^m\sum _{\ell =1}^mS(m,\ell )u^\ell R^{(\ell )}_u(u). \end{aligned}$$

(2.6)

The derivatives $R^{(\ell )}_u(u)$ are computed efficiently from the following stable recursion relation:

$$\begin{aligned} R^{(\ell )}_u(u)={\displaystyle {\frac{f^{(\ell )}_u(u)-\sum \limits _{j=0}^{\ell -1}\left( {\begin{array}{c}\ell \\ j\end{array}}\right) R^{(j)}_u(u)g^{(\ell -j)}_u(u)}{g(u)}}}, \end{aligned}$$

(2.7)

where $\ell \ge 0$ and $\sum _{j=0}^{-1}(\cdots )=0.$ The initialization to this recursion reads as:

$$\begin{aligned} R^{(1)}_u(u)={\displaystyle {\frac{f^{(1)}_u(u)-R(u)g^{(1)}_u(u)}{g(u)}}}. \end{aligned}$$

(2.8)

In the case of the parametric dFPT, we obtained an explicit analytical expression for the $m\,$th derivative of the components and the corresponding envelope. The starter is the Heaviside partial fraction decomposition of the envelope in the nonderivative parametric FPT:

$$\begin{aligned} R(u)=\frac{p_0}{q_0}+\sum _{k=1}^KG(k,u)\,,\quad G(k,u)=\frac{d_ku}{u-u_k}\,,\quad u_k=\mathrm{e}^{\gamma \nu _k}, \end{aligned}$$

(2.9)

where G(k, u) is the $k\,$th component spectrum. Following notation (2.5), the $m\,$th derivative of G(k, u) is denoted by $G^{(m)}_\nu (k,u):$

$$\begin{aligned} G^{(m)}_\nu (k,u)= \left( \frac{\text {d}}{\text {d}\nu }\right) ^mG(k,u). \end{aligned}$$

(2.10)

Then, the explicit calculations of $G^{(m)}_\nu (k,u)$ for an integer $m\ge 1$ yields the expression:

$$\begin{aligned} G^{(m)}_\nu (k,u)= d_k\gamma ^m\sum _{\ell =1}^m(-1)^m\ell !S(m,\ell )\frac{v^\ell_k}{(v_k-1)^{\ell +1}}\,,\quad v_k=\frac{u}{u_k}. \end{aligned}$$

(2.11)

Here, the sum over $\ell$ can be carried out explicitly to give the result:

$$\begin{aligned} G^{(m)}_\nu (k,u)=d_k(-\gamma )^m\frac{A_m(v_k)}{(v_k-1)^{m+1}}, \end{aligned}$$

(2.12)

where $A_m(v)$ is the Eulerian polynomial whose one of the classical definitions reads as [11]:

$$\begin{aligned} A_m(v)=\sum _{\ell =1}^m \ell !S(m,\ell )v^\ell (1-v)^{m-\ell }. \end{aligned}$$

(2.13)

Finally, the $m\,$th derivative of the Heaviside partial fraction representation $R^{(m)}_\nu (u)$ from Eq. (2.9) becomes:

$$\begin{aligned} R^{(m)}_\nu (u)&= \sum _{k=1}^KG^{(m)}_\nu (k,u) \\&= (-\gamma )^m\sum _{k=1}^Kd_k\frac{A_m(v_k)}{(v_k-1)^{m+1}}\quad (m=1,2,3,...), \end{aligned}$$

(2.14)

where $v_k$ is defined in Eq. (2.11). This is the general derivative of the arbitrary order m of the envelope in the parametric dFPT. It is seen from this result that, in the parametric dFPT, the derivative envelope $R^{(m)}_\nu (u)$ is the sum of its K derivative component spectra $G^{(m)}_\nu (k,u).$

3 Results and discussion

3.1 Input, time domain data

Time and frequency domain data are strictly separated in conventional MRS. Time signals are measured (encoded). Frequency spectra (spectral lineshapes) are predicted by theory and computed by various methods (Fourier, Padé, ...). This difference needs to be emphasized since very often an incorrect terminology, “acquired spectra”, is used in the MRS literature. In customary MRS, spectra are never acquired, i.e. encoded or measured. They are reconstructed from the encoded time signals or FIDs. This is to be distinguished from the nomenclature of the dawn of NMR, when in the 1940s and 1950s spectra were recorded directly on oscilloscopes by slowly sweeping across the preassigned intervals of the external magnetic field strength $B_0.$

As stated, we presently use the same polyethylene Philips Phantom A (Proton Phantom) [2, 3] as in Ref. [1]. Therein, this phantom is described and the procedure is given for encoding the time signals. The specifics of these FIDs used here are the same as outlined in Ref. [1]. Thus, such information shared by [1] and the present studies need not be repeated here. However, the only essential dissimilarity, and this is a huge difference between Ref. [1] and the current work, is that the presently used FIDs have been encoded without water suppression. There is no need either that we again expound on the pattern of J-splitting (spin-spin interaction), which has been detailed in the Results Section of Ref. [1].

Based upon the theory of high-resolution NMR spectroscopy, it is expected that in the spectrum of the polyethylene Philips Phantom A the following resonances should be found (excluding the ethanol OH peak obscured by the giant water resonance) [2] (p. 51):

• 1 (singlet, s): water ($\mathrm{H}_2\mathrm{O}$),

• 2-5 (quartet, q): methylene protons from the $\mathrm{CH}_2$ group of ethanol (EtOH, $\mathrm{CH}_3\mathrm{CH}_2\mathrm{OH}$),

• 6 (singlet, s): methanol (MeOH, $\mathrm{CH}_3\mathrm{OH}$),

• 7 (singlet, s): acetate or acetic acid (Ace, $\mathrm{CH}_3\mathrm{COOH}$) and

• 8-10 (triplet, t): methyl protons from the $\mathrm{CH}_3$ group of ethanol (EtOH, $\mathrm{CH}_3\mathrm{CH}_2\mathrm{OH}$).

3.2 Output, frequency-domain data

As in Ref. [1], both Padé and Fourier reconstructions will be presented in this subsection. As is well-known, the fast Fourier transform (FFT) can autonomously give the total shape spectra alone. In other words, the FFT is a shape estimator only and, as such, belongs to the group of nonparametric signal processors. The adjective ’nonparametric’ indicates that the FFT, on its own, cannot generate the peak parameters (peak position, width, height, phase) for exponentially damped sinusoids/cosinusoids that are routinely encountered in NMR spectroscopy (and in many other areas of signal processing) [4,5,6]. This is at variance with the fact that such parameters are the key reconstructed information in NMR spectroscopy.

By contrast, Padé spectral estimations can be nonparametric and parametric. Both variants predict the envelopes. Additionally, the parametric Padé processing gives the components whose sum represents the parametrically reconstructed envelope. The component spectral lineshapes themselves are built from the peak position, width, height and phase of each constituent resonance [1]. These latter peak parameters are obtained by solving the quantification problem. In the parametric Padé signal processing, the quantification problem is solved exactly for the given input FID. Consequently, the ensuing peak parameters for each resonance in the component spectra are unique.

In this article, the spectral reconstructions are displayed through 8 figures, combining the representative sets of the Padé and Fourier results:

• Figure 1: Padé, nonderivative FPT (nonparametric, no zero filling), real parts of complex spectra,

• Figure 2: Fourier, nonderivative FFT (no zero filling), real parts of complex spectra,

• Figure 3: Padé, nonderivative FPT (nonparametric, no zero filling), additional spectral modes (magnitudes and imaginary parts of complex spectra),

• Figure 4: Fourier, nonderivative FFT (no zero filling), additional spectral modes (magnitudes and imaginary parts of complex spectra),

• Figure 5: Padé, nonderivative FPT and derivative dFPT (nonparametric, no zero filling) vs. Fourier, nonderivative FFT and derivative dFFT (no zero filling),

• Figure 6: Padé, nonderivative FPT and derivative dFPT (nonparametric, no zero filling) vs. Fourier, nonderivative FFT and derivative dFFT (FID zero filled once),

• Figure 7: Padé, nonderivative FPT and derivative dFPT (no zero filling); nonparametric envelopes vs. parametric envelopes,

• Figure 8: Padé, nonderivative FPT and derivative dFPT (no zero filling); nonparametric envelopes vs. parametric components.

Throughout this study, no zero filling of the FIDs is made for the Padé-processed spectra (be they nonderivative or derivative). Moreover, the input data for the encoded FIDs are free from any other modification, e.g. apodization, filtering, etc., that usually accompany and plague other signal processors (notably FFT) in NMR spectroscopy [12,13,14]. In computations, convergence of Padé spectra (nonparametric, parametric) is monitored by systematically increasing the model order K. As a result, the converged model order $K=190$ is retained in all the present illustrations¹.

Fig. 1

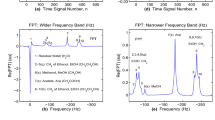
MRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Time signals or FIDs (a,d) of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonparametric Padé envelopes (b,c,e,f) with no zero filling of the FID. Wider (b,c) and narrower (e,f) frequency ranges. Spectral envelopes: abscissae in Hz (b,e) and ppm (c,f), ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

Fig. 2

MRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Time signals or FIDs (a,d) of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Fourier envelopes (b,c,e,f) with no zero filling of the FID. Wider (b,c) and narrower (e,f) frequency ranges. Spectral envelopes: abscissae in Hz (b,e) and ppm (c,f), ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

Fig. 3

MRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonparametric Padé envelopes with no zero filling in various modes (real, imaginary, their squares, magnitude). Wider (a,d,e) and narrower (b,c,f-h) frequency ranges. Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

3.2.1 Nonderivative shape estimators for total shape spectra

The encoded average time signal $\{c_n\}\ (0\le n\le N-1\,, N=512)$ is depicted in Fig. 1 (no phase correction) alongside the predictions by the nonparametric Padé. Therein, panels (a) and (d) show the real (Re) and imaginary (Im) parts of the FID, respectively. Both panels, (a) and (d), contain the encoding specifics. The quantity on the abscissae is usually time (given as integer increments of the sampling or dwell time $\tau$). Alternatively, the signal number n can be used on the abscissae, according to panels (a) and (d). As to the ordinates, it is customary to use arbitrary units (au) as on panels (a) and (d). It is seen from panels (a) and (d) that $\mathrm{Re}(c_n)$ is about an order of magnitude larger than $\mathrm{Im}(c_n).$

Both the real and imaginary parts of the FID are seen to be strictly positive definite, $\mathrm{Re}(c_n)>0$ and $\mathrm{Im}(c_n)>0$ for $0\le n\le N-1\, (N=512).$ As emphasized, water has not been suppressed in the course of encoding time signals nor in processing. For this reason, the FID exhibits predominantly water characteristics. It falls off rapidly with increased n for $0\le n\le 100$ in $\mathrm{Re}(c_n)$ (panel a) and for $0\le n\le 40$ in $\mathrm{Im}(c_n)$ (panel d).

However, a drastic slope change is seen on panel (a) for $\mathrm{Re}(c_n)$ at $n>100$ and thereafter there is a much slower decrease of the FID with augmentation of the time signal number n. If water were the only ingredient of the phantom, the decline of the FID on panel (a) would continue sharply also after $n=100.$ It is then the remaining substance in the phantom that causes the observed slope change of $\mathrm{Re}(c_n)$ around $n=100.$

As to $\mathrm{Im}(c_n)$ on panel (d), after a sharp decline for $0\le n\le 40,$ there is an oscillatory behavior at $n>40.$ Therein, two maxima are seen, first near $n=100$ and the second close to $n=250$ with the former being narrower and taller than the latter. Possibly, the maximum of $\mathrm{Im}(c_n)$ at $n=100$ could be associated with a particular ingredient in the phantom. The broader structure around $n=250$ has some undulations on its top that are seen to continue all the way to the end of the total acquisition time, $T=512$ ms.

To come closer to positive-definiteness of the real parts of the complex spectra, the encoded FIDs can be phase corrected. In the Padé-based reconstructions (unlike all the fitting techniques in signal processing), phase correcting the FID is optional. The so-called zero-order phase correction is done through multiplication of each time signal point $c_n$ by $\exp {(i\phi _0)}.$ Either a manual or an algorithmic phase $\phi _0$ can be selected. The former is user-subjective as it consists of plotting the real part of a complex envelope for different values of $\phi _0.$ Eventually, one of these values of $\phi _0$ is chosen because it appears visually to give the real part of the spectrum close to some positive-definite lineshape in the frequency window of interest.

An alternative is to compute $\phi _0$ in an objective way by finding an extremum (e.g. the minimum) of the real part $\mathrm{Re}$(FFT) of the complex Fourier spectrum, which is obtained from the originally encoded, phase-uncorrected FID data points. Presently, using the FIDs from panels (a) and (d) and computing the complex FFT spectrum, then identifying $\phi _0$ as $\min\{{\mathrm{Re(FFT)}}\},$ we find $\phi _0\approx 3.0185$ rad. From here and on, all the complex Fourier and Padé spectra are reconstructed from the zero-order phase corrected FID given by $\{c_n\exp {(i\phi _0)}\}\, (0\le n\le N-1).$ Of course, this phase correction is inconsequential for all magnitude spectra because these are the same for both $\{c_n\}$ and $\{c_n\exp {(i\phi _0)}\}$ since $\phi _0$ is constant for every $n\,(0\le n\le N-1).$ We use the FFT to find $\phi _0$ because the originally encoded FID and the FFT spectrum are directly retrievable from each other (exact information preservation).

The real parts $(\mathrm{Re}$(FPT)) of complex Padé envelopes are shown on panels (b), (c), (e) and (f). These graphs are intensities (ordinates in au) as a function of the sweep frequencies (abscissae). We display the abscissae in two different ways depending on the length of the frequency windows and the employed frequency units. The wider and narrower frequency intervals are on panels (b,c) and (e,f), respectively. Frequency in hertz (Hz) and parts per million (ppm) are on panels (b,e) and (c,f), respectively.

For a wider frequency window on panels (b) and (c), only the giant water peak (#1) is visible in the Padé envelope. The multi-component structure of the FID, so clearly manifested on e.g. $\mathrm{Re}(c_n)$ after $n=100$ on panel (a), does not influence at all the Padé envelopes on (b) and (c). The entire phantom’s content, other than water, may yield the constituent, partial Padé spectra, but they are completely buried in the long tail of the water resonance peak.

This occurs because of the magnitudes of the ordinates (0-600 au) for spectra on the left column within a wider frequency window, e.g. $\nu \in [-0.5,5.5]$ ppm on panel (c). Even though only the dominant water peak is visible on panels (b) and (c), for referencing and for an easier follow-up, we still list therein the chemical names of the expected hidden resonances of primary concern. For the same reason, besides water, also given are the numbers of all the anticipated relevant nine hidden resonances and their approximate positions.

The situation is very different for a narrower frequency interval on panels (e) and (f) outside the immediate region of the water peak. For example, the narrower frequency window on panel (f) is $\nu \in [0.5,4.0]$ ppm, which is to be compared to its wider counterpart, $\nu \in [-0.5,5.5]$ ppm on panel (c). The Padé envelope on the right column rides on an elevated baseline due to the long tail of the water resonance. On that baseline climbing in the upfield direction (increased frequencies by going from the right to the left), superimposed are several resonances, some clearly delineated, some partially or completely obscured. For example, both acetate, Ace, $\mathrm{CH}_3\mathrm{COOH}$ (#7) near 2.1 ppm and methanol, MeOH, $\mathrm{CH}_3\mathrm{OH}$ (#6) around 3.4 ppm are identifiable with certainty as the two isolated single resonances.

Moreover, the methyl $\mathrm{CH}_3$ (near 1.25 ppm) and the methylene $\mathrm{CH}_2$ (close to 3.5 ppm) of ethanol, EtOH, $\mathrm{CH}_3\mathrm{CH}_2\mathrm{OH},$ also show their fine structures on panel (f) for the Padé envelope, hinting at the expected triplet and quartet resonances, respectively. In particular, regarding the anticipated triplet in the $\mathrm{CH}_3$ group, the middle peak (#9) is observed. Also clearly visible are the tops of the two side peaks (##8,10). The remaining portions of these edge peaks (##8,10), however, are totally masked by the dominant resonance #9 in the $\mathrm{CH}_3$ group of ethanol. The tops of the two shouldered peaks (##8,10) appear to be close to the halved peak height of the middle peak #9. This is in the spirit of the exact peak height ratios 1:2:1 for the triplet in the methyl $\mathrm{CH}_3$ of ethanol. Nevertheless, a direct comparison on the level of peak heights would be meaningful only for the same peak widths of all the three resonances in the triplet from $\mathrm{CH}_3$ reconstructed by the nonparametric FPT. However, these widths are not available from the nonparametric FPT [1].

Regarding the expected quartet in the methylene $\mathrm{CH}_2$ group of ethanol, panel (f) for the Padé envelope shows that the upper parts of the two middle peaks (##3,4) of the same heights are clearly separated. However, the neighboring anticipated resonances (##2,5) in the $\mathrm{CH}_2$ group, as two crude shoulders, appear to be immersed into the steep sides of the peaks #3 and #4, respectively. The peak heights of the two shouldered resonances (##2,5) are about one third of the peak heights of the two middle resonances (##3,4), thus approximately satisfying the corresponding predicted exact ratios 1:3:3:1.

To make this observation quantitative within the peak heights, it would be necessary to have the same peak widths for all the four resonances in $\mathrm{CH}_2,$ retrieved by the FPT as a shape estimator which, however, provides no peak parameters [1]. Regarding panel (f), we do not discuss the hydroxyl OH group of ethanol. The reason is in the occurrence that the OH lineshape is lost under the giant water resonance located at 4.87 ppm. Moreover, the chemical shift of the OH group is outside of the shown frequency window [0.5,4.0] ppm in panel (f) of Fig. 1.

The outlined analysis of the estimation results from Fig. 1 is to be evaluated by taking into account the severe restrictions in the input data (short FID of 0.5KB, no zero filling, no water suppression, encoding at a relatively weak magnetic field $B_0=$1.5T). Due to these limitations of the studied FID, the computed nonparametric Padé envelopes from Fig. 1 should be considered as qualitative. Such a view refers especially to the qualitative reconstruction of the exact quantitative ratios 1:2:1 and 1:3:3:1 of the peak heights in the triplet and quartet resonances for methyl $\mathrm{CH}_3$ and methylene $\mathrm{CH}_2$ protons in ethanol, respectively. We say ’qualitative’ because the peak heights in the plotted envelopes are judged here only upon their visual appearance in the absence of any information about the peak widths.

Accurate checks of the peak heights as the measures for the proton abundance proportions 1:2:1 and 1:3:3:1 in the $\mathrm{CH}_3$ and $\mathrm{CH}_2$ groups of ethanol, respectively, is justified only for the resonances of the same width which is, however, not the case in Fig. 1. For unequal widths, peak areas should be used, as originally pointed out in the key study on ethanol from Ref. [15]. The issue of precise proton abundance or concentration is vital to data analysis in NMR spectroscopy and this will be addressed in a separate report analyzing simultaneously the FIDs with and without water suppression for the Proton Phantom [2, 3].

Fourier envelopes are displayed in Fig. 2 which is of the type of Fig. 1. Here too, similarly to the Padé spectra in Fig. 1, the employed FIDs have been phase-corrected, but no zero-filling was made. Thus, the same type of discussion on Fig. 1 can be taken over to Fig. 2. Still, there is a need to single out a few characteristics salient to the FFT. This is justified for the cases where certain clear discrepancies exist between the Fourier and Padé total shape spectra. The first such case emerging from comparing Figs. 1 and 2 points to the Padé higher resolving power than that in Fourier processing. This coheres with the well-documented general feature that Padé estimations of envelopes outperform those from Fourier processing when it comes to visual frequency resolution of spectral lines [4,5,6].

Additionally, several other insights can be illuminated. For instance, there is no clear indication in Fig. 2f about the existence of the separate peaks in the triplet and quartet resonances for the $\mathrm{CH}_3$ and $\mathrm{CH}_2$ groups of ethanol, respectively. Instead, only two rough structures (##8,10) are seen as being glued to each side of the prevailing middle peak $(\#9).$

Similarly, the expected quartet (##2-5) in the $\mathrm{CH}_2$ group of ethanol is seen to be in obscurity in Fig. 2f. Therein, the intensities of the two central resonances (##3,4) are crude and unequal. This is opposed to the corresponding doublet of sharp resonances (##3,4) of similar peak heights in the Padé envelope from Fig. 1f. Moreover, the peak heights of the prominent resonances are systematically lower in the FFT (Fig. 2) relative to those in FPT (Fig. 1).

For example, the peak heights (say h, in au) of these resonances, which are read off from $\mathrm{Re(FFT)}$ in Fig. 2 and $\mathrm{Re(FPT)}$ in Fig. 1, run as follows. Peak # 1: FFT $\sim$520 (FPT $\sim$560) $\{7.1\%\},$ # 3: FFT $\sim$0.72 (FPT $\sim$0.75) $\{4.0\%\},$ # 7: FFT $\sim$1.10 (FPT $\sim$1.25) $\{12.0\%\}$ and # 9: FFT $\sim$0.76 (FPT $\sim$0.78) $\{2.6\%\},$ where the relative errors, $100\%(h_{\mathrm{FPT}}-h_{\mathrm{FFT}})/h_{\mathrm{FPT}}$ are written in the parentheses for each of the peak pairs.

All told, there are some perceivable differences between the Padé (Fig. 1) and Fourier (Fig. 2) envelopes. Nevertheless, the found differences in the reconstructed envelopes are not dramatic and they stay within the realm of qualitative descriptions for both processors in nonparametric estimations. What is most needed in NMR spectroscopy, however, is retrieval of quantitative data, primarily the abundance of the resonating protons contributing to the observed resonance.

To try to achieve this goal on a sound theoretical basis, we exclude, from the onset, any attempt to fit the reconstructed spectral envelopes because such procedures invariably lead to nonunique quantification results. An alternative is to resort to parameter estimators. They would give the sought peak position, height, width and phase of every found resonance. For example, the parametric FPT is the method of choice due to its exact quantification capabilities with the underlying unique set of peak parameters and noise suppression advantages [4,5,6,7,8].

However, since the main emphasis in this article is on shape estimators, there is a possibility to use nonparametric derivative signal processing, which crosses the conventional borders in data analysis. Namely, for a longtime now, a sharp division existed between shape and parameter estimators. The former are limited to qualitative reconstructions of lineshape profiles alone. The latter are primarily devoted to component spectra with the prior determination of peak positions, widths, heights and phases of physical, genuine resonances. The dFPT in its role of a shape estimator can, in principle, perform both the qualitative (prediction of lineshapes) and quantitative (extraction of peak parameters) estimations. A realistic problem with encoded time signals that contain the known answer for spectral resonances is an ideal set up to find out how well derivative shape estimators can quantify.

In this regard, a remarkable success of the Padé derivative shape estimations has already been achieved in Ref. [1] for the Proton Phantom [2, 3] in the work on time signals encoded with partial suppression of water. After mastering this latter problem, one then wonders what else could possibly be accomplished with the same phantom? The present study raises the bar even higher. We want to find out whether the accomplishment from Ref. [1] could also be feasible for this phantom in conjunction with demanding time signals encoded without water suppression.

3.2.2 Intricacies of the magnitude mode of spectra

In Figs. 1 and 2, we displayed only the real parts $\mathrm{Re(FPT)}$ and $\mathrm{Re(FFT)}$ of Padé and Fourier complex spectra, respectively. However, in derivative estimations, the main theme of the present study, we shall deal with the magnitude spectral mode alone. For this reason, it is instructive to compare the real and magnitude modes of envelopes. This is the topic of Figs. 3 and 4 concerned with the Padé and Fourier estimations, respectively.

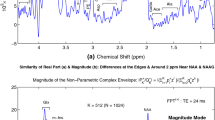
Figure 3 shows a wider and a narrower frequency interval, $\nu \in [-0.5,5.5]$ ppm and $\nu \in [0.5,4.0]$ ppm, on panels (a,d,e) and (b,c,f-h), respectively. For the wider window, the real $\mathrm{Re(FPT)}$ and imaginary $\mathrm{Im(FPT)}$ parts of the complex Padé envelope are on panels (a) and (e), respectively, whereas the magnitude mode $|\mathrm{FPT}|$ is on panel (d). As seen on panels (a) and (d), the lineshapes of both $\mathrm{Re(FPT)}$ and $|\mathrm{FPT}|$ are of a characteristic absorption-like profile.

Staying still with the wider sweep frequency band, $\nu \in [-0.5,5.5]$ ppm, panel (e) displays yet another spectral mode, the imaginary part $\mathrm{Im(FPT)}$ of the underlying complex spectrum. This appears as a typical dispersion-like mode. Pure absorption and dispersion profiles of spectral lineshapes cannot be obtained from encoded FIDs. This occurs because the encoded time signals contain some unknown phases that mix the absorption and dispersion modes when taking either the real or imaginary part of the given complex spectrum.

As is usual with a pure dispersion or dispersion-like profile, the lineshape of $\mathrm{Im(FPT)}$ on panel (e) appears as if the positive-definite $\mathrm{Re(FPT)}$ from panel (a) is cut through its central, vertical line with the left wing being inverted and pushed below the abscissa into the negative part of the plane. The intensities of the positive and negative “half” peaks of water in $\mathrm{Im(FPT)}$ can be read on panel (e) as being approximately 190 au and -230 au, respectively. By comparison, the water peak height in $\mathrm{Re(FPT)}$ from panel (a) is about 560.

However, what matters is not the resonance of water (# 1). Rather, the other nine resonances (##2-10) are of primary interest and they belong to ethanol, methanol and acetate. However, these are all opaque, when plotted on the same panels (a), (d) and (e) of Fig. 3 together with the overwhelming water peak. To make ethanol, methanol and acetate visible, the mentioned narrower window is needed, $\nu \in [0.5,4.0]$ ppm. The end (4 ppm) of this latter window is indicated by an encircled dot in the wider window $\nu \in [-0.5,5.5]$ ppm on panels (a) and (e) for $\mathrm{Re(FPT)}$ and $\mathrm{Im(FPT)}$, respectively. Therein, it is seen that at 4 ppm, $\mathrm{Im(FPT)}$ dominates (15.5 au) over $\mathrm{Re(FPT)}$ (0.29 au). The reason for such a large discrepancy between $\mathrm{Im(FPT)}$ and $\mathrm{Re(FPT)}$ is in their dispersion-like and absorption-like lineshapes, respectively. In particular, both wings of $\mathrm{Im(FPT)}$ are much more elevated from the abscissa than the tail of $\mathrm{Re(FPT)}.$ In fact, the lineshape of $\mathrm{Re(FPT)}$ is very near the abscissa even at 4.7 ppm as seen on panel (a).

For continuity, the encircled dots from panels (a) and (e) are also shown in the narrower window $\nu \in [0.5,4.0]$ ppm for $\mathrm{Re(FPT)}$ on panel (b) and for $\mathrm{Im(FPT)}$ on panel (f). Panel (b) for $\mathrm{Re(FPT)},$ which has already been seen and analyzed in Fig. 1f, indicates the clear presence of 7 out of 9 resonances. This is not the case at all on panel (f) for $\mathrm{Im(FPT)}.$ Therein, several barely notable stair-wise kinks of resonances $\#\#2-6$ are observed to ride on a high tail inherited from panel (e) for $\mathrm{Im(FPT)}.$ Moreover, the resonances ##8-10 in $\mathrm{Im(FPT)}$ appear merely as some bumps. Thus, despite zooming to the narrower band $\nu \in [0.5,4.0]$ ppm, the lineshape of $\mathrm{Im(FPT)}$ is unable to delineate most of the resonances (##2-6, 8-10). Only the dispersion-like profile of acetate (#7) can clearly be seen.

Both $\mathrm{Re(FPT)}$ and $\mathrm{Im(FPT)}$ enter into the magnitude mode $|\mathrm{FPT}|$ of the envelope by way of their squares $\{\mathrm{Re(FPT)}\}^2$ and $\{\mathrm{Im(FPT)}\}^2$ in the standard expression $|\mathrm{FPT}|=\sqrt{\{\mathrm{Re(FPT)}\}^2+\{\mathrm{Im(FPT)}\}^2}.$ Before displaying the magnitude spectral mode, we first show its two components, $\{\mathrm{Re(FPT)}\}^2$ and $\{\mathrm{Im(FPT)}\}^2.$ Expectedly, $\{\mathrm{Re(FPT)}\}^2$ and $\{\mathrm{Im(FPT)}\}^2$ from panels (c) and (g) exacerbate the difference between $\mathrm{Re(FPT)}$ and $\mathrm{Im(FPT)}$ seen on panels (b) and (f), respectively. Comparing first $\mathrm{Re(FPT)}$ and $\{\mathrm{Re(FPT)}\}^2,$ we see that the ordinates are the same on panels (b) and (c). Moreover, $\{\mathrm{Re(FPT)}\}^2$ preserves all the resonances from $\mathrm{Re(FPT)}.$ Further, the baseline is lower in $\{\mathrm{Re(FPT)}\}^2$ compared to that in $\mathrm{Re(FPT)}.$ Specifically, resonances in $\{\mathrm{Re(FPT)}\}^2$ are superimposed on a notably less steep background than in $\mathrm{Re(FPT)},$ implying a better SNR in the former relative to the latter.

By contrast, in $\{\mathrm{Im(FPT)}\}^2$ on panel (g), the ordinate appears to be much larger than that in $\mathrm{Im(FPT)}$ on panel (f). In such a circumstance, the bumps in $\mathrm{Im(FPT)}$ on panel (f) become significantly smoothed in $\{\mathrm{Im(FPT)}\}^2$ on panel (g). Replotting $\{\mathrm{Re(FPT)}\}^2$ on panel (g) alongside $\{\mathrm{Im(FPT)}\}^2,$ makes in evidence that the former (being practically embedded in the abscissa), is completely negligible relative to the latter.

Finally, after the comparative analyses of the real and imaginary parts of the complex Padé spectrum, we come to the magnitude mode $|\mathrm{FPT}|,$ the main concern in Fig. 3. Here too, we show the wider and narrower frequency bands $\nu \in [-0.5,5.5]$ ppm and $\nu \in [0.5,4.0]$ ppm on panels (d) and (h), respectively. For the wider window $\nu \in [-0.5,5.5]$ ppm, comparing panels (a) and (d), it is seen, as per theory, that the water peak in $|\mathrm{FPT|}$ is wider by about a factor of $\sqrt{3}$ than that in $\mathrm{Re(FPT)}.$ Moreover, these two panels show that the baseline is higher in $|\mathrm{FPT}|$ than in $\mathrm{Re(FPT)}.$

For the narrower frequency band $\nu \in [0.5,4.0]$ ppm on panel (h), $|\mathrm{FPT}|$ is basically a replica of $\mathrm{Im(FPT)}$ from panel (f). This is expected from panel (g) due to the dominance of $\{\mathrm{Im(FPT)}\}^2$ over $\{\mathrm{Re(FPT)}\}^2$ in computing $|\mathrm{FPT}|$ via $|\mathrm{FPT}|=\sqrt{\{\mathrm{Re(FPT)}\}^2+\{\mathrm{Im(FPT)}\}^2}.$ We see now that systematically going through panels (a-c,e-g), step by step, as a prelude to introducing $|\mathrm{FPT}|$ on panels (d) and (h), was necessary and instructive for the narrower frequency band $\nu \in [0.5,4.0]$ ppm of principal interest.

In retrospect, the said systematics help understand why $|\mathrm{FPT}|$ on panel (h) is so drastically different from $\mathrm{Re(FPT)}$ on panel (b). It is important to make this difference (and especially the reason behind it) apparent prior to passing to derivative estimation for which the magnitude spectral envelopes from Fig. 3h is the reference spectrum. Potential gains by derivative envelopes in the magnitude mode $|\mathrm{dFPT}|$ are judged by reference to the corresponding nonderivative magnitude total shape spectrum, $|\mathrm{FPT}|,$ from Fig. 3h.

Figure 4 deals with the same theme of different spectral modes as in Fig. 3, except that it is based on Fourier processing. In Fig. 4, for both the wider (panel a) and narrower (panel b) frequency windows, the features of $\mathrm{Re(FFT)}$ have already been addressed in Fig. 2. Further characteristics of Fourier envelopes are seen in the remaining plots for $\{\mathrm{Re(FFT)}\}^2$ (narrower window: panel c), $|\mathrm{FFT}|$ (wider window: panel d) as well as for $\mathrm{Im(FFT)}$ (wider window: panel e, narrower window: panel f), $\{\mathrm{Im(FFT)}\}^2$ (narrower window: panel g) and $|\mathrm{FFT}|$ (narrower window: panel h). As in Fig. 3g, we plot also $\{\mathrm{Re(FFT)}\}^2$ in Fig. 4g. Qualitatively, these Fourier characteristics on all the panels in Fig. 4 are much of the same type as their counterparts in Padé envelopes from Fig. 3. Of course, there are some quantitative differences between the two groups of envelopes from Figs. 3 and 4. However, since these differences are not of a very pronounced kind, there is no need to repeat the analysis from Fig. 3. Nevertheless, it is necessary to include Fig. 4 in the exposition. The reason is in observing that the reference spectra for both the subsequent Padé and Fourier derivative estimations have the comparable and wholly uninformative nonderivative magnitude envelopes from Figs. 3h and 4h, respectively.

Fig. 4

MRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without suppression at a 1.5T GE clinical scanner. Fourier envelopes with no zero filling in various modes (real, imaginary, their squares, magnitude). Wider (a,d,e) and narrower (b,c,f-h) frequency ranges. Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

3.2.3 Derivative shape estimators: Padé versus Fourier

Figures 5-8 are devoted to derivative signal processing. Thus, the dFPT faces the dFFT in Figs. 5 and 6. Regarding Figs. 7 and 8, they are concerned only with the dFPT. The two versions of the dFPT for envelopes (nonparametric and parametric) are compared with each other in Fig. 7. At last, the ultimately key information is sought in Fig. 8 by juxtaposing the envelopes (nonparametric dFPT) and components (parametric dFPT). As stated earlier, the magnitude mode of spectra (envelopes, components) is used in the present derivative estimations, similarly to Ref. [1]. This is convenient since the magnitude spectral mode is insensitive to an overall phase correction of lineshapes. In other words, the magnitude spectra are the same for the raw, encoded time signal, $\{c_n\},$ and its phased counterpart, $\{c_n\}\exp {(i\phi _0)}$ for any $\phi _0.$

On the other hand, the real parts $\mathrm{Re(FPT)}$ and $\mathrm{Re(FFT)}$ of the corresponding complex spectra are not of practical use for derivative estimations. The reason has been pointed out in our earlier studies on derivative signal processing [16,17,18,19,20]. Therein, it was found that more or less symmetric side lobes always accompany every resonance from the real and imaginary parts of the given complex derivative envelope. Such side lobes are wider than the width of the central resonance. They complicate extraction of the resonance peak parameters and this obstacle is even exacerbated for higher derivative orders.

Fig. 5

MRS and dMRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonderivative and derivative envelopes with no zero filling for two processors: Fourier (a,b,c,g,i) and nonparametric Padé (d,e,f,h,j). Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

Fig. 6

MRS and dMRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonderivative and derivative envelopes: Fourier with one zero filling (a,b,c,g,i) and nonparametric Padé with no zero filling (d,e,f,h,j). Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

Fig. 7

MRS and dMRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonderivative and derivative Padé envelopes with no zero filling: parametric (a,b,c,g,i) and nonparametric (d,e,f,h,j). Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

One of the salient features of the dFPT for augmented derivative order is in a systematic narrowing of the peak widths and in a simultaneous rising of the peak heights of all resonances [16,17,18]. This leads to clear separation of adjacent resonances and to flattening of the background. As a result, the signal to noise ratio (SNR) is systematically improved by increasing the derivative order in the dFPT.

Variations in resonance widths impact on this trend. Thus, for higher derivatives, a narrower resonance will become taller with a faster rate of its increased peak height for the augmented derivative order m than in the case of a wider resonance. Such a property implies that the mentioned wider side lobes will be suppressed and practically invisible next to the associated sharper central peak in the given resonance. Moreover, here too, the magnitude mode proves useful since therein side lobes are significantly diminished by combining the real and imaginary parts of the given complex spectrum. With side lobes gone in the magnitude spectral mode, the isolated thin central peak per each resonance can unambiguously be interpreted and quantified. This benefit and the phase-insensitiveness make the magnitude mode best suited for derivative estimations.

In nonderivative estimations, the magnitude mode is usually considered disadvantageous relative to an absorption spectrum, because the former is wider than the latter by a factor of $\sqrt{3}.$ However, this is a short-lived drawback as already the magnitude of the first derivative envelope has exactly the same width as the corresponding absorption mode spectrum. With higher derivatives, the magnitude envelope quickly becomes the spectral mode of choice. From here and on, only the magnitude mode is of relevance for derivative signal processing.

The nonderivative as well as derivative Padé and Fourier magnitude envelopes are set to compete with each other in Figs. 5 and 6. No zero filling of the FID is made for Padé processing in either of these two figures. In Fourier estimations, no zero-filing is made for Fig. 5, whereas the FID is zero-filled once for Fig. 6. In Figs. 5 and 6, the Fourier and Padé envelopes are on the left and right columns, respectively.

By reference to Figs. 1f (Padé) and 2f (Fourier), we saw that the real part of complex nonderivative spectral envelopes in the FFT and FPT exhibit several recognizable resonances. According to Figs. 3h and 4h, however, all the sought spectral features are almost completely absent from the magnitude modes of the same complex nonderivative spectral envelopes. This information is also repeated on panels (a) and (d) of Fig. 5. What is left therein are merely a few bumps near the main resonances even though the narrower frequency band is considered, outside the location (4.87 ppm) of the giant water peak. The reasons for such an occurrence have already been understood from the analyses of Figs. 3 (Padé) as well as 4 (Fourier) and need not be repeated here.

This opens more space for exposition on derivative estimations whose reconstructions are shown on panels (b,c,e-j). Throughout, the derivative orders are relatively low: $m=1$ (panel b: Fourier, e: Padé), $m=2$ (c: Fourier, f: Padé), $m=3$ (g: Fourier, h: Padé) and $m=4$ (i: Fourier, j: Padé). The nomenclature for Padé and Fourier derivative envelopes in the magnitude mode is $|\mathrm{D}_m\mathrm{FPT}|$ and $|\mathrm{D}_m\mathrm{FFT}|,$ respectively, where $\mathrm{D}_m$ is the $m\,$th order derivative operator with respect to the sweep linear frequency $\nu ,$ i.e. $\mathrm{D}_m=(\text {d}/\text {d}\nu )^m\, (m=1,2,3,...).$

Relative to the FFT (panel a), it is seen that the Fourier first derivative ($|\mathrm{D}_1\mathrm{FFT}|,$ panel b) and likewise the second derivative ($|\mathrm{D}_2\mathrm{FFT}|$, panel c) give no hope for the sought resolution improvement. Instead of a clearer delineation of e.g. ethanol and methanol lineshapes, for these resonances, Fourier yields merely some more pronounced wiggles at the expected chemical shifts of the sought resonances on panels (b) and (c). Even worse, the long tail from the water resonance peak survived in both $|\mathrm{D}_1\mathrm{FFT}|$ and $|\mathrm{D}_2\mathrm{FFT}|.$ This applies also to any higher derivative order m as exemplified on panels (g) and (i) in the vicinity of acetate for $m=3$ and $m=4,$ respectively. Whatever structures may hide in $|\mathrm{D}_m\mathrm{FFT}|$ for $m\ge 1,$ they are either completely embedded into the steep water peak tail or ride on it, barely visible above the highly elevated baseline.

In other words, the dFFT is seen to flagrantly fail in derivative estimations. The breakdown of the dFFT can be traced back to the action of the derivative operator $\mathrm{D}_m.$ This operator forces the dFFT to abandon processing the input time signal $\{c_n\}.$ Instead, the function $\{c_n (n\tau )^m\}$ is processed by the dFFT. The power function $(n\tau )^m,$ multiplying $\{c_n\},$ puts emphasis on higher time signal points n for a fixed derivative order m. It is here that the problem in the dFFT arises because the tails of encoded FIDs are dominated by noise. This means that the dFFT will eventually end up by processing essentially noise alone. Apodizations of the FIDs might somewhat mitigate the disastrous situation with the derivative Fourier processing, but modifications of encoded data do not constitute an acceptable basis for well-founded estimations.

Instead, an alternative way to proceed is to use the dFPT where the Padé spectrum $|\mathrm{D}_m\mathrm{FPT}|$ stems from processing the unmodified encoded FID, i.e. $\{c_n\}\, (0\le n\le N-1).$ The results of the dFPT are plotted on panels (e), (f), (h) and (j) for $m=1,2,3$ and 4, respectively. Comparing $|\mathrm{FPT}|$ (panel d) with $|\mathrm{D}_1\mathrm{FPT}|$ (panel e), it is seen that already the first Padé derivative shows a stunning improvement in resolution. For example, while the acetate, Ace, and the $\mathrm{CH}_3$ group of ethanol, EtOH, were buried in the elevated baseline of $|\mathrm{FPT}|$ on panel (d), they appear on panel (e) for $|\mathrm{D}_1\mathrm{FPT}|$ as sharply delineated peaks.

Further, the anticipated J-splitting via the triplet in the $\mathrm{CH}_3$ group of ethanol is accomplished in $|\mathrm{D}_1\mathrm{FPT}|$ on panel (e). Therein, the result $|\mathrm{D}_1\mathrm{FPT}|$ becomes all the more important by comparing it to the flawed Fourier counterpart $|\mathrm{D}_1\mathrm{FFT}|$ from panel (b). Regarding the baseline, it is considerably flattened in $|\mathrm{D}_1\mathrm{FPT}|$ (panel e) throughout a sizable range, 0.5-2.5 ppm. This is to be contrasted to the ever rising high baseline in $|\mathrm{D}_1\mathrm{FFT}|$ (panel b) at all frequencies. As to methanol and the $\mathrm{CH}_2$ group of ethanol, their dispersion-like profiles begin to emerge at approximately the correct locations. However, these lineshapes are completely uninterpretable as they are immersed in the still present, steep tail of the water peak.

Evidently, for methanol and the $\mathrm{CH}_2$ group of ethanol on panel (e), Padé derivatives higher than the first order should be tried. This brings us to panel (f) for Padé second derivative, $|\mathrm{D}_2\mathrm{FPT}|.$ Herein, several key advances are patently clear. The prerequisite for the overall improvement of $|\mathrm{D}_2\mathrm{FPT}|$ (panel f) over $|\mathrm{D}_1\mathrm{FPT}|$ (panel e) is in maximally flattening the baseline in the narrower window of primary focus, 0.5-4.25 ppm. This is manifested by massive suppression of the long tail of the water peak. The most striking effect of this occurrence in $|\mathrm{D}_2\mathrm{FPT}|$ is seen in the range 3.3-3.8 ppm, which hosts methanol and the $\mathrm{CH}_2$ group of ethanol. These resonances popped out with their unambiguous profiles, including the fully resolved J-coupled quartet of the $\mathrm{CH}_2$ group of ethanol.

Moreover, regarding the triplet of the $\mathrm{CH}_3$ group of ethanol around 1.25 ppm, there is also a significant resolution improvement when passing from $|\mathrm{D}_1\mathrm{FPT}|$ (panel e) to $|\mathrm{D}_2\mathrm{FPT}|$ (panel f). One can note here that the derivative operator $\mathrm{D}_2$ in $|\mathrm{D}_2\mathrm{FPT}|$ has symmetrized and straightened up all the three resonances in the ethanol $\mathrm{CH}_3$ group through suppression of the sidebands that occur in $|\mathrm{D}_1\mathrm{FPT}|$ on panel (e). Further, it can be seen on panel (f) that the bell-shaped Lorentzian profiles characterize all the nine peaks (##2-10) in the Padé second derivative magnitude spectrum. In $|\mathrm{D}_2\mathrm{FPT}|,$ there are two minor symmetric satellite resonances around the acetate peak (#7, $\sim$2.1 ppm). These satellites disappear from the next two derivatives, $|\mathrm{D}_3\mathrm{FPT}|$ (panel h) and $|\mathrm{D}_4\mathrm{FPT}|$ (panel j).

As can be seen from panels (e) and (f), already with $|\mathrm{D}_2\mathrm{FPT}|,$ the dFPT is extremely fast in finalizing the complete derivative processing for all the nine peaks (##2-10). Therefore, there is no need for considering higher derivatives. Nevertheless, panels (h) and (j) in Fig. 5 are plotted for $|\mathrm{D}_m\mathrm{FPT}|\, (m=3,4),$ but only within a small frequency band around acetate. The reason for this zooming is in a better visualization of the two satellite lineshapes on each side of the acetate resonance. Panels (h) and (j) testify that these satellite have not survived in $|\mathrm{D}_m\mathrm{FPT}|\, (m=3,4)$ on the scale of the displayed ordinates whose size is guided by the acetate peak height, i.e. by the tallest resonance in the shown window of interest, $\nu \in [0.5,4.25]\,\mathrm{ppm}.$

The side product of this fruitful experience is a definition of the stopping criterion in the dFPT with respect to increasing the derivative order m. The resulting rule of thumb is to stop progressing with derivative estimations at the lowest feasible derivative order $m=m_{\mathrm{min}}$ for which all the genuine (physical) resonances are completely resolved, preferably to the level of a minimal background baseline. Presently, as per panels (e) and (f) in Fig. 5, this criterion is remarkably well satisfied at $m_{\mathrm{min}}=2.$

Conventional processing by means of the FFT is almost invariably connected with zero filling of the analyzed FIDs. Thus far, we have not adhered to this practice. However, inspecting especially panels (g) and (i), zero-padding may improve somewhat the lineshapes of $|\mathrm{D}_3\mathrm{FFT}|$ and $|\mathrm{D}_4\mathrm{FFT}|,$ respectively. To check for this possibility, the encoded FID is zero filled once for Fourier processing in Fig. 6. Therein, as throughout this article, no zero filling is made for Padé processing.

In general, zero filling of time signals may impact adversely on lineshapes of Fourier spectral envelopes. The FFT processing of zero-filled FIDs is associated with a trigonometric interpolation in the frequency domain [21,22,23,24]. This interpolation may lead to distortions of lineshapes in the FFT through the appearance of some ripples and wiggles. Such deformations can be severe for weak physical resonances lying close to the background baseline. A particularly troublesome situation is with lineshape distortions occurring for frequencies at which the wiggle intensities (as spurious information) are comparable to the strengths of the genuine spectral structures, associated with the physical part of the FID (prior to its zero filling). This is actually the case almost at all frequencies (0.5-4.25 ppm) for the nonderivative Fourier envelope, $|\mathrm{FFT}|,$ on panel (a) in Fig. 6. Therein, the most obvious distortion is a nearly complete obliteration of the low-lying structures around 1.25 ppm, the location of the $\mathrm{CH}_3$ group of ethanol.

The wiggle artifacts due to zero filling of the FID are also seen in $|\mathrm{D}_1\mathrm{FFT}|$ from panel (b) of Fig. 6. They are most visible around acetate and the $\mathrm{CH}_3$ group of ethanol. It seems that there are no wiggles in $|\mathrm{D}_2\mathrm{FFT}|$ (panel c). Also, Fig. 6c shows that the appearance of $|\mathrm{D}_2\mathrm{FFT}|,$ with the FID zero-filled once, is slightly better than the associated second Fourier derivative in Fig. 5c with no zero filling. Moreover, panels (g) and (i) in Fig. 6 show that the wiggles are absent from $|\mathrm{D}_3\mathrm{FFT}|$ and $|\mathrm{D}_4\mathrm{FFT}|,$ respectively. Further, as per panels (g,i) of both Figs. 5 and 6, as expected, the acetate peaks in $|\mathrm{D}_3\mathrm{FFT}|$ and $|\mathrm{D}_4\mathrm{FFT}|$ are taller with zero-filled FID than with no zero filling of the time signal.

Overall, the presented nonderivative Fourier spectra employing the $|\mathrm{FFT}|$ with one zero filling (Fig. 6a) are worsened (via the appearance of densely packed ripples and wiggles) in relation to the retrieval by the $|\mathrm{FFT}|$ without zero filling (Fig. 5a). Further, Figs. 5b and 6b show that the Fourier first derivative, $|\mathrm{D}_1\mathrm{FFT}|,$ is also deteriorated by zero filling. In fact, according to panels (c), (g) and (i) in Figs. 5 and 6, merely the lineshapes of acetate in $|\mathrm{D}_m\mathrm{FFT}|\, (m=2,3,4)$ are somewhat improved when the encoded FID is zero filled once. As to ethanol and methanol, however, zero filling of the FID for Fourier derivative processing is not helpful at all.

Thus, comparing Figs. 5 and 6, it can be concluded that neither the nonderivative nor derivative Fourier processing is ameliorated by zero filling of the input time signal. Evidently, padding an FID with some virtual data points of zero amplitude (an alternative wording for zero-filling), cannot increase information since the encoded time signal already contains the entire information [24].

As mentioned, the FPT and dFPT with no zero filling are identical in Figs. 5 and 6. They are fully addressed in Fig. 5, so that there is no need for discussing them again in Fig. 6. Nevertheless, the Padé results from the FPT and dFPT appear in Fig. 6, but solely as the reference spectra to assist with the discussion of the Fourier reconstruction data. Moreover, as a guidance, it is sufficient to write the molecule numbers and acronyms for all the resonances $\#\#2-10$ only on the Padé panels in Fig. 6.

All told, Figs. 5 and 6 demonstrate irrespective of whether or not zero filling is used in the time domain, the dFFT does not represent a valid derivative estimator of spectral envelopes. This setback is caused by multiplication of the input FID, $\{c_n\},$ by the power function of time, $\{(n\tau )^m\},$ which predominantly weighs the noisy part of the encoded time signal. This worsens the SNR of the dFFT relative to the FFT. Another drawback is broadening of spectral widths of resonances in the dFFT with respect to the FFT. These awkward properties of the dFFT are orthogonal to the beneficial concept of derivative estimations.

In contradistinction, the dFPT (through its reliance exclusively on the intact encoded FID, $\{c_n\},$ without zero padding) is consistent in yielding the most dramatically enhanced performance in derivative estimations. This accomplishment is made possible by a steady trend of narrowing of resonance widths and concomitant increasing of the peak heights for rising derivative order m. This synergism leads to the emergence of very sharp Padé derivative resonances. As a net advantage, the overlapped resonances from the FPT become distinctly separated in the dFPT.

In turn, the background baseline is lowered in the dFPT relative to the FPT as clear from panels (d-f,h,j) in Figs. 5 and 6. Taken in concert, the massively suppressed background baselines, the strongly narrowed resonance widths and the sharply enhanced peak heights are responsible for simultaneously improved resolution and SNR in the dFPT. Unprecedentedly, this success of the dFPT is achieved despite using the time signals encoded without water suppression.

3.2.4 Derivative Padé processing of envelopes: nonparametric versus parametric estimations

Up to now, we dealt with shape estimations alone. This is the only type of signal processing (nonparametric estimations) that can be done by the FFT. In other words, the farthest the FFT can go is to predict the total shape spectra. No underlying components can be reconstructed solely by Fourier processing on its own (i.e. without fitting envelopes from the FFT in post-processing). Fitting techniques suffer from a number of drawbacks, including subjectivity through arbitrary imposition of various constraints. To reduce the components’ wide variations (due to nonuniqueness) of the employed adjustable parameters, different constraints are imposed that can modify the true fundamental frequencies and amplitudes $\{\nu _k,d_k\}$ by some undetermined amount.

However, due to over-fitting (over-modeling) and/or under-fitting (under-modeling), such constraints would always overestimate and/or underestimate some (if not all) the true values of the peak parameters. Under-fitting implies missing some of the physical (genuine) resonances in the guessed components from the used mathematical model. On the other hand, over-fitting means that some unphysical (spurious) resonances, foreign to the investigated sample, are included in the initialization of modeling. This invariably leads to underestimation and/or overestimation of concentrations of metabolites in clinical applications of signal processsing to in vivo MRS for which, therefore, the use of any fitting recipe could hardly be reliable.

Regarding signal processing by the FPT and dFPT, both shape and parameter estimations are possible within the realm of the versatile Padé methodologies. Here, envelope spectra can be computed both nonparametrically (shape estimations) and parametrically (solving the quantification problem). By contrast, component spectra, within the nonderivative FPT, can be reconstructed only by parameter estimations. This is the parametric FPT which sets and solves the quantification problem explicitly yielding the peak signatures (position, width, height and phase of every resonance). The situation is fundamentally different in derivative estimations, where the dFPT as a shape estimator (nonparametric processing) can quantify the envelopes (without fitting) and, thus, extract the mentioned peak parameters.

Therefore, the focus of the rest of the exposition shall be on derivative estimations by the dFPT alone in its two variants, parametric and nonparametric. Normally, once the quantification problem is solved by the parametric FPT, there is no reason to resort additionally to the parametric dFPT. However, the nonparametric FPT necessitates its derivatives if the natural goal is quantification without fitting total shape spectra. In such a case, to cross-validate the findings from the nonparametric dFPT, we use the parametric dFPT.

Analyzing the results from Fig. 5, we concluded that the second derivative in the nonparametric dFPT suffices for a successful ending of the spectral estimations. However, to accurately quantify by the nonparametric dFPT, reconstruction of components by shape estimations is needed.

This poses a key question, which runs as follows. How can we be sure that the single total shape spectrum $|\mathrm{D}_2\mathrm{FPT}|$ from Fig. 5f actually coincides with the sought sharp component spectral lineshapes reconstructed by the parametric dFPT?

In the case under study, there are nine component spectra to retrieve. This is precisely the reconstruction finding by the nonparametric dFPT via $|\mathrm{D}_2\mathrm{FPT}|$ in Fig. 5f. Thus, regarding at least the number of resonances, the nonparametric estimate $|\mathrm{D}_2\mathrm{FPT}|$ (Fig. 5f) is correct. Nevertheless, this is necessary, but not sufficient. The sufficient condition would be fulfilled if the difference between the nonparametric envelope $|\mathrm{D}_2\mathrm{FPT}|$ and the underlying (but unknown) components is negligible (e.g. buried in the background baseline).

The only way to find this out, within the same Padé estimation methodology, is to first solve the quantification problem by the parametric FPT. This would provide the nonderivative component spectra. These latter spectra should be subjected to the differentiation operator $\mathrm{D}_m$ to arrive at the second derivative in the parametric dFPT. Finally, the found second derivative components from the parametric dFPT should be compared with the nonparametric envelope $|\mathrm{D}_2\mathrm{FPT}|$ from the mere shape estimation in Fig. 5f.

To closely follow this roadmap for the ultimate cross-validation of the nonparametric dFPT, we first make a preparatory step, still staying within the realm of envelopes alone. This step consists of using the FPT and dFPT to compare their envelopes computed parametrically and nonparametrically. Figure 7 addresses this matter within the FPT and dFPT showing the parametric and nonparametric total shape spectra in these two versions of Padé processing. Finally, Fig. 8 compares the component spectra from the parametric FPT and dFPT with the corresponding envelopes from the nonparametric FPT and dFPT, respectively. In both the parametric and nonparametric Padé estimations in Figs. 7 and 8, the magnitude mode is adopted for all these spectra, reconstructed for the derivative orders $0\le m\le 4,$ using the model order $K=190,$ as in Figs. 5 and 6.

Of course, magnitude derivative spectra are not built from the magnitude nonderivative spectrum. Rather, derivative complex spectra are generated first by applying the differentiation operator $\mathrm{D}_m$ to the complex nonderivative spectrum. Subsequently, the absolute values are taken of the resulting complex derivative spectra and these are plotted as the lineshapes in the magnitude mode.

As announced, Fig. 7 (for the envelopes alone) compares the Padé predictions in the parametric (panels a-c,g,i) and nonparametric (panels d-f,h,j) estimations. Panels (a) and (d) depict the results of the nonderivative processing by the parametric and nonparametric FPT, respectively. Panels (b,c,e,f,g-j) are allocated to the dFPT dealing with the parametric (panels b,c,g,i) and nonparametric (panels e,f,h,j) versions. It is pleasing to observe that the nonparametric and parametric Padé envelopes are in complete harmony in Fig. 7, including the tiniest spectral structures. Crucially, this highest level of conformity between the two totally different computations within Padé processing encompasses not only the main nonderivative resonances (panels a,d), but also the displayed four derivatives, $|\mathrm{D}_1\mathrm{FPT}|$ (b,e), $|\mathrm{D}_2\mathrm{FPT}|$ (c,f), $|\mathrm{D}_3\mathrm{FPT}|$ (g,h) and $|\mathrm{D}_4\mathrm{FPT}|$ (i,j).

Such a benchmarking completely cross-validates the Padé nonparametric derivative estimations on the envelope level. The importance of the found accord between the parametric and nonparametric dFPT for total shape spectra surpasses a routine check of one computational algorithm against the other within Padé signal processing. This verification runs deeper because the parametric dFPT first computes the components and then sums them up to obtain an envelope, as detailed in e.g. Refs. [1, 16]. On the other hand, an envelope is computed by the nonparametric dFPT without recourse to components that are, in principle, foreign to shape estimations. Explicit quantification (with extraction of the numerical values of the peak positions, widths and heights of all the physical resonances) of the nonparametric dFPT envelope $|\mathrm{D}_2\mathrm{FPT}|$ (Fig. 7f), with the appropriate conversion to the absorptive mode of the nonderivative FPT, will be reported shortly.

In the first reported spectrum of ethanol from the key study by Arnold, Dharmatti and Packard [15], the measurements detected three resonances (one per group) for methyl $\mathrm{CH}_3,$ methelene $\mathrm{CH}_2$ and hydroxyl OH protons, satisfying the approximate peak area ratios 3:2:1, respectively, with no fine splitting. The subsequent, much improved measurements on ethanol by Arnold [25] observed the multiplets with fine splitting: a triplet in $\mathrm{CH}_3$ (1:2:1), a quartet in $\mathrm{CH}_2$ (1:3:3:1) and a singlet in OH. Here, in the methyl and methylene multiplets, the proportions in the parentheses represent the ratios of the peak areas extracted from the recorded spectrum [25]².

The most remarkable observation is that the upper panel of Fig. 6b from Ref. [25] for the measured spectrum of ethanol is in full accord with all seven resonances (3 for $\mathrm{CH}_3$ and 4 for $\mathrm{CH}_2$) from the theoretical prediction in the present Fig. 7f using the dFPT through its second derivative³. This implies that in the Proton Phantom [2, 3] under investigation, the presence of methanol and acetate does not alter the internal spectrum of ethanol. This occurs because of a presumably negligibly small J-coupling among protons from any group from ethanol with protons from methanol and acetate [1].

Important as it is, relying solely upon envelope benchmarking would not necessarily suffice. For this reason, it is critical to consider component shape spectra, as well. The unique component spectra obtained by the nonderivative parametric FPT can serve as the gold standard to be compared with derivative components reconstructed by other means. When the components from the nonderivative parametric FPT are subjected to the derivative operator $\mathrm{D}_m,$ the results would automatically be the gold standards for any derivative components. We will now use these gold standards for the derivative components from the parametric dFPT to test the reliability of the total shape spectra from the nonparametric dFPT.

At first, such unusual comparisons might seem not to make much sense as they intend to confront spectra of vastly different categories (a single spectrum for an envelope versus a number of spectra each representing a component of an envelope). The puzzle is resolved by the notion of ’sequential reconstructions’ which shall be introduced shortly.

In principle, all the component spectra are inherently contained in the nonparametric envelopes from the FPT and dFPT and yet they are invisible in panels (d-f) of Fig. 7. Likewise, the components of envelopes in the parametric FPT and dFPT are not visualized either on panels (a-c) of Fig. 7 for total shape spectra. Neither of these two statements implies that the opaque components cannot be made transparent. In the parametric envelopes from the FPT and dFPT, the envelopes are constructed from the prior reconstructions of all the components [1]. Hence, the components from the nonderivative and derivative parametric Padé estimations can be visualized directly by plotting the lineshape of each individual resonance, as shall be done in Fig. 8.

On the other hand, the situation is more complicated in the nonparametric FPT and dFPT because of the unavailability of the component spectra during the envelope computations. Nevertheless, we can rely upon some inferences to gain insight into the hidden components in nonparametrically computed Padé envelopes. Such inferences might be possible by checking the extent within which a nonparametric envelope might visually resemble the parametrically reconstructed components (the latter being taken as the reference spectra).

To proceed with this check, Fig. 8 is plotted for the component spectra (parametric FPT and dFPT) on panels (a-c,g,i) alongside the envelopes (nonparametric FPT and dFPT) on panels (d-f,h,j). Of prime importance are the reference component spectra on panel (a) stemming from nonderivative parametric FPT as the gold standard for component spectra retrieved by any other signal processor. However, already the first inspection of Fig. 8 necessitates an explanation for panels (a) and (d) before proceeding further with the analysis. Herein, looking merely at the ordinates, 0-0.65 au (left) and 0-20 au (right), it is clear that the sum of the components plotted on panel (a) cannot yield the nonparametric envelope from panel (d).

Before drawing Fig. 8a, we verified that, in the parametric nonderivative FPT, the sum of all the components (including the giant water resonance) is equal to the envelope in Fig. 7a. Moreover, as per Figs. 7a and 7d, the envelopes are the same in the nonderivative parametric and nonparametric FPT, respectively. The implication is that in Fig. 8d, the plotted nonparametric envelope (being identical to the parametric envelope) should coincide with the sum of the components from the parametric nonderivative FPT (Fig. 8a) at any chemical shift. That this is evidently not so indicates that something is missing in Fig. 8a. Indeed, to avoid clutter in Fig. 8a and, further, to devote the prime attention to ethanol, methanol and acetate, the uninformative, long tails of hugely elevated derivative components from the giant water resonance are left out altogether. However, by adding such ignored tails to the sum of the shown components from Fig. 8a, the nonparametric envelope from Fig. 8d would be found.

Fig. 8

MRS and dMRS for the standard Philips Phantom A [2, 3] with the main content: ethanol, methanol, acetate and water. Processing of time signals of short length $N=512$ encoded without water suppression at a 1.5T GE clinical scanner. Nonderivative and derivative fast Padé transform with no zero filling: parametric components (a,b,c,g,i) and nonparametric envelopes (d,e,f,h,j). Abscissae in ppm, ordinates in arbitrary units (au). For details, see the main text. (Color figure online)

Almost throughout Fig. 8, the red and blue curves are reserved for the parametric FPT and dFPT (components) and nonparametric FPT and dFPT (envelopes), respectively. The exception is Fig. 8a where, to highlight, the brown curves are used for the nine resonance component lineshapes $\#\#2-10$ (ethanol, methanol, acetate). It is seen on panel (a) of Fig. 8 that, in addition to the main, narrow resonances ($\#\#2-10$), the displayed frequency range [0.5,4.25] ppm houses also several wide peaks. The most pronounced among these broad resonances are located around the principal peaks due to ethanol, methanol and acetate. Such an occurrence is reminiscent of macromolecules present in spectra from in vivo proton MRS and it is usually assigned to proteins and lipids at 0.93, 1.24, 1.43, 2.04 and 3.00 ppm) [1, 26,27,28]. These macromolecules often reside near the main diagnostically relevant metabolites, e.g. lactate, Lac (1.33 ppm, methyl $\mathrm{CH}_3$), nitrogen acetyl aspartate, NAA (2.02 ppm, methyl $\mathrm{CH}_3$ and 2.47-2.66 ppm, methylene $\mathrm{CH}_2$), glutamate, Glu (2.04, 2.11 ppm, methylene $\mathrm{CH}_2$ and 2.35 ppm, methyl $\mathrm{CH}_3$), creatine, Cre (3.04 ppm, methylene $\mathrm{CH}_2$ and 3.93 ppm, methyl $\mathrm{CH}_3$), choline, Cho (3.22 ppm, methyl $\mathrm{CH}_3$ and 4.05 ppm, methylene $\mathrm{CH}_2$), etc.

Even though the broad peaks are pronounced in Fig. 8a, no assignment is given to them hereafter. This is justified by the circumstance that, together with the extended tails of water components, these broad resonances constitute the background on top of which the main resonances ($\#\#2-10$) are superimposed. The peak heights of broad and narrow resonances grow slower and faster, respectively by increasing the derivative order m. As a result, due to an increased dynamic range between the intensities (shown on the ordinates) of the wide and sharp peaks, these two groups of resonances cannot be simultaneously visualized on the same graph for a sufficiently high derivative order m. In other words, the derivative operator $\mathrm{D}_m$ in the dFPT is capable of making a distinct separation of resonances of narrow and broad widths, associated in e.g. in vivo MRS with the diagnostically relevant metabolites and macromolecules.

Figure 8 provides an example of such a clear separation of sharp and wide resonances for the component spectra from the parametric dFPT in its first two derivatives $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ (panel b) and $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (panel c). It can be observed in panel (b) that, to a large extent, all the broad tall peaks are diminished already in the first derivative $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}.$ Moreover, the remainders of broad taller peaks from their first huge reductions on panel (b), have disappeared in $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (panel c) throughout the chemical shift range [0.5, 4.25] ppm. The exception is the triple of minor bumps underneath the acetate resonance. However, such minuscule leftovers are entirely suppressed in the third and fourth derivatives $|\mathrm{D}_3\mathrm{FPT}|_{\mathrm{Comp}}$ (panel h) and $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Comp}}$ (panel i).

All told, by recapitulating the left column in Fig. 8, it is evident that the component nonderivative spectra $|\mathrm{FPT}|_{\mathrm{Comp}}$ on panel (a) are congested because they are filled with broad resonances. However, such spectra are seen on panel (b) for $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ to be sparser and eventually become free from wide resonances on panel (c) for $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}.$ It is in this way that the derivative estimations by the dFPT can significantly mitigate the so-called “spectral crowding” [29,30,31] which hampers particularly in vivo MRS.

This also implies that visual separation of sharp and broad peaks is accomplished by the dFPT in a sequential fashion. Sharper resonances are visualized first since their smaller widths dictate the size of the ordinates when plotting spectral intensities versus chemical shifts. Subsequently, broader resonances can be made transparent. For instance, one can gradually shrink the ordinates until wider resonances begin to pop out.

In any case, the occurrence that $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ on panel (c) is void of broad resonances should not be interpreted as if they were irretrievably lost. Quite the contrary, they are all present on panel (c), but remain hidden, i.e. invisible alongside much taller sharp resonances on the same plot. Besides the said ordinate shrinking, there is another way to make broader resonances apparent. It consists of subtracting the sharp resonance components from the components of all the resonance components (broad+sharp) from panel (c). This defines the second derivative broad components spectra ($|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Broad\, Comp}}$), which is void of sharp resonances ($|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Sharp\, Comp}}$), as the difference between all the component spectra ($|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{All\, Comp}}$) shown in panel (c) and those due to sharp resonances alone, i.e. $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Broad\, Comp}}=|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{All\, Comp}}-|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Sharp\, Comp}}.$ By construction, the profiles $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Broad\, Comp}}$ can alternatively be called ’the annulled sharp resonance component spectra’ [1].

As to the first derivative within the dFPT in Fig. 8, inspecting in parallel the components $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ (panel b) and the envelope $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}$ (panel e), significant differences are evident. The largest discrepancy is at the locations of the $\mathrm{CH}_2$ group of ethanol (##2-5) and methanol (#6). These resonances are closer to the water peak (#1, 4.87 ppm) and, therefore, they are heavily distorted with no recognizable absorption-like profiles. By contrast, acetate (#7) and the $\mathrm{CH}_3$ group of ethanol (##8-10) are farther away from the water resonance and, thus, less prone to deformations. As a result, the singlet of acetate and the triplet of the $\mathrm{CH}_3$ group of ethanol are well delineated and notably lifted above the baseline.

Nevertheless, the resonance intensities of the latter four peaks (##7-10) on panel (b) for $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ (components) and $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}$ (envelope) on panel (e) are different. They are lower in $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ than in $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}.$ This is caused by the small remainders of wider resonances near the peaks ##7-10 on panel (b) for $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}.$ Focusing on the band 1.1-2.2 ppm, these latter spectral leftovers are added to the lineshapes of the peaks ##7-10 (components) to produce the parametric lineshape $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}$ (envelope, Fig. 7b). The latter parametric total shape spectrum, in turn, coincides with the nonparametric envelope $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}$ according to panels (b) and (e) of Fig. 7. Figure 8e also shows the nonparametric envelope $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}.$ We can then say that the peak heights of resonances ##2-10 in Fig. 8e for envelope $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Tot}}$ (nonparametric dFPT) are higher than those in Fig. 8b for components $|\mathrm{D}_1\mathrm{FPT}|_{\mathrm{Comp}}$ (parametric dFPT) because the former as the total shape spectrum accounts for the leftovers of the invisible wider resonances.

Next, we pass to the second derivative spectra in Fig. 8 for components $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (panel c, parametric dFPT) ) and the total shape spectrum $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Tot}}$ (panel f, nonparametric dFPT). It is seen here that, near methanol (#6) as well as close to the $\mathrm{CH}_2$ and $\mathrm{CH}_3$ groups of ethanol, there is a remarkably high level of agreement between all the components $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (panel c) and the single envelope $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Tot}}$ (panel f). Specifically, the peak heights in the triplet $\mathrm{CH}_3$ group of ethanol (##8-10), the singlet of methanol (# 6) and the quartet $\mathrm{CH}_2$ group of ethanol (##2-5) in the parametric dFPT for the components (panel c) are the same as the corresponding resonances in the envelope from the nonparametric dFPT (panel f).

Merely the acetate resonance appears slightly taller on panel (f) for the envelope $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Tot}}$ than on panel (c) for the components $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}.$ The only reason for this is in the appearance of a small peak beneath the line profile of acetate. At last, this minor discrepancy is remedied by going to the third derivative of the parametric (components) and nonparametric (envelopes) in the dFPT. The pertinent illustrations are depicted on panels (g) and (h) for $|\mathrm{D}_3\mathrm{FPT}|_{\mathrm{Comp}}$ and $|\mathrm{D}_3\mathrm{FPT}|_{\mathrm{Tot}},$ respectively. Likewise, the fourth derivatives $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Comp}}$ and $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Tot}}$ in the parametric dFPT (panel i) and nonparametric dFPT (panel j), respectively, give the coincident peak heights of acetate. Although the third derivatives on panels (g) and (h) concluded the inquiry about the peak height of acetate, the fourth derivatives for this resonance on panels (i) and (j) are shown as an optional verification of stability of concordance between $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Comp}}$ (parametric dFPT) and $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Tot}}$ (nonparametric dFPT).

All told, regarding the peaks ##2-6 and ##8-10 in Fig. 8, it is indeed comforting to see the highest levels of agreement between the components $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (panel c, parametric dFPT) and the envelope $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Tot}}$ (panel f, nonparametric dFPT). This observation applies equally well to the acetate peak (#7) from $|\mathrm{D}_3\mathrm{FPT}|_{\mathrm{Comp}}$ (panel g) and $|\mathrm{D}_3\mathrm{FPT}|_{\mathrm{Tot}}$ (panel h) as well as from $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Comp}}$ (panel i) and $|\mathrm{D}_4\mathrm{FPT}|_{\mathrm{Tot}}$ (panel j). Resonances ##2-6 or ##8-10 are not displayed by $|\mathrm{D}_{3,4}\mathrm{FPT}|_{\mathrm{Comp}}$ nor $|\mathrm{D}_{3,4}\mathrm{FPT}|_{\mathrm{Tot}}.$ This was unnecessary since these resonances (methanol and the two groups of ethanol) already have their final lineshapes on panels (c) and (f) for $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Comp}}$ (parametric dFPT) and $|\mathrm{D}_2\mathrm{FPT}|_{\mathrm{Tot}},$ (nonparametric dFPT), respectively.

4 Conclusion

This study is in magnetic resonance spectroscopy, MRS, with a focus on separating the overlapped J-coupled multiplets from nuclear spin-spin interactions. Such separations can be heavily challenged by the stringent encoding conditions for the input data, the time signals, as is actually the case in the present work.

The stringency of measurements is reflected in the use of short time signals of length $N=512,$ encoded without water suppression at a clinical scanner of a low magnetic field strength (1.5T). The peculiar nature of such time signals is dictated by an overwhelming dominance of water relative to the remaining substance of the scanned sample. This is where the greatest challenge comes for any signal processor.

In data analysis through spectral reconstructions, we apply the standard, nonderivative fast Padé transform, FPT, and the derivative fast Padé transform, dFPT. Computations in the FPT and dFPT are carried out relying upon both the shape and parameter estimations. For comparisons, also reported are the corresponding reconstructions by the nonderivative and derivative fast Fourier transforms, FFT and dFFT, respectively. Among these estimators, the dFPT is our principal focus.

For the encoding object, we chose a spectroscopic phantom. This is the Philips Phantom A designed for proton MRS. It contains a number of known chemical compounds dissolved in demineralized water and filled in a plastic sphere. The main molecules in this polyethylene phantom are ethyl alcohol (ethanol), methyl alcohol (methanol) and acetic acid (acetate). Their principal nine resonances are the two singlets, one for methanol and one for acetate, as well as the multiplets from ethanol with the methyl triplet (1:2:1) and the methylene quartet (1:3:3:1). Herein, according to the Pascal triangle, the proportions written in the parentheses are the peak intensity ratios of the individual lines in the methyl triplet and the methylene quartet. We do not address the third ethanol group, the hydroxyl OH singlet because of its proximity to the dominant water resonance.

Our goal is full separation of all these nine resonances, down to the negligibly small background baseline, with the help of shape estimations alone by the dFPT. This task is aimed to be accomplished using the time signals encoded without water suppression. Moreover, the customary artificial devices (zero filling, apodization,...) are avoided altogether.

It turned out that Fourier derivative processing by the dFFT flagrantly failed to resolve the nine resonances with and without zero filling of the encoded time signals. Further, the dFFT is significantly deteriorated relative to the FFT, the nonderivative Fourier. The demise of the dFFT can readily be traced back to weighting the time signal with a time dependent power function which emphasizes the noisy part of encoding. This weight function worsens the resolution and signal-to-noise ratio, SNR, with augmentation of the derivative order.

On the other hand, the nonparametric dFPT, in its role of a shape estimator, accurately resolved all the expected nine resonances. Of special importance is to highlight the handling of the J-coupled resonances by the dFPT. This shape estimator, already with its second derivative, resolved these multiplets and determined their true peak area ratios. The resolving power and SNR are simultaneously improved by the dFPT on account of reconstructing narrower and taller resonances accompanied by a largely flattened background baseline. Remarkably, relative to Ref. [1], the same degree of success of the second derivative is achieved in the nonparametric dFPT applied to time signals encoded with and without water suppression.

As a consequence, water suppression in the course of encoding time signals might not be necessary, even though it is a standard nowadays. In fact, any difference found between reconstructions using time signals encoded with and without water suppression should be attributed to the uncertainties caused by the former measurement.

Derivative envelopes from the dFPT are dramatically improved with respect to the associated nonderivative spectra in the FPT. Such findings lend firm support to further elaboration and explorations within the dFPT. This boost refers to time signals with the known answers (synthesized data or data encoded from phantoms of the given content). It equally concerns data acquired from samples whose content is unknown or from patients for diagnostic purposes in medicine.

The mentioned goal of the present study is fully attained by reconstructing all the physical components by means of the nonderivative parametric FPT. The components from this parameter estimator represent the exact, unique solution of the quantification problem. They represent the gold standard, which can be used to cross-validate all other estimators. Among these, the most stunning is the outcome of the present analysis yielding the identical second derivatives in the dFPT from the nonparametric envelopes and parametric components. It is fascinating that this result is obtained against all the odds from encoding time signals without water suppression.

Conceptually, such a finding is far reaching since it promotes the nonparametric dFPT, as a shape estimator, to a pedestal of an exact solver of the quantification problem. In other words, the nonparametric FPT is automatically quantification-equipped without any fitting of spectral envelopes. This de facto erases the traditional division between the shape and parameter estimators.

There are at least two straight ways to extract the peak parameters from magnitude envelopes in shape estimations by the dFPT. As a first approximation, sole visual resolutions of resonances can be used. Herein, the magnitude mode of well resolved, separated, isolated Lorentzian resonances in the envelopes from the nonparametric dFPT yields their parameters in a streamlined fashion. This is done directly on the displayed screen merely by clicking the cursor at the needed places to read off, i.e. to extract the peak positions (chemical shifts), peak heights and the full widths and half maxima. The peak area is given by the product of the peak height and the full width at halved peak height. Then the proton abundance for the given resonance can be deduced using the found peak area. Alternatively, more precise peak parameters can be obtained by the same computer program which generates the mentioned Lorentzian line profiles. At last, the sought nonderivative peak parameters associated with absorptive Lorentzians are deduced using the found derivative peak parameters from reconstructions in the magnitude mode by means of the known conversion expressions [18].

In MRS for diagnostic medicine, extraction of metabolite concentrations is of vital importance. For this purpose the peak areas are the main prerequisite. The concentration of a metabolite is given by the product of the peak area and the predetermined concentration of a substance serving as a standard for calibration. Information on metabolite concentrations can greatly be improved by derivative magnetic resonance spectroscopy, dMRS, based on signal processing by the dFPT. This is a long awaited upgrade of nuclear magnetic resonance spectroscopy in the clinic.

Conventional MRS suffers from insufficient resolution, relatively low signal-to-noise ratio, macromolecular baselines, overlapping resonances, abundant J-unresolved multiplets, etc. The expounded derivative upgrade through the dFPT-based dMRS is deemed sufficiently powerful to simultaneously surmount all these most severe stumbling blocks of nuclear magnetic resonance spectroscopy in its versatile clinical applications.