Abstract
This review is on the fast Padé transform (FPT) for magnetic resonance spectroscopy (MRS). It is structured into two portions. Firstly, we give an introductory overview, emphasizing the conceptual framework. Secondly, we cover the specific, concrete accomplishments with detailed analysis and selected illustrations. Key advances have been achieved by the FPT for MRS in the most recent period. These consist of direct applications of the FPT to time signals encoded by in vivo MRS from tumorous tissues. We focus on the robust and comprehensive Padé-based solutions for the thorniest problems (overlapping resonances, resolution, noise) that have hampered progress of in vivo MRS for a very long time. Both parametric and non-parametric aspects of signal processing in the FPT are thoroughly covered. The FPT, as a parameter estimator, solves exactly the quantification problem by reconstructing the positions, widths, heights and phases of all the physical peaks. This gives the component lineshapes of all the true resonances. The non-parametric FPT, as a shape estimator, has thus far predicted the total lineshapes alone without separating the individual components. Finally, we discuss the most recent advances in signal processing for MRS using the derivative fast Padé transform (dFPT). This upgrade is of utmost importance, as the dFPT exactly reconstructs all the peak parameters for every physical resonance by carrying out estimation of total shape spectra alone. The derivative operator within the dFPT narrows the linewidths and concomitantly enhances the peak heights, while simultaneously suppressing noise. This leads to separation of overlapping peaks, resolution improvement and noise reduction. Far-reaching ramifications of such an achievement within MRS are highlighted with the prospects for further explorations to the benefit particularly of cancer medicine.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Basic sciences and their versatile applications are like two sides of the same coin. Vastly varying intertwining is also present in basic sciences themselves, where theory and measurements are the twin roads to the same goal of deciphering the laws of nature. For instance, the Radon transform from 1913 in pure mathematics laid the foundation of computed tomography (CT) in the 1960s and 1970s (Cormack, Hounsfield) to dramatically improve radiographs from X-ray diagnostics in medicine. As an even more striking example, discovery of nuclear magnetic resonance (NMR) from the 1940s and 1950s in physics (Rabi, Bloch, ...) changed analytical chemistry forever in decrypting the structure of proteins and other big molecules (Ernst, Wutrich, ...). It revolutionized medicine, as well, through magnetic resonance spectroscopy (MRS) beginning already in the 1950s (Odenblad, ...) and magnetic resonance imaging (MRI) from the 1970s (Lauturber, Mansfield) for diagnostics, surgery and post-therapeutic follow-up. Lauturber (chemist) and Mansfield (physicist) shared the 2003 Nobel Prize on Medicine and Physiology for their contribution to the development of MRI.
“All science is interdisciplinary” declared Lauturber in his Nobel lecture. Therein, remarkably, he stated that the key ingredient to MRI (locating resonating nuclei) has been benefited from his experience with two-center molecular integrals in chemistry. Nothing is more practical than theory, the truth which passed the test of time.
Going beyond MRI is the task of MRS. Anatomical/morphological findings from MRI are complemented by MRS which informs on the chemical content of the scanned tissue. The method of determining the molecular composition of the examined sample by NMR spectroscopy in analytical chemistry has enriched medical diagnostics through MRS. This pathway of bonding basic research on MRS by way of mathematics, physics and chemistry with the applications in early cancer detection is the topic of the present review. To have a specific focus, we review the most recent progress within the last five years in mathematical optimization of MRS by advanced signal processing based upon quantum physics and chemistry, the fast Padé transform (FPT). With the stated goal, the selected problem areas of major public health concern in cancer medicine will be addressed while dealing with four human organs: brain, breast, prostate and ovary.
2 Theory
2.1 Mathematics of the fast Padé transform
Here, we will give a synopsis of the salient mathematics of the FPT as it applies to MRS. For full in-depth presentations, the reader is referred to Refs. [1, 2]. In a hypothetical situation with ideal encoding conditions (no magnetic field inhomogeneities, perfect magnet shimming, complete water and/or lipid suppression, etc.), the waveforms of the measured MRS time signals are expected to be sums of complex-valued attenuated exponentials:
Here, \(\tau \) is the sampling rate (with the continuous time t discretized as \(t=n\tau \)), K is the model order as well as the total number of non-degenerate resonances, and N is the full signal length. Quantities \(\omega _k\) and \(d_k\) are the complex fundamental frequency and amplitude, respectively. Alongside K, the pairs \(\omega _k\) and \(d_k\) are the nodal constituents of each signal point \(c_n.\) It is the quantum-mechanical origin of MRS that dictates the mathematical form (2.1) for the time signal \(c_n,\) which can equivalently be conceived as an auto-correlation function.
All the inaccuracies arising from any MRS encoding would be disguised through various uncertainties (deterministic, systematic, stochastic, etc.). Under this circumstance, the task of a reliable spectral analyzer is to recover the true spectral parameters \(\{K,\omega _k,d_k\}\) from a given noisy time signal. Importantly, the form (2.1) is not limited to time signals originating from phenomena of a purely quantum-mechanical nature. Quite the contrary, the stability of any system (classical or quantum) can be steadily maintained only through some internal motions of the constituents, as most frequently manifested by damped oscillations (2.1). Moreover, the dynamics of all systems are mathematically described by some differential or difference equations. For example, (2.1) is the exact solution of the \(K\,\)th degree difference equation with constant coefficients. The uniqueness of (2.1) for the latter difference equation is guaranteed by the prescribed initial conditions that determine all the amplitudes \(\{d_k\}\, (1\le k\le K).\) Time signal (2.1) is linear in \(d_k\) and non-linear in \(\omega _k.\) In spectral analysis, neither the \(K\,\)th degree difference equation nor the K boundary conditions is known. All that is known are the signal points \(\{c_n\}\, (0\le n\le N-1)\) for the fixed values of \(\tau \) and magnetic field strength \(B_0.\) This is what makes quantification an inverse problem: reconstruction of the unknown parametrization \(\{K,\omega _k,d_k\}\, (1\le k\le K)\) of the given time signal \(\{c_n\}\, (0\le n\le N-1),\) also called free induction decay (FID), satisfying relationship (2.1). In (2.1), it is the non-linearity in \(\omega _k\) which causes the non-uniqueness of all the fitting procedures for retrieval of spectral parameters. By contrast, for equidistantly sampled time signal points (2.1), the FPT uniquely solves the non-linear quantification problem by pure linear algebra (which is also computationally the most stable). To this end, a single system of linear equations needs to be solved. Even the only remaining non-linear operation in the parametric FPT, i.e. polynomial rooting, is solved by a linear operation through the equivalent eigenvalue problem of the extremely sparse Hessenberg (or companion) matrix [1].
2.2 Generation of a spectrum
A spectrum in the FPT is generated from the encoded, raw, unedited time signal \(\{c_n\}\, (0\le n\le N-1)\) by transformation into the equivalent frequency domain. In MRS, this spectrum is a reflection of the reaction or response of the tissue to external perturbations by the radio-frequency (RF) pulse as well as by the static and gradient magnetic fields. This phenomenon is described by the response function, also known as the Green function. The running (or sweep) angular frequency \(\omega \) is the independent variable of the spectrum, in terms of which the linear frequency \(\nu \) is given by \(\nu =\omega /(2\pi ).\) This frequency \(\omega \) is embedded in the harmonic variable \(z=\exp {(i\tau \omega )}.\) For a given MRS time signal, \(\{c_n\},\) of total length N, the exact, complex-valued spectrum is represented by the following sum in harmonic variable \(z^{-1}=\exp {(-i\tau \omega )}:\)
The system’s response function is this truncated Maclaurin series, or equivalently, the finite-ranked Green function, which is also called the discrete, finite \(z-\)transform [1]. In the FPT, there are two equivalent spectra denoted by \(G^\pm _K(z^{\pm 1})\) corresponding to the same input response function (2.2). This depends on whether the variable z or its reciprocal \(z^{-1}\) is employed:
where
Here, \(r_+=1, r_-=0, z^{+1}\equiv z\) with \(\{p^\pm _r\}\) and \(\{q^\pm _s\}\) being the expansion coefficients of the polynomials \(P^\pm _K(z^{\pm 1})\) and \(Q^\pm _K(z^{\pm 1}),\) respectively. In the \(\mathrm{FPT}^{(+)},\) the numerator polynomial \(P^+_K(z)\) does not have a free, constant term, i.e. \(p^+_0=0.\) When the polynomial degree K is the same for both \(P^\pm _K(z^{\pm 1})\) and \(Q^\pm _K(z^{\pm 1}),\) the spectra from Eq. (2.3) are termed the diagonal forms of the \(\mathrm{FPT}^{(\pm )}.\) These Padé spectra approximate the input Green function \(G_N(z^{-1})\) from Eq. (2.2) through \(G_N(z^{-1})\approx G^\pm _K(z^{\pm 1}).\) From this latter relationship, the ensuing two quotients \(P^+_K/Q^+_K\) and \(P^-_K/Q^-_K\) are both uniquely extracted using Eq. (2.2). Prior to convergence, for the same truncation level of the input time signal \(\{c_n\}\) from (2.1), the polynomial ratios \(P^+_K/Q^+_K\) and \(P^-_K/Q^-_K\) are different. However, upon achieving convergence, the complex spectra \(P^+_K/Q^+_K\) and \(P^-_K/Q^-_K\) are always the same, implying equivalence of the \(\mathrm{FPT}^{(+)}\) and \(\mathrm{FPT}^{(-)}.\) Regarding envelopes, this is one aspect of the utility of the intrinsic cross-validation within the FPT.
2.3 Non-parametric signal processing
Non-parametric analysis via the \(\mathrm{FPT}^{(\pm )}\) is performed as soon as the expansion coefficients \(\{p^\pm _r\}\) and \(\{q^\pm _s\}\) of the polynomials \(P^\pm _K(z^{\pm 1})\) and \(Q^\pm _K(z^{\pm 1}),\) respectively, are generated from the time signal \(\{c_n\}.\) If all the phases \(\varphi ^\pm _k\) of the signal amplitudes (i.e. the FID intensities) \(d_k=|d_k|\exp {(i\varphi ^\pm _k)}\) are equal to zero, \(\varphi ^\pm _k=0\, (1\le k\le K),\) then the real and imaginary parts \(\mathrm{Re}(P^\pm _K/Q^\pm _K)\) and \(\mathrm{Im}(P^\pm _K/Q^\pm _K)\) would be of purely absorptive and dispersive spectral lineshapes, respectively. However, the phases of encoded MRS time signals are non-zero due to various reasons, e.g. delay between the excitation and the beginning of data acquisition, mechanical oscillations of the receiver coil, static magnetic field inhomogeneity, etc. Thus, for encoded FIDs, there will invariably be a mixture of absorption and dispersion lineshapes in \(\mathrm{Re}(P^\pm _K/Q^\pm _K)\) and \(\mathrm{Im}(P^\pm _K/Q^\pm _K).\)
2.3.1 Partitioning of spectral envelopes
The explicit expressions in e.g. the \(\mathrm{FPT}^{(+)}\) for \(\mathrm{Re}(P^+_K/Q^+_K)\) and \(\mathrm{Im}(P^+_K/Q^+_K)\) can be analytically extracted from \(P^+_K/Q^+_K\) and the results are the so-called “partitioned envelopes”. They are given by:
where,
The corresponding partitioned spectra in the \(\mathrm{FPT}^{(-)}\) are obtained directly from Eqs. (2.5)–(2.9) by changing the superscript \((+)\) into \((-).\) The compartmentalization of \(\mathrm{Re}(P^+_K/Q^+_K)\) and \(\mathrm{Im}(P^+_K/Q^+_K)\) is a redistribution of the full interference between the two partitioned envelopes. Therefore, a smaller interference effect in \(\{A^+_K, B^+_K\}\) and \(\{C^+_K, D^+_K\}\), when each of these spectra is viewed separately, can unfold certain hidden resonances in compound peaks. Note, that the complex-valued spectrum \(P^+_K/Q^+_K\) is itself sectioned into two spectra. One is the moving average (MA) given by \(P^+_K\) and the other is auto-regression (AR) provided by \(Q^+_K.\) Their combination is the auto-regressive moving average (ARMA), which is equivalent to the \(\mathrm{FPT}^{(+)}.\) The MA and AR sections describe zeros and poles of the ARMA process. Thus, alternatively, the MA and AR models are called the “All zeros” and “All poles” models [1]. In fact, it is the reciprocal \(1/Q^+_K\) that is a spectrum with all the poles, whereas \(P^+_K\) yields the valleys in between spectral peaks. Overall, we see that the partitioned spectra \(\{A^+_K, B^+_K\}\) and \(\{C^+_K, D^+_K\}\) from Eqs. (2.6)–(2.9) are various direct and mixed products of the real and imaginary parts of the MA and AR pathways in the ARMA process, i.e. in the \(\mathrm{FPT}^{(+)}.\) We emphasize that \(\mathrm{Re}(P^+_K/Q^+_K)\) and \(\mathrm{Im}(P^+_K/Q^+_K)\) are not decomposed arbitrarily into \(\{A^+_K, B^+_K\}\) and \(\{C^+_K, D^+_K\},\) respectively. Rather, each of these decompositions is unique [3, 4], being motivated by the AR and MA compartments of the ARMA process.
2.3.2 Derivatives of spectral envelopes
Very recently [5,6,7], we proposed yet another way to separate overlapping peaks by Padé-based non-parametric estimations. This is called the derivative fast Padé transform (dFPT). It consists of applying the derivative operator \(D^m_\nu =(\text {d}/\text {d}\nu )^m\) of order \(m>0\) to the given non-parametrically generated total shape spectrum from the conventional FPT \((m=0)\):
We re-emphasize that in (2.11), the input envelopes \(P^\pm _K(z^{\pm 1})/Q^\pm _K(z^{\pm 1})\) from the customary FPT are computed non-parametrically. It is for this reason that the output envelopes \(D^m_\nu (P^\pm _K(z^{\pm 1})/Q^\pm _K(z^{\pm 1}))\) from (2.11) are called the “non-parametric” derivative envelopes in the dFPT. Advantageously, however, as demonstrated in Ref. [6], the non-parametric derivative envelopes \(D^m_\nu (P^\pm _K(z^{\pm 1})/Q^\pm _K(z^{\pm 1}))\) in (2.11) provide the exact peak parameters (positions, widths, heights and phases) of all the physical resonances. This has been benchmarked in Ref. [7] by the complete agreement between the lineshapes of the non-parametric derivative envelopes and the derivative component spectra in the dFPT. The latter spectra refer to the lineshapes obtained by applying the derivative operator \(D^m_\nu \) to the component spectra constructed after solving the quantification problem in the parametric FPT. The relationships between the two sets of the peak parameters, one for the dFPT \((m>0)\) and the other for the FPT \((m=0),\) derived in Ref. [6], permit reconstruction of the exact peak positions, widths, heights and phases of every physical resonance by relying exclusively upon the non-parametric derivative envelopes. The spectra in the dFPT are given by the analytical expressions and, moreover, the derivative operator \(D^m_\nu \) never applies to the input time signals. This is the reason for enhanced signal-to-noise-ratio (SNR) in the dFPT. Overall, the dFPT simultaneously increases resolution (through separation of all the overlapped peaks) and suppresses noise. By contrast, in the derivative fast Fourier transform (dFFT), the operator \(D^m_\nu \) is applied directly to exp(\(-2\pi i\nu t\)) and this via \(t^{m}c(t)\) dramatically decreases SNR in the already poorly resolved Fourier envelopes [5,6,7]. These features will also be illuminated and elaborated in the detailed upcoming analyses of the specific results from reconstructions.
2.4 Parametric signal processing
Quantification is achieved via polynomial rooting within the \(\mathrm{FPT}^{(\pm )}.\) The roots of the characteristic equations of the polynomials in the numerators \((P^\pm _K)\) and denominators \((Q^\pm _K)\) provide the respective zeros and poles of the Padé spectra \(P^\pm _K/Q^\pm _K.\) The fundamental or eigen-frequencies \(\{\omega ^\pm _k\}\) contained in the set \(\{c_n\}\) are reconstructed via the roots of equations \(Q^\pm _K(z^{\pm 1})=0.\) The amplitudes \(\{d^\pm _k\}\) are generated through the analytical expression for the Cauchy residues of the Padé quotients \(P^\pm _K(z^{\pm 1})/Q^\pm _K(z^{\pm 1})\) taken at the \(k\,\)th pole \(z^{\pm 1}_k\equiv z^{\pm }_k.\) By definition, the poles \(z^{\pm 1}_k\) satisfy the corresponding characteristic equations, \(Q^\pm _K(z^\pm _k)=0\) [8, 9]. It has been systematically verified that the computed total shape complex spectra \(P^\pm _K/Q^\pm _K\) are identical for parametric and non-parametric signal processing in the \(\mathrm{FPT}^{(\pm )}.\) This is yet another cross-validation within the FPT. This cross-check retrospectively validates the reconstructed frequencies and amplitudes. In such a way, the entire quantification process is corroborated and benchmarked.
Finding the zeros of polynomials is a non-linear operation. For high degree polynomials, computation can be both excessively long and insufficiently accurate. This difficulty can be avoided altogether by solving the equivalent linear problem of highly efficient and numerically exact computation of the eigenvalues of the corresponding Hessenberg matrix. This latter square matrix (also called the companion matrix) is extremely sparse, having the polynomial coefficients on its first row, unity on the main diagonal and zero elsewhere. This sparseness permits large matrix dimension (\(K\times K\)) and, thus, enables fast and accurate generation of a huge size of the set of the eigenvalues that are equal to the roots of the \(K\,\)th degree polynomials \(Q^\pm _K.\) As to the amplitudes \(\{d^\pm _k\},\) their analytical Cauchy residue formulae \(d^\pm _k=P^\pm _K(z^{\pm 1}_k)/Q^{\pm \prime }_K(z^{\pm 1}_k)\) with \(Q^{\pm \prime }_K(z^{\pm 1})=(\text {d}/\text {d}z^{\pm 1})Q^{\pm }_K(z^{\pm 1})\) are especially appealing. Here, the amplitude \(d^+_k\) is built from the single pole \(z_k\) and, similarly, \(d^-_k\) depends only on \(z^{-1}_k.\) By contrast, in some other parametric methods, e.g. the linear predictor (LP) and the Hankel-Lanczos singular value decomposition (HLSVD), the \(k\,\)th amplitude relies upon the entire set of all the reconstructed poles (spurious and genuine). As such, the presence of the spurious poles reconstructed by the LP and HLSVD unavoidably undermines the accuracy of the amplitudes. Namely, instead of the analytically available Padé-based amplitudes, the LP and HLSVD solve the second system of linear equations obtained by inserting all the retrieved frequencies \(\{\omega _k\}\) (true and false) into (2.1).
2.5 Signal-noise separation and Froissart doublets
After the stabilized value of degree K has been attained in the \(\mathrm{FPT}^{(\pm )}\) insofar as the computation is continued, all the subsequently reconstructed terms from the canonical representations of the Padé numerators \(P^\pm _K\) and denominator \(Q^\pm _K\) in the ratios \(P^\pm _K/Q^\pm _K\) cancel each other [10, 11]. The stability of the total shape complex spectra is thereby achieved as indicated by:
As mentioned, the amplitudes are the Cauchy residues of the quotients \(P^\pm _{K}(z^{\pm 1})/Q^\pm _{K}(z^{\pm 1}),\) and they have two equivalent analytical expressions:
Here, \(z^{\pm }_{k,P}\) and \(z^{\pm }_{k,Q}\) are the roots of the characteristics equations of the numerator and denominator polynomials \(P^\pm _{K}(z^{\pm }_{k,P})=0\) and \(Q^\pm _{K}(z^{\pm }_{k,Q})=0,\) respectively, where \(z^{\pm }_{k,P}\equiv z^{\pm 1}_{k,P}\) and \(z^{\pm }_{k,Q}\equiv z^{\pm 1}_{k,Q}.\) The subscripts P and Q in \(z^{\pm }_{k,P}\) and \(z^{\pm }_{k,Q}\) are used to distinguish the solution of the characteristic equations for the numerator and denominator polynomials \(P^\pm _K\) and \(Q^\pm _K,\) respectively. As per either of the two formulae in Eq. (2.13), whenever \(z^{\pm }_{k,Q}=z^{\pm }_{k,P},\) it follows:
Zeros and poles in the FPT spectrum draw their meaning from the fact that \(P^\pm _K/Q^\pm _K\) are meromorphic functions. Functions whose poles are their only singularities are called meromorphic functions. Alternatively, pole-zero coincidence can be viewed as cancellation between resonances (peaks due to \(1/Q^\pm _K\)) and anti-resonances (dips due to \(P^\pm _K\)).
Besides pole-zero coincidences and zero or near-zero amplitudes, the “stability test” further helps identify unphysical resonances. The \(\mathrm{FPT}^{(\pm )}\) always generate two distinct sets of resonances. With the smallest change in the partial signal length N / M with \(M > 1\) (i.e. by truncating the total signal length and preserving the same bandwidth), one set of resonances emerges as stable, while the other is unstable. Stable and unstable resonances are characterized as genuine and spurious, respectively. With any change in e.g. partial signal length or varying the level of external noise, spurious resonances characteristically exhibit fluctuations of their spectral parameters in \(P^\pm _K\) and \(Q^\pm _K.\) Moreover, albeit showing stochastic behavior, spurious resonances also display a certain order in these fluctuations (“order in chaos” so to speak). The reason is that polynomials \(P^\pm _K\) and \(Q^\pm _K\) are actually inter-dependent, since the expansion coefficients \(\{p^\pm _r\}\) of \(P^\pm _K\) are deduced by convolution of time signal points with the expansion coefficients \(\{q^\pm _s\}\) of \(Q^\pm _K\) [1, 2]. This latter folding is dictated by the defining relations \(P^\pm _K(z^{\pm 1})=G_N(z^{-1})Q^\pm _K(z^{\pm 1})\) where the latter product is treated as a convolution. Consequently, there is an association of \(P^\pm _K\) with \(Q^\pm _K\) and this generates a correlation between the spurious subsets of the complete set of the reconstructed harmonics \(\{z^\pm _{k,P}\}\) and \(\{z^\pm _{k,Q}\}.\) In other words, the spuriousness generated by \(P^\pm _K\) is correlated to the like spuriousness produced by \(Q^\pm _K.\) Therefore, the noise-like distributions are limited since there is a connection between spuriousness stemming from \(P^\pm _K\) and \(Q^\pm _K.\) The natural limit of the dominant population of spurious poles and zeros is the circumference (\(|z|=1\)) of the unit circle in the complex plane of the harmonic variable \(z=\exp {(i\tau \omega )}.\) It is precisely on the same circumference \(|z|=1\) that all the Fourier non-damped harmonics (unattenuated sinusoids) \(\{\exp {(-2\pi ik/N)}\}\, (0\le k\le N-1)\) from the fast Fourier transform (FFT) are located and, thus, maximally mixed with noise. The convergence radii of the \(\mathrm{FPT}^{(+)}\) and \(\mathrm{FPT}^{(-)}\) are also separated by this limit, having their initially defined convergence regions inside (\(|z|<1\)) and outside (\(|z|>1\)) the unit circle, respectively. However, by way of the Cauchy analytical continuation, the \(\mathrm{FPT}^{(+)}\) and \(\mathrm{FPT}^{(-)}\) also converge in their complementary regions \(|z|>1\) and \(|z|<1,\) respectively. The \(\mathrm{FPT}^{(+)}\) testifies to the power of this concept, as it is an analytical continuator by design, working with the variable z at \(|z|<1\) precisely where the input Green function \(G_N(z^{-1})\) from (2.2) diverges. The correlation between \(P^\pm _K\) and \(Q^\pm _K\) is the most apparent for spurious resonances for which the roots \(z^{\pm }_{k,Q}\) and \(z^{\pm }_{k,P}\) coincide via the pole-zero equality, \(z^{\pm }_{k,Q}=z^{\pm }_{k,P}\) or near equality, \(z^{\pm }_{k,Q}\approx z^{\pm }_{k,P}.\) A fluctuating pole is linked to a fluctuating zero, and they collapse into each other via \(z^{\pm }_{k,Q}=z^{\pm }_{k,P},\) such that in the quotients \(P^\pm _K/P^\pm _K\) all the unstable spectral structures are canceled out. Pole-zero coincidence produces the pole-zero cancellation. This is evident in the canonical form of the Padé spectra:
These cancellations take place on the rhs of Eq. (2.15) through:
whenever
Thus, pole-zero coincidence (2.17), as a signature of Froissart doublets, leads to pole-zero cancellation (2.16). Through these cancellations, all the spurious resonances are removed from the spectra (2.15) in the \(\mathrm{FPT}^{(\pm )}.\) It is in this way that noise is, de facto, eliminated from the \(\mathrm{FPT}^{(\pm )}.\) Thus, through signal-noise-separation (SNS), all the genuine resonances (\(z^\pm _{k,Q}\ne z^\pm _{k,P}\)) are retained, while all the spurious resonances (\(z^\pm _{k,Q}=z^\pm _{k,P}\) or \(z^\pm _{k,Q}\approx z^\pm _{k,P}\)) are annihilated, i.e. automatically removed from the spectral envelopes. Therefore, we see that noise suppression is inherent in the \(\mathrm{FPT}^{(\pm )}\) due to the polynomial ratios for the spectra [1, 2].
2.6 Interference effects in the “Usual” and “Ersatz” spectra
To generate pure absorptive Lorentzians, the interference effects can be externally suppressed. This is achieved by setting the reconstructed phases \(\varphi ^\pm _k\) to zero “by hand”, \(\varphi ^\pm _k=0\, (1\le k\le K)\) in the final list of the reconstructed spectral parameters. The so-called “Ersatz” (E) total shape spectra are thereby produced in the \(\mathrm{FPT}^{(\pm )}.\) As an example, we can illustrate this in the \(\mathrm{FPT}^{(+)}\) where the Heaviside partial fraction decomposition of the Ersatz total shape spectrum is given by:
On the other hand, the “Usual” (U) Heaviside partial fraction decomposition of the spectrum in the \(\mathrm{FPT}^{(+)}\) reads as:
The corresponding component spectra inherent in Eqs. (2.18) and (2.19) are extracted via:
By replacing \(d^+_k\equiv |d^+_k|\exp {(i\varphi ^+_k)}\) with \(|d^+_k|\) in Eqs. (2.18) and (2.20), the real parts of the total and component shape spectra of the Ersatz form \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{E}\) and \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{E}_k\) from Eqs. (2.18) and (2.20), respectively, are produced in the purely absorption modes. Their associated counterparts in the Usual form \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}\) and \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}_k\) from Eqs. (2.19) and (2.21), respectively, contain absorption as well as dispersion modes of the spectral lineshape.
It should be emphasized that peak heights are particularly important in MRS. In the fitting techniques, these peak heights are estimated from graphs for the Fourier amplitudes versus chemical shifts in the given FFT envelope. However, the FPT does not rely at all upon visual display of spectral lineshapes to determine the peak heights, since the Padé envelope and component lineshapes are provided by their mathematical, closed formulae that explicitly contain the peak heights as the analytical expressions. Peak height is defined as the value of the component spectrum taken at the position where the running linear frequency \(\nu \) matches the reconstructed chemical shift \(\mathrm{Re}(\nu ^+_{k,Q})\) of the considered \(k\,\)th resonance. In the \(\mathrm{FPT}^{(+)},\) we set \(\omega =\mathrm{Re}(\omega ^+_{k,Q})\) or \(\nu =\mathrm{Re}(\nu ^+_{k,Q})\) in (2.20) and (2.21) to derive the peak heights, \(\{H^+_k\}^\mathrm{E}\) and \(\{H^+_k\}^\mathrm{U},\) of the \(k\,\)th resonance in the Ersatz and Usual component spectra, respectively. The results are the following analytical expressions for the \(k\,\)th peak amplitude in the Ersatz spectrum:
and in the Usual spectrum
In Eqs. (2.22) and (2.23), the quantity \(T^{\star +}_{2,k}\) is the \(T^\star _2\) relaxation time due to spin-spin interactions for the k th resonance retrieved by the \(\mathrm{FPT}^{(+)}\) as:
The Ersatz peak height is the ratio of the amplitude \(|d^+_k|\) and the factor \(1-\exp {(-\tau /T^{\star +}_{2,k})},\) which can equivalently by written as \(1-\exp {(-\tau \mathrm{Im}(\omega ^+_{k,Q})})\). The peak “height” \(\{H^+_k\}^\mathrm{U}\) from (2.23) in the Usual component spectrum is complex-valued, due to the amplitude \(d^+_k\) therein being complex. Consequently, \(\{H^+_k\}^\mathrm{U}\) is the peak height amplitude which, like every other amplitude, can be real- or complex-valued. The Usual peak height magnitude \(|\{H^+_k\}^\mathrm{U}|\) is equal to the the Ersatz peak height \(\{H^+_k\}^\mathrm{E}.\) The Ersatz peak height \(\{H^+_k\}^\mathrm{E}\) is real-valued, and differs from \(\mathrm{Re}\{H^+_k\}^\mathrm{U}\) according to:
and
where the relation \(d^+_k = |d^+_k|\mathrm{e}^{i\varphi ^+_k}\) is used. The mathematical background of the FPT is expounded in this section with the aim of facilitating the analyses of the applications of this signal processor to several problem areas in cancer diagnostics, as detailed in the subsequent sections of this review.
3 Aspects of magnetic resonance of relevance to medicine
3.1 Magnetic resonance phenomena as non-ionizing radiation
In medical diagnostics, NMR spectroscopy from physics and chemistry is renamed as MRS. This is done for the reason of diverting the potential fear that some patients might have when hearing the word “nuclear”. Such an issue belongs merely to nomenclature, since MRS invokes no nuclear radiation whatsoever. It is only the nuclear spin states that are excited by RF pulses during scanning of the examined tissue. The RF part of the electromagnetic field spectrum is of weak intensity, which is below the excitation and ionization thresholds of the tissue molecules, thus resulting in no damage. Moreover, in magnetic resonance (MR) scans of patients, none of the three simultaneously applied external fields (RF, static and gradient magnetic fields) has the strength to ionize atoms or molecules in the tissue. It is for this reason that MRS, as well as MRI, are in the category of non-ionizing radiations. Such a feature is essential for medical diagnostics because it allows the patients to undergo repeated monitoring by MRS and MRI examinations within short time intervals, if needed. This is contrasted to ionizing radiations, the most well-known example of which in medical diagnostics are CT and positron emission tomography-computerized tomography (PET-CT). Ionizing radiation used in X-ray-based diagnostics and radiotherapy (by gamma-rays, electrons, atomic nuclei) can disrupt the internal structure of molecules and cells from the tissue by causing changes that might yield irreparable damages, undergo mutations and/or induce secondary cancers.
3.2 Hardware upgrades versus advanced signal processing
In the past, much attention has been paid to improvements of hardware for MR phenomena used in medical diagnostics by increasing the magnetic field strength \(B_0\) above 1.5T. However, this has not improved the overall status of MRS in the clinic. Despite being known for decades now, this MR modality is still awaiting to become a part of the standard diagnostic armamentarium in everyday medical diagnostics. The prime reason for such a drawback is the lack of the necessary coupling of the enhanced hardware capabilities (stronger magnets) to more reliable data analyses than those based upon the FFT, and various equivocal fitting techniques.
The present article reviews the recent efforts aimed at bridging this gap by focusing upon the fast Padé transform, FPT [1, 2, 12]. We address the limitations of the FFT that impacted adversely on the expected progress in MRS. The multi-faceted parametric and non-parametric estimations of spectral envelopes (total shape spectra), and their components are thoroughly presented within the FPT. A veritable Padé-conceived paradigm shift has been revealed by achieving super high-resolution with lower magnetic fields, and short data acquisition times. This tandem accomplishment is poised to make MRS both clinically reliable and cost-effective. Clinical reliability is conveyed by trustworthy reconstructions of diagnostically relevant quantifiers of metabolite molecules (abundance/concentrations, chemical shifts, relaxation times, etc). Cost-effectiveness is guaranteed by significant reductions of the total examination time for the patient and, hence, much better turnout in the hospital management.
It is hoped that such favorable circumstances will establish the long anticipated standing of MRS as the modality capable of revolutionizing not only diagnostics (particularly in cancer medicine), but also screening, as well as image-guided surgery and post-operative surveillance of patients [12, 13].
3.3 Inter-disciplinarity in MRS
By judiciously intertwining mathematics, physics, chemistry and biology, research in MRS offers the possibilities to improve tumor diagnostics. The fate and overall success of all MR phenomena in medicine ultimately depends on the way in which the data are evaluated and interpreted by the theoretically designed spectral analysis. No measurement itself, irrespective of the extent of hardware innovations, and perfecting the sequence encoding, can provide decision-making information without accurate and reliable signal processing. This has also been emphasized by the U.S. National Cancer Institute [13] stating that more robust signal processing is vital for achieving the fuller potential of MRS. Without such signal processing, the diagnostic accuracy of MRS is insufficient to meet the stringent clinical requirements.
The encoded MRS data are time signals and, hence, their evaluation is within the realm of the interdisciplinary research area known as signal processing. Mathematical optimization helps realize the potential of MRS in a more individualized approach for patients afflicted with and/or at risk of malignancy, a clinical approach termed “personalized cancer medicine” (PCM). We continue this review with a conceptual framework, which provides the needed connection between the sought clinical information and the necessary mathematical optimization [1, 2].
With this background, the specific, concrete results are presented for Padé-optimized MRS relevant to four problem areas of major public health concerns within cancer diagnostics: prostate cancer, breast cancer, primary brain tumors and ovarian cancer. We mainly focus on the period from 2013 onward, succinctly including earlier salient results. A very brief overview of each of these four areas is first provided, noting their profound importance for timely and accurate diagnosis, which can impact upon patients’ survival and quality of life. The relevant results are reviewed as the process of benchmarking the FPT, which includes handling noise-corrupted MRS time signals. This key problem is addressed first in the controlled setting with noise-corrupted synthesized MRS time signals, and subsequently explored using the corresponding encoded data from a standard test phantom head on a clinical MR scanner. Such a review sets the stage for the detailed investigations on the applications of the FPT to MRS time signals encoded in vivo on 1.5 and 3T MR scanners. This paves the road for practical clinical implementation within the themes of the mentioned four problem areas.
Firstly, it should be emphasized that MRI provides high spatial resolution, such that morphology, i.e. anatomy is very well visualized. This is why MRI has become one of the key modalities for all aspects of cancer diagnostics and care. Whereas MRI is generally extremely sensitive in detecting abnormalities, its specificity is often low, such that many benign lesions are not confidently distinguished from malignancy. However, through MRS, the status of the metabolic features of tissues or organs can be assessed, and this enables proceeding beyond morphology. Thus, MRS can potentially tap into the biochemical changes associated with the cancer processes, i.e. the “hallmarks of cancer” [14, 15]. This is particularly critical for early tumor detection, because the malignant changes on the molecular level invariably precede their observable manifestations on anatomical images of the scanned tissue.
In most applications within the MRS literature, single-voxel encoding is used. However, for the purpose of volumetric coverage of the scanned tissue, multiple-voxels are employed to combine MRI and MRS into magnetic resonance spectroscopic imaging (MRSI). This is alternatively called chemical shift imaging (CSI), because of the explicit reference to resonating frequencies called chemical shifts. Whenever there is a suspicion that a single voxel is not sufficiently representative of the status of the imaged tissue, MRSI is used for the corresponding volumetric coverage [16].
3.4 Complementing MRI: improved specificity by way of MRS
Analytical chemistry, resonance physics and the mathematics of time signal processing are all intertwined in MRS, and this requires team work of basic science researchers and clinicians. Radiologists were quick to accept MRI and use it routinely as a standard diagnostic modality. The reason is twofold. Firstly, MRI scans can be viewed directly on the screen much in the same familiar way as the conventionally observed X-ray images. Secondly, there is an added value consisting of superiority of soft tissue discrimination by MRI over that of CT, implying timelier diagnosis, e.g. earlier tumor detection.
No similar automatic service with the necessary diagnostic certainty is provided by MRS without the mentioned interdisciplinary approach. The most important extra bonus of MRS relative to MRI is differential diagnosis by the former modality. Namely, some lesions that are non-specific on MRI could be differentiated by MRS. For instance, brain tumor and benign lesions might appear similar on conventional MRI. However, these two lesions could often be distinguished by MRS on the basis on the level of two diagnostically important metabolites, N-acetyl aspartate (NAA) and choline (Cho). Neuronal activity, reflected by NAA molecules, is generally decreased in tumors. On the other hand, Cho as a marker of cell membrane turnover, is usually elevated in tumors. This biochemical information obtained in a non-invasive way, by mathematical/physical/chemical analyses of the scanned tissue, translates into the specificity improvement of MRS with respect to MRI. An illustration of this type was previously given in the first figure of Ref. [17], through juxtaposing the information from MRI and MRS. Therein, two hyperlucent brain lesions appeared quite alike, and thus gave no hint as to which of them might be associated with a pathology. However, MRS from that figure helped tell the difference between the two lesions. The analysis of the MRS data suggested that one lesion was benign, whereas the other could be tumorous according to the decreased NAA and increased Cho levels. The latter lesion was then diagnosed to be a low-grade astrocytoma, as confirmed histopathologically.
3.5 Strategic issues for MRS within metabolomics and translational research
Molecular imaging can vitally contribute to offering patients with cancer (or at high cancer risk), the best possible care [18,19,20]. Molecular imaging is becoming well-recognized “as a tool that has the capacity to improve every facet of cancer care. The growing demands among physicians, patients and society for personalized care are increasing the importance of molecular imaging and shaping the development of biomedical imaging as a whole” [15] (p. 182). As such, PCM could particularly benefit from metabolomic (i.e. metabolic) profiles provided by MRS-based molecular imaging. However, this potential is yet to be realized in full [18, 21]. Metabolomics refers to the global quantitative assessment of endogenous metabolites within a biological system or tissue. Therein, MRS, MRSI and mass spectrometry are the main methods used, either individually or grouped as a metabolomic profile, to detect metabolites in cells, tissues and biofluids. A multi-faceted potential exists for metabolomics within oncology, especially for timely detection of cancer, as well as a predictive and pharmacodynamic marker of drug effect. When used as a translational research tool, metabolomics can provide a link among basic science research, the laboratory and the clinic. This is the case because metabolic and molecular imaging, such as MRS, MRSI and positron emission tomography (PET), enable the identification of metabolic markers non-invasively in vivo [22]. However, while PET is focused on one selected metabolite at a time, MRS and MRSI deal simultaneously with many metabolites by identifying the whole spectrum of diagnostically informative molecules.
Notwithstanding the many important achievements, the diagnostic accuracy of MRS is still generally insufficient for the stringent requirements of PCM [18, 21, 23, 24]. One of the prime reasons for this situation is reliance upon ambiguous fitting techniques for analyzing MRS data (encoded time signals and/or computed Fourier-based spectra).
3.6 The need for accurate molecular imaging through MR modalities
Among the most pressing needs within the framework of PCM is early assessment of response to therapy and, in particular, to identify non-responders in order to facilitate timelier therapeutic decision-making. Target definition for radiation therapy (RT) with identification of tumor regions that should receive a boost is another important area for molecular imaging through MR, as is pre-surgical staging. The potential of MRS and MRSI to distinguish high from low risk malignancy (notably prostate cancer) and to do so non-invasively and without exposure to ionizing radiation has also been underscored. Further, post-therapeutic monitoring as well as intensive surveillance of persons at high risk for certain cancers are critical areas for molecular imaging through MR.
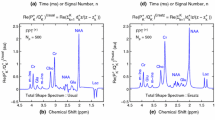
Regarding all these issues for PCM, the diagnostic biochemical information, i.e. the concentrations of metabolites contained within the tissue, as reconstructed through MRS, needs to be of the highest possible accuracy. However, within MRS, none of the sought clinical information is conventionally obtainable in a direct way from the encoded data. From an MR scanner, a time signal, as a multi-modal heavily-packed exponentially damped function is customarily encoded. This is shown on panels (a) and (b) of Fig. 1 related to MRS for normal brain tissue. Such time signals are not amenable to direct, clinically meaningful interpretation. The measured data must be mathematically processed in either the time or frequency domain in order to extract the clinically useful information. For example, the encoded data from the time domain can be transformed into the frequency domain giving the spectral representation, which exhibits a number of relatively discernable peaks called resonances as seen on panels (c) and (d) in Fig. 1 for the predictions by the FFT and FPT, respectively. The estimated areas of the components of these peaks in Fig. 1(d) are associated with metabolite concentrations (abundance), that constitute the clinically most interpretable information.
Already the introductory Fig. 1 embodies the salient features of the main story behind MRS. It tells us, on panels (a) and (b), what is being encoded (uninterpretable real and imaginary parts of the time signal) as well as, on panel (d), what is being sought (metabolite concentrations via spectral components). Further, on panels (c) and (d), the key finding of signal processing of the encoded data is conveyed through a comparison of the FFT and FPT. Therein, the FFT from Fig. 1(c) has only the total shape spectrum with no components, thus failing to autonomously fulfill the main task of MRS: reconstruction of diagnostically pivotal metabolite concentrations. In sharp contrast, as per panel (d) of Fig. 1, the FPT simultaneously yields the envelopes and component shape spectra, thus providing metabolite concentrations en route. This gives little doubt as to which of these two processors is more suitable for MRS.
Conceptual illustration of normal brain MRS data showing what is measured and what is computed. The real and imaginary parts of the encoded (or synthesized) time signal are shown on (a) and (b), respectively. Neither can be directly interpreted. These time signals are used to compute the spectral lineshapes displayed on (c) and (d) where a number of the reconstructed peaks (resonances) are assigned to the known molecules (metabolites). Under the best of circumstances, the FFT can give only total shape spectra or envelopes, such as the lineshape on (c). The FPT, however, yields both the total and component shape spectra on (d). The component shape shape are of greatest clinical relevance as they can provide the diagnostically informative metabolite concentrations. The acronym au stands for arbitrary units (color online)
3.7 Limitations of the fast Fourier transform for encoded MRS data
The customary approach has been to directly process all the encoded MRS signals by the FFT, a low-resolution, non-parametric processor. Subsequently, the obtained set of resonances in the Fourier envelope is often fitted by a given mathematical model to assess the number of components of each peak. Such a non-unique approach inevitably guesses the number of components and, thus, gives biased, inaccurate estimates of metabolite concentrations. Illustrations of the limited information gleaned from several Fourier envelopes are presented later in this review. The quantification problem in MRS is extremely difficult, being “mathematically ill-conditioned”, meaning that even small external perturbations (noise and noise-like impurities or corruptions) yield large variations of the sought solution. This leads to large variances of the extracted concentrations of metabolites. None of “the FFT plus fitting” techniques is capable of unambiguously solving the problem of spectral analysis which is alternatively called quantification. However, the main reason for resorting to MRS and MRSI is to solve the quantification problem, which amounts to reconstructing a set of spectral parameters (for each physical resonance), comprised of chemical shifts, relaxation times, oscillation amplitudes and phases, from which the metabolite concentrations are computed. For example, chemical shifts inform about the molecular compounds in which the MR-sensitive nuclei (e.g. protons in proton MRS) are bound in the scanned tissue. Albeit difficult, the quantification problem is nevertheless solvable and the unique solution does exist. The challenge is to find the correct mathematical method which surmounts the ill-conditioning of the MRS quantification problem.
3.8 A more advanced method by the fast Padé transform
The existing estimators in the MRS literature were unable to simultaneously as well as unequivocally solve the quantification problem, and separate the physical (signal) from unphysical (noise) part of the examined FID. Therefore, we sought an alternative method which, from the onset, would be more suitable for time signal processing than the Fourier analysis. An important reason for being utterly inadequate in representing functions with peaks is the lack of a polar structure of the FFT. A polar representation of a function is built from a set of its pole-type singularities at which the function acquires its maximum values. Polynomial representations, such as the FFT, are conventionally applicable to smooth, periodic functions without singularities. If a function is polar, then the FFT requires a huge number of sampled data points of that function to mimic its poles by exhaustive interference effects. Such a demanding severity on the size of MRS data makes the FFT ineffective, as it involves exceedingly long acquisition time. In practical terms regarding MRS, long scanning time is required, which is a burden to the patient as well as to health care resources. Hence the lack of cost-effectiveness of the FFT-based MRS.
A distinct advantage is provided by rational polynomials as a quotient of two polynomials that have the polar representation automatically built-in. Therefore, rational polynomials are the most suitable candidates for describing functions with peaks, such as spectra in MRS. A quotient of two polynomials is the Padé approximant [1]. Such a quotient is unique for the known input power series expansion of the given function. This has long been recognized in interdisciplinary research, where the Padé approximant is known as the front runner in spectral analysis: in mathematics, physics, chemistry, engineering (response functions), mass spectrometry via ion cyclotron resonance mass spectrometry (ICRMS) and technology. We have employed the Padé approximant over the years in physics and chemistry [25,26,27,28].
Thus, we transferred this versatile method of rational polynomials to MRS diagnostics in clinical oncology. This new approach to signal processing in MRS is termed the fast Padé transform, FPT [1]. Here, “fast” is used to indicate a quasi-linear scaling of the computational complexity with the total signal length, using the Euclid algorithm for extracting the numerator and denominator polynomials. Moreover, “transform” implies that the time and frequency representations of the FPT are deducible from each other by inversion, similarly to the FFT. Firstly, in the parametric FPT, the quantification problem is solved uniquely yielding the complex-valued fundamental frequencies and amplitudes. Secondly, the corresponding component spectra as well as the total shape spectrum (the sum of all the component shape spectra) are constructed in any mode (absorption, magnitude, power, etc.). Thus, by design, the parametric FPT separates all the overlapping peaks.
As outlined in the theory section, splitting apart the overlapping peaks can also be achieved by the two forms of the non-parametric FPT, both using only the envelopes, one dealing with qualitative, partitioned spectra [3, 4], and the other with quantitative, derivative spectra [5,6,7]. In particular, the higher-order derivative fast Padé transform, dFPT, is capable of reconstructing exactly all the spectral parameters without explicitly solving the quantification problem [5,6,7], as will further be discussed in the present review.
3.9 Adaptation of the Padé approximant to MRS for medical applications
A great deal was at stake when adapting the Padé approximant to MRS in oncology, because of the high demands for reliability aimed at aiding clinicians in making the most delicate decisions, in particular to distinguish cancerous from non-malignant pathologies. To achieve this goal, the FPT was broadened to provide fully self-contained cross-checking. This was accomplished by encompassing two equivalent and complementary variants of the same Padé methodology. They are termed the causal \(\mathrm{{FPT}}^{(+)}\) (inside the unit circle, \(|z|<1\)) and anti-causal \(\mathrm{{FPT}}^{(-)}\) (outside the unit circle, \(|z|>1\)) estimators, with the “circle” referring to the harmonic complex variable z. Only the common set of spectral parameters reconstructed by these two versions of the FPT is accepted as the final output list or line-list. The same applies to the dFPT, which itself is a yet another check of the outcome of the MRS quantification problem solved by the non-derivative parametric FPT. The necessary mathematical outlines of the FPT and dFPT are given in theory section and more fully in Refs. [1, 2, 5,6,7, 29, 30].
To complete our clinically-designed signal processing, two additional crucial elements were implemented: (i) the exact reconstruction of the true number of resonances with the ensuing unequivocal retrieval of all the metabolites that are physically present in the scanned tissue, and (ii) unambiguous signal-noise separation, SNS. Features (i) and (ii) of the FPT secure that no false (unphysical, spurious) metabolites would be present in the output list of spectral analysis of the MRS data, nor would any true (physical, genuine) metabolite be missing. This is of key importance, because the last thing clinicians would need is a new data analyzer which cannot reliably indicate whether the information is true or false.
3.10 Benchmarking the FPT
The essence of MR is the introduction of various types of perturbations to gain insight into the system (i.e. tissue) under study. Based upon the abundant literature on stability of systems under external perturbations, Padé-designed response functions were benchmarked via three rigorous, systematic steps. Step 1 was on noiseless synthesized (simulated) MRS time signals. This was followed by step 2 on noise-corrupted synthesized time signals. Only after completing steps 1 and 2, could the actual benchmarking proceed to the final step 3 using experimentally (in vitro or in vivo) encoded MRS time signals.
We first used simulated MRS time signals that are fully reminiscent of the corresponding encoded data. Our earlier work with noiseless simulated MRS time signals, similar to the FIDs from several cancerous, benign and normal tissues, showed that the FPT can reconstruct with machine accuracy all the input spectral parameters for any set of genuine resonances. In parallel, we performed a number of early studies on MRS time signals encoded in vivo from volunteers, further demonstrating the full reliability of the high resolution performance of the FPT [1, 2, 29,30,31,32,33,34,35,36]. The next critical step in benchmarking the FPT for clinical diagnostics within oncology was our detailed, systematic studies of noise-corrupted time signals. This was still in a controlled setting by using noisy simulated time signals. We also employed FIDs encoded with phantoms placed in clinical 1.5T MR scanners [37]. In a comprehensive group of studies [10, 38,39,40,41,42,43,44,45,46,47,48], the FPT has been shown to effectively handle MRS time signals from brain, prostate, ovarian and breast cancer, as well as the FIDs from the corresponding normal and/or benign tissues. Overall, the high resolution of the FPT and its capability to exactly reconstruct the spectral parameters from which all the metabolite concentrations are precisely computed was demonstrated for these malignant, benign and normal tissues over a wide chemical shift region. This encompasses regions where completely overlapping resonances, including cancer biomarkers, are located.
The clear superiority of the FPT in detailed comparisons with the FFT helps explain why the FFT has not yielded the long sought added value of MRS needed for cancer diagnostics. This is particularly evident regarding clinical decision-making within oncology. As such, the hoped-for contribution of MRS and MRSI to individualized cancer care has remained largely unrealized. This is mainly due to inadequate processing of MRS time signals, i.e. the exclusive reliance upon the FFT with post-processing by various fitting techniques that are all equivocal by invariably failing to detect some of true metabolites (via under-fitting) and predicting non-existent ones (via over-fitting). Irrespective of whether using certain selected lineshapes for the individual peaks or employing some linear combination of model spectra (synthesized or encoded), all the existing fitting-based signal processing methods are ambiguous. This fact occurs because even some minor changes in the input data (e.g. alteration of the initial or starting values of the unknown spectral parameters, imposing various types of minimization constraints, etc.) can yield vastly different results of reconstructions, as manifested by typically huge standard deviations in e.g. the linear combination of model in vitro spectra (LCModel). As stated earlier, such non-uniqueness evidenced by the instability of predictions is a direct manifestation of the ill-posedness of quantification as a non-linear inverse problem. Mathematical ill-posedness or ill-conditioning refers to the lack of a continuous dependence of the output on the input data. The FPT has been successfully applied to quantify MRS data from clinical MR scanners using: (i) time signals encoded by way of low field strength \(B_0=1.5\mathrm{T}\) on the General Electric (GE) head phantom with several metabolites that are also detected in the human brain [37], and (ii) FIDs measured in vivo from human brain with the help of stronger (\(B_0=4\) and \(B_0=7\mathrm{T}\) [1, 2, 30, 33, 34] as well as weaker (\(B_0=1.5\mathrm{T}\)) static magnets [8, 9, 36, 49].
Pattern recognition of MR spectra from brain, prostate, ovarian and breast cancer, as well as from benign and normal tissues, with appropriate illustrations (tables, graphs) can greatly facilitate rapid interpretation in the clinician setting. This is in conjunction with the quantitative information with maps of metabolite concentrations, as reliably produced by the FPT. Crucially, with the FPT, a set of cancer biomarkers widely considered as being diagnostically informative can confidently be identified, together with their metabolite concentrations. We can mention here a few such biomarkers: phosphocholine (PC), which often completely underlies other metabolites, lactate (Lac) reflecting anaerobic glycolysis, as well as \(\beta -\)glucose (\(\beta -\)Glc) for which altered glucose metabolism is a typical feature of cancer cells (with low levels of glucose generally seen in malignancy), also taurine (Tau), a possible indicator of apoptosis, and rapidly-decaying myoinositol (m-Ins), which may help distinguish malignant breast tissues from fibroadenomas, and aid in identifying primary brain tumors and prostate cancer. Through the FPT, extensive possibilities emerge for multivariate exploration to find combined metabolite patterns that best characterize various types and grades of these malignancies versus diverse benign pathologies that cause differential diagnostic dilemmas.
4 Noise as one of the greatest difficulties for MRS in the clinical setting
Let us begin by noting some of the essential points regarding noise encountered in MRS. As stated, for a hypothetically ideal encoding, the MRS time signals are expected from quantum mechanics to be sums of complex-valued attenuated exponentials, as in (2.1). In practice, of course, no such ideal measurement can ever be carried out. Nevertheless, since quantum physics predicts precisely this representation for an FID, it is also necessary to use Eq. (2.1) for non-ideal time signals from MRS encoding, and to subsequently devise robust safeguards against various imperfections arising from the measurement. We have demonstrated how noise is handled in practice with the FPT. We first simulate the hypothetical noiseless situation just described, and that is what is meant by the controlled setting. This benchmarking approach is well established in other disciplines, such as engineering: the first test of a model is its validation on a problem with an exactly known solution [1, 2]. In engineering, recovering the system’s parametrized characteristics from the given input data is known as “reverse engineering”.
The ideal time signal is equidistantly sampled with the known set of spectral parameters \(\{K,\omega _k,d_k\}\, (1\le k\le K),\) where K is the model order, \(\{\omega _k\}\) are the complex frequencies and \(\{d _k\}\) are the corresponding complex amplitudes. This constitutes the noiseless MRS time signal. The mentioned compound noise in an MRS encoding of FIDs is mimicked by perturbing the noiseless input data \(\{c_n\}\, (0\le n\le N-1)\) with random Gaussian complex-valued zero-mean white noise \(\{g_n\}\, (0\le n\le N-1)\) of a prescribed standard deviation \(\sigma .\) When \(\{g_n\}\) is added to \(\{c_n\}\) to create the data set \(\{c_n+g_n\}\,(0\le n\le N-1),\) the initially known spectral parameters \(\{K,\omega _k,d_k\}\, (1\le k\le K)\) are subsequently treated as if they were never available. The objective of such studies is to exactly reconstruct all the physical parameters \(\{K,\omega _k,d_k\}\, (1\le k\le K)\) by applying the FPT to the noisy time signal \(\{c_n+g_n\}\,(0\le n\le N-1)\) of systematically increased standard deviation \(\sigma .\) In order to more closely conform to the realistically encoded FIDs, we have varied \(\sigma \) within three orders of magnitude [10, 23, 24, 47, 48].
4.1 The reasons for high resolution and noise suppression within the FPT
As elaborated in detail in Refs. [1, 2, 30, 48], there are several reasons for high resolution and noise suppression in signal processing by the FPT. One is that the ratio of two polynomials, say \(P_K/Q_K,\) for the complex non-linear spectrum in the FPT, possesses an extra degree of freedom to cancel noise from the numerator by the noise in the denominator. In contrast, being a single polynomial, the FFT does not have this capability and, therefore, by this method, the noise imported directly from the input time domain data to the frequency spectrum cannot be removed nor suppressed. Moreover, the FPT can simultaneously interpolate as well as extrapolate, and this further enhances its resolution capacities. By comparison, the FFT lacks both interpolation and extrapolation. Zero-filling of time signals might eventually improve the formal appearance of spectral envelopes, but cannot enhance the resolution since the entire information is already contained in the data points from the FID.
4.2 Signal-noise separation within the FPT
Especially with very closely-overlapping peaks, as is abundantly the case for MRS spectra from the brain, prostate, breast and the ovary, the number of true metabolites is always a very small percentage of the total number of resonances generated using the noise-corrupted time signal \(\{c_n+g_n\}\,(0\le n\le N-1).\) The genuine resonances are often on the order of merely 1% as will be exemplified in this review. Distinguishing such false, noisy peaks from those that are genuine is a critical problem for accurate diagnostics. Mathematically, this means that for MRS quantification problems (especially with noisy time signals) solved without windowing, an over-determined system of linear equations becomes inevitable in any parametric processor, with the price of reconstructing many spurious resonances. In the FPT, this problem is solved algorithmically by identifying pole-zero confluences [2, 50, 51]. For a fixed model order K, the FPT generates the unique set of spectral poles and zeros. The zeros of the numerator polynomial \(P_K\) correspond to valleys in-between any two adjacent peaks in the same spectrum, and the system zeros are described thereby. The roots of the denominator polynomial \(Q_K\) are the system poles and represent the positions (chemical shifts) and widths of peaks in a spectrum. It is precisely here that the FPT meets the metabolomics branch of system theory in biomedicine. Namely, by detecting the system characteristics through recovery of the parametrized system poles and system zeros, the FPT carries out metabolic profiling, as a quantitative study of a group of metabolites, previously known or unknown (unassigned) within or related to a particular metabolic pathway. The entire information about the generic system (cell, tissue, organism, ...) is contained in the system poles and zeros.
Poles and zeros that coincide, i.e. Froissart doublets [51], are unstable with no convergence in sight (as they wander haphazardly in the complex frequency plane) after exposition to the slightest perturbation. Hence, this is evidently unphysical information. These spurious resonances exhibit noise-like behavior, and need to be identified as such in order to be removed from the final results of the analysis. On the one hand, in an attempt to mitigate the detrimental effect of noise inherently present in the encoded FIDs, it is necessary to resort to over-determination. This latter notion signifies that the number of linear equations to be solved exceeds the number of the sought, unknown quantities (solutions). On the other hand, as stated earlier, over-determination itself produces noise-like information by reconstruction of spurious resonances. The FPT simultaneously overcomes both these obstacles (in fact, conundrums), by its very form of the spectrum as a polynomial ratio \(P_K/Q_K.\) Crucially, there is a complementary set of retrieved poles and zeros that are non-coincident and stable. These are called physical or genuine.
The mechanism for this signal-noise binning is the SNS concept manifested in a two-fold way: (a) pole-zero cancellation (in the canonical representation of \(P_K/Q_K\) for spurious resonances, i.e. Froissart doublets) arising from over-determination, and (b) suppression of noise from the input FID itself by the non-linearity of the rational response function \(P_K/Q_K.\) Elimination of spurious resonances also occurs in the alternative Heaviside partial fraction representation of the Padé spectrum \(P_K/Q_K.\) Therein, the numerator of each partial fraction contains the amplitude \(d_k,\) which is zero for any spurious resonance. So, yet another signature or fingerprint of a spurious resonance is its zero-valued amplitude. The amplitude is proportional to the pole-zero difference and, thus, we have \(d_k=0\) for coincident poles and zeros. It is pertinent to recall that any error, including noise, in two experimentally measured quantities A and B (or computationally generated with finite precision arithmetic), is often largely canceled in their quotient A / B. Similar quotients are also encountered in the FPT spectrum, \(P_K/Q_K.\) The FPT exactly reconstructs the number K by way of convergence of the physical information. Namely, when all the fundamental or eigen-parameters \(\{\omega _k,d_k\}\) in every physical or genuine resonance stabilize, the sought number K is automatically determined.
In summary, pole-zero cancellation is achieved by gradually increasing the degree K of the Padé polynomials \(P_K\) and \(Q_K\) to monitor fluctuations of the reconstructed spectra until stabilization is attained. Thus, the FPT accompanied by SNS appears as a multi-pronged strategy for distinguishing false from true content of the investigated time signals. Overall, we see that the methodology rooted in the FPT provides added value of utmost importance to the whole metabolomics in system biomedicine. This bonus is unique to the FPT because of its possibility to discriminate or indeed separate in a mathematically and clinically reliable manner, the true from the false part of the extracted information within the examined system. With such a differentiation, metabolic profiling is enriched via an invaluable complement to data quantification by a novel design of filtering out the unphysical (spurious, false, incoherent) and retaining the physical (genuine, true, coherent) information in data evaluation.
Noise is also systematically suppressed in the dFPT albeit by a different mechanism. Namely, in the dFPT, we take the derivatives of the analytically available formula for the non-parametrically reconstructed envelope \(P_K/Q_K\) from the non-derivative FPT. This automatically secures that no noise is invoked by repeated differentiation of any order. Noise, which is initially transferred from the input time signal to the seed total shape spectrum \(P_K/Q_K\) is systematically suppressed by higher order derivatives of the starting envelope \(P_K/Q_K.\) This is possible because differentiation suppresses broad background and separates overlapped peaks by narrowing peak widths and increasing peak heights of physical resonances. In contradistinction, the derivative fast Fourier transform, dFFT, amplifies noise with increased derivative orders. The reason for such a severe disadvantage is that, in the dFFT, one first takes the derivative \(D^m_\nu \) of exp(\(-2\pi i\nu t\)) and then applies the FFT to the ensuing product \((\tau n)^{m} c_{n}\). However, the term \((\tau n)^{m}\) weighs heavily the tail of noisy time signal, \(c_n\). Therefore, the dFFT drastically deteriorates SNR since noise in enhanced with augmentation of the differentiation order.
4.3 Two complementary, self-checking and auto-correcting variants of the FPT: special relevance to SNS
As stated, there are two variants of the FPT, denoted by \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)}\) defined inside (\(|z|<1\)) and outside (\(|z|>1\)) the unit circle for the causal and anti-causal representation, respectively. The spectra in the \(\mathrm{{FPT}}^{(\pm )}\) are the frequency-dependent polynomial quotients \(P^\pm _K/Q^\pm _K\) extracted from a common, truncated Maclaurin series in powers of \(z^{-1}\) as per (2.2).
The \(\mathrm{{FPT}}^{(-)}\) operates with variable \(z^{-1}\) and, hence, it is an accelerator of convergence of the input slowly converging series (2.2) expanded in powers of \(z^{-1}.\) In the presence of higher levels of noise, the pole-zero coincidence may be close, but not complete. Moreover, some spurious resonances may show near-zero amplitudes (\(d_k\approx 0\)), instead of their expected zero values, \(d_k=0\) [44, 48]. This requires the “stability test” to confidently achieve SNS also at higher noise levels with incomplete pole-zero coincidences. Furthermore, in the \(\mathrm{{FPT}}^{(-)},\) there is a mixing of the spurious and genuine resonances within the same positive imaginary frequency region, \(\mathrm{Im}(\omega _k)>0.\)
The \(\mathrm{{FPT}}^{(+)}\) works with variable z, and is designed to numerically perform analytical continuation of the input series (2.2). As such, from an algorithmic standpoint, the \(\mathrm{{FPT}}^{(+)}\) has a more difficult task because it must induce convergence into a divergent series [1, 2, 29]. Consequently, in order to converge, the \(\mathrm{{FPT}}^{(+)}\) typically requires more signal points than the \(\mathrm{{FPT}}^{(-)}.\) However, the \(\mathrm{{FPT}}^{(+)}\) achieves more stringent SNS than the \(\mathrm{{FPT}}^{(-)}.\) This occurs because in the \(\mathrm{{FPT}}^{(+)},\) the genuine and spurious resonances are located in two separate domains with the positive and negative imaginary frequencies, \(\mathrm{Im}(\omega _k)>0\) and \(\mathrm{Im}(\omega _k)<0,\) respectively. Pole-zero coincidences of spurious resonances have been reported with the \(\mathrm{{FPT}}^{(+)}\) to be accurately maintained at higher noise levels. Whenever this occurs, a denoised spectrum can automatically be generated [10].
These two variants provide an internal cross-validation within the same Padé methodology. Upon convergence of the \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)},\) their reconstructions are compared, and the final output list is produced from the spectral parameters that are common to both variants. Since this checking procedure is entirely self-contained, the results of the \(\mathrm{{FPT}}^{(\pm )}\) need no comparison with any other signal processor for verification [1, 2, 34]. We have clearly demonstrated the practical usefulness of the outlined self-contained cross-validation by the two different and equivalent variants, \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)},\) through their complementary capabilities to separate genuine signal from noise. In particular, within the \(\mathrm{{FPT}}^{(+)}\) the special property of analytical continuation by numerical means has been illuminated for successful handling of heavily noise-corrupted synthesized MRS time signal data [10, 23]. These results represent a critical step towards efficient implementations of in vivo MRS, where there are no known input spectral parameters with which to check the results of reconstruction. The \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)}\) are always employed together for a fully self-contained cross validation, using different algorithms in numerical computations.
4.4 Solutions by the FPT to noise-related and other problems with encoded in vivo MRS time signals
A number of major problems arise with in vivo encoding in MRS, the solutions to which through Padé-based strategies are described later and with full detail in our recent publications [8, 9, 11, 49, 52,53,54]. Among the most difficult of these problems are those related to noise from encoding itself plus from unphysical resonances that arise in data reconstruction by any processor. Noise-like spikes emerge, and they are often much larger than the genuine spectral content. A key aspect of the FPT for in vivo encoded MRS time signals is spectra averaging [9] in which the arithmetic average is taken of a pre-computed sequence of the retrieved envelopes for varying model order K. For different values of K, each envelope is computed at the same number of sweep or running chemical shifts. It is this flexibility of the FPT which enables taking the arithmetic average of the envelopes for varying K at the same fixed sweep frequency. Spectra averaging stabilizes the total shape spectra that are otherwise highly sensitive to model order K. Averaging these envelopes yields a total shape spectrum void of spikes, that themselves stem from the random, noise-like nature of spurious resonances with changes in K. Averaging of spectra is not possible in the FFT because Fourier vectors in the frequency domain are not of the same length for different truncation of the total acquisition time \(T=N\tau .\) Namely, the number of sampling frequencies in an FFT spectrum is the same as the total number N of the FID points in the time domain. Thus, by keeping the sampling time \(\tau \) fixed, truncating T amounts to lowering N and this, in turn, leads to a smaller number of sticks in an FFT spectrum. Hence, the FFT spectra at different truncations of T cannot be added together to perform averaging.
Yet another obstacle exists in MR spectra, and that is a still large remnant or residual part of the giant water resonance after its partial removal during the encoding procedure. Suppression of the giant water resonance, as a highly problematic issue for in vivo MRS (especially of the brain) is achieved through several Padé-based strategies [8, 9], as will be presented in this review.
Further, within the FPT, we have recently introduced a partitioning procedure to non-parametrically identify the cancer biomarkers, such as PC which has heretofore been a hidden component of total choline (tCho) in spectral envelopes [3, 4]. Within the non-parametric FPT, this partitioning procedure can be applied to in vivo encoded MRS time signals. The purpose of such a pre-processing, as the first-stage application of the Padé analysis of total shape spectra, would be to quickly visualize whether the biomarkers of interest are qualitatively detectable (present or absent). If e.g. PC is present, this would be followed by a detailed quantitative reconstructions of the Padé-based processing.
Most recently, we have shown that even the non-parametric FPT can retrieve all the peak parameters without ever attempting to solve explicitly the quantification problem per se. This is achieved by the dFPT [5,6,7]. In benchmark computations, we have demonstrated that high derivatives of total shape spectra coincide with high derivatives of component shape spectra. This fact and the existence of the relationships among the peak parameters of the derivative and non-derivative component spectra, permit exact reconstruction of positions, widths, heights and phases of all physical resonances using only total shape spectra computed by the non-parametric dFPT. Such an achievement is due to the main mathematical features of the dFPT that lead to the peak width narrowing and the concomitant peak high enhancement with a strong suppression of the noisy background. Crucially, the dFPT simultaneously solves all the three major problems in MRS: unequivocal separation of overlapping resonances, noise elimination and resolution enhancement. Thus far, the dFPT has been illustrated on synthesized time signals reminiscent of the corresponding FIDs encoded by in vivo MRS for breast cancer [5,6,7]. The dFPT is now envisaged to be directly applied to time signals from in vivo MRS encodings. This powerful approach is anticipated to contribute to practical improvements for diagnosis and management of breast cancer and other malignancies.
5 Padé-optimized MRS for four cancer problems
We have aimed to improve cancer diagnostics on a quantitative molecular basis within the newly emerging discipline called “molecular imaging”. As noted, molecular imaging is rapidly gaining recognition as a key tool for the realization of more personalized cancer care. Our goal is the retrieval of key information that is not detected using the FFT and post processing via fitting and/or peak integrations. Accurate quantification is needed to determine metabolite concentrations, so that MRS can be better used to detect and characterize cancers, with clear distinction from non-malignant processes. We have heretofore focused on four cancers (brain, prostate, breast and ovarian) for which the added value of early detection through Padé-optimized MRS would have a major clinical-public health impact. The Padé methodology is also applicable to a number of other problem areas in oncology, and beyond. The as yet unrealized possibilities of MRS for improved diagnostics are underscored, particularly early detection, for a wider range of cancers [54,55,56]. We herein will first briefly highlight some salient issues regarding the four selected problem areas.
5.1 Diagnostics by MRS: salient highlights on the four cancer problems
5.1.1 Prostate cancer
Prostate cancer is one of the most frequently occurring malignancies and is cited as the sixth leading cause of cancer deaths among men worldwide [57]. Mortality rates from prostate cancer have been declining since the late 1980s in Western Europe and North America [58, 59]. This favorable trend is attributed, at least in part, to early detection using prostate specific antigen (PSA). Data from the U.S. indicate that during this time period, the percentage of men with distant metastases at initial prostate cancer diagnosis dramatically decreased [60]. The importance of early detection and treatment of prostate cancer has been further underscored by longitudinal findings that radical prostatectomy confers a significant survival advantage compared to “watchful waiting” [61]. On the other hand, active surveillance of “low risk” prostate cancer continues to be investigated as a potentially viable option [62].
By providing insight into the metabolic characteristics of prostate tissue, MRS and MRSI are being increasingly used for many aspects of prostate cancer diagnostics and management. Among the areas in which MRS and MRSI have been helpful include distinguishing malignant prostate from benign prostatic hypertrophy (BPH), as well as high risk from low risk prostate cancer, identifying the optimal site for biopsy, detecting extracapsular extension, selecting treatment modality as well as timing and assessing tumor regression versus recurrence after treatment [63,64,65]. The concentration ratio between two MR-observable metabolites, Cho at \(\sim 3.2\) parts per million (ppm) and citrate (Cit) at \(\sim 2.5\) to 2.7 ppm has been the cornerstone of prostate cancer detection. Citrate indicates healthy prostate epithelial secretory activity. Choline is a cell proliferation marker. However, important exceptions are: with metabolic atrophy due to radiation or hormonal therapy or in stromal prostate, Cit is low without cancer being present. With BPH, it occurs that Cit can be high despite coexistent malignancy. Moreover, there is no consensus as to cutoff values of these metabolite concentration ratios that best identify prostate cancer [66].
Expanded protocols have been developed, e.g. including polyamines (PA) which are MR-visible metabolites resonating at about 3.1 ppm. Normal healthy prostate contains high concentrations of PA, whereas with prostate cancer PA levels are low [67, 68]. However, assessment of PA in the in vivo MR spectrum has been problematic with the FFT plus fitting, since PA are broad resonances that overlap with other metabolites. Overall, limitations in resolution and data interpretation from MRS are recognized as major challenges in prostate cancer diagnostics, staging and surveillance [69]. In vitro MRS applied to prostate specimens yields more insight, but abundant multiplets and closely-overlapping resonances of different metabolites are very troublesome for quantification. These problems are not solved by the FFT followed by fitting [70]. Therefore, the full potential of molecular imaging through MRS and MRSI for a more individualized approach to various dilemmas associated with prostate cancer remains to be realized. Overall, for MRS time signals encoded in vivo from the prostate, inadequate processing by the FFT followed by fitting is a major reason for this unrealized potential [23].
5.1.2 Breast cancer
Worldwide, breast cancer is the most commonly diagnosed malignancy among women and a major cause of death [24]. Improved survival has been consistently attributed to breast cancer screening, in particular since there are greater chances for early detection, such that appropriate care can be offered to the patient without undue delay [71, 72].
Although having low specificity, mammography is widely employed for breast cancer diagnostics. As a consequence of this insufficient specificity (false positives), further examination is often required [73]. When breast density is high, as is frequently the case among younger women, there is also a considerable chance that the mammogram yields a false negative result [42]. Among the standard anatomic imaging modalities, MRI has the highest sensitivity for breast cancer detection. This advantage of MRI is particularly seen for women at high risk [74, 75]. Recall, that another benefit of MR-based modalities is that they entail no exposure to ionizing radiation. Although contrast-enhanced MRI is usually very sensitive for detecting breast cancer, false negatives can occur for small breast cancers, especially if there is no selective contrast uptake. The major problem with MRI is poor specificity.
In vivo MRS implemented with the FFT envelopes has the potential to improve the specificity of MRI for breast cancer diagnostics [2, 76, 77]. However, most applications of FFT-based MRS for breast cancer diagnostics have assessed only a single composite peak, namely total choline, tCho. The latter may be increased in benign breast lesions or lactation, and is often undetected in small cancers [77]. As we recently reviewed [3], in FFT-based MRS, pooled estimates of sensitivity and specificity vis-à-vis breast cancer diagnosis are below 90%. Attempts to improve resolution and SNR for MRS of the breast via higher field scanners [78, 79] have not yielded the sought degree of accuracy in identifying breast cancer. Thus, there are still no sufficiently trustworthy standards to diagnose a breast lesion as cancerous versus benign thereby.
There is abundant information in closely-overlapping resonances for detecting breast cancer. The FPT applied to synthesized MRS time signals (noiseless and noise-corrupted) similar to the corresponding FIDs encoded in vitro from extracted breast cancer specimens [80] accurately reconstructed the sought biochemical content. This includes PC, a breast cancer biomarker [81], which very closely overlaps with neighboring peaks [2, 41, 42, 47].
5.1.3 Primary brain tumors
Although primary malignant brain tumors are relatively rare in adults compared to other cancers, they generate much attention. This is because of the fear associated with the location, the young age at which these can occur, and the often poor prognosis [12, 37]. In the pediatric population, primary brain tumors are the leading cause of solid tumor-related morbidity and mortality [82,83,84].
Molecular imaging through MRS and MRSI has been of seminal importance for neuro-oncology. There has been a great “explosion” of information in recent years on MRS and MRSI for primary brain tumor diagnostics, as reviewed in Refs. [2, 37, 82, 85,86,87]. Magnetic resonance spectroscopy and MRSI are now among the key modalities for nearly all aspects of brain tumor diagnostics and management for both the adult and pediatric populations. This includes initial diagnosis [82], tumor characterization [85] and grading [88], treatment planning in RT [89], surgical guidance [90], as well post-therapeutic follow-up [91,92,93].
Within this framework, the limitations of the FFT and fitting become all the more striking. Thus, e.g. rather than obtaining accurate quantitative information for at least 25 metabolites, as can readily be achieved by the FPT [2, 8, 9, 31, 32, 49], much of neuro-diagnostics through MRS based on the FFT and fitting has been reduced to a semi-quantitative approach, with concentration ratios of a very small number of metabolites. With this situation, many diagnostic dilemmas remain. A notable example is that recurrent primary brain tumors are quite often misclassified as radiation necrosis, and vice verse, according to meta-analysis from Refs. [91,92,93]. Another example of great importance for PCM is to distinguish non-tumorous cerebral hypoxia/ischemia from brain tumors. The latter also often contain hypoxic regions that promote genomic instability and are associated with the invasive/metastatic process [8, 9, 49].
5.1.4 Ovarian cancer
The ovary is a small, moving ellipsoid organ with its normal mean volume in adult females ranging from 6.1 to 1.8 \(\mathrm{cm}^3\) depending on age. Particularly in early-stage cancer, the ovary may be only slightly enlarged or of normal size [94]. Cancers in this tiny organ are the sixth most often occurring malignancy among women throughout the world. In many parts of the world, including the U.S., Scandinavia and Israel, ovarian cancer is even more common, and in a number of countries the incidence of ovarian cancer appears to be increasing [95,96,97,98]. Ovarian cancer has a very high case fatality rate [99]. For example, only in the U.S. over 14000 women die each year from ovarian cancer [100]. In 2013 alone, about 158000 women worldwide died of ovarian cancer. Among the risk factors for ovarian cancer is heredity, which accounts for up to 25 % of cases [101,102,103,104,105]. Familial ovarian cancer has been most widely identified in relation to the hereditary breast and ovarian cancer (HBOC) syndrome, with germline mutations in BRCA1 and BRCA2 tumor suppressor genes being responsible for the vast majority of HBOC. Several other gene mutations also appear to be associated with HBOC or other hereditary ovarian cancers. The Lynch syndrome characterized by non-polyposis colorectal cancer also includes increased risk of ovarian cancer, as well as endometrial cancer [102, 105]. Non-hereditary risk factors for ovarian cancer include use of hormone replacement therapy [104, 106], unhealthy life-style (smoking, high-saturated fat diet intake, obesity) [104], late childbirth, nulliparity, endometriosis [107, 108], and possibly exposure to diagnostic ionizing radiation, as well as to talc, pesticides or herbicides [104, 108,109,110]. Nightshift work may also increase the risk of ovarian cancer [111], possibly in relation to circadian genes that are highly expressed in the ovaries, since these genes regulate ovulation.
Early detection of ovarian cancer is an urgent public issue. Ovarian cancer has an excellent prognosis if found at an early stage [112]. However, due to the lack of accurate early detection methods, the majority of ovarian cancers are diagnosed late, which is the main reason for the very high case fatality rate [113, 114]. The potential for in vivo MRS as a method for early ovarian cancer detection has been suggested for nearly two decades [115, 116]. However, especially due to the small size and motion of this organ, in vivo MRS data processed by the FFT together with fitting have been greatly hindered by problems of poor resolution and bad SNR [2, 117].
\(\bullet \) Meta-analysis of in vivo MRS studies on benign and cancerous ovarian lesions
We recently carried out a meta-analysis [52] of the published in vivo MRS investigations for altogether 134 cancerous, 114 benign and 3 borderline ovarian lesions, all encoded via clinical (1.5 or 3T) MR scanners. In the reviewed studies, the encoded FIDs were all analyzed by the FFT followed, in some instances, by post-processing via fitting. A very small number of peaks were identified, and only Cho at 3.2 ppm and Lac at 1.3 ppm were significantly more often detected in malignant compared to benign ovarian lesions. However, based upon detection of Cho alone, 50 benign lesions would be erroneously categorized as cancerous (false positive), with a positive predictive value (PPV) of 66%. The 20 malignant ovarian lesions would be incorrectly considered benign due to lack of Cho detection (false negative), with a negative predictive value (NPV) of 57.4%. Although Lac provided better PPV and NPV, data were available for only 25% of the patients. A model with both Lac and Cho, adjusting for age and static magnetic field strength \(B_0,\) with a total of fifty patients, yielded the best PPV, NPV and overall accuracy. Nevertheless, four of twenty-six patients with benign ovarian lesions were still erroneously predicted to have ovarian cancer and four of twenty-four patients with ovarian cancer were wrongly predicted to have benign lesions. We concluded on the basis of this meta-analysis that in vivo MRS with the FFT alongside fitting did not adequately distinguish malignant versus non-cancerous ovarian lesions [52].
\(\bullet \) More promising results from in vitro MRS for identifying ovarian cancer
As we systematically reviewed in Ref. [52], via in vitro MRS utilizing methods from analytical chemistry with stronger static magnetic fields, more metabolic insight can be garnered to identify cancerous versus benign ovarian lesions [118,119,120,121]. Moreover, in human epithelial ovarian carcinoma cell lines compared to normal or immortalized ovarian epithelial cells, the levels of the MR-visible metabolite and cancer biomarker PC [81] were three- to eight-fold higher [122]. These findings further motivated our investigations of how Padé-optimization of MRS could contribute to improved ovarian cancer diagnostics. We now proceed to the actual results of Padé-optimized MRS applied to the four problem areas, starting with prostate cancer diagnostics.
5.2 The FPT applied to MRS time signals associated with normal glandular, normal stromal and cancerous prostate
As noted, MRS data from the prostate is a highly demanding signal processing problem since the spectra are very dense, with abundant multiplets of resonances. The FPT was first applied to noiseless MRS data similar to in vitro encoding from normal glandular as well as normal stromal prostate and from prostate cancer [70]. With a very small fraction of the full signal length, the FPT resolved all the physical resonances, including multiplets and overlapping peaks of different metabolites, yielding the exact metabolite concentrations to distinguish normal from cancerous prostate [2, 40].
Recently [23, 54], the convergence performance of the FPT was examined in detail for MRS time signals reminiscent of FIDs encoded in Ref. [70] from prostate cancer and from normal glandular as well as normal stromal prostate. In Refs. [23, 54], comparisons were made between Fourier and Padé processing for noise-free and noise-corrupted MRS time signals from the prostate. In-depth assessment was also undertaken of how the \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)}\) handle noise-corrupted MRS data from the prostate [23].
\(\bullet \) Construction of the MRS time signals associated with prostate cancer, normal glandular and normal stromal prostate
Fourier-reconstructed spectra for the noiseless MRS time signal from normal glandular prostate [70] at \(N_{\mathrm{P}}=\)608 (green), 632 (black) and 706 (red) on (a) between 2.45 and 3.75 ppm. Converged Padé-reconstructed spectra of envelopes (b) and components (c) for normal glandular prostate as generated using the \(\mathrm{FPT}^{(-)}\) which gives the same results for \(N_{\mathrm{P}}=608, 632\) and 706. On (d), converged Padé-reconstructed components for prostate cancer with the three sets of coincident curves at \(N_{\mathrm{P}}=608,632,706\) (color online)
Illustrations of the SNS concept on (a) and (b) by the \(\mathrm{{FPT}}^{(-)}\) for MRS data from normal glandular prostate, \(N_{\mathrm{P}} = 1210,\) where \(N = 2048,\) with added noise of standard deviation \(\sigma = 0.00514\) RMS. The Argand plot (a), as \(\mathrm{Im}(\nu ^-_{k,X})\) versus \(\mathrm{Re}(\nu ^-_{k,X}),\) where \(X=P\) and \(X=Q,\) shows complete pole-zero coincidence (symbolized by \(\odot \)) for the spurious resonances and exact agreement of the input and the Padé-reconstructed genuine poles (indicated as \(\otimes \)). Magnitude plot as \(|d^-_k|\) versus chemical shift (b), where all the genuine resonances have non-zero magnitudes, while the spurious resonances have zero-valued magnitudes. Converged absorption components generated via the \(\mathrm{{FPT}}^{(-)}\) for noise-corrupted MRS time signal (\(\sigma = 0.00514\) RMS) corresponding to normal glandular prostate with \(N_{\mathrm{P}} = 1210\) (c) and stromal prostate \(N_{\mathrm{P}} = 1220\) (d). The MRS time signals are similar to those encoded in Ref. [70] (color online)
Three FIDs were generated, corresponding to the MRS data encoded for prostate cancer, normal glandular and normal stromal prostate. This was a sum of \(K=27\) damped complex exponentials \(\mathrm{e}^{in\tau \omega _k}\, (1\le k\le K)\) multiplied by their amplitudes \(d_k.\) The time signals from Ref. [70] were recorded at a Larmor frequency of 500 MHz (static magnetic field strength \(B_0=11.7\mathrm{T}\)). Herein, a bandwidth (BW) of 6000 Hz was used, with sampling time \(\tau =1/\mathrm{{BW}}.\) The phases \(\varphi _k\, (1 \le k\le 27)\) of \(d_k\) were all set to zero, so that \(d_k=|d_k|.\) Note that for the illustrations in Figs. 2 and 3, the resonances of Lac at 1.330 and at 4.120 ppm, as well as alanine (Ala) at 1.490 ppm and m-Ins at 4.07 ppm are not shown, since the displayed spectra herein are for the spectral region of interest (SRI) between 2.45 and 3.75 ppm, where the other 23 resonances are located [2, 23, 40].
5.2.1 Comparison of Padé and Fourier processing of MRS time signals from the prostate
Comparing the resolution performance of the FPT on MRS time signals from the prostate with that of the FFT is particularly helpful in illustrating why the yield of MRS as well as MRSI in prostate cancer diagnostics has not yet been sufficiently reliable to confidently inform clinical decision-making.
Figure 2 shows the results of processing noiseless MRS time signals [23] from normal glandular prostate and prostate cancer, similar to the corresponding encoded FIDs reported in Ref. [70]. Therein, we compare the FPT with the discrete Fourier transform (DFT). Here, the employed partial signal lengths \(N_{\mathrm{P}} = 608, 632, 706\) are not of the composite form \(2^m\) (m being a positive integer), and this is the reason for using the DFT instead of the FFT. As is well-known, in the FFT, the fast Tukey-Cooley computational algorithm [1] employs the signal length \(N=2^m\, (m=1,2,3,\ldots ),\) which reduces the initial huge number multiplications \((N^2),\) for N large, to a much smaller number \((N\mathrm{{log}}_2N)\) of multiplications. The displayed chemical shift interval is 2.45–3.75 ppm. Shown on panel (a) of Fig. 2 are the DFT envelopes at partial signal lengths \(N_{\mathrm{P}} = 608, 632\) and 706, where the total signal length is \(N=1024.\) Therein, not only are all these Fourier spectra rudimentary, but a comparison of the green, black and red curves reveals that at the three different partial signal lengths, the total shape spectra have changed substantially. Most notably, the height of the creatine (Cr) peak at around 3.0 ppm has markedly diminished at the longer signal lengths, and the ratio of heights of the peaks corresponding to Cit, centered at around 2.5 and 2.7 ppm, have changed, as well. Thus, it is clearly seen that no convergence is achieved through the DFT for these partial signal lengths.
In sharp contrast, panel (b) of Fig. 2 reveals that at the same partial signal lengths (\(N_{\mathrm{P}} = 608, 632, 706\)) within the same chemical shift interval, the FPT-generated total shape spectra converged (the three lines for the said three values of \(N_{\mathrm{P}}\) are indistinguishable). Therein, two Cit doublets centered at about 2.52 ppm (peaks ## 3 and 4) and 2.73 ppm (peaks ## 5 and 6) are clearly seen. Creatine, Cr, at 3.04 ppm is a thin, smooth peak. There is also a hint of two PA peaks (## 8 and 9) at 3.10 and 3.14 ppm. The Cho peak (# 10) at about 3.2 ppm is well-defined. Serrated structures (peaks ## 11–14) centered at 3.25 ppm can be observed, and these are followed by a more rounded peak (# 15), and then scylloinositol (s-Ins) as peak # 16 is clearly defined at 3.35 ppm. Further, the three triple serrated peaks centered at 3.43 ppm (peaks ## 17–19), 3.55 ppm (peaks ## 20–22) and 3.64 ppm (peaks ## 23–25) are also well-delineated and these would correspond to a Tau triplet and two m-Ins triplets, respectively.
Notwithstanding the clarity of the converged total shape spectra, some uncertainties still remain. However, these uncertainties are resolved by the converged component spectra in the FPT. This is seen on panel (c) of Fig. 2 at the partial signal lengths \(N_{\mathrm{P}} = 608, 632\) and 706 for which the three sets of component curves are identical. It is confirmed that there are two Cit doublets, with a total of four individual resonances, and that there is a partial overlap between peaks ## 3 and 4 and between peaks ## 5 and 6. The overlap between the PA peaks ## 8 and 9 is now clearly seen. The dense region between 3.23 and 3.28 ppm is revealed from the component spectra to be comprised of five overlapping resonances (## 11–15), including the small PC peak (# 11), for which there is little or no suggestion from the total shape spectrum. At the higher chemical shift region, s-Ins (# 16) is unequivocally observed as a single resonance, also Tau (## 17–19) and the two m-Ins structures (## 20–22) and (## 23–25) are unquestionably triplets, whose overlapping peaks are well-defined only via the component shape spectra as reconstructed by parametric analysis provided by the FPT. The general spectral pattern of the malignant prostate in panel (d) of Fig. 2 differs noticeably from normal glandular prostate on panel (c). This is particularly seen in the attenuation of the Cit doublets and the two PA resonances. In prostate cancer, the tCho components at 3.21–3.24 ppm are prominent. Importantly, PC at 3.23 ppm (peak # 11) is much larger than its immediate neighbors that are Cho (peak # 10) at 3.210 ppm and glycerophosphocholine (GPC) at 3.24 ppm (peak # 12). The middle components of the two Tau triplets (peaks ## 14 and 18) are much taller in malignant prostate than in the normal glandular prostate. The full names of the metabolites are given in the list of abbreviations for this and subsequent figures.
5.2.2 Padé-based signal-noise separation for MRS time signals from the prostate
Signal-noise separation, SNS, for MRS time signals from the prostate is exceedingly challenging. As noted, spectra from the prostate are very dense, with numerous multiplet resonances and closely overlapping peaks of different metabolites. In the presence of noise, as encountered in clinical MR scanning, including organ motion in the pelvic region, this problem becomes daunting. The capabilities of the FPT to reliably disentangle the copious spurious resonances from genuine spectral structures were put to a most stringent test. A full presentation of the performance of both variants, the \(\mathrm{{FPT}}^{(+)}\) and \(\mathrm{{FPT}}^{(-)},\) in handling noise-corrupted MRS time signals similar to those encoded from the prostate, can be found in Ref. [23]. Therein, using the \(\mathrm{{FPT}}^{(\pm )},\) the genuine resonances were identified and precisely quantified, despite the inundation of the reconstructions with spurious content. Signal-noise separation is illustrated in panels (a) and (b) of Fig. 3 for MRS data of the type of those encoded in Ref. [70] for normal glandular prostate, with added noise \(\sigma = 0.00514\) RMS (root mean square). Here, the partial signal length is \(N_{\mathrm{P}} = 1210,\) whereas the full signal length is \(N = 2048.\) Panel (a) displays the Argand plot, \(\mathrm{Im}(\nu ^-_{k,X})\) versus \(\mathrm{Re}(\nu ^-_{k,X}),\) with \(X=P\) and \(X=Q,\) for the chemical shift region between 2.45 and 3.70 ppm. Therein, pole-zero coincidence of every spurious resonance is observed (symbolized by \(\odot \)). Moreover, all the genuine poles are correctly reconstructed (as indicated by \(\otimes \)). Panel (b) of magnitudes \(|d^-_k|\) (the absolute values of the amplitudes \(d^-_k\) of all the genuine resonances) versus chemical shift shows the exact reconstruction (denoted by \(\otimes \)). Recall that for zero-valued phase \(\varphi ^-_k\) of \(d^-_k,\) i.e. for \(\varphi ^-_k=0,\) we have \(d^-_k=|d^-_k|\) from the definition \(d^-_k=|d^-_k|\exp {(i\varphi ^-_k)}.\) Notably, the very small magnitudes of PC (peak # 11) at 3.23 ppm, and one of the Tau triplets (peak # 15) at 3.275 ppm were accurately reconstructed, as were the retrieved magnitudes of all the other metabolites in the entire spectrum. The Tau triplet and two m-Ins triplets were also clearly identified and quantified in the region between 3.33 and 3.63 ppm, despite several spurious resonances in close proximity. All the spurious resonances are seen to have zero magnitudes, and are symbolized as open circles (via \(\circ \)).
5.2.3 Component spectra retrieved by the FPT using noisy MRS data corresponding to the prostate
The converged absorption component spectra are also shown in Fig. 3 for the noise-corrupted time signals (\(\sigma = 0.00514\) RMS) associated with normal glandular prostate on panel (c) and normal stromal prostate on panel (d), as generated by the \(\mathrm{{FPT}}^{(-)}\) using the FID sampled at \(N = 2048.\) The high resolution of the \(\mathrm{{FPT}}^{(-)}\) is evident, in that convergence was achieved at short partial signal lengths \(N_{\mathrm{P}} = 1210\) and \(N_{\mathrm{P}} =1220\) on panels (c) and (d), respectively. For the normal glandular case in panel (c), the tallest structures are resonances ## 4 and 5 from Cit doublets near 2.5 and 2.75 ppm, Cr (peak # 7) at \(\sim 3.04\) ppm and the very narrow Cho resonance # 10 at around 3.21 ppm. The two PA peaks (## 8 and 9) are also well delineated. A very small PC peak # 11 is observed in the component spectra. Normal stromal prostate, as shown on Fig. 3(d), also markedly differs from normal glandular prostate. The doublets of Cit doublets are much smaller, as is the PA doublet. However, unlike prostate cancer, the components of Cho are also considerably attenuated in normal stromal prostate.
5.2.4 Clinical relevance of prostate MRS data processed by the FPT
In Refs. [23, 54], we applied the FPT for the first time to noise-corrupted MRS time signals from the prostate. The capability of the FPT to handle this difficult quantification problem (which has multiplets and other overlapping resonances) with very high resolution and fidelity has been demonstrated. This provides full confidence to apply the FPT to in vivo MRS time signals encoded from the prostate, with expectations of improved diagnostic yield. The information obtained thereby is fully expected to help clinicians tackle the numerous dilemmas that arise in decision-making during and after treatment of prostate cancer [23]. There are many benefits of this research for patients at high risk or afflicted with prostate cancer. Clearly, the anticipated increased accuracy with which Padé-optimized MRS could identify patients with coexisting prostate cancer and prostatic hypertrophy versus those with only the benign condition would be a major benefit for both groups of patients. Confidence that prostate cancer is not present would be highly beneficial in that false-positive findings regarding prostate cancer are well recognized to have adverse effects, including psychological distress [123]. On the other hand, accurate and timely identification of prostate cancer is generally considered to be associated with improved prognosis [58, 59].
It should also be emphasized that there is a frequent need for volumetric coverage in prostate cancer diagnostics. Thus, the higher resolution of the FPT for MRS becomes even more critical for MRSI, since spectroscopic imaging measurements coupled with 3-dimensional spatial resolution must be done within a reasonable total acquisition time to be clinically useful. Note that the FPT applies directly also to time signals from MRSI. As mentioned, the difference between MRS and MRSI is in that the former is encoded on a single voxel, whereas the latter is the corresponding multi-voxel modality which amounts to volumetric coverage. Recall, that whenever there is a suspicion that a single voxel is not sufficiently representative of the status of the imaged tissue, MRSI is used for the corresponding volumetric coverage.
We anticipate further and broader contributions of Padé-optimization of MRS and MRSI to a more personalized approach for patients at risk or afflicted with prostate cancer. Distinguishing high from low risk prostate cancer is one of the most critical challenges. The role of MRS in active surveillance, within the “watchful waiting” option, has been emphasized [124], with its non-invasiveness being an obvious advantage over biopsy. In order to realize this potential, the precision offered by Padé-based MRS and MRSI would be a vital contribution.
Optimization of MRS and MRSI through the FPT could also be used to more confidently identify the best site(s) for prostate biopsy. Pre-surgical staging, radiation treatment planning, particularly identification of the sites for a boost dose, could be more precisely determined (target definition), with better sparing of the surrounding normal tissues. Other applications of MRS and MRSI for prostate cancer, such as detection of extracapsular extension, selecting treatment modality as well as timing and assessing tumor regression versus recurrence after treatment [63,64,65, 125] are also expected to be much more effective with the accuracy provided by the FPT.
5.3 The FPT applied to noisy MRS time signals from breast cancer
We will herein summarize the results of our investigations [24, 47, 54] applying the FPT to synthesized noise-corrupted MRS time signals, based upon encoded in vitro data from extracted breast cancer specimens [80]. In Fig. 4, we recapitulate the procedure of signal processing. The input data are comprised of simulated, noise-corrupted complex time signals, the real part of which is shown on panel (a). The corresponding imaginary part (not shown to avoid clutter) is similar. This time signal is associated with the breast cancer specimen. Gaussian random zero-mean white noise was added with the standard deviation \(\sigma = 0.0289\) RMS.
Most importantly, it should be noted that metabolic content of this cancerous breast tissue is all contained within the input MRS time signal. However, this information cannot be visualized without mapping the time signal into the frequency domain, so that a spectrum can be constructed. This mapping through mathematical transforms is permitted, since time and frequency constitute a pair of “conjugate variables”.
Signal processing in MRS with data reminiscent of those encoded from breast cancer in Ref. [80]. The real part of the FID, \(\{c_n\},\) from Eq. (2.1) with added noise \(\sigma =0.0289\) RMS (a). Non-converged absorption envelopes reconstructed by the FFT at \(N=2048\) (b). Converged absorption envelopes reconstructed by the \({\text{ FPT }}^{(-)}\) at \(N_{\text{ P }} = 1700\) (c). Converged components in the \({\text{ FPT }}^{(-)}\) at \(N_{\text{ P }} = 1700\) (d). On (e) and (f), genuine metabolites (within the dashed frames) are stable at two noise levels \(\sigma =0.00289\) RMS and \(\sigma =0.0289\) RMS differing by a factor of 10, notwithstanding occasional proximity of poles and zeros. Spurious resonances, outside the frames on (e) and (f) show complete pole-zero coincidence and are unstable across the said 2 noise levels. Converged metabolite concentrations (g) as computed at \(N_{\text{ P }} = 1700\) via the \({\text{ FPT }}^{(-)}\) (circles). On (h), seen are the non-zero peak heights for genuine resonances and zero heights for spurious peaks. The input data are denoted throughout by the exes (x) (color online)
5.3.1 Construction of the MRS time signals related to breast cancer
Using Eq. (2.1), we constructed the simulated FID corresponding to the MRS time signals encoded for breast cancer [80]. The time signal was comprised of \(K=9\) damped complex exponentials \(\exp {(i\tau \omega _k)}\) multiplied by stationary amplitudes \(\{d_k\},\) with \(|d_k|=C_k/C_{\mathrm{ref}}\) where \(C_k\) is the concentration of the \(k\,\)th metabolite and \(C_{\mathrm{ref}}\) is the reference concentration, \(C_{\mathrm{ref}} = 0.05\) mM/g. The input data for the magnitudes \(\{|d_k|\}\) were derived from the \(k\,\)th median concentrations expressed in \(\mu \) M/g of wet weight (ww) of metabolites, as reported in Ref. [80]. Further, in Ref. [80], the MRS time signals of length \(N = 65536\) (64 kB) were recorded at a Larmor frequency \(\nu _{\mathrm{L}}=\)600 MHz corresponding to a static magnetic field strength \(B_0=14.1 \mathrm{T}.\) The used bandwidth is BW=6 kHz. The linewidths were set to be 0.0008 ppm. The peaks in the spectrum were Lorentzians. The phases \(\varphi _k (1\le k\le 9)\) from generally complex amplitudes were all set to zero, so that \(d_k=|d_k|\) [24, 47, 54].
Note that here, in the illustrations, Lac and Ala are not shown, since their resonant frequencies are 1.332 and 1.471 ppm, respectively, while the spectra in Fig. 4 are for the SRI between 3.2 and 3.3 ppm, where the other seven metabolites are located [2, 24, 41, 47].
5.3.2 Comparison of the performance of the FFT and FPT for breast cancer MRS data
Comparing the performance of FFT with the FPT for noise-corrupted data associated with breast cancer clearly demonstrates the superior resolution capacity of the FPT relative to the FFT under the same conditions [21, 24, 45, 47]. It is via the FFT that mapping from the time to the frequency representation is performed automatically in MR scanners. Consequently, FIDs such as that in panel (a) are not even viewed. In panel (b) of Fig. 4, the FFT spectrum is shown at the full signal length \(N = 2048,\) where it is comprised of crude peaks and a jagged baseline, from which no diagnostic conclusion could be drawn.
In panel (c), the converged total shape spectrum is generated via the FPT at \(N_{\mathrm{P}} = 1700\) from which six peaks can be identified at their correct chemical shift locations. Already from the heights of these peaks, substantial information can be extracted concerning the relative concentrations of several metabolites including some of the components of tCho. This information is provided by the FPT at a very short signal length, while the FFT would need a 32 times longer signal (\(32 \times 2048 = 65536,\) corresponding to 64 kB) to produce a spectrum such as that from the FPT on panel (c).
The converged envelope shown in panel (c) of Fig. 4 is the most that the FFT could ever generate at 64 kB, insofar as conditions were optimal, namely high magnetic field strength, ideal coil design, maximum care taken to properly encode the time signals, with excellent shimming and other technical aspects. In particular, from the envelopes due to both the FFT and FPT on panels (b) and (c), respectively, in the chemical shift region between 3.2 and 3.3 ppm, there is no clue that PC lies therein, i.e. that there is a PC peak buried under the much larger phosphoethanolamine (PE) resonance, as shown in the Padé component shape spectra of panel (d).
5.3.3 Signal-noise-separation by the FPT for MRS data from breast cancer
For simulated noiseless data associated with breast cancer, as per encoding in Ref. [80], convergence was achieved at a partial signal length \(N_{\mathrm{P}} = 1500,\) such that some 741 spurious resonances were generated [2, 41]. With added random noise of \(\sigma = 0.0289\) RMS, a bit longer partial signal length was needed (\(N_{\mathrm{P}} = 1700)\) [24]. Consequently, there were 841, i.e. 100 more spurious resonances. In order to distinguish these copious non-physical resonances from the genuine metabolites, all facets of the SNS were utilized, i.e. pole-zero coincidence, zero amplitude as well as instability with change in noise level and/or with varying truncations of the total acquisition time, T.
The SNS process is illustrated in panels (e), (f) and (h) of Fig. 4 for the chemical shift region between 3.16 and 3.34 ppm. Slightly wider chemical shifts are used in panels (e), (f) and (h) to display more spurious resonances. In panels (e) and (f) to obviate clutter, the full width at half maximum (FWHM) is doubled at the location of PC at 3.220 ppm, with PC denoted as PC*. A question could arise for the near zero peak height and pole-zero proximity of Cho (peak # 3), but its complete stability with a tenfold increase in noise level on panel (f) relative to panel (e) firmly indicates that this is a genuine metabolite. In sharp contrast, the spurious resonances exhibited not only zero peak heights and pole-zero coincidence, but also marked change in their FWHM with the tenfold increase in noise levels by reference to panels (e) and (f). Thus, stability is key for full confidence in distinguishing true from false resonances. Overall, through the Padé-based SNS procedure, the genuine metabolites comprising barely 1% of the generated resonances were not only identified, but also exactly quantified. The latter include the strongly overlapping PE and PC resonances.
5.3.4 The FPT identifies and quantifies phosphocholine as the prime breast cancer biomarker
The FPT can go beyond tCho, identifying and quantifying the breast cancer biomarker PC. As shown in Refs. [2, 24, 41, 47], PC was unequivocally identified and its concentration computed exactly through the parametric \(\mathrm{FPT}^{(+)}\) with the presence of random noise of \(\sigma = 0.0289\) RMS. The \(\mathrm{FPT}^{(+)}\) also accomplished this task for breast data with 100 times higher noise levels (\(\sigma = 2.89\) RMS) [24]. Panel (g) of Fig. 4 displays a metabolite map for the exactly Padé-reconstructed concentrations (as symbolized by \(\otimes \)), within the chemical shift region between 3.2 and 3.3 ppm on the abscissa. Here, the ordinate is metabolite concentration. In addition to the graphic representation via the symbols of open circles, the corresponding retrieved numerical data are also listed next to each of the seven metabolites. Therein lie seven genuine metabolites, including PC which resonates at nearly the same chemical shift (3.220 ppm) as PE (3.221 ppm).
In this analysis, we have considered diagnostically informative metabolites whose concentrations are exactly computed via the FPT. Besides the breast cancer biomarker PC, these concentrations also refer to \(\beta -\)Glc [126], Tau (a possible biomarker of apoptosis) [127] and m-Ins (a rapidly-decaying metabolite that may help identify fibroadenomas) [42, 128], as well as Lac [42]. Padé optimization opens many possibilities for multi-variate exploration to identify metabolite patterns that best characterize various types and grades of breast cancer and distinguish these from benign breast pathology that often pose differential diagnostic dilemmas.
5.3.5 Visualization of PC in partitioned envelopes from the non-parametric FPT
Recently, we introduced and tested a new procedure for visualizing hidden components of envelopes non-parametrically through the partitioned spectra [3, 4]. The pertinent mathematical features are briefly presented in the theory section. Heretofore, in all the studies applying the FPT to process MRS data associated with breast cancer, it was exclusively through parametric processing that the PC resonance could be identified. As indicated, from an inspection of the absorption total shape spectrum provided by the non-parametric FPT, the smooth peak at \(\sim 3.22\) ppm gives no hint whatsoever that there might be a PC peak beneath the far more abundant PE resonance, as per Fig. 4(c) and the top panel of Fig. 5.
The partitioned and non-partitioned absorption envelopes computed non-parametrically in the \(\mathrm{FPT}^{(+)}\) by using the noiseless FID, sampled at \(N = 16384\) and truncated at \(N_{\mathrm{P}} = 6000\, (K = 3000).\) Along the abscissae of each panel are the input chemical shifts. The definitions of the displayed spectra \(A^+_K\) and \(B^+_K\) are on the titles of (b) and (c), respectively. On (d), displayed again are the data from (b) and (c) alongside the curve for \(A^+_k+B^+_K.\) On (a), the black and blue curves for \(\mathrm{Re}(P^+_K/Q^+_K),\) computed with and without partitioning, respectively, are indistinguishable. For a discussion and the meaning of color-coding for circles, see the main text (color online)
We have noted that the key advantage of the FPT, as a quotient of two polynomials \(P_K/Q_K,\) is its automatically included polar representation. We thus raised the question as to whether more information could be gleaned via the non-parametric FPT applied to MRS time signals than has heretofore been the case. Namely, would it be possible to further explore the additional degree of freedom via the two polynomials of the FPT relative to the single polynomial of the FFT vis-à-vis reconstruction of spectral envelopes alone?
With or without spectra partitioning, the non-parametric analysis through the \(\mathrm{FPT}^{(\pm )}\) is the necessary initial step for processing MRS time signals. This step generates the expansion coefficients \(\{p^\pm _r\}\) and \(\{q^\pm _s\}\) of the Padé polynomials \(P^\pm _K\) and \(Q^\pm _K,\) respectively. Therefore, the total shape spectra or envelopes \(P^\pm _K/Q^\pm _K\) can immediately be computed at any desired set of the sweep frequencies, not just those from the Fourier grid, \(2\pi k/T\, (k=0,1,2,\ldots , N-1).\) The polynomial expansion coefficients are reconstructed directly from the input time signal \(\{c_n\}.\) The non-parametric signal processing by the \(\mathrm{FPT}^{(\pm )}\) requires no polynomial rooting and, thus, no solving of the MRS quantification problem.
Within the concept of partitioning, the mentioned additional degree of freedom in the non-parametric complex spectrum \(P_K/Q_K\) consists of an alternative way of computing \(\mathrm{Re}(P_K/Q_K)\) and \(\mathrm{Im}(P_K/Q_K).\) Conventionally, for \(d_k=|d_k|\) with \(\varphi _k=0\), these latter absorption and dispersion spectra are obtained directly from the computer using the complex-valued entry \(P_K/Q_K.\) Alternatively, the analytical expression for e.g. \(\mathrm{Re}(P_K/Q_K)\) can be derived first in the form of two partitioned spectra, \(A_K\) and \(B_K.\) Similarly, the analytical expression for \(\mathrm{Im}(P_K/Q_K)\) also contains its own two partitioned spectra, \(C_K\) and \(D_K.\) The sum of the partitioned spectra \(A_K\) and \(B_K\) is the complete absorption spectrum, \(A_K+B_K=\mathrm{Re}(P_K/Q_K).\) Likewise, when the partitioned spectra \(C_K\) and \(D_K\) are added together, the complete dispersion spectrum \(C_K+D_K=\mathrm{Im}(P_K/Q_K)\) is obtained. Thus, our nomenclature is to call \(\mathrm{Re}(P_K/Q_K)\) the complete absorptive envelope when generated by way of the sum \(A_K+B_K.\) By the same token, \(\mathrm{Im}(P_K/Q_K)\) is termed the complete dispersive envelope if it is obtained from the sum \(C_K+D_K.\) It is the analytical expressions for \(A_K, B_K, C_K\) and \(D_K\) that we feed separately into the computer. The ensuing numerical results are graphed to visualize the partitioned absorption envelopes \(A_K\) and \(B_K,\) as well as the partitioned dispersion envelopes \(C_K\) and \(D_K.\) The partitions \(A_K\) and \(B_K\) in \(\mathrm{Re}(P_K/Q_K)\) as well as \(C_K\) and \(D_K\) in \(\mathrm{Im}(P_K/Q_K)\) redistribute the interference effect. It is the interference of \(A_K\) and \(B_K\) in \(A_K+B_K\) that prevents splitting of adjacent overlapping resonances. In a rearranged interference followed by plotting \(A_K\) and \(B_K\) separately, the individual resonances have a chance to “pop up” and, thus, split apart the compound peaks in \(A_K+B_K.\) Therefore, we computed the partitioned envelope spectra from \(A_K, B_K, C_K\) and \(D_K.\) As a check, the results for the complete absorption partition \(A_K+B_K\) and the complete dispersion partition \(C_K+D_K\) must be shown to coincide with the conventional absorption \(\mathrm{Re}(P_K/Q_K)\) and the conventional dispersion \(\mathrm{Im}(P_K/Q_K)\) envelopes, respectively.
Figure 5 displays the partitioned and non-partitioned absorption envelopes computed non-parametrically in the \(\mathrm{FPT}^{(+)}.\) All the reconstructions are performed using a partial signal length \(N_{\mathrm{P}} = 6000\, (K=3000)\) of the full signal length \(N=16384.\) This N itself is only a quarter of its encoded counterpart from Ref. [80]. Along the abscissae of each panel are the input chemical shifts in the spectral region between 3.205 and 3.290 ppm. These are symbolized by circles that are mainly open and shown in black. The two exceptions with the filled green and magenta circles relate to PC and PE, respectively. The colored filling is shown only when the PC and PE lineshapes are peaked practically at their correct locations 3.220 and 3.221 ppm, respectively. This is the case in panels (b) and (c), where PC and PE are separately visualized, although both circles are not simultaneously filled. Therein, the PC and PE peaks are centered almost precisely at 3.220 and 3.221 ppm only on panels (b) and (c), respectively. For this reason, panels (b) and (c) each have only one filled circle. On panel (b), the PE peak is slightly shifted to the left from the associated input fundamental frequency 3.221 ppm, and its circle if left unfilled. Similarly, on panel (c), the PC peak is slightly shifted to the right of its exact location at 3.220 ppm, and the open circle is seen therein. However, on panel (d), both circles for PC and PE are filled, since therein the entire partitioned spectra from panels (b) and (c) are displayed together. Panel (b) shows the partial envelope spectrum for \(A^+_K.\) Therein, PC and PE are clearly distinguished as two separate peaks of fairly comparable heights, and the five other resonances are also identified. Panel (c) exhibits the partitioned envelope spectrum for \(B^+_K.\) Here, once again, PC and PE are clearly seen to be two separate, adjacent peaks, with PE being more prominent than PC.
Further, taurine and \(\beta -\)Glc show much smaller peak heights in the partial envelope spectrum for \(B^+_K\) compared to that for \(A^+_K.\) These latter two partial envelope spectra are displayed jointly in panel (d), with the same color coding as in panels (b) and (c): green for \(A^+_K\) and magenta for \(B^+_K.\) In addition, shown on panel (d) is the summed envelope \(A^+_K+B^+_K,\) indicated in black, where only a single compound peak PC + PE can be identified in the interval [3.220, 3.221] ppm. It can be seen on panel (a), that the complete absorption envelope \(A^+_K+B^+_K\) is indistinguishable from the related non-partitioned absorption envelope \(\mathrm{Re}(P^+_K/Q^+_K),\) both of which display a symmetrical and smooth single Lorentzian peak in the range [3.220, 3.221] ppm, without any indication whatsoever that more than one peak may be present therein.
The most notable feature of the absorption spectra displayed in Fig. 5 is that the PC and PE peaks appearing in both partitions \(A^+_K\) and \(B^+_K\) are so well delineated that the dips between them descend all the way down to the background or baseline of zero-valued ordinates. On panel (b), it appears as if \(A^+_K\) were in need to push PE a bit upstream in order to place PC at its correct position, 3.220 ppm. Likewise, on panel (c), it is seen that \(B^+_K\) acts as if it were necessary to push PC a bit downstream so that PE could be centered at the corresponding correct location, 3.221 ppm. These slight dislocations in PE or PC within \(A^+_K\) or \(B^+_K\) on panels (b) or (c) are due to the minimal distance of merely 0.001 ppm between the input chemical shifts of 3.220 and 3.221 ppm of PC and PE, respectively. Moreover, such an incremental separation of 0.001 ppm between the two values of chemical shift, \(\mathrm{Re}(\nu _k),\) for PC and PE is smaller than the sum 0.0016 ppm of their associated individual values of \(\mathrm{Im}(\nu _k).\) All the resonances have the same exceedingly small values for \(\mathrm{Im}(\nu _k)\) that are \(\mathrm{Im}(\nu _k)=0.0008\) ppm. Given that the imaginary frequency \(\mathrm{Im}(\nu _k)\) is the measure of the breadth of an absorptive Lorentzian resonance, it is understandable why the individuality of PC and PE is masked under the combined PC and PE peak on panel (a) of Fig. 5.
Detailed analysis in Refs. [3, 4] confirmed the trustworthiness of this partitioning procedure by reference to the Padé parametric processing. The latter estimation is the gold standard which not only visually separates the overlapping peaks, but also performs their exact quantification. These findings have a clear intrinsic significance for signal processing. At the same time, they possess a practical importance. Namely, partitioning would be a convenient initial, qualitative “screening” step (in the sense of pre-processing) to assess whether or not the cancer biomarker PC is identifiably present or absent. Subsequently, the retrieval of the physical peak positions, widths, heights and phases would follow in two totally different, cross-checking ways via parametric and non-parametric Padé estimations. In the customary parametric FPT for explicitly solving the quantification problem, one can have a special focus upon those cases in which PC was identified firstly by non-parametric partitioned envelopes. On the other hand, the dFPT deals exclusively with non-parametrically computed envelopes, to which the higher-order derivative transforms are applied, yielding the exact peak positions, widths, heights and phases of all the genuine resonance. On the basis of the obtained concordant quantitative results, from these two complementary procedures (parametric/non-derivative and non-parametric/derivative), it would be important to apply such a multi-faceted Padé methodology to in vivo data, aimed at validation of partitioned spectra for breast cancer diagnostics, and beyond.
5.3.6 Exact quantification by non-parametric derivative envelopes in the dFPT
The salient features of the dFPT have been illustrated for noiseless and noisy time signals reminiscent of data encoded by in vitro MRS from excised breast cancer tissue [5,6,7]. In breast tumor diagnostics via MRS reliable identification and quantification of PC is a very demanding task for any non-parametric signal processor. This occurs because the PC resonance is completely invisible in customary zeroth-order (\(m=0\)) derivative envelopes due to the dominant adjacent resonance of phosphoethanolamine, PE. Recall that the PC-to-PE chemical shift separation is only 0.001 ppm. These latter two metabolites sharply differ in abundance. Their respective concentrations are \(C_{\mathrm{PC}} = 0.3\) and \(C_{\mathrm{PE}} = 2.25\, \mu \mathrm{M/g}\) of wet weight, ww, of the scanned tissue. The dFPT successfully solves this problem by clearly identifying and quantifying all the genuine resonances, including that of PC. Thereby, on the same screen, not only is the PC-PE separation visualized and exactly quantified, but so are the concentrations of these two metabolites, alongside the corresponding numerical parameters for all the other molecules. Thus, the higher-order differentiation transform, when used in conjunction with the dFPT simultaneously achieves resolution enhancement, noise suppression and exact quantification, despite explicit non-parametric processing of envelope lineshapes alone (i.e. without solving the quantification problem at all). This high resolution implies higher specificity of dMRS relative to MRS, which, in itself, is already more specific than MRI.
Derivative magnetic resonance spectroscopy, dMRS, for breast cancer diagnostics. Derivative fast Padé transform, dFPT, versus derivative fast Fourier transform, dFFT, for a wider range with 9 peaks. Derivative operator \(D_\nu \equiv {\text{ d }}/{\text{ d }}\nu \) (relative to the sweep frequency \(\nu \)) of order m is \(D^m_\nu =({\text{ d }}/{\text{ d }}\nu )^m.\) On (a) and (b), for two different frequency intervals, shown are the absorption spectra in the non-derivative \({\text {FPT}}^{(-)}\) computed with a synthesized FID corrupted by random zero-mean Gaussian white noise of standard deviation \(\sigma =0.0289\) RMS. All the peak heights for the derivative spectra in the \({\text {dFPT}}^{(-)}\) with \(m=6,24\) and 50 on (c), (d) and (e), respectively, are normalized to the non-derivative \((m=0)\) absorptive peak height of lactate at 1.332 ppm from (b). On (f), the dFFT amplifies noise even at a low order, \(m=6\) (color online)
Derivative magnetic resonance spectroscopy, dMRS, for breast cancer diagnostics. Non-parametric (blue) versus parametric (red) dFPT for a narrow range with 2 overlapped peaks, phosphoethalomine, PE and phosphocholine, PC, separated by mere 0.001 ppm of chemical shift. Derivative operator \(D_\nu \equiv \mathrm{d}/\mathrm{d}\nu \) (relative to the sweep frequency \(\nu \)) of order m is \(D^m_\nu =(\mathrm{d}/\mathrm{d}\nu )^m.\) The peak heights for derivative spectra (\(m>0\)) on (e) are normalized to the non-derivative \((m=0)\) absorptive peak height of lactate at 1.332 ppm from Fig. 6(b). No normalization on (a)–(d) nor on (f)–(h) (color online)
These results are illustrated in Figs. 6 and 7 for an extended and narrow frequency range, respectively. Both Figs. 6 and 7 consider the same noisy time signal (with added white noise of \(\sigma = 0.0289\) RMS) used in Figs. 4 and 5, as generated on the basis of the corresponding encoded FID from Ref. [80]. The spectral envelopes from non-parametric, non-derivative FPT in the absorption mode are shown on panels (a) and (b) of Fig. 6 in two different frequency intervals, where Lac peak on panel (b) appears as the largest resonance. On panel (a), all the isolated resonances (Cho at 3.21 ppm, GPC at 3.23 ppm, \(\beta -\)Glc at 3.25 ppm, Tau at 3.27 ppm and m-Ins at 3.28 ppm) are clearly resolved and correctly quantified by the FPT. However, the Lorentzian absorption lineshape (i.e. completely symmetrical) at 3.22 ppm gives no hint that there is a PC peak underlying PE. Panel (c) is the magnitude of the 6th derivative of the complex envelope in the dFPT, with a rightward bulge near 3.220 ppm suggesting the presence of PC. All the singlet resonances are exactly reconstructed and the baseline is flattened, especially when juxtaposed to panel (a). At two high-order derivatives, \(m = 24\) and \(m = 50\) on panels (d) and (e), respectively, in addition to all the singlet resonances, it is observed that also PC and PE are completely resolved and exactly quantified. The extremely narrow symmetric Lorentzian peaks (from their tips to bottoms) in the magnitudes of the \(m\,\)th derivative complex envelopes for \(m = 24\) and \(m = 50\) solve a practical problem encountered with conventional non-derivative \((m=0)\) lineshapes. Namely, extended Lorentzian tails mask adjacent and even distant spectral structures of potentially informative content. This is recognized as the “leakage problem” in MRS. The high-order derivative envelopes circumvent this problem by nullifying the tails and exactly determining the peak areas, thus yielding the correct concentrations.
In sharp contrast to the noise suppression achieved by the dFPT, the derivative fast Fourier transform, dFFT, hugely amplifies noise even at low differentiation order m, such that all genuine information is lost, as seen on panel (f) in Fig. 6. This is because the dFFT processes the product of the power function \(t^m\) with the time signal c(t), where \(t^m\, (m=1,2,3,\ldots )\) puts higher weight on the later time signal points, dominated by noise.
Figure 7 zooms into the region [3.219, 3.222] ppm containing only PE and PC. On panel (a) of Fig. 7, the non-derivative, non-parametric FPT \((m=0)\) gives a broad peak where PC is completely hidden (blue). Here, the components from the parametric FPT are in red. On panel (e) of Fig. 7, the dashed line displays the 6th derivative envelope with narrower lineshapes and a rightward bulge corresponding to PC. The full line is the 50th derivative envelope, where PC and PE are fully separated and their peak heights exactly quantified. Panels (b–d) and (f–h) of Fig. 7 compare the parametric dFPT (red) and non-parametric dFPT (blue). With increased derivative order m, the non-parametric dFPT for envelopes exactly reconstructs the components of the parametric dFPT, as seen for \(m=24\) and \(m=48\) on panels (g) and (h), respectively. The peak signatures (positions, heights, widths) reconstructed by the non-parametric dFPT in the magnitude mode of any derivative order \(m>0\) are uniquely related to their absorptive parametric counterparts from the parametric FPT (\(m = 0\)) [6, 7]. This is critical as it permits straightforward interpretation and extraction of peak areas and associated metabolite concentrations from the dFPT. This demonstrates that in the controlled setting, the higher order non-parametric dFPT is a stand-alone, streamlined method for clear display with identification and exact quantification of key metabolic information, including that for PC [5,6,7].
5.4 Applications of the FPT to MRS time signals from the brain
5.4.1 Initial proof-of-principle studies on brain MRS
Extensive controlled studies [2, 31, 32, 35, 129] have been performed applying the FPT to synthesized MRS time signals typical of those encoded in vivo from the brain of a healthy volunteer at 1.5T [130]. Therein, the input set of some 100 spectral parameters (4 real-valued entries per resonance) was reconstructed from which the concentrations of 25 metabolites were accurately computed. Metabolites were included for which chemical shifts differed only by 0.001 ppm. It was demonstrated that even the closest of overlapping resonances can be precisely quantified by the FPT. The SNS procedure was also effectively carried out through the \(\mathrm{FPT}^{(+)}\) and \(\mathrm{FPT}^{(-)}\) on simulated noiseless and noise-corrupted MRS time signals similar to those encoded from normal human brain [2, 31, 32, 35, 50, 51].
In the more recent proof-of-concept study [37], the \(\mathrm{FPT}^{(+)}\) was applied to MRS time signals encoded from the standard GE phantom head on a 1.5T MR scanner. Six among the major metabolites, i.e. NAA, glutamate (Glu), Cr, Cho, m-Ins and Lac that are also detectable via MRS scans of in vivo human brain were contained in the phantom head. Using the parametric \(\mathrm{FPT}^{(+)},\) fully accurate quantification was achieved. We scrutinized the convergence process to verify the stability of the reconstructed spectral parameters. Through “parameter averaging”, it was shown that the reconstructed complex-valued fundamental frequencies \(\{\nu ^+_k\}\) and amplitudes \(\{d^+_k\}\) were accurately determined. This was the case even for dense spectral regions, where small and/or very closely overlapping resonances were located. Such results justified applying Padé-optimized MRS to encoded in vivo data within neuro-oncology, as discussed next.
5.4.2 Padé processing of in vivo MRS time signals encoded from healthy human brain
\(\bullet \) High resolution of the FPT in reconstructing total shape spectra
Several of our early investigations applying the FPT were performed on MRS time signals encoded in vivo [1, 2, 30, 33, 34, 131]. These initial studies analyzed FIDs from normal healthy brain, and were carried out on high field MR scanners (4 and 7T). Comparisons with the FFT revealed a markedly superior performance of the FPT in generating fully converged total shape spectra [1, 2, 30, 33, 34]. Notably, the FPT showed better resolution than the FFT for the same signal length. Moreover, the FPT could attain the same resolution as the FFT by utilizing twice shorter signals. These findings were noted to be particularly important for MRSI. Self-contained error analysis was demonstrated using the two FPT variants, the \(\mathrm{FPT}^{(+)}\) and \(\mathrm{FPT}^{(-)},\) whereby their difference was on the level of background noise [131].
\(\bullet \) Practical implementation of SNS using data from a clinical scanner at 1.5T
In a subsequent study carried out on a 1.5T scanner [36], by adding noise to the already noisy MRS time signal, signal-noise-separation, SNS, was achieved. Namely, the FID was corrupted by adding random zero-mean 5% Gaussian white noise. Good statistics were achieved via 50 distinct realizations of this noise by altering the input seed numbers to the computer generator of random numbers, yielding 50 noisy FIDs of the same type, but comprised of different random numbers. When these different noisy sets were added to the original MRS time signal, 50 noise-corrupted time signals were generated. Each FID was subjected to parametric analysis by the FPT, with reconstruction of 50 sets of frequencies and amplitudes. When the fundamental frequencies and amplitudes were nearly the same for all the 50 FIDs, this binned the reconstructions as genuine. Concordantly, all the retrieved unstable spectral parameters were associated with spurious resonances. Via this procedure, some 23 stable resonances were identified from the in vivo encoded MRS time signals [36]. Further parametric analysis by the FPT has been performed by other investigators on in vivo encoded MRS data from healthy human brain in Refs. [132,133,134,135]. Two of these studies are PhD Theses [133, 134].
5.4.3 The FPT applied to encoded in vivo MRS time signals: pediatric brain tumor and cerebral asphyxia
More recently, the FPT has been used to process MRS time signals encoded in vivo on a 1.5T MR scanner from a child with a brainstem glioma [8] and from a child who had suffered cerebral asphyxia [9, 49]. Therein, through the FPT, closely overlapping resonances, including cancer biomarkers [8, 9, 49], were successfully resolved and quantified. As noted, the choice of these clinical problems is of utmost importance for PCM. Specifically, this refers to distinguishing non-tumorous cerebral hypoxia/ischemia from brain tumors, which also often contain hypoxic regions that promote genomic instability and are associated with the invasive/metastatic process.
At the shortest echo time (TE) for which spectra are most dense, the \(\mathrm{FPT}^{(-)}\) resolved the abundant overlapping resonances, including short-lived metabolites such as m-Ins. By activating protein C kinase, it occurs that m-Ins causes production of proteolytic enzymes and, therefore, it has been considered to be associated with brain tumors. Heretofore, however, uncertainties associated with the use of short TEs have rendered conclusions tenuous concerning the diagnostic significance of m-Ins. Closely-overlapping resonances were also resolved by the \(\mathrm{FPT}^{(-)},\) such as NAA, Glu and N-Acetylaspartylglutamic acid (NAAG) centered near 2.04 ppm, Cr and phosphocreatine (PCr) at \(\sim 3.0\) ppm as well as free Cho and PC at \(\sim 3.2\) ppm. Thus far, cancer biomarker PC has not been detected by the FFT with in vivo proton MRS of the brain, or elsewhere, as noted, due to close overlap with the neighboring resonances.
\(\bullet \) Successful strategies for handling the residual of the giant water resonance
The real (a) and imaginary (b) parts of the FID, \(\{c_n\},\) encoded in vivo on a 1.5T scanner (corrected for zero-order phase \(\varphi _0=-2.2220\) rad) from a brainstem glioma in a 4 year old patient at TE = 136 ms, with 512 data points. Water residual distorts these wave forms. Real (c) and imaginary (d) parts of the reconstructed FID with a box window suppression of the water residual. Therein, the wave forms are regularized and seen as being symmetric around the abscissae. The real part of the complex envelope reconstructed by the non-parametric \(\mathrm{FPT}^{(-)}\) (e) from the encoded FID. The real part of the envelope computed by the non-parametric \(\mathrm{FPT}^{(-)}\) from the reconstructed FID (f) (color online)
A major problem with MRS data encoded from clinical 1.5T scanners is the large residual water resonance. We initially introduced an information-preserving windowing procedure via a step function using the non-parametric FPT to suppress residual water. A new time signal was generated by inverting the windowed spectrum. Importantly, the components within the SRI were not affected. Some expected shape distortions at the edges, outside the SRI, were inconsequential [8]. These findings are illustrated in Fig. 8, where panels (a) and (b) display the real and imaginary parts, respectively, of the raw time signal encoded at TE = 136 ms from the patient with a glioma. This FID was subsequently corrected by the zero-order phase \(\varphi _0=-\,2.2220\) rad, where “rad” denotes radian. The water residual is unsuppressed in these FIDs, such that the wave forms are asymmetrical around the abscissae. The real and imaginary parts of the complex reconstructed FID, \(\{c_n\},\) on panels (c) and (d), respectively, are seen as being regularized around the abscissae. From these encoded and reconstructed FIDs, the real part of the total shape spectrum is displayed on panels (e) and (f), respectively, as generated by the non-parametric \(\mathrm{FPT}^{(-)}.\) In panel (e), the real part of the total shape spectrum is presented, as reconstructed by the non-parametric \(\mathrm{FPT}^{(-)}\) from the FID without suppression of residual water. The total shape spectra in panels (e) and (f) are identical in the SRI between \(\sim \) 0.5 and 4.0 ppm. At the edges outside the SRI, some anticipated, but non-essential discrepancies can be observed, as stated. For further insight, see also panel (c) of Fig. 9, where these two curves are overlain (green: residual water unsuppressed, blue: residual water suppressed). The same Padé envelope from panel (f) of Fig. 8 has also been reconstructed by parametric processing in the \(\mathrm{FPT}^{(-)}.\)
Shown on (a) and (b) are the real parts of the complex envelopes reconstructed by the non-parametric \(\mathrm{FPT}^{(-)}\) and the FFT, respectively, from the encoded, water-unsuppressed FID, as per Fig. 8. On (c), we display the real parts of the envelopes generated by the non-parametric \(\mathrm{FPT}^{(-)}\) without residual water suppression (green curve) and from the reconstructed FID with suppressed water (blue curve). The real part of the Usual and Ersatz component spectra are on (d) and (e), respectively, computed by the parametric \(\mathrm{FPT}^{(-)}\) from the reconstructed FID with residual water suppressed (color online)
Overall, complete equivalence of the total shape spectra generated non-parametrically and parametrically in the FPT was confirmed within the SRI. Having this confirmation, we subsequently applied the parametric FPT [9] using only the components with chemical shifts from the SRI chosen to avoid the residual water resonance. In this way, computing the parametrically generated envelopes via \(P^+_K/Q^+_K\) by utilizing the Heaviside partial fraction sum from Eq. (2.19), the water residual suppression problem could be entirely solved without any windowing.
\(\bullet \) Practical importance of suppressing spectral structures around water residual
Whether via the CHEmical Shift Selective (CHESS) pulses, inversion recovery, ”Water suppression through the enhanced \(T_1\) effects” (WET), or other techniques for suppressing water during the encoding, a huge water residual still remains. The originally giant water resonance (\(\sim \) 10000 times larger than any other resonance) is explained by the fact that tissue contains \(\sim \) 70% water. With Fourier-based processing, the procedure for handling residual water is usually via the HLSVD whereby the residual water structures are partially suppressed by fitting them to 3–10 unphysical resonances. As a consequence, the HLSVD procedure introduces spuriousness into the spectral analysis. We have now confirmed that the best strategy is via the expounded parametric FPT. Thereby, the spectral region of interest, SRI, can be chosen to bypass the giant water resonance, automatically generating spectral envelopes (using only the components from the SRI) without the need for windowing. This solves yet another important stumbling block for wider clinical applications of in vivo MRS using the FPT.
\(\bullet \) High resolution of the FPT in reconstructing envelopes and their components
In Fig. 9, we continue with analysis of the processing of the FID encoded from the patient with a brainstem glioma. Therein we present the real parts of the total shape spectrum in the frequency window between 0.75 and 4.25 ppm, as reconstructed by the non-parametric \(\mathrm{FPT}^{(-)}\) and the FFT on panels (a) and (b), respectively, at TE = 136 ms, employing the full signal length \(N = 512\) with the residual water content retained.
As is typical of brain tumors, the peak at \(\sim \) 3.2 ppm, corresponding to Cho plus PC, is notably larger than the peaks centered at \(\sim \) 2.0 ppm, assigned to NAA, and at \(\sim \) 3.0 ppm associated with Cr plus PCr. However, with the FFT, the peaks at \(\sim \) 3.0 and 3.2 ppm are severely blunted, as are most of the structures in the chemical shift region to the left of the Cho plus PC peak.
Besides the superior resolution of the \(\mathrm{FPT}^{(-)}\) in computing the total shape spectrum, further insights are provided by the Padé parametric analysis from which the Usual and Ersatz spectra on panels (d) and (e), respectively, are reconstructed (with residual water suppressed). In panel (d), the amplitudes \(\{d^-_k\}\) are all complex-valued because the reconstructed amplitude phases \(\{\varphi ^-_k\}\) are non-zero as are the phases \(\{\varphi _k\}\) in the encoded FIDs. Consequently, there is an admixture of absorption and dispersion components, especially in the spectrally dense region from \(\sim \) 3 to \(\sim \) 4.3 ppm. The small Lac doublet at \(\sim \) 1.3 ppm is seen on panels (c) and (d) to be inverted below the baseline (\(180^\circ \) out of phase) due to \(J-\)coupling.
The Ersatz component spectra are helpful for recognizing closely overlapping resonances, such as Cho and PC at \(\sim \) 3.2 ppm, as well as NAA, NAAG and gamma amino butyric acid (GABA) at \(\sim \) 2.0 ppm and the abundant resonances in the crowded region from 3.8 to 4.2 ppm. Note, however, that insofar as the phases are non-zero, which is most often the case, the interference effects must be considered, such that the Usual components with complex amplitudes should be employed to compute metabolite concentrations.
\(\bullet \) Spectra averaging as a successful strategy for separating signal from noise with in vivo encoded MRS
For in vivo MRS, large noise-like spikes often appear when model order K is changed, as noted. We developed an averaging procedure with the aim of regularizing spectra. The average envelope versus frequency can be viewed as analogous to “signal averaging” done in the time domain to enhance SNR. Advantageously, however, spectra averaging can be repeated any number of times due to efficient reconstructions in the FPT once the encoding has been completed. This is in sharp contrast to signal averaging, where repetition will lengthen the patients’ examination time, whose existing length is already one of the main drawbacks in encoding by MRS.
We use a sequence of values of the model order K to produce the 1st average envelope (by way of the arithmetic average). Via the inverse fast Fourier transform (IFFT) or the inverse discrete Fourier transform (IDFT), depending on whether N is \(2^m (m = 0,1,2,\ldots )\) or not, the complex average envelope is inverted. A reconstructed FID is thereby produced, which is then subjected to the FPT to generate the next set of envelopes for the same sequence of values of K as considered in the previous iteration.
The real (a) and imaginary (b) parts of the FID, \(\{c_n\},\) encoded in vivo on a 1.5T scanner (corrected for zero-order phase \(\varphi _0=1.7499\) rad at TE = 272 ms, with 512 data point) from the parietal temporal brain region in an 18 month old patient with cerebral asphyxia. Water residual distorts these wave forms. The real (c) and imaginary (d) parts of the FID are given by the inverted complex 1st average envelope in the SRI between 0.75 and 4.5 ppm. The resonance frequency of water is at 4.61 ppm and is excluded from the SRI. Therein, both parts of the FID reconstructed by the parametric \(\mathrm{FPT}^{(+)}\) are regularized, and symmetrically distributed around the abscissae. The real parts \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}\) of 31 Usual complex envelopes plotted on (e) for \(K = 385(1)415\) from the FID depicted in (a) and (b). Numerous spikes are observed. The associated 31 complex envelopes \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}\) are averaged and denoted by \(\mathrm{Re}(\mathrm{FPT}^{(+)})^\mathrm{U}_{\mathrm{Av}}\) whose real part is displayed on (f) (color online)
In Fig. 10, the various effects of spectra averaging are illustrated for the FIDs encoded in vivo on a 1.5T scanner from the pediatric patient who had suffered cerebral asphyxia [9]. The real and imaginary parts of the encoded FID in panels (a) and (b), respectively, are asymmetric around the abscissae due to the large residual water peak. The phase correction of the encoded FID is \(\varphi _0=1.7499\) rad. Panels (c) and (d) display the real and imaginary parts, respectively, of the FID created by the IFFT-based inversion of the complex 1st average envelope. In the reconstructed time signal, the phase correction \(\varphi _0=1.7499\) rad of the encoded FID is preserved. The residual water resonance at 4.61 ppm is above the SRI, and thus has been excluded from the reconstructed FID. Consequently, there is full regularization of the FIDs on panels (c) and (d), i.e. they are now symmetrical around the abscissae, as was the case in panels (c) and (d) of Fig. 8. In panel (e), the first set of iterates is displayed, with the real parts of 31 Usual envelopes \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}\) for \(K = 385,386,\ldots ,415\) from the FID encoded with 512 data points and subsequently doubled in its length by zero-filling once to \(N=1024.\) Large noise-like spikes are seen therein. Note, that the explicit writing, e.g. \(K= 385,386,\ldots ,415\) is abbreviated in Fig. 10 as \(K=385(1)415,\) where (1) in between \(K_{\mathrm{min}}=385\) and \(K_{\mathrm{max}}=415\) indicates the increment \(\Delta K\) for K.
A “clean” spectrum is generated by taking the arithmetic average of these 31 envelopes with the result denoted by \(\mathrm{Re}\{\mathrm{FPT}^{(+)}_K\}^\mathrm{U}_{\mathrm{Av}}.\) This is shown in panel (f) of Fig. 10. The stable structures remain in this average spectrum, whereas the spikes are markedly diminished or have almost disappeared.
In Fig. 11, signal-noise separation, SNS, is shown to be successfully achieved via iterative spectra averaging for the MRS time signals encoded in vivo from the pediatric patient with cerebral asphyxia. In the component spectra, the peak heights are displayed on panels (a) and (b) for the Usual and Ersatz lineshapes, as per Eqs. (2.21) and (2.20), respectively. Panel (c) shows pole-zero coincidences, through the \(\mathrm{FPT}^{(+)}\) from the FID generated by the inverted complex 12th average envelope. This panel is the Argand plot, as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q}).\) Blue open circles and red dots represent the poles and zeros, respectively. For spurious resonances these symbols coincide (Froissart doublets), and are located in the negative imaginary frequency region below the abscissa (horizontal green line). The genuine poles and zeros lie in the positive imaginary frequency region above the abscissa and are non-coincident, albeit sometimes close to each other. The pole-zero coincidences lead to annihilation of the amplitudes for spurious resonances, as shown in the magnitude plot on panel (d).
Signal-noise separation illustrated from the 12th average envelope \(\{\mathrm{FPT}^{(+)})\}^\mathrm{U}_{\mathrm{Av}}\) with the encoded FID, as per Fig. 10. Pole-zero coincidences lead to zero-valued peak heights (open circles in red) in the Usual and Ersatz component spectra on (a) and (b), respectively. Argand plot (c) as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) showing full separation of the genuine from spurious frequencies reconstructed by the \(\mathrm{FPT}^{(+)}.\) All the spurious resonances exhibit pole-zero coincidence as symbolized by \(\odot \) on (c) as well as zero-valued magnitudes on (d) via open circles in red (color online)
Spectral parameters generated by the \(\mathrm{FPT}^{(+)}\) from the complex FIDs given by the inverted complex 10th, 11th and 12th average envelopes whose real parts, by reference to Fig. 10, are in green, magenta and blue, respectively. Argand plot (a) as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q}).\) The magnitude plot (b) as \(|d^+_k|\) versus chemical shift. The phase plot (c) as \(\varphi ^+_k\) versus chemical shift. The Ersatz components and their peak heights (d) (color online)
In Ref. [9], with successive iterations, there was further suppression of spurious spectral structures. Besides the total shape spectra, all four Padé-reconstructed spectral parameters for each genuine resonance displayed progressively diminished fluctuations with consecutive iterations, until the spectral parameters were completely stabilized to the level of variances consistent with data stochasticity. At that point, full convergence was robustly achieved [9].
Figure 12 displays the convergence of the reconstructions of the spectral parameters from the FIDs given by the complex inverted 10th, 11th and 12th average envelopes. These reconstructions are also for in vivo encoded MRS time signals from the pediatric patient with cerebral asphyxia. For all the results, including Argand plots on panel (a), magnitude plots on panel (b), phase plots on panel (c) and Ersatz components with peak heights versus chemical shifts on panel (d), convergence has been attained. In this convergence, the deviations are exceedingly small, to within the realm of data stochasticity. In other words, there is nearly complete concordance among the 10th, 11th and 12th reconstructions of the spectral parameters, which are each color coded, but coincide so closely that all the structures appear to be blue (the last plotted curve is blue). This is especially remarkable for very weak resonances (seen between 3.2 and 3.4 ppm), indicating that precise quantification of very low levels of PC can be achieved.
Spectra averaging (performed iteratively or only once) reduces the unphysical, non-coherent portion of the extracted information coming from many sources (noise from the encoding, round-off errors in computation, unstable resonances, etc.). These random errors are considerably diminished via the stabilized quotient \(P^+_K/Q^+_K,\) through the unique coupling of averaging of Padé spectra and the form of the rational response function of the examined system to external perturbations [11]. As stated earlier, spectra averaging cannot be done in the FFT for different values of \(N_{\mathrm{P}},\) since Fourier vectors in the frequency domain are not of equal length for various truncation levels of the total acquisition time T [9].
All told, through the iterative averaging procedure, exceedingly small variances were obtained for the four Padé-reconstructed parameters for genuine resonances, once convergence was achieved. Via the parametric FPT, the spectral region of interest was chosen to bypass the large residual water resonance, automatically generating spectral envelopes without the need for windowing. This now fully validated methodology can generate denoised spectra and accurate spectral parameters for in vivo MRS data encoded within neuro-diagnostics. Therefore, this type of mathematical optimization through the FPT can be successfully applied to MRS time signals encoded in vivo from brain tumors using standard clinical scanners at 1.5 or 3T. Improved diagnostic yield of MRS within neuro-oncology is anticipated thereby.
5.5 Applications of the FPT to MRS time signals from the ovary
5.5.1 Initial proof-of-concept studies for ovary MRS
We began with studies of noise-controlled MRS time signals from the ovary [2, 10, 38, 39, 43, 44]. The FPT was first applied to synthesized noiseless FIDs associated with MRS data for benign and cancerous ovarian cyst fluid of the kind similar to in vitro encoded from Ref. [118], where some 12 resonances have been assigned to the known metabolites. The FPT resolved all the 12 input resonances with only 64 time signal points, and exactly computed the related metabolite concentrations [2, 38, 39]. In contrast, with 64 time signal points, the FFT generated rough, uninformative spectra. Strikingly, the FFT required 32768 signal points for convergence of envelopes. These results confirmed the high resolving power of the FPT. With increasing levels of added noise, the FPT was shown to resolve and accurately quantify all the 12 input resonances associated with MRS data from Ref. [118] for non-cancerous and malignant ovarian cyst fluid [10, 43, 44]. From these and the earlier described proof-of-principle studies on other tissues, in addition to the promising results of the FPT applied to in vivo MRS of the brain, it was deemed that Padé-optimized in vivo MRS should also be implemented where the added value would likely be the greatest. One such problem area is ovarian cancer diagnostics, where, as discussed, the need for an effective in vivo MRS-based screening method has been underscored for many years [115, 116], but thus far this hope has remained largely unrealized.
5.5.2 The FPT applied to in vivo MRS time signals encoded from the ovary
The first step for the FPT applied to in vivo MRS time signals encoded from the ovary was to compare its resolution capability with that of the FFT. The encoded FID time signal of total length \(N=1024\) are from a patient with an enlarged left ovary as detected on transvaginal ultrasound [136]. Subsequent histopathologic analysis indicated that this was a borderline serous cystic ovarian lesion. In Ref. [52], the non-parametric FPT gave better resolved total shape spectra than the FFT when applied to MRS time signals encoded in vivo on a 3T scanner at TE = 30 ms from the borderline serous cystic ovarian tumor. The spectra averaging procedure was then applied to these FIDs from the ovary.
As seen on Fig. 13(a), noise-like spikes appear in the display of the real parts of 6 complex envelopes reconstructed non-parametrically by the \(\mathrm{FPT}^{(+)}\) at partial signal lengths \(N_{\mathrm{P}} = 1150, 1170,\ldots , 1250\) corresponding to the model orders \(K = 575(10)625.\) These spectra are shown with color-coding as black (\(K=575\)), green (\(K=585\)), cyan (\(K=595\)), red (\(K=605\)), magenta (\(K=615\)) and blue (\(K=625\)). Here, all the values of \(N_{\mathrm{P}}\) are larger than the total FID length, \(N=1024.\) The additional data for \(N_{\mathrm{P}}-N\) are the time signal points with zero-valued amplitudes. A magenta-coded spike at \(\sim \) 3.3 ppm is a noticeable structure, with many other pronounced spikes interspersed throughout the SRI of 0.75–3.75 ppm. Arithmetic averaging of the 6 complex envelopes yields the average complex envelope, the real part of which is displayed in Fig. 13(b). The noisy spikes are greatly attenuated therein such that only genuine peaks are visible. The largest peaks are N-acetylneuraminic acid (acNeu) at 2.06 ppm and NAA at 2.03 ppm. Numerous other resonances are also seen.
The real parts of 6 usual envelopes \(\mathrm{Re}(P^+_K/Q^+_K)\) are shown on (a) for the SRI = [0.75, 3.75] ppm in the \(\mathrm{FPT}^{(+)}\) at \(K = 575(10)625\) using the FID encoded in vivo on a 3T MR scanner from a borderline serous cystic ovarian lesion [136], with color-coding: black (\(K = 575\)), green (\(K = 585\)), cyan (\(K = 595\)), red (\(K = 605\)), magenta (\(K = 615\)) and blue (\(K = 625\)). Here, numerous prominent noise-like spikes are seen. On (b), the corresponding 6 complex envelopes are averaged and the result of the real part is denoted as \(\mathrm{Re}\{\mathrm{FPT}^{(+)}\}^\mathrm{U}_{\mathrm{Av}}\) in which noisy spikes are either greatly reduced or disappeared altogether. The FID from the IDFT-based inversion of the complex average envelope is subjected to the \(\mathrm{FPT}^{(+)}\) to generate the Usual and Ersatz component spectra for the 6 model orders K on (c) and (d), respectively (color online)
We proceed beyond shape estimation of envelopes to component spectra generated from the fundamental frequencies and amplitudes reconstructed by the \(\mathrm{FPT}^{(+)}.\) The complex average envelope is inverted to generate a new MRS complex time signal to which the FPT is applied. For processing this latter reconstructed FID, the partial signal lengths used were, as above, \(N_{\mathrm{P}} = 1150, 1170, \ldots , 1250\) associated with the model orders \(K = 575(10)625.\) The real parts of the Usual complex mode, as per Eq. (2.21), are shown on panel (c) of Fig. 13. Strikingly, nearly full convergence to the level of data stochasticity was attained throughout the SRI. Thus, most of the Usual components appear entirely as blue (the last plotted curve for \(K = 625\) is in blue). The only exception is at about 3.4 ppm, where magenta color is seen to top the up-going peaks, and a smaller green down-going peak (a dip) can be noticed. Next, in panel (d) of Fig. 13, the real parts of the Ersatz component spectra are displayed, by reference to Eq. (2.20), helping to visualize overlap of closely-lying or hidden resonances. Almost complete convergence to the level of data stochasticity was also attained throughout the SRI for these Ersatz components that mainly appear as blue, except for around 3.4 ppm, where a pronounced magenta-coded up-going resonance is observed to top the peaks. Within the depicted SRI, remarkably, over 90 peaks are seen with Ersatz component spectra in Fig. 13(d).
\(\bullet \) Spectra averaging and extrapolation for processing in vivo MRS time signals encoded from the ovary
In Ref. [11], we examined the role of spectra averaging in conjunction with Padé-based extrapolation. Therein, the spectra were computed at sweep frequencies whose number considerably exceeds the number of data points in the encoded time signal. The study [11] was also carried out directly on the in vivo MRS time signals encoded from the ovary. The complex average envelope was then inverted to yield a new complex time signal which is longer than the encoded data. The Padé-extrapolated time signal is then quantified for a sequence of model orders K to monitor convergence of the reconstructed parameters. It was then demonstrated that spectra averaging together with Padé-based extrapolation yielded more sharply delineated pole-zero coincidences compared to the case without averaging and extrapolation, thereby improving signal-noise separation, SNS, and also signal-noise ratios, SNR. This detailed comparison of the results for Padé reconstruction was carried out for six FIDs with the same model orders K generated without averaging and without extrapolation. Variances are visibly reduced for the reconstructed parameters (complex frequencies and complex amplitudes) when spectra averaging and extrapolation were performed. Another very important practical finding from Ref. [11] was that a single averaging combined with extrapolation appeared to be entirely sufficient to attain convergence of spectral parameters coherent with averaging through multiple iterations.
Comparisons along these lines are presently made in Figs. 14 and 15. In Fig. 14, the encoded data are employed directly by the \(\mathrm{FPT}^{(+)}\) without averaging or extrapolation. Panel (a) shows the real parts of 6 complex envelopes generated non-parametrically by the \(\mathrm{FPT}^{(+)}\) for \(K=575(10)625\) from the encoded FID, as in panel (a) of Fig. 13. Panel (b) of Fig. 14 displays the Argand plot as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) for the 6 sets of complex frequencies generated by the parametric \(\mathrm{FPT}^{(+)}\) applied to the encoded FID for \(K= 575(10)625\) and displayed with the same color coding as the envelopes. The 6 FIDs differ from each other only in the number of added zeros. Notably, the color of each imaginary frequency, \(\mathrm{Im}(\nu ^+_{k,Q}),\) at a specified chemical shift, \(\mathrm{Re}(\nu ^+_{k,Q}),\) can quite often be identified. In panel (c) for magnitudes \(\{|d^+_k|\}\) versus chemical shift, significant spread is also observed, particularly in the regions around 1.3, 2.1, 3.4 and 3.6 ppm. Phases \(\{\varphi ^+_k\}\) versus chemical shift are presented on panel (d) where throughout the SRI, the 6 sets of spectral parameters exhibit noticeable discrepancies.
The real parts of 6 Usual envelopes \(\mathrm{Re}(P^+_K/Q^+_K)^\mathrm{U}\) are presented on (a) at \(K = 575(10)625.\) The FIDs used on (a), containing 2 parts via 1024 encoded time signal points and \(2K - 1024\) zeros (\(2K\ge 1150\)), are quantified by the \(\mathrm{FPT}^{(+)}\) at \(K = 575(10)625\) to yield the Argand plot (b) as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q}),\) the magnitude plot (c) as \(|d^+_k|\) versus chemical shift, and the phase plot (d) as \(\varphi ^+_k\) versus chemical shift. Color coding is the same as in Fig. 13 (color online)
The envelope \(\{\mathrm{FPT}^{(+)}\}^\mathrm{U}_{\mathrm{Av}}\) at \(K = 575(10)625,\) whose real part is shown on (a) is inverted via the IDFT producing an FID, which is quantified by the \(\mathrm{FPT}^{(+)}\) at \(K = 575(10)625\) to give the Argand plot (b) as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q}),\) the magnitude plot (c) as \(|d^+_k|\) versus chemical shift, and the phase plot (d) as \(\varphi ^+_k\) versus chemical shift. Convergence to the level of data stochasticity is attained for all these spectral parameters. Color coding is the same as in Fig. 14 (color online)
The findings of Fig. 14 are sharply contrasted with those in Fig. 15, where the convergence of the spectral parameters is illustrated for 6 model orders \(K= 575(10)625\) when spectra averaging and extrapolation are carried out. On panel (a), the real part of the complex average envelope, as in Fig 13(b), is shown once again. The corresponding complex average envelope is inverted to create a new complex FID which is longer than the encoded data. This latter, extrapolated FID is then quantified for \(K= 575(10)625\) to assess convergence of the reconstructed parameters. Panel (b) of Fig. 15 displays the Argand plot as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) for the 6 sets of complex frequencies in the interval \(K= 575(10)625\) with color coding as in Figs. 13 and 14. Except for extremely few instances, at about 1.2, 3.4 and 3.6 ppm showing minor deviations, there is complete agreement among the 6 sets of reconstructed complex frequencies. For the plot of magnitudes \(\{|d^+_k|\}\) versus chemical shift depicted in panel (c) of Fig. 15, apart from very slight variations at around 1.2, 3.4 and 3.6 ppm, concordant with panel (b), agreement among the 6 sets of reconstructed magnitudes is complete. In panel (d), the plot of phases \(\{\varphi ^+_k\}\) versus chemical shift also shows complete agreement among the 6 sets of reconstructed phases, except for minimal variations at \(\sim \) 1.2, 3.4 and 3.6 ppm.
\(\bullet \) Examination of spectral poles and zeros as the key to stability
In a recent work [53], applying the FPT to in vivo MRS time signals encoded from the ovary, we examined the essential features of the response function, namely both the spectral poles as well as the zeros, as the key to stability of the system to external perturbations. Noise was separated from signal by reliance upon the multi-level signature of Froissart doublets (pole-zero confluence). Note that due to the special form of the rational polynomials for the Padé spectra, stabilization via pole-zero cancellation is a very unique feature of the FPT. Our focus was upon eliminating the over-sensitivity to alterations in model order K, through systematic examination of poles and zeros, as well as Padé-reconstructed spectral parameters and component shape spectra. This comprehensive examination of convergence of all variables under study includes further investigation of the role of spectra averaging and time signal extrapolation.
On panel (a) of Fig. 16, the 6 sets of genuine poles plotted as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) in the Argand diagrams, generated by the \(\mathrm{FPT}^{(+)}\) using the encoded FID at \(K = 575(10)625,\) show noticeable spread. In contrast, the 6 sets of physical poles, visualized through \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) utilizing the reconstructed FID, have converged (to the level of stochasticity) on panel (b). Analogous findings are seen for the physical zeros. Thus, on panel (c), the 6 sets of genuine zeros, shown as \(\mathrm{Im}(\nu ^+_{k,P})\) versus \(\mathrm{Re}(\nu ^+_{k,P})\) in the Argand diagrams employing the encoded FID at \(K = 575(10)625,\) are noticeably dispersed. On the other hand, on panel (d), there is almost complete agreement among the 6 sets of genuine zeros seen through \(\mathrm{Im}(\nu ^+_{k,P})\) versus \(\mathrm{Re}(\nu ^+_{k,P})\) due to the \(\mathrm{FPT}^{(+)}\) applied to the reconstructed FID.
Genuine poles as \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) are on (a) generated by the \(\mathrm{FPT}^{(+)}\) applied to the encoded FID at \(K = 575(10)625.\) Genuine poles \(\mathrm{Im}(\nu ^+_{k,Q})\) versus \(\mathrm{Re}(\nu ^+_{k,Q})\) are on (b) predicted by the \(\mathrm{FPT}^{(+)}\) using the reconstructed FID at \(K=575(10)625.\) Genuine zeros \(\mathrm{Im}(\nu ^+_{k,P})\) versus \(\mathrm{Re}(\nu ^+_{k,P})\) are on (c) due to the \(\mathrm{FPT}^{(+)}\) employing the encoded FID at \(K = 575(10)625.\) Genuine zeros \(\mathrm{Im}(\nu ^+_{k,P})\) versus \(\mathrm{Re}(\nu ^+_{k,P})\) are on (d) obtained by the \(\mathrm{FPT}^{(+)}\) with the reconstructed FID at \(K = 575(10)625.\) Color coding is the same as in Fig. 15 (color online)
Overall, it was demonstrated in Ref. [53] that for the reconstructed poles and zeros, as well as for magnitudes and phases, spectra averaging and Padé-based extrapolation of time signals are essential for checking the stability of the system and for the accurate reconstruction of resonances. Full convergence was achieved when spectra averaging and extrapolation were applied together. Spectra averaging and extrapolation were also shown to be needed to obtain stabilized results to the level of data stochasticity for the Usual and Ersatz component spectra for the 6 model orders. Without spectra averaging and extrapolation, there were noticeable variances for the 6 model orders with regard to all the variables under study. This scrutiny and the ensuing results have important implications for firmly establishing the robustness of quantification by the FPT, applied directly to MRS time signals encoded in vivo from the ovary. The outlined systematics of spectra averaging and time signal extrapolation, carried out one after the other, is a practical and expedient solution to the most important obstacle for all parametric methods. This obstacle is a marked instability of reconstructions to changes in model order K. Our procedure of spectra averaging and time signal extrapolation was suggested and implemented in the FPT [53], but can also be applied to any other parametric estimator. Nevertheless, the advantage of the FPT over the other existing parametric methods is in the most accurate quantification and time signal extrapolation based on Padé rational polynomials.
5.5.3 A twofold damper on early ovarian cancer detection by MRS
In Ref. [137], we sought to reach a wider audience, in particular, clinicians, disseminating the key results applying the FPT for MRS time signals encoded in vivo from the ovary. We introduced the term “FPT-MRS” to more succinctly denote Padé-optimized in vivo MRS. Here, optimization encompasses both data analysis and data acquisition. Our emphasis was on the added diagnostic value of FPT-MRS for early ovarian cancer detection. Note, parenthetically, that it is not unusual to add the name of a signal processor to a spectroscopy modality, like FPT-MRS. This is customary when the given processor not only performs data evaluation, but also guides the encoding, i.e. measurements. Another example is Fourier transform ion cyclotron resonance mass spectrometry (FT-ICRMS) [138].
There are several chemical shift regions for which these insights are the most salient. Around 1.3 ppm, the component spectra are seen to clarify the overlap among lipid (Lip), threonine (Thr), Lac and other resonances. These insights may help resolve uncertainty as to whether or not the presence of Lip is helpful for distinguishing benign from cancerous lesions. Although Lip at 1.3 ppm was more often identified in malignant lesions, this difference was not statistically significant in our meta-analysis [52]. Conversely, Lac also resonating at 1.3 ppm was found in Ref. [52] to be significantly associated with cancerous as opposed to benign ovarian lesions, but data regarding Lac were sparse. The key to clarification is to perform Padé-based quantification using a short TE, as done in the presently reviewed publications from our studies. Thereby, Lip, Lac, and other metabolites around 1.3 ppm, can be reliably identified and quantified. In the chemical shift region around 2.0 ppm, there have also been uncertainties that obscure interpretation of MR spectra from the ovary. Via Padé reconstructions, the two resonances between 2.0 and 2.1 ppm corresponding to NAA and acNeu were unambiguously distinguished, such that we may now be able to ascertain the actual significance of NAA versus acNeu for distinguishing cancerous from benign ovarian lesions. Not only was Cho at 3.2 ppm identified and its peak parameters reconstructed via the FPT, but also PC and GPC were detected from in vivo MRS of the ovary for the first time. The genuine nature of these two resonances was confirmed by their positive imaginary frequencies, lack of pole-zero coincidence and non-zero, albeit small, magnitudes. Yet another confirmation of the physical nature of these two resonances was stability of their spectral parameters. Since PC is identified as an indicator of malignant transformation [81, 122], possibly mediated, at least in part, by a loss of the tumor suppressor p53 function [139], it becomes now feasible via the FPT to non-invasively assess this biomarker for ovarian cancer diagnostics. In Ref. [137], we illuminated the two-fold obstacle with ovarian MRS related to both measurements and interpretation. First, it is difficult to encode good quality MRS time signals from a small, moving organ such as ovaries. Second, the noisy encoded time signals are conventionally analyzed and interpreted with the exclusive reliance upon the ambiguous processing by the FFT and fitting. As a repercussion, such a double difficulty has put a damper on efforts to explore MRS for early ovarian cancer detection.
Consequently, the MR community has not prioritized this problem area. We underscored that the results applying FPT-MRS to the ovary strongly indicate that this situation can and should change. There is now justification to further apply FPT-MRS for early ovarian cancer detection and better identification of benign ovarian lesions. The goal of effective in vivo MRS-based screening for ovarian cancer, the potential for which has been highlighted for nearly two decades [115, 116], as stated, could thereby become a reality.
6 Discussion
In detailed studies, Padé-optimized MRS has been fully validated within the in vivo setting for applications to tumorous tissue. An essential innovation is spectra averaging, with the help of which, for the very first time, key cancer biomarkers (most notably PC) have been identified and quantified through in vivo MRS [8, 9, 11, 49, 52,53,54, 137]. Even greater precision in quantifying these biomarkers is achieved when Padé-based extrapolation is combined with spectra averaging, and then applied to in vivo MRS time signals encoded from tumorous tissue [11].
Our recent work [3, 4] indicates that this process can be markedly streamlined by first qualitatively identifying these otherwise hidden cancer biomarkers through partitioning of the spectral envelopes non-parametrically. In what follows, we are going to present some further considerations on this development.
The passage from the time to the frequency representation is information preserving. Thus, it has been customary in the MRS literature to argue, when e.g. PC is not seen in an FFT total shape spectrum, that this metabolite should be absent from the corresponding FID, as well. Such reasoning is misleading since, in fact, PC can be one of the constituents of an FID, and still be invisible on the FFT envelope, or any other envelope, for that matter. This is evidenced in e.g. Fig. 4(c) for breast cancer. Therein, the total shape spectrum in the FPT does not show any trace of PC which is, however, present in the corresponding component spectra in Fig. 4(d). This is in concordance with the synthesized input FID, which, by design, contains the PC metabolite.
The intriguing question which emerges from here is: could PC somehow be visualized on an envelope reconstructed non-parametrically, i.e. by shape estimation alone? The answer is in the affirmative, as shown in Fig. 5 and in Refs. [3, 4], within the FPT. The way in which this can be achieved is provided by first understanding the reason behind the appearance of PC and PE as a single peak in a total shape spectrum computed either parametrically or non-parametrically. It is the interference or interaction between PC and PE that causes these two adjacent metabolites (separated by a mere 0.001 ppm) to blend together into a single resonance. Thus, by intercepting the process of this interference before its completion, it might be possible to disentangle PC and PE without recourse to quantification, i.e. by relying solely upon non-parametric estimation. The said interception comes naturally in the Padé complex-valued total shape spectrum \(P_K/Q_K,\) where the analytical expression from absorption and dispersion each contains two unique partitions. Each partitioned envelope exhibits a reduced interference effect. It is such an interference reduction which splits PC and PE apart all the way down to the background baseline level in the envelopes, as seen in Fig. 5.
Here, it could be asked: Why would this phenomenon matter, given that the parametric FPT can reconstruct the component spectra and, thus, exactly separate PC from PE? It matters because of both the intrinsic and practical clinical reasons. As to the intrinsic reason, partitioned spectra provide a procedure by way of mathematical physics to weaken a strong coupling of the overlapping resonances. This weakening unfolds the hidden spectral structures masked by the intact, complete interference effect. Regarding the practical reasons, the power of partitioning is in its uniqueness and expedience, since the hidden resonance(s) can be visualized as soon as the polynomials \(P_K\) and \(Q_K\) are extracted from the input time signals. This should be compared to the parametric estimation requiring a number of additional steps through polynomial rooting, signal-noise separation, SNS, assessing pole-zero coincidence (Froissart doublets), etc.
Clinically, partitioned spectra are useful for the initial, qualitative insight into the existence of e.g. PC in an envelope. Namely, prior to learning about the concentration of PC, by way of quantification, the radiologist would like to know whether PC is present at all. If PC is visualized in the partitioned envelope, then the next step could be to zoom around PC in a narrow SRI and perform a local quantification explicitly by the parametric FPT and/or implicitly by the non-parametric dFPT. This stepwise approach to spectra is deemed practical because it begins with a more familiar shape estimation, but with a bonus of partitioning which can visualize separation of tightly overlapping resonances. Such a strategy is reminiscent of the radiologist’s approach to the passage from MRI to MRS. Namely, when a suspicious lesion is observed on MRI, further investigation is often needed due to the inadequate specificity of MRI. Employing MRS can help gain insight into the metabolic features of the suspicious lesion, thereby assisting in the differential diagnostic procedure [17].
Overall, these developments are possible because of the mathematical capabilities associated with the FPT and dFPT. Neither spectra averaging, nor extrapolation, nor quantification are possible with the FFT. This is due to the mathematical structure of the FFT: no extrapolation nor interpolation features, limiting to the equidistant Fourier grid frequencies, no spectra averaging due to different numbers N / M of the FFT sticks for the varying truncation level M of the full FID length, N, providing only non-parametric analysis, etc. Instead of the FFT, the critical step to realize the potential of molecular imaging through MR, is to apply Padé-optimization to in vivo MRS, which we denote by “FPT-MRS” as a compact acronym. Software upgrades with unbiased quantifying signal processing by the FPT are indispensable for achieving these long-sought goals of MRS [48, 137].
The FPT has been applied by several research groups within various areas of MR methodologies [132,133,134,135, 140,141,142]. It is hoped that this review will motivate the use of the FPT by many more researchers within MR community and far beyond across interdisciplinary fields. In fact, our Padé-based signal processing has already found many applications in different research branches in science and technology. Some examples are in acoustics with time signals corresponding to the so-called room impulse response (RIR) [143], or in recurrence spectra of multi-electron atoms in an electric field [144], or in leak location and leak area determination in water, oil and gas pipelines [145].
The non-parametric derivative fast Padé transform, dFPT [5,6,7], is of prime importance because it can disentangle spectrally crowded regions, by splitting apart closely packed peaks. Hidden resonances, even those that are very weak, are not only visualized but also exactly quantified, despite performing shape estimation alone. This streamlined methodology would allow clear quantified visualization of the entire MRS information, including concentrations of all the diagnostically-relevant metabolites. Such a new modality called derivative magnetic resonance spectroscopy (dMRS) is poised to become a standard, reliable and practical part of the diagnostic armamentarium for cancer and other pathologies. In order to realize this potential, it would be extremely important to widely apply dFPT to quantify phosphocholine as well as other cancer biomarkers heretofore undetected in vivo. This is especially important at short echo times, TE, due to increased overlap with other resonances that have not yet decayed. These include isoleucine (Iso) and valine (Val), resonating at 1.02 and 1.04 ppm, respectively, lipid, Lip and lactate, Lac, at \(\sim \) 1.3 ppm, alanine, Ala, overlapping with other resonances at \(\sim \) 1.5 ppm, lysine (Lys), closely overlapping with several other metabolites between 1.67-1.78 ppm, taurine, Tau, overlapping with myoinositol, m-Ins, Cho and glucose, Glc, between 3.3 and 3.4 ppm, etc. [56, 118, 120, 121, 127]. For FFT-based in vivo MRS, longer TEs are generally used to ease interpretation of the computed sparser, simpler spectra with, however, much information lost due to decay of short-lived resonances representing metabolites [9].
Both the FPT and dFPT process the same original time signal points \(\{c_n\}.\) In the dFPT, the derivatives of order m are taken on the analytical expression for the conventional Padé spectrum, \(R_K(z)=P_K(z)/Q_K(z).\) Therefore, the spectrum in the dFPT is also an analytical formula given by \(G^{(m)}=D^m_\nu R_K(z),\) where \(D_\nu =\text {d}/\text {d}\nu \) is the differentiation operator with respect to linear frequency \(\nu \). This is the reason for which no additional noise is introduced by \(D_\nu .\) As per Ref. [5], normalization in the dFPT is performed, so that the increased peak heights on derivative spectra for \(m>0\) can still be plotted on the same graphs with the non-derivative envelopes \((m=0).\) This normalization to a reference peak e.g. Lac in the example from Fig. 6(b) requires that the Padé-reconstructed spectral envelopes have converged with respect to model order m for both \(m=0\) and \(m>0.\)
In the dFPT, for the higher-order derivative envelopes, the reconstructed peak positions do not alter, whereas simultaneously, the peak widths decrease and the peak heights increase. These latter two trends for \(m>0\) are concomitant, such that their product can reconstruct the peak parameters of the absorption mode of the non-derivative \((m=0)\) version of the FPT. Here, emphasis is placed on high derivative orders of magnitude spectra, which are strictly positive-definite and thus do not require any phase correction. These are, therefore, the most straightforward for clinical interpretation and extraction of metabolite concentrations.
In Refs. [5,6,7], we proceed beyond traditionally conceived shape estimators in MRS to show that there is a way of making non-parametric processors intrinsically quantitative. This is possible in the dFPT by accurate reconstruction of the position, width, height and phase of each component peak of all physical resonances without solving the quantification problem. The ensuing derivative magnetic resonance spectroscopy, dMRS, moves this research forward by providing unambiguously interpretable spectra for clinicians with all needed quantitative information readily at hand. Our most recent results [7] suggest that this will be the stand-alone signal processing strategy of choice for cancer diagnostics within MRS. Being computationally fast, with robust noise suppression, the high-resolution dFPT is fully ready to be implemented in clinical MR scanners. With this, the long sought hope of clinicians would at last be realized: to visualize the entire MRS information by seeing directly on the screen the clearly disentangled overlapping peaks and then inspecting the displayed concentrations of all the diagnostically relevant metabolites. This vision would enable the entry of MRS as a standard, clinically reliable part of the diagnostic armamentarium for cancer and other pathologies.
A key consideration, as discussed, is that a single voxel in MRS may not be representative of the scanned tissue. Multi-voxels are then employed for volumetric coverage through magnetic resonance spectroscopic imaging, MRSI [16]. Typically, however, SNR is deteriorated in MRSI relative to MRS. Moreover, MRSI is more time-consuming and analysis of the encoded data is computationally more demanding because MRSI is tasked with reconstructing and interpreting thousands of spectra to extract the diagnostically relevant information. Via MRSI the chemical specificity of MRS is joined with the spatial localization techniques of MRI to yield multiple MRS time signals. We anticipate that this efficient strategy by way of derivatives of total shape spectra via the dFPT would be particularly appropriate for putting molecular imaging through MRSI into practice. This would yield the derivative magnetic resonance spectroscopic imaging (dMRSI). As stated, the FIDs from MRSI are of the same type as from MRS and, thus, can be processed by the dFPT. Moreover, MRI itself would greatly benefit from the derivative transform in conjunction with dFPT. The resulting high-order derivative magnetic resonance imaging (dMRI) may well reduce noise and make the images simultaneously sharper and brighter, as we plan to investigate.
Attempts have been made to use higher field scanners aimed at improving SNR in MRS and MRSI for cancer diagnostics. These attempts were motivated by insufficient accuracy of Fourier-based in vivo MRS and MRSI with clinical (1.5 or 3T) MR scanners for identifying cancers and distinguishing these from benign lesions. Higher field scanners have, thus far, not provided the anticipated improved cancer detection [78, 79]. Furthermore, the huge costs would preclude such an approach for widespread applications. In sharp contrast, via dFPT-based dMRS and dMRSI, improved SNR is achieved together with narrowing of the linewidths yielding separation of overlapping peaks. This results in improved resolution. Such a powerful and efficient approach is anticipated to be applicable on standard clinical scanners (1.5 T), offering the further benefit of cost-effectiveness. Overall, the dFPT simultaneously solves the two stumbling blocks of MRS and MRSI, by enhancing resolution and improving SNR with shorter encoded data.
7 Conclusions
We review the fast Padé transform, FPT, for magnetic resonance spectroscopy, MRS, in personalized cancer medicine, PCM. The present main focus is on early malignant transformations within molecular levels of the examined human tissue of brain, breast, prostate and ovary. Their timelier detection is likely to significantly reduce the fatality rates.
Mathematics can come to the rescue through clinically reliable signal processing of proven validity for MRS time signals encoded from patients. This is critical to an adequate analysis and interpretation of MRS data prior to the diagnosis of eventual pathologies.
Over the years, it has been demonstrated that the FPT can fully be trusted in achieving the long sought mathematical optimization of MRS. Through robust computational algorithms with self-checking (causal vs anti-causal estimates) and auto-correcting (pole-zero cancellations), this powerful signal processor gives ultimately the most accurate molecular content of the MRS-scanned tissue. This content is entirely quantitative providing the diagnostically relevant information on metabolite concentrations, chemical shifts (environment of resonating nuclei bound to different molecules), relaxation times (notably different for benign and tumorous lesions), etc.
It has been established that the FPT can provide this needed quantification by parametric estimation signal processing reconstructing the exact positions, widths and phases of the peaks/resonances of all the metabolite molecules that are physically present in the investigated tissue. What has begun to emerge very recently, however, was the possibility to retrieve all the mentioned quantitative data in MRS by shape estimation of envelopes alone. This is provided by the derivative fast Padé transform, dFPT, which then gives birth to derivative magnetic resonance spectroscopy, dMRS. The novelty brought by the dFPT is the use of higher-order derivatives of non-parametric Padé-based envelopes (total shape spectra) to exactly reconstruct all their physical components with their peak positions, widths, heights and phases. In particular, each peak height is proportional to the abundance of resonating nuclei, or equivalently, to the concentrations of molecules assigned to the known metabolites according to their recovered chemical shifts.
We have benchmarked the dFPT on noise-corrupted synthesized MRS time signals, reminiscent of the corresponding encoded in vitro data. The outcome is very encouraging since the dFPT works as per theory by extracting the trustworthy and stable quantitative results. This strongly motivates the further applications of the dFPT to encoded MRS time signals, both in vitro and in vivo. We are currently pursuing this task and the results shall be reported shortly.
Abbreviations
- Ace:
-
Acetate
- acNeu:
-
N-acetylneuraminic acid
- Ala:
-
Alanine
- AR:
-
Auto-regression
- ARMA:
-
Auto-regressive moving average
- Asp:
-
Aspartate
- au:
-
Arbitrary units
- Av:
-
Average
- BPH:
-
Benign prostatic hypertrophy
- BW:
-
Bandwidth
- CHESS:
-
CHEmical Shift Selective
- Cho:
-
Choline
- Cit:
-
Citrate
- Cr:
-
Creatine
- Crn:
-
Creatinine
- CSI:
-
Chemical shift imaging
- CT:
-
Computerized tomography
- dFPT:
-
Derivative fast Padé transform
- DFT:
-
Discrete Fourier transform
- dFFT:
-
Derivative fast Fourier transform
- dMRI:
-
Derivative magnetic resonance imaging
- dMRS:
-
Derivative magnetic resonance spectroscopy
- dMRSI:
-
Derivative magnetic resonance spectroscopic imaging
- E:
-
Ersatz
- FFT:
-
Fast Fourier transform
- FID:
-
Free induction decay
- FPT:
-
Fast Padé transform
- FT-ICRMS:
-
Fourier transform ion cyclotron resonance mass spectrometry
- FWHM:
-
Full width at half maximum
- GABA:
-
Gamma amino butyric acid
- GE:
-
General Electric
- Glc:
-
Glucose
- Gln:
-
Glutamine
- Glu:
-
Glutamate
- Glx:
-
Glutamine plus glutamate
- Gly:
-
Glycine
- GPC:
-
Glycerophosphocholine
- GSH:
-
Glutathione
- HBOC:
-
Hereditary breast and ovarian cancer
- His:
-
Histidine
- HLSVD:
-
Hankel-Lanczos singular value decomposition
- ICRMS:
-
Ion cyclotron resonance mass spectrometry
- IDFT:
-
Inverse discrete Fourier transform
- IFFT:
-
Inverse fast Fourier transform
- Iso:
-
Isoleucine
- Lac:
-
Lactate
- LCModel:
-
Linear combination of model in vitro spectra
- Leu:
-
Leucine
- Lip:
-
Lipid
- LP:
-
Linear predictor
- Lys:
-
Lysine
- MA:
-
Moving average
- Mann:
-
Mannose
- Met:
-
Methionine
- m-Ins:
-
Myoinositol
- MR:
-
Magnetic resonance
- MRI:
-
Magnetic resonance imaging
- MRS:
-
Magnetic resonance spectroscopy
- MRSI:
-
Magnetic resonance spectroscopic imaging
- NAA:
-
N-acetyl aspartate
- NAAG:
-
N-acetyl aspartyl glutamic acid
- NMR:
-
Nuclear magnetic resonance
- NPV:
-
Negative predictive value
- PA:
-
Polyamine
- PC:
-
Phosphocholine
- PCM:
-
Personalized cancer medicine
- PCr:
-
Phosphocreatine
- PE:
-
Phosphoethanolamine
- PET:
-
Positron emission tomography
- PET-CT:
-
Positron emission tomography-computerized tomography
- ppm:
-
Parts per million
- PPV:
-
Positive predictive value
- PSA:
-
Prostate specific antigen
- Pyr:
-
Pyruvate
- Rad:
-
Radian
- RF:
-
Radiofrequency
- RIR:
-
Room impulse response
- RMS:
-
Root-mean-square
- RT:
-
Radiation therapy
- s-Ins:
-
Scylloinositol
- SNR:
-
Signal-to-noise ratio
- SNS:
-
Signal-noise-separation
- SRI:
-
Spectral region of interest
- Tau:
-
Taurine
- tCho:
-
Total choline
- TE:
-
Echo time
- Thr:
-
Threonine
- Tyr:
-
Tyrosine
- U:
-
Usual
- Val:
-
Valine
- WET:
-
Water suppression through enhanced \(T_1\) effects
- ww:
-
Wet weight
References
Dž. Belkić, Quantum-Mechanical Signal Processing and Spectral Analysis (Institute of Physics Publishing, Bristol, 2005)
Dž. Belkić, K. Belkić, Signal Processing in Magnetic Resonance Spectroscopy with Biomedical Applications (Taylor & Francis Publishers, London, 2010)
Dž. Belkić, K. Belkić, Visualizing hidden components of envelopes non-parametrically in magnetic resonance spectroscopy: phosphocholine, a breast cancer biomarker. J. Math. Chem. 55, 1698–1723 (2017)
Dž. Belkić, K. Belkić, Robust identification of the cancer biomarker phosphocholine through partitioned envelopes in magnetic resonance spectroscopy by the non-parametric fast Padé transform. J. Math. Chem. 55, 2004–2047 (2017)
Dž. Belkić, K. Belkić, Exact quantification by the nonparametric fast Padé transform using only shape estimation of high-order derivatives of envelopes. J. Math. Chem. 56, 268–314 (2018)
Dž. Belkić, K. Belkić, Explicit extraction of absorption peak positions, widths and heights using higher order derivatives of total shape spectra by nonparametric processing of time signals as complex damped multi-exponentials. J. Math. Chem. 56, 932–977 (2018)
Dž. Belkić, K. Belkić, Validation of reconstructed component spectra from non-parametric derivative envelopes: comparison with component lineshapes from parametric derivative estimations with the solved quantification problem. J. Math. Chem. 56, 2537–2578 (2018)
Dž. Belkić, K. Belkić, Improving the diagnostic yield of magnetic resonance spectroscopy for pediatric brain tumors through mathematical optimization. J. Math. Chem. 54, 1461–1513 (2016)
Dž. Belkić, K. Belkić, Iterative averaging of spectra as a powerful way of suppressing spurious resonances in signal processing. J. Math. Chem. 55, 304–348 (2017)
Dž. Belkić, K. Belkić, How the fast Padé transform handles noise for MRS data from the ovary: importance for ovarian cancer diagnostics. J. Math. Chem. 54, 149–185 (2016)
Dž. Belkić, K. Belkić, Synergism of spectra averaging and extrapolation for quantification of in vivo MRS time signals encoded from the ovary. J. Math. Chem. 55, 1067–1109 (2017)
K. Belkić, Molecular Imaging Through Magnetic Resonance for Clinical Oncology (Cambridge International Science Publishing, Cambridge, 2004)
J. Evelhoch, M. Garwood, D. Vigneron, M. Knopp, D. Sullivan, A. Menkens, L. Clarke, G. Liu, Expanding the use of magnetic resonance in the assessment of tumor response to therapy: workshop report. Cancer Res. 65, 7041–7044 (2005)
D. Hanahan, R.A. Weinberg, Hallmarks of cancer: the next generation. Cell 144, 646–674 (2011)
M.F. Kircher, H. Hricak, S.M. Larson, Molecular imaging for personalized cancer care. Mol. Oncol. 6, 182–195 (2012)
R. Prost, Magnetic resonance spectroscopic imaging, in Magnetic Resonance Imaging and Spectroscopy, Comprehensive Biomedical Physics, vol. 3, ed. by Dž. Belkić, K. Belkić (Elsevier, Amsterdam, 2014), pp. 331–345
Dž. Belkić, K. Belkić, The general concept of signal-noise separation (SNS): mathematical aspects and implementation in magnetic resonance spectroscopy. J. Math. Chem. 45, 563–597 (2009)
Dž. Belkić, K. Belkić, Molecular imaging in the framework of personalized cancer medicine. Isr. Med. Assoc. J. 15, 665–672 (2013)
T. Jones, The spectrum of medical imaging. Eur. J. Cancer 38, 2067–2069 (2002)
K. Pinker, A. Stadlbauer, W. Bogner, S. Gruber, T.H. Helbich, Molecular imaging of cancer: MR spectroscopy and beyond. Eur. J. Radiol. 81, 566–77 (2012)
Dž. Belkić, K. Belkić, The role of optimized molecular imaging in personalized cancer medicine. Diag. Imaging Eur. 30, 28–31 (2014)
J.L. Spratling, N.J. Serkova, S.G. Eckhardt, Clinical applications of metabolomics in oncology: a review. Clin. Cancer Res. 15, 431–440 (2009)
Dž. Belkić, K. Belkić, The fast Padé transform for noisy magnetic resonance spectroscopic data from the prostate: potential contribution to individualized prostate cancer care. J. Math. Chem. 54, 707–764 (2016)
implications for personalized cancer medicine, Dž. Belkić, K. Belkić, Mathematically-optimized magnetic resonance spectroscopy in breast cancer diagnostics. J. Math. Chem. 54, 186–230 (2016)
Dž. Belkić, P.A. Dando, J. Main, H.S. Taylor, Three novel high-resolution nonlinear methods for fast signal processing. J. Chem. Phys. 113, 6542–6556 (2000)
Dž. Belkić, Principles of Quantum Scattering Theory (Institute of Physics Publishing, Bristol, 2004)
J. Main, P.A. Dando, Dž. Belkić, H.S. Taylor, Semi-classical quantization by Padé approximant to periodic orbit sums. Europhys. Lett. 48, 250–256 (1999)
J. Main, P.A. Dando, Dž. Belkić, H.S. Taylor, Decimation and harmonic inversion of periodic orbit signals. J. Phys. A 33, 1247–1263 (2000)
Dž. Belkić, Analytical continuation by numerical means in spectral analysis using the fast Padé transform (FPT). Nucl. Instrum. Meth. A 525, 372–378 (2004)
Dž. Belkić, Strikingly stable convergence of the fast Padé transform (FPT) for high-resolution parametric and non-parametric signal processing of Lorentzian and non-Lorentzian spectra. Nucl. Instr. Meth. A 525, 366–371 (2004)
Dž. Belkić, Exact quantification of time signals in Padé-based magnetic resonance spectroscopy. Phys. Med. Biol. 51, 2633–2670 (2006)
Dž. Belkić, Exponential convergence rate (the spectral convergence) of the fast Padé transform for exact quantification in magnetic resonance spectroscopy. Phys. Med. Biol. 51, 6483–6512 (2006)
Dž. Belkić, K. Belkić, The fast Padé transform in magnetic resonance spectroscopy for potential improvements in early cancer diagnostics. Phys. Med. Biol. 50, 4385–4408 (2005)
Dž. Belkić, K. Belkić, In vivo magnetic resonance spectroscopy by the fast Padé transform. Phys. Med. Biol. 51, 1049–1075 (2006)
Dž. Belkić, Machine accurate quantification in magnetic resonance spectroscopy. Nucl. Instrum. Meth. A 580, 1034–1040 (2007)
Dž. Belkić, K. Belkić, The potential for practical improvements in cancer diagnostics by mathematically-optimized magnetic resonance spectroscopy. J. Math. Chem. 49, 2408–2440 (2011)
Dž. Belkić, K. Belkić, Quantification by the fast Padé transform of magnetic resonance spectroscopic data encoded at 1.5T: implications for brain tumor diagnostics. J. Math. Chem. 54, 602–655 (2016)
K. Belkić, Resolution performance of the fast Padé transform: potential advantages for magnetic resonance spectroscopy in ovarian cancer diagnostics. Nucl. Instr. Meth. A. 580, 874–880 (2007)
Dž. Belkić, K. Belkić, Mathematical modeling applied to an NMR problem in ovarian cancer detection. J. Math. Chem. 43, 395–425 (2008)
Dž. Belkić, K. Belkić, Unequivocal resolution of multiplets in MR spectra for prostate cancer diagnostics achieved by the fast Padé transform. J. Math. Chem. 45, 819–858 (2009)
Dž. Belkić, K. Belkić, Exact quantification of time signals from magnetic resonance spectroscopy by the fast Padé transform with applications to breast cancer diagnostics. J. Math. Chem. 45, 790–818 (2009)
K. Belkić, Dž. Belkić, Possibilities for improved early breast cancer detection by Padé-optimized MRS. Isr. Med. Assoc. J. 13, 236–243 (2011)
Dž. Belkić, K. Belkić, Magnetic resonance spectroscopy with high-resolution and exact quantification in the presence of noise for improving ovarian cancer detection. J. Math. Chem. 50, 2558–2576 (2012)
Dž. Belkić, K. Belkić, Resolution enhancement as a key step towards clinical implementation of Padé-optimized magnetic resonance spectroscopy for diagnostic oncology. J. Math. Chem. 51, 2608–2637 (2013)
Dž. Belkić, K. Belkić, Optimized spectral analysis in magnetic resonance spectroscopy for early tumor diagnostics. J. Phys. Conf. Ser. 565, Art. ID 012002 (2014)
Dž. Belkić, K. Belkić, Padé-optimization of noise-corrupted magnetic resonance spectroscopic time signals from fibroadenoma of the breast. J. Math. Chem. 52, 2680–2713 (2014)
Dž Belkić, K. Belkić, Proof-of-the-concept study on mathematically optimized magnetic resonance spectroscopy for breast cancer diagnostics. Technol. Cancer Res. Treat. 14, 277–297 (2015)
Dž. Belkić, K. Belkić, Strategic steps for advanced molecular imaging with magnetic resonance-based diagnostic modalities. Technol. Cancer Res. Treat. 14, 119–142 (2015)
Dž. Belkić, K. Belkić, High-resolution quantum-mechanical signal processing for in vivo NMR spectroscopy. Adv. Quantum Chem. 74, 353–386 (2017)
Dž. Belkić, K. Belkić, Unequivocal disentangling genuine from spurious information in time signals: clinical relevance in cancer diagnostics through magnetic resonance spectroscopy. J. Math. Chem. 44, 884–912 (2008)
Dž. Belkić, Exact signal-noise separation by Froissart doublets in the fast Padé transform for magnetic resonance spectroscopy. Adv. Quantum Chem. 56, 95–179 (2009)
Dž. Belkić,K. Belkić, In vivo magnetic resonance spectroscopy for ovarian cancer diagnostics: quantification by the fast Padé transform. J. Math. Chem. 55, 349–405 (2017)
Dž. Belkić, K. Belkić, Encoded in vivo time signals from the ovary in magnetic resonance spectroscopy: poles and zeros as the cornerstone for stability of response functions of systems to external perturbations. J. Math. Chem. 55, 1110–1157 (2017)
Dž. Belkić, K. Belkić, Robust high-resolution quantification of time signals encoded by in vivo magnetic resonance spectroscopy. Nucl. Instr. Methods A 878, 99–128 (2018)
Dž. Belkić, K. Belkić (eds.), Magnetic Resonance Imaging and Spectroscopy, Comprehensive Biomedical Physics, vol. 3 (Elsevier Publishers, Amsterdam, 2014)
K. Belkić, Inter-disciplinarity of MR and future perspectives with a focus on screening. In: Magnetic Resonance Imaging and Spectroscopy, Comprehensive Biomedical Physics, vol. 3, Dž. Belkić, K. Belkić (eds.), (Amsterdam, Elsevier, 2014), pp. 417–433
M. Center, A. Jemal, J. Lortet-Tieulent, E. Ward, J. Ferlay, O. Brawley, F. Bray, International variation in prostate cancer incidence and mortality rates. Eur. Urol. 61, 1079–1092 (2012)
C. Bouchardy, G. Fioretta, E. Rapiti, H. Verkooijen, C. Rapin, F. Schmidlin, R. Miralbell, R. Zanetti, Recent trends in prostate cancer mortality show a continuous decrease in several countries. Int. J. Cancer 123, 421–429 (2008)
C. Bosetti, P. Bertuccio, F. Levi, F. Lucchini, E. Negri, C. La Vecchia, Cancer mortality in the European Union, 1970–2003, with a joinpoint analysis. Ann. Oncol. 19, 631–640 (2008)
F. Pinto, A. Totaro, G. Palermo, A. Calarco, E. Sacco, A. D’Addessi, M. Racioppi, A. Valentini, B. Gui, P, Bassi, Imaging in prostate cancer staging: present role and future perspectives. Urol. Int. 88, 125–136 (2012)
A. Bill-Axelson, L. Holmberg, H. Garmo, J. Rider, K. Taari, C. Busch, S. Nordling, M. Häggman, S.-O. Andersson, A. Spångberg, O. Andrén, J. Palmgren, G. Steineck, H.-O. Adami, J. Johansson, Radical prostatectomy versus watchful waiting in early prostate cancer. New Engl. J. Med. 364, 1708–1717 (2011)
C.H. Bangma, M. Bul, M. Roobol, The prostate cancer research international: active surveillance study. Curr. Opin. Urol. 22, 216–221 (2012)
L. Boesen, E. Chabanova, V. Løgager, I. Balslev, K. Mikines, H.S. Thomsen, Prostate cancer staging with extracapsular extension risk scoring using multiparametric MRI: a correlation with histopathology. Eur. Radiol. 25, 1776–1785 (2015)
V. Kumar, N. Jagannathan, S. Thulkar, R. Kumar, Prebiopsy MRS and imaging in the diagnosis of prostate cancer. Int. J. Urol. 19, 602–613 (2012)
A.C. Westphalen, G.D. Reed, P.P. Vinh, C. Sotto, D.B. Vigneron, J. Kurhanewicz, Multiparametric 3T endorectal MRI after external beam radiation therapy for prostate cancer. J. Magn. Reson. Imaging 36, 430–437 (2012)
A. Rincon Mayans, B. Diaz-Tejeiro, J. Rioja Zuazu, L. Diaz Dorronsoro, M. Rodriguez Fraile, A. Boillos, J. Zudaire Bergera, How do endorectal MRI, PET-CT and transrectal ultrasound contribute to diagnostic and management of localized prostate cancer? Arch. Esp. Urol. 64, 746–764 (2011)
A. Shukla-Dave, H. Hricak, C. Moskowitz, N. Ishill, O. Akin, K. Kuroiwa, J. Spector, M. Kumar, V. Reuter, J. Koutcher, K. Zakian, Detection of prostate cancer with MR spectroscopic imaging: an expanded paradigm incorporating polyamines. Radiology 245, 499–506 (2007)
S. Verma, A. Rajesh, J. Fütterer, B. Turkbey, T. Scheenen, Y. Pang, P. Choyke, J. Kurhanewicz, Prostate MRI and 3D MR spectroscopy: How we do it. Am. J. Roentgenol. 194, 1414–1426 (2010)
V. Kundra, P.M. Silverman, S.F. Matin, H. Choi, Imaging in oncology from the University of Texas M.D. Anderson Cancer Center: diagnosis, staging, and surveillance of prostate cancer. Am. J. Roentgenol. 189, 830–844 (2007)
M.G. Swanson, A.S. Zektzer, Z.L. Tabatabai, J. Simko, S. Jarso, K.R. Keshari, L. Schmitt, P.R. Carroll, K. Shinohara, D.B. Vigneron, J. Kurhanewicz, Quantitative analysis of prostate metabolites using 1H HRMAS spectroscopy. Magn. Reson. Med. 55, 1257–1264 (2006)
L. Pace, N. Keating, A systematic assessment of benefits and risks to guide breast cancer screening decisions. J. Am. Med. Assoc. 311, 1327–1335 (2014)
R.A. Smith, K.S. Andrews, D. Brooks, S.A. Fedewa, D. Manassaram-Baptiste, D. Saslow, O.W. Brawley, R.C. Wender, Cancer screening in the United States, 2018: a review of current American Cancer Society guidelines and current issues in cancer screening. CA Cancer J. Clin. 68, 297–316 (2018)
T. Salz, J.T. DeFrank, N.T. Brewer, False positive mammograms in Europe: do they affect reattendance? Breast Cancer Res. Treat. 127, 229–231 (2011)
D.G. Evans, N. Kesavan, Y. Lim, S. Gadde, E. Hurley, N.J. Massat, A.J. Maxwell, S. Ingham, R. Eeles, M.O. Leach, A. Howell, S.W. Duffy, MRI breast screening in high-risk women: cancer detection and survival analysis. Breast Cancer Res. Treat. 145, 663–672 (2014)
K. Belkić, M. Cohen, B. Wilczek, S. Andersson, A.H. Berman, M. Márquez, V. Vukojević, M. Mints, Imaging surveillance programs for women at high breast cancer risk in Europe: are women from ethnic minority groups adequately included? Int. J. Oncol. 47, 817–839 (2015)
J.K. Begley, T.W. Redpath, F.J. Gilbert, In vivo proton MRS of breast cancer: a review of the literature. Breast Cancer Res. 14, Art. ID 207 (2012)
H. Allouche-Arnon, T. Arazi-Kleinman, S. Fraifeld, B. Uziely, R. Katz-Brull, MRS of the Breast. In: Magnetic Resonance Imaging and Spectroscopy, Comprehensive Biomedical Physics, vol. 3, Dž. Belkić, K. Belkić (eds.), (Elsevier, Amsterdam, 2014), pp. 299–314
P.A. Baltzer, M. Dietzel, Breast lesions: diagnosis by using proton MR spectroscopy at 1.5 and 3.0T—systematic review and meta-analysis. Radiology 267, 735–746 (2013)
D. Klomp, B. van de Bank, A. Raaijmakers, M. Korteweg, C. Possanzini, V. Boer, C. van de Berg, M. van de Bosch, P. Luijten, 31P and 1H MRS at 7T: initial results in human breast cancer. NMR Biomed. 24, 1337–1342 (2011)
I.S. Gribbestad, B. Sitter, S. Lundgren, J. Krane, D. Axelson, Metabolite composition in breast tumors examined by proton nuclear magnetic resonance spectroscopy. Anticancer Res. 19, 1737–1746 (1999)
K. Glunde, J. Jiang, S.A. Moestue, I.S. Gribbestad, MRS/MRSI guidance in molecular medicine: targeting choline and glucose metabolism. NMR Biomed. 24, 673–690 (2011)
L.A. Brandão, T.Y. Poussaint, Pediatric brain tumors. Neuroimaging Clin. N. Am. 23, 499–525 (2013)
J. Crawford, Childhood brain tumors. Pediatr. Rev. 34, 63–78 (2013)
E. Bouffet, U. Tabori, A. Huang, U. Bartels, Possibilities of new therapeutic strategies in brain tumors. Cancer Treat. Rev. 36, 335–341 (2010)
W. Hollingworth, L. Medina, R. Lenkinski, D. Shibata, B. Bernal, D. Zurakowski, B. Comstock, J. Jarvik, Systematic review of MRS for the characterization of brain tumors. Am. J. Neuroradiol. 27, 1404–1411 (2006)
N. Morita, M. Harada, H. Otsuka, E. Melhem, H. Nishitani, Clinical application of MR spectroscopy and imaging of brain tumor. Mag. Reson. Med. Sci. 9, 167–175 (2010)
M. Castillo, History and evolution of brain tumor imaging: insights through radiology. Radiology 273, S111–S125 (2014)
M. Caulo, V. Panara, D. Tortora, P.A. Mattei, C. Briganti, E. Pravatá, S. Salice, A.R. Cotroneo, A. Tartaro, Data-driven grading of brain gliomas: a multiparametric MR imaging study. Radiology 272, 494–503 (2014)
S. Ken, L. Vieillevigne, X. Franceries, L. Simon, C. Supper, J.A. Lotterie, T. Filleron, V. Lubrano, I. Berry, E. Cassol, M. Delannes, P. Celsis, E.M. Cohen-Jonathan, A. Laprie, Integration method of 3D MR spectroscopy into treatment planning system for glioblastoma IMRT dose painting with integrated simultaneous boost. Radiat. Oncol. 8, 1 (2013). https://doi.org/10.1186/1748-717X-8-1
M.N. Pamir, K. Özduman, E. Yildiz, A. Sav, A. Dinçer, Intraoperative magnetic resonance spectroscopy for identification of residual tumor during low-grade glioma surgery. J. Neurosurg. 118, 1191–1198 (2013)
Dž Belkić, K. Belkić, A meta-analysis of studies using MR spectroscopy for evaluating suspicious lesions after radiation therapy of primary brain tumors. J. Math. Chem. 50, 2527–2557 (2012)
X. Wang, X. Hu, P. Xie, X. Li, L. Ma, Comparison of magnetic resonance spectroscopy and positron emission tomography in detection of tumor recurrence in posttreatment glioma: a diagnostic meta-analysis. Asia Pac. J. Clin. Oncol. 11, 97–105 (2015)
H. Zhang, L. Ma, Q. Wang, X. Zheng, C. Wu, B.-N. Xu, Role of magnetic resonance spectroscopy for the differentiation of recurrent glioma from radiation necrosis: a systematic review and meta-analysis. Eur. J. Radiol. 83, 2181–2189 (2014)
J.D. Seidman, B.G. Wang, Evaluation of normal-sized ovaries associated with primary peritoneal serous carcinoma for possible precursors of ovarian serous carcinoma. Gynecol. Oncol. 106, 201–206 (2007)
M. Åkeson, A. Jakobsen, B. Zetterqvist, E. Holmberg, M. Brannström, G. Horvath, A population-based 5-year cohort study of epithelial ovarian cancer in western Sweden: 10-year survival and prognostic factors. Int. J. Gynecol. Cancer 19, 116–123 (2009)
D. Kisić-Tepavčević, B. Matejić, T. Gazibara, T. Pekmezović, Trends and patterns of ovarian cancer mortality in Belgrade, Serbia: a joinpoint regression analysis. Int. J. Gynecol. Cancer 21, 1018–1023 (2011)
A. Sharifian, M.A. Pourhoseingholi, M. Norouzinia, M. Vahedi, Ovarian cancer in Iranian women, a trend analysis of mortality and incidence. Asian Pac. J. Cancer Prev. 15, 10787–10790 (2014)
J.M. Schildkraut, A.J. Alberg, E.V. Bandera, J. Barnholtz-Sloan, M. Bondy, M.L. Cote, E. Funkhouser, E. Peters, A.G. Schwartz, P. Terry, K. Wallace, L. Akushevich, F. Wang, S. Crankshaw, P.G. Moorman, A multi-center population-based case-control study of ovarian cancer in African-American women: the African American Cancer Epidemiology Study (AACES). BMC Cancer 14, Art. ID 688 (2014)
A. Chetrit, G. Hirsh-Yechezkel, Y. Ben-David, F. Lubin, E. Friedman, S. Sadetzki, Effect of BRCA1/2 mutations on long-term survival of patients with invasive ovarian cancer: the National Israeli Study of Ovarian Cancer. J. Clin. Oncol. 26, 20–25 (2008)
N. Wentzensen, S. Wacholder, Talc use and ovarian cancer: epidemiology between a rock and a hard place. J. Natl. Cancer Inst. 106, 1–2 (2014). https://doi.org/10.1093/jnci/dju260
E.J. Mališić, R.N. Janković, K.V. Jakovljević, S. Radulović, Association of TP53 codon 72 polymorphism with susceptibility to ovarian carcinomas in Serbian women. Eur. J. Obstet. Gynceol. Reprod. Biol. 166, 90–93 (2013)
L.E. Minion, J.S. Dolinsky, D.M. Chase, C.L. Dunlop, E.C. Chao, B.J. Monk, Hereditary predisposition to ovarian cancer, looking beyond BRCA1/BRCA2. Gynecol. Oncol. 137, 86–92 (2015)
P.D.P. Pharoah, The potential for risk stratification in the management of ovarian cancer risk. Int. J. Gynecol. Cancer 22, S16–S17 (2012)
F. Salehi, L. Dunfield, K. Phillips, D. Krewski, B. Vanderhyden, Risk factors for ovarian cancer: an overview with emphasis on hormonal factors. J. Toxicol. Environ. Health 11, 301–321 (2008)
J.O. Schorge, S.C. Modesitt, R.L. Coleman, D.E. Cohn, N.D. Kauff, L.R. Duska, T.J. Herzog, SGO White paper on ovarian cancer: etiology, screening and surveillance. Gyncol. Oncol. 119, 7–17 (2010)
N. Wentzensen, B. Trabert, Hormone therapy: short-term relief, long-term consequences. Lancet 385, 1806–1808 (2015)
Å. Klint, L. Tryggvadottir, F. Bray, M. Gislum, T. Hakulinen, H. Storm, M. Enghol, Trends in the survival of patients diagnosed with cancer in female genital organs in Nordic countries. Acta Oncol. 49, 632–643 (2010)
P.M. Webb, Environmental (nongenetic) factors in gynecological cancers: update and future perspectives. Future Oncol. 11, 295–307 (2015)
J.E. Muscat, M.S. Huncharek, Perineal talc use and ovarian cancer: a critical review. Eur. J. Cancer Prev. 17, 139–146 (2008)
D.W. Cramer, A.F. Vitonis, K.L. Terry, W.R. Welch, L.J. Titus, The association between talc use and ovarian cancer: a retrospective case-control study in two US states. Epidemiology 27, 334–346 (2016)
P. Bhatti, K.L. Cushing-Haugen, K.G. Wicklund, J. Doherty, M.A. Rossing, Nightshift work and risk of ovarian cancer. Occup. Environ. Med. 70, 231–237 (2013)
G. Chornokur, E. Armankwah, J. Schildkraut, C. Phelan, Global ovarian cancer health disparities. Gynecol. Oncol. 129, 258–264 (2013)
P. Mohaghegh, A.G. Rockall, Imaging strategy for early ovarian cancer: characterization of adnexal masses with conventional and advanced imaging techniques. Radiographics 32, 1751–1773 (2012)
D.K. Armstrong, S.C. Plaxe, R.D. Alvarez, J.N. Bakkum-Gamez, L. Barroilhet, K. Behbakht, L.-M. Chen, M.A. Crispens, M. Cristea, M. DeRosa, D.M. Gershenson, H.J. Gray, A. Hakam, L.J. Havrilesky, C. Johnston, M.B. Jones, C.A. Leath III, S. Lele, L. Martin, U.A. Matulonis, D.M. O’Malley, R.T. Penson, S. Percac-Lima, M. Pineda, M.A. Powell, E. Ratner, S.W. Remmenga, P.G. Rose, P. Sabbatini, J.T. Santoso, S. Shahabi, T.L. Werner, J.Burns, M. Hughes, NCCN Clinical practice guidelines in oncology (NCCN guidelines): ovarian cancer, including fallopian tube cancer and primary peritoneal cancer, Version 4.2017, November 9, 2017. https://www2.tri-kobe.org/nccn/guideline/gynecological/english/ovarian.pdf
L.F.A.G. Massuger, P.B.J. van Vierzen, U. Engelke, A. Heerschap, R. Wevers, 1H magnetic resonance spectroscopy. A new technique to discriminate benign from malignant ovarian tumors. Cancer 82, 1726–1730 (1998)
K. Belkić, M. Cohen, M. Márquez, M. Mints, B. Wilczek, A.H. Berman, E. Castellanos, M. Castellanos, Screening of high-risk groups for breast and ovarian cancer in Europe. Oncol. Rev. 4, 233–267 (2010)
A. Esseridou, G. Di Leo, L.M. Sconfienza, V. Caldiera, F. Raspagliesi, B. Grijuela, F. Hanozet, F. Podo, F. Sardanelli, In vivo detection of choline in ovarian tumors using 3D MRS. Investig. Radiol. 46, 377–382 (2011)
E.A. Boss, S.H. Moolenaar, L.F. Massuger, H. Boonstra, U.F. Engelke, J.G. de Jong, R.A. Wevers, High-resolution proton nuclear magnetic resonance spectroscopy of ovarian cyst fluid. NMR Biomed. 13, 297–230 (2000)
E. Kolwijck, R.A. Wevers, U.F. Engelke, J. Woudenberg, J. Bulten, H.J. Blom, L.F.A.G. Massuger, Ovarian cyst fluid of serous ovarian tumors contains large quantities of the brain amino acid N-acetylaspartate. PLoS ONE 5, Art. ID e10293 (2010)
D. Ben Sellem, K. Elbayed, A. Neuville, F.-M. Moussallieh, G. Lang-Averous, M. Piotto, J.-P. Bellocq, I.J. Nameret, Metabolomic characterization of ovarian epithelial carcinomas by HRMAS-NMR spectroscopy. J. Oncology 2011, Art. ID 174019, (2011)
M. Kyriakides, N. Rama, J. Sidhu, H. Gabra, H.C. Keun, M. El-Bahrawy, Metabonomic analysis of ovarian tumour cyst fluid by proton nuclear magnetic resonance spectroscopy. Oncotarget 7, 7216–7226 (2016)
E. Iorio, D. Mezzanzanica, P. Alberti, F. Spadaro, C. Ramoni, S. D’Ascenzo, D. Millimaggi, A. Pavan, V. Dolo, S. Canevari, F. Podo, Alterations of choline phospholipid metabolism in ovarian tumor progression. Cancer Res. 65, 9369–9376 (2005)
U.S. Preventive services task force screening for prostate cancer, U.S. Preventive services task force recommendation statement. Ann. Intern. Med. 149, 185–191 (2008)
D. Bonekamp, S. Bonekamp, J.K. Mullins, J.I. Epstein, H.B. Carter, K.J. Macura, Multiparametric magnetic resonance imaging characterization of prostate lesions in the active surveillance population: incremental value of magnetic resonance imaging for prediction of disease reclassification. J. Comput. Assist. Tomogr. 37, 948–956 (2013)
A. Shukla-Dave, H. Hricak, O. Akin, Y. Changhonget, K.L. Zakian, U. Kazuma, P.T. Scardino, J. Eastham, M.W. Kattan, Preoperative nomograms incorporating magnetic resonance imaging and spectroscopy for prediction of insignificant prostate cancer. BJU Int. 109, 1315–1322 (2012)
D. Rivenzon-Segal, R. Margalit, H. Degani, Glycolysis as a metabolic marker in orthotopic breast cancer, monitored by in vivo 13C MRS. Am. J. Physiol. Endocrinol. Metab. 283, E623–E630 (2002)
K.S. Opstad, B.A. Bell, J.R. Griffiths, F.A. Howe, Taurine: a potential marker of apoptosis in gliomas. Br. J. Cancer 100, 789–794 (2009)
P.J. Bolan, Magnetic resonance spectroscopy of the breast: current status. Magn. Reson. Imaging Clin. N. Am. 21, 625–639 (2013)
Dž. Belkić, K. Belkić, Optimized molecular imaging through magnetic resonance for improved target definition in radiation oncology. In: Radiation Damage to Biomolecular Systems, G. Gómez-Tejedor, M.C. Fuss (eds.), (Springer, Heidelberg, 2012), pp. 411–430
J. Frahm, H. Bruhn, M.L. Gyngell, K.D. Merboldt, W. Hänicke, R. Sauter, Localized high-resolution proton NMR spectroscopy using stimulated echoes: initial applications to human brain in vivo. Magn. Reson. Med. 9, 79–93 (1989)
Dž Belkić, Error analysis through residual frequency spectra in the fast Padé transform (FPT). Nucl. Instrum. Methods A 525, 379–386 (2004)
D.C. Williamson, H. Hawesa, N. Thacker, S.R. Williams, Robust quantification of short echo time 1H magnetic resonance spectra using the Padé approximant. Magn. Reson. Med. 55, 762–771 (2006)
A.C. Ojo, The analysis and automatic classification of nuclear magnetic resonance signals. Ph.D. Thesis, University of Edinburgh (2010), Edinburgh Research Archive. http://hdl.handle.net/1842/4109
J.M. Zhang, Human brain glutamate, glutamine, \(\gamma \)-aminobutyric acid: proton magnetic resonance spectral quantification with the fast Padé transform. PhD Thesis, University of California Los Angeles (2013). https://escholarship.org/uc/item/1np12339
E.S.S. Hansen, S. Kim, J.J. Miller, M. Geferath, G. Morrell, C. Laustsen, Fast Padé transform accelerated CSI for hyperpolarized MRS. Tomography 2, 117–124 (2016)
E. Kolwijck, U.F. Engelke, M. van der Graaf, A. Heerschap, J. Henk, H.J. Blom, M. Hadfoune, W.A. Buurman, L.F. Massuger, R.A. Wevers, N-acetyl resonances in in vivo and in vitro NMR spectroscopy of cystic ovarian tumors. NMR Biomed. 22, 1093–1099 (2009)
K. Belkić, Dž Belkić, The challenge of ovarian cancer: steps towards early detection through advanced signal processing in MRS. Isr. Med. Assoc. J. 19, 517–525 (2017)
Dž Belkić, P.A. Dando, H.S. Taylor, S.-K. Shin, Decimated signal diagonalization for Fourier transform spectroscopy. J. Phys. Chem. A 104, 11677–11684 (2000)
N. Mori, R. Delsite, K. Natarajan, M. Kulawiec, Z. Bhujwalla, K. Singh, Loss of p53 function in colon cancer cells results in increased phosphocholine and total choline. Mol. Imaging 3, 319–323 (2004)
M.F. Callaghan, D. Larkman, J.V. Hajnal, Padé-methods for reconstruction of feature extraction in magnetic resonance imaging. Magn. Reson. Med. 54, 1490–1502 (2005)
S. Kim, G. Morell, Reconstruction of NMR spectra from truncated data with the fast Padé transform, in Proceedings of the International Society for Magnetic Resonance in Medicine (ISMRM), 17th Meeting, p. 2352 (2009)
S. Williams, Dž. Belkić, K. Belkić, Potential and obstacles of MRS in the clinical setting. In: Magnetic Resonance Imaging and Spectroscopy, Comprehensive Biomedical Physics, vol. 3, Dž. Belkić, K. Belkić (eds.), (Amsterdam, Elsevier, 2014) pp. 315–329
E.A. O’Sullivan, C.N. Cowan, Modeling room transfer functions using the decimate Padé approximant. Sign. Process. IET 2, 49–58 (2008)
S. Gao, X.-Y. Xu, H.-Y. Li, Y.-H. Zhang, S.-L. Lin, Harmonic inversion of recurrence spectra of non-hydrogenic atoms in an electric field. Commun. Theor. Phys. 49, 1291–1294 (2008)
A. Lay-Ekuakille, P. Vergallo, G. Griffo, A robust algorithm based on the decimated Padé approximant for processing sensor data in leak detection in waterworks. IET Sci. Meas. Technol. 7, 256–264 (2013)
Acknowledgements
This work is supported by the research grants from Radiumhemmet at the Karolinska University Hospital, the City Council of Stockholm (FoUU) and the Marsha Rivkin Center for Ovarian Cancer Research (Seattle, USA).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
OpenAccess This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Belkić, D., Belkić, K. Review of recent applications of the conventional and derivative fast Padé transform for magnetic resonance spectroscopy. J Math Chem 57, 385–464 (2019). https://doi.org/10.1007/s10910-019-01001-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10910-019-01001-8