Structural and Magnetic Characterizations of Ruddlesden–Popper Family (Ca_2-xNd_xMnO₄) Compound Synthesized by Ceramic Route

Abstract

In this work, we were interested in the Ca_2−xNd_xMnO₄ compounds when (0.1 ≤ x ≤ 0.4). These oxides are synthesized through the solid-state method. In this study, we investigated the evolution of the structure, the magnetic properties and the Mn³⁺/Mn⁴⁺ ratio with the Nd content. The morphological study shows a decrease in the size of the grain in relation to x. The X-ray diffraction reveals a transition from the tetragonal phase to the orthorhombic phase when x = 0.4. Magnetic measurements have been taken for all the compounds in the temperature range between 2 and 300 K. The temperature-dependent magnetic susceptibility shows the presence of three transitions T_N, T_C and T_CO. A dramatic difference in magnetic susceptibility between ZFC and FC was observed below the Neel temperatures for Ca_2-xNd_xMnO₄, which shows the onset of a ferromagnetic moment below these temperatures. This moment is caused by the Dzyaloshinskii–Moriya interaction.

1 Introduction

The interest in materials with a perovskite structure is explained by their potential technological applications arising from their various and interesting physical properties [1,2,3]. The Mn-based perovskite oxides have been a renewed subject of numerous investigations in recent years [4,5,6,7] because of their colossal magnetoresistance and giant volume magnetostriction near room temperature, which is required by the technology of various sensors and magnetomechanical devices. The Ca₂MnO₄ also has a layered perovskite structure. However, it does not have an ideal Ruddlesden–Popper-type structure, i.e., the octahedra MnO₆ of the compound rotate slightly around the c axis from an ideal Ruddlesden–Popper-type structure with the space group I/4mmm. As a result, it takes a tetragonal unit cell with the space group I41/acd, and its unit cell is related to the K₂NiF₄-type unit cell in the following way: $a = \sqrt 2 a^{\prime}$ and $c = 2c^{\prime}$ (where $a^{\prime}$ and $c^{\prime}$ are the lattice parameters for the K₂NiF₄-type unit cell) [8]. Ca₂MnO₄ shows an unusual magnetic susceptibility behavior, with a very shallow maximum around 220 K and a fairly sharp peak at 114 K [9, 10]. A powder neutron diffraction study of this compound has revealed that three-dimensional ordering sets in at 114 K with an antiferromagnetic structure different from that of K₂NiF₄ [9].

The layered perovskite manganite Ca₂MnO₄ containing only Mn⁴⁺ ions has the K₂NiF₄-type of structure [11]. The doping of divalent ions by the trivalent ions, which made ​​ a change in the structural and magnetic properties of the first one and the structure of solid solutions of Ca_2-x Ln_xMnO₄ (Ln = Pr, Nd, Sm, Eu and Gd) at room temperature, was first investigated by Daoudi and Le Flem [12] and Chaumont et al. [13]. In this family, there are two kinds of crystal structure: One is the tetragonal phase and the other is the orthorhombic phase. The former appears in Pr at X = 0 [3], and also for Y, but on the other hand this transition varies according to the element of substitution: For example, for Sm, this transition is reported at x = 0.3 [14]. The latter has axes of a₀ and b₀ which are related to the tetragonal axis of a_T by a₀≈b₀≈ √2 at. Otherwise, this substitution leads to a ferromagnetic double-exchange interaction between Mn³⁺ and Mn⁴⁺ that results from the motion of an eg electron between the two partially filled d shells with a strong on-site Hund’s coupling [15, 16].

In this mechanism, the kinetic energy of the eg electrons increases at the cost of an enhancement of an antiferromagnetic coupling via the t_2g electrons. Recent studies have shown that these exchange mechanisms cannot, by themselves, explain the observed behavior in these systems and suggested that the canted moments [17], the spin structures [18], the magnetic clusters [19], the strong electron–phonon interaction arising from the lattice distortion associated with the Jahn–Teller splitting of the Mn e_g level [20] and the spin glass [21] play a crucial role in changing the number of Mn³⁺ and Mn⁴⁺ ions in the samples.

The purpose of this work is to report on the effect of the substitution of the trivalent Nd³⁺ ion for the divalent Ca²⁺ ion on the crystallographic and magnetic properties of the Ca_2−xNd_xMnO₄ (0.1 ≤ x ≤ 0.4) compounds. It also aims to determine the anisotropy constants of the studied compounds.

2 Experimental Techniques

2.1 Synthesis

The Ca_2-x Nd_xMnO₄ samples were prepared by means of a solid-state reaction method [22]. The precursors of CaO, Nd₂O₃ and MnO₂ (all of 99℅ purity) were mixed in appropriate ratios. The obtained powders were pressed under 4 tones into pellets about 1 mm in thickness and 8 mm in diameter and calcined at 1100 °C for 4 days in air with several intermediate regrinding and repressing into pellet. Finally the mixtures were sintered in the air at 1523 K for 24 h.

2.2 Apparatus

The phase purity, homogeneity and lattice structure of the synthesized compound were obtained by X-ray diffraction (XRD) analysis, using an X-ray powder diffractometer (Siemens D5000) with CuKα radiations (λ = 1.54056 Å).

Microstructures and grain sizes were observed by means of a scanning electron microscope (SEM). The pictures were taken at room temperature on a Philips XL 30 equipped with a field emission gun at 19.7 kV.

The magnetization measurements were taken using a vibrating sample magnetometer in the temperature range 5-300 K with an applied field up to 0.05 T. A domain study at low temperature was performed using the protocol ZFC/FC, which is an experimental procedure that allows to take measurements of magnetization as a function of the temperature M (T) under the action of a weak magnetic field of about 500Oe (FC) or without magnetic field (ZFC). The range of temperature explored extends from 5 to 300 K. These measurements were taken using an extraction magnetometer (BS₂).

3 Results and Discussion

3.1 Structural Properties

3.1.1 X-ray Diffraction

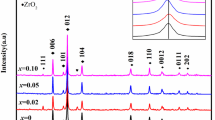
The X-ray diffraction (XRD) profiles (see Fig. 1) were indexed with a tetragonal structure (I/4mmm space group) for x ≤ 0.3 and an orthorhombic one (Pnma space group) for x = 0.4. Such behavior is in agreement with Takahaski’s results [23]. This transition type is also observed with other rare earth doping such as Pr [24], Nd and Y [25].

Fig. 1

X-ray diffraction data for polycrystalline CNMO (Color figure online)

In order to confirm the structure of materials, Goldschmidt’s tolerance factor t_G as an indicator for the stability and distortion of crystal structure was calculated [26]:

$$t_{G} = \frac{{r_{A} + r_{O} }}{{(r_{B} + r_{O} )\sqrt 2 }}$$

where r_A, r_B and r_O are the radii of A, B and O site ions in the ABO₄ structure, respectively.

The arithmetic values of the ionic rays of ions occupying sites A, B and O, respectively.

Are calculated as follows:

$$\langle {r}_{O}\rangle ={r}_{{O}^{2-}}$$

$$\langle {r}_{B}\rangle ={r}_{{Mn}^{3+}}$$

$$\langle {r}_{A}\rangle =\left(2-x\right) {r}_{C{a}^{2+}}+x {r}_{{Nd}^{3+}}$$

The calculated tolerance factor values are given in Table 1. According to this table, it can be seen that the t_G values decrease with the increase in the Nd rate due to a decrease in the average ionic radius of the site A. The decrease in the tolerance factor t_G brings about the system to the most symmetrical structure.

Table 1 Mean ion radii (< rA >) and tolerance factors

In order to determine the average crystallite size, we have used the Scherer method [27]; below is a detailed explanation of this method of calculation.

$${D}_{SC}=\frac{0.9\times \lambda }{\beta \times cos\theta }$$

(1)

where (λ = 1.541 A) is the wave length of the CuK ∝ radiation, θ is the diffraction angle for the most intense peak (2 0 0) and β is defined as:

$$\beta^{2} = \beta^{2}_{m} - \beta^{2}_{s}$$

(2)

Here, β_m is the experimental full width at half maximum (FWHM) of a standard silicon sample [28].

The mean values of the crystallite size, summarized in Table 2, confirm that all compounds are of nanometer size.

Table 2 Grain size

4 Morphological Study

4.1 Scanning electron microscope (SEM)

The morphology and the size of the particles for the compounds 0.1 ≤ x ≤ 0.4 are observed with the SEM photograph (inset Fig. 2). The obtained micrographs show that the samples are constituted of homogenous particles. Histograms displayed in Fig. 2 shows that the particles are distributed according to a Lorentzian function. Particle size distribution can significantly affect the magnetic properties of samples [29]. Table 2 presents the values obtained from the grain size, determined using ImageJ software.

Fig. 2

Typical scanning electron micrographs (SEM) of CNMO samples (Color figure online)

Obviously, the particle sizes observed by SEM are several times larger than those calculated by XRD, which indicates that each particle observed by SEM consists of several crystallized grains.

5 Magnetic Study

Figure 3 shows the variation of the magnetization as a function of the temperature for all compositions which were measured under an applied magnetic field of 0.05 T. All samples undergo a PM–FM transition upon lowering of the temperature. On the other hand, the variation of dM/dT shows that there are three transitions: The first two are defined from the minimum of the first derivative of the magnetization as a function of the temperature denoted, respectively, as T_N and T_C. The third is the T_CO charge control temperature (defined from the maximum of the first derivative of the magnetization as a function of temperature) which occurs at high temperature. The T_N, T_C and T_CO values ​​for the samples (0.1 ≤ x ≤ 0.4) are given in Table 3. Note that the substitution has no effect for x = 0.1 and x = 0.2 on the transition temperatures, on the other hand it increases progressively for x = 0.3 and 0.4: The compound Ca₂MnO₄ contains only the Mn⁴⁺ ions which are responsible for the antiferromagnetic interaction by the super-exchange interaction via 2p orbitals of oxygen. The substitution of trivalent Nd³⁺ ions for divalent Ca²⁺ ions led to the appearance of Mn³⁺ ions. Therefore, the coexistence of Mn³⁺ and Mn⁴⁺ ions promotes a ferromagnetic coupling by the super-exchange interaction, via oxygen 2p orbitals. As the Nd replaces the Ca sites, this causes a gain in the Mn^{3 +}/Mn^{4 +} ratio. The population of electrons hopping and the number of available jump sites increase. Therefore, the double-exchange becomes important, thus implying the growth of ferromagnetism as the Nd content increases [30]. To better explain the origin of ferromagnetism, according to the double-exchange interaction introduced by Zener in 1951 [16], an electron of the 2p orbital of oxygen was delocalized on the level of e_g (Mn⁴⁺) and the orbital, thus evacuated, was filled by an electron from the level of e_g (Mn³⁺) with conservation of the spin orientation (Rule of Hund). Finally, in our compound we have a competition between a weak antiferromagnetic interaction and the ferromagnetic interaction, which necessitates a ZFC/FC study.

Fig. 3

Magnetization variation as a function temperature for CNMO and derivative of magnetization as a function of temperature (Color figure online)

Table 3 Values of the transitions temperatures for different concentrations (x)

Figure 4 illustrates the low-temperature magnetic behavior of Ca_2-xNd_xMnO₄ in the temperature range 2 K–300 K. The zero-field-cooled (ZFC) and field-cooled (FC) data are measured by a BS₂ magnetometer. The sample was first cooled to 2 K, and then, the ZFC and FC magnetizations were measured during heating without a magnetic field and applying a field of 500 Oe, respectively, with intermediate cooling. Both the ZFC and FC variations are characteristic of a complex magnetic behavior with maximum values goes from 0.74 uem/g to 0.165 uem/g in the ZFC curve.

Fig. 4

Irreversibility magnetization vs temperature for CNMO (Color figure online)

The temperature-dependent irreversibility magnetization for all the compounds is shown in Fig. 5. For all compounds, the divergence between the ZFC and FC magnetization increases with the decrease in temperature, as also can be seen from M–T plots. The percentage change in irreversibility magnetization, i.e., the bifurcation between ZFC and FC is 40% in x = 0.1, is significantly high in comparison with 6% x = 0.2 and 0.3. This large divergence generally depicts the presence of competing FM and AFM interactions and the presence of magnetic anisotropy in the compound [31, 32]. A small peak in the vicinity of Neel temperature (~ 110 K) of CNMO also corresponds to the AFM behavior of the compound.

Fig. 5

Temperature dependence of the reciprocal magnetization (1/M) of CNMO measured under H = 0.05 T T. The solid lines are fits to the Curie–Weiss law (Color figure online)

In set Fig. 5, the variation of the ZFC curve shows that when the temperature is decreased, a maximum followed by a drastic reduction is produced. This behavior is observed for all compounds. This maximum corresponds to the temperature of spin glass T_SG, which decreases as x increases. This moment can be related to the spin glass state enhanced by the Dzyaloshinskii–Moriya interaction [33] (Fig. 6).

Fig. 6

Phase diagram of CNMO with 0 < x < 0.4, where PM, CO, FM and AF represent the paramagnetic phase, charge ordering phase, ferromagnetic phase and antiferromagnetic phase, respectively (Color figure online)

For T lower than T_B, a phenomenon of super-paramagnetic relaxation is observed due to the reduced size of the grains. The super-paramagnetic relaxation time is given by this formula:

$$\tau = \tau_{0} \exp ( - \frac{{E_{a} }}{{k_{B} T}})$$

(3)

where E_a is the energy barrier separating the energy minima, T is the temperature, ${\uptau }_{0}\sim {10}^{-12}-{10}^{-9}\mathrm{s}$ and k_B is the Boltzmann constant [34].

The critical size for a particle is super-paramagnetic and is defined by considering the magnetization switches once per second, which corresponds to [35]:

$$E_{a} = KV = 25k_{B} T$$

(4)

The particles are assumed to be spherical. The volume (V) of a particle is of the order of d_s³, where d_s is the diameter of a particle and it is related to the anisotropy constant by:

$$d_{S} \approx \left( {\frac{{25k_{B} T}}{K}} \right)^{1/3}$$

(5)

Table 3 shows that the blocking temperature and the anisotropy energy increase with the rate of substitution of neodymium. Finally, the anisotropy constant is calculated using the values ​​of d_s calculated by means of the Scherrer method. Since the anisotropy constants are positive, we will have three easy magnetization directions which are the three crystallographic directions similar to the case of Fe (centered cubic structure) [36].

The susceptibility presents the Curie–Weiss-type behavior $\chi = {C \mathord{\left/ {\vphantom {C {T - \theta_{CW} }}} \right. \kern-\nulldelimiterspace} {T - \theta_{CW} }}$ for the temperatures little above 55 K. Here, C and $\theta_{CW}$ are Curie constant and Curie–Weiss temperature, respectively.

The value of $\theta_{CW}$ is negative (see Fig. 4), indicating that the local magnetization maximum is associated with the antiferromagnetic AF–ferromagnetic FM transition.

With the increase in the Sr content, this signature of AF ordering shifts slightly to low temperature and appears as a subtle shoulder. In this case, Neel temperature (TN) can be defined as the temperature corresponding to the minimum of dM/dT around that shoulder. At high temperatures, the M– T curve exhibits a distinct maximum at a certain temperature (T_CO).

At high temperatures, the M– T curve exhibits a distinct maximum at a certain temperature (T_CO). With the introduction of a Sr ion, T_CO increases almost linearly. It is 231 K for x = 0.1 and 246 K for x = 0.4, which means that 2% Nd causes a increase in T_CO by about 9 K. For the temperatures between T_CO and T_N, the susceptibilities of all the compounds show Curie–Weiss-type behaviors with a positive $\theta_{CW}$ value, signaling a local ferromagnetic correlation. The theoretical effective moment is calculated through the equation:

$$\mu^{the}_{eff} = g\sqrt {J\left( {J + 1} \right)}$$

(6)

where $g = 1 + \frac{{J\left( {J + 1} \right) + S\left( {S + 1} \right) - L\left( {L + 1} \right)}}{{2J\left( {J + 1} \right)}}$ Landé factor, $J = \left| {S + L} \right|$ total moment, $L = \sum {m_{l} }$ orbital moment and $S = \sum {m_{s} }$ spin moment.

The theoretical value of the magnetic moments is too low compared to that observed experimentally. In order to obtain magnetic moments which are close to those of the experiment, one can imagine the formation of polarons containing four manganese cations (4Mn) which are coupled ferromagnetically, and the value of the magnetic moment associated to the polarons is given by the following formula:

$$\mu_{eff} \left( {4Mn} \right) = \sqrt {\mu^{2}_{eff} \left( {4Mn} \right)}$$

(7)

These results are given in Table 4. The difference between T_C and $\theta_{WC}$ could be better explained by the appearance of a magnetic inhomogeneity which may be due to the formation of polarons between Zener manganese cations, e.g., sharing two electrons suggests the formation of magnetic clusters above T_C.

Table 4 Temperature blocking energy anisotropy, anisotropy constant, the Curie constant, the Curie–Weiss temperature, the theoretical and experimentally value of the magnetic moments, for compound Ca_2−xNd_xMnO₄

Knowledge of the paramagnetic Curie temperature $\theta_{WC}$ provides access to the molecular field constant λ which is defined as the ratio of the molecular field to the magnetization M. This molecular field is related to the Curie constant by λ = $\theta_{WC}$ /C, where C denotes the Curie–Weiss constant (Table 3).

Based on the above studies, a phase diagram of CNMO system is presented in Fig. 6. It demonstrates the evolution of magnetic structure with the content of Nd. According to the previous reports, by the doping of Nd, ferromagnetic microregions can be produced in the matrix of CO phase due to an AF spin coupling between Nd³⁺ and Mn⁴⁺. Besides, the doping of trivalent ions also introduces the B-site randomness and causes the deviation of Mn⁴⁺/Mn³⁺ ratio from 1:1, which is disadvantageous to the coherence of the CO phase [36,37,38,39,40] Thus, these two factors are the main reasons for the depression of CO phase. On the other hand, the smaller Nd³⁺ ion in the Mn³⁺-O-Mn⁴⁺ bond not only changes Mn³⁺/Mn⁴⁺ ratio, but also causes the neighboring Mn–O bond length and Mn³⁺-O-Mn⁴⁺ angle to deviate from the undoped case, then leads to lattice distortions. These lattice distortions may disfavor the FM interaction between Mn ions. The competition between FM ordering and AF ordering presumably determines the variation of T_N. For the case of low Nd content, the FM ordering could be weak and its effects may be canceled out by those associated with the lattice distortion.

6 Conclusion

In this work, we studied the role of the doping effect in the structural and magnetic properties of Ca_2-xNd_xMnO₄ oxides. Doping x produces a structural and magnetic phase transition. We found that when x increases, for x < 0.3, we have a tetragonal structure and for x > 0.3 an orthorhombic system. The magnetic measurement shows that the Curie temperature T_C increases with an increasing concentration of Nd doping. In addition, magnetization decreases when x is increased. This effect can be explained by a big ferromagnetic double-exchange interaction between the ions of Mn⁴⁺ and Mn³⁺.