Metropolis–Hastings Monte Carlo Method for Neutron Emissivity Tomographic Inversion in Tokamak Plasma

Abstract

The article presents a new approach to plasma neutron emissivity reconstruction based on the Metropolis–Hastings Monte Carlo algorithm. The algorithm is based on a biased random walk. A dedicated computer code generates pseudo-random samples within the domain that contains the solution. The properly chosen objective function ensures convergence to the desired solution. The method allows to overcome the problem of trapping in local minima by accepting, with some finite probability, changes in the direction opposite to that indicated by the objective function. The developed method was tested using a synthetic data set. The results show that the method provides reliable reconstructions and thus can be used as an alternative or complementary method to the commonly applied ones. The method capabilities were also tested against noise present in the line-integrated projections.

Introduction

Tomographic reconstruction of neutron emissivity distribution in a poloidal cross-section of a fusion device such as tokamak is of great importance for retrieving information on spatially resolved fusion rates. Moreover, the reconstruction of 14.1 MeV neutron emissivity provides an insight into alpha particle profile birth. Such an inversion is performed from line-integrated quantities (projections, in tomography terms) measured by a set of cameras equipped with neutron detectors. Due to technical and financial constraints, the total number of neutron cameras as well as the number of lines of sight (LoS) in most of existing tokamaks is very limited. The task of tomographic reconstruction for thermonuclear plasma, as a source of fusion neutrons, is thus very challenging due to ill-posed nature of the problem and sparse spatial resolution of the measured plasma projections. In mathematical terms, the inversion is a non-trivial, ill-posed problem of the limited angle tomography. In this case, the standard tomographic methods, known from medical computed tomography (CT) field, such as Filtered Back Projection (FBP) or Algebraic Reconstructed Technique (ART) fail. Thus, several dedicated approaches to the reconstruction of neutron emissivity in magnetic-confinement fusion (MCF) devices have been developed and applied. Perhaps, the most commonly used methods are based on Tikhonov regularization (TR) [1, 2], minimization of Fisher Information (MFI) [3, 4] or maximization of entropy (ME) or likelihood (ML) [4, 5]. Recently other approaches such as genetic algorithms [6] or neural networks [7] were successfully applied. In [8] the authors proposed a Monte Carlo (MC) algorithm for neutron and gamma emissivity reconstruction. The authors called this method Monte Carlo Back-projection Technique. It is based on a simple iterative scheme and, for complex shapes of numerically simulated emissivity distributions, provides usually poorer results than TR or ML methods [8].

In this paper, a new approach to plasma neutron emissivity reconstruction based on the Metropolis–Hastings [9, 10] MC algorithm is presented. Large non-trivial systems, such as systems involved in the ill-posed problems of plasma tomographic reconstruction, suffer from the ‘curse of dimensionality’. This means that the number of possible configurations is very large with numerous of local minima, and therefore a straightforward sampling of these configurations is impractical. In neutron emission tomography from limited data sets measured in tokamak devices, the applied Metropolis–Hastings MC algorithm can overcome this problem, avoiding trapping of the random walk in local minima. In fact, the algorithm offers a possible method for jumping out of a local minimum by accepting, with some finite probability, changes in the direction opposite to indicated by the objective function. Moreover, in this approach, an additional a priori information e.g. about the smoothness or non-negativity of the solution can be easily incorporated by a proper choice of the objective function.

The primary aim of this work was to develop a new reconstruction method based on MC approach, to test the feasibility of its application in a tokamak plasma as well as to evaluate its accuracy and robustness. The rest of the article is structured as follows. “General Definition of Tomographic Problem” section provides the general definition of the tomographic inversion problem. In “The Inversion Method” section, details on the developed reconstruction method are presented. In “Synthetic Emissivity Models” section, a set of synthetic emissivity models used for the method evaluation is defined. “Results” section provides the results of tests obtained with the modelled neutron emissivity patterns. Finally, “Conclusions” section contains conclusions and future plans.

General Definition of Tomographic Problem

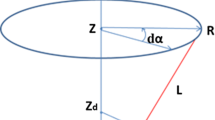
In this paper, in order to develop and evaluate the new method we use a generic experimental setup presented in Fig. 1. The system consists of two cameras with vertical and horizontal views. Each camera features 16 neutron detectors. It is worth noting that the method can be relatively easily adapted and applied to any other tokamak’s neutron diagnostic geometry. In our approach, the ill-posed inversion problem is solved in a discrete Cartesian coordinate system (i.e. using a local pixel basis set). Thus, the emissivity is discretized on a grid as a matrix $\varvec{F}$ of $N \times N$ square elements. Each element is associated with a value of the emissivity that is assumed to be constant within the pixel. The grid size $N$ is a parameter that can be tuned and it should be sensibly chosen as a trade-of between the number of degrees of freedom of ill-conditioned problem, the desired resolution of the reconstructed neutron emissivity, and the required computing time (see Sect. 5).

Fig. 1

Geometrical layout of LoS of the generic neutron tomographic system. The neutron imaging system consists of two cameras with 32 LoS in total

The discrete inverse problem of tomographic reconstruction is defined by the following set of linear equations:

$$p_{k} = \mathop \sum \limits_{i = 1}^{{N_{p} }} w_{ki} f_{i} , \quad k = 1 \ldots N_{d} .$$

(1)

In Eq. (1) $f_{i}$ is the i-th element of the plasma neutron emissivity represented by $N^{2} \times 1$ column vector $\varvec{f}$, i.e. $\varvec{f}$ is a row-major ordered vector form of emissivity matrix $\varvec{F}$, $N_{p} = N^{2}$ is the total number of elements (pixels) for the discrete representation of the neutron emissivity, $N_{d}$ is the total number of LoS (detectors) and $p_{k}$ is the k-th element of $N_{d} \times 1$ column vector $\varvec{p}$ that represents the available data (projections) along the LoS. The element $w_{ki}$ of the geometrical matrix $\varvec{W}$ represents the contribution of i-th element of emissivity to the k-th projection. The matrix $\varvec{W}$ (of size $N_{d} \times N_{p}$) is constructed based on the geometrical layout of the LoS.

The Inversion Method

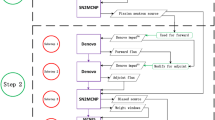
Solving of Eq. (1) by the direct matrix inversion is impossible due to its ill-posed nature and thus some kind of regularization is usually applied. In the current approach, we take advantage of stochastic MC approach, instead of solving the problem by Tikhonov Regularization (TR) with Singular Value Decomposition (SVD) as it was proposed in [2] and other reports. The proposed method is based on an iterative approach. The workflow of the reconstruction method is presented in Fig. 2. The reconstruction starts with the initialization phase. In this step, an initial guess of the solution $\varvec{f}^{\left( 0 \right)}$ is created. In the developed code, a $N_{p} \times 1$ null vector is taken as the initial guess. In the subsequent step, an element $f_{i}$ of the solution is selected randomly in order to be modified. The probability distribution for selecting the random element is defined according to projections $\varvec{p}$, similarly as proposed in [8]. Such an approach ensures that the modifications are more frequently introduced in regions where greater values of the reconstructed emissivity function are expected and less frequent modifications are performed in region where lower values are expected. The value of the selected element is then modified by adding a random number $r$ drawn from a uniform distribution in the interval $\left( {a,b} \right).$ The lower $a$ and upper $b$ limits of the interval are determined experimentally and in this work were set as − 0.001 and 0.001, respectively. In general, the smaller steps of modifications the better reconstruction accuracy can be achieved, however, at the same time, more iterations are needed to obtain the convergence. In each iteration, the unmodified solution $\varvec{f}^{\left( k \right)}$ and the modified solution $\varvec{f}^{{\left( {trial} \right)}}$ are evaluated using the Tikhonov-like objective function given as:

$$E\left( {\varvec{f}^{\left( k \right)} } \right) = \| \varvec{Wf}^{\left( k \right)} - \varvec{p}^{2} \| + \lambda\| \varvec{Lf}^{{\left( k \right)}}\|^{2}.$$

(2)

Fig. 2

Workflow diagram of the developed tomographic inversion method

In Eq. (2), $\varvec{L}$ is a matrix representation of the second-order derivative operator that imposes a smoothness constraint on the reconstructed solutions, $\lambda$ is the regularization parameter and the superscript (k) denotes the iteration number.

In principle, the regularization parameter $\lambda$ can be chosen using one of the standard methods, e.g. the Generalized Cross Validation technique [11], L-curve method [12] or Morozov’s Discrepancy Principle [13].

Generalized Cross Validation is based on the idea that if arbitrary element of the projection vector $\varvec{p}$ is left out then the corresponding solution should reflect this observation. The mean-square error of the predicted k-th projection from the estimated emissivity function, reconstructed using the regularization parameter, can be used to find the optimal regularization parameter. However, due to the fact that problem of tomographic inversion from only 32 detectors is highly ill-posed, this technique seems not to be a reliable tool for choosing of the regularization parameter. The L-curve method relies on a plot, for all valid regularization parameters, of the magnitude of the regularized solution versus the magnitude of the corresponding residual. The L-curve plotted in log–log scale should have a characteristic L-shaped appearance with a distinct corner separating the vertical and horizontal parts of the curve. The optimal choice of the regularization parameter corresponds to the L-curve’s corner [14]. Unfortunately, in the case of the plasma tomography with such a limited number of LoS, the highly ill-posed character of the problem causes the L-curve to be very often concave, and consequently, its L-vertex cannot be reliably defined. Similar conclusions have been also drawn by Craciunescu et al. [8] and Jardin et al. [15]. Finally, the Morozov’s Discrepancy Principle states that if we know an estimate on the magnitude of error in the input data, then any solution that produces a measurement with error of the same magnitude is acceptable.

From the three above mentioned methods, only the last one can be successfully applied. However, its application would additionally increase the computational cost of the method. Thus, in the presented approach, a simple alternative heuristic method of finding approximated optimum of $\lambda$ was applied. At first, two Gaussian functions are fitted to the projection data set (one for the vertical view, another for the horizontal view) as shown in Fig. 3. The regularization parameter $\lambda$ is then taken as a function of the variations $\sigma_{{\left( {reg} \right)_{1} }}^{2}$ and $\sigma_{{\left( {reg} \right)_{2} }}^{2}$ of the two Gaussian distributions:

$$\lambda \left( {\sigma_{{\left( {reg} \right)_{1} }}^{2} ,\sigma_{{\left( {reg} \right)_{2} }}^{2} } \right) = \frac{{\sigma_{{\left( {reg} \right)_{1} }}^{2} + \sigma_{{\left( {reg} \right)_{2} }}^{2} }}{l},$$

(3)

where $l$ is a constant that has been determined experimentally, based on scans for several test phantoms (in this study $l = 1.4$). Dynamic selection of $\lambda$, based on the widths of the projection functions, ensures increased smoothness for a wider emissivity function and prevents from over-smoothing when the emissivity function is more peaked.

Fig. 3

Illustration of the regularization parameter selection procedure based on the widths of Gaussian functions fitted to the projections

Let $E(\varvec{f}^{\left( k \right)} )$ denotes the value of the objective function before introducing the modification and $E(\varvec{f}^{{\left( {trial} \right)}} )$ be the value of the objective function when the modification of selected element $f_{i}$ is considered (i.e. $f_{i}^{{\left( {trial} \right)}} = f_{i}^{\left( k \right)} + r$). Then, the modification is accepted only if:

$$exp\left( { - \frac{{E\left( {\varvec{f}^{{\left( {trial} \right)}} } \right) - E\left( {\varvec{f}^{\left( k \right)} } \right) }}{c}} \right) > d ,$$

(4)

where $d$ is a uniformly distributed random number in the interval (0,1) and $c$ is a small constant parameter ($c = 0.001$ taken in this study). If condition 4 is fulfilled, the modified solution $\varvec{f}^{{\left( {trial} \right)}}$ is taken for the next iteration (i.e. $\varvec{f}^{{\left( {k + 1} \right)}} = \varvec{f}^{{\left( {trial} \right)}}$). Otherwise, the unmodified solution is used in the next iteration (i.e. $\varvec{f}^{{\left( {k + 1} \right)}} = \varvec{f}^{\left( k \right)}$). In order to prevent from unphysical solutions containing negative elements, every $s > 0$ iterations ($s = 100$, in this study) the negative values of $\varvec{f}^{\left( k \right)}$, if exist, are penalized by taking the absolute value of the solution. The iteration procedure continues until the objective function $E(\varvec{f}^{\left( k \right)} )$ is lower than a given threshold value $T$.

Figure 4a shows the evolution of objective function value as a function of the iteration number. After $\sim8 \times 10^{4}$ iterations the convergence criterion ($E(\varvec{f}^{\left( k \right)} ) < T)$ was met. Globally, the objective function decreases with the iteration number, however, locally the objective function can increase as it is shown in Fig. 4b. Figure 4c shows the change in the objective function value $\Delta E = E\left( {\varvec{f}^{{\left( {trial} \right)}} } \right) - E(\varvec{f}^{\left( k \right)} )$ as a function of the iteration number. Figure 4d presents the rejected trials (i.e. those trials for which the condition in Eq. (4) has not been fulfilled) as a function of the iteration number. It can be clearly seen, that number of the rejected events increases when the iterative process converges to the desired solution. This is quite obvious, since when the current solution becomes more similar to the final solution, there is much less possibilities to implement random changes that would decrease the objective function.

Fig. 4

Convergence of the solution in developed reconstruction method: a the objective function value as a function of the iteration number, b zoom of plot a to show that the objective function value can locally increase, c the change in the objective function value $\Delta E$ as a function of the iteration number, d rejected trials (black vertical lines) as a function of the iteration number

Synthetic Emissivity Models

The developed method was tested using a set of synthetic emissivity models. Analytic neutron emissivity models were used to produce input projections for the reconstruction algorithm. After performing the reconstruction, the model and the reconstruction results were compared using root mean square error of the reconstructed emissivity:

$$RMS_{em} = \sqrt {\frac{1}{{N^{2} }}\mathop \sum \limits_{i} \left( {f_{i}^{{\left( {mod} \right)}} - f_{i}^{{\left( {rec} \right)}} } \right)^{2} } ,$$

(5)

as a figure of merit. In Eq. (4), denotes the emissivity in the i-th element of the model, $f_{i}^{{\left( {rec} \right)}}$ is the emissivity in the i-th element of the reconstruction result.

Three phantom models were used to mimic the most commonly observed neutron emissivity distributions in tokamak plasma. The phantom models include: Gaussian, hollow, and banana shapes. The simple Gaussian model is given by the following formula:

$${\mathfrak{S}}\left( {R,Z} \right) = \exp \left( { - \frac{{\left( {R - \Delta R} \right)^{2} }}{{2\sigma^{2} }} - \frac{{\left( {Z - \Delta Z} \right)^{2} }}{{2\sigma^{2} }}} \right),$$

(6)

where $\left( {\Delta R, \Delta Z} \right)$ are the plasma center coordinates and $\sigma$ represents the standard deviation of the Gaussian. The hollow model is obtained by subtracting two Gaussian phantoms with the same emissivity center but different variances $\sigma_{1}^{2} > \sigma_{2}^{2}$:

$${\mathcal{H}}\left( {R,Z} \right) = {\mathfrak{S}}_{1} \left( {R,Z} \right) - {\mathfrak{S}}_{2} \left( {R,Z} \right).$$

(7)

Then, the banana model is derived from the hollow model by introducing a High-Field Side (HFS) poloidal asymmetry as follows:

$${\mathcal{B}}\left( {R,Z} \right) = {\mathcal{H}}\left( {R,Z} \right)\exp \left( { - \frac{{\left( {R - \Delta R_{as} } \right)^{2} }}{{2\sigma_{as}^{2} }} - \frac{{\left( {Z - \Delta Z_{as} } \right)^{2} }}{{2\sigma_{as}^{2} }}} \right),$$

(8)

where the point $\left( {\Delta R_{as} , \Delta Z_{as} } \right)$ denotes the center of the asymmetry chosen on the corona of the corresponding hollow profile, and σ_as represents the asymmetry spatial extent. The phantom shapes were selected to model, in relatively realistic way, the commonly observed distributions of neutron emissivity. While the simple Gaussian shape represents neutron emission of thermal plasma, the hollow and banana phantoms reflect more complicated cases of the neutron emissivity. The intention of the banana phantom was to model profile shapes of 14.1 MeV neutron emission observed in the ohmic deuterium discharge during tritium gas puffing (trace tritium experiments) [16, 17]. Emissivity profiles are normalized, such that $RMS_{em}$ equal to one represents 100% of global reconstruction error while zero represents a perfect reconstruction.

Results

The presented method was tested with the set of plasma neutron emissivity phantom models defined in the previous section. Test reconstructions were performed for two different phantom sizes: small (S) ($i.e. \sigma = 0.15a,\; \left( {\Delta R, \;\Delta Z} \right) = \left( {0,\;0} \right), \;\sigma_{2} = \sigma , \;\sigma_{1} = \sqrt 2 \sigma ,\; \sigma_{as} = \sqrt 3 \sigma , \;\left( {\Delta R_{as} , \;\Delta Z_{as} } \right) = \left( {\sqrt 2 \sigma ,\;0} \right)$) and large (L) ($i.e. \sigma = 0.21a,\; \left( {\Delta R, \;\Delta Z} \right) = \left( {0,\;0} \right),\;\sigma_{2} = \sigma ,\; \sigma_{1} = \sqrt 2 \sigma ,\;\sigma_{as} = \sqrt 3 \sigma ,\; \left( {\Delta R_{as} , \;\Delta Z_{as} } \right) = \left( {\sqrt 2 \sigma ,\;0} \right)$, where $a$ is the system minor radius). Figures 5 and 6 show the reconstruction results of the modelled neutron emissivity, along with the relative errors, for small and large phantoms size, respectively. Figures 7a–f summarize the reconstruction quality, in terms of $RMS_{em}$, as a function of the reconstruction grid size, for all the considered models. Since the presented method is of a stochastic nature, the presented results are the average values from 10 independent reconstructions. Error bars representing the standard deviation are also plotted in the figure, but often they are too small to be visible. For comparison, also the $RMS_{em}$ values for the results obtained with TR method as implemented in [2] have been included in the figure.

Fig. 5

Three phantom models (small size) reconstructed using the developed MC method and the relative error in reconstruction

Fig. 6

Three phantom models (large size) reconstructed using the developed MC method and the relative error in reconstruction

Fig. 7

$RMS_{em}$ as a function of the grid size for the developed MC method (in red) and TR (in blue). a small Gaussian model, b large Gaussian model, c small banana model, d large banana model, e small hollow model, f large hollow model (Color figure online)

It can be noted that, in most cases, grid size of 24 or 26 is optimal and further increase of the grid resolution does not lead to better quality (i.e. lower $RMS_{em}$) of the obtained results. In general, the developed MC method provides slightly better results of reconstruction than TR for more complex models (banana and hollow). However, $RMS_{em}$ is higher for MC method (~ 0.06) than for TR method (~ 0.02) when large Gaussian model is considered. Both methods give almost equal $RMS_{em}$ values for small Gaussian model. In general, TR method seems to better reconstruct larger phantoms while in case of the MC method slightly lower $RMS_{em}$ is obtained for the small phantoms set. For both sizes of hollow and banana models, regions with the highest relative reconstruction error are located in the central part of the model. In these regions, the modelled emissivity drops to zero, however, due to the smoothness constraint implemented in the objective function, the reconstructed emissivity has small non-zero value in these regions. This leads to the situation that the relative error locally reaches ~ 0.35, in the central part of the reconstructed emissivity (see Figs. 5 and 6).

Since the proposed approach to $\lambda$ selection is based on the heuristic method, it gives a rough estimation of $\lambda$ rather than the exact optimal value. Therefore, additional tests have been performed in order to verify the accuracy of $\lambda$ selection and its influence on the method accuracy. For all the phantoms, optimal $\lambda$ parameters were found by scanning and then compared with the $\lambda$ values selected by the developed method. The results showed that $\frac{{\left| {\lambda_{OPT} - \lambda_{SEL} } \right|}}{{\lambda_{OPT} }}$ can reach up to ~ 0.9, where $\lambda_{OPT}$ is the value of $\lambda$ that minimizes $RMS_{em}$ and $\lambda_{SEL}$ is the value selected by the developed method. The discrepancy between $\lambda_{OPT}$ and $\lambda_{SEL}$ can increase $RMS_{em}$ by up to ~ 0.2%.

Tokamak plasma diagnostics and associated data acquisition systems usually work in noisy environment due to the operation of high-power Neutral Beam Injection and Radio Frequency Heating systems. Thus, in the next step, the resilience of the developed method against noise was checked. For this purpose, the small hollow phantom model was used. The line-integrated projection data set $\varvec{p}$ was constructed using the phantom and random noise was intentionally added to the projection data. It was assumed that each detector acquired a signal with an addition of relative noise. In principle, the neutron detector signals exhibit noise resulting from statistical fluctuations in the finite number of neutrons detected, described by the Poisson distribution. In practice, however the noise can be modelled using the Gaussian distribution since for small neutron counts, the noise is generally dominated by other signal-independent sources of noise (e.g. electronics-noise), and for larger counts, the central limit theorem ensures that the Poisson distribution approaches the Gaussian distribution. Thus, the simulated noise had the Gaussian distribution with standard deviation equal to a fraction $nl$ of the signal $p_{k}$ in a particular projection channel. The noise level was varied from 0.01 to 0.1. For each noise level, the reconstruction accuracy, in terms of $RMS_{em}$, was evaluated by performing 10 reconstructions of the small hollow phantom (grid size $N = 24$) using synthetic projections affected by the noise. The results of this test are shown in Fig. 8, where $RMS_{em}$ is plotted as a function of the noise level $nl$. As a reference, the results from TR method are also included in the figure. The developed MC method features almost linear dependence of $RMS_{em}$ with increasing noise level $nl$. The resilience to noise present in the input data for the developed method is comparable to the resilience of TR method. For $nl > 0.05$ significant distortions of the emissivity shape were observed. Additionally, since the developed MC method is of a stochastic nature, the significant deviations from the mean $RMS_{em}$ values were observed, as indicated by the error bars.

Fig. 8

$RMS_{em}$ as a function of the noise level $nl$ for the developed MC method (in red) and TR method (in black). Results for the small hollow phantom model (Color figure online)

At the development stage the presented method has been implemented into a MATLAB code. A standard notebook computer (Mid 2011 Macbook Air) equipped with a dual core 1.7 GHz CPU (Intel i5-2557M) and 4 GB of DDR3 RAM memory was used for the development and tests. In general, the computation time required for reconstructions depends on many factors such as implementation (e.g. programing language, numerical libraries, sequential or parallel computing), and machine used (e.g. CPU, GPU, FPGA). Moreover, the computation time depends also on selection of the parameters that can be tuned in the method e.g. $c$ constant, reconstruction grid size $N$, convergence criterion $T$, etc. Finally, the method is of a stochastic nature itself, thus slightly different computation time can be required for different runs of the same code, even if the same input data and parameters were used. However, in order to provide at least a rough estimate on the computational demands, tests with all three phantom models (L size) were carried out. Figure 9 shows the number of iterations required to achieve the convergence and the time spent on the computations for all the modelled emissivity patterns. The presented results are the average from 10 independent runs (error bars are of the size of the symbols). In the investigated range of the grid size parameter $N$, the presented implementation of the algorithm is almost of linear time complexity ${\mathcal{O}}\left( n \right)$. For comparison, the maximal reconstruction time of the phantoms when using TR method as implemented in [2] was 78 s. In general, the reconstruction time is roughly an order of magnitude lower for TR than for the developed method.

Fig. 9

Computational time and number of iterations required to achieve convergence for reconstruction of the three phantom models (L size) using the MC-based method

Conclusions

The method of neutron emissivity reconstruction based on Metropolis–Hastings MC algorithm has been developed. The algorithm is based on a biased random walk and has been implemented using MATLAB programing language. The code generates pseudo-random samples within the domain that contains the solution. The properly chosen objective function ensures convergence to the desired solution and allows to incorporate a priori knowledge about the solution (i.e. smoothness condition). The method allows to overcome the problem of trapping in local minima by accepting, with some finite probability, changes in the direction opposite to indicated by the objective function.

The developed method was tested using a set of emissivity patterns that are commonly observed in a tokamak plasma. The results show that the method provides reliable reconstructions and thus can be used as an alternative or complementary method to the commonly applied ones. The root mean square difference between the modelled and reconstructed emissivities $RMS_{em}$ varies from ~ 0.06, for the simple Gaussian model, to ~ 0.13, for the more complicated hollow model. It must be however clearly stressed that the presented tests were performed in somewhat ideal and simplified conditions i.e. perfect models of neutron emissivity were used, input projections were not affected by noise, the full knowledge of geometrical layout of LoS was assumed, etc. In the real situation, the error estimation is much more difficult. The presented results however give at least the lower limit of the expected reconstruction errors.

The conducted tests show also that the developed method performs well when the additive noise present in the input projections $nl$ is below ~ 5%. After the promising results obtained at this development and testing stage, in the next step, a faster implementation of the method and its application with experimental data from a real tokamak diagnostic system is foreseen.