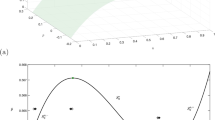
We investigate traveling wave solutions in a family of reaction-diffusion equations which includes the Fisher–Kolmogorov–Petrowskii–Piscounov (FKPP) equation with quadratic nonlinearity and a bistable equation with degenerate cubic nonlinearity. It is known that, for each equation in this family, there is a critical wave speed which separates waves of exponential decay from those of algebraic decay at one of the end states. We derive rigorous asymptotic expansions for these critical speeds by perturbing off the classical FKPP and bistable cases. Our approach uses geometric singular perturbation theory and the blow-up technique, as well as a variant of the Melnikov method, and confirms the results previously obtained through asymptotic analysis in [J.H. Merkin and D.J. Needham, (1993). J. Appl. Math. Phys. (ZAMP) A, vol. 44, No. 4, 707–721] and [T.P. Witelski, K. Ono, and T.J. Kaper, (2001). Appl. Math. Lett., vol. 14, No. 1, 65–73].
Similar content being viewed by others
References
Abramowitz, M. A., and Stegun, I. A. (eds.), (1974). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover Publications, Inc., New York, Ninth printing.
Bender C.M., Orszag S.A. (1978). Advanced Mathematical Methods for Scientists and Engineers. Mc Graw-Hill, Inc., New York
Billingham J., Needham D.J. (1991). A note on the properties of a family of travelling-wave solutions arising in cubic autocatalysis. Dynam. Stabil. Sys. 6(1): 33–49
Britton N.F. (1986). Reaction-Diffusion Equations and Their Applications to Biology. Academic Press Inc., London
Carr, J. (1981). Applications of Centre Manifold Theory, volume 35, in Applied Mathematical Sciences. Springer-Verlag, New York.
Casten R.G., Cohen H., Lagerstrom P.A. (1975). Perturbation analysis of an approximation to the Hodgkin-Huxley theory. Quart. Appl. Math. 32, 365–402
Chow S.N., Lin X.B. (1990). Bifurcation of a homoclinic orbit with a saddle-node equilibrium. Diff. Int. Equ. 3(3): 435–466
Chow S.N., Li C., Wang D. (1994). Normal Forms and Bifurcation of Planar Vector Fields. Cambridge University Press, Cambridge
Denkowska Z., Roussarie R. (1991). A method of desingularization for analytic two-dimensional vector field families. Bol. Soc. Bras. Mat. 22(1): 93–126
Diener M. (1994). The canard unchained or how fast/slow dynamical systems bifurcate. Math. Intelligencer 6(3): 38–49
Dumortier, F. (1993). Techniques in the theory of local bifurcations: Blow-up, normal forms, nilpotent bifurcations, singular perturbations, In Schlomiuk, D. (ed.), Bifurcations and Periodic Orbits of Vector Fields, number 408 in NATO ASI Series C, Mathematical and Physical Sciences, Dordrecht, Kluwer Academic Publishers.
Fenichel N. (1971). Persistence and smoothness of invariant manifolds for flows. Indiana Univ. Math. J. 21, 193–226
Fenichel N. (1979). Geometric singular perturbation theory for ordinary differential equations. J. Diff. Equs. 31(1): 53–98
Fisher R.A. (2000). The wave of advance of advantageous genes. Ann. Eugenics 7, 355–369
Guckenheimer J., Hoffman K., Weckesser W. (2000). Numerical computation of canards. Int. J. Bifur. Chaos Appl. Sci. Engrg. 10(12): 2669–2687
Jones, C. K. R. T. (1995). Geometric singular perturbation theory. In Dynamical Systems, volume 1609 of Springer Lecture Notes in Mathematics, Springer-Verlag, New York.
Kolmogorov A.N., Petrowskii I.G., Piscounov N. (1997). Etude de l’équation de la diffusion avec croissance de la quantité de matiére et son application à un problème biologique. Moscow Univ. Math. Bull. 1, 1–25
Krupa M., Szmolyan P. (2001). Extending geometric singular perturbation theory to nonhyperbolic points—fold and canard points in two dimensions. SIAM J. Math. Anal. 33(2): 286–314
Merkin J.H., Needham D.J. (1993). Reaction-diffusion waves in an isothermal chemical system with general orders of autocatalysis and spatial dimension. J. Appl. Math. Phys. (ZAMP) A 44(4): 707–721
Murray J.D. (2002). Mathematical Biology, I: An Introduction, volume 17 of Interdisciplinary Applied Mathematics. Springer-Verlag, Berlin Heidelberg, third edition
Needham D.J., Barnes A.N. (1999). Reaction-diffusion and phase waves occurring in a class of scalar reaction-diffusion equations. Nonlinearity 12(1): 41–58
Robinson C. (1983). Sustained resonance for a nonlinear system with slowly varying coefficients. SIAM J. Math. Anal. 14(5): 847–860
Salam F.M.A. (1987). The Mel’nikov technique for highly dissipative systems. SIAM J. Appl. Math. 47(2): 232–243
Sherratt J.A., Marchant B.P. (1996). Algebraic decay and variable speeds in wavefront solutions of a scalar reaction-diffusion equation. IMA J. Appl. Math. 56(3): 289–302
Witelski T.P., Ono K., Kaper T.J. (2001). Critical wave speeds for a family of scalar reaction-diffusion equations. Appl. Math. Lett. 14(1): 65–73
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Popović, N., Kaper, T.J. Rigorous Asymptotic Expansions for Critical Wave Speeds in a Family of Scalar Reaction-Diffusion Equations. J Dyn Diff Equat 18, 103–139 (2006). https://doi.org/10.1007/s10884-005-9002-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10884-005-9002-1
Keywords
- Reaction-diffusion equations
- FKPP equation
- traveling waves
- critical wave speeds
- geometric desingularization
- blow-up technique