Skip to main content
SpringerLink
Log in

Finite element modeling of effective thermomechanical properties of Al–B4C metal matrix composites

  • Original Paper
  • Published:
Journal of Materials Science Aims and scope Submit manuscript

A Correction to this article was published on 20 November 2023

This article has been updated

Abstract

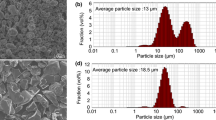
The present work aims to investigate the influences of thermal residual stresses and material properties on the thermomechanical deformation behavior of Al–B4C composites. Boron carbide-reinforced aluminum matrix composites having 4, 8, and 12 vol% boron carbide were fabricated using squeeze liquid stir casting method for experimental characterization of their microstructure, effective elastic moduli and effective CTEs at room temperature as well as elevated temperatures. Next, the thermomechanical behavior of fabricated composites was investigated using finite element modeling. The effects of thermal residual stresses on the effective material properties were examined by simulating the cooling process of MMCs from processing temperature to room temperature. The effective elastic moduli and the effective CTEs were predicted considering linear elastic as well as elastoplastic deformation of aluminum matrix, and the results obtained were compared with the experimental values. The effects of voids on effective material behavior are studied by simulating the void growth and nucleation using Gurson–Tvergaard–Needleman model.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Figure 1
Figure 2
Figure 3
Figure 4
Figure 5
Figure 6
Figure 7
Figure 8
Figure 9
Figure 10
Figure 11

Similar content being viewed by others

Change history

References

  1. Banks-Sills L, Leiderman V, Fang D (1997) On the effect of particle shape and orientation on elastic properties of metal matrix composites. Compos B Eng 28(4):465–481

    Article  Google Scholar 

  2. Park B, Crosky A, Hellier A (2008) High cycle fatigue behaviour of microsphere Al2O3–Al particulate metal matrix composites. Compos B Eng 39(7):1257–1269

    Article  Google Scholar 

  3. Park B, Crosky A, Hellier A (2008) Fracture toughness of microsphere Al2O3–Al particulate metal matrix composites. Compos B Eng 39(7):1270–1279

    Article  Google Scholar 

  4. Kaczmar J, Kainer K (1991) Properties of PM-manufactured 6061 Al-base composite materials strengthened with r-alumina fibers. Compos Eng 1(6):363–374

    Article  Google Scholar 

  5. Karbalaei Akbari M, Mirzaee O, Baharvandi H (2013) Fabrication and study on mechanical properties and fracture behavior of nanometric Al2O3 particle reinforced A356 composites focusing on the parameters of vortex method. Mater Des 46:199–205

    Article  Google Scholar 

  6. Sharma NK, Pandit SN, Vaish R, Srivastava V (2014) Effective Young’s Modulus of Ni–Al2O3 composites with particulate and interpenetrating phase structures: a multiscale analysis using object oriented finite element method. Comp Mater Sci 82:320–324

    Article  Google Scholar 

  7. Sharma NK, Misra RK, Sharma Satpal (2014) Thermal expansion behavior of Ni–Al2O3 composites with particulate and interpenetrating phase structures: an analysis using finite element method. Comp Mater Sci 90:130–136

    Article  Google Scholar 

  8. Langer SA, Fuller JE, Carter WC (2001) OOF: an image-based finite-element analysis of material microstructures. Comput Sci Eng 3:15–23

    Article  Google Scholar 

  9. Reid ACE, Langer SA, Lua RC, Coffman VR, Haan S-III, Garcia RE (2008) Image-based finite element mesh construction for material microstructures. Comput Mater Sci 43:989–999

    Article  Google Scholar 

  10. Sharma NK, Pandit SN, Vaish R (2012) Microstructural modeling of Ni-Al2O3 composites using object-oriented finite-element method. Int Sch Res Net Ceram 52:247–252

    Google Scholar 

  11. Chawla N, Chawla KK (2006) Microstructure-based modeling of the deformation behavior of particle reinforced metal matrix composites. J Mater Sci 41:913–925. doi:10.1007/s10853-006-6572-1

    Article  Google Scholar 

  12. Chawla N, Patel BV, Koopman M, Chawla KK, Saha R, Patterson BR, Fuller ER, Langer SA (2003) Microstructure-based simulation of thermomechanical behavior of composite materials by object-oriented finite element analysis. Mater Charact 49:395–407

    Article  Google Scholar 

  13. Gudlur Pradeep, Muliana Anastasia, Radovic Miladin (2014) Effective thermo-mechanical properties of aluminum–alumina composites using numerical approach. Compos B 58:534–543

    Article  Google Scholar 

  14. Zhang XX, Xiao BL, Andra H, Ma ZY (2014) Homogenization of the average thermo-elastoplastic properties of particle reinforced metal matrix composites: the minimum representative volume element size. Comp Struc 113:459–468

    Article  Google Scholar 

  15. Sharma NK, Misra RK, Sharma Satpal (2016) 3D micromechanical analysis of thermo-mechanical behavior of Al2O3/Al metal matrix composites. Comp Mater Sci 115:192–201

    Article  Google Scholar 

  16. Dvorak G, Wafa A, Bahei-El-Din Y (1994) Implementation of the transformation field analysis for inelastic composite materials. Comput Mech 14(3):201–228

    Article  Google Scholar 

  17. Torquato S (1998) Effective stiffness tensor of composite media: II. Applications to isotropic dispersions. J Mech Phys Solids 46(8):1411–1440

    Article  Google Scholar 

  18. Dvorak GJ, Srinivas MV (1999) New estimates of overall properties of heterogeneous solids. J Mech Phys Solids 47(4):899–920

    Article  Google Scholar 

  19. Yin HM, Sun LZ (2005) Elastic modeling of periodic composites with particle interactions. Philos Mag Lett 85:163–173

    Article  Google Scholar 

  20. Yi Hua, Linxia Gu (2013) Prediction of the thermomechanical behavior of particle-reinforced metal matrix composites. Comp Part B 45:1464–1470

    Article  Google Scholar 

  21. Weglewski Witold, Basista Michał, Chmielewski Marcin, Pietrzak Katarzyna, (2012) Modeling of thermally induced damage in the processing of Cr–Al2O3 composites. Comp Part B 43:255–264

    Article  Google Scholar 

  22. Gurson AL (1977) Continum theory of ductile rupture by void nucleatoin and growth—Part I: yield criteria and flow rules for porous ductile media. J Eng Mater Technol Trans ASME 99 (Ser H) 2–15

  23. Gurson A.L (1977b) Porous rigid-plastic materials containing rigid inclusions—Yield function, plastic potential, and void nucleation. In: Proceedings of the International Conference on Fracture, vol. 2A 357–364

  24. Tvergaard V (1981) Influence of voids on shear band instabilities under plane strain conditions. Int J Fract 17:389–407

    Article  Google Scholar 

  25. Needleman A, Tvergaard V (1984) An analysis of ductile rupture in notched bars. J Mech Phys Solids 32:461–490

    Article  Google Scholar 

  26. Tsagareishvili GV, Nakashidze TG, JobavaJSh Lomidze GP, Khulelidze DE, Tsagareishvili DSh, Tsagareishvili OA (1986) Thermal expansion of boron and boron carbide. J Less Common Met 117:159–161

    Article  Google Scholar 

  27. Domnich Vladislav, Reynaud Sara, Haber RA, Chhowalla Manish (2011) Boron carbide: structure, properties, and stability under stress. J Am Ceram Soc 94(11):3605–3628

    Article  Google Scholar 

  28. Moosbrugger C (2000) Atlas of stress–strain curves. 2nd ed. ASM International

Download references

Acknowledgements

We confirm that the present manuscript is the authors’ original work and that the content of this manuscript or a major portion thereof has not been published in a refereed journal, and it is not being submitted fully or partially for publication elsewhere. The manuscript has been read and approved by all listed authors.

Author information

Authors and Affiliations

  1. BML Munjal University, Gurgaon, 122413, India

    Neeraj Kumar Sharma

  2. Gautam Buddha University, Greater Noida, 201306, India

    R. K. Misra & Satpal Sharma

Authors
  1. Neeraj Kumar Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. K. Misra
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Satpal Sharma
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Neeraj Kumar Sharma.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sharma, N.K., Misra, R.K. & Sharma, S. Finite element modeling of effective thermomechanical properties of Al–B4C metal matrix composites. J Mater Sci 52, 1416–1431 (2017). https://doi.org/10.1007/s10853-016-0435-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10853-016-0435-1

Keywords

Search

Navigation