Introduction

When martensite transformation occurs in a sample of shape memory alloy (SMA), the heat of transformation should be removed from the sample to keep the temperature constant or lowering it at constant rate. The heat transfer occurs from the sample to surroundings and may cause some time-dependent phenomena in shape memory effect. Note that the martensite of SMA shows the typical thermoelasticity, which is characterized by the time-independence of its transformation kinetics [1]. It follows that the temperature is the only variable of the kinetics, as it has been verified by carefully temperature-controlled X-ray diffraction measurements, for example, in [2]. Thus, most of the time-dependent phenomena observed might have originated from the heat transfer, except for a few cases involving the relaxation in microstructure [3] and diffusional processes [4]. In fact, the strain-rate dependence of mechanical properties was observed in some respects, which were explained in terms of the local disturbance of temperature due to the heat transfer; see the examples [5–9].

In most of thermal measurements, the heat effect is observed as thermal inertia (thermal effect) [10–13]. This effect can be realized according to the Newton’s law of cooling. Namely, let us consider a substance being heated up/cooled down at constant rate by means of a heat reservoir in contact with it. When phase transformation occurs in the substance, the heat of transformation is generated, and thus the temperature shows the delay in reaching that of the heat reservoir owing to the existence of thermal resistance between them.

As a result, when the latent heat of transformation of SMA is measured with differential scanning calorimetry (DSC), the heat flow versus temperature curve shows apparent cooling-rate dependence. Kwarciak and Morawiec [14] first pointed out the effect in Nickel–Titanium (Ni–Ti) and Copper–Zinc–Aluminum (Cu–Zn–Al) SMAs such that the Mf appeared to be decreased with increasing the cooling rate, while the Ms was unaffected. It was concluded that the great part of the dependence should be caused by thermal inertia, since the kinetics was rate-independent. In this way, the possibility of DSC for the purpose of determining the Mf is substantially limited.

Now that DSC is widely used as a rapid technique for determining the transformation temperatures of SMA [15–17]; see the industrial standards [18, 19]. The inertia effect is, however, still an unresolved problem. In fact, recently Benke et al. [20, 21] applied an empirical rule of excluding the inertia effect from the Mf measured with DSC. Eventually, they discarded the tangent line method [15, 16], which has been used as the standard method of dealing with the data of DSC [18, 19]. Though the method they proposed on the basis of the empirical rule may be quite useful for practical purposes, its physical meaning is not clear.

A similar problem was formerly studied by Kempen et al. [22]. They determined the isothermal kinetics of Fe–Mn alloy martensite by differential thermal analysis (DTA) [13]. This technique includes, however, no thermal inertia. Details of the difference between DSC and DTA is described in references [10, 11, 14]. Besides the methodology, the kinetics of transformation is quite different between the ferrous alloy and SMAs; the isothermal transformation of ferrous martensite is typically time-dependent. It follows that their analysis cannot be applied directly to the present problem.

We are now dealing with the problem to determine the transformation kinetics by means of DSC. This may be similar to the typical inverse problem in thermal physics to estimate the magnitude of a heat source by measuring the temperature at distance from the source [23]. Here, the heat of transformation and the DSC curve correspond to the source and the temperature, respectively. In general, the difficulty in solving an inverse problem can be fairly reduced, if the equation relating the source and the temperature is prescribed in the form with a finite number of parameters [23].

Therefore, this study will start the analysis with defining the kinetics in the form with a few parameters. Next, the heat equation for the heat transfer in DSC will be derived. Since the general heat equation has been obtained by previous authors [10–13], what we have to do is just to consider the kinetics of martensite transformation in the equation. Then, this equation will be solved analytically or numerically. Finally, these parameters will be determined by comparing the solution with experimental results.

Model analysis

Modeling heat transfer in DSC

The DSC cell used in this study was a typical heat-flux type, and is illustrated in Fig. 1a. There were two stages for a sample and a reference material in close positions on the top surface of heat reservoir, which was a solid cylinder. The temperature of the solid cylinder was controlled to change at any fix-rate below 50 K min−1. Two thermocouples connected in series measured the difference between the temperature of the sample stage and that of the reference stage. This study assumes that the temperature of the sample, the sample stage, the reference stage, and the reservoir were uniform; they are designated as T,   T s,   T r, and T w. The heat capacity of the sample is C s and that of the reference C r.

Fig. 1
figure 1

A schematic drawing of the sample’s cell of the present DSC instrument (a), and the heat transfer diagram (b). The temperature of the sample stage, the reference stage, and the heat reservoir is denoted as T s,  T r,  and T w, respectively

Full size image

Figure 1b is the diagram of the heat transfer occurring in the DSC cell. The sample and the reference were thermally insulated from ambient. Let the thermal resistance to the heat flux between the sample stage and the reservoir be R (W−1 K).

The temperature of sample T (K) may be different from that of the stage T s owing to the heat resistance. This study deals with the austenite to martensite transformation by lowering the temperature of the heat reservoir T w at constant rate: \(\dot{T}_{\rm w} = -\alpha\,(\hbox{K}\,{\text {s}}^{-1}).\) The measurement begins at t = 0. When t 0 (s) is elapsed, the temperature of sample T is decreased to T 0 (K). Then, the temperature at arbitrary time t > t 0 is:

$$ T-T_{0} = -\alpha (t-t_{0}). $$
(1)

This relation is discussed more in detail in Appendix 1.

Let us consider the latent heat of transformation, of which amount is ℓ (J) and its time derivative \(\dot{L}\) (J s−1). The former is a numerical value, while the latter is a function of time.

$$ \ell =\int\limits^{\infty}_{0}\dot{L}{\text {d}}t > 0. $$
(2)

A DSC measures the difference in the temperatures between the sample stage and the reference stage T r − T s as a function of the duration of cooling (or heating), and outputs the difference in the heat flow between the two stages:

$$ \frac{T_{\rm r}-T_{\rm s}}{R}\quad [W]. $$
(3)

Let us set a new variable u ≡ T r − T s + constant. By taking appropriate constant, see Appendix 1, we obtain the equation of the continuity in a simple form:

$$ \tau\dot{u} +u-R\dot{L} =0, $$
(4)

where the time constant τ is defined as τ = RC s (s). This expression is essentially the same to those derived by previous authors [10–13, 22].

Before discussing Eq. 4 in this general form, we shall examine the trivial solution; in case that the transformation is absent, \(\dot{L}=0, \) thus Eq. 4 becomes a homogeneous differential equation. Suppose that the initial value of u is 0 at t = 0 and the stationary value \(\bar{u}\) at \(t=\infty,\) the solution is:

$$ u = \bar{u}\left(1-{e}^{-t/\tau}\right), $$
(5)

which expresses a relaxation process with the delay constant τ (s).

Latent heat of martensitic transformation

Now we shall consider the nonhomogeneous term \(\dot{L}\) in Eq. 4 when R ≠ 0. We can rewrite this term by chain rule:

$$ \dot{L}=\dot{T} \frac{{\text {d}}L}{{\text {d}}T}. $$
(6)

Let us denote the temperature profile of the volume fraction of martensite:

$$ \xi=\xi(T)\quad \hbox{s.t.} \quad 0\leq \xi \leq 1. $$
(7)

Here, ξ = 0 means the 100% austenite phase and ξ = 1 the 100% martensite. Since the derivative of latent heat with respect to temperature is:

$$ \frac{{\text {d}}L}{{\text {d}}T}=\ell \frac{{\text {d}}\xi}{{\text {d}}T}, $$
(8)

the nonhomogeneous term becomes

$$ \dot{L}=\ell\dot{T} \frac{{\text {d}}\xi}{{\text {d}}T}. $$
(9)

An expression similar to this was seen in a previous article [13]. Substituting it into Eq. 4, we obtain the heat equation:

$$ \tau\dot{u}+u+\alpha\ell R\cdot \frac{{\text {d}}\xi}{{\text {d}}T}=0. $$
(10)

Kinetics of martensitic transformation and simulation of DSC curve

This differential equation can be solved if the transformation kinetics ξ = ξ(T) is given in explicit form. Several mathematical functions were proposed for the kinetics [24–28]. Among the functions proposed so far we define the three trial functions, type I, II, and III:

  1. (1)

    Type I is the step function,

    $$ \xi= \left\{ \begin{array}{ll} 1,&\quad T \leq T_{0},\\ 0,&\quad T > T_{0}.\end{array} \right. $$
    (11)

    This profile has no hysteresis. The transformation starts and finishes at a temperature T 0.

  2. (2)

    Type II is an exponential decay function [24, 27],

    $$ \xi =\left\{\begin{array}{ll} 1-{e}^{\gamma(T-T_{0})},&\quad T \leq T_0,\\ 0,&\quad T> T_0.\end{array}\right. $$
    (12)

    This profile has hysteresis. Obviously, the temperature T 0 is equal to the Ms temperature. The parameter γ is the decay constant. A fast decay means a large γ. In the limit of \(\gamma \rightarrow \infty,\) this profile becomes the step function of type I.

  3. (3)

    Type III is the linear function of temperature connecting the Ms and Mf temperatures [25–27].

    $$ \xi = \left\{\begin{array}{ll} 1,& T< \hbox{Mf},\\ (\hbox{Ms}-T)/(\hbox{Ms}-\hbox{Mf}),&\quad \hbox{Mf}\leq T \leq \hbox{Ms},\\ 0,& T> \hbox{Ms}.\end{array}\right. $$
    (13)

This study defines these simple functions because of the simplicity and the usefulness for the application to form more complicated functions. Namely, they can be used as the basis functions to express arbitrary function by the linear combination of them. If the simulation could not provide satisfactory result, then the linear combination of the function probably yields more successful simulation.

Taking the derivatives, substituting these into Eq. 10, and exchanging the variable from temperature T to time t according to Eq. 1, we obtain the first-order ordinary differential equation with respect to time. The solution of this equation can be obtained in an analytic form, which is described in Appendix 2. The solutions are:

  1. (1)

    The model DSC curve for type I in the absence of martensite transformation is:

    $$ \frac{T_{\rm r}-T_{\rm s}}{R}=\alpha \left(C_{\rm r}-C_{\rm s}\right)\left(1-{e}^{-t/\tau}\right),\quad 0< t\leq t_{0}. $$
    (14)

    The right hand side of this equation represents the baseline. All the model curves have this term in common. If the reference material is absent, it is equal to Eq. 5 by letting \(\bar{u}=-\alpha C_{\rm s}.\)The curve during martensitic transformation is:

    $$ \frac{T_{\rm r}-T_{\rm s}}{R}=\alpha \left(C_{\rm r}-C_{\rm s}\right)\left(1-{e}^{-t/\tau}\right)-{\frac{\alpha \ell}{\tau}} {e}^{-(t-t_{0})/\tau},\quad t\geq t_{0}. $$
    (15)

    The second term expresses the peak due to the heat of transformation. The minus sign means it is an exothermic reaction (upward peak). According to Eq. 1, this term can be expressed as a function of temperature:

    $$ -\frac{\alpha \ell}{\tau} {e}^{(T-T_0)/(\alpha \tau)},\quad T \leq T_{0}, $$
    (16)

    and 0 for T > T 0. Hereafter, the baseline will not be shown.

  2. (2)

    The peak term for type II is:

    $$ -\frac{\alpha \gamma \ell}{1-\alpha \gamma \tau}\left[{e}^{\gamma (T-T_{0})}-{e}^{(T-T_{0})/(\alpha \tau)}\right],\quad T \leq T_{0}, $$
    (17)

    and 0 for T > T 0.

  3. (3)

    For type III:

    $$ \left\{\begin{array}{ll} -\frac{\alpha \ell}{\hbox{Ms}-\hbox{Mf}} \left[-{e}^{(T-\hbox{Ms})/(\alpha\tau)}+{e}^{(T-\hbox{Mf})/(\alpha \tau)} \right],& \quad T<\hbox{Mf}\\ -\frac{\alpha \ell}{\hbox{Ms}-\hbox{Mf}}\left[1-{e}^{(T-\hbox{Ms})/(\alpha\tau)}\right], &\quad \hbox{Mf}\leq T \leq \hbox{Ms} \\ 0,&\quad T>\hbox{Ms} \end{array}\right. $$
    (18)

Figure 2 illustrates the three trial functions, the derivatives with respect to temperature, and the model DSC curves of Eqs. 16–18. Note that the baselines are not shown. The three types have the following characteristics in common:

  1. (1)

    if the inertia effect was absent, the peak should have the same shape that of the derivative of the trial function.

  2. (2)

    with decreasing the cooling rate α, the height of peak is decreased. In the limit of \(\alpha \rightarrow 0\), the peak height becomes zero.

  3. (3)

    with increasing α, the Mf is decreased, while the Ms is unaffected. Namely, the hysteresis becomes wider as α becomes larger.

  4. (4)

    if the curve is drawn as a function of the duration of measurement, the area of the peak is ℓ (J), which is unaffected by the rate.

Fig. 2
figure 2

Three trial functions, I, II, and III, their time derivatives, and the model DSC curves at cooling rates, a 1 > a 2 > a 3. Note that the baselines are not drawn

Full size image

As these model curves are compared with those observed in this study and also those by previous authors [14–16, 20], it is concluded that the model curve of type II is most appropriate for the present purpose. Both type I showing the λ-type peak and type III showing peak with a plateau were seldom observed in experiments.

The model curve of Eq. 17 has the three parameters, the scanning rate α, the delay constant τ, and the decay constant γ. The influence of these parameters on the shape of the model curve for the Cu–Al–Ni alloy is shown in Fig. 3. The upper, the middle, and the lower figure shows the effect of α,   τ, and γ, respectively. It is seen that

  1. (1)

    the peak height is increased with increasing α, decreasing τ or increasing γ,

  2. (2)

    the Mf is decreased with increasing α, increasing τ or decreasing γ,

  3. (3)

    the Ms is virtually unaffected by these parameters.

Fig. 3
figure 3

The model DSC curves of the Cu–Al–Ni alloy. The dependence on the cooling rate (upper figure), the delay constant (middle), and the decay constant (lower) is shown

Full size image

Determining the Mf temperature in DSC curves

The Ms and Mf temperatures were measured in the DSC curves with the tangent line method [14–16]; drawing two tangent lines having the largest slopes on both side of a DSC peak, and taking the crossing points with the extended baseline. This method was proposed in early works [29], examined by several researchers and has been adopted in some industrial standards [18, 19]. Since the Mf measured with this method in DSC may include the error due to thermal inertia, we hereafter use the symbol Mf* to distinguish it from the real value of the Mf.

As the tangent line method is applied to the model curve of Eq. 17, the Mf* is calculated as:

$$ \hbox{Mf}^{\ast}=\hbox{Ms}-\left[\frac{1}{\gamma}+\alpha\tau\left(1- \frac{2\hbox{ln}(\gamma\alpha\tau)}{1-\gamma\alpha\tau}\right) \right]. $$
(19)

The first term in the parenthesis is left after taking the limit of \(\alpha \rightarrow 0. \) This term can also be obtained by drawing the tangent line to the exponential decay function of Eq. 12, as illustrated in Fig. 2. The second term in the parenthesis represents the inertia effect in the DSC peak. Letting the non-dimensional number χ ≡ γατ be a variable, the above relation becomes:

$$ \gamma(\hbox{Ms}-\hbox{Mf}^{\ast})-1= \chi\left(1- \frac{2\hbox{ln}\chi}{1-\chi}\right). $$
(20)

The right hand side of this expression is plotted against χ in the range 0 ≤ χ ≤ 3 in Fig. 4. It is a monotonic increasing function for χ > 0. Thus, the Mf* is a monotonic decreasing function of χ. The parameter χ can represent the combined effect of the three parameters on thermal inertia.

Fig. 4
figure 4

The right hand side of Eq. 20 as a function of χ

Full size image

As long as the kinetics is expressed by exponential decay, the Ms is well defined at the starting point of the peak, while the Mf cannot be distinctly located in the wake of the peak. If we define the cut-off by the volume fraction of martensite f, s.t. 0 ≤ f ≤ 1, then we can define the Mf according to Eq. 12:

$$ \hbox{Mf}=\hbox{Ms}+\frac{\hbox{ln}(1-f)}{\gamma}. $$
(21)

Formerly Tanaka [24] thought that the volume fraction of martensite was 99% at the Mf. If so, the interval between the Ms and Mf is 4.6/γ (K). If it is 95% in volume, then the interval is 3.0/γ (K).

Experimental

A ϕ 3 rod of Copper–27at.%Aluminum–4at.%Nickel alloy nearly [001] oriented single crystal grown by the Bridgman method [30] was used, since single crystal is a pre-requisite for good mechanical properties in this SMA. The DSC samples having a disk shape of 3 mm in diameter and 1–2 mm in thickness were cut from the ingot, solution treated for 1 h at 1223 K (950 °C) in air and quenched in water. The as-quenched samples were annealed at 573 K (300 °C) for 3 min to reduce possible short time aging effect and the cycling effect in case measurements were repeated for a few times [31].

A Titanium–50.5at.%Nickel alloy cold drawn wire was supplied by Furukawa Techno Material Co. Ltd., Japan. Two different heat treatments were applied. One was annealed at 773 K (500 °C) for 1 h (aged sample), and the other was annealed at 1173 K (900 °C) for 1 h and quenched in ice water (quenched sample). The aged sample showed the austenite (B2) to the R phase transformation at high temperature, and the R-phase to the B19′ martensite transformation at low temperature [16]. The quenched sample showed only the martensitic transformation [32]. We shall call the aged alloy the R-phase Ni–Ti alloy, and the quenched alloy the martensitic Ni–Ti alloy, respectively.

Calorimetric study was carried out using a Shimadzu DSC-60 heat-flux type DSC [10, 14]. The reading of temperature and latent heat was calibrated by those in the melting reaction of a 99.999% Indium. The instrument was operated at constant rate in the range between 2  and 30 K min−1 (0.033–0.5 K s−1). In conformity with the previous reports [14–16, 20], we shall use the unit of K min−1 in dealing with DSC data, and K s−1 in the model analysis.

As the reference method for the transformation temperatures, the electrical resistance [29] was measured with four-point method. The dimension of the Cu–Al–Ni sample was a rectangle of 40 mm in length and 2.5 mm in width and 0.5 mm in thickness, and that of Ni–Ti alloy a wire of 40 mm in length and 0.6 mm in diameter. Copper lead wires were spot welded to both ends and a K-type thermocouple to the center of gauge part. Therefore, no thermal effect should be involved in the measurement [10, 14, 22, 29]. The rate of heating/cooling was below 0.2 K min−1.

Results and discussion

The Ms and Mf temperatures measured by resistance and DSC method

The electrical resistance versus temperature curves of the Cu–Al–Ni alloy, the martensitic Ni–Ti, and the R-phase Ni–Ti alloys are shown in Fig. 5a, b, and c, respectively. The martensitic transformation temperatures (Ms, Mf, As, and Af) are indicated by arrows in the figures. They were determined in the same way as in the previous studies using those alloys [16, 29, 30, 32–36]. The present results are listed in Table 1.

Fig. 5
figure 5

Electrical resistance curves of the Cu–Al–Ni alloy (a), the martensitic Ni–Ti alloy (b), and the R-phase Ni–Ti alloy (c)

Full size image
Table 1 The result of resistance and DSC measurements
Full size table

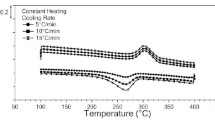
The heat flow versus temperature curves (DSC curves) of these alloys are shown in Fig. 6. These curves were measured at cooling rate of 2,  5,  10,  20, and 30 K min−1. Both the martensitic and the R-phase transformation are exothermic reactions. Those are drawn as the peaks in the upward direction [18, 19]. It is seen that both the height and the width of the peak were increased with increasing the rate. Figure 6a and b is taken in cooling runs. The thermal effect was similar to those observed by previous authors [14, 20]. Figure 6c shows the DSC curves of the R-phase transformation in cooling run and the reverse R-phase transformation in heating run. The inertia effect appeared symmetrically between heating and cooling runs. Such symmetric appearance of inertia effect was formerly reported in Cu–Al–Ni SMA [20].

Fig. 6
figure 6

Experimental DSC curves of the Cu–Al–Ni alloy (a), the martensitic Ni–Ti alloy (b), and the R-phase Ni–Ti alloy (c)

Full size image

The Ms and Mf* (or Rs and Rf*) were determined by the tangent line method as illustrated in Fig. 6c. These temperatures are plotted with respect to the cooling rate for the Cu–Al–Ni alloy, the martensitic Ni–Ni–Ti, and the R-phase Ni–Ti alloy, in Fig. 7a, b, and c, respectively. The Mf determined by resistance method is indicated by arrows in the figures. It is seen that the Mf was found within the range of the variation of the Mf* at various cooling rates.

Fig. 7
figure 7

The Ms and Mf* (or Rs and Rf*) temperatures versus cooling rate relations measured by DSC for the Cu–Al–Ni alloy (a), the martensitic Ni–Ti alloy (b), and the R-phase Ni–Ti alloy (c). Arrows indicate the Mf (Rf) determined in the resistance curves of Fig. 5. Solid lines are the plots of Eq. 19

Full size image

The latent heat of transformation was calculated from the area of DSC peak plotted as a function of time, according to the definition of Eq. 2. The calculation was performed numerically with the operating software of the DSC. Although the shape of the peak was changed by the rate, the latent heat was unaffected. The values are listed in Table 1.

Data fitting to solve inverse problem

The two parameters γ and τ included in Eq. 17 has not been determined yet. They can be determined by seeking for the best fitting of the model DSC curves to those in experiments. Let us start with fitting the height of peak, which is the distance between the summit and its baseline. The heights measured in Fig. 6 (H exp) are plotted by open symbols in the left figures of Fig. 8. As for the height of the model curve, it is calculated as the maximum of Eq. 17:

$$ H_{\rm model}=\frac{\ell}{\tau}(\gamma \alpha \tau)^{1/(1-\gamma\alpha\tau)}=\frac{\ell}{\tau}\chi^{1/(1-\chi)}, $$
(22)

which occurs at the temperature:

$$ \frac{\alpha\tau\hbox{ln}(\gamma\alpha\tau)}{1-\gamma\alpha\tau}= \frac{\chi\hbox{ln}\chi}{\gamma(1-\chi)}. $$
(23)

The optimal values of τ and γ yielding the best fitting of H model to H exp were obtained as follows:

  1. (1)

    measure the latent heat of martensite transformation ℓ,

  2. (2)

    measure the Ms temperature in DSC curve or in resistance curve and substitute it to T 0,

  3. (3)

    calculate H model using the values of ℓ and Ms, and assuming τ in the range from 0.1 to 20 s at a regular increment of 0.1 s, and γ in the range from 0.01 to 5 K−1 at a regular increment of 0.01 K−1,

  4. (4)

    take the difference between H exp and H model for the same α, and calculate the sum of the square errors over all set of data, and find τ and γ minimizing the sum.

    $$ \sum\limits_{\alpha}|H_{\rm exp}-H_{\rm model}|^2\rightarrow \hbox{min}. $$
    (24)

The results are listed in Table 2. First, the height H model calculated using the optimal parameters are drawn as the solid lines in the left figures of Fig. 8. Close agreement with the experimental result is obtained. Next, substituting the parameters into Eq. 17, the model DSC curves are drawn in the right figures of Fig. 8. The experimental (solid lines) and the model curves (dotted lines) for α = 5 and 20 K min−1 are compared. In this figure, the baseline of the model curve was not that calculated from Eq. 17, but just adjusted equal to the experimental curve.

Table 2 Determining parameters and the Mf temperature in the present method
Full size table

It is seen that the temperatures of the peaks showed disagreement of a few degree. The disagreement may originate from the difference between the trial function and the real kinetics. A better fitting could be obtained using more complicated trial function as mentioned before. In spite of the disagreement, we obtained close agreement with respect to the temperature range of the peak, i.e., the interval between the Ms and Mf*. Therefore, for the present purpose of simulating the Mf* including the inertia effect, the disagreement in the peak temperatures could be tolerated.

Two methods of extrapolation for determining the Mf temperature

The Mf* temperatures calculated from Eq. 19 are drawn as the solid lines in Fig. 7. Close agreement between the measured and the calculated Mf* is ensured. In this figure, the extrapolation to the zero cooling rate yields a value between the Ms and Mf determined by resistance measurement. The Mf* thus extrapolated are listed in Table 2. They are 5, 6, and 3 K below the Ms.

This result can be realized from the kinetics showing exponential decay. As mentioned before, in the limit of \(\alpha\rightarrow 0, \)the value of the Mf* in Eq. 19 is:

$$ \lim_{\alpha \rightarrow 0}\hbox{Mf}^{\ast}=\hbox{Ms}-1/\gamma. $$
(25)

According to this relation, the values of γ estimated by the extrapolation applied to Fig. 7 are 0.20,  0.17,  and 0.33 K−1. These are almost equal to the γ determined by the data fitting performed in Fig. 8, see the values in Table 2.

Fig. 8
figure 8

The left figures are the peak height versus cooling rate relation measured in experiments (open symbols) and those calculated from Eq. 22 (solid and dotted lines). The right figures are the experimental DSC curves (solid lines) and the model curves (dotted lines)

Full size image

It should be noted that linear extrapolation, if we apply it, may cause significant error. Instead, we have found that the approximation by means of the fourth-order polynomial provides result with more reasonable accuracy. For example, the linear extrapolation in the range of α between 2 and 30 K min−1 in the Cu–Al–Ni sample gives Ms − 1.53/γ (K), while the forth order polynomial Ms − 1.094/γ (K). If the range of α is limited below 10 K min−1, more accurate results can be obtained; Ms − 1.24/γ (K) by the former and Ms − 1.047/γ (K) by the latter extrapolation.

Now we shall examine how the Mf was determined in the resistance curves of Fig. 5. According to Eq. 21, the Ms and Mf in Table 1 and the γ in Table 2 means that 94% volume was transformed in the Cu–Al–Ni alloy, 92% in the martensitic Ni–Ti alloy, and 97% in the R-phase Ni–Ti alloy. Thus, in average, the resistance method determines the Mf as the temperature when 95% volume is transformed. The Mf defined for 95% transformation in Eq. 21 is listed in Table 2.

In summary, the procedure of the extrapolation method is,

  1. (1)

    measure the Ms and Mf* by taking DSC curves at various rates,

  2. (2)

    extrapolate the Mf* into \(\alpha\rightarrow 0\),

  3. (3)

    determine γ through Eq. 25,

  4. (4)

    estimate the Mf through the relation:

    $$ \hbox{Mf}=\hbox{Ms}-3/\gamma, $$
    (26)

    which derives the temperature when 95% of the sample becomes martensite.

The other method of extrapolation is letting the mass of a sample to zero. Since the heat capacity C s is in proportion to the mass of sample M, the delay constant τ = C s R is in the same proportion to M. Since \(\tau \rightarrow 0\) as \(M\rightarrow 0, \) the extrapolation is expected to derive the temperature:

$$ \lim_{M \rightarrow 0}\hbox{Mf}^{\ast} =\hbox{Ms}-1/\gamma. $$
(27)

In order to check if the relation holds in experiment, we carried out DSC using a sample of the Cu–Al–Ni alloy in a shape of round disk. The thickness was gradually reduced by grinding the top surface while keeping the thermal contact of the bottom surface unchanged. The result is shown in Fig. 9. The upper figure (Fig. 9a) is the DSC curves. It is seen that the thermal effect was decreased with decreasing the mass of the sample.

Fig. 9
figure 9

a DSC curves of Cu–Al–Ni alloy with different weights, and b the Ms and Mf* temperatures were plotted as functions of the weight M (mg)

Full size image

The lower figure (Fig. 9b) is the Ms and Mf* temperatures plotted against the mass. Again, the Ms was unaffected, while the Mf* was decreased with increasing the mass M (mg). The prediction of Eq. 19, which is drawn as the solid and dotted lines, shows close agreement with the measured Mf*. This calculation was done by assuming that the delay constant τ was equal to 13.3M/46 (s), since τ = 13.3 s in Table 2 was obtained in the Cu–Al–Ni sample of 46 mg. This method estimates γ equal to 0.2 K−1, and thus the Mf equal to Ms − 3/γ = 393 K, which is fairly close to that determined by the resistance method in Table 1.

Conclusion

Using two representative SMAs, Cu–Al–Ni and Ni–Ti, simulation and experiment of the thermal effect in DSC were carried out. Exponential decay was likely appropriate for expressing the kinetics of the martensitic transformation in these alloys. Using this kinetics, two methods of determining the Mf temperature were proposed. One was the extrapolation of the Mf* measured at various cooling rates to the zero rate. The other was the extrapolation of the Mf* measured in samples with various weights to the zero mass. Both methods derived a temperature just below the Ms. Letting the interval between the Ms and the temperature equal to 1/γ (K), we obtained the value of decay constant γ (K−1). Then we could estimate the Mf through the relation Ms − 3.0/γ (K) as the temperature when 95% volume was transformed. The result showed close agreement with the Mf determined by electrical resistance method.