Size of oxide vacancies in fluorite and perovskite structured oxides

Abstract

An analysis of the effective radii of vacancies and the stoichiometric expansion coefficient is performed on metal oxides with fluorite and perovskite structures. Using the hard sphere model with Shannon ion radii we find that the effective radius of the oxide vacancy in fluorites increases with increasing ion radius of the host cation and that it is significantly smaller than the radius of the oxide ion in all cases, from 37 % smaller for HfO₂ to 13 % smaller for ThO₂. The perovskite structured LaGaO₃ doped with Sr or Mg or both is analyzed in some detail. The results show that the effective radius of an oxide vacancy in doped LaGaO₃ is only about 6 % smaller than the oxide ion. In spite of this the stoichiometric expansion coefficient (a kind of chemical expansion coefficient) of the similar perovskite, LaCrO₃, is significantly smaller than the stoichiometric expansion coefficient of the fluorite structured CeO₂. Our analysis results indicate that the smaller stoichiometric expansion coefficient of the perovskites is associated with the restraining action of the A-O sub-lattice to dimensional changes in the B-O sub-lattice and vice versa.

1 Introduction

The performance of fluorite and perovskite structured metal oxide ceramics is very dependent on the volume changes that are associated with the necessary substitution of some of the host ions with lower valent metal ions to introduce ionic conductivity via the oxide vacancies formed as charge compensating defects. Furthermore, reduction of Ce⁴⁺ to Ce³⁺ in CeO_2-x expands the crystal lattice to an extent that may mechanically damage components of ceria, e.g. dense oxygen separation membranes. Important features like oxide ion conductivity, thermal expansion coefficient and mechanical stability are very dependent on the defect chemistry and in particular the properties of the substituting cations and the associated oxide vacancies. Examples of features related to the type of cation substitutes are: 1) the crystal lattice shrinks if a fluorite like CeO₂ is doped with a 2 or 3-valent cation of approximately the same size as Ce⁴⁺; 2) mechanical failure due to stress gradients caused by volume change gradients during reduction of substituted CeO₂; and 3) the oxide ion conductivity reaches its maximum as a function of dopant radius for a dopant radius - the matching radius - that does not change the lattice parameter of the host crystalline compound, i.e. the highest conductivity occurs if Vegard’s slope is zero or the conductivity—for a given dopant concentration—is highest in the stress free lattice [1–4]. Thus, knowledge on volumetric aspects of the crystal defects may help us in optimizing devices that utilize such materials, e.g. solid oxide electrolysers and fuel cells and dense oxygen separation membranes.

Even though the basic knowledge behind these phenomena was available several decades ago [5–7] there has been a lot of discussion and disagreement about the volume of the oxide vacancies including many years of debate about whether the volume of a vacancy is larger or smaller than that of the oxide ion. Now, it seems agreed that the oxide vacancies in fluorite oxides are always smaller than the oxide ion [8, 9], but still the detailed relationships between ionic sizes and vacancy size may be debated. Furthermore, less knowledge is available on oxide vacancies in perovskite structured oxides.

This paper is written in memory of Prof. A. S. Nowick, who dedicated almost all of his science to the study of how the crystal defects determine the physical, chemical and mechanical properties of metal oxides, in particular fluorite and perovskite structured oxides, see [10–12] as examples. Following in Prof. Nowick’s footsteps, we here analyze data from the literature for fluorites and perovskites with different degrees of metal ion substitution, different substitutes and different host ions with respect to the volumetric changes due to doping, and in particular estimate the volume of the oxide vacancy as a function of ion size and crystal structure. We show that the oxide vacancy volume is related to the type of structure and to the oxygen-metal bond strength (and length) of the host lattice. Based on this we are discussing some of the detailed claims in the literature. Furthermore, shortcomings of the models are elucidated.

2 Empirical relations between lattice constants, cation radii and vacancy size

We have chosen to estimate the size of vacancies using the Shannon radii of the ions [13] and represent them as hard spheres in direct contact in the crystal unit cell (hard sphere model) because this is a simple method that is very easy to apply in ceramic engineering. It should in this context be noted that the Shannon radius is a kind of average that depends on coordination number (CN) of the given ion. The radius is found by analyzing a large number of different crystal structures and different compositions in which a given ion has a given CN. As a matter of fact the hard sphere model usually does not give the exact bond lengths and unit cell volumes measured using X-ray or neutron diffraction (XRD, NRD), but the approximation is sufficiently good for many purposes. This model seems very useful even in case of crystals with relatively high concentrations of vacancies that introduce a significant additional uncertainty because the oxide vacancy will change the CN of the cations. As the detailed defect structure of the nonstoichiometric crystals is usually not known, we assume that the vacancies and dopant are distributed randomly, and we cannot make any direct reliable correction if this is not the case. Therefore, we have decided to use this model in spite of its limitations at least within the validity range of Vegard’s law. We touch upon deviations that appear at high degree of cation substitutions below. As it appears below some extra “tools” are unavoidable in the case of perovskites. It is also worth noting that the properties that we are interested in are often those of the oxides at elevated temperatures (such as 500–1000 °C), whereas the Shannon radii are for room temperature.

2.1 Fluorites

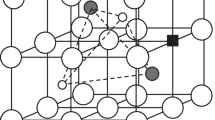
The fluorite structure is a relatively open structure. The positions of the ion centers are shown in Fig. 1, but naturally the metal and the oxide ions “touch” each other and also the O²⁻ in the cubic sublattice “touch” each other when perceiving the ions as hard spheres. Using CeO₂ as example the lattice parameter is 5.41134 Å [14] giving an O-O distance of 2.71 Å compared to the Shannon diameter of O²⁻ of 2.76 Å, i.e. the O-O distance is slightly smaller than given by the hard sphere approximation. This may be taken as indicative of the degree of accuracy of this approximation.

Fig. 1

Structure of MO₂ fluorite unit cell, M = Hf⁴⁺, Zr⁴⁺, Ce⁴⁺, U⁴⁺ or Th⁴⁺; M is black, O is gray

Based on a comprehensive data material Kim [7] established the following empirical relation between the unit cell parameter, a, of the doped oxide, the unit cell parameter of the pure undoped fluorite structured oxide, a₀, the difference in cation radius, Δr_cat, the difference in cation charge, Δz_cat, between the host and the substitutional, and the fraction of substituted cations, x:

$$ a={a}_0+\left(A\cdot \Delta {r}_{cat}+B\cdot \Delta {z}_{cat}\right)\cdot x $$

(1)

A and B are constants that are dependent on host cation type.

Using the hard sphere approximation, with oxide vacancies treated as substituents in the anion sublattice, the effective radius of the oxide vacancies in doped ceria and zirconia was calculated first by Hong and Virkar [15] and later by Marrocchelli et al. [8], who also presented a DFT derived structural relaxation model that rationalizes why the effective radius of the oxide vacancy is smaller than the oxide ion radius in contrast to the perception of many workers in the area. The formulas derived from the hard sphere model are (assuming 3-valent cation substituents):

$$ a=\frac{4}{\sqrt{3}}\left({r}_{cat}+{r}_{an}\right) $$

(2)

$$ {r}_{cat}=\left(1-x\right)\cdot {r}_h+x\cdot {r}_s $$

(3)

$$ {r}_{an}=\left(\frac{2-\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{2}\right)\cdot {r}_O+\left(\frac{\raisebox{1ex}{$x$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}{2}\right)\cdot {r}_V $$

(4)

where h stands for host and s for substitutional, and r_V is the oxide ion vacancy radius. Equating Kim’s lattice constant expression (Eq. 1) to that of the hard sphere model (Eq. 2), and substituting Eqs. 3 and 4, results in the following relation between the vacancy radius and the parameters A and B used in Kim’s empirical relation:

$$ {r}_v={r}_O-\sqrt{3}\cdot B\cdot \Delta {z}_{cat}+\left(4-\sqrt{3}\cdot A\right)\cdot \Delta {r}_{cat} $$

(5)

The above expressions are for a single substituent, but generalizing to multiple substituents is trivial. The expression derived from Kim’s empirical formula (Eq. 5) indicates that the vacancy radius depends on the ionic radius of the substituent. This is different from the implementation of the hard sphere model by Hong and Virkar [15] and by Marrocchelli et al. [8], where r_V was treated as a constant.

The results of calculations of effective vacancy radii for a selection of compositions using Kim’s formulas are shown in Table 1 and compared with those found by Hong and Virkar [15] and by Marrocchelli et al. [8]. In order to visualize the outcome of these relations the data have also been plotted in Fig. 2.

Table 1 Oxide ion vacancy radii in MO₂ (M = Hf, Zr, Ce, U, Th) type fluorite structured oxides calculated using different approaches from the literature. The Shannon radii of the host and dopant cations with CN = 8 are in Å: Hf⁴⁺ 0.83; Zr⁴⁺ 0.84; Ce⁴⁺ 0.97; U⁴⁺ 1.00; Th⁴⁺ 1.21; Y³⁺ 1.02; Gd³⁺ 1.05, La³⁺ 1.16. The radius of O²⁻ (CN = 4) is 1.38 Å

Fig. 2

Dependence of oxide ion vacancy effective radius, r_V, on host cation radius, r_h, in MO₂ fluorite structured oxides using Kim’s formula. Calculated values of r_V for three selected dopants (Y, Gd and La) are also shown. r_V values calculated by Hong and Virkar [15] and by Marrocchelli et al. [8] are also included

The first trend seen in Fig. 2 is that the bigger the host cation is, the bigger is the oxide ion vacancy. The next observed trend is that (as a consequence of Kim’s formula) the bigger the dopant ion is, the smaller is the effective vacancy radius. A qualitative explanation of the first trend might simple be that Born-Haber energy (to a large extent the result of the coulombic attraction) is the bigger, the smaller the host cations are. The lattice “collapses” locally around the vacancy, and the degree of collapse is the bigger, the bigger the coulombic forces are. By this the unit cell shrinks even though only the first 2 to 3 coordination shells are affected by the vacancy. The main force counteracting a further collapse is the Pauli repulsion by the oxide ions. DFT calculations supporting this in the case of ceria were recently published by Marrocchelli et al. [8].

The second trend—r_V decreases with increasing r_s—may be explained by a stronger association of vacancies to big dopant ions than to small ones due to the compressive stress that will form around dopants with radius larger than the matching radius, r_m, the dopant radius giving zero Vegard’s slope.

The finding that r_V in general increases with increasing r_h, is in conflict with molecular dynamics (MD) modeling results published by Marrocchelli, Bishop and Kilner [9], for host ionic radii larger than that of Ce. They model the same fluorite structured oxides as we treat here, but they also include the high temperature δ-phase of Bi₂O₃. They find that of the oxide vacancies in this series of fluorites the vacancy in doped ceria is the biggest. Again, using the data for δ-phase of Bi₂O₃ they claim that the model results are supported by experiments. Based on the analysis above we are skeptical to these model results being valid for doped MO₂ type fluorites. Apart from the outcome of our analysis, we have further the following arguments against using δ-Bi₂O₃ in this context: 1) δ-Bi₂O₃ is not an MO₂ type of fluorite structured oxide; 2) the δ-Bi₂O₃ crystal structure does not contain oxide vacancies, even though it is a very good oxide ion conductor due to disorder. It contains 25 % empty oxide ion sites that are inherent to the structure and thus not charged as is the case for e.g. a vacancy in Gd₂O₃ doped ceria; 3) the concept of ionic radius may not be very useful in the case of the Bi³⁺-ion, which has a so-called lone pair of 6s electrons. The volume of this lone pair constitutes a significant fraction of the whole volume of the ion, i.e. Bi³⁺ might be better described as having the shape of two balls, which are to some extent grown together. The lone pair is very polarizable. All in all this lone pair of 6s electrons makes Bi³⁺ to form a high temperature oxide crystal with fluorite structure that has properties very different from those formed by other cations with same charge and very similar Shannon radius. Note for instance that La₂O₃ does not attain a fluorite structure at any temperature even though the Shannon radius of La³⁺ (1.16 Å) is very close to that of Bi³⁺ (1.17 Å).

2.2 Perovskites

Another group of metal oxides that is about equally tolerant to nonstoichiometry as the fluorites, is the perovskite structured oxides with the general formula ABO₃, where A is a big and B is a small metal ion. The ideal perovskite is cubic and in this the A-ions must have the same Shannon radius (CN = 12) of 1.40 Å as that of O²⁻ with CN = 6. In this case the A and O ions form together a cubic closed packed lattice and the small B-ions are accommodated in the cavity inside the oxygen octahedra as shown in Fig. 3.

Fig. 3

Structure of perovskite, ABO₃, where A (gray) is a big ion, B (black) is a small ion; O is blue. The O + A ions form together a cubic closest packed structure if the size of the A-ion is close to the size of the oxide ion

This means that the perovskite structure is a very compact structure with strong B-metal-oxygen bonds. The ideal perovskite has thus the following ion size data: r_O2- = r_A,ideal = 1.40 Å; r_B,ideal = 0.58 Å; lattice parameter a = 3.96 Å. In contrast to the cubic fluorite, which stays cubic on substitution of metal ions until the solubility limit is reached, the perovskites are often changing away from the exact cubic structure by a slight change in the shape of the precise oxygen octahedra, which easily may be compressed, elongated, tilted or twisted. This makes it even more difficult to make an accurate model for evaluating the size of oxide vacancies than in the case of fluorites. In spite of this we are here using again a kind of hard sphere approximation in an equivalent cubic representation for estimating the size of oxide vacancies, because the deviations from the cubic structure are often very small.

2.3 “Relaxed” hard sphere approximation

The (weighted) average A, B and anion radii in A^h _1-xA^s _xB^h _1-yB^s _yO_{3–0.5x-0.5y} (where the valency difference between h and s is 1) can be defined as:

$$ {r}_A=x\cdot {r}_A^s+\left(1-x\right)\cdot {r}_A^h $$

(6)

$$ {r}_B=y\cdot {r}_B^s+\left(1-y\right)\cdot {r}_B^h $$

(7)

$$ {r}_{anion}=\frac{3-0.5\cdot x-0.5\cdot y}{3}\cdot {r}_O+\frac{0.5\cdot x+0.5\cdot y}{3}\cdot {r}_V $$

(8)

The lattice constant of a cubic perovskite in the hard sphere approximation is related to the average A, B and anion radii according to the following relations:

$$ a=\sqrt{2}\left({r}_A+{r}_O\right)=2\left({r}_B+{r}_O\right) $$

(9)

This leads to a tolerance factor $t=\frac{\left({r}_A+{r}_O\right)}{\sqrt{2}\left({r}_B+{r}_O\right)}$ of 1 for the ideal cubic perovskite structure.

Two “sensitivity” factors p₁ and p₂ are introduced to the expression for the unit cell parameter (Eq. 9) in order to account for i) the offset of the effective ionic radii in the real perovskite structured compounds from the ones calculated from the Shannon radii [13] and ii) the deviation of the A-O and B-O sub-lattices from the hard sphere approximation, thereby forming a “relaxed” hard sphere approximation:

$$ {a}_{AO}=\sqrt{2}{p}_1\left({r}_A+{r}_{anion}\right) $$

(10)

$$ {a}_{BO}=2{p}_2\left({r}_B+{r}_{anion}\right) $$

(11)

$$ a=\frac{a_{AO}+{a}_{BO}}{2} $$

(12)

In this description the lattice constant (12) is assumed to be given by a “compromise” (simple average) between the one that would be dictated considering the A-O lattice only (Eq. 10) and the B-O lattice only (Eq. 11). The above set of equations (Eqs. 10–12) includes three unknown parameters, p₁, p₂ and r_V. Their values (assumed constants) have been determined by fitting Eqs. 10 and 11 to experimental data for La_1-xSr_xGa_1-yMg_yO_{3–0.5x-0.5y} [16–18] in the equivalent cubic representation. In order to enable a comparison between the unit cells of the different La_1-xSr_xGa_1-yMg_yO_3-δ materials the volume per A and B site was used. The unit cell volumes of the orthorhombic and monoclinic perovskite materials were transformed to an equivalent cubic unit volume by dividing by the number of formula units (Z = 4). This gives the unit cell volume per A and B site, similar to the high symmetry Pm-3 m structure, and an equivalent cubic unit cell parameter (a’) was calculated as the cube root of the volume. The unit cell parameters from [17] were systematically lower than the other reported values, and in order to use these in the calculations, they were brought to the same absolute scale by scaling to the unit cell volume of the undoped LaGaO₃ material, using a factor of 1.0033.

The quality of the fitting to the experimental data is illustrated in Fig. 4 below. The fitted lines in this figure correspond to the average values determined from Eqs. 10–12. The relative difference between experimental and calculated value is less than 0.15 % for any data point. This is considered a fair agreement given i) the inherent scattering in the experimental data from different sources reaching a value of up to 0.13 % and ii) the simplifying assumptions imposed to the “relaxed” hard sphere approximation. The assumption of constant p₁ and p₂ is considered particularly weak, as their values may be expected to pass through a discrete step for t = 1, which separates the regime where the A-O sub-lattice is intimately packed (t > 1) from the regime where the B-O sub-lattice is intimately packed (t < 1). This assumption was not problematic for the lanthanum gallate series considered here as t ≈ 1 for the examined compositions, but varying p₁ and p₂ values upon treating other perovskite compositions may be required.

Fig. 4

Fitting of the “relaxed” hard sphere approximation to the experimental data. x = 0.1 data with open, x = 0.15 with half filed and x = 0.2 with filled triangles. The fitted lines correspond to the average values determined from Eqs. 10–12. The values of the fitted parameters are also shown in the figure

Indeed, the values for both p₁ and p₂ fitted very close to unity, being 0.998 and 0.963, respectively, which indicates that i) the deviation from the hard sphere approximation is not significant for either sub-lattice and that ii) the Shannon ionic radii offer a good representation of the ionic radii in these perovskites. The oxide ion vacancy assumes an effective radius of 1.31 Å, smaller than the oxide ion radius of 1.4 Å. The relative difference is only 6 %, as compared to ca. 20 to 30 % for ceria and zirconia, respectively.

Figure 5 compares the experimental data for the equivalent cubic unit cell parameter with the values estimated from the A-O sub-lattice (a_AO), the B-O sub-lattice (a_BO) and their average value (used in Fig. 4) for the A-site and B-site acceptor substituted series, as well as for the end member LaGaO₃. It is obvious that the average value (a) comes much closer to the experimental data than the individual a_AO or a_BO values. It is further seen that the equivalent cubic unit cell parameter for the A-site acceptor substituted series is overestimated by a_AO and underestimated by a_BO, and vice versa for the B-site acceptor substituted series.

Fig. 5

Comparison of the experimental data for the equivalent cubic unit cell parameter with the values estimated from the A-O sub-lattice (a_AO), the B-O sub-lattice (a_BO), and their average value (a)

When substituting La with Sr, the average A-site radius increases, the B-site radius remains unchanged and oxide ion vacancies are introduced. The combination of increasing r_A and decreasing r_anion with increasing Sr substitution on the A-O sub-lattice, results in a tendency for the equivalent cubic unit cell parameter to expand. On the other hand, the decreasing r_anion with increasing Sr substitution on the B-O sub-lattice, results in a tendency for the equivalent cubic unit cell parameter to contract. The experimental data suggest that the equivalent cubic unit cell parameter remains constant within experimental uncertainty. This is interpreted as the effort of the lattice to find an optimum minimum energy configuration that compromises the trends induced by the two sub-lattices, and explains why the average value (a) provides a better representation of the experimental data than either a_AO or a_BO. This means that both sub-lattices are strained, or shifted from the configuration that would provide minimum free energy for each individual sub-lattice, such that the overall structure reaches a minimum energy configuration. In reality this strain is partly released by coordinated distortions that lower the symmetry of the structure from cubic to orthorhombic. Similar arguments hold for the B-site substituted series.

A number of studies have previously attempted to provide empirical (or semi-empirical) expressions for the equivalent cubic unit cell parameter of perovskites by fitting experimental data for perovskite oxides and halides [19–22]. Nevertheless, our analysis differs from the previous in taking into account also anion sub-stoichiometry. This consideration enables us to derive the apparent value of the oxide ion vacancy radius for a class of perovskite oxides showing fast oxide ion conduction. Furthermore, the expression proposed here for the equivalent cubic unit cell parameter has the advantage of being directly derived from geometrical structural considerations, thereby enabling a straightforward interpretation of the empirical parameters p₁ and p₂ (see preceding discussions). The expression proposed here (Eq. 12) is similar to that proposed by Ubic et al. [22], with the difference that we have avoided the use of an additional constant term. Furthermore, we have utilized A-site ionic radii in the correct 12-fold coordination rather than the erroneous 6-fold coordination often chosen in previous studies.

3 Stoichiometric expansion

In spite of the fact that the oxide vacancies are smaller than O²⁻ the lattice will expand if O²⁻-vacancies are formed together with reduction of Ce⁴⁺ in CeO₂ to Ce³⁺ at low oxygen partial pressure. This is due to the fact that the radius of Ce³⁺ (1.14 Å, CN = 8) is bigger than r_m,CeO2 = 1.04 Å. The expansion on reduction due to a gradual change in stoichiometry is called stoichiometric expansion (sometimes “expansion on reduction” or “chemical expansion”, which is in fact a broader phenomenon [23]) and can be described by the “stoichiometric expansion coefficient” (SEC or α_S) in analogy to the thermal expansion coefficient.

The stoichiometric expansion coefficient, α_S, is defined by:

$$ \upvarepsilon =\Delta \mathrm{L}/\mathrm{L}={\alpha}_{\mathrm{S}}\cdot \delta $$

(13)

where ε is the measured strain, L is the sample length, and ΔL is the change due to a change in oxygen stoichiometry of δ e.g. in reduced CeO_2-δ or in doped La_1-xSr_xCrO_3-δ [24].

In case of ceria this may have very serious consequences because α_s = 0.1 mol⁻¹, i.e. per mole oxide removed from 1 mol CeO₂, which is the same as δ in CeO_2-δ. Thus, reducing CeO₂ to CeO_1.9 expands the lattice by 1 %. If this is not done extremely slowly then the induced strain/stress gradients will mechanically crack any item made of CeO₂. This phenomenon is most probably the reason behind the (previously) widely spread conception that O²⁻ vacancies should be bigger than O²⁻. In contrast α_S is in the range of 0.023 – 0.03 per vacant O for reduction of various doped LaCrO₃ [24].

Since the perovskite structure adopts a configuration that compromises the trends induced by the two sub-lattices, it is reasonable to expect that it will be less prone to expansion induced by a cation radius increase (by substitution or reduction) in one of the two sub-lattices as compared to the fluorite structure where a single M-O (sub-)lattice exists. This hypothesis is explored in Fig. 6 by comparing the relative change in lattice parameter (strain) upon reduction of Ce (equivalent to substitution of Ce⁴⁺ by Ce³⁺) in the ceria fluorite lattice and A- or B-site acceptor substituted LaGaO₃. To achieve a fair comparison, the A- or B-site substitutional was selected to have the same relative ionic radius difference to the host as in the ceria case, i.e.:

Fig. 6

Comparison of the relative change in lattice parameter (strain) upon acceptor substitution in the CeO_2-x/2 fluorite lattice and the A- or B-site of LaGaO₃, for substitutionals with the same relative ionic radius difference and valency difference to the host cation. The black dots represent the experimentally determined total strain development upon reduction of ceria, deduced as the average value form two investigations [25, 26]

$$ \frac{r_{C{e}^{3+}}-{r}_{C{e}^{4+}}}{r_{C{e}^{4+}}}=\frac{r_{A^{2+}}^s-{r}_{L{a}^{3+}}}{r_{L{a}^{3+}}}=\frac{r_{B^{2+}}^s-{r}_{G{a}^{3+}}}{r_{G{a}^{3+}}}=0.178 $$

as well as the same valency difference of 1. This corresponds to ${r}_{A^{2+}}^s=1.6\ \mathring{\mathrm{A}} \approx {r}_{Ba}=1.61\ \mathring{\mathrm{A}}$, and ${r}_{B^{2+}}^s=0.73\ \mathring{\mathrm{A}} \approx {r}_{Mg}=0.72\kern0.30em \mathring{\mathrm{A}}$. The different lines in Fig. 6 have been extended to the same substitution level of x = 0.2, corresponding to the same oxygen nonstoichiometry level of δ = x/2 = 0.1. The calculated trends for the perovskite structure are based on the “relaxed” hard sphere approximation with p₁ = 0.998, p₂ = 0.963, and r_V = 1.31 Å, as determined for the Sr and/or Mg substituted LaGaO₃. The hard sphere approximation was used for CeO_2-x/2 (Eqs. 2–4) with r_V = 1.169 Å [8]. Furthermore, the total strain has been separated into its two constituent parts, relating to the change in cation radius (due to substitution) and anion radius (due to vacancy formation), respectively, in order to enable a deeper insight into the origins of the total strain.

The contribution from the formation of oxide ion vacancies is negative in both cases, due to the smaller effective vacancy radius as compared to the oxide ion. The magnitude of this contribution is significantly larger in the fluorite than the perovskite case though, due to the significantly smaller value of r_V in CeO_2-x/2. The increased average cation radius upon partial substitution of the host cation with a larger one (either by substitution or by reduction of the host) leads to the development of positive strain in all cases, as expected. This contribution is a factor of 2 or 3 smaller (for A- or B-site substitution, respectively) in the perovskite case as compared to the fluorite. This striking difference is largely attributed to the restricting/opposing influence of the B-O sub-lattice for A-site substitution and of the A-O sub-lattice upon B-site substitution in the perovskite structure. The combined cation and anion induced total strain comes closer for the two structures, but remains smaller by a factor of 1.3 or 2.3 for the perovskite (for A- or B-site substitution, respectively).

The total strain upon B-site substitution in LaGaO₃ normalized to the change in oxygen stoichiometry attains a value of 0.044. This value is indeed within the range of 0.017–0.06, quoted in a recent review article [23] as the values of the stoichiometric expansion coefficient for a broad range perovskite compounds. (The cation that expands on reduction in the perovskites is in almost all cases B-ion and hence this is the relevant value to discuss when addressing expansion on reduction).

Experimental data for measured expansions in CeO_2-x/2 upon reduction are also plotted in Fig. 6. The data fall on the line predicted from the hard sphere model using the vacancy radius given in Table 1 illustrating the validity of the description of the response of the lattice constant to changes in average cation radii regardless if this is introduced by substitution or by partial valence change of the host. (The Gallate series discussed here contains only elements that are valence stable in the structure and hence for these materials no expansion on reduction data exists). The stoichiometric expansion coefficient of CeO_2-x/2 deduced from the experimental data in Fig. 6 is ~ 0.105 which is ~ 2.3 times larger than the value estimated for a similar stoichiometry change in the perovskite model compound by B-site acceptor substitution corresponding to the same relative cation radius change. The dominating reason for the weaker response of the perovskites to changes in cation ionic radii than for the fluorites was as argued above the restraining action of the A-O lattice to the B-O and vice versa, which is also the primary reason for their weaker response to reduction (i.e. their smaller values of stoichiometry expansion coefficients).

A simpler way of looking at this is saying that the concentration of reducible ions in the perovskites is one half of what it is in the fluorites because only the B-ions are reduced. As it is the expansion by reduction of the cation that primarily determines the expansion on reduction of the entire structure, one can expect α_S to be a factor of 2 smaller for the perovskites. If we were to relate α_S to the fraction of reduced cations instead of δ then α_S of the perovskites would become 2 times bigger, approaching that of the fluorites. It should also be noted that the relative increase in cation radius is often smaller in the case of the small B-ions, e.g. only ca. 12 % relative expansion upon reduction of Cr⁴⁺ (0.55 Å) to Cr³⁺ (0.615 Å) as compared to ca. 18 % for Ce⁴⁺ (0.97 Å) reducing to Ce³⁺ (1.143 Å). This can account for the fact that the stoichiometric expansion coefficient of perovskites is often found to be more than 2 times smaller than CeO_2-x/2.

The stoichiometric expansion coefficient for a relative expansion of the B-site ion by 12 % (Cr⁴⁺ to Cr³⁺), calculated using the relaxed hard sphere model developed for La_1-xSr_xGa_1-yMg_yO_3-δ, is 0.023 in good agreement with the experimental values of 0.023–0.03 determined for various doped LaCrO₃ [24].

4 Discussion

The above analysis shows that - even though the approximation of hard sphere ions with Shannon radii is not accurate and has no solid physical (quantum mechanical) foundation - this approximation seems still quite efficient in describing the actual changes in unit cell volumes (expansion or contraction) by partial substitution of a host cation with another cation with different size and charge or by change of the oxidation state (and thus also size) of the host cation (reduction/oxidation). The calculated effective oxide vacancy radius seems to be an operational quantity, which can even be qualitatively rationalized in terms of changes in lattice energy.

However, we do not claim that we can calculate the exact size of a vacancy, and certainly not the shape. In fact it seems difficult to us to define which volume belongs to a given vacancy when examined on the atomic level. Thus, we are not challenging models like Nakamura’s model [27], which e.g. takes into account the non-random coordination of the different cations and is constrained to fulfill the average cation coordination that corresponds to the amount of doping. The result of Nakamura’s modeling is that the vacancy is larger than or equal to the oxide ion in the fluorite structure.

The relaxation model of Marrocchelli et al. [8] also gives vacancies bigger than oxide ions (locally), but because of the displacement of the first anion coordination shell the combined result is that the vacancy formation causes a negative change in the unit cell volume. Thus, the effective vacancy volume and radius reflects the volumetric effect of the vacancy in interaction with the nearest 2–3 coordination shells and not the physical size and shape of the actual vacancy.

5 Conclusion

An analysis of fluorite and perovskite structured oxides using the hard sphere approximation and the Shannon ion radii has shown that

• The concept of “the effective oxide vacancy radius” is found practical in describing and rationalizing the changes in lattice unit cell volume and thus the changes in volume of macroscopic items of the oxides associated with doping and stoichiometry changes by reduction or oxidation.

• The effective oxide vacancy radius in fluorites increases with increasing radius of the host cation and decreases with increasing radius of the dopant cation

• The effective oxide vacancy radius in doped LaGaO₃ perovskites is much closer to the size of the oxide ion. The perovskite vacancy is only ca. 6 % smaller than the oxide ion whereas the vacancy in the fluorite is 13–37 % smaller.

• In spite of the bigger effective vacancy radius of the perovskite this very compact structure has a lower stoichiometric expansion coefficient than the fluorite. According to our analysis this arises from the restraining action of the A-O sub-lattice to dimensional changes in the B-O and vice versa.