Effects of spike-triggered negative feedback on receptive-field properties

Abstract

Sensory neurons are often described in terms of a receptive field, that is, a linear kernel through which stimuli are filtered before they are further processed. If information transmission is assumed to proceed in a feedforward cascade, the receptive field may be interpreted as the external stimulus’ profile maximizing neuronal output. The nervous system, however, contains many feedback loops, and sensory neurons filter more currents than the ones representing the transduced external stimulus. Some of the additional currents are generated by the output activity of the neuron itself, and therefore constitute feedback signals. By means of a time-frequency analysis of the input/output transformation, here we show how feedback modifies the receptive field. The model is applicable to various types of feedback processes, from spike-triggered intrinsic conductances to inhibitory synaptic inputs from nearby neurons. We distinguish between the intrinsic receptive field (filtering all input currents) and the effective receptive field (filtering only external stimuli). Whereas the intrinsic receptive field summarizes the biophysical properties of the neuron associated to subthreshold integration and spike generation, only the effective receptive field can be interpreted as the external stimulus’ profile maximizing neuronal output. We demonstrate that spike-triggered feedback shifts low-pass filtering towards band-pass processing, transforming integrator neurons into resonators. For strong feedback, a sharp resonance in the spectral neuronal selectivity may appear. Our results provide a unified framework to interpret a collection of previous experimental studies where specific feedback mechanisms were shown to modify the filtering properties of neurons.

Appendices

Appendix A

The convention used here to operate with the Fourier transform is

$$ \hat{f}(\omega) = \frac{1}{\sqrt{2\pi}}{\int}_{-\infty}^{+\infty} f(t) \mathrm{e}^{-i\omega t} \mathrm{d}t. $$

(40)

From this definition, the following properties follow:

• – The Fourier transform of a constant signal of magnitude r ₀ is $\hat {f}(\omega ) = \sqrt {2 \pi } \ r_{0} \ \delta (\omega )$.

• – If a signal f(t) is equal to the convolution of two other signals g(t) and h(t), then $\hat {f}(\omega ) = \sqrt {2\pi } \ \hat {g}(\omega ) \ \hat {h}(\omega )$.

• – If a signal f(t) is equal to another signal but delayed, f(t)=g(t−Δ), then $\hat {f}(\omega ) = \mathrm {e}^{-i \omega {\Delta }} \hat {g}(\omega )$.

• – If a signal f(t) is the derivative of another signal f(t)=dg/dt, then $\hat {f}(\omega ) = i \omega \hat {g}(\omega )$.

The Laplace transform, in turn, is defined as

$$ \tilde{f}(s) = {\int}_{0}^{\infty} f(t) \mathrm{e}^{-s t} \mathrm{d}t, $$

(41)

where s=σ+i ω is a complex number. In the particular case where s is evaluated at a purely imaginary number (σ=0), the Laplace transform is proportional to the Fourier transform for temporally positive functions. The Laplace transform, hence, can be seen as a generalization of the Fourier transform to the whole complex plane. Related properties hold:

• – The Laplace transform of a constant signal of magnitude r ₀ is $\tilde {f}(s) = r_{0} / s$.

• – If a signal f(t) is equal to the convolution of two other signals g(t) and h(t), then $\tilde {f}(s) = \tilde {g}(s) \ \tilde {h}(s)$.

• – If a signal f(t) is the derivative of another signal f(t)=dg/dt, then $\tilde {f}(s) = s \ \tilde {g}(s) - g(0)$.

Using these properties, it is easy to see that if the signals r(t) and x(t) are governed by Eqs. (4) and (8), the Laplace transform of r(t), for an initial zero feedback contribution x(0)=0, is

$$ \tilde{r}(s) = \frac{r_{0} / s + \tilde{h}(s) \ \tilde{s}_{1}(s) } {1 + g \ \tilde{h}(s) / (s + 1/\tau_{\mathrm{d}})}. $$

(42)

According to control theory (Franklin et al. 1994), this feedback system becomes unstable when at least one pole of $\tilde {r}(s)$ has positive real part. It is important to search for instabilities in the Laplace representation, since they may not be evident in the Fourier space. In addition to the fixed pole s=0 given by the constant signal term, the poles of $\tilde {r}(s)$ are those complex points s where the denominator of Eq. (42) vanish, that is,

$$ 1 + g \frac{\tilde{h}(s)}{s + 1/\tau_{\mathrm{d}}} = 0. $$

(43)

This equation holds in the complex plane, so both the real and the imaginary part of the equality must vanish. Feedback gives rise to unstable behavior whenever at least one solution of Eq. (43) has positive real part. The onset of instability, hence, appears when the pole (or pair of conjugate poles) with largest real part crosses the imaginary axis, from left to right. At the crossing, σ=0, so the real and imaginary parts of Eq. (43) become

$$\begin{array}{@{}rcl@{}} \text{Im}[\hat{h}(\omega)] - \tau_{\mathrm{d}} \omega \text{Re} [\hat{h}(\omega)] &=& 0, \end{array} $$

(44)

$$\begin{array}{@{}rcl@{}} 1 + \sqrt{2\pi} g \tau_{\mathrm{d}} \text{Re} [\hat{h}(\omega)] &=& 0, \end{array} $$

(45)

where now, $\hat {h}(\omega )$ is the Fourier transform of the intrinsic filter, obtained when evaluating the Laplace transform at a purely imaginary point and dividing by $\sqrt {2\pi }$. The frequencies satisfying Eq. (44) are independent of the feedback strength, g. Note that, in addition, Eq. (45) can only be fulfilled by those frequencies ω _i , from the set of solutions to Eq. (44), that result in $\text {Re}[\hat {h}(\omega _{i})] < 0$. Even among these, if g is small, no frequency ω satisfies Eq. (45), and the system is stable (the pole with largest real part is on the stable semi-plane). For a critical value of feedback strength, the condition imposed by Eq. (45) can be finally reached and the system becomes unstable. This means that for feedback strengths beyond the critical value, there is at least one pole on the unstable semi-plane and therefore the inverse Fourier transform diverges.

Appendix B

In this section, we describe the temporal processing of slow stimuli. We arrive at the same results as the ones derived by (Urdapilleta and Samengo 2009), but here we base the analysis on the spectral properties of filters. In the absence of feedback,

$$ r(t) = h_{0} + {\int}_{-\infty}^{+\infty} h(\tau) s(t-\tau) \mathrm{d}\tau, $$

(46)

$$ \hat{r}(\omega) = \sqrt{2\pi}\left[ h_{0} \delta(\omega) + \hat{h}(\omega) \hat{s}(\omega) \right]. $$

(47)

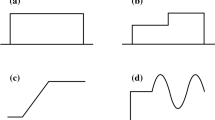
In the present context, a slow stimulus is one that does not contain high frequency components. In other words, the input/output relation of the cell is only determined by the lowest frequency components of the filter $\hat {h}(\omega )$, since the higher frequencies are not explored. The stimulus, hence, has to remain fairly constant throughout the time scale of the filter (given by the non-zero portions in the temporal filters shown in Fig. 1). If only low frequencies matter, we may take the limit ω→0. In this context, we prove that

• ON cells behave as low-pass filters, see Fig. 1a. For $\omega \rightarrow 0$, the Fourier transform of these filters is

  $$\begin{array}{@{}rcl@{}} \hat{h}(\omega) &=& \frac{1}{\sqrt{2\pi}} {\int}_{-\infty}^{+\infty} h(\tau) \mathrm{e}^{-i \omega \tau} \mathrm{d}\tau \\ &=& \frac{1}{\sqrt{2\pi}} {\int}_{-\infty}^{+\infty} h(\tau) [\cos(\omega \tau)-i \sin(\omega \tau)] \mathrm{ d}\tau\\ &\approx& \frac{1}{\sqrt{2\pi}} {\int}_{-\infty}^{+\infty} h(\tau) [1 - i \omega \tau] \mathrm{d}\tau = \frac{1}{\sqrt{2\pi}} (H + i \omega H_{1} ) \end{array} $$

  (48)

  where $H = {\int }_{-\infty }^{+\infty } h(\tau ) \mathrm {d}\tau$ and $H_{1} = - {\int }_{-\infty }^{+\infty } \tau h(\tau ) \mathrm {d}\tau$. The small angle approximation can be used again,

  $$\begin{array}{@{}rcl@{}} \hat{h}(\omega) &\approx& \frac{H}{\sqrt{2\pi}} \left[ 1 + i \omega \frac{H_{1}}{H} \right] \\ &\approx& \frac{H}{\sqrt{2\pi}} \left[ \cos\left(\omega \frac{H_{1}}{H}\right) + i \sin\left(\omega \frac{H_{1}}{H}\right)\right] \\ &\approx& \frac{H}{\sqrt{2\pi}} \,\mathrm{e}^{-i \omega \delta_{0}}, \end{array} $$

  (49)

  where we have defined the (positive) delay δ ₀=−H ₁/H. From this expression, it is easy to check that the gain of the Fourier transform for ON cells at low frequencies is constant and equal to $H/\sqrt {2\pi }$. In addition, the phase decreases linearly with ω, starting at 0 with slope −δ ₀ (in Fig. 1a, a linear graph instead of the semi-logarithmic one would clearly show this linear relationship).

  To relate $\hat {h}(\omega )$ to the neural response in the temporal domain, we simply make use of the Fourier transform of a delayed signal (see Appendix A),

  $$ r(t) \approx h_{0} + \mathcal{F}^{-1} \left\{ H \mathrm{e}^{-i \omega \delta_{0}} \hat{s}(\omega)\right\} \approx h_{0} + H s(t-\delta_{0}). $$

  (50)

  According to Eq. (50), the amplitude of the response is exclusively determined by H; simultaneously, neural processing introduces a fixed delay δ ₀ between the response and the stimulus.

• ON biphasic cells behave as band-pass filters, see Fig. 1c. In the limit $\omega \rightarrow 0$, $\hat {h}(\omega )$ is still given by Eq. (47). However, symmetric biphasic filters satisfy H=0, so to obtain a meaningful description we have to perform the expansion around ω=0 up to the second order,

  

  (51)

  where $H_{2} = {\int }_{-\infty }^{+\infty } \tau ^{2} h(\tau ) \mathrm {d}\tau$. Proceeding as before and defining a corresponding (positive) delay δ ₁=−H ₂/(2H ₁), we obtain

  $$\begin{array}{@{}rcl@{}} \hat{h}(\omega) &\approx& \frac{H_{1} \omega}{\sqrt{2\pi}} \, \mathrm{e}^{i \pi/2} \left[ \cos\left( \omega \frac{H_{2}} {2H_{1}}\right) + i \sin\left(\omega \frac{H_{2}} {2H_{1}}\right)\right]\\ &\approx& \frac{H_{1} \omega}{\sqrt{2\pi}}\, \mathrm{e}^{i \pi/2} \mathrm{e}^{-i \omega \delta_{1}} = \frac{H_{1} \omega}{\sqrt{2\pi}} \, \mathrm{e}^{i(\pi/2-\omega \delta_{1})}. \end{array} $$

  (52)

  Hence, in the limit $\omega \rightarrow 0$, the gain of symmetric biphasic filters depends linearly on the angular frequency, with a positive slope $H_{1}/\sqrt {2\pi }$. In addition, the filter phase is a linearly decreasing function of ω, with intercept at the origin π/2 and slope −δ ₁. Both characteristics can be observed in Fig. 1C.

  To relate $\hat {h}(\omega )$ to the neural response in the temporal domain, it is useful to recover the imaginary unit as a factor and rewrite Eq. (52) as

  $$\begin{array}{@{}rcl@{}} \hat{h}(\omega) &\approx& \frac{H_{1}}{\sqrt{2\pi}} \, \mathrm{e}^{-i \omega \delta_{1}} (i \;\omega). \end{array} $$

  (53)

  In this case, given that the Fourier transform of a convolution becomes a product in Fourier space, the term (i ω) can be effectively associated to the stimulus, $\hat {s}(\omega )$. In turn, by applying the Fourier transform of a derivative, and proceeding as before, it is easy to check that r(t) is proportional to the delayed stimulus derivative, with a factor of proportionality given by H ₁ and a fixed delay δ ₁. Explicitly,

  $$ r(t) \approx h_{0} + \mathcal{F}^{-1}\left\{ H_{1} \mathrm{e}^{-i \omega \delta_{1}} \left[i \omega \hat{s}(\omega) \right]\right\} \approx h_{0} + H_{1} \left[ \frac{\mathrm{d}s}{\mathrm{d}t} \right]_{(t-\delta_{1})}. $$

  (54)

• Corresponding OFF cells behave analogously to monophasic and biphasic ON cells (see Fig. 1b and d). Specifically, the Fourier transforms of these filters are exactly given by Eqs. (48) and (51), in the limit $\omega \rightarrow 0$. The only difference with the previous ON cells is that the proportionality factors H and H ₁ for monophasic and biphasic cells, respectively, are now negative. The presence of a factor (−1) affecting the whole expression can be incorporated into a multiplicative term, $\exp {(\pm i \pi )}$, which shifts the phase of the Fourier transform in ±π. This shift can be observed in Fig. 1 by comparing phases of corresponding filters (monophasic ON/OFF filters and biphasic ON/OFF filters). Additionally, the factor (−1) does not affect the magnitude of the Fourier transform of ON or OFF cells. In the temporal domain, this factor simply means that the relationships obtained for ON cells are also valid, but associated to the negative of the stimulus or its derivative. These results agree our previous analysis (Urdapilleta and Samengo 2009).