How well do mean field theories of spiking quadratic-integrate-and-fire networks work in realistic parameter regimes?

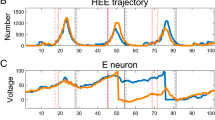
Abstract

We use mean field techniques to compute the distribution of excitatory and inhibitory firing rates in large networks of randomly connected spiking quadratic integrate and fire neurons. These techniques are based on the assumption that activity is asynchronous and Poisson. For most parameter settings these assumptions are strongly violated; nevertheless, so long as the networks are not too synchronous, we find good agreement between mean field prediction and network simulations. Thus, much of the intuition developed for randomly connected networks in the asynchronous regime applies to mildly synchronous networks.

Appendices

Appendix A: Statistics of the synaptic drive

In the main text we approximated h¯ _{L i} as a Gaussian random variable with respect to index, i, and the right hand side of Eq. (2.16) as Gaussian white noise. With this approximation, all we need are the variance of h¯ _{L i} and the covariance of the right hand side of Eq. (2.16). Here we compute those quantities.

We start with the variance of h¯ _{L i} , Eq. (2.12). To isolate the index-independent and index-dependent terms, we write

$$ J_{LM}^{ij} = \epsilon J_{LM} + \delta J_{LM}^{ij} $$

(A.1)

where 𝜖J _LM is the population averaged value of $J_{LM}^{ij}$ (see Eq. (2.7)) and δ $J_{LM}^{ij}$ ≡ $J_{LM}^{ij}$ − 𝜖J _LM represents the index-dependent fluctuations around that average (sometimes referred to as the quenched noise). Making this substitution, using Eq. (2.15a) for the mean firing rate, and recalling that 𝜖 = K _M / N _M , Eq. (2.12) becomes

$$ \bar{h}_{Li} = {h_{L}} + \delta \mu_{Li} + \sum\limits_{M,j} \frac{\tau_m}{K_{M}^{1/2}} \, \delta J_{LM}^{ij} \, \nu_{Mj} $$

(A.2)

where h _L is given in Eq. (2.13b) and the sum is over M = E, I and X. The last term in this expression is the sum of a large number of variables. The weights inside the sum are truly random, so if the firing rates and the weights are sufficiently weakly correlated, this sum is a Gaussian random variable with respect to index, i. Here we assume they are, although this is clearly an approximation: the firing rates, ν _Mj , are functions of the connection strengths, and so the variables inside the sum are not quite independent. However, in practice this is a good approximation, especially if 𝜖 (which is a measure of the sparseness of the connectivity; see Eq. (2.7)) is small, something that tends to reduce correlations. Given this approximation, and the fact that, by construction, the mean is zero, all we need is the variance. This variance (plus the variance of δ μ _Li , which, by construction, is $\Delta _{mu _L }^{2}$ (see Eq. (2.8)), is given by

$$ \Delta^{2}_{h_{L}} = \Delta_{\mu_{L}}^{2}+ \sum\limits_{M,M', j,j'} \frac{\tau_{m}^{2}}{(K_{M} K_{M'})^{1/2}}\, \nu_{Mj} \nu_{M'j'} \frac{1}{N_{L}} \sum\limits_i \delta J_{LM}^{ij} \delta J_{LM'}^{ij'} $$

(A.3)

where, as in Eq. (2.13a), we use $\Delta^{2}_{h_{L}}$ for the total variance. When j ≠ j′ or M ≠ M′, in the large K limit the sum is approximately zero; when j = j′ and M = M′, the sum over i is just the variance of $J_{LM}^{ij}$. Thus, using Eq. (2.7) for the variance of $J_{LM}^{ij}$, Eq. (A.3) becomes, after a small amount of algebra,

$$ \Delta^{2}_{h_{L}} = \Delta_{\mu_{L}}^{2}+ \sum\limits_M J_{LM}^{2} \left(1 + \Delta^{2} - \epsilon \right) \tau_{m}^{2} \nu_{M}^{2} $$

(A.4)

where $\nu_{M}^{2}$ is the second moment of the firing rate (Eq. (2.15b)).

We next compute the covariance of the right hand side of Eq. (2.16). Using $C_{LL'}^{ii'}(\tau )$ to denote the covariance between neuron i of type L and neuron i’ of type L’ at times separated by τ, we have

$$\begin{array}{@{}rcl@{}} C_{LL'}^{ii'}(\tau) &=& \sum\limits_{M,M', j,j'} \frac{\tau_{m}^{2} }{(K_{M} K_{M'})^{1/2}} \, J_{LM}^{ij} J_{L'M'}^{i'j'}\\ &&\times \left\langle \sum\limits_{l,l'} \left[\delta\left(t-t_{j}^{l}\right) - \nu_{Mj}\right] \left[\delta\left(t + \tau -t_{j'}^{l}\right) - \nu_{M'j'}\right] \right\rangle. \end{array} $$

(A.5)

The angle brackets represent an average over the distribution of spike times. Real neurons have a nontrivial correlational structure; if nothing else, there is a refractory period. However, we ignore that and make the approximation that the neurons are Poisson. In that case, as shown by (Rice 1954), and as is relatively easy to derive, the average over the distribution of spikes yields

$$ \left\langle \sum\limits_{l,l'} \left[\delta\left(t-t_{j}^{l}\right) - \nu_{Mj} \right] \left[\delta\left(t + \tau-t_{j'}^{l'}\right) - \nu_{M'j'}\right] \right\rangle = \nu_{Mj} \delta(\tau) \delta_{jj'} \delta_{MM'} $$

(A.6)

where δ _{i j} is the Kronecker delta ( δ _{i j} = 1 if i = j and 0 otherwise). Thus, Eq. (A.5) becomes

$$ C_{LL'}^{ii'}(\tau) = \delta(\tau) \sum\limits_{M,j} \frac{\tau_{m}^{2}}{K_{M}} \, J_{LM}^{ij} J_{L'M}^{i'j} \nu_{Mj}. $$

(A.7)

Assuming, as usual, that the connections strengths are approximately independent of the firing rates, we may average the connection strengths and firing rates separately. Using Eq. (2.7) for the distribution of connection strengths, we have

$$\begin{array}{rll} C_{LL'}^{ii'}(\tau) &=& \delta(\tau)\tau_{m}^{2} \sum\limits_{M} \frac{\nu_{M}}{K_{M}}\, \sum\limits_j J_{LM}^{ij} J_{L'M}^{i'j} \\ &=&\delta(\tau)\tau_{m}^{2} \sum\limits_M J_{LM}^{2} \left[ \epsilon (1-\delta_{ii'} \delta_{LL'}) + \left(1+\Delta^{2}\right) \delta_{ii'} \delta_{LL'} \right] {\nu_{M}}. \end{array} $$

(A.8)

An important observation is that $C_{LL'}^{ii'}(\tau )$ is nonzero even when i ≠ i′ and/or L ≠ L′. Thus, the driving terms for different neurons are correlated; this in turn implies that spike times are correlated across neurons. This would seem to imply that our independence approximation is badly violated. However, as shown by (Renart et al. 2010; Hertz 2010), for balanced networks operating in the asynchronous regime, correlations between excitatory and inhibitory neurons largely cancel, leaving the mean correlation on the order of 1 / N. Thus, in large networks the independence approximation tends to work relatively well. This means we can focus on the autocorrelation, $C_{LL}^{ii}$, which is somewhat simpler than the full covariance,

$$ C_{LL}^{ii}(\tau) = \delta(\tau) \tau_{m}^{2} \sum_M J_{LM}^{2} \left(1+\Delta^{2}\right) {\nu_{M}}. $$

(A.9)

This expression leads to Eqs. (2.17) and (2.18).

Appendix B: Transforming from the quadratic integrate and fire neuron to the θ-neuron

For quadratic integrate and fire neurons, action potentials are emitted when the voltage reaches + ∞, at which point the voltage is reset to − ∞. Integrating to infinity, however, poses a problem numerically. To get around this, we make the change of variables

$$ V_{Li} = \bar{v} + (V_{th} - V_r) \tan(\theta_{Li}/2). $$

(B.1)

This moves the points at V _Li = ± ∞ to θ _Li = ± π, and also removes the singularities at ± ∞. Inserting this into Eq. (2.6a) we see that θ _Li evolves according to

$$\tau_m \frac{d \theta_{Li}}{dt} = (1-\cos \theta_{Li}) + (1 + \cos \theta_{Li})(\mu_L + \mu_{Li} + h_{Li}). $$

(B.2)

A spike is emitted when θ _Li = π, at which point it is reset to − π.

Appendix C: White noise approximation to external input

To speed up the simulations, we use Gaussian white noise instead of actual spike trains for the external input (the term with M = X in Eq. (2.6b)). To do that, we make the replacement

$$\begin{array}{@{}rcl@{}} &&\frac{\tau_m}{K_{X}^{1/2}}\sum\limits_{j,l} J_{LX}^{ij} \, \delta\left(t-t_{Xj}^{l}\right)\rightarrow \; \\ &&J_{LX} \tau_m \overline{\nu}_{X}\left( K_{X}^{1/2} + ( 1 + \Delta^{2} - \epsilon )^{1/2} \eta_{LXi} + \left[\frac{1 + \Delta^{2}}{\tau_m \overline{\nu}_{X}} \right]^{1/2} \xi_{LXi}(t) \right) \end{array} $$

(C.1)

where η _LXi is a zero mean, unit variance Gaussian random variable with respect to index, i, ξ _LXi (t) is Gaussian white noise, and we assumed that all the external neurons have the same firing rate ν _X (which allowed us to replace νX2^{1 / 2} with ν _X ); see Eqs. (2.13b), (2.14) and (2.18).