Abstract
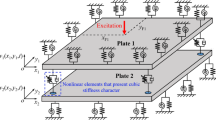
The problem of vibrations of a viscoelastic plate with concentrated masses is studied in a geometrically nonlinear formulation. In the equation of motion of the plate, the action of the concentrated masses is taken into account using Dirac δ-functions. The problem is reduced to solving a system of Volterra type ordinary nonlinear integrodifferential equations using the Bubnov-Galerkin method. The resulting system with a singular Koltunov-Rzhanitsyn kernel is solved using a numerical method based on quadrature formulas. The effect of the viscoelastic properties of the plate material and the location and amount of concentrated masses on the vibration amplitude and frequency characteristics is studied. A comparison is made of numerical calculation results obtained using various theories.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
C. L. Amba-Rao, “On the vibration of a rectangular plate carrying a concentrated mass,” J. Appl. Mech., 31,No. 3, 550–551 (1964).
R. Chen, “Vibration of cylindrical panels carrying a concentrated mass,” Trans. ASME, Ser. E, J. Appl. Mech., 37,No. 3, 874–875 (1979).
L. V. Andreev, A. L. Dyshko, and I. D. Pavlenko, Dynamics of Plates and Shells with Concentrated Masses [in Russian], Mashinostroenie, Moscow (1988).
E. Dowell and S. M. Doherty, “Experimental study of asymptotic modal analysis applied to a rectangular plate with concentrated masses,” J. Sound Vibr., 170, 671–681 (1994).
P. D. Cha, “Free vibration of a rectangular plate carrying a concentrated mass,” J. Sound Vibr., 207, 593–596 (1997).
J. S. Wu and S. S. Luo, “Use or the analytical-and-combined method in the free vibration analysis of a rectangular plate with any number of point masses and translational springs,” J. Sound Vibr., 200, 179–194 (1997).
P. A. Bondarev, “Vibrations of a plate with concentrated masses on a nonlinear elastic foundation,” Ukr. Mat. Zh., 1, 61–66 (1974).
A. A. Il’yushin and B. E. Pobedrya, Foundations of Mathematical Theory of Thermoviscoelasticity [in Russian], Nauka, Moscow (1970).
T. Kocaturk, S. Sezer, and C. Demir, “Determination of the steady state response of viscoelastically point-supported rectangular specially orthotropic plates with added concentrated masses,” J. Sound Vibr., 278, 789–806 (2004).
M. A. Koltunov, Creep and Relaxation [in Russian], Vysshaya Shkola, Moscow (1976).
A. S. Vol’mir, Nonlinear Dynamics of Plates and Shells [in Russian], Nauka, Moscow (1972).
H. M. Berger, “A new approach to the analysis of large deflection of plates,” J. Appl. Mech., 22,No. 4, 465–472 (1955).
F. B. Badalov, Kh. Éshmatov, and M. Yusupov, “Some methods of solving the integrodifferential equations encountered in viscoelasticity problems,” Prikl. Mat. Mekh., 51,No. 5, 867–871 (1987).
B. Kh. Éshmatov, “Nonlinear vibrations of viscoelastic orthotropic plates from composite materials,” in: Proc. of the 3rd MIT Conf. on Comput. Fluid and Solid Mech. (Boston, June 14–17, 2005), Cambridge Univ., Cambridge (2005), p. 93.
B. Kh. Éshmatov, “Dynamic stability of viscoelastic plates under increasing compressing loads,” J. Appl. Mech. Tech. Phys., 47,No. 2, 289–297 (2006).
B. Kh. Éshmatov, “Nonlinear vibration analysis of viscoelastic plates based on a refined Timoshenko theory,” Int. Appl. Mech., 42,No. 5, 596–605 (2006).
F. B. Badalov and Kh. Éshmatov, “Nonlinear vibrations of viscoelastic plates with initial irregularities,” Prikl. Mekh., 28,No. 8, 99–105 (1990).
Author information
Authors and Affiliations
Corresponding author
Additional information
__________
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 48, No. 6, pp. 158–169, November–December, 2007.
Rights and permissions
About this article
Cite this article
Khodzhaev, D.A., Éshmatov, B.K. Nonlinear vibrations of a viscoelastic plate with concentrated masses. J Appl Mech Tech Phy 48, 905–914 (2007). https://doi.org/10.1007/s10808-007-0115-7
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/s10808-007-0115-7