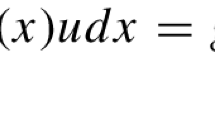To analyze the stability in probability of perturbed dynamical systems, it is necessary to find the transient probability density of the components of the vector process, which can be calculated from the stationary solutions of the associated Fokker–Planck–Kolmogorov equations. For multi-dimensional systems, explicit forms for these solutions are difficult to find. The paper presents a numerical scheme that computes these solutions. As a comparison criterion, a numerical simulation of the Itô equations is carried out using the Monte-Carlo simulation (MCS) method. Both methods are applied to a parametrically excited three-dimensional system subjected to a combined effect of harmonic excitations and stochastic perturbations. As an example, the instability of a cylindrical shell under axial force and internal pressure is considered
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
S. T. Ariaratnam and Wei-Chau Xie, “Lyapunov exponents and stochastic stability of two-dimensional parametrically excited random systems,” Trans. ASME, Ser. E. J. Appl. Mech., 60, No. 3, 667–682 (1993).
V. V. Bolotin (ed.), Vibrations in Engineering: Handbook [in Russian], Mashinostroenie, Moscow (1978).
M. F. Dimentberg, Stochastic Processes in Dynamic Systems with Variable Parameters [in Russian], Nauka, Moscow (1989).
R. Z. Khasminskii, “A limit theorem for the solutions of differential equations with random right-hand sides,” Theor. Probab. Its Appl., No. 11, 390–406 (1966).
R. Z. Khasminskii, Stability of System of Differential Equations with Random Perturbations of Their Parameters [in Russian], Nauka, Moscow (1969).
M. M. Klosek-Dygas, B. J. Matkowsky, and Z. Schuss, “Stochastic stability of nonlinear oscillators,” SIAM J. Appl. Math., 48, N 5, 1115–1127 (1988).
G. A. Korn and T. M. Korn, Mathematical Handbook for Scientists and Engineers, McGraw-Hill. New York (1968).
H. J. Kushner, Stochastic Stability and Control, London, Academic Press, New York (1967).
J. La Salle and S. Lefschetz, Stability by Lyapunov’s Direct Method with Applications, Academic Press, New York (1961).
M. Labou, “Stochastic stability of parametrically excited random systems,” Int. Appl. Mech., 40, No. 10, 1175–1183 (2004).
M. Labou and T-W. Ma, “Lyapunov exponents of coupled two-DOF stochastic linear systems and related stability problems,” J. Sound Vibr., 325, 421–435 (2009).
M. Labou, “Stochastic stability of three-dimensional linear systems under parametric random action,” Int. Appl. Mech., 46, No. 4, 124–143 (2010).
M. Labou, “On stability of parametrically excited linear stochastic systems,” Int. Appl. Mech., 47, No. 10, 1440–1453 (2011).
A. A. Samarskii and A. V. Gulin, Numerical Methods [in Russian], Nauka, Moscow (1989).
T. T. Soog and M. Grigoriu, Random Vibration of Mechanical and Structural Systems, Prentice Hall, New Jersey (1992).
R. L. Stratonovich, Topics in the Theory of Random Noise, Vol. 1, Gordon and Breach, New York (1963).
A. C. Vol’mir, Stability of Deformable Systems [in Russian], Nauka, Moscow (1967).
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Prikladnaya Mekhanika, Vol. 48, No. 4, pp. 126–144, July–August 2012.
Rights and permissions
About this article
Cite this article
Labou, M. Numerical schemes for stability in probability of perturbed dynamical systems. Int Appl Mech 48, 465–483 (2012). https://doi.org/10.1007/s10778-012-0534-x
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-012-0534-x