Skip to main content
SpringerLink
Log in

Harmonic thickness vibrations of inhomogeneous elastic layers with curved boundaries

  • Published:
International Applied Mechanics Aims and scope

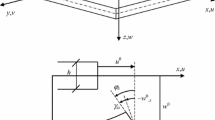
The thickness vibrations of elastic inhomogeneous bodies of different geometry under dynamic harmonic loading are studied. The dependence of the amplitude–frequency characteristics of homogeneous and inhomogeneous bodies on excitation frequency is analyzed in detail. The frequency spectra for plane, cylindrical, and spherical layers are determined

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. W. Nowacki, Theory of Elasticity [in Polish], PWN, Warsaw (1970).

    Google Scholar 

  2. M. A. Pavlovskii, Theoretical Mechanics [in Ukrainian], Tekhnika, Kyiv (2002).

    Google Scholar 

  3. G. M. Savin and J. J. Rushchitsky, Elements of the Mechanics of Hereditary Media [in Ukrainian], Vyshcha Shkola, Kyiv (1976).

    Google Scholar 

  4. V. M. Shul’ga, “Solving the equations of elasticity in cylindrical coordinates,” Dop. NAN Ukrainy, No. 6, 80–82 (1998).

  5. M. O. Shul’ga, “Theory of thickness vibrations of elastic layers with curved boundaries,” Dop. NAN Ukrainy, No. 5, 72–75 (2010).

  6. M. O. Shul’ga and L.O. Grigor’eva, “Vibrations of elastic layers with curved boundaries,” Opir Mater. Teor. Sporud, 84, 120–126 (2009).

    Google Scholar 

  7. N. A. Shul’ga, Fundamentals of the Mechanics of Periodically Layered Media [in Russian], Naukova Dumka, Kyiv (1981).

    Google Scholar 

  8. M. Kashtalyan and J. J. Rushchitsky, “General Hoyle–Yougdahl and Love solutions in the linear inhomogeneous theory of elasticity,” Int. Appl. Mech., 46, No. 1, 1–17 (2010).

    Article  ADS  Google Scholar 

  9. M. Kashtalyan and J. J. Rushchitsky, “Love solutions in the linear inhomogeneous transversely isotropic theory of elasticity,” Int. Appl. Mech., 46, No. 2, 121–129 (2010).

    Article  ADS  Google Scholar 

  10. M. Kashtalyan and J. J. Rushchitsky, “General Love solution in the linear isotropic inhomogeneous theory of radius-dependent elasticity,” Int. Appl. Mech., 46, No. 3, 245–254 (2010).

    Article  ADS  Google Scholar 

  11. M. Kashtalyan and J. J. Rushchitsky, “General Love solution in the linear inhomogeneous transversely isotropic theory,” Int. Appl. Mech., 46, No. 4, 367–376 (2010).

    Article  ADS  Google Scholar 

  12. N. A. Shul’ga, “Theory of dynamic processes in mechanical systems and materials of regular structure,” Int. Appl. Mech., 45, No. 12, 1301–1330 (2009).

    Article  Google Scholar 

  13. N. A. Shul’ga, “A mixed system of equations of elasticity,” Int. Appl. Mech., 46, No. 3, 264–268 (2010).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. S. P. Timoshenko Institute of Mechanics, National Academy of Sciences of Ukraine, 3 Nesterov St., Kyiv, Ukraine, 03057

    N. A. Shul’ga, L. O. Grigor’eva & V. F. Kornienko

Authors
  1. N. A. Shul’ga
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. L. O. Grigor’eva
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. F. Kornienko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to N. A. Shul’ga.

Additional information

Translated from Prikladnaya Mekhanika, Vol. 47, No. 1, pp. 81–89, January 2011.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Shul’ga, N.A., Grigor’eva, L.O. & Kornienko, V.F. Harmonic thickness vibrations of inhomogeneous elastic layers with curved boundaries. Int Appl Mech 47, 62–69 (2011). https://doi.org/10.1007/s10778-011-0443-4

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10778-011-0443-4

Keywords

Search

Navigation