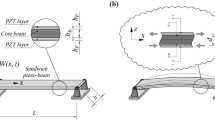
The problem of forced vibration of a hinged beam with piezoelectric layers is solved. Issues of mechanical and electric excitation of vibration and the possibility of damping mechanically induced vibration by applying a voltage to the electrodes of the piezolayers are studied. The effect of the physically nonlinear behavior of the passive layers on the response of the sensor layer and entire structure and the effect of geometric nonlinearity on the behavior of the structure and sensor layer are analyzed. The interaction of physical and geometrical nonlinearities for transient and stationary processes is studied
Similar content being viewed by others
References
Ya. A. Zhuk and I. K. Senchenkov, “Equations of a coupled dynamic thermoviscoplastic problem for thin-walled shells with piezoelectric layers,” Teor. Prikl. Mekh., 34, 115–121 (2001).
Ya. A. Zhuk and I. K. Senchenkov, “Modeling the stationary vibrations and dissipative heating of thin-walled inelastic elements with piezoactive layers,” Int. Appl. Mech., 40, No. 5, 546–556 (2004).
V. G. Karnaukhov, Ya. O. Zhuk, and T. V. Karnaukhova, “Refined thermomechanical model of a physically nonlinear shell with distributed transversely isotropic sensors undergoing forced harmonic vibration,” Dop. NAN Ukrainy, No. 5, 70–75 (2007).
V. G. Karnaukhov, Ya. O. Zhuk, and T. V. Karnaukhova, “Refined thermomechanical model of a physically nonlinear shell with distributed transversely isotropic actuators undergoing forced harmonic vibration,” Dop. NAN Ukrainy, No. 6, 50–55 (2007).
N. A. Shul’ga and A. M. Bolkisev, Vibration of Piezoelectric Bodies [in Russian], Naukova Dumka, Kyiv (1990).
V. T. Grinchenko, A. F. Ulitko, and N. A. Shul’ga, Electroelasticity, Vol. 5 of the five-volume series Mechanics of Coupled Fields in Structural Members [in Russian], Naukova Dumka, Kyiv (1989).
S. I. Pugachev (ed.), Piezoceramic Transducers: A Handbook [in Russian], Sudostroenie, Leningrad (1984).
I. K. Senchenkov and Ya. A. Zhuk, “Thermodynamic analysis of one thermoviscoplastic model,” Prikl. Mekh., 33, No. 2, 41–48 (1997).
S. Bodner and Y. Partom, “Constitutive equations for elastoviscoplastic strain hardening material,” Trans. ASME, J. Appl. Mech., 42, 385–389 (1975).
L. O. Grigor’eva, “Vibrations of a piezoceramic cylinder subjected to nonstationary electric excitation,” Int. Appl. Mech., 43, No. 3, 303–309 (2007).
I. A. Guz and K. P. Herrmann, “On the lower bounds for critical loads under large deformations in non-linear hyperelastic composites with imperfect interlaminar adhesion,” Eur. J. Mech., A/Solids, 22, No. 6, 837–849 (2003).
V. L. Karlash, “Planar electroelastic vibrations of piezoceramic rectangular plate and half-disk,” Int. Appl. Mech., 43, No. 5, 547–553 (2007).
V. G. Karnaukhov and Ya. V. Tkachenko, “Damping the vibrations of a rectangular plate with piezoelectric actuators,” Int. Appl. Mech., 44, No. 2, 182–187 (2008).
V. G. Karnaukhov and Ya. V. Tkachenko, “Studying the harmonic vibrations of a cylindrical shell made of a nonlinear elastic piezoelectric material,” Int. Appl. Mech., 44, No. 4, 442–447 (2008).
I. F. Kirichok, “Flexural vibrations and vibrational heating of a ring plate with thin piezoceramic pads under single-frequency electromechanical loading,” Int. Appl. Mech., 44, No. 2, 200–207 (2008).
G. R. Liu, X. Q. Peng, R. Y. Lam, and J. Tani, “Vibration control simulation of laminated composite plates with integrated piezoelectrics,” J. Sound Vibr., 220, No. 5, 827–846 (1999).
S. S. Rao and M. Sunar, “Piezoelectricity and its use in disturbance sensing and control of flexible structures: A survey,” Appl. Mech. Rev., 47, No. 4, 113–123 (1994).
D. H. Robbins and J. N. Reddy, “Analysis of piezoelectrically actuated beams using a layer-wise displacement theory,” Comp. Struct., 41, No. 2, 265–279 (1991).
J. Tani, T. Takagi, and J. Qui, “Intelligent material systems: Application of functional materials,” Appl. Mech. Rev., 51, No. 8, 505–521 (1998).
H. F. Tiersten, “On the thickness expansion of the electric potential in the determination of two–dimensional equations for the vibration of electroded piezoelectric plates,” J. Appl. Phys., 91, No. 4, 2277–2283 (2002).
H. S. Tzou, Piezoelectric Shells (Distributed Sensing and Control of Continua), Kluwer, Boston–Dordrecht (1993).
H. S. Tzou and R. Ye, “Piezothermoelectricity and precision control of piezoelectric systems: Theory and finite element analysis,” J. Vibr. Acoust., 116, 489–495 (1994).
S. Vidoli and F. dell’Isola, “Vibration control in plates by uniformly distributed PZT actuators interconnected via electric networks,” Eur. J. Mech., A/Solids, 20, 435–456 (2001).
H. Y. Zhang and Y. P. Shen, “Vibration suppression of laminated plates with 1–3 piezoelectric fiber-reinforced composite layers equipped with integrated electrodes,” Comp. Struct., 79, 220–278 (2007).
Ya. A. Zhuk and I. K. Senchenkov, “On linearization of the stiffness characteristics of flexible beams made of physically nonlinear materials,” Int. Appl. Mech., 42, No. 2, 196–202 (2006).
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated from Prikladnaya Mekhanika, Vol. 45, No. 1, pp. 118–136, January 2009.
Rights and permissions
About this article
Cite this article
Zhuk, Y.A., Guz, I.A. Active damping of the forced vibration of a hinged beam with piezoelectric layers, geometrical and physical nonlinearities taken into account. Int Appl Mech 45, 94–108 (2009). https://doi.org/10.1007/s10778-009-0162-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10778-009-0162-2