Cosmic matter flux may turn Hawking radiation off

Abstract

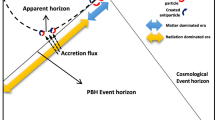
An astrophysical (cosmological) black hole forming in a cosmological context will be subject to a flux of infalling matter and radiation, which will cause the outer apparent horizon (a marginal trapping surface) to be spacelike spacelike (Ellis et al., arXiv:1407.3577). As a consequence the radiation emitted close to the apparent horizon no longer arrives at infinity with a diverging redshift. Standard calculations of the emission of Hawking radiation then indicate that no blackbody radiation is emitted to infinity by the black hole in these circumstances, hence there will also then be no black hole evaporation process due to emission of such radiation as long as the matter flux is significant. The essential adiabatic condition (eikonal approximation) for black hole radiation gives a strong limit to the black holes that can emit Hawking radiation. We give the mass range for the black holes that can radiate, according to their cosmological redshift, for the special case of the cosmic blackbody radiation (CBR) influx (which exists everywhere in the universe). At a very late stage of black hole formation when the CBR influx decays away, the black hole horizon becomes first a slowly evolving horizon and then an isolated horizon; at that stage, black hole radiation will start. This study suggests that the primordial black hole evaporation scenario should be revised to take these considerations into account.

Appendices

Appendix 1: Junction condition inside the horizon

To construct the Oppenheimer-Snyder model inside the Schwarzchild horizon, we need a coordinate system that does not have a singularity on the horizon. We choose the Lemaître coordinate system [39] which is similar to the FLRW and LTB comoving coordinates. Then

$$\begin{aligned} ds^2= -dt^2 + R'^2dr^2 + R(t,r) d\Omega ^2 \end{aligned}$$

(58)

where

$$\begin{aligned} R= ( 2M)^{1/3} \left( \frac{3}{2} ( r-(t-t_0)) \right) ^{2/3}. \end{aligned}$$

(59)

The singularity is at $R=0$. Since the induced metric must be the same on both sides of the star surface at $\chi _0$ , we get

$$\begin{aligned} R(\tau )|_{\chi _0} = a(\tau ) \chi _0 \end{aligned}$$

(60)

and

$$\begin{aligned} \left( \frac{dt}{d\tau }\right) ^2\left| _{\chi _0} - R'^2\left( \frac{dr}{d\tau }\right) ^2 \right| _{\chi _0} = 1 \end{aligned}$$

(61)

The unit normals ($n_{\mu } n^{\mu }=1$) to the star surface are $n_-^\mu =(0,a,0,0)$ and $n_{+\mu }=(-\frac{dr}{d\tau }, \frac{dt}{d\tau },0,0)$. Using these normal vectors to calculate the extrinsic curvature lead us to these equations:

$$\begin{aligned} K_{-\theta }^{\theta } =K_{-\phi }^{\phi } = \frac{1}{a \chi } \end{aligned}$$

(62)

and

$$\begin{aligned} K_{+\theta }^{\theta } =K_{+\phi }^{\phi } = \frac{dr}{d\tau }\frac{\dot{R}}{R} +\frac{dt}{d\tau }\frac{1}{R'R} \end{aligned}$$

(63)

Matching the two extrinsic curvatures on the star surface we get,

$$\begin{aligned} \left. \left( \frac{dr}{d\tau }\frac{\dot{R}}{R} +\frac{dt}{d\tau }\frac{1}{R'R}\right) \right| _{\chi _0}= \frac{1}{a \chi _0} \end{aligned}$$

(64)

The equations (60, 61, 64) give the evolution of the star surface in the two space times.

Appendix 2: Areal coordinate for dynamical metric

The $r$ coordinate which we used as a radial coordinate in the fluid is a comoving coordinate, where the time coordinate is proper time for this observer. In contrast to the stationary metric in the vacuum, which has a preferred Killing observer, there is no preferred observer in the general dynamical metric. In the case that we want to calculate the redshift for a CBR photon which comes from a large distance to the apparent horizon, we need better coordinates. In the spherically symmetric case, there is a well defined family of observers which can be attributed to the areal coordinate $R(t,r)$ [52], and which are Kodama observers. The function $R(t,r)$ is a good candidate to describe the particle distance from center, and is called an areal coordinate (it is the angular diameter distance in cosmology). By taking the areal radius as a new coordinate and using the relation $dR=R'dr+\dot{R}dt$ for the LTB metric one obtains

$$\begin{aligned} ds^{2}=\left( \frac{\dot{R}^{2}}{1+f}-1\right) dt^{2}+\frac{dR^{2}}{1+f} -\frac{2\dot{R}}{1+f}dR dt +R(t,r)^{2}d\Omega ^{2}. \end{aligned}$$

(65)

The (t,R) coordinates are usually called areal coordinates. This LTB metric form is similar to the Painlev$\acute{e}$ form of the Schwarzschild metric. In the case of $f = 0$, the metric is the same as the Painlev$\acute{e}$ metric form.

The redshift (43) measured by Kodama observer with 4-velocity $K^{i}=\frac{\sqrt{1+f}}{\left( \sqrt{1-\frac{2m}{R}}\right) R'}(R',-\dot{R})$ [21, 22], can be written as

$$\begin{aligned} 1+z&= c_0 ~\frac{\left( \frac{\sqrt{\frac{2m}{R}+f}-\sqrt{1+f}}{\sqrt{1-\frac{2m}{R}}}\right) _e}{\left( \frac{\sqrt{\frac{2m}{R}+f}-\sqrt{1+f}}{\sqrt{1-\frac{2m}{R}}}\right) _o}~ exp \left( -\int _o^e \frac{\dot{R}'}{\sqrt{1+f}}dr \right) \nonumber \\&= c_0~ exp \left( -\int _o^e \pm \frac{\dot{R}'}{\dot{R}+\sqrt{1+f}} dR \right) . \end{aligned}$$

(66)

The $\pm$ refer to the outgoing and ingoing null geodesic respectively. Using the Einstein equation (25), we get the following equation:

$$\begin{aligned} 1+z = c_0~\frac{\left( \frac{\sqrt{\frac{2m}{R}+f}-\sqrt{1+f}}{\sqrt{1-\frac{2m}{R}}}\right) _e}{\left( \frac{\sqrt{\frac{2m}{R}+f}-\sqrt{1+f}}{\sqrt{1-\frac{2m}{R}}}\right) _o}~ exp \left( -\int _o^e \pm \frac{\dot{R}'}{- \sqrt{\frac{2M}{R}+f}+\sqrt{1+f}} dR \right) .\qquad \end{aligned}$$

(67)

The exponential part can be either $e^{-\infty }$ or $e^{+\infty }$ on the apparent horizon. For the ingoing null geodesic (with - sign), which comes from a large distance $e$ to the apparent horizon $o$, light becomes infinitely blue shifted: $(1+z)\rightarrow 0$. Note that the coordinate $R$ (comoving for a Kodama observer), like the Schwarzchild areal coordinate given by the $R=constant$ surface, is a spatial coordinate outside the horizon ($R>2M$) but becomes a time coordinate inside the horizon. Therefore, this coordinate cannot be used for inside the apparent horizon $R<2M$.

Appendix 3: Adiabatic condition for dynamical metric

An equivalent statement to the eikonal approximation is an adiabatic condition [19, 20, 25]. This condition says that the need for slow evolution of the geometry is hidden in the approximation used to write the modes as $e^{iwt}$ multiplied by a position-dependent fact or. This makes sense only if the geometry is quasi-static on the timescale set by $w$. This condition can be used as a criterion for having Hawking radiation [53]. Since this condition is an essential condition for black hole radiation, we want to examine it for a dynamical metric in the Painlev$\acute{e}$-Gullstrand coordinates,

$$\begin{aligned} ds^2=-(c(t,r)^2-v(t,r)^2)~dt^2-2 v dt~dR +dR^2+R^2 d\Omega ^2 \end{aligned}$$

(68)

The adiabatic condition says that the peak in the Planck spectrum is meaningful when

$$\begin{aligned} k T\approx w_{peak} \gg max\lbrace |\dot{c}/c|,|\dot{v}/v|\rbrace \end{aligned}$$

(69)

Now we examine this condition for the LTB metric (65) in this coordinate. The left hand side of this equation is proportional to the surface gravity [21, 22] which is finite. Without giving the details of the calculation for the $v=\frac{\dot{R}}{1+f}$ function, we get

$$\begin{aligned} \kappa _{AH} \gg |\dot{v}/v|= \frac{M'}{\sqrt{1+f}RR'} \end{aligned}$$

(70)

Using the surface gravity for the LTB metric [21, 22]

$$\begin{aligned} \kappa _H=\frac{1}{2}g^{\mu \nu } \nabla _\mu \nabla _\nu R=\frac{1}{2R}-\frac{M'}{2RR'}, \end{aligned}$$

(71)

and the $C$ function for LTB [38], $C=2\sqrt{1+f}\frac{M'}{R'-M'}$, one gets

$$\begin{aligned} 1 \gg C . \end{aligned}$$

(72)

Therefore, to examine the adiabatic condition for the LTB metric, it is sufficient to check the $C$ function.

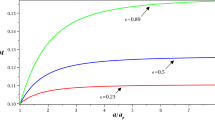
Conclusion: Surprisingly, only in the case of a slowly evolving horizon obeying (72) can a LTB dynamical black hole radiate. As a result, the adiabatic condition is also satisfied for an isolated horizon where $C=0 \Leftrightarrow M'=0$.

As another example, assume that we have ingoing radiation falling into the black hole. The suitable metric for this case is Vaidya ingoing form:

$$\begin{aligned} ds^2=-\left( 1-\frac{2M(v)}{r}\right) dv^2+2dvdr+r^2 d\Omega ^2, \end{aligned}$$

(73)

where the apparent horizon is located at $r=2M$. Using equation (71), we get $\kappa _H=\frac{1}{4M(v)}$ for the surface gravity. Hence, the adiabatic condition (69) says

$$\begin{aligned} 1 \gg \frac{dM(v)}{dv}. \end{aligned}$$

(74)

This means that the incoming matter flux must be small to satisfy the adiabatic condition. On the other hand, the $C$ function for a Vaidya metric that has a slowly evolving horizon is [49]

$$\begin{aligned} 1 \gg C=\frac{dM(v)}{dv}. \end{aligned}$$

(75)

As a result, similarly to the LTB case, the adiabatic condition allows Hawking radiation for a Vaidya black hole that has a slowly evolving horizon or an isolated horizon.