Reflection and Transmission of Plane Elastic Waves at an Interface Between Two Double-Porosity Media: Effect of Local Fluid Flow

Abstract

We obtain the reflection and transmission coefficients for inhomogeneous plane waves incident on a flat interface separating two double-porosity media described by the Biot–Rayleigh model, which takes into account the effect of local fluid flow (LFF). Three longitudinal and one transverse waves are reflected and transmitted, represented by potential functions specified by the propagation and attenuation directions. The continuity of the energy at the interface for sealed and open-boundary conditions yields a system of equations for the coefficients, and the expressions of the energy ratios for the reflected and refracted waves are derived in closed form. Numerical examples showing the magnitude, phase and energy ratio as a function of frequency and incidence angle are carried out to investigate the influence of the inhomogeneity angle, boundary condition, type of incidence wave and LFF effect. The results confirm that the LFF affects the reflection and transmission behaviors for the incident P1 and SV waves, irrespective of whether the interface is open or sealed. The effect causes interference fluxes between different waves, a consequence of energy conservation at the interface. We also perform full-waveform simulations to validate the results.

Appendices

Appendix 1

Let us denote the volume fractions of the two phases by $\nu_{1}$ and $\nu_{2}$ ($\nu_{2} = 1 - \nu_{1}$), the two local porosities in the host and inclusions by $\phi_{10}$ and $\phi_{20}$, the densities of solid grain and fluid by $\rho_{s}$ and $\rho_{f}$, the grain bulk and shear moduli by $K_{s}$ and $\mu_{s}$, the fluid bulk modulus by $K_{f}$, the two kinds of permeability by $\kappa_{1}$ and $\kappa_{2}$, the fluid viscosity by $\eta$, the radius of the inclusion by $R_{0}$, and the three consolidation parameters by $c_{1}$, $c_{2}$ and $c_{s}$.

In uniform porosity case, the two partial porosities are defined by Ba et al. (2011)

$$ \phi_{1} = \nu_{1} \phi_{10} ,\phi_{2} = \nu_{2} \phi_{20} ,\phi = \phi_{1} + \phi_{2} , $$

(51)

where $\phi$ is the total porosity. The five density parameters in Eq. (1) are defined as

$$ \begin{aligned} \rho_{11} & = \left( {1 - \phi } \right)\rho_{s} - {{\left( {\phi - 1} \right)} \mathord{\left/ {\vphantom {{\left( {\phi - 1} \right)} {\left( {2\rho_{f} } \right)}}} \right. \kern-0pt} {\left( {2\rho_{f} } \right)}} \\ \rho_{22} & = {{\left( {\phi_{1} + \nu_{1} } \right)\rho_{f} } \mathord{\left/ {\vphantom {{\left( {\phi_{1} + \nu_{1} } \right)\rho_{f} } 2}} \right. \kern-0pt} 2},\;\rho_{33} = {{\left( {\phi_{2} + \nu_{2} } \right)\rho_{f} } \mathord{\left/ {\vphantom {{\left( {\phi_{2} + \nu_{2} } \right)\rho_{f} } 2}} \right. \kern-0pt} 2} \\ \rho_{12} & = {{\left( {\phi_{1} - \nu_{1} } \right)\rho_{f} } \mathord{\left/ {\vphantom {{\left( {\phi_{1} - \nu_{1} } \right)\rho_{f} } 2}} \right. \kern-0pt} 2},\;\rho_{13} = {{\left( {\phi_{2} - \nu_{2} } \right)\rho_{f} } \mathord{\left/ {\vphantom {{\left( {\phi_{2} - \nu_{2} } \right)\rho_{f} } 2}} \right. \kern-0pt} 2}. \\ \end{aligned} $$

(52)

The stiffness parameters are

$$ \begin{aligned} K_{b1} & = \frac{{\left( {1 - \phi_{10} } \right)K_{s} }}{{1 + c_{1} \phi_{10} }},K_{b2} = \frac{{\left( {1 - \phi_{20} } \right)K_{s} }}{{1 + c_{2} \phi_{20} }},\mu_{b} = \frac{{\left( {1 - \phi } \right)\mu_{s} }}{{1 + c_{s} \phi }}, \\ {1 \mathord{\left/ {\vphantom {1 {K_{b} }}} \right. \kern-0pt} {K_{b} }} & = {{\nu_{1} } \mathord{\left/ {\vphantom {{\nu_{1} } {K_{b1} }}} \right. \kern-0pt} {K_{b1} }} + {{\nu_{2} } \mathord{\left/ {\vphantom {{\nu_{2} } {K_{b2} }}} \right. \kern-0pt} {K_{b2} }}, \\ \beta & = \frac{{\phi_{20} \left[ {1 - \left( {1 - \phi_{10} } \right){{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{b1} }}} \right. \kern-0pt} {K_{b1} }}} \right]}}{{\phi_{10} \left[ {1 - \left( {1 - \phi_{20} } \right){{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{b2} }}} \right. \kern-0pt} {K_{b2} }}} \right]}},\gamma = \frac{{K_{s} \left[ {\phi_{2} + \beta \phi_{1} } \right]}}{{K_{f} \left[ {1 - \phi - {{K_{b} } \mathord{\left/ {\vphantom {{K_{b} } {K_{s} }}} \right. \kern-0pt} {K_{s} }}} \right]}}, \\ Q_{1} & = \frac{{\beta \phi_{1} K_{s} }}{\beta + \gamma },Q_{2} = \frac{{\phi_{2} K_{s} }}{1 + \gamma },R_{1} = \frac{{\phi_{1} K_{f} }}{{1 + {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0pt} \gamma }}},R_{2} = \frac{{\phi_{2} K_{f} }}{{1 + {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0pt} \gamma }}}, \\ A & = \left( {1 - \phi } \right)K_{s} - {{2\mu_{b} } \mathord{\left/ {\vphantom {{2\mu_{b} } 3}} \right. \kern-0pt} 3} - {{K_{s} \left( {Q_{1} + Q_{2} } \right)} \mathord{\left/ {\vphantom {{K_{s} \left( {Q_{1} + Q_{2} } \right)} {K_{f} }}} \right. \kern-0pt} {K_{f} }},\;\;N = \mu_{b} . \\ \end{aligned} $$

(53)

$b_{1}$ and $b_{2}$ are

$$ b_{1} = \phi_{1} \phi_{10} {\eta \mathord{\left/ {\vphantom {\eta {\kappa_{1} }}} \right. \kern-0pt} {\kappa_{1} }},b_{2} = \phi_{2} \phi_{20} {\eta \mathord{\left/ {\vphantom {\eta {\kappa_{2} }}} \right. \kern-0pt} {\kappa_{2} }}. $$

(54)

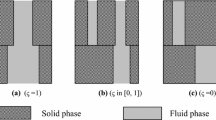
In the non-uniform porosity case (Wang et al. 2019),

$$ \alpha_{1} = \phi_{1} + \frac{{\beta \phi_{1} K_{s} }}{{\gamma K_{f} }},\alpha_{2} = \phi_{2} + \frac{{\phi_{2} K_{s} }}{{\gamma K_{f} }},M_{1} = \frac{{K_{f} }}{{\phi_{1} \left( {1 + {\beta \mathord{\left/ {\vphantom {\beta \gamma }} \right. \kern-0pt} \gamma }} \right)}},M_{2} = \frac{{K_{f} }}{{\phi_{2} \left( {1 + {1 \mathord{\left/ {\vphantom {1 \gamma }} \right. \kern-0pt} \gamma }} \right)}}. $$

(55)

Parameter $\lambda_{c}$ is

$$ \begin{aligned} \lambda_{c} & = - \frac{2}{3}\mu + \left( {1 - \phi } \right)K_{s} \\ & \quad + \,\left( {1 - {{K_{s} } \mathord{\left/ {\vphantom {{K_{s} } {K_{f} }}} \right. \kern-0pt} {K_{f} }}} \right)\left( {\alpha_{1} M_{1} \phi_{1} + \alpha_{2} M_{2} \phi_{2} - M_{1} \phi_{1}^{2} - M_{2} \phi_{2}^{2} } \right) + \left( {\alpha_{1} M_{1} \phi_{1} + \alpha_{2} M_{2} \phi_{2} } \right). \\ \end{aligned} $$

(56)

Following Eqs. (55) and (53), the relations among $Q_{i}$, $R_{i}$, $\alpha_{i}$, and $M_{i}$ are

$$ Q_{i} = \phi_{i} M_{i} \left( {\alpha_{i} - \phi_{i} } \right),R_{i} = \phi_{i}^{2} M_{i} ,\;\;i = 1,2. $$

(57)

The density $\rho$ is

$$ \rho = \left( {1 - \phi } \right)\rho_{s} + \phi \rho_{f} . $$

(58)

Appendix 2

The elements of matrix G in Eq. (33) are

$$ G_{1l} = \, s_{z}^{l} ,\;\left( {l = 1,2,3} \right),\quad G_{14} = s_{x}^{4} ,\quad G_{1l} = - \,s_{z}^{l} ,\;\left( {l = 5,6,7} \right){\kern 1pt} ,\quad G_{18} = - \,s_{x}^{8} . $$

(59)

$$ G_{2l} = {\kern 1pt} s_{x}^{l} ,\;{\kern 1pt} \left( {l = 1,2,3} \right),\quad G_{24} = - s_{z}^{4} ,{\kern 1pt} \quad G_{2l} = - s_{x}^{l} ,\;\left( {l = 5,6,7} \right),\quad G_{28} = s_{z}^{8} . $$

(60)

$$ \begin{aligned} G_{3l} & = \left( {D_{1}^{\rm I} + D_{2}^{\rm I} \delta_{f1s}^{l} + D_{3}^{\rm I} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right) - 2\mu_{{}}^{\rm I} \left( {s_{z}^{l} } \right)^{2} ,\left( {l = 1,2,3} \right) \\ G_{34} & = - \,2\mu_{{}}^{\rm I} s_{x}^{4} s_{z}^{4} \\ G_{3l} & = - \,\left[ {\left( {D_{1}^{\rm II} + D_{2}^{\rm II} \delta_{f1s}^{l} + D_{3}^{\rm II} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right) - 2\mu_{{}}^{\rm II} \left( {s_{z}^{l} } \right)^{2} } \right],\left( {l = 5,6,7} \right) \\ G_{38} & = 2\mu_{{}}^{\rm II} s_{x}^{8} s_{z}^{8} . \\ \end{aligned} $$

(61)

$$ \begin{aligned} G_{4l} & = 2\mu_{{}}^{\rm I} s_{x}^{l} s_{z}^{l} ,\left( {l = 1,2,3} \right),G_{44} = \mu_{{}}^{\rm I} \left( {\left( {s_{x}^{4} } \right)^{2} - \left( {s_{z}^{4} } \right)^{2} } \right) \\ G_{4l} & = - \,2\mu_{{}}^{\rm II} s_{x}^{l} s_{z}^{l} ,\left( {l = 5,6,7} \right),G_{48} = - \mu_{{}}^{\rm II} \left( {\left( {s_{x}^{8} } \right)^{2} - \left( {s_{z}^{8} } \right)^{2} } \right). \\ \end{aligned} $$

(62)

For the open boundary,

$$ \begin{aligned} G_{5l} & = \,\phi_{1}^{\rm I} \left( {\delta_{f1s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 1,2,3} \right),G_{54} = \phi_{1}^{\rm I} \left( {\delta_{f1s}^{4} - 1} \right)s_{x}^{4} \\ G_{5l} & = - \,\phi_{1}^{\rm II} \left( {\delta_{f1s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 5,6,7} \right),G_{58} = - \phi_{1}^{\rm II} \left( {\delta_{f1s}^{8} - 1} \right)s_{x}^{8} . \\ \end{aligned} $$

(63)

$$ \begin{aligned} G_{6l} & = \left( {D_{4}^{\rm I} + D_{5}^{\rm I} \delta_{f1s}^{l} + D_{6}^{\rm I} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right),\left( {l = 1,2,3} \right),G_{64} = 0 \\ G_{6l} & = - \,\left[ {\left( {D_{4}^{\rm II} + D_{5}^{\rm II} \delta_{f1s}^{l} + D_{6}^{\rm II} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right)} \right],\left( {l = 5,6,7} \right),G_{68} = 0. \\ \end{aligned} $$

(64)

$$ \begin{aligned} G_{7l} & = \phi_{2}^{\rm I} \left( {\delta_{f2s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 1,2,3} \right),G_{74} = \phi_{2}^{\rm I} \left( {\delta_{f2s}^{4} - 1} \right)s_{x}^{4} \\ G_{7l} & = - \,\phi_{2}^{\rm II} \left( {\delta_{f2s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 5,6,7} \right),G_{78} = - \,\phi_{2}^{\rm II} \left( {\delta_{f2s}^{8} - 1} \right)s_{x}^{8} . \\ \end{aligned} $$

(65)

$$ \begin{aligned} G_{8l} & = \left( {D_{7}^{\rm I} + D_{8}^{\rm I} \delta_{f1s}^{l} + D_{9}^{\rm I} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right),\left( {l = 1,2,3} \right),G_{84} = 0 \\ G_{8l} & = - \,\left[ {\left( {D_{7}^{\rm II} + D_{8}^{\rm II} \delta_{f1s}^{l} + D_{9}^{\rm II} \delta_{f2s}^{l} } \right)\left( {\left( {s_{x}^{l} } \right)^{2} + \left( {s_{z}^{l} } \right)^{2} } \right)} \right],\left( {l = 5,6,7} \right),G_{88} = 0. \\ \end{aligned} $$

(66)

For the sealed boundary,

$$ \begin{aligned} G_{5l} & = \phi_{1}^{\rm I} \left( {\delta_{f1s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 1,2,3} \right),G_{54} = \phi_{1}^{\rm I} \left( {\delta_{f1s}^{4} - 1} \right)s_{x}^{4} \\ G_{5l} & = 0,\left( {l = 5,6,7} \right),G_{58} = 0. \\ \end{aligned} $$

(67)

$$ \begin{aligned} G_{6l} & = 0,\left( {l = 1,2,3} \right),G_{64} = 0 \\ G_{6l} & = - \,\phi_{1}^{\rm II} \left( {\delta_{f1s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 5,6,7} \right),G_{68} = - \,\phi_{1}^{\rm II} \left( {\delta_{f1s}^{8} - 1} \right)s_{x}^{8} . \\ \end{aligned} $$

(68)

$$ \begin{aligned} G_{7l} & = \phi_{2}^{\rm I} \left( {\delta_{f2s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 1,2,3} \right),G_{74} = \phi_{2}^{\rm I} \left( {\delta_{f2s}^{4} - 1} \right)s_{x}^{4} \\ G_{7l} & = 0,\left( {l = 5,6,7} \right),G_{78} = 0. \\ \end{aligned} $$

(69)

$$ \begin{aligned} G_{8l} & = 0,\left( {l = 1,2,3} \right),G_{84} = 0 \\ G_{8l} & = - \,\phi_{2}^{\rm II} \left( {\delta_{f2s}^{l} - 1} \right)s_{z}^{l} ,\left( {l = 5,6,7} \right),G_{88} = - \phi_{2}^{\rm II} \left( {\delta_{f2s}^{8} - 1} \right)s_{x}^{8} . \\ \end{aligned} $$

(70)

In the case of an incident P1 wave, irrespective of the boundary being open or sealed, the first four elements in y are

$$ \begin{aligned} y_{1} & = - \,s_{z}^{0} ,y_{2} = {\kern 1pt} - s_{x}^{0} , \\ y_{3} & = - \,\left[ {\left( {D_{1}^{\rm I} + D_{2}^{\rm I} \delta_{f1s}^{0} + D_{3}^{\rm I} \delta_{f2s}^{0} } \right)\left( {\left( {s_{x}^{0} } \right)^{2} + \left( {s_{z}^{0} } \right)^{2} } \right) - 2\mu_{{}}^{\rm I} \left( {s_{z}^{0} } \right)^{2} } \right],\;y_{4} = - 2\mu_{{}}^{\rm I} s_{x}^{0} s_{z}^{0} \\ \end{aligned} $$

(71)

For the open boundary,

$$ \begin{aligned} y_{5} & = - \,\phi_{1}^{\rm I} \left( {\delta_{f1s}^{0} - 1} \right)s_{z}^{0} ,\;y_{6} = - \left[ {\left( {D_{4}^{\rm I} + D_{5}^{\rm I} \delta_{f1s}^{0} + D_{6}^{\rm I} \delta_{f2s}^{0} } \right)\left( {\left( {s_{x}^{0} } \right)^{2} + \left( {s_{z}^{0} } \right)^{2} } \right)} \right], \\ y_{7} & = - \,\phi_{2}^{\rm I} \left( {\delta_{f2s}^{0} - 1} \right)s_{z}^{0} ,\;y_{8} = - \left[ {\left( {D_{7}^{\rm I} + D_{8}^{\rm I} \delta_{f1s}^{0} + D_{9}^{\rm I} \delta_{f2s}^{0} } \right)\left( {\left( {s_{x}^{0} } \right)^{2} + \left( {s_{z}^{0} } \right)^{2} } \right)} \right]. \\ \end{aligned} $$

(72)

For the sealed boundary,

$$ y_{5} = - \,\phi_{1}^{\rm I} \left( {\delta_{f1s}^{0} - 1} \right)s_{z}^{0} ,\;y_{6} = 0,\;y_{7} = - \,\phi_{2}^{\rm I} \left( {\delta_{f2s}^{0} - 1} \right)s_{z}^{0} ,\;y_{8} = 0. $$

(73)

In the case of an incident SV wave, irrespective of the boundary being open or sealed, the elements in y are

$$ y_{1} \,{ = }\,{\kern 1pt} \, - \,s_{x}^{0} ,\;y_{2} \,{ = }\,{\kern 1pt} s_{z}^{0} ,\;y_{3} \,{ = }\,2\mu_{{}}^{\rm I} s_{x}^{0} s_{z}^{0} ,\;y_{4} \,{ = }\, - \mu_{{}}^{\rm I} \left( {\left( {s_{x}^{0} } \right)^{2} - \left( {s_{z}^{0} } \right)^{2} } \right). $$

(74)

$$ y_{5} = - \,\phi_{1}^{\rm I} \left( {\delta_{f1s}^{0} - 1} \right)s_{x}^{0} ,\;y_{6} = 0,\;y_{7} = - \,\phi_{2}^{\rm I} \left( {\delta_{f2s}^{0} - 1} \right)s_{x}^{0} ,\;y_{8} = 0. $$

(75)

The parameters $D_{i}^{\rm I}$ and $D_{i}^{\rm II}$ in Eqs. (61), (64), (66), (71), and (72) are given in “Appendix 3”.

Appendix 3

The expressions for $D_{i}^{\rm I} \left( {i = 1,2, \ldots ,8,9} \right)$ in Eq. (38) in medium $\varOmega_{ 1}$ are

$$ \begin{aligned} D_{ 1}^{\rm I} & = - \,\lambda_{c}^{\text{I} } { + }\alpha_{1}^{\text{I} } M_{1}^{\text{I} } \phi_{1}^{\text{I} } { + }\alpha_{2}^{\text{I} } M_{2}^{\text{I} } \phi_{2}^{\text{I} } \\ & \quad { + }\,\frac{{3\phi_{10}^{\text{I} } }}{{{\text{F}}^{\text{I} } }}\phi_{1}^{\text{I} } \phi_{2}^{\text{I} } \left( {\alpha_{1}^{\text{I} } M_{1}^{\text{I} } - \alpha_{2}^{\text{I} } M_{2}^{\text{I} } } \right)\left( {\alpha_{1}^{\text{I} } M_{1}^{\text{I} } - \alpha_{2}^{\text{I} } M_{2}^{\text{I} } + M_{2}^{\text{I} } \phi_{2}^{\text{I} } - M_{1}^{\text{I} } \phi_{1}^{\text{I} } } \right), \\ \end{aligned} $$

(76)

$$ D_{2}^{\rm I} = - \,\alpha_{1}^{\rm I} M_{1}^{\rm I} \phi_{1}^{\rm I} + \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}\phi_{1}^{\rm I} \phi_{2}^{\rm I} \left( {\alpha_{1}^{\rm I} M_{1}^{\rm I} - \alpha_{2}^{\rm I} M_{2}^{\rm I} } \right)M_{1}^{\rm I} \phi_{1}^{\rm I} , $$

(77)

$$ D_{3}^{\rm I} = - \,\alpha_{2}^{\rm I} M_{2}^{\rm I} \phi_{2}^{\rm I} - \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}\phi_{1}^{\rm I} \phi_{2}^{\rm I} \left( {\alpha_{1}^{\rm I} M_{1}^{\rm I} - \alpha_{2}^{\rm I} M_{2}^{\rm I} } \right)M_{2}^{\rm I} \phi_{2}^{\rm I} , $$

(78)

$$ D_{4}^{\rm I} = \alpha_{1}^{\rm I} M_{1}^{\rm I} - M_{1}^{\rm I} \phi_{1}^{\rm I} - \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{1}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} \left( {\alpha_{1}^{\rm I} M_{1}^{\rm I} - \alpha_{2}^{\rm I} M_{2}^{\rm I} + M_{2}^{\rm I} \phi_{2}^{\rm I} - M_{1}^{\rm I} \phi_{1}^{\rm I} } \right), $$

(79)

$$ D_{5}^{\rm I} = M_{1}^{\rm I} \phi_{1}^{\rm I} - \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{1}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} M_{1}^{\rm I} \phi_{1}^{\rm I} , $$

(80)

$$ D_{6}^{\rm I} = \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{1}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} M_{2}^{\rm I} \phi_{2}^{\rm I} , $$

(81)

$$ D_{7}^{\rm I} = \alpha_{2}^{\rm I} M_{2}^{\rm I} - M_{2}^{\rm I} \phi_{2}^{\rm I} + \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{2}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} \left( {\alpha_{1}^{\rm I} M_{1}^{\rm I} - \alpha_{2}^{\rm I} M_{2}^{\rm I} + M_{2}^{\rm I} \phi_{2}^{\rm I} - M_{1}^{\rm I} \phi_{1}^{\rm I} } \right), $$

(82)

$$ D_{8}^{\rm I} = \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{2}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} M_{1}^{\rm I} \phi_{1}^{\rm I} , $$

(83)

$$ D_{9}^{\rm I} = M_{2}^{\rm I} \phi_{2}^{\rm I} - \frac{{3\phi_{10}^{\rm I} }}{{F^{\rm I} }}M_{2}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} M_{2}^{\rm I} \phi_{2}^{\rm I} , $$

(84)

where

$$ F^{\rm I} = \phi_{20}^{\rm I} \left( {R_{0}^{\rm I} } \right)^{2} \rho_{f}^{\rm I} \phi_{1}^{\rm I} \omega^{2} - i\omega \phi_{20}^{\rm I} \left( {R_{0}^{\rm I} } \right)^{2} \frac{{\phi_{10}^{\rm I} \phi_{1}^{\rm I} \eta_{1}^{\rm I} }}{{\kappa_{1}^{\rm I} }} + 3\phi_{10}^{\rm I} \phi_{1}^{\rm I} \phi_{2}^{\rm I} \left( {M_{1}^{\rm I} + M_{2}^{\rm I} } \right). $$

(85)

By replacing index I with II in Eqs. (76)–(85), the corresponding formulae for medium $\varOmega_{ 2}$ can be obtained.