1 Introduction

A slight overload can induce brittle fracture when a crack initiates at the point of maximum stress and then propagates. The crack development through the structure depends on the loading conditions, and a crack can propagate as a single crack, change its original trajectory, or split into two or multiple branches (Cotterell 1965). In the literature, several experimental studies have been performed and reported (Bowden et al. 1967; Döll 1975; Chandar and Knauss 1982; Ramulu and Kobayashi 1985; Suzuki et al. 1997; Suzuki and Sakaue 2004) to analyse the fracture behaviour. Very high crack propagation speeds, approaching the speed of sound in the material, are observed during the experiments (Bowden et al. 1967). Such behaviour is named as fast fracture when a sudden failure occurs in the structure with a rapid crack growth after crack nucleation. Theoretically, the Rayleigh wave speed is the limiting speed for tensile failure. Moreover, the experimental results (Fineberg et al. 2003) show that crack instability occurs at speeds lower then Rayleigh wave speed and the micro-branching occurs at critical velocity. Before branching occurs, an increase in fracture surface roughness is observed (Döll 1975; Ramulu and Kobayashi 1985), and after branching, the crack propagation speed reduces by 5 to 10% (Bowden et al. 1967).

Significant efforts have been made to determine the crack growth direction and the maximum energy release rate by means of classical continuum mechanics, including Finite Element Method (FEM). The applicability of the FEM on fracture mechanics problems showed difficulties in the treatment of singularities in discontinuous stress and strain fields. Furthermore, FEM requires external crack growth criteria and prior knowledge of crack propagation direction and speed (Charalambides and McMeeking 1987; Ortiz and Pandolfi 1999). Instead, Extended FEM (XFEM) was developed to overcome problems, including mesh-dependency (Fries and Belytschko 2010; Belytschko et al. 2013). XFEM has been applied to various problems (Mariani and Perego 2003; Menouillard and Belytschko 2010; Geniaut and Galenne 2012; Nicak et al. 2015) and become a good alternative to the cohesive zone model. However, in XFEM, local mesh refinement is necessary before each propagation step, and the branching point has to be identified from the stresses which sometimes makes the technique inefficient (Mariani and Perego 2003; Zi and Belytschko 2003; Zhou et al. 2005; Geniaut and Galenne 2012; Ren and Guan 2017).

As an alternative approach, peridynamics (PD) was introduced by Silling (2000) and demonstrated success in modelling dynamic fracture problems. For the material failure predictions, integration, rather than differentiation, is used to calculate the total force-density acting on each material point and spatial derivatives are not used in the formulation. Material points are interacting with each other in a non-local manner, and each interaction is called a peridynamic bond. Moreover, the damage in the PD model is usually introduced by using a critical stretch based failure criterion for each bond between interacting material points. If the stretch of a bond exceeds a critical stretch value, failure occurs for that particular bond. The critical stretch is directly related to the material’s critical energy release rate. Various peridynamic bond failure, coupled strength and energy failure criteria are available in the literature (Zhang and Qiao 2018a, b, 2019). PD model does not require crack tip tracking and specification of the crack behaviour when the crack changes its direction or crack branching occurs.

There are currently various peridynamic formulations available in the literature. Amongst these “Bond-based” PD has been widely used for predicting crack initiation and propagation patterns (Silling et al. 2010; Ha and Bobaru 2011; Bobaru and Hu 2012; Huang et al. 2015) as well as branching problems (Bobaru et al. 2009; Ha and Bobaru 2010, 2011; Agwai et al. 2011; Bobaru and Zhang 2015) of brittle materials, for example, PMMA, soda-lime glass and Homalite 100. Peridynamic results showed a good match of damage maps and crack propagation speeds with the experimental results (Bowden et al. 1967; Chandar and Knauss 1982; Ramulu and Kobayashi 1985; Suzuki and Sakaue 2004). It was noticed that the amplitude of the loading has a significant impact on the crack initiation and propagation behaviour (Bobaru and Zhang 2015). The bond-based PD model has a limitation on material properties, especially for Poisson’s ratio being 1/3 in the 2D model and 1/4 in the 3D model for isotropic materials. To eliminate this limitation, “Ordinary state-based” PD was proposed by Silling et al. (2007). The improved “Ordinary state-based” PD model provides more realistic results when Poisson’s ratio is different from 1/3 (2D model) and 1/4 (3D model).

In this study, the ordinary state-based PD model is used for fracture mechanics problems under static and dynamic loading conditions. Moreover, an in-depth investigation of the critical stretch based failure criterion is performed. Seven different cases are considered to determine the most accurate bond force definition if a failure occurs for a particular bond. In Sect. 3, Crack Opening Displacement (COD) values for a pre-cracked isotropic plate are obtained for seven different cases and compared against FEM results. In Sect. 4, convergence studies are presented for different horizon and discretisation sizes. Moreover, in Sect. 5, PD results are compared with the experimental results (Suzuki et al. 1997) for dynamic fracture problems (Freund 1998). Furthermore, PD results are presented for different dynamic loading conditions and the evaluated crack propagation speeds, crack branching patterns, and branching angles from PD model are compared with experimental results (Suzuki and Sakaue 2004). The conclusions are given in Sect. 6.

2 Ordinary state-based peridynamics formulation

The ordinary state-based peridynamics (Silling et al. 2007) is a reformulation of the fundamental equations of classical continuum mechanics to solve problems with discontinuities. Peridynamics model uses integro-differential equations instead of partial differential equations as in the classical continuum mechanics. This widens the possibility of solving fracture mechanics problems ranging from prediction of crack initiation to propagation (Kilic and Madenci 2010).

The peridynamic equation of motion can be expressed in the form of integro-differential equation as:

$$\begin{aligned} \rho {\ddot{{\varvec{u}}}}\left( {{\varvec{x}},t} \right)= & {} \mathop \int \limits _{H} \left( {\varvec{t}}\left( {{\varvec{{u}'}}-{\varvec{u}},{\varvec{{x}'}}-{\varvec{x}},t} \right) -{\varvec{{t}'}}\left( {\varvec{u}}-{\varvec{{u}'}},{\varvec{x}} \right. \right. \nonumber \\&\left. \left. -{\varvec{{x}'}},t \right) \right) d{V}'+{\varvec{b}}\left( {{\varvec{x}},t} \right) \end{aligned}$$
(1)

which can be discretised as

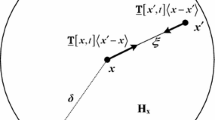
$$\begin{aligned} \rho _{\left( i \right) } {\ddot{{\varvec{u}}}}_{(i)}= & {} \mathop \sum \limits _{j=1}^{N} \left( {\varvec{t}}_{\left( {{\varvec{i}}} \right) \left( {{\varvec{j}}} \right) } \left( {{\varvec{u}}_{\left( {{\varvec{j}}} \right) } -{\varvec{u}}_{\left( {{\varvec{i}}} \right) } ,{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } ,t} \right) \right. \nonumber \\&\left. -{\varvec{t}}_{\left( {{\varvec{j}}} \right) \left( {{\varvec{i}}} \right) } \left( {{\varvec{u}}_{\left( {{\varvec{i}}} \right) } -{\varvec{u}}_{\left( {{\varvec{j}}} \right) } ,{\varvec{x}}_{\left( {{\varvec{i}}} \right) } -{\varvec{x}}_{\left( {{\varvec{j}}} \right) } ,t} \right) \right) V_{\left( j \right) } +{\varvec{b}}_{\left( {{\varvec{i}}} \right) }\nonumber \\ \end{aligned}$$
(2)

from which the acceleration \({\ddot{{\varvec{u}}}}_{(i)} \) of the material point at a time t can be obtained. Each material point at \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \) interacts with other material points at \({\varvec{x}}_{\left( {{\varvec{j}}} \right) } \) within its horizon, \(H_{x_{\left( i \right) } } \), as shown in Fig. 1. The coordinates of the material point i are identified as \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \) with the incremental volume \(V_{\left( i \right) } \). \({\varvec{u}}_{\left( {{\varvec{i}}} \right) } \), \({\varvec{b}}_{\left( {{\varvec{i}}} \right) } \) and \(\rho _{\left( i \right) } \) are the displacement, body load and mass density of the material point at \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \), respectively.

In the ordinary state-based peridynamics, force density vectors of interacting material points have unequal magnitudes (Madenci and Oterkus 2014), and for the material point at \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \) they can be written as:

$$\begin{aligned} t_{\left( i \right) \left( j \right) }= & {} 2\delta \left\{ {d\frac{\Lambda _{\left( i \right) \left( j \right) } }{\left| {{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } } \right| }a\theta _{\left( i \right) } +2\delta bs_{\left( i \right) \left( j \right) } } \right\} \nonumber \\&\times \frac{{\varvec{y}}_{\left( {{\varvec{j}}} \right) } -{\varvec{y}}_{\left( {{\varvec{i}}} \right) } }{\left| {{\varvec{y}}_{\left( {{\varvec{j}}} \right) } -{\varvec{y}}_{\left( {{\varvec{i}}} \right) } } \right| } \end{aligned}$$
(3)
$$\begin{aligned} t_{\left( j \right) \left( i \right) }= & {} -2\delta \left\{ {d\frac{\Lambda _{\left( i \right) \left( j \right) } }{\left| {{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } } \right| }a\theta _{\left( j \right) } +2\delta bs_{\left( i \right) \left( j \right) } } \right\} \nonumber \\&\times \frac{{\varvec{y}}_{\left( {{\varvec{j}}} \right) } -{\varvec{y}}_{\left( {{\varvec{i}}} \right) } }{\left| {{\varvec{y}}_{\left( {{\varvec{j}}} \right) } -{\varvec{y}}_{\left( {{\varvec{i}}} \right) } } \right| } \end{aligned}$$
(4)

where s is the stretch between the material points, a, b, d are the peridynamic parameters, \(\delta \) is the horizon size and the dilatation \(\theta \) can be expressed as:

$$\begin{aligned} \theta _{\left( i \right) } =d\delta \mathop \sum \nolimits _{j=1}^{N} \Lambda _{\left( i \right) \left( j \right) } s_{\left( i \right) \left( j \right) } V_{\left( j \right) } \end{aligned}$$
(5)

and the parameter \(\Lambda _{\left( i \right) \left( j \right) } \) is defined as

$$\begin{aligned} \Lambda _{{\left( i \right) \left( j \right) }} = \left( {\frac{{{\varvec{y}}_{{\left( {\varvec{j}} \right) }} - {\varvec{y}}_{{\left( {\varvec{i}} \right) }} }}{{\left| {{\varvec{y}}_{{\left( {\varvec{j}} \right) }} - {\varvec{y}}_{{\left( {\varvec{i}} \right) }} } \right| }}} \right) \square \left( {\frac{{{\varvec{x}}_{{\left( {\varvec{j}} \right) }} - {\varvec{x}}_{{\left( {\varvec{i}} \right) }} }}{{\left| {{\varvec{x}}_{{\left( {\varvec{j}} \right) }} - {\varvec{x}}_{{\left( {\varvec{i}} \right) }} } \right| }}} \right) \end{aligned}$$
(6)
Fig. 1
figure 1

Peridynamic material points and interaction of points \({x_{\left( i \right) }}{\text { and }}{x_{\left( j \right) }}\)

Full size image
Fig. 2
figure 2

Deformation of Peridynamic material points \({x_{\left( i \right) }}{\text { and }}{x_{\left( j \right) }}\)

Full size image

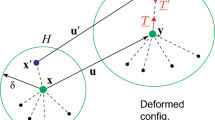
After the point \({\varvec{x}}_{\left( {{\varvec{j}}} \right) }\) experiences the displacement, its new location is specified as \({\varvec{y}}_{\left( {{\varvec{j}}} \right) }\) in the deformed configuration, as shown in Fig. 2.

Peridynamic parameters a, b, d are the material constants identified by comparing classical continuum mechanics and peridynamic models for isotropic expansion and simple shear loading conditions (Madenci and Oterkus 2014). These parameters can be specified in terms of bulk modulus \(\kappa \), shear modulus \(\mu \), thickness and horizon size for a 2D problem, with plane stress conditions:

$$\begin{aligned} a=\frac{1}{2}\left( {\kappa -2\mu } \right) , ~b=\frac{6\mu }{\pi h\delta ^{4}}, ~d=\frac{2}{\pi h\delta ^{3}} \end{aligned}$$
(7)

The stretch between the material points \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \) and \({\varvec{x}}_{\left( {{\varvec{j}}} \right) } \) can be expressed as

$$\begin{aligned} s_{\left( i \right) \left( j \right) } =\frac{\left( {\left| {{\varvec{y}}_{\left( {{\varvec{j}}} \right) } -{\varvec{y}}_{\left( {{\varvec{i}}} \right) } } \right| -\left| {{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } } \right| } \right) }{\left| {{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } } \right| } \end{aligned}$$
(8)

The failure parameter introduced by Silling and Bobaru (2005) can be represented by the history-dependent scalar-valued function \(\mu \) for the peridynamic equation of motion given in Eq. (2). The failure parameter \(\mu \) is defined as

$$\begin{aligned} \mu \left( {{\varvec{x}}_{{\left( {\varvec{j}} \right) }} - {\varvec{x}}_{{\left( {\varvec{i}} \right) }} ,t} \right) = \left\{ {\begin{array}{*{20}l} {1{~}} \\ 0 \\ \end{array} } \right. ~~~\begin{array}{*{20}l} {if{{~~~}}s_{{\left( i \right) \left( j \right) }} \left( {{\varvec{x}}_{{\left( {\varvec{j}} \right) }} - {\varvec{x}}_{{\left( {\varvec{i}} \right) }} ,t^{\prime }} \right)< s_{c} ~{\text {for all}}~~~0 < t^{\prime }} \\ {{\text {otherwise}}} \\ \end{array} \end{aligned}$$
(9)

where for a 2-D problem the critical stretch \(s_{c} \) in connection with the material fracture energy \(G_{c} \) is given by (Madenci and Oterkus 2014):

$$\begin{aligned} s_{\text{ c }} =\sqrt{\frac{G_{c} }{\left( {\frac{6}{\pi }\mu +\frac{16}{9\pi ^{2}}\left( {\kappa -2\mu } \right) } \right) \delta }} \end{aligned}$$
(10)

The introduced parameter of the critical stretch \(s_{c} \) is predefining the limit of the bond stretch, at which the bonds between material points can be broken. According to Silling and Askari (2005) the bonds are broken irreversably once they are stretched beyond the critical limit and the bond no longer sustains the tensile force. With the applied tension forces on the sides of the plate, the fracture energy \(G_{c} \) in peridynamic model is required to break the bonds connected at the opposite halves of the crack. In the current study, a constant critical stretch is used and the values of the fracture energy are obtained from the tests (Suzuki et al. 1997). Note that some studies indicated the variation of fracture energy with the propagating crack (Sharon et al. 1996), but the performed experiments (Ravi-Chandar and Knauss 1984a) on Homalite-100 suggested that the the increase of the fracture energy occurs due to the voids ahead of the crack front. Nevertheless, the relation between the crack propagating speed and the critical energy is not taken into account in the current study, and critical stretch is kept constant.

Table 1 Seven cases of damage parameter initiation
Full size table

The constant \(s_{c} \) in “Bond-based” peridynamics models was used in the multiple studies of brittle fracture (Bobaru et al. 2009; Ha and Bobaru 2010, 2011; Silling et al. 2010; Agwai et al. 2011; Bobaru and Hu 2012; Bobaru and Zhang 2015; Huang et al. 2015) and showed good agreement with experimental profiles. The study of Ha and Bobaru (2011) introduced a damage-dependent peridynamic model with a correction factor for \(s_{c} \), which showed closer results to experimental crack path and branching.

Ordinary state-based peridynamics has several fundamental differences with respect to the original bond-based peridynamic formulation. In bond-based peridynamics, the peridynamic force between two material points is calculated based on the relative displacements between these two material points. In other words, only the motion of the interacting material points has an effect on the peridynamic force between the interacting material points. On the other hand, in ordinary state based peridynamics, peridynamic force between two interacting material points has two components as in Eqs. (3) and (4). The second component is similar to the one in bond-based peridynamics which is depending on the motion of the interacting material points only. The first component is based on the peridynamic dilatation term which brings into the effect of family members of the interacting material points on the peridynamic force between them. When the bond is broken, it is logical to eliminate the second component which is only dependant on the motion of the interacting material points. However, it is not obvious how to deal with the first term which is related with the motions of family members. In addition, even if the peridynamic force between two material points (first and second components) is fully eliminated, it is not intuitive to decide how the bond breakage should be taken into account for peridynamic dilatation calculation. Therefore, it is essential to consider all possibilities about the peridynamic force and dilatation calculations by considering the failure parameter and compare peridynamic solutions for a benchmark problem to determine the best option. Such an in-depth investigation is currently not available in the literature. In order to investigate the effect of the failure parameter on the dilatation term and the bond force between interacting material points, seven different cases are considered as presented in Table 1. The local damage of the material point \({\varvec{x}}_{\left( {{\varvec{i}}} \right) } \) ranges from 0 to 1, can be identified as

$$\begin{aligned} \varphi \left( {{\varvec{x}}_{\left( {{\varvec{i}}} \right) } ,t} \right) =1-\frac{\sum \nolimits _{j=1}^N {\mu \left( {{\varvec{x}}_{\left( {{\varvec{j}}} \right) } -{\varvec{x}}_{\left( {{\varvec{i}}} \right) } ,t} \right) V_{\left( {{\varvec{j}}} \right) } } }{\sum \limits _{j=1}^N {V_{\left( {{\varvec{j}}} \right) } } }. \end{aligned}$$
(11)

Local damage is dependent on the relationship between the horizon size and the distance between the material points. For an initial crack, the failure parameter becomes zero if a bond is passing through the crack represented by a red line. Local damage is evaluated for three different horizon sizes, when \(\delta =m\Delta x\), with \(m= 3, 4, 5\), as shown in Fig. 3. As the horizon size increases, the material point interacts with an increased number of points within the horizon.

The local damage \(\varphi \) at a material point on the crack plane will converge to a value of 0.5 as m parameter increases.

Fig. 3
figure 3

Local damage at a material point on the crack plane, when horizon size is a \(\delta = 3\Delta x\) \( \rightarrow \varphi = 0.38\), b \(\delta = 4\Delta x \rightarrow \varphi = 0.41\), c \(\delta = 5\Delta x \rightarrow \varphi = 0.43\)

Full size image
Fig. 4
figure 4

Sample geometry of the pre-cracked square plate a under displacement and velocity boundary conditions and b its spatial discretisation under imposed boundary conditions

Full size image

3 Determination of the best case for the critical stretch based failure criterion

To determine the best case amongst seven cases in Table 1 for the damage parameter implementation in the ordinary state-based equation of motion, the failure parameter \(\mu \) is added or not in the dilatation term and the bond force between interacting material points. To verify the models, PD numerical results are compared against FEA solution. A PD numerical model is considered for a square plate with a central crack under the quasi-static loading condition as shown in Fig. 4a. The initial length of the crack is selected as \(2a=0.1~\text {m}\). The square plate is \(L=0.5~\text {m}\) long, \(W=0.5~\text {m}\) wide and \(h=0.01~\text {m}\) thick. The following material properties of the plate are specified: Young’s modulus \(E=200~\text {GPa}\), mass density \(\rho =7850~\text {kg/m}^{3}\) and Poisson’s ratio \(\nu =0.25\).

As shown in Fig. 4a, the plate is subjected to displacement constraints of \(v\left( {x,\text{ y }=W/2,t} \right) =v^{*}=5\times 10^{-4}~\text {m}\) and \(v\left( {x,\text{ y }=-W/2,t} \right) =v^{*}=-5\times 10^{-4}~\text {m}\). The boundary conditions are applied by introducing fictitious boundary layers \(R_{f} \) as demonstrated in Fig. 4b. The size of the \(R_{f} \) region is equal to the horizon size, which is \(\delta =3.015~\Delta x\). The displacements in the fictitious regions are specified as (Madenci and Oterkus 2016):

$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =u\left( {x,y,t} \right) \quad \text{ with } \quad y_{f} \in R_{f\left( {\text{ y }=\frac{W}{2}} \right) } \end{aligned}$$
(12)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =2v^{*}\left( {x,\text{ y }=\frac{W}{2},t+\Delta t} \right) -v\left( {x,y,t} \right) \end{aligned}$$
(13)
$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =u\left( {x,y,t} \right) \quad \text{ with } \quad y_{f} \in R_{f\left( {\text{ y }=-\frac{W}{2}} \right) } \end{aligned}$$
(14)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =2v^{*}\left( {x,\text{ y }=-\frac{W}{2},t+\Delta t} \right) -v\left( {x,y,t} \right) \end{aligned}$$
(15)

The peridynamic model is discretised with 250,000 material points with a uniform spacing between them \(\Delta x=0.001~\hbox {m}\). Adaptive dynamic relaxation method (Kilic and Madenci 2010)    with a total time step of 52,000 is used to reach the quasi-static loading condition with a time step size of \(\Delta t=~1\) s.

Fig. 5
figure 5

Crack opening displacement comparison near the crack tip when \(\delta = 3.015{~}\Delta x\) for Cases 1–3

Full size image
Fig. 6
figure 6

Crack opening displacement comparison near the crack tip when \(\delta = 3.015{~}\Delta x\) for a Case 4 and a Cases 5–7

Full size image

The current study is performed to determine the best case for the critical stretch based failure criterion by implementing the failure parameter \(\mu \) in Table 1 and analysing the crack opening displacement (COD) of the pre-existing crack without its further propagation. As the pre-condition to the model, all bonds crossing the pre-existing crack in the system as shown in Fig. 3 are considered to be broken which is a similar condition of bond stretch exceeding the critical stretch value. Due to uniaxial tensile loading, location of the pre-existing crack being in the middle of the plate and the allocation of the global axis at the centre of the crack, the COD is symmetrical along the vertical and horizontal axes. For this reason, the presented COD results are for the edge of the pre-existing crack located in the \(+\text{ x }\) and \(+\text{ y }\) part of the coordinate system. As shown in Fig. 5, although the first three case results, Case 1–3, are following the same pattern of the COD with FEA results, Case 1 has the best agreement compared to FEA where for all broken bonds both the force density vector and their contribution to the dilatation term are dropping to 0. Fig. 7 presents the horizontal and vertical displacements of the PD Case 1 results with respect to FEA solution which shows a very good agreement between PD and FEA results. On the other hand, Case 2 and 3 do not sufficiently eliminate the interaction between the material points when the bonds are broken. Implementation of Case 4 yields large COD with up to 0.025 m in the middle of the plate (Fig. 6a), which is not realistic compared to only \(2\times 10^{-4}\text {m}\) in FEA results. On the other hand, Cases 5–7 result in COD values lower than \(10^{-6}\text {m}\) within the crack area (Fig. 6b) which again do not match well with FEA solution. This shows that in Cases 5–7 the bonds are not properly broken in the location of the pre-existing crack and do not accurately represent the existence of the crack.

Based on the comparisons of PD results for seven cases against FEA results, Case 1 is selected as the best case for critical stretch based failure criterion in the ordinary state-based PD model and is used in the following sections for further studies.

Fig. 7
figure 7

FEA for horizontal (left) and vertical (right) displacement. PD solution for horizontal (left) and vertical (right) displacement for Case 1

Full size image

4 Convergence studies

The convergence studies are performed to identify suitable spacing between the material points \(\Delta x\) and the parameter m, defining horizon size \(\delta \), \(\delta =m\Delta x\), for a square plate in Fig. 4 with a central crack.

4.1 Numerical studies of convergence in COD

The geometrical and material properties are the same as in the previous section. The plate in Fig. 4a is loaded symmetrically by applying displacement constraints of \(~v^{*}=5\times 10^{-4} \text{ m }\) along \(\text{ y }=W/2\) and of \(~v^{*}=-5\times 10^{-4} \text{ m }\) along \(\text{ y }=-W/2\). The boundary conditions are applied in the fictitious region \(R_{f} \) using the equations given in Eqs. (12–15). The peridynamic steady-state solutions after 4000-time steps are compared with FEA as shown in Fig. 8.

Fig. 8
figure 8

Convergence of PD predictions in COD with a fixed value of horizon size \(\delta = 0.003{~\text {m}}\) and varying \(\Delta x = 1 \times {10^{ - 3}},{~}0.75 \times {10^{ - 3}},{~}0.6 \times {10^{ - 3}}{~\text {m}}\); b fixed value of \(\Delta x = 1 \times {10^{ - 3}}{~\text {m}}\) and varying \(m = 3,{~}4,{~}5\)

Full size image

Fig. 8a shows the convergence of the solutions for a fixed horizon size of \(\delta =0.003~\text {m}\) and varying the spacing between material points, \(\Delta x=1\times 10^{-3},~0.75\times 10^{-3},~0.6\times 10^{-3} \text{ m }\). All spacing values provide good agreement with FEA results. Based on \(\Delta x=1\times 10^{-3}\,\text{ m }\), Fig. 8b presents a convergence of PD predictions in COD for varying \(m=3,~4,~5\). All horizon sizes values yield similar results.

4.2 Numerical studies of convergence in dynamic crack propagation speed

In this section, the plate shown in Fig. 4a is subjected to dynamic loading and loaded symmetrically by applying velocity boundary condition of \(\dot{{v}}\left( {x,\text{ y }=W/2,t} \right) =\dot{{v}}^{*}=1.0~\text{ m/s }\) and \(\dot{{v}}\left( {x,\text{ y }=-W/2,t} \right) =\dot{{v}}^{*}=-1.0~\text{ m/s }\). The velocity boundary conditions (BC) are enforced in the fictitious boundary layer \(R_{f} \) (Fig. 4b) as (Madenci and Oterkus 2016):

$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =u\left( {x,y,t} \right) \quad \text{ with } \quad y_{f} \in R_{f\left( {\text{ y }=\frac{W}{2}} \right) } \end{aligned}$$
(16)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =2\dot{{v}}^{*}\left( {x,\text{ y }=\frac{W}{2},t+\Delta t} \right) \times \Delta t-v\left( {x,y,t} \right) \nonumber \\\end{aligned}$$
(17)
$$\begin{aligned}&u_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =u\left( {x,y,t} \right) \quad \text{ with } \quad y_{f} \in R_{f\left( {\text{ y }=-\frac{W}{2}} \right) } \end{aligned}$$
(18)
$$\begin{aligned}&v_{f} \left( {x_{f} ,y_{f} ,t+\Delta t} \right) \nonumber \\&\quad =2\dot{{v}}^{*}\left( {x,\text{ y }=-\frac{W}{2},t+\Delta t} \right) \times \Delta t-v\left( {x,y,t} \right) \nonumber \\ \end{aligned}$$
(19)

The plate is made from PMMA material with the following material properties: Young’s modulus \(E=3.24~\text{ GPa }\), mass density \(\rho =1200~\text{ kg/m}^{{3}}\) and Poisson’s ratio \(\nu =0.35\). The dynamic stress intensity factor and the critical energy release rate are taken as \(\text{ K}_{\text{ I }} =1.35~\text {MPa} \surd \text {m}\) and \(G_{0} =570~\text{ J/m}^{{2}}\), respectively.

Fig. 9
figure 9

Crack propagation speed V evaluation

Full size image
Fig. 10
figure 10

m-convergence of PD predictions with a fixed value of horizon size \(\delta = 0.003{~}\text {m}\) and varying \(\Delta x = 1 \times {10^{ - 3}},{~}0.75 \times {10^{ - 3}},{~}0.6 \times {10^{ - 3}}{~}\text {m}\) a crack growth vs time and b crack propagation speed V vs crack growth distance

Full size image
Fig. 11
figure 11

\(\left( {\delta m} \right) \) - convergence of PD predictions with a fixed value of \(\Delta x = 1 \times {10^{ - 3}}{~}\text {m}\) and varying \(m = 3,{~}4,{~}5\) a crack growth vs time and b crack propagation speed V vs crack growth distance

Full size image

The crack propagation speed is calculated as (see Fig. 9):

$$\begin{aligned} V=\frac{x_{tp} -x_{tp-1} ~}{t_{tp} -t_{tp-1} ~}=\frac{L_{ext} }{\tau _{ext} } \end{aligned}$$
(20)

where \(x_{tp}\,\text{ and }\,x_{tp-1} \) are the crack tip positions at the current time \(t_{tp} \) and the previous time \(t_{tp-1} \). \(L_{ext}\) represents the extension length of the crack propagation during the time interval \(\tau _{ext}\) between \(t_{tp} \) and \(t_{tp-1}\). For the crack propagation speed calculations, the extension length is specified as \(L_{ext} =10~\text{ mm }\), which means that data-dumps are performed every 10 mm of crack tip progression.

A single propagating crack is obtained for all the PD simulations of both convergence studies. Note that the crack growth distance is evaluated from the pre-crack tip. Figure 10 shows the convergence for crack propagation time and speeds of the solutions for a fixed horizon size of \(\delta =3\times 10^{-3}~\text{ m }\) with varying \(\Delta x=1\times 10^{-3},~0.75\times 10^{-3},~0.6\times 10^{-3} \text{ m }\). With an increasing number of material points within the horizon, the local damage is increasing, respectively, such as \(\varphi =0.38\), 0.41 and 0.43 (Fig. 3). The solutions for selected types of \(\Delta x\) show very similar behaviour of the crack propagation and \(\Delta x=1\times 10^{-3}\,\text{ m }\) is chosen for the next convergence study for varying \(m=3,~4,~5\). The results for \(\left( {\delta m} \right) \)—convergence study of crack propagation time and speeds are shown in Fig. 11. It can be noted that there is no significant difference in crack growth distance and crack propagation speeds between the models with different horizon sizes. Therefore, in the following sections, PD numerical models with \(m=3\) and \(\Delta x=1\times 10^{-3}\,\text{ m }\) will be utilised for numerical efficiency.

4.3 Numerical studies of convergence in dynamic crack branching

The \(\delta \) and m-convergence studies are selected to observe the dynamic crack branching. The problem set up is the same as stated in Sect. 4.2 with the increased velocity boundary condition of \(\dot{v}(x,y=W/2,t)=\dot{v}^{*}=3.0~\text {m/s}\) and \(\dot{v}(x,y=-W/2,t)=\dot{v}^{*}=-3.0~\text {m/s}\)

Fig. 12
figure 12

\(\delta \)-convergence of PD crack path predictions with a fixed value of \(m = 3\) and varying horizon size \(\delta \). a \(\delta = 3 \times {10^{ - 3}}~\text {m}\), b close-up for \(\delta = 3 \times {10^{ - 3}}~\text {m}\) c \(\delta = 2.3 \times {10^{ - 3}}~\text {m}\) d close-up for \(\delta = 2.3 \times {10^{ - 3}}~\text {m}\) e \(\delta = 1.8 \times {10^{ - 3}}~\text {m}\) f close-up for \(\delta = 1.8 \times {10^{ - 3}}~\text {m}\)

Full size image

The \(\delta \) convergence study is performed for a fixed \(m=3\) and three different horizon sizes \(\delta =3\times 10^{-3}, 2.3\times 10^{-3}, 1.8\times 10^{-3}\text {m}\) with corresponding uniform grid spacing and total number of material points of \({\Delta }x=1\times 10^{-3} \text {m}~\left( {253,000~nodes} \right) ,{\Delta }x=0.75\times 10^{-3} \text {m}~\left( {447,552~nodes} \right) \), \( {\Delta }x=0.6\times 10^{-3} \text {m}~\left( {698,880~nodes} \right) \). The critical stretch is dependent on the horizon size in Eq. (10), and \( s_{c} \) is changing with the decrease in horizon. Moreover, the same number of material points are interacting within the specified horizon in all the simulations and the local damage is \(\varphi =0.38\). The uniform time step size of \(\Delta t=2\times 10^{-7}~\text{ s }\) is applied and all three PD simulations are stopped at \(t=28\times 10^{-3}~\text {s}\).

Fig. 13
figure 13

Crack propagation speed vs crack growth distance for \(\delta \)-convergence studies with a fixed value of \(m = 3\) and varying horizon size \(\delta \)

Full size image
Fig. 14
figure 14

m-convergence of PD crack path predictions with a fixed value of \(\delta =3\times 10^{-3}~\text {m}\) and varying grid spacing. a \(\Delta x=1\times 10^{-3}~\text {m}, (m=3)\) , b close-up for \(\Delta x=1\times 10^{-3}~\text {m}, (m=3)\) c \(\Delta x=0.75\times 10^{-3}~\text {m}, (m=4)\) d close-up for \(\Delta x=0.75\times 10^{-3}~\text {m}, (m=4)\) e \(\Delta x=0.6\times 10^{-3}~\text {m}, (m=5)\) f close-up for \(\Delta x=0.6\times 10^{-3}~\text {m}, (m=5)\)

Full size image

The crack propagation path for \(\delta \)-convergence study is shown in Fig. 12. For all the horizons the crack branching pattern is almost identical and the crack branches are symmetrical along the x-axes. Evaluating the crack branching in Fig. 12a, c, d the branching angle of 20\(^\circ \) is noted for all three studies. Moreover, looking closer at crack propagation pattern in Fig. 12b, d, f thicker damage is observed before branching, followed by crack bifurcation with thinner damage zones of both branches. The crack thickening can be the roughening of the crack surface noticed during the experimental studies on dynamic crack propagation (Döll 1975; Ramulu and Kobayashi 1985; Park and Chen 2011). With the increased grid spacing the thickening damage zone is getting wider, but overall the damage maps are very similar. The crack propagation speeds for three different horizon sizes are shown in Fig. 13. The crack propagation speeds are evaluated by Eq. (20) and the results are very close for all three studies. Moreover, the crack thickening and bifurcation initiation (vertical lines at the plot) are starting almost at the same distance from the pre-crack and are independent of the horizon size. For this reason, the horizon size of \(\delta =3\times 10^{-3}\) and uniform grid spacing of \({\Delta }x=1\times 10^{-3}~\text {m}\) can be used for further PD simulations.

The m-convergence study is carried out for a fixed \(\delta =3\times 10^{-3}~\text {m}\) and three different models with \({\Delta }x=1\times 10^{-3}~\text {m}~\left( {253,000~nodes} \right) , {\Delta }x=0.75\times 10^{-3}~\text {m}~\left( {447,552~nodes} \right) \), \( {\Delta }x=0.6\times 10^{-3}~\text {m}~\left( {698,880~nodes} \right) \). With increasing number of material points within the horizon, the local damage is increasing, respectively, such as \(\varphi =0.38\), 0.41 and 0.43 (Fig. 3). Figure 14 shows the results of PD predicted crack path at \(t=28\times 10^{-3}~\text {s}\) and Fig. 15 shows the crack propagation speeds for all three models. It can be noticed that increased material points discretization of \({\Delta }x=0.6\times 10^{-3}~\text {m}\) and the horizon size performed in a similar manner compared to the model with \({\Delta }x=1\times 10^{-3}~\text {m}\). All damage maps look very similar, with the thickening area of the propagating crack and its further bifurcation with the angle of 20\(^\circ \). As the crack path and the crack propagation speed at the crack tip are similar among the different solutions, \(m=3\) can be used.

As a result of all convergence studies for COD, crack propagation speed and bifurcation, \(\delta =3{\Delta }x\) with \({\Delta }x=1\times 10^{-3}~\text {m}\) is selected for the following studies to reduce the computational cost, while results of the numerical simulations are not being effected.

Fig. 15
figure 15

Crack propagation speed vs crack growth distance for m-convergence studies with a fixed value of \(\delta = 3 \times {10^{ - 3}}~\text {m}\) and varying grid spacing \({{\Delta }}x\)

Full size image
Fig. 16
figure 16

Pre-cracked rectangular PMMA plate a under velocity boundary conditions and b its spatial discretisation under imposed boundary conditions

Full size image

5 Comparison of peridynamic crack propagation speed, crack opening displacement (COD) and crack bifurcation with experiments

5.1 Crack propagation speed and COD

In this section, crack propagation speed and COD from the PD simulations are compared with those from the experiments (Suzuki et al. 1997). The pre-notched thin rectangular poly(methyl methacrylate) PMMA plate in Fig. 16a is chosen for this case with the following geometric parameters: length \(L=0.22~\text{ m }\), width \(W=0.31~\text{ m }\) and thickness \(h=0.003~\text{ m }\). The plate has a pre-crack at the left side with a size of \(2a=0.07~\text {m}\). The properties of the PMMA material are specified as Young’s modulus of \(E=3.24~\text{ GPa }\), mass density of \(\rho =1200~\text{ kg/m}^3\), Poisson’s ratio of \(\nu =0.35\) (Kalthoff 1987).

Fig. 17
figure 17

Damage maps for PMMA plate when \({K_I} = 1.6~\text {MPa}\surd \text {m}\) under different velocity BCs: a \({\dot{v}^*} = 0.50~\text {m/s}\), c \({\dot{v}^*} = 0.10~\text {m/s}\), e \({\dot{v}^*} = 0.02~\text {m/s}\), and when \({K_I} = 1.0~\text {MPa}\surd \text {m}\): b \({\dot{v}^*} = 0.50~\text {m/s}\), d \({\dot{v}^*} = 0.10~\text {m/s}\), f \({\dot{v}^*} = 0.02~\text {m/s}\)

Full size image

Several methods are proposed to compute the dynamic stress intensity factor (SIF) and their overview is presented by Aliabadi and Rooke (1991). For the current study two methods are selected to evaluate the SIF for the crack opening mode. Firstly, the dynamic stress intensity factor is evaluated by using the formulation of Irwin (1957) which links SIF and COD presented in Eq. (21):

$$\begin{aligned} K_{I} =\sqrt{\frac{2\pi }{r}} \frac{E}{8}d_{r} \end{aligned}$$
(21)

where r is the distance from the crack tip and \(d_{r} \) is the COD or a relative displacement between two corresponding points on opposite sides of the crack. The values of COD and r are identified from the presented experimental data (Suzuki et al. 1997) and SIF of \(K_{I} =1.0~\text {MPa}\surd \text {m}\) is evaluated. The second method is introduced by Freund (1998) where the relation is established between the stress intensity factor and energy release rate \(G_{c} \) for the dynamic crack growth:

$$\begin{aligned} G_{c} =\frac{1-\nu ^{2}}{E}A_{I} \left( V \right) K_{I}^{2} \end{aligned}$$
(22)

and the SIF can be expressed in the following form:

$$\begin{aligned} K_{I} \left( V \right) =\sqrt{\frac{\pi }{8 r}} \frac{G}{1-\nu _{1} }\frac{1}{L\left( V \right) }d_{r} \end{aligned}$$
(23)

where \(\nu \) and E are the Poisson’s ratio and Young’s modulus, G is the modulus of rigidity, \(\nu _{1} =\nu / \left( {1+\nu } \right) \) for the plane stress condition, \(A_{I} \left( V \right) \) and \(L\left( V \right) \) are the functions of crack speed V. Suzuki et al. (1997) used Eq. (23) to evaluate the dynamic SIF for the propagating crack and identified the SIF of \(K_{I} =1.6~\text {MPa}\surd \text {m}\) at crack propagation speed of \(V=180~\text {m/s}\).

It is not easy to predict the crack behaviour since the propagating crack can change its trajectory, branch or curve. The crack propagation behaviour depends on the applied BC or the test method during experiments (Ramulu and Kobayashi 1985). To have a single propagating crack, a carefully controlled BC should be applied. If impulsive loading is applied, it can lead to an increase of crack propagation speed as well as single or multiple branching (Bowden et al. 1967). For the current section, low velocities are applied as the tension loading, and the following velocity BCs are enforced on the boundary edges at \(\text{ y }=W/2\) and \(\text{ y }=-W/2\): \(\dot{v}^*= 0.50~\text {m/s}\), \(\dot{v}^*= 0.10~\text {m/s}\) and \(\dot{v}^*= 0.02~\text {m/s}\). The plate is loaded symmetrically by applying velocity constraints in fictitious boundary layer \(R_{f}\) (Fig. 16b) in the y-direction by using Eqs. (16–19).

The peridynamic models are discretised with 69,520 material points with a uniform spacing between them \(\Delta x= 0.001\) m and horizon size of \(\delta =3.015\Delta ~x\). A uniform time step size of \(\Delta t=2 \times 10^{-7}~\text{ s }\) is used. The critical stretch is evaluated by Eq. (10) for specified SIF of \(K_{I} =1.0~\text {MPa}\surd \text {m}\) as \(s_{c} =0.0067\) and for \(K_{I} =1.6~\text {MPa}\surd \text {m}\) as \( s_{c} =0.0107\). Critical elongation \(s_{c} \) is constant for propagating crack.

With the applied velocity BCs and both SIFs, self-similar crack propagation patterns are observed in Fig. 17. The lower velocities lead to delays in crack propagation as shown in Fig. 18, but the pattern of crack propagation is similar for different velocity BCs. The crack propagation speeds in Fig. 19a with different velocity BCs demonstrate that higher velocity BCs lead to increased crack propagation speeds. For example, for the models with \(K_{I} =1.6~\text {MPa}\surd \text {m}\) and the applied \(\dot{{v}}^{*}=0.5~\text{ m/s }\) the maximum crack propagation speed reaches \(V=560~\text{ m/s }\) and for \(\dot{v}^{*} = 0.02~\text {m/s} \) the maximum crack speeds are around \(V=370~\text {m/s}\). This proves that the crack propagation behaviour is force dependant (Suzuki et al. 1997) and increase in tension loading leads to higher crack propagation speeds. The data is presented for every \(L_{ext} =10~\text {mm}\) when the location of the crack tip is extended each 10 mm starting from the pre-existing crack.

Fig. 18
figure 18

Crack growth distance for different velocity BC and SIF

Full size image
Fig. 19
figure 19

Numerical results for PMMA plate under different velocity BCs and SIF. a Crack propagation speed vs. crack growth distance; b The ratio of numerically computed speed to the Rayleigh wave speed

Full size image
Table 2 Ratios of experimental fracture speeds and numerically computed at 25 mm from the pre-existing crack
Full size table

The numerical crack propagation speed is compared to the Rayleigh wave speed in Fig. 19b. The approximate expression for the Rayleigh wave speed \(c_{R} \) (Freund 1998) is:

$$\begin{aligned} \frac{c_{R} }{c_{2} }=\frac{0.862+1.14\nu }{1+\nu } \end{aligned}$$
(24)

where \(\nu \) is the Poisson ratio. In terms of shear modulus G and material density \(\rho \), the speed of shear waves is defined as:

$$\begin{aligned} c_{2} =\sqrt{\frac{G}{\rho }} \end{aligned}$$
(25)

The PD numerical velocities are normalised by the Rayleigh wave speed \(c_{R} \) of the material which is \(c_{R} \approx 934~\text {m/s}\) for the PMMA material.

For the applied velocity BC less than \(\dot{v}^{*}= 0.50~\text {m/s}\), fractions of 0.5 and lower of the Rayleigh wave speed are observed in Fig. 19b and crack propagation is stable in Fig. 17cf. However, with the increased velocity BC of \(\dot{{v}}^{*}=0.50~\text {m/s}\) and SIF of \(K_{I} =1.0~\text {MPa}\surd \text {m}\), the crack propagation speed reaches 60% of the Rayleigh wave speed that occurs at the location of the crack tip \(x_{tp} \ge 0.08~\text {m} \) , and thickening of the crack can be noticed (Fig. 17a).

During the experiments by Suzuki et al. (1997), PMMA specimen is under tensile loading and high-speed holographic microscopy is used to evaluate the results in the observation area. It was specified that the observation area is 25 mm away from the pre-existing crack. In the PD model, the lower velocity BC of \(\dot{v}^{*}= 0.02~\text {m/s}\) resulted in the crack propagation speed around \(V=190~\text {m/s}\) in the observation area, which is within the range of experimentally measured value of \(V= {186 \pm 19}~\text{ m/s }\). The other BC showed higher crack speeds \(V>250~\text {m/s}\) at the crack tip position \(x_{tp} =25.5\times 10^{-3}~\text {m}\), as shown in Fig. 19a. Table 2 presents the numerical crack propagation speeds in the observation area.

The COD is analysed in Fig. 20 and compared to the experiments (Suzuki et al. 1997) in the observation area and within the range of \(1<\text{ r }< 12~\text {mm}\). According to the theoretical results of the linear elastic fracture mechanics (Freund 1998), the CODs are proportional to the square root of the distance r from the crack tip.

$$\begin{aligned} \text{ COD } = \sqrt{r} \end{aligned}$$
(26)

Figure 20b presents the numerical results for three different loading conditions and two SIF. The straight lines are indicating the calculated relation between the COD and r, and it can be noticed from that the PD numerical model results are in good agreement with the theory.

The SIF evaluated from the Eq. (21) with the applied \(\dot{v}^{*}= 0.02~\text {m/s}\) showed very good agreement with the experimental results in the crack propagation speed and the COD in the observation area.

The use of two different SIF showed that for the low velocity BC with the fracture initiation starting later then \(t_{in} >1.5\times 10^{-3}~\text {s}\) the crack propagation speeds are almost the same. On the other hand, the analysis with the higher loading of \(\dot{{v}}^{*}=0.50~\text {m/s}\) showed different ranges of crack propagation speeds. Moreover, the use of non-dependent SIF on the loading rate does not represent the COD accurately as the higher fracture energy is required for the higher tension loads. It can be noted from Fig. 20b that the COD is almost the same for different boundary conditions. The experimental data (Ravi-Chandar and Knauss 1984b) on dynamic fracture showed that the high loading rate significantly increases the SIF at initiation stage. This means that critical SIF has to be identified for dynamic fracture initiation and as the strain rate at the crack tip is dependent on internal load the critical crack opening displacement can be a possible criterion for fracture initiation. To implement the critical COD is a plan for a future work.

Fig. 20
figure 20

The COD when crack propagation speed is \(V = 190~{\text {m/s}}\) at the observation area and velocity BC is \({\dot{v}^*} = 25 \times {10^{ - 3}}~{\text {m/s}}\): a Deformation map of the propagating crack at \({x_{tp}} = 25.5~{\text {mm}}\). Displacements are magnified by 100. b Experimental (Suzuki et al. 1997) and PD results of the COD

Full size image

5.2 Crack propagation speed and crack bifurcation

In this section, a comparison between PD simulations and experimental tests (Suzuki and Sakaue 2004) is carried out. In particular, the crack propagation speeds, and bifurcation angles are evaluated in order to assess the accuracy of the numerical model with the constant value of critical fracture energy. The other focus is on the response of the structure to the small changes in tensile loads.

Theoretical studies (Freund 1998) have proposed to introduce the limiting velocity of the crack (Eq. 24), where the crack accelerates until arriving to the Rayleigh wave speed \(c_{R} \). Experimental studies indicated variations of the critical velocities for different brittle materials. It was observed (Yoffe 1951) that crack instabilities occur at \(V\sim 0.6\, c_{R} \) and similar crack branching behaviour was noticed in different numerical (Abraham et al. 1994) and experimental studies (Fineberg et al. 1992; Sharon et al. 1995). Cotterell (1965) observed that the branching velocities for PMMA are about \(V\sim 0.78\,c_{R} \). On the other hand, Ravi-Chandar and Knauss (1984c) determined the critical velocities of up to \(V\sim 0.9\,c_{R} \) with non-steady crack propagation. Multiple experiments on brittle fracture showed the occurrence of the crack instabilities with different fracture patterns. The authors (Cotterell 1965; Fineberg et al. 1992; Suzuki and Sakaue 2004) observed micro-branching phenomena with variation of branching angles of 10–15\(^\circ \) whereas (Sharon et al. 1995) showed the macro-branching angles of 30\(^\circ \). Similar microscopic branches were observed in other brittle materials like Homalite-100 (Ravi-Chandar and Knauss 1984a) and polystyrene (Hull 1970).

When the crack propagation speed is reaching the critical velocity, the crack branches into two or multiple micro- and macro-cracks. However, the aforementioned experiments indicated a big variation of critical velocity criteria, which could be affected by the size of the samples, as well as the dynamic loading. The current study is showing the effect of the different velocity BC on crack behaviour and the boundaries of the plate should not have effect on fracture process.

Geometrical and material properties are the same as in the previous case with the SIF of \(K_{I} =1.3~\text {MPa}\surd \text {m}\). However, an impulsive loading is applied to obtain fast crack propagation and further bifurcation. To investigate the crack response to the tensile loads, multiple cases of the velocity boundary conditions are selected, starting with \(\dot{{v}}^{*}=1.00~\text {m/s}\) and increased by 0.2 m/s. The velocity is applied on the boundary edges at \(\text{ y }=W/2\) and \(\text{ y }=-W/2\) ranging from \(\dot{{v}}^{*}=1.00~\text {m/s}\) to \(\dot{v}^{*}= 1.00~\text {m/s}\) to \(\dot{v}^{*}= 6.8~\text {m/s}\). The plate is loaded symmetrically by applying velocity constraints in fictitious boundary layer \(R_{f} \) (Fig. 16b) in the y-direction by using Eqs. (16–19).

The peridynamic models are discretised with 275,440 material points with a uniform spacing between them \({\Delta }x=5\times 10^{-4}\) m and horizon size of \(\delta =3.015\Delta x\). A uniform time step size of \(\Delta t=2\times 10^{-7}~\text{ s }\) is used.

Based on the damage plots given in Fig. 21 under different velocity BCs, it is remarkable to see the dependency of the crack propagation behaviour on the applied loading conditions. As the intensity of the loading increases the thickening of the damage zone is observed, which is followed by further branching (Fig. 21 , from \(\dot{v}^{*}=1.4~\text {m/s}\) to \(\dot{v}^{*}=2~\text {m/s}\)) or fish-bone pattern with multiple micro-branches or/and macro-branches (Fig. 21, from \(\dot{v}^{*}=2.2~\text {m/s}\)). Similar behaviour of crack propagation was observed by Bobaru and Zhang (2015) for brittle materials for Soda-lime glass and Homalite 100 under velocity boundary conditions. It was also observed that the increase of the loading intensity speeds up the crack propagation and branching. Figure 21 presents the damage maps of all simulations. Note that the negative x-axis indicates the pre-crack location.

Firstly, to evaluate the crack propagation behaviour of a single crack bifurcation, the comparison is made with the brittle fracture experiments on PMMA performed by Suzuki and Sakaue (2004) where the fracture speeds were evaluated within 5 mm before and after bifurcation as well as the bifurcation angle. It was mentioned that the mean crack speed before the bifurcation is \(V=688\pm 45~\text {m/s}\) which drops by 42 m/s after the bifurcation with the mean crack speed of \(V=647\pm 35~\text {m/s}\) and the bifurcation angle of 15\(^\circ \).

Fig. 21
figure 21

Damage maps for PMMA plate under different velocities BC. The applied velocities are specified on top of each figure

Full size image
Fig. 22
figure 22

Crack propagation speeds and the ratios of numerically computed speed to the Rayleigh wave speed for PMMA plate under velocity BCs of: a \({\dot{v}^*} = 1.4~\text {m/s}\) and \({\dot{v}^*} = 2.0~\text {m/s}\) b \({\dot{v}^*} = 2.4~\text {m/s}\) and \({\dot{v}^*} = 3.2~\text {m/s}\) and c \({\dot{v}^*} = 5.4~\text {m/s}\)

Full size image

Based on the crack behaviour under the applied loading BC between \(\dot{{v}}^{*}=1.40~\text {m/s}\) and \(\dot{{v}}^{*}=2.0~\text {m/s}\) when the crack is bifurcating, it can be noted that the crack propagation speeds from numerical PD model are in the range of the fracture speeds from the experimental results (Suzuki and Sakaue 2004). The crack propagation speeds under \(\dot{{v}}^{*}=1.40~\text {m/s}\) and \(\dot{{v}}^{*}=2.0~\text {m/s}\) velocity loading conditions are given in Fig. 22a. Under specified loading conditions, the thickening of the damaged area is noticed before the bifurcation with the mean crack propagation speed of \(V=500\pm 5~\text {m/s}\). The bifurcation occurs when the mean crack propagation speed is \(V=560 \pm 10~\text {m/s}\). The data in Fig. 22 is presented every \(L_{ext} =5~\text {mm}\), when the location of the crack tip is extended each 5 mm starting from the pre-existing crack. The predicted crack branching angles around 16\(^\circ \)–20\(^\circ \) are noted for all four loading boundary conditions between \(\dot{{v}}^{*}=1.40~\text {m/s}\) and \(\dot{{v}}^{*}=2.0~\text {m/s}\). The predicted crack speeds and crack bifurcation angle are quite close to the experimental observations.

Based on the experimental studies, a large decrease of crack propagation speeds relative to the single crack speeds is observed. Döll (1975) and Ramulu and Kobayashi (1985) stated that before the bifurcation occurs the crack propagation speed may accelerate and after bifurcation it drops by 5–10%. The recent experiments on Soda-lime glass by Sundaram and Tippur (2018) showed the same pattern of the crack propagation behaviour with a drop of crack propagation speed by 30% prior to bifurcation and followed by a significant increase at branching and a fast drop by 30% after the bifurcation. Numerical studies, by means of peridynamics (Ha and Bobaru 2010; Bobaru and Zhang 2015), showed a similar trend of the fracture speeds in the bifurcation zone. Evaluating the crack bifurcation of PMMA in Fig. 22 from the numerical PD model, the crack propagation speed decreases when the thickening occurs and increases rapidly before bifurcation following by a drop of 6% after bifurcation for both loading conditions. Moreover, two branches propagate with higher crack speeds than a single crack. The results for the crack propagation speed and crack growth distance after the bifurcation are analysed for the upper crack branch.

Secondly, the dynamic stretch of the plate under higher velocity BC in Fig. 21 showed formation of multiple micro-branches. It can be noticed that as the velocity of the crack is increasing, the length of the branches as well as their number is increasing. The branching angles are varying, and in most of the cases, lower crack speeds result in smaller angles. For example, the PD damage plot with the velocity BC increase of \(\dot{v}^{*}=2.4~\text {m/s}\) resulted in first crack branching of around 30\(^\circ \) and at \(V\sim 0.57\,c_{R} \) (Fig. 22b), followed by longer branch of around the same angle of 30\(^\circ \), but the second branch initiated at a higher crack speed of \(V\sim 0.76\,c_{R} \) with the distance between two branches is 0.03 m. On the other hand, the velocity of \(\dot{v}^{*}=3.2~\text {m/s}\) resulted in three branches (Fig. 22b): the first one at the crack tip location of \(x_{tp} =0.058~\text {m}\) with branching angle of 30\(^\circ \) at \(V\sim 0.74\,c_{R} \) and the other two branches with increasing branching angles by 5\(^\circ \) at \(V\sim 0.75\,c_{R} ~\left( {x_{tp} =0.07~m} \right) ,~\) and 10\(^\circ \) at \(V\sim 0.77\,c_{R} ~\left( {x_{tp} =0.085~m} \right) .\) The trend of higher branching angle with the longer branches can be noticed in all simulations as well as the occurrence of micro-branches with 12\(^\circ \) angles followed by the long crack bifurcation as shown in Fig. 22c. All the results of crack propagation are having the same trend of the crack bifurcation, starting at \(V\sim 0.57\,c_{R} \) and upper with further drop and after the recovery. The variation in branching patterns and angles is dependent on fluctuations in crack velocity and when the velocity is reaching the critical value, crack is branching.

The performed PD simulations showed the dynamic instability of the propagating crack. It can be seen that the branching is a function of the crack velocity and the branching is not observed below the critical velocity. The experiments performed by Sharon et al. (1995) analysed the effect of the crack velocity on occurrence of branching which shows that the increase of velocity is the result of the micro-branching instability. The following characteristic can be explained as the energy release from the potential energy with the increased crack speed resulting in creating of new crack branches. While the energy is distributing over the new cracks, the crack propagation velocity is decreasing. Moreover, the PD study showed the relation between the branch initiation and the branching angles and lengths as the higher crack propagation speeds bring wider and longer crack bifurcations. On the other hand, the constant critical elongation parameter was used in the presented numerical simulations which is simplified and not dependent on the loading condition and crack propagation speeds. Having this in mind, additional studies have to be performed.

6 Conclusion

This study presents an in-depth investigation of critical stretch based failure criterion in ordinary state-based peridynamics for both static and dynamic fracture problems. Seven different cases were considered to investigate the effect of the failure parameter on the dilatation term and force between material points. Based on crack opening displacement (COD) results obtained from both peridynamics and finite element analysis under static loading conditions, it was found that one the seven cases provide the best agreement between the two different approaches. This conclusion was further confirmed by performing a convergence study in terms of horizon size and spacing between material points. The results further demonstrated that ordinary state based peridynamic model using a critical stretch based failure criterion captures the fracture phenomena in brittle materials, such as PMMA material, under dynamic loading conditions including both crack propagation and crack branching. COD achieved from PD simulations agrees with the theory of the linear elastic fracture mechanics and a close match was obtained with experimental results. It was also observed that crack behaviour is loaddependent, and crack patterns change by increasing the magnitude of loading. The comparison of PD simulations with experiments showed remarkably close agreement of the crack propagation speeds, with 6% difference, and captured similar patterns of the crack behaviour. PD model represents the crack propagation accurately with the increase of crack propagation speeds which leads to further branching. Moreover, in both experimental literature and PD model, the speed of crack propagation reduces when thickening occurs, and after a sharp increase of the speed before bifurcation follows a drop in the crack speed after branching, and further recovery occurs with the rise of the crack propagation speeds in both branches. Finally, it can be concluded that the ordinary state-based PD model using the critical stretch based failure criterion can capture the correct COD and crack propagation behaviour for both static and dynamic loading conditions. For the future work, the critical COD will be introduced in the dynamic ordinary state-based PD model to address the velocity dependent fracture energy.