Selling mode choice and information sharing in an online tourism supply chain under channel competition

Abstract

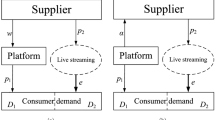
This paper examines the selling mode choice and information sharing in an online tourism supply chain with an online travel platform (OTP) that holds private demand information and a tourism service provider under demand uncertainty. By developing a game-theoretic model, we examine the OTP’s information sharing incentive under different selling modes (i.e. agency mode, reselling mode or hybrid mode), then study the OTP’s selling mode preference. Our analysis shows that the OTP may share information even if the double marginalization of information sharing exists under the hybrid mode. The OTP’s selling mode choice changes in response to the channel competition intensity and the commission rate, and is also critically affected by the demand fluctuation and forecast accuracy under certain conditions. In particular, although the channel competition is intense under the hybrid mode, the OTP may choose the hybrid mode rather than the agency/reselling mode without channel competition.

Appendix

Proof of Theorem 1

Under $AN$ strategy, as $\partial^{2} E[\pi_{TSP}^{AN} ]/\partial^{2} p_{A}^{AN} = - 2 + 2\lambda < 0$, $E[\pi_{TSP}^{AN} ]$ is concave in $p_{A}^{AN}$. Then, by solving $\partial E[\pi_{TSP}^{AN} ]/\partial p_{A}^{AN} = (1 - \lambda )(\overline{a} - 2p_{A}^{AN} ) = 0$, we get $p_{A}^{AN} = \overline{a}/2$. Similarly, under $AI$ strategy, we derive $p_{A}^{AI} = E[a\left| {Y]} \right./2$. Finally, substituting optimal prices into Eqs. (6), (7) and (8), we get $E[\pi_{TSP}^{AX} ]$ and $E[\pi_{OTP}^{AX} ]$.

Proof of Theorem 2

Under $RN$ strategy, $E[\pi_{OTP}^{RN} ]$ is concave in $p_{R}^{RN}$ since $\partial^{2} E[\pi_{OTP}^{RN} ]/\partial^{2} p_{R}^{RN} = - 2 < 0$. Then, by solving $\partial E[\pi_{OTP}^{RN} ]/\partial p_{R}^{RN} = E[a\left| {Y]} \right. - 2p_{R}^{RN} + w^{RN} = 0$, we can easily get $p_{R}^{RN} (w^{RN} ) = (E[a\left| {Y]} \right. + w^{RN} )/2$. Substituting $p_{R}^{RN} (w^{RN} )$ into the TSP’s expected profits function, we obtain $E[\pi_{TSP}^{RN} ] = w^{RN} (E[a] - w^{RN} )/2$. From $\partial^{2} E[\pi_{TSP}^{RN} ]/\partial^{2} w^{RN} = - 1 < 0$, we know that $E[\pi_{TSP}^{RN} ]$ is concave in $w^{RN}$. Accordingly, we get $w^{RN} = \overline{a}/2$ based on the first order condition $\partial E[\pi_{TSP}^{RN} ]/\partial w^{RN} = (\overline{a} - 2w^{RN} )/2 = 0$. Substituting $w^{RN} = \overline{a}/2$ into $p_{R}^{RN} (w^{RN} )$, we derive $p_{R}^{RN} = (\overline{a} + 2E[a\left| {Y]} \right.)/4$. Following the similar argument, we get the optimal pricings under $RI$ strategy. Finally, substituting optimal pricings into Eqs. (9), (10) and (11), we get $E[\pi_{TSP}^{RX} ]$ and $E[\pi_{OTP}^{RX} ]$.

Proof of Theorem 3

Under $CN$ strategy, since $\partial^{2} E[\pi_{OTP}^{CN} ]/\partial^{2} p_{R}^{CN} = - 2/(1 + \gamma )(1 - \gamma ) < 0$, we get that $E[\pi_{OTP}^{CN} ]$ is concave in $p_{R}^{CN}$. Then, we derive $p_{R}^{CN} (p_{A}^{CN} ,w^{CN} ) = ((1 - \gamma )E[a\left| {Y]} \right. + (1 + \lambda )\gamma p_{A}^{CN} + w^{CN} )/2$. Substituting it into Eq. (12), we find that $E[\pi_{TSP}^{CN} ]$ is joint concave in $p_{A}^{CN}$ and $w^{CN}$. Hence, $p_{A}^{CN} = \overline{a}/2$ and $w^{CN} = (1 - \lambda \gamma )\overline{a}/2$ are derived based on the first order condition. Substituting $p_{A}^{CN} = \overline{a}/2$ and $w^{CN} = (1 - \lambda \gamma )\overline{a}/2$ into $p_{R}^{CN} (p_{A}^{CN} ,w^{CN} )$, we obtain $p_{R}^{CN} = ((1 + \gamma )\overline{a} + 2(1 - \gamma )E[a\left| {Y]} \right.)/4$. Similarly, we can easily obtain the optimal pricings under $CI$ strategy. Finally, substituting optimal pricings into Eqs. (12), (13) and (14), we get $E[\pi_{TSP}^{CX} ]$ and $E[\pi_{OTP}^{CX} ]$.

Proof of Proposition 1

Under the agency mode, we have $V_{OTP}^{AI} = \lambda \rho^{2} \Delta^{2} \overline{a}^{2} /4 > 0$ from Theorem 1.

Under the reselling mode, we get $V_{OTP}^{RI} = - 3\rho^{2} \Delta^{2} \overline{a}^{2} /16 < 0$ from Theorem 2.

Under the hybird mode, the OTP’s information shairng profits are $V_{OTP}^{CI} = (3(\gamma - 1) + 4\lambda (1 + \gamma ))\rho^{2} \Delta^{2} \overline{a}^{2} /16(1 + \gamma )$. There is a unique $\lambda_{1}$ making $3(\gamma - 1) + 4\lambda_{1} (1 + \gamma ) = 0$, and then $V_{OTP}^{CI} < 0$ when $0 < \lambda < \lambda_{1}$; $V_{OTP}^{CI} > 0$ when $\lambda_{1} < \lambda < 1$.

Proof of Proposition 2

Firstly, the agency mode are compared with the hybrid mode. From Proposition 1, we know that when $0 < \lambda < \lambda_{1}$, we only need to compare $AI$ and $CN$ strategies. On the one hand, as for the risk-free profits, we have $\overline{\pi }_{OTP}^{C} - \overline{\pi }_{OTP}^{A} = (1 - \gamma )\overline{a}^{2} /16(1 + \gamma ) > 0$. As for risky profits, we get $F_{OTP}^{C} - V_{OTP}^{AI} = (1 - \gamma - \lambda - \lambda \gamma )\rho^{2} \Delta^{2} \overline{a}^{2} /4(1 + \gamma )$. It is obvious that $F_{OTP}^{C} - V_{OTP}^{AI} > 0$ when $0 < \lambda < \lambda_{1}$. As a result, when $0 < \lambda < \lambda_{1}$, $CN$ strategy always dominates $AI$ strategy. When $\lambda_{1} < \lambda < 1$, we need to compare $AI$ and $CI$ strategies. We can easily get that $\overline{\pi }_{OTP}^{C} - \overline{\pi }_{OTP}^{A} = (1 - \gamma )\overline{a}^{2} /16(1 + \gamma ) > 0$ and $F_{OTP}^{C} + V_{OTP}^{CI} - V_{OTP}^{AI} = (1 - \gamma )\rho^{2} \Delta^{2} \overline{a}^{2} /16(1 + \gamma ) > 0$. Hence, $CI$ strategy also dominates $AI$ strategy when $\lambda_{1} < \lambda < 1$. Combining the above comparison results, we derive that the hybrid mode is more profitable than the agency mode.

Next, we compare the reselling mode and the hybrid mode. From Proposition 1, when $0 < \lambda < \lambda_{1}$, we only need to compare $WN$ and $CN$ strategies. For the risk-free profits, we have $\overline{\pi }_{OTP}^{C} - \overline{\pi }_{OTP}^{R} = (2\lambda - \gamma + 2\lambda \gamma )\overline{a}^{2} /8(1 + \gamma )$. Its sign depends on the sign of $2\lambda - \gamma + 2\lambda \gamma$. There is a unique $\lambda_{2} = \gamma /2(1 + \gamma )$, which satisfies $2\lambda - \gamma + 2\lambda \gamma = 0$, such that $\overline{\pi }_{OTP}^{C} < \overline{\pi }_{OTP}^{R}$ when $0 < \lambda < \min \{ \lambda_{1} ,\lambda_{2} \}$; $\overline{\pi }_{OTP}^{C} > \overline{\pi }_{OTP}^{R}$ when $\lambda_{2} < \lambda < \lambda_{1}$. For the risky profits, we get $F_{OTP}^{C} - F_{OTP}^{R} = - \gamma \rho^{2} \Delta^{2} \overline{a}^{2} /2(1 + \gamma ) < 0$. Based on the above comparison results, we find that when $0 < \lambda < \min \{ \lambda_{1} ,\lambda_{2} \}$, $\overline{\pi }_{OTP}^{C} < \overline{\pi }_{OTP}^{R}$ and $F_{OTP}^{C} < F_{OTP}^{R}$. Therefore, $RN$ strategy dominates $CN$ strategy when $0 < \lambda < \min \{ \lambda_{1} ,\lambda_{2} \}$. In addition, we also obtain that $\overline{\pi }_{OTP}^{C} > \overline{\pi }_{OTP}^{R}$ and $F_{OTP}^{C} < F_{OTP}^{R}$ when $\lambda_{2} < \lambda < \lambda_{1}$, and thus the forecast variability affects choices in this case. We have $\partial \left( {E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ]} \right)/\partial (\rho \Delta )^{2} < 0$, and $\max \left( {E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ]} \right) > 0$ when $(\rho \Delta )^{2} = 0$. When $(\rho \Delta )^{2} = 1$, there exists a unique $\lambda_{3}$, which makes $\min \left( {E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ]} \right) = 0$. Then, when $\lambda_{3} < \lambda < \lambda_{1}$ (i.e. in R2), $\min \left( {E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ]} \right) > 0$, and $CN$ strategy is optimal. When $\lambda_{2} < \lambda < \min \{ \lambda_{1} ,\lambda_{3} \}$ (i.e. in R3), $\min \left( {E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ]} \right) < 0$. Obviously, there exists a unique $\tau_{1}$, which makes $E[\pi_{OTP}^{CN} ] - E[\pi_{OTP}^{RN} ] = 0$, such that $CN$ strategy is optimal when $0 < \rho \Delta < \tau_{1}$; otherwise, when $\tau_{1} < \rho \Delta < 1$, $RN$ strategy is optimal.

When $\lambda_{1} < \lambda < 1$, we need to compare $RN$ and $CI$ strategies. For the risk-free profits, we have $\overline{\pi }_{OTP}^{C} - \overline{\pi }_{OTP}^{R} = (2\lambda - \gamma + 2\lambda \gamma )\overline{a}^{2} /8(1 + \gamma )$. Its sign is the same as the previous case when $0 < \lambda < \lambda_{1}$. Hence, when $\lambda_{1} < \lambda < \lambda_{2}$, we have $\overline{\pi }_{OTP}^{C} < \overline{\pi }_{OTP}^{R}$; when $\max \{ \lambda_{1} ,\lambda_{2} \} < \lambda < 1$, we get $\overline{\pi }_{OTP}^{C} > \overline{\pi }_{OTP}^{R}$. As for the risky profits, we get $F_{OTP}^{C} + V_{OTP}^{CI} - F_{OTP}^{R} = ((4\gamma + 4)\lambda - 5\gamma - 3)\rho^{2} \Delta^{2} \overline{a}^{2} /16(1 + \gamma )$. Its sign depends on the sign of $(4\gamma + 4)\lambda - 5\gamma - 3$. There exists a unique $\overline{\lambda } = (3 + 5\gamma )/4(1 + \gamma )$ making $F_{OTP}^{C} + V_{OTP}^{CI} - F_{OTP}^{R} = 0$. Then, when $\lambda_{1} < \lambda < \overline{\lambda }$, we have $F_{OTP}^{C} + V_{OTP}^{CI} < F_{OTP}^{R}$; when $\overline{\lambda } < \lambda < 1$, we get $F_{OTP}^{C} + V_{OTP}^{CI} > F_{OTP}^{R}$. Based on the above comparison results, we find that when $\lambda_{1} < \lambda < \lambda_{2}$, we have $\overline{\pi }_{OTP}^{C} < \overline{\pi }_{OTP}^{R}$ and $F_{OTP}^{C} + V_{OTP}^{CI} < F_{OTP}^{R}$, and thus $RN$ is the optimal strategy for the OTP. When $\overline{\lambda } < \lambda < 1$, we get $\overline{\pi }_{OTP}^{C} > \overline{\pi }_{OTP}^{R}$ and $F_{OTP}^{C} + V_{OTP}^{CI} > F_{OTP}^{R}$; therefore $CI$ is the optimal strategy for the OTP. However, when $\max \{ \lambda_{1} ,\lambda_{2} \} < \lambda < \overline{\lambda }$, we have $\overline{\pi }_{OTP}^{C} > \overline{\pi }_{OTP}^{R}$ and $F_{OTP}^{C} + V_{OTP}^{CI} < F_{OTP}^{R}$, and thus the forecast variability affects selection in this case. Then, we have $\partial (E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ])/\partial (\rho \Delta )^{2} < 0$, and when $(\rho \Delta )^{2} = 0$, we have $\max \left( {E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ]} \right) > 0$. When $(\rho \Delta )^{2} = 1$, there is a unique $\lambda_{4} = (3 + 7\gamma )/8(1 + \gamma )$, which satisfies $\min \left( {E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ]} \right) = 0$. Accordingly, when $\lambda_{4} < \lambda < \overline{\lambda }$, we get $\min \left( {E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ]} \right) > 0$, and the OTP prefers $CI$ strategy. When $\max \{ \lambda_{1} ,\lambda_{2} \} < \lambda < \lambda_{4}$(i.e. in R4), we have $\min \left( {E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ]} \right) < 0$. It indicates that in R4, there is a unique $\tau_{2}$, which satisfies $E[\pi_{OTP}^{CI} ] - E[\pi_{OTP}^{RN} ] = 0$. Therefore, in R4, when $0 < \rho \Delta < \tau_{2}$, $CI$ is the optimal strategy; when $\tau_{2} < \rho \Delta < 1$, $RN$ is the optimal strategy.

Proof of Proposition 3

Firstly, we derive the TSP’s optimal strategy. For the information sharing profits, we have $V_{TSP}^{AI} = (1 - \lambda )\rho^{2} \Delta^{2} \overline{a}^{2} /4 > 0$, $V_{TSP}^{RI} = \rho^{2} \Delta^{2} \overline{a}^{2} /8 > 0$ and $V_{TSP}^{CI} = (3 + \gamma - 2\lambda (1 + \gamma ))\rho^{2} \Delta^{2} \overline{a}^{2} /8(1 + \gamma ) > 0$. That is, regardless of the selling mode, the TSP always prefers information sharing. Next, we analyze the TSP’s optimal selling mode. Comparing $AI$ and $CI$ strategies, we get $E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{AI} ] = (1 - \gamma )(1 + \rho^{2} \Delta^{2} )\overline{a}^{2} /8(1 + \gamma ) > 0$, and thus $CI$ strategy dominates $AI$ strategy. Next, comparing the TSP’s expected profits under $RI$ and $CI$ strategies, we get $E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RI} ] = (1 - (1 + \gamma )\lambda )(1 + \rho^{2} \Delta^{2} )\overline{a}^{2} /4(1 + \gamma )$. Its sign depends on the sign of $1 - (1 + \gamma )\lambda$. Therefore, there exists a unique $\lambda_{5} = 1/(1 + \gamma )$, which satisfies $1 - (1 + \gamma )\lambda { = }0$. When $0 < \lambda < \lambda_{5}$, we have $E[\pi_{TSP}^{CI} ] > E[\pi_{TSP}^{RI} ]$, and thus $CI$ strategy is optimal; when $\lambda_{5} < \lambda < 1$, we get $E[\pi_{TSP}^{CI} ] < E[\pi_{TSP}^{RI} ]$, and thus $RI$ strategy is optimal.

For the TSC, we have $V_{TSC}^{AI} = \rho^{2} \Delta^{2} \overline{a}^{2} /4 > 0$, $V_{TSC}^{RI} = - \rho^{2} \Delta^{2} \overline{a}^{2} /16 < 0$ and $V_{TSC}^{CI} = (3 + 5\gamma )\rho^{2} \Delta^{2} \overline{a}^{2} /16(1 + \gamma ) > 0$. As for the optimal selling mode, comparing $AI$ and $CI$ strategies, we get $E[\pi_{TSC}^{CI} ] - E[\pi_{TSC}^{AI} ] = 3(1 - \gamma )(1 + \rho^{2} \Delta^{2} )\overline{a}^{2} /16(1 + \gamma ) > 0$, so $CI$ strategy dominates $AI$ strategy. Then, we compare $RN$ and $CI$ strategies. For the risk-free profits, we have $\overline{\pi }_{TSC}^{C} - \overline{\pi }_{TSC}^{R} = (2 - \gamma )\overline{a}^{2} /8(1 + \gamma ) > 0$. For the risky profits, we get $F_{TSC}^{C} + V_{TSC}^{CI} - F_{TSC}^{R} = 3(1 - \gamma )\rho^{2} \Delta^{2} \overline{a}^{2} /16(1 + \gamma ) > 0$. As a result, $CI$ strategy also dominates $RN$ strategy.

Proof of Proposition 4

One can easily identify the Pareto improvement regions by comparing Propositions 2 and 3. To achieve Pareto improvement, the fixed fee charged to the TSP should at least make up for the loss suffered by the OTP because of the strategy adjustment (i.e., $T_{\min } = \pi_{OTP}^{ZB} - \pi_{OTP}^{ZA}$), whereas it cannot be higher than the TSP’s benefits from adopting the Pareto improvement strategy (i.e., $T_{\max } = \pi_{TSP}^{ZA} - \pi_{TSP}^{ZB}$).

Proof of Proposition 5

When $0 < \lambda < \lambda_{1}$, we only need to compare $CN$, $RN$ and $AI$ strategies. Firstly, we compare $CN$ and $RN$ strategies. The TSP only gains the risk-free profits under $CN$ and $RN$ strategies, and then we have $\overline{\pi }_{TSP}^{C} - \overline{\pi }_{TSP}^{R} = (1 - (1 + \gamma )\lambda )\overline{a}^{2} /4(1 + \gamma )$. One can easily derive that when $0 < \lambda < \lambda_{1}$, $\overline{\pi }_{TSP}^{C} > \overline{\pi }_{TSP}^{R}$. That is, $CN$ strategy dominates $RN$ strategy. Then, comparing $CN$ and $AI$ strategies, we have $\overline{\pi }_{TSP}^{C} - \overline{\pi }_{TSP}^{A} = (1 - \gamma )\overline{a}^{2} /8(1 + \gamma ) > 0$. For the risky profits, the OTP shares (withholds) information under the agency mode (hybrid mode). Hence, the TSP possesses risky profits advantage under the agency mode. When $0 < \lambda < \lambda_{1}$, we have $\overline{\pi }_{TSP}^{C} > \overline{\pi }_{TSP}^{A}$ and $V_{TSP}^{AI} > 0$. So, the TSP’s preference depends on the forecast variability. It is easy to identify that $\partial (E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ])/\partial (\rho \Delta )^{2} < 0$, and when $(\rho \Delta )^{2} = 0$, we have $\max \left( {E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ]} \right) > 0$. When $(\rho \Delta )^{2} = 1$, there exists a unique $\lambda_{6} = (1 + 3\gamma )/2(1 + \gamma )$, which makes $\min \left( {E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ]} \right) = 0$. Therefore, when $\lambda_{6} < \lambda < \lambda_{1}$ (in R7), we get $\min \left( {E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ]} \right) > 0$, and thus the TSP prefers $CN$ strategy. When $0 < \lambda < \min \{ \lambda_{1} ,\lambda_{6} \}$ (i.e. in R6), we have $\min \left( {E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{WN} ]} \right) < 0$. It indicates that in R6, there is a unique $\tau_{3}$ making $E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ] = 0$. As a result, when $0 < \rho \Delta < \tau_{3}$, the TSP prefers $CN$ strategy; when $\tau_{3} < \rho \Delta < 1$, the TSP chooses $AI$ strategy.

Next, when $\lambda_{1} < \lambda < 1$, we only need to compare $CI$, $RN$ and $AI$ strategies. Firstly, we compare $CI$ and $AI$ strategies. We have $E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{AI} ] = (1 - \gamma )(1 + \rho^{2} \Delta^{2} )\overline{a}^{2} /8(1 + \gamma ) > 0$, and thus $CI$ strategy is optimal. Then, we compare $CI$ and $RN$ strategies. We have $\overline{\pi }_{TSP}^{C} - \overline{\pi }_{TSP}^{R} = (1 - (1 + \gamma )\lambda )\overline{a}^{2} /4(1 + \gamma )$ for the risk-free profits. Its sign depends on the sign of $1 - (1 + \gamma )\lambda$. We can easily derive that when $\lambda_{1} < \lambda < \lambda_{5}$ (i.e. in R8), $\overline{\pi }_{TSP}^{C} > \overline{\pi }_{TSP}^{R}$; when $\lambda_{5} < \lambda < 1$, $\overline{\pi }_{TSP}^{C} < \overline{\pi }_{TSP}^{R}$. For the risky profits, the OTP shares information under the hybrid mode, but withholds information under the reselling mode. Therefore, the TSP possesses the risky profits advantage under the hybrid mode when compared with the reselling mode. Based on the above comparison results, inR8, we have $\overline{\pi }_{TSP}^{C} > \overline{\pi }_{TSP}^{R}$ and $V_{TSP}^{CI} > 0$, and thus the TSP prefers $CI$ strategy. When $\lambda_{5} < \lambda < 1$, we have $\overline{\pi }_{TSP}^{C} < \overline{\pi }_{TSP}^{R}$ and $V_{TSP}^{CI} > 0$; therefore, the forecast variability affects choice. We verify that $\partial (E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RN} ])/\partial (\rho \Delta )^{2} > 0$, and when $(\rho \Delta )^{2} = 0$, $\min \left( {E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RN} ]} \right) < 0$. When $(\rho \Delta )^{2} = 1$, there exists a unique $\lambda_{7} = (5 + \gamma )/4(1 + \gamma )$, which satisfies $\max \left( {E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RN} ]} \right) = 0$. Accordingly, when $\lambda_{7} < \lambda < 1$ (i.e. in R10), we have $\max \left( {E[\pi_{TSP}^{CN} ] - E[\pi_{TSP}^{AI} ]} \right) < 0$, and thus the TSP prefers $RN$ strategy. While when $\lambda_{5} < \lambda < \min \{ \lambda_{7} ,1\}$(i.e. in R9), $\max \left( {E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RN} ]} \right) > 0$. Therefore, there exists a unique $\tau_{4}$, which satisfies $E[\pi_{TSP}^{CI} ] - E[\pi_{TSP}^{RN} ] = 0$ in R9, such that when $0 < \rho \Delta < \tau_{4}$, the TSP prefers $RN$ strategy; otherwise, when $\tau_{4} < \rho \Delta < 1$, the TSP prefers $AI$ strategy.

Proof of Proposition 6

One can easily identify the Pareto improvement regions by comparing Propositions 5 and 3.