Liquidity in Financial Networks

Abstract

This study investigates the amount of liquidity that is necessary to settle a given network of financial obligations. In our analysis, we assume sequential settlement, which is standard in real-world interbank settlement systems, instead of simultaneous settlement, which is typically assumed in relevant research. We develop a graph-theoretic model and apply a flow network technique to investigate how the interconnected feature could affect the required liquidity. Our main contribution is to show that the effect of the interconnected feature is characterized with our original concepts regarding “twist” properties—arc-twisted and vertex-twisted—that are defined on the basis of the concept of “cycles.” Each of the “twist” properties refers to certain inconsistency in the dynamics of settlements. The characterization provides a consistent and fundamental perspective of how a hub or other network structures affect the required liquidity. We further investigate the quantitative implications of the “twist” properties for real-world networks of obligations by examining networks with clustered structures and small-world structures. We show that “twist” properties have non-linear effects on the required liquidity against an increase in the amount of obligations.

1 Introduction

The financial crisis of 2008 raised the concern that default of a bank may cause a “domino” of default through interconnected financial obligations among banks. To ensure the resilience of financial system, the Basel Committee introduced a liquidity regulation under the framework of Basel lll; banks are required to hold sufficient liquidity against short-term liquidity shocks. For the purpose of liquidity regulation in general, it is crucial to assess the required liquidity appropriately. The assessment hinges on, among other things, the assumption of an underlying settlement system. In this respect, seminal theoretical studies in the literature on financial contagion¹ effectively assume “simultaneous” settlement, by which financial obligations are canceled out whenever possible, although “sequential” settlement is the standard in the modern interbank settlement systems. The assumption of simultaneous settlement leaves the relevant analyses highly tractable by allowing fixed-point arguments, although it could considerably underestimate the amount of funds to prevent a “domino” effect of default.

Purpose and Framework

This study offers a framework to evaluate the amount of liquidity—funds available for settlements—that is necessary to prevent default under “sequential” settlement. Our aim is to clarify how the interconnected feature of financial obligations could affect the required amount of funds. For this purpose, we assume an exogenous network of obligations and abstract their formation. We focus on the total amount of funds necessary to settle all obligations, and investigate how the amount depends on network topologies. We perform our investigation along with two polar liquidity scenarios. One is assumed as a situation in times of financial distress, by which funds circulate least efficiently. The other is assumed as a benchmark situation in times of non-distress, by which funds circulate most efficiently. In our formulation as graph problems, the pair of scenarios amounts to deriving the upper bound and lower bound of the required amount of funds against possible “orders” of settlements.

Approach and Technique

We characterize each lower bound and upper bound, applying a basic technique to analyze “flow” networks. Specifically, we decompose a network of obligations on the basis of cycles. This helps to separate mathematically the relevant “ordering” factor from the relevant “flow” factor. We refer to the former as the synchronization factor, and the latter as the domain factor, for reasons that become clearer soon. In terms of the interconnection of network, the synchronization factor captures the interconnected feature of network, while the domain factor—cycles and the relevant amount of obligations—serves as the reference basis for the interconnection.

Main Results: Qualitative Aspects

The main contribution of this study is to reveal the qualitative aspect of the synchronization factor with two of our original concepts, arc-twisted and vertex-twisted, which are formally defined on a directed graph. Specifically, with regard to the lower bound, the domain factor refers to the efficient recycling of funds within each domain—a cycle of obligations—without considering the interrelation between domains, while the synchronization factor, which is characterized by arc-twisted, refers to the additional amount of funds required that is sourced from the interrelation between domains. With regard to the upper bound, the domain factor refers to the least efficient recycling of funds within a domain without considering the interrelation between domains, while the synchronization factor, which is characterized by vertex-twisted, refers to the amount of subtraction that is sourced from the interrelation between domains.

Thus, the interconnected feature of network is essentially captured by arc-twisted for the case of the lower bound, and by vertex-twisted for the case of the upper bound. A natural concern is the relation between the two concepts. In this respect, we show a simple relation, such that vertex-twisted indicates arc-twisted but not vice-versa. This result consolidates our findings on the qualitative implications of the interconnected feature. We illustrate that our characterization with the “twist” concepts provides a consistent and fundamental perspective on the underlying mechanism for a hub or other network structures to affect each lower/upper bound.

Results: Quantitative Aspects

We further analyze the quantitative implications of the “twist” concepts for real-world payment networks. Our approach is to focus on classes of network that capture key properties of real-world payment networks. The key properties observed in real-world payment networks have been discussed as a combination of high degree of clustering and relatively short average path lengths, as highlighted by Soramäki et al. (2007) with regard to Fedwire, by Rordam and Bech (2009) with regard to Danish interbank money flows, and by Inaoka et al. (2004) and Imakubo and Soejima (2010) with regard to BOJ-NET. This pair of properties is typically referred to as a small-world structure.² We show that for each lower and upper bound, an increase of obligations has a non-linear effect on the required amount of funds through the synchronization factor. This result suggests that appropriate consideration of the synchronization factor is indispensable in evaluating the funds required for real-world payment networks.

Interbank Settlement Systems

Here, we elaborate on the background of our assumption of “sequential” settlement. A traditional interbank settlement system used to be a simultaneous-type system called a designated-time net settlement system, whereby settlements are conducted on a designated-time basis and the obligations are offset against each other as much as possible. Against the backdrop of the expanding volume of obligations and technological advances for real-time transactions, many interbank settlement systems have changed and now adopt a sequential-type system called real-time gross settlement (RTGS), which settles obligations on a real-time basis.³ In the RTGS system, obligations are no longer offset against each other but instead are settled on an individual gross basis. Although several interbank settlement systems further adopt systems that partially combine the offsetting service to the RTGS system, they still operate on the basis of RTGS system.⁴ Our assumption of “sequential” settlement simulates the RTGS system without any offsetting service, and is intended to serve as a benchmark analysis for applications that incorporate the offsetting service.

Literature and Contribution

In the literature of financial network, a distinctive feature of our two concepts, arc-twisted and vertex-twisted, is their reference to dynamics. Such existing concepts as connectivity and concentration are largely static,⁵ because the main focus of such research is examination of the consequence of balance-sheet linkage, effectively assuming “simultaneous” settlement. Few theoretical studies explicitly assume certain “sequential” settlement to discuss the relevance of network topologies. An exception is Rotemberg (2011), whose analysis is most relevant to the present study. Rotemberg (2011) theoretically examines the lower bound of the required amount of funds in a different setting. The author assumes “sequential” settlement, which allows an obligation to be settled in arbitrary installments.⁶ However, in reality, the unit of settlements is not flexibly adjusted in many interbank settlements.⁷ In our study, we do not allow arbitrary installments “ex-post,” that is, the unit of settlement is fixed when a network of obligations is given; when the given obligations are settled, each obligation needs to be settled at once in each given unit.⁸ Rotemberg (2011) shows that multiplicity of cycles could be a source of inefficient circulation of funds in deriving the lower bound. From the perspective of our characterization, multiplicity of cycles corresponds to the “domain” factor. The assumption of flexible installments fails to capture the “synchronization” factor.⁹ Indeed, the key contribution of our study is to reveal that the static concept of “domain” factor is insufficient; however, a dynamic concept regarding the “synchronization” factor is indispensable for examining RTGS systems. The implications of the dynamic aspect of RTGS systems have also been examined in simulation-based studies, such as Beck and Soramäki (2001) and Galbiati and Soramäki (2011).¹⁰ Our theoretical analysis complements these works by clarifying the source of complications relevant to the dynamics.

Applications of the Framework

Hayakawa (2018) applies our framework to discuss the liquidity issues of introducing central clearing counterparties (CCPs), and discusses how a CCP’s offsetting service could affect (i.e. increase or decrease) overall liquidity needs. By understanding CCPs’ offsetting service as the elimination of arcs in the network model, Hayakawa (2018) reveals potential negative effects of introducing a CCP, and discusses the effects quantitatively in relation to network topologies. The study illustrates the usefulness of the framework in discussing the liquidity issues of settlements from the perspective of network topologies.

The rest of the paper is structured as follows. Section 2 introduces our model and mathematical framework. Section 3 provides motivational observations, especially regarding several example “networks” that are particularly relevant to our analysis. Section 4 overviews our main results in reference to the relevant theorems, and provides preliminary analysis. Section 5 shows our main results, formally introducing the “twist” properties—arc-twist and vertex-twist. Section 6 presents additional results regarding the quantitative implications of the “twist” properties. Section 7 provides concluding remarks. The appendix includes proofs of the relevant results.

2 Model and Framework

There are a finite number of banks. We consider two stages for the formation of interbank obligations and their settlements. In Stage 1, debts among banks are exogenously given. The contracts specify that all relevant obligations be settled in Stage 2. We discuss the required amount of funds in Stage 2 along with two polar liquidity scenarios that are intended to capture settlements in each “good time” and “bad time,” as we elaborate in Sect. 2.3.

We express interbank obligations formed in Stage 1 utilizing a flow network representation, which we introduce in Sect. 2.1. Then, the settlements of interbank obligations in Stage 2 are expressed as a network with additional elements that specify “orders” and “liquidity inputs,” which we introduce in Sect. 2.2. Section 2.3 introduces our liquidity scenarios and presents our formulation as a pair of graph problems.

2.1 Interbank Obligations: f-network $\langle V,A,f\rangle$

We express the obligations formed in Stage 1 utilizing a flow network representation.¹¹ The obligations are expressed with a flow network (f-network)$\mathcal {N}^f=\langle V,A,f \rangle$. V specifies a set of vertices, which corresponds to banks. $A=\left\{ (v,w,n)|v,w\in V, n=1,2,\ldots \right\}$ specifies a set of arcs, where each arc $(v,v',k)$ shows that v has some amount of obligation to $v'$, and k is used as an index that distinguishes among multiple arcs for $(v,v')$. The indices are not usually mentioned in order to avoid being notationally cumbersome; however, the multiplicity of the arcs is not trivial for our analysis, as discussed in the analysis section. Then, flow$f:A\rightarrow \mathcal {R}_{+}$ expresses the amount of the relevant obligations.

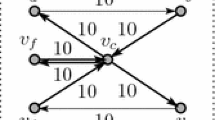
Throughout the study, we confine ourselves to a class of f-networks that are closed. In words, an f-network $\langle V,A,f\rangle$ is closed when for each $v\in V$, the total amount of obligations owed by v to the others equals the total amount of claims held by v. We show the formal definition below. Figure 1 provides examples of closed f-networks. The left f-network is later used to illustrate our analytical method. The right f-network is presented simply as a reminder that our framework allows multiple arcs between the same two vertices in the same direction.

Definition 1

(Closed f-network)

f-network $\langle V,A,f\rangle$ is closed if $f^{I}_{v}=f^{O}_{v}$ for every $v\in V$, where $f^{I}_{v}\equiv \sum _{v'\in V}\sum _{l=1,2,\ldots } f((v',v, l))$, $f^{O}_{v}\equiv \sum _{v' \in V}\sum _{m=1,2,\ldots } f((v, v', m))$.

In the above Definition 1, $f^I_v$ denotes the total amount of claims held by v—the total amount of funds that should flow into v. Meanwhile, $f^O_v$ denotes the total amount of obligations v owes to the others—the total amount of funds that should flow out of v. To clarify the definition, we could restate it as follows: for each $v\in V$, the weighted node input degree (i.e. $f^{I}_{v}$) equals the weighted node output degree (i.e. $f^{O}_{v}$).

Remark

The main reason we confine our focus to the class of closed f-networks is their mathematical tractability in our analysis. We consider our findings to be essentially applicable also to f-networks that are not closed, as we discuss in the analysis section. In addition, the class of closed f-networks serves as a benchmark to examine the implications of “sequential” settlement, particularly in comparison to “simultaneous” settlement, since no funds would be required under “simultaneous” settlement for arbitrary closed f-networks.

Fig. 1

Examples of closed f-networks: graphical representation. Notes: On the left side of the figure, $V=\left\{ v_{a}, v_{b}, v_{c}, v_{d}\right\}$, $A=\left\{ (v_{a}, v_{b}), (v_{a}, v_{c}), (v_{b}, v_{c}),(v_{c}, v_{d}), (v_{d}, v_{a}) \right\} , f((v_{a}, v_{b}))=f((v_{b}, v_{c}))=10, f((v_{a}, v_{c}))=20, f((v_{c}, v_{d}))=f((v_{d}, v_{a}))=30$. The right side of the figure shows a situation with multiple obligations between $v_{c}$ and $v_{d}$. Each is distinguished as $f((v_{c},v_{d},1))=25$, $f((v_{c},v_{d},2))=5$ while the other obligations are the same as on the left

2.2 Settlement of Obligations: fsp-network $\langle V,A,f,s,p\rangle$

In Stage 2, the interbank obligations are settled sequentially on a gross basis. Given interbank obligations $\langle V,A,f\rangle$, we let one-to-one mapping (sequence) $s:A\rightarrow \left\{ 1,2,\ldots ,|A|\right\}$ show the relative order of settlements. It states that the obligations specified by A are settled individually in this order such that obligation $a\in A$ with $s(a)=k$ is settled in k-th order.

Fig. 2

Examples of e-covered fsp-networks: graphical representation. Notes: These two fsp-networks are defined on the same f-network$\langle V,A,f\rangle$ shown on the left side of Figure 1. The left-hand fsp-network shows $\langle V,A,f,s,p \rangle$ with $s((v_{d},v_{a}))=1$, $s((v_{a},v_{b}))=2$, $s((v_{a},v_{c}))=3$, $s((v_{b},v_{c}))=4$, $s((v_{c},v_{d}))=5$, $p(v_{a})=p(v_{b})=p(v_{c})=0$, $p(v_{d})=30$. The right fsp-network shows $(V,A,f,s',p')$ with $s'((v_{d},v_{a}))=1$, $s'((v_{a},v_{b}))=5$, $s'((v_{a},v_{c}))=3$, $s'((v_{b},v_{c}))=4$, $s'((v_{c},v_{d}))=2$, $p'(v_{a})=0$, $p'(v_{b})=10$, $p'(v_{c})=p'(v_{d})=30$. The order specified by s is shown on the upper right of the amount of corresponding obligation, and each initial liquidity holding specified by p is shown in boldface alongside each vertex

In order to evaluate the required liquidity, we assume that funds are input to each bank only initially in Stage 2, and that lending/borrowing funds between banks is not allowed. Thus, funds that can be used by a bank for its payments are either those initially put to the bank, or those the bank has received in the course of settlements. Along with this assumption, let (potential) $p:V\rightarrow \mathcal {R}_{0+}$ indicate the amount of funds put to each bank initially in Stage 2 (e.g. $p(v)=10$ indicates $v\in V$ initially holds 10 units of funds.)

We form a different concept of network called the fsp-network$\mathcal {N}^{fsp}=\langle V,A,f,s,p \rangle$. We define the e-covered (exact covered) property for fsp-networks, such that for e-covered $\langle V,A,f,s,p\rangle$, $\sum _{v\in V} p(v)$ indicates the total amount of required funds for $\langle V,A,f,s\rangle$. The e-covered property consists of two requirements: first, there is no shortage of funds at any point of settlement, and second, there are no redundant funds that are not used for any of the settlements. Before proceeding to our formal definition, Fig. 2 shows examples of e-covered fsp-networks. For each f-network $\langle V,A,f\rangle$ in the figure, the order specified by $s:A\rightarrow \left\{ 1,2,\ldots ,|A|\right\}$ is shown on the upper right of the amount of corresponding obligation, and each initial liquidity holding specified by $p:V\rightarrow \mathcal {R}_{0+}$ is shown in boldface alongside each vertex. It is easily confirmed for the fsp-network shown on the left that 30 units of funds put to the vertex on the bottom-left is sufficient to settle all the obligations given the indicated orders of settlements, and any amount smaller than this falls short of the required amount for the corresponding settlements. For the right-hand fsp-network, it is similarly confirmed that the indicated funds are sufficient to settle all obligations, and any smaller amount of funds for any vertex causes a shortage for the corresponding settlement.

We prepare to define covered property, then proceed to our formal definition of e-covered property. Given fsp-network $\langle V,A,f,s,p\rangle$, let $t=0,1,\ldots , |A|$ be a period in which obligation $a\in A$ with $s(a)=t$ is settled at the beginning of each period. The aggregate amount of funds received by $v\in V$ in period t is denoted as $f^{I}_{v,t}=\sum _{v'\in V}\sum _{l=1,2,\ldots } 1_{\left\{ s((v',v,l))=t\right\} }f((v',v,l))$, while the aggregate amount paid to other banks is denoted as $f^{O}_{v,t}=\sum _{v'\in V}\sum _{m=1,2,\ldots }1_{\left\{ s((v,v',m))=t\right\} }f((v,v',m))$. We denote $p^{t}(v)$ as the amount held by $v\in V$ at the end of period t, by letting $p^{t}(v)=p^{t-1}(v)+(f^{I}_{v,t}-f^{O}_{v,t})$ for $t=1,2,\ldots , |A|$ and $p^{0}(v)=p(v)$. Now, we say $\langle V,A,f,s,p\rangle$ is covered if $p^{t}(v)\ge 0$ for every $v\in V$ and every $t=0,1,\ldots ,|A|$. Based on the covered property, the e-covered property is defined as follows.

Definition 2

(E-covered property of fsp-networks)

fsp-network $\langle V,A,f,s,p\rangle$ is e-covered (exact covered) if (no shortage): $\langle V,A,f,s,p\rangle$ is covered, and (no redundancy): There is no other $p':V\rightarrow R_{0+}$ such that $\langle V,A,f,s,p'\rangle$ is covered, $p'(v)\le p(v)$ for every $v\in V$, and $p'(v')<p(v')$ for some $v'\in V$.

In words, the e-covered fsp-network $\langle V,A,f,s,p\rangle$ indicates that the amount of funds initially assigned to each vertex v (i.e. p(v)) is just sufficient to settle all the obligations owed by v, given the order of the settlements specified by s.

We proceed to clarify the implication of the e-covered property by presenting a minimization problem (Problem A) and associated lemma.

(Problem A: Minimization Among Covered fsp-Networks)

For a given $\langle V,A,f,s\rangle$ where $\langle V,A,f\rangle$ is closed,

$$\begin{aligned} \begin{aligned} \min _{p}&\sum _{v\in V}p(v),\\ \hbox {s.t.,}\,&\langle V,A,f,s,p\rangle \hbox { is covered}. \end{aligned} \end{aligned}$$

Lemma 1

Given $\langle V,A,f,s\rangle$ where $\langle V,A,f \rangle$ is closed, $\langle V,A,f,s,p\rangle$ that attains the value for Problem A is e-covered and unique.

The result is immediate based on the definition of e-covered. Based on the lemma, we examine the required amount of funds in terms of the uniquely derived e-covered fsp-network for a given closed f-network and sequence. When $\langle V,A,f,s,p\rangle$ is e-covered, we call $\sum _{v\in V}p(v)$ its circulation.

2.3 Liquidity Scenarios and the Relevant Graph Problems

We focus on two polar scenarios for our analysis: one in the good time, and the other in the bad time. The good time refers to the financial state in which settlements are executed under the best coordination, and the total required funds are the minimum possible. By contrast, the bad time refers to the state in which settlements are executed under the worst coordination, and the total required funds are the maximum possible. The bad time is meant to represent a period of financial distress, while the good time is interpreted as a benchmark state for a time of non-distress.

Formally, the total required funds in each scenario are derived by each of the following minimization and maximization problems, called min/max settlement fund circulation problems (MIN-SFC and MAX-SFC).¹² For a given closed f-network, MIN-SFC (MAX-SFC) derives the lower (upper) bound of the total required funds against every possible “order” of settlement. For the formulation, let S(A) denote the set of available sequences for given $\langle V,A,f\rangle$.

(MIN-SFCin Original Form)

Given a closed f-network$\langle V,A,f\rangle$,

$$\begin{aligned} \begin{aligned} \min _{s\in S(A) }&\sum _{v\in V}p(v),\\ {\textit{s.t. }}&{\textit{fsp-network }}\langle V,A,f,s,p\rangle {\textit{ is e-covered.}} \end{aligned} \end{aligned}$$

(MAX-SFCin Original Form)

Given a closed f-network$N^{f}=\langle V,A,f\rangle$,

$$\begin{aligned} \begin{aligned} \max _{s\in S(A) }&\sum _{v\in V}p(v),\\ {\textit{s.t. }}&{\textit{fsp-network }}\langle V,A,f,s,p\rangle {\textit{ is e-covered.}} \end{aligned} \end{aligned}$$

For example, for the closed f-network shown on the left side of Fig. 1, the left side of Fig. 2 shows an fsp-network that gives the value derived by MIN-SFC, while the right side of the figure shows an fsp-network that gives the value derived by MAX-SFC. Throughout the study, we call the value derived by each MIN-SFC and MAX-SFCmin/max-circulation and denote them as $x^{min}(N^{f})$, $x^{max}(N^{f})$ for the input closed f-network $N^{f}$.

Remark on the Formulation

Our particular focus in setting up the problems of MIN-SFC and MAX-SFC is on analyzing the implications of the sequential feature of settlements given the level of coordination. In this regard, the good and bad liquidity scenarios are meant to be analytical scenarios, and there are limitations in applying our approach to real-world scenarios. For one thing, our formulation ignores the endogenous nature of the timing decision by banks themselves. In particular, bank-run behavior might spread among financial institutions with regard to their mutual obligations, which could switch the situation suddenly from the good to bad liquidity scenario. Meanwhile, in bad scenarios, banks could simply claim their pending debts, while attempting to postpone their own debts at the same time. Such a “simultaneous” claim situation is not captured in our sequential setting; however, we note that our analysis could still help in discussing the necessary amount of liquidity that would cease or prevent the “simultaneous” claim situation.

3 Motivational Observations

In this section, we motivate the introduction of our “twist” properties—arc-twisted and vertex-twisted—and illustrate their relevance to min/max-circulation, referring to several example f-networks.

3.1 Min-Circulation and arc-twisted

For the fsp-network shown on the left side of Fig. 2, we observe that the min-circulation for the underlying f-network equals the largest obligation in the amount (i.e. $max _{a\in A} f(a)$) for the underlying closed f-network. Actually, the following result is immediate.

Observation 1

(Lower bound of min-circulation)

For an arbitrary closed f-network $N^f=\langle V,A,f\rangle$, we have $x^{min}(N^f) \ge max _{a\in A} f(a)$.

The inequality arises for other f-networks. For example, see Fig. 3, where $x^{min}(N^f)=40$ > $max _{a\in A} f(a)=30$ for the given $N^f=\langle V,A,f\rangle$. We show that, for this specific example f-network, the additionally required funds $x^{min}(N^f)-max _{a\in A} f(a)= 10$ sources from the “twist” property of arc-twisted.¹³ To explain the arc-twisted property informally, for the f-network in Fig. 3, take two “cycles,” as shown in Fig. 4. We say that the two cycles are in arc-twisted relation, based on certain inconsistency between the two cycles. The formal definition is shown in our analysis section. The following results illustrate the relevant inconsistency for our example f-network.

Fig. 3

Notes: $V=\{v_a,v_b,v_c,v_d,v_e,v_f\}$, $A=\{(v_a,v_b), (v_b,v_c), (v_c,v_d), (v_d,v_e), (v_e,v_f), (v_f,v_a), (v_a,v_d), (v_c,v_f),(v_e,v_b)\}$, $f((v_f,v_a))=f((v_b,v_c))=f((v_d,v_e))=30$, $f((v_a,v_b))=f((v_c,v_d))=f((v_e,v_f)=20, f((v_a,v_d)=f((v_c,v_f))=f((v_e,v_b))=10$

Fig. 4

Notes: This figure shows two cycles included in the f-network shown in Fig. 3

Observation 2

(Arc-twisted cycles)

• i. (Cycle on the left side of Fig. 4) Take a closed f-network $N^f=\langle V,A,f\rangle$ where $\langle V,A\rangle$ is given as the cycle shown on the left side of Fig. 4.

If sequences starting with $s((v_f,v_a))=1$ attains the min-circulation of $N^f$, then we have $s((v_b,v_c)) < s((v_d,v_e))$.

• ii. (Cycle on the right of Fig. 4) Take a closed f-network $N^f=\langle V,A,f\rangle$ where $\langle V,A\rangle$ is given as the cycle shown in the right side of Fig. 4.

If sequences starting with $s((v_f,v_a))=1$ attains the min-circulation of $N^f$, then we have $s((v_b,v_c)) > s((v_d,v_e))$.

Remember that in the original f-network shown in Fig. 3, each of the three arcs $(v_f,v_a)$, $(v_b,v_c)$, and $(v_d,v_e)$ needs be settled at once, that is, not in any multiple installments. Thus, Observation 2 implies that an efficient order of funds to circulate for each cycle cannot be realized at the same time for the original f-network, and this inconsistency generates the additionally required funds. In our analysis section, we show how this observation is formally generalized.

Implications of slicingandhub

Here, we further observe that several different changes on the f-network shown in Fig. 3 serve to eliminate the “additionally required” funds. First, see Fig. 5, where an arc $(v_b, v_c)$ for the original f-network is sliced into two arcs. A comparison of the two f-networks indicates that the “additionally required” funds source from the restriction such that an arc in the amount of 30 units (e.g. $(v_b,v_c)$ ) need be settled at once, whereas when stated from the perspective of the f-network in Fig. 5, the restriction is interpreted as the sliced arcs $(v_b,v_c,1)$ and $(v_b,v_c,2)$ needing to be synchronized to settle.

Figure 6 shows a different way to avoid the additional funds. There, a hub vertex $v_g$ is added to the original f-network. The fsp-network shown on the right side of the figure attains the min-circulation, indicating that the added hub serves to coordinate the timing of settlements. These observations indicate that the “twist” property of arc-twisted is more fundamental in discussing min-circulation than the other concepts are, such as hub.

Fig. 5

Slicing. Notes: The figure shows an f-network constructed from the f-network shown in Figure 3, by letting an arc $(v_b, v_c)$ be sliced into two

Fig. 6

Hub. Notes: The figure shows an f-network that constructed from the f-network shown in Fig. 3, by adding a hub vertex $v_g$ such that the vertex is added in the middle of each of $(v_a,v_d)$, $(v_c,v_f)$, and $(v_e, v_b)$ to separate one arc into two (e.g. $(v_a,v_d)$ is separated into $(v_a,v_g)$ and $(v_g,v_d)$)

The Non-linearity Brought by arc-twisted Cycles

Now, we proceed to observe a notable consequence of the existence of arc-twisted cycles. For the f-network shown in Fig. 3, we consider an increase in the amount of obligations on the basis of a cycle. Suppose that we increase the amount of obligations on the basis of the cycle shown on the right side of Fig. 4 such that each arc in the cycle has an additional 5 units of funds, which we show on the left side of Fig. 7. Observe that the sequence that attains the min-circulation for the original f-network shown in Fig. 3 also attains the min-circulation for that in Fig. 7, where a corresponding fsp-network is shown on the right side. However, when we keep increasing the amount on the basis of the same cycle, at a certain point, the same sequence no longer attains min-circulation. For example, see the f-network shown on the left side of Fig. 8, where an amount of 15 units is added instead of 5 units in the previous figure. Now, the circulation attained for the same sequence is 70 units as shown in the middle of the figure; however, the min-circulation is smaller in this case, at 65 units, for which a corresponding fsp-network is shown on the right side of the figure. We summarize these observations below.

Fig. 7

Notes: Compared to Fig. 3, flow is increased in the amount of 5 units with respect to each arc in the cycle $(v_a, v_d, v_e, v_b, v_c,v_f,v_a)$ (e.g. $f((v_a,v_d))=10+5$ and $f((v_d, v_e))=30+5)$)

Fig. 8

Notes: Compared to Fig. 3, flow is increased in the amount of 15 units with respect to each arc in the cycle $(v_a, v_d, v_e, v_b, v_c,v_f,v_a)$. The fsp-network shown in the middle of the figure implies that the sequence that attains the min-circulation for the original f-network shown in Fig. 3 no longer attains the min-circulation of the f-network shown on the left side of this figure, where the circulation is shown as $70(=20+25+25)$ units. The min-circulation turns to 65 units, for which a corresponding fsp-network is shown on the right side of the figure

Observation 3

(Non-linearity associated with arc-twisted)

Given f-network $N^f$ shown on the left side of Fig. 3, suppose that flow is increased for the arcs in cycle $(v_a, v_d, v_e, v_b, v_c,v_f,v_a)$ by the amount of $m>0$.¹⁴ Denote the derived f-network as $\tilde{N}^{f}$. Then, we have as follows:

• i. if $m\le 10$, then any sequence that attains the min-circulation for $N^f$ also attains the min-circulation for $\tilde{N}^f$, and $x^{min}(\tilde{N}^f)=x^{min}(N^f)+2m$.

• ii. if $m> 10$, then none of the sequences that attain the min-circulation for $N^f$ attains the min-circulation for $\tilde{N}^f$, and $x^{min}(\tilde{N}^f)=x^{min}(N^f)+20+ (m-10)$.

According to Observation 3, the marginal effect of increasing flow on the cycle is 2 if $m \le 10$, while it is 1 if $m >10$. To observe the intuition, note for the fsp-network shown in Fig. 3, the funds are “efficiently circulated” on the basis of the cycle $(v_a,v_b,v_c,v_d,v_e,v_f,v_a)$ shown on the left side of Fig. 4. (i.e. the sequence for the cycle is monotonically increasing when we start by $s((v_a,v_b))=1$, which is followed by $s((v_b,v_c))=2,s((v_c,v_d))=4,s((v_d,v_e))=5,s((v_e,v_f))=7,s((v_f,v_a))=8$.) By contrast, the funds are not efficiently circulated on the basis of the cycle shown on the right side of Fig. 4 (i.e. the sequence for the cycle is never monotonically increasing when we start by any of the vertices.). The reason that the former cycle—$(v_a,v_b,v_c,v_d,v_e,v_f,v_a)$—is “chosen” to attain efficient circulation is that the flow endowed to the cycle is basically larger than that endowed to the other cycle (e.g. $f((v_e,v_f))=20 > f((v_a,v_d))=10$). The former cycle should be chosen as long as $m\le 10$ in the notation of Observation 3; but once $m>10$, the other cycle should now be chosen, and thus, sequences that attain the min-circulation need to be changed accordingly, as illustrated on the right side of Fig. 8. Note that such non-linearity is not observed for the f-networks shown in Fig. 2, for any pair or set of the cycles included.

Implications of Non-linearity for Interbank Settlements

The observed non-linearity has implications for real-world settlements, specifically regarding the effect of partial offsetting. In real-world settlements, it is plausible that offsetting is executed only partially.¹⁵ Using the notation in Observation 3, suppose $m>10$ at first, and then, m decreases to track the change of the marginal effect of offsetting obligations on the basis of the cycle. The observation states that once $m<10$, the marginal effect doubles.

To see the implications of the same observation in a different context, compare two ways of partial offsetting for the f-network shown in Fig. 3; that is, offsetting on the basis of the cycle shown on the left side of Fig. 4, or the right side of the figure. Related to Observation 3, we observe that the marginal effect of offsetting is twice as large for the right cycle as for the left cycle.

3.2 Max-Circulation and vertex-twisted

As observed for the fsp-network shown on the right side of Fig. 2, the max-circulation for the underlying f-network is strictly less than the aggregate amount of obligations (i.e. $\sum _{a\in A} f(a)$). Specifically, for the shown f-network, the max-circulation equals $\sum _{a\in A} f(a)-max _{a\in A} f(a)$. Actually, we obtain the following result.

Observation 4

For an arbitrary closed f-network $N^f=\langle V,A,f\rangle$, we have $x^{max}(N^f) \le \sum _{a\in A} f(a)-max _{a\in A} f(a)$.

Again, the inequality arises for other f-networks. For example, see Fig. 9, where $x^{max}(N^f)=110$ < $\sum _{a\in A} f(a)-max _{a\in A} f(a)=140-20$ for the given $N^f=\langle V,A,f \rangle$. We show that the subtracted amount $10 (=120-110)$ is sourced from the “twist” property, which we term vertex-twisted for the case of max-circulation. To explain the vertex-twisted property informally, for the f-network shown in Fig. 9, take the two “cycles” shown in Fig. 10. We say that the two cycles are in vertex-twisted relation, based on a certain inconsistency arising between the two cycles. The following observations are relevant to the inconsistency.

Observation 5

• i. (Cycle on the left side of Fig. 10) Take a closed f-network $N^f=\langle V,A,f\rangle$ where $\langle V,A\rangle$ is given as the cycle shown on the left side of Fig. 10.

If sequences starting with $s((v_f,v_a))=1$ attains the max-circulation of $N^f$, then, we have $s((v_d,v_e)) < s((v_b,v_c))$.

• ii. (Cycle on the right side of Fig. 10) Take a closed f-network $N^f=\langle V,A,f\rangle$ where $\langle V,A\rangle$ is given as the cycle shown on the right side of Fig. 10.

Fig. 9

Notes: $V=\{v_a,v_b,v_c,v_d,v_e,v_f\}$, $A=\{(v_a,v_b), (v_b,v_c), (v_c,v_d), (v_d,v_e), (v_e,v_f), (v_f,v_a), (v_b,v_f), (v_f,v_d), (v_d,v_b)\}$, $f((v_a,v_b))=f((v_b,v_c))=f((v_c,v_d))=f((v_d,v_e))=f((v_e,v_f))=f((v_f,v_a)=20, f((v_b,v_f)=f((v_f,v_d))=f((v_d,v_b))=10$

Fig. 10

Notes: The above figure shows two cycles included in the f-network shown in Fig. 9

If sequences starting with $s((v_f,v_a))=1$ attains the max-circulation of $N^f$, then, we have $s((v_d,v_b)) > s((v_b,v_f))$.

Fig. 11

Notes: Compared to Fig. 9, the direction of the inner cycle is reversed

For the case of max-circulation, the implied order of vertices is relevant. In order to clarify this point, proceed to Fig. 11, where the direction of the inner cycle is now reversed. The max-circulation becomes 120 units, where there is no longer a subtracted amount. Focus on vertices $v_f$ and $v_d$; each has multiple outgoing and incoming arcs. For the case of $v_f$, we observe that all outgoing arcs—$(v_f,v_a)$ and $(v_f,b)$—are settled before all incoming arcs—$(v_d,v_f)$ and $(v_e,v_f)$. The same observation holds for the case of $v_d$. In words, we could say that the outgoing arcs for the vertex are synchronized to be settled before any incoming arc. This would be an instruction for the least efficient circulation of funds to be attained; however, Observation 5 indicates that such synchronization is not fully executable for the f-network shown in Fig. 9. This is essentially because there is an arc—$(v_f,v_d)$—between two vertices $v_d$ and $v_f$. With regard to $v_f$, when all outgoing arcs are settled before all incoming arcs, $(v_f,v_d)$ needs be settled before $(v_f,v_e)$. Then, the instruction is for $(v_d,v_e)$ to be settled after $(v_e,v_f)$ for the purpose of the least efficient circulation of funds. Combining these, the instruction is that $(v_f,v_d)$ is settled before $(v_d,v_e)$. Now, we observe inconsistency; with regard to $v_d$, in order for all outgoing arcs to be settled before all incoming arcs, $(v_d,v_e)$ needs be settled before $(v_f,v_d)$. Thus, with regard to $v_f$, all outgoing arcs cannot be settled before all incoming arcs. This inconsistency that arises between the two cycles is formally referred to as vertex-twisted relation.

Non-linearity Brought by Vertex-Twisted Cycles

Now, we proceed to observe the non-linearity for the case of max-circulation, which is brought by vertex-twisted cycles. For the f-network shown in Fig. 9, we consider to increase the amount of obligations on the basis of a cycle. Suppose that we increase the amount of obligations on the basis of the cycle shown on the right side of Fig. 10 such that each arc in the cycle is given an additional 5 units, which we show on the left side of Fig. 12. Observe that the sequence that attains the max-circulation for the original f-network shown in Fig. 9 also attains the max-circulation for that in Fig. 12, where a corresponding fsp-network is shown on the right side. However, when we keep increasing the amount on the basis of the same cycle, at a certain point, the same sequence no longer attains the max-circulation. For example, see the f-network shown on the left side of Fig. 13, where an amount of 15 units is added instead of 5 units in the previous figure. Now, the circulation attained for the same sequence is 125 units as shown in the middle of the figure; however, the max-circulation is smaller in this case, at 130 units, for which a corresponding fsp-network is shown on the right side of the figure. We summarize these observations below.

Fig. 12

Notes: Compared to Figure 9, flow is increased in the amount of 5 with respect to each arc in cycle $(v_b, v_f, v_d, v_b)$ (e.g. $f((v_b,v_f))=10+5$)

Fig. 13

Notes: Compared to Fig. 9, flow is increased in the amount of 15 with respect to each arc in cycle $(v_b, v_f, v_d, v_b)$. The fsp-network shown in the middle of the figure implies that the sequence that attains the max-circulation for the original f-network shown in Fig. 9 no longer attains the max-circulation of the f-network shown on the left side of this figure, where the circulation is shown as $125(=45+20*4)$ units. The max-circulation becomes 130 units, for which a corresponding fsp-network is shown on the right side of the figure

Observation 6

(Non-linearity associated with vertex-twisted)

Given f-network $N^f$ shown on the left side of Fig. 9, suppose that flow is increased for the arcs in cycle $(v_a, v_d, v_e, v_b, v_c,v_f,v_a)$ by the amount of $m>0$.¹⁶ Denote the derived f-network as $\tilde{N}^{f}$. Then, we have:

• i. if $m\le 10$, then any of the sequences that attain the max-circulation for $N^f$ also attains the max-circulation for $\tilde{N}^f$, and $x^{max}(\tilde{N}^f)=x^{max}(N^f)+m$.

• ii. if $m> 10$, then none of the sequences that attain the max-circulation for $N^f$ attains the max-circulation for $\tilde{N}^f$, and $x^{max}(\tilde{N}^f)=x^{max}(N^f)+10+2(m-10)$.

According to Observation 6, the marginal effect of increasing flow on the cycle is 1 if $m \le 10$, while it is 2 if $m >10$. To observe the intuition, note for the fsp-network shown in Fig. 9 that the funds are least efficiently circulated on the basis of cycle $(v_a,v_b,v_c,v_d,v_e,v_f,v_a)$, which is shown on the left side of Fig. 10 (i.e. for each arc except one—$(v_a,v_b)$, initially held funds are used at the timing of the settlement.). By contrast, the funds are not least efficiently circulated on the basis of the other cycle $(v_b,v_f,v_d,v_b)$ shown on the right side of Fig. 10 (i.e. for each arc except two—$(v_f,v_d)$ and $(v_d,v_b)$, initially held fund is used at the timing of the settlement. The reason that the former cycle–$(v_a,v_b,v_c,v_d,v_e,v_f,v_a)$—is chosen to attain least efficient circulation is that the flow endowed to the cycle is basically larger than that endowed to the other cycle. The former cycle should be chosen as long as $m\le 10$ in the notation of Observation 6; but once $m>10$, the other cycle should now be chosen, and thus, the sequence that attains the max-circulation needs to be changed accordingly, as illustrated on the right side of Fig. 13. Note that such non-linearity is not observed for the f-networks shown in Fig. 2, regarding any pair or set of the cycles included. In the same manner as the case of min-circulation, the observed non-linearity associated with the max-circulation has implications for partial offsetting in the context of interbank settlements.

3.3 Arc-twisted and vertex-twisted

We later formally state that arc-twisted indicates vertex-twisted, but not vice versa. Specifically, the two cycles in Fig. 4 are arc-twisted, and thus, they are also vertex-twisted. The two cycles in Fig. 10 are vertex-twisted, but they are not arc-twisted. This result consolidates the observations regarding arc-twisted and vertex-twisted.

4 Overview and Preliminary Analysis

4.1 Overview of the Main Results

Since we need to take several steps to present our main results, we provide an overview in this section. With regard to min/max-circulation, our base results are summarized as follows.

$$\begin{aligned} x^{min/max}(.)={\mathop {(\mathbf{``flow'' relevant part })}\limits _{\textit{domain}~\mathrm{factor}}} + {\mathop {(\mathbf{``order'' relevant part })}\limits _{\textit{synchronization}~\mathrm{factor}}}. \end{aligned}$$

Based on the preliminary results provided in Theorems 1, 2, and 3, Theorem 4 presents our formal presentation of the above separation into two parts. The theorem also shows our characterization of the first part of the equation with the concept of domain, which refers to the extent that each unit of settlement funds can circulate; a cycle is shown as the unit for funds to circulate. With regard to the second part of the equation, which is our main focus, our characterization is presented in Theorem 5 for min-circulation with our arc-twisted concept, and in Theorem 6 for max-circulation with our vertex-twisted concept. Theorem 7 consolidates our main findings by showing the relation between the “twist” concepts, as mentioned in the last part of Sect. 3. Further results focusing on the quantitative aspects of the “twisted” properties—non-linearity in min/max-circulation—are discussed in Sect. 6.

Remark

• Our summary equation implies that a specific change of an underlying network can be decomposed into two effects. In the discussion paper version of this paper (Hayakawa 2014), we define a group of network transformations, which includes the operations of slicing and separation—letting one arc be two by adding a vertex in the middle of the arc—mentioned in Sect. 3, and present the effects in terms of the domain and synchronization factors. The following statement summarizes the relevant results with the symbolic expression $\varDelta _{transform}$, which refers to the extent to which min/max-circulation is changed by each of our network transformation operations on the input closed f-network.¹⁷

  $$\begin{aligned} \varDelta _{{\textit{transform}}}x^{min/max}(.) = ({\textit{domain}}\hbox { effect}) + ({\textit{synchronization}}\hbox { effect}). \end{aligned}$$

4.2 Preliminary Analysis

We say that an f-network is not connected when we can separate its vertices into two groups with no arc between them. Throughout this article, without loss of generality we focus on f-networks that are connected.

Our approach is based on the observation that a closed f-network can be decomposed into several closed f-networks. For the formal statement, we first define decomposition of the f-network as follows.

Definition 3

(Decomposition of f-network)

f-network $N^{f}=\langle V,A,f\rangle$ is decomposed into $\left\{ N^{f}_{k}=\langle V_{k},A_{k},f_{k}\rangle \right\} _{k=1,2,\ldots ,K}$ if

• i) $V=\cup _{1\le k\le K} V_{k}$, $A=\cup _{1\le k\le K}A_{k}$, and

• ii) $\forall a\in A$, $f(a)=\sum _{k\in K'} f_{k}(a)$, where $K'=\left\{ k''|a\in A_{k''}\right\}$.

We simply denote a decomposition of f-network $N^f$ as $N^{f}=\sum _{k=1}^{K} N^{f}_{k}$. Figure 14 shows an example of decomposition of an f-network.

Fig. 14

Example of decomposition of an f-network. Notes: $N^{f}_{1}=\langle V_{1},A_{1},f_{1}\rangle$, where $V_{1}=\left\{ v_{a}, v_{c}, v_{d}\right\}$, $A_1=\left\{ (v_{a}, v_{c}), (v_{c}, v_{d}), (v_{d}, v_{a}) \right\}$, $f_1(a\in A_1)=20$. $N^{f}_{2}=\langle V_{2},A_{2},f_{2}\rangle$, where $V_{2}=\left\{ v_{a}, v_{b}, v_{c}, v_{d}\right\}$, $A_2=\left\{ (v_{a}, v_{b}), (v_{b}, v_{c}) (v_{c}, v_{d}), (v_{d}, v_{a}) \right\}$, $f_2(a\in A_2)=10$. For each decomposed f-network, the constant value of flow (i.e. 20 and 10 units respectively) is shown in the center

A specific type of decomposition, which we term closed-cycle decomposition, is the basis for our analyses. For closed-cycle decomposition, each decomposed f-network is closed, and consists of one cycle. The decomposition in Fig. 14 is actually a closed-cycle decomposition. Below, we prepare to define cycle and the relevant concepts, before proceeding to define closed-cycle decomposition.

Given a multi-arc directed graph $\langle V,A\rangle$, we denote the set of vertices included in $A'\subseteq A$ as $V_{A'}$ and the set of arcs that includes $v\in V$ as $A_{v}$. $A'\subseteq A$ is a path from $v\in V_{A'}$ to $v'\in V_{A'}$ if we can order vertices $V_{A'}$ such that $(v,v_{1},v_{2},\ldots ,v_k, v')$ where the consecutive ordered pairs of vertices $(v,v_1)$, $(v_1,v_2)$..., $(v_k,v')$ constitute $A'$. The same arc cannot appear more than once in a path, but the same vertex can. $A'\subseteq A$ is a cycle if $A'$ is a path that starts and ends at the same vertex. We say that a cycle is punctured if the same vertex appears more than once (except the vertex that appears both at the start and the end), and is non-punctured otherwise. For a directed graph G, we denote $C_{G}$ as the set of cycles included in G and refer to it as the cycle set of G.

Our formal definition of closed-cycle decomposition is as follows.

Definition 4

(Closed-cycle decomposition¹⁸)

An f-network $N^{f}=\langle V,A,f\rangle$ with $G=\langle V,A\rangle$ is closed-cycle decomposed into $\left\{ N^{f}_{k}=\langle V_{k},A_{k},f_{k}\rangle \right\} _{k=1,2,\ldots ,K}$ if

• i) $N^{f}=\sum _{k=1}^{K}N^{f}_{k}$ is a decomposition, and

• ii) $\forall k=1,2,\ldots ,K$, each $N^{f}_{k}$ is closed and consists of one cycle, where the same cycle does not constitute more than one f-network, that is, for $1\le k, k'\le K$, $\langle V_k,A_k\rangle \ne \langle V_{k'},A_{k'}\rangle$ if $k\ne k'$.

With a slight abuse of notation, we let $N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle$ denote a closed-cycle decomposition with $C\subseteq C_{G}$, where $f^{c}$ denotes a constant function.

We have the following result for closed-cycle decomposition.

Theorem 1

(Ford and Fulkerson 1962)

Any closed f-network can always be closed-cycle decomposed.

Note that Theorem 1 does not ensure uniqueness¹⁹ of closed-cycle decomposition, although Fig. 14 shows a case of uniqueness.

We now define decomposition of fsp-networks.

Definition 5

(Decomposition of fsp-networks)

$N^{fsp}{=}\langle V,A,f,s,p\rangle$ is decomposed into $\left\{ N^{fsp}_{k}{=}\langle V_{k},A_{k},f_{k},s_{k},p_{k}\rangle \right\} _{k=1,2,\ldots ,K}$ if

• i. $\langle V,A,f\rangle$ is decomposed into $\left\{ \langle V_{k},A_{k},f_{k}\rangle \right\} _{k=1,2,\ldots ,K}$,

• ii. each sequence$s_{k}$ is consistent with s in the sense that the ordering is preserved, and

• iii. $\sum _{k} p_{k}(v) = p(v)$ for every $v\in V$.

When a decomposition of fsp-network $N^{fsp}=\langle V,A,f,s,p\rangle$ is also a closed-cycle decomposition of the corresponding f-network such as $\langle V,A,f\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},\rangle$, we extend to write $\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$.

Figures 15 and 16 show examples of decomposition of an fsp-network.

Fig. 15

Example of decomposition of fsp-network

Fig. 16

Example of decomposition of fsp-network

Observe that in both Figs. 15 and 16, all decomposed fsp-networks are e-covered. The following Lemma 2 states that it is always possible to perform such decomposition when the given fsp-network is e-covered.

Lemma 2

(E-covered decomposition)

Given a closed f-network $\langle V,A,f\rangle$, for any e-covered fsp-network $N^{fsp}=\langle V,A,f,s,p\rangle$, there exists a decomposition $N^{fsp}=\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$ such that $\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$ is e-covered for every $c\in C$.

Proof

See Appendix A.1. $\square$

We say that $N^{fsp}=\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$ is an e-covered decomposition when $N^{fsp}$ is e-covered and each decomposed $\langle V^{c},c,f^{c},s^{c},p^{c} \rangle$ is also e-covered.

5 Characterization of Min/Max-Circulation

The purpose of this section is to present our characterization of min/max-circulation. The first step is to rearrange the original minimization/maximization problems utilizing closed-cycle decomposition.

Note that in Fig. 15, an e-covered fsp-network that attains the min-circulation for the underlying f-network is expressed with an e-covered decomposition, where the min-circulation is read as $30=20+10$. Similarly, Fig. 16 shows the case of the max-circulation, where the value is read as $70=40+30$. This observation implies the following procedure to find the min/max-circulation. First, for a given closed f-network, take a closed-cycle decomposition, and then, let each decomposed f-network be an e-covered fsp-network. We could recover an fsp-network for the given f-network by “adding up”the e-covered fsp-networks—the reverse view of fsp-decomposition. By searching every possible closed-cycle decomposition for the given closed f-network, we can find an fsp-network that attains the min/max-circulation.

The following two Theorems 2 and 3 ensure that such a procedure successfully finds the min/max-circulation. Below, $C_{N^{f}}$ represents the power set of “the set of cycles” for $N^{f}$; the reformulated problems find a set of cycle $C\in C_{N^{f}}$ that constitutes a closed-cycle decomposition such that $N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle$.

Theorem 2

(MIN-SFC in decomposed form)

Given a closed f-network $N^{f}=\langle V,A,f\rangle$, the following problem gives the same value as $x^{min}(N^{f})$.

$$\begin{aligned} \begin{aligned} \min _{s\in S(A), C\in C_{N^{f}},\left\{ f^{c}\right\} _{c\in C} }&\sum _{c\in C}\sum _{v\in V^{c}} p^{c}(v).\\ \hbox {s.t. }&N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle \hbox { is a closed-cycle decomposition,}\\&\langle V^{c},c,f^{c},s^{c},p^{c}\rangle \hbox { is e-covered for every }c\in C,\hbox { and}\\&\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle \end{aligned} \end{aligned}$$

Proof

See Appendix A.2. $\square$

Theorem 3

(MAX-SFC in decomposed form)

Given a closed f-network $N^{f}=\langle V,A,f\rangle$, the following problem gives the same value as $x^{max}(N^{f})$;

$$\begin{aligned} \begin{aligned} \max _{s\in S(A), C\in C_{N^{f}},\left\{ f^{c}\right\} _{c\in C} }&\sum _{c\in C}\sum _{v\in V^{c}} p^{c}(v).\\ \hbox {s.t. }&N^{f}=\sum _{c\in C}(V^{c},c,f^{c})\hbox { is a closed-cycle decomposition,}\\&\langle V^{c},c,f^{c},s^{c},p^{c}\rangle \hbox { is e-covered for every }c\in C,\hbox { and}\\&\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle \hbox { is e-covered.} \end{aligned} \end{aligned}$$

Proof

See Appendix A.3. $\square$

For each problem in the original form, it is sufficient to search within the e-covered fsp-networks for a given f-network. Lemma 2 ensures that every such e-covered fsp-network is decomposed into e-covered fsp-networks on the basis of closed-cycle decomposition. Thus, essentially, it is sufficient to search within the closed-cycle decomposition for a given f-network.

We could interpret that a redundant procedure that finds a closed-cycle decomposition is inserted for each problem in decomposed form. The decomposed forms need be rearranged once again to proceed to our characterization. There, each of the decomposed form problems is separated into a decomposition choice part and a sequence choice part. First, we define a sub-problem for each MIN-SFC and MAX-SFC, each of which corresponds to the sequence choice part that is characterized with our “twist” properties.

In the sub-problems, as shown formally below, a closed-cycle decomposition $\langle V,A,f\rangle =\sum _{c\in C}\langle V^c,c,f^c\rangle$ is given. Observe that for each decomposed f-network $\langle V^c,c,f^c \rangle$, the min-circulation is $f^c$. Now, for each decomposed f-network, suppose to take a corresponding e-covered fsp-network $\langle V^c,c,f^c,s^c,p^c \rangle$ such that $\sum _{v\in V^c}p^c(v)=f^c$. If we can “add up” the fsp-networks to construct an e-covered fsp-network $\langle V,A,f,s,c \rangle$, then, the min-circulation is proved as $\sum _{c\in C}f^c$; however, this is not always possible. The sub-problem for the case of minimization is used to derive the minimum value of the discrepancy ($\sum _{c\in C} (\sum _{v\in V^{c}} p^{c}(v)-f^{c})$), which we call the residual. Observe that for the closed-cycle decomposition shown in Fig. 15, the residual equals zero, as we easily confirm. The sub-problem for the case of maximization similarly is used to derive the residual, and again, an example case of zero residual is shown in Fig. 16.

(Sub-problem for MIN-SFC)

Given a closed f-network$N^{f}$and a closed-cycle decomposition$\{C\in C_{N^{f}}$, $\left\{ f^{c}\right\} _{c\in C}\}$,

$$\begin{aligned} \begin{aligned} \min _{\left\{ s^{c}\in S(c)\right\} _{c\in C}}&\sum _{c\in C} \left( \sum _{v\in V^{c}} p^{c}(v)-f^{c}\right) \\ {\textit{s.t. }}&\langle V^{c},c,f^{c},s^{c},p^{c}\rangle {\textit{ is e-covered for every }}c\in C,{\textit{ and}}\\&\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle . \end{aligned} \end{aligned}$$

(Sub-problem for MAX-SFC)

Given a closed f-network$N^{f}$and a closed-cycle decomposition$\{C\in C_{N^{f}}$, $\left\{ f^{c}\right\} _{c\in C}\}$,

$$\begin{aligned} \begin{aligned} \min _{\left\{ s^{c}\in S(c)\right\} _{c\in C}}&\sum _{c\in C} \left( (|c|-1)f^{c}-\sum _{v\in V^{c}} p^{c}(v)\right) ,\\ {\textit{s.t. }}&\langle V^{c},c,f^{c},s^{c},p^{c}\rangle {\textit{ is e-covered for every }}c\in C,{\textit{ and}}\\&\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle {\textit{ is e-covered.}} \end{aligned} \end{aligned}$$

where |c| denotes the number of arcs that constitute cycle c.

We denote the derived value, residual, as $R^{min/max}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})$.

Now, we rewrite MIN-SFC and MAX-SFC as follows.

(MIN-SFCin Separated Form)

Given a closed f-network$N^{f}=\langle V,A,f\rangle$,

$$\begin{aligned} \begin{aligned} \min _{C\in C_{N^{f}},\left\{ f^{c}\right\} _{c\in C} }&\sum _{c\in C}f^{c} + R^{min}\left( N^{f}, C,\left\{ f^{c}\right\} _{c\in C}\right) \\ {\textit{s.t. }}&N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle {\textit{ is a closed-cycle decomposition.}} \end{aligned} \end{aligned}$$

(MAX-SFCin Separated Form)

Given a closed f-network$N^{f}=\langle V,A,f\rangle$,

$$\begin{aligned} \begin{aligned} \max _{C\in C_{N^{f}},\left\{ f^{c}\right\} _{c\in C} }&\sum _{c\in C}(|c|-1)f^{c} - R^{max}\left( N^{f},C,\left\{ f^{c}\right\} _{c\in C}\right) \\ {\textit{s.t. }}&N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle {\textit{ is a closed-cycle decomposition }}, \end{aligned} \end{aligned}$$

The above separated form is still not well separated in that it does not explicitly refer to which kind of closed-cycle decomposition is to be chosen. We address this issue in the next subsection.

5.1 Property of domination and Min/Max-Circulation

In this subsection, we present our characterization for the decomposition choice part of the separated form MIN-SFC and MAX-SFC. We introduce the concept of domination that refers to a relation between closed-cycle decompositions for the same f-network. Before proceeding to the formal definition, we see an example f-network shown in Fig. 17 to illustrate the concept. Observe that the f-network shown on the left side of the figure is closed-cycle decomposed into different sets of closed f-networks shown in the right side. The summation of the flow on each cycle is $30(=20+10)$ for the upper decomposition, while it is $40(=10+10+10+10)$ for the lower decomposition. In terms of the smaller value, we say that the lower decomposition is dominated by the upper decomposition,²⁰ which is formally defined below.

Fig. 17

closed-cycle decomposition and domination. Notes: For the f-network shown on the left, two closed-cycle decompositions are shown on the right. The lower-right closed-cycle decomposition is dominated by the upper-right closed-cycle decomposition

Definition 6

(dominated, undominated²¹)

Given a directed graph $G=\langle V,A\rangle$ and the sets of cycles $C_{G}$, a set of cycles $C\subseteq C_{G}$ is dominated by another set of cycles $C' \subseteq C_{G}$ (equivalently, $C'$dominatesC) if

• i) we can take a closed f-network $N^{f}$ such that $N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle =\sum _{c'\in C'}\langle V^{c'},c',f^{c'}\rangle$, and

• ii) we have $\sum _{c\in C}f^{c}<\sum _{c'\in C'}f^{c'}$.

Given the power set of “a set of cycles” $\tilde{C}$, we further say that a set of cycles $C\in \tilde{C}$ is undominated in $\tilde{C}$ if C is not dominated by any $C'\subseteq \tilde{C}$.

For a closed f-network $N^{f}=\langle V,A,f\rangle$, let $C_{ N^{f} }$ denote the power set of the set of cycles for $N^f$. Let $C^{und}_{N^{f}} \subseteq C_{ N^f}$ denote the set of undominated sets of cycles within $C_{N^f}$. Then, let $\{C\in C^{und}_{N^f },\left\{ f^{c}\right\} _{c\in C}\}$ denote an undominated closed-cycle decomposition for $N^f$.

The following Theorem 4 presents our characterization of the decomposition choice part. Essentially, for each case of min/max-circulation, in choosing closed-cycle decomposition along with the MIN-SFC/MAX-SFC in separated form, arbitrary undominated closed-cycle decomposition suffices. This implies that min-circulation might not be attained with a dominated decomposition. This is actually the case of the decomposition shown in the lower-right of Fig. 17. It is similarly confirmed for the case of max-circulation.

Theorem 4

(Min/max-circulation with undominated closed-cycle decomposition)

Given a closed f-network $N^{f}=\langle V,A,f\rangle$, regarding the min-circulation, we have:

• i) $x^{min}(N^{f})= F^{min}(N^{f}) + min_{C\in C^{und}_{N^{f}}, \left\{ f^{c}\right\} _{c\in C}} R^{min}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})$, where $F^{min}(N^{f}) = \sum _{c\in C'}f^{c}$ for an arbitrary undominated closed-cycle decomposition $N^{f}=\sum _{c\in C'}\langle V^{c},c,f^{c}\rangle$.

Regarding max-circulation, we have:

• ii) $x^{max}(N^{f})= F^{max}(N^{f}) - min _{C\in C^{und}_{N^{f}}, \left\{ f^{c}\right\} _{c\in C}} R^{max}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})$, where $F^{max}(N^{f}) = \sum _{c\in C'}(|c|-1)f^{c}$ for an arbitrary undominated closed-cycle decomposition $N^{f}=\sum _{c\in C'}\langle V^{c},c,f^{c}\rangle$.

Proof

See Appendix A.4. $\square$

Note that $F^{min}(N^f)$ and $F^{max}(N^f)$ indicate that arbitrary undominated closed-cycle decomposition has the same value.

5.2 Property of arc-twisted and Min-Circulation

As an input for MIN-SFC, take the f-network shown on the left side of Fig. 18, which is a reprint of Fig. 3. We mention in Sect. 3 that the fsp-network shown on the right side of Fig. 18 achieves a min-circulation of 40. Now, from the perspective of closed-cycle decomposition, the min-circulation is derived using the decomposition shown in Fig. 19. We confirm that the residual is not zero ($10>0$). As the source of the non-zero residual, we mention certain inconsistency between the two cycles, which we formally define as arc-twisted relation between cycles. We prepare to define arc-reverse number.

Arc-Reverse Number

For a given $G=\langle V,A\rangle$ together with a sequences on A, let cycle $c\in A$ consist of arcs $(a_{1},a_{2},\ldots a_{n},a_{n+1}=a_{1})$, where $a_{k}=(v_{k},v_{k+1})$ for $k=1,2,\ldots ,n$. Then, the arc-reverse number is defined as $r^{atwi}(c,s)=\sum _{k=1}^{n}1_{\left\{ s(a_{k})>s(a_{k+1})\right\} }$. When there are multiple ways to index arcs for a cycle and accordingly multiple values of the arc-reverse number (which is possible when the cycle is punctured), we set the arc-reverse number as the minimum among them.

Arc-Twisted

We say that cycles in $C\subseteq C_{G}$ are in arc-twisted relation, or simply that they are arc-twisted, if we cannot take any sequences on A such that $r^{atwi}(c,s)=1$ for every $c\in C$. We say that the cycles included in $C\subseteq C_{G}$ are minimum arc-twisted when there are no arc-twisted cycles $C' \subset C$. Returning to Fig. 19, the two decomposed cycles are arc-twisted and minimum arc-twisted. Note that minimum arc-twisted cycles are not always a pair, as confirmed in Fig. 20.

The following theorem is our main result on the relevance of the arc-twisted property for the residual part of min-circulation.

Theorem 5

(arc-twisted and $R^{min}(.)$)

Given a closed f-network $N^{f}$ and a closed-cycle decomposition, which is characterized by $C\in C_{N^{f}}$ and $\left\{ f^{c}\right\} _{c\in C}$, $R^{min}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})=0$ if and only if C is not arc-twisted.

Proof

When C is not arc-twisted, we can always take a sequence such that the arc-reverse number for every $c\in C$ is 1. This lets us take $\sum _{v\in V^{c}}p^{c}(v)=f^{c}$ for every $c\in C$. Conversely, when $R^{min}(.)=0$, we can always take the arc-reverse number as 1 for all $c\in C$ under any sequence that realizes $R^{min}(.)=0$. $\square$

Fig. 18

Example f-network to show the property of arc-twisted

Fig. 19

Closed-cycle decomposition for the f-network shown in Figure 18

Fig. 20

Examples of three cycles in arc-twisted relation. Notes: For the directed graph on the left, the three cycles on the right are minimum arc-twisted

5.3 Property of vertex-twisted and Max-Circulation

Let the f-network shown on the left side of Fig. 21, which is a reprint of Fig. 9, be our input for the MAX-SFC. We mention in Sect. 3 that the fsp-network shown on the right side of the figure attains the max-circulation as 110. From the perspective of closed-cycle decomposition, the max-circulation is derived using the decomposition shown in Fig. 22. We confirm that the residual is not zero ($10>0$). As the source of the non-zero residual, we mention certain inconsistency between the two cycles, which we formally define as vertex-twisted relation between cycles. We prepare to define the vertex-reverse number.

Vertex-Reverse Number

For $\langle V,A\rangle$, define the vertex-sequence$s_{v}:V\rightarrow \left\{ 1,2,\ldots ,|V|\right\}$ as a one-to-one mapping. For a given $\langle V,A\rangle$ together with a vertex-sequence$s_{v}$ on V, let cycle $c\in A$ consist of $(v_{1},v_{2},\ldots ,v_{n},v_{n+1})$, where $v_{n+1}=v_{1}$. Then, the vertex-reverse number is defined as $r^{vtwi}(c,s_{v})=\sum _{k=1}^{n}1_{\left\{ s_{v}(v_{k})>s_{v}(v_{k+1})\right\} }$. When there are multiple ways to index the vertices for a cycle and accordingly multiple values of the vertex-reverse number (which is possible when the cycle is punctured), we set the vertex-reverse number for the cycle as the minimum among them.

Vertex-Twisted

Cycles in $C\subseteq C_{G}$ are in vertex-twisted relation, or simply that they are vertex-twisted if we cannot take any vertex-sequence$s_{v}$ such that $r^{vtwi}(c,s_v)=1$ for every $c\in C$. Cycles in $C\subseteq C_{G}$ are minimum vertex-twisted when there are no vertex-twisted cycles $C' \subset C$.

Note that although any punctured cycle as in Fig. 23 is vertex-twisted by itself, the notion of vertex-twisted is not trivial in the sense that cycles that are not punctured can also be vertex-twisted, as shown in Figs. 22 and 24.

The following Theorem 6 is our main result on the relevance of the vertex-twisted property for the residual part of max-circulation.

Theorem 6

(Vertex-twisted and $R^{max}(.)$)

Given a closed f-network $N^{f}$ and its closed-cycle decomposition, which is characterized by $C\in C_{N^{f}}$ and $\left\{ f^{c}\right\} _{c\in C}$, $R^{max}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})=0$ if and only if C is not vertex-twisted.

Proof

When C is not vertex-twisted, then from its definition, we can always take vertex-sequence$s_{v}$ on vertices in C such that the vertex-reverse number is $|c|-1$ for all $c\in C$. Denote each set of vertices as $V_{k}=arg _{v\in V}s_{v}(v)=k$ for $k=1,2,\ldots ,|V|$. Take a sequence on arcs $a_{k}\in A$, which starts from $v\in V_{k}$ such that $\sum _{1}^{k-1}|V_{k-1}|< s(a_{k})< \sum _{1}^{k}|V_{k}|$. Since there is no vertex-twisted cycle, such a sequences lets us take $p^{c}$ such that each decomposed fsp-network is e-covered and $\sum _{v\in V^{c}}p^{c}(v)=(|c|-1)f^{c}$. What needs to be shown is that the combined fsp-network with the decomposed fsp-network is e-covered. For each vertex $v\in V$, take any two out-arcs $a'=(v,v'), a''=(v,v'')\in A$. Then, there is no in-arc $a'''=(v''',v)\in A$ such that $s(a')< s(a''')<s(a'')$. This is true for any two out-arcs. Thus, the combined fsp-network is e-covered.

For the converse direction, take a sequences that realizes $R^{max}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})=0$. Under the sequences, for each cycle $c\in C$ with its set of vertices $V^{c}$, take a vertex $v^{c}\in V^{c}$ such that $s((v,v^{c}))=argmin_{a\in c}s(a)$ and call it the head-vertex for c. Then, for every vertex $v'\in V^{c}\setminus v^{c}$ with its arc $(v',v)\in c$, there is no arc $a=(v'',v')\in C$ such that $s(a)<s((v',v))$ since otherwise it would immediately lead to $R^{max}(N^{f}, C,\left\{ f^{c}\right\} _{c\in C})> 0$. This is true for every cycle $c\in C$. Then, we can naturally define partial order < on $v\in V^{c}$ from sequences such that each head-vertex is the largest and becomes smaller in the direction opposite to that indicated by the arcs. We can always take the vertex-sequence to be consistent with the order <, and under such a vertex-sequence, the vertex-reverse number is 1 for every cycle $c\in C$. Thus, C is not vertex-twisted. $\square$

Fig. 21

Example f-network showing the property of vertex-twisted

Fig. 22

Closed-cycle decomposition for the f-network shown in Fig. 21

Fig. 23

Examples of vertex-twisted cycles. Notes: Each directed graph itself constitutes a punctured cycle

Fig. 24

Example directed graph of two vertex-twisted cycles. Notes: For the directed graph shown on the left, we can take the two cycles shown on the right, which are vertex-twisted

5.4 Arc-twisted and vertex-twisted

Note that if the cycles in C are arc-twisted, then they are also vertex-twisted as stated in the following Theorem 7. The opposite is not always true, as is easily confirmed.

Theorem 7

(arc-twisted and vertex-twisted)

For any set of cycles C, C is vertex-twisted if C is arc-twisted.

Proof

Suppose that C is not vertex-twisted. Then, by definition, we can take a vertex-sequence$s_{v}$ on the vertices in C such that the vertex-reverse number is 1 for all $c\in C$. Take a sequence$s^{c}$ for each $c\in C$ such that $s^{c}((v,v'))=s_{v}(v)$. We have $r^{atwi}(c,s^{c})=1$ for every $c\in C$. Since we can always take a sequence on the arcs in C such that the sequence is consistent with all $s^{c}$, C is not arc-twisted. $\square$

Policy Implications

In implementing policies that reduce the required liquidity for settlements, the base implication of Theorems 5, 6, and 7 is that the effect of each relevant “twist” property is scenario dependent. For the part of the arc-twisted property, which also indicates the vertex-twisted property, it would serve to increase the min-circulation but decrease the max-circulation. Thus, even if there is some policy that effectively “adds” the arc-twisted property, the implementation of the policy is not always recommended. For the part of the vertex-twisted property without the arc-twisted property, it would serve to decrease the max-circulation, while would not increase the min-circulation. Thus, it is recommended that a policy that adds such a property should always be implemented.

6 Quantitative Implications of the “twist” Properties

In this section, we show the quantitative implications of the “twist” properties in the context of a real-world payment network by examining certain classes of networks. First, we show the results associated with clustering, and then, we proceed to show the results associated with small-world feature.

6.1 Networks with clustered Structure

We consider two classes of f-networks with clustered structure, each of which highlights the quantitative implications of the “twist” properties.

6.1.1 Type-1 clustered Structure

First, as a generalization of the f-network shown on the left side of Fig. 18, we construct type-1 clustered f-network$\langle V,A,f\rangle$ as follows.

• Let $V=\left\{ v_{1},v_{2},\ldots ,v_{2n-1},v_{2n}\right\}$ for some integer $n\ge 3$. Let $A=A_{1}\cup A_{2}\cup A_{3}$.

• Take arcs of $(v_{2k-2},v_{2k-1})$ for $k=1,2,\ldots ,n$ with $v_{0}\equiv v_{n}$, and let this set of arcs be $A_{1}$. Take $f(a)=f_{1}$ for $a\in A_{1}$.

• Take arcs of $(v_{2k},v_{2k-3})$ for $k=1,2..,n$, with $v_{-1}\equiv v_{n-1}$, and let this set of arcs be $A_{2}$. Take $f(a)=f_{2}$ for $a\in A_{2}$.

• Take arcs of $(v_{2k-1},v_{2k})$ for $k=1,2,\ldots ,n$, and let this set of arcs be $A_{3}$. Take $f(a)=f_{3}=f_{1}+f_{2}$ for $a\in A_{3}$.

Figure 25 shows the underlying directed graph for a type 1 clustered f-network with $n=6$. Note that the f-network shown in Fig. 18 is an example of type 1 clustered f-network with; $n=3$, $A_{1}=\{(v_a,v_b), (v_c,v_d), (v_e,v_f)\}$ with $f_1=f(a\in A_{1})=20$, $A_{2}=\{(v_a,v_d), (v_e,v_b),(v_c,v_f)\}$ with $f_2=f(a\in A_{2})=10$, and $A_{3}=\{(v_f,v_a),(v_b,v_c),(v_d,v_e)\}$ with $f_3=f(a\in A_{3})=f(a\in A_{1})+f(a\in A_{2})=30$.

Fig. 25

Type-1 clustered f-network: $n=6$

Observation 7

Type-1 clustered f-network$\langle V,A,f\rangle$ is closed.

Furthermore, we have the following closed-cycle decomposition. $\langle V,A,f\rangle =\langle V,A_{1}\cup A_{3},f_{1}\rangle +\langle V,A_{2}\cup A_{3},f_{2}\rangle$, which we simplify as $\langle V,A,f\rangle =\langle V,c_{1},f_{1}\rangle + \langle V,c_{2},f_{2} \rangle$, where $c_1$ and $c_2$ are arc-twisted.

The following result explicitly shows the quantitative implications of the property of arc-twisted regarding this class of network.

Theorem 8

For a given type-1 clustered f-network$N^{f}=\langle V,A,f\rangle$ with $f_{1}\ge f_{2}$ in its construction, we have:

• i) $x^{min}(N^{f})=f_{1}+(n-1)f_{2}=(f_{1}+f_{2})+(n-2)f_{2}$.

• ii) Furthermore, for the case $f_{1}>f_{2}$, if the above value is realized with sequences on A, then $r^{atwi}(c_{1},s)=1$.

Proof

See Appendix A.5$\square$

The theorem is interpreted as revealing the following two features.²²

• Non-proportional feature

  For a given type-1 clustered f-network $N^f$ with $f_{1}>f_{2}$, take another type-1 clustered f-network $\tilde{N}^f$ with $f_{1}>f_{2}+m$. Then, we have

  • i) if $f_1>f_2+m$, then, $x^{min}(\tilde{N}^f)=x^{min}(N^f)+(n-2)m$, while

  • ii) if $f_1<f_2+m$, then, $x^{min}(\tilde{N}^f)=x^{min}(N^f)+(n-2)(f_2-f_1)+ (m-f_1)$.

This states that the marginal effect on the min-circulation against an increase in flow regarding the cycle $c_2(=A_2\cup A_3)$ is $(n-2)$ until $m< f_1-f_2$; but once $m>f_1-f_2$, the marginal effect turns to 1.

• Regime-change feature

  For a given type-1 clustered f-network $N^f=\langle V,A,f\rangle$ with $f_{1}>f_{2}$, let sequence$s^*$ on A attain the min-circulation. Take another type-1 clustered f-network $\tilde{N}^f$ with $f_{1}>f_{2}+m$; then, we have

  • i) if $f_1>f_2+m$, then, $s^*$ attains the min-circulation also for $\tilde{N}^f$, while

  • ii) if $f_1<f_2+m$, then, $s^*$ no longer attains the min-circulation for $\tilde{N}^f$.

6.1.2 Type-2 clustered Structure

Now, we construct another class of clustered f-network. It is intended to capture a key feature of the f-network shown on the left side of Fig. 21, which is introduced as type-2 clustered f-network$\langle V,A,f\rangle$ as follows.

• Let $V=\left\{ v_{1},v_{2},\ldots ,v_{n-1},v_{n}\right\}$ for some integer $n\ge 3$. Let $A=A_{1}\cup A_{2}$.

• Take arcs of $(v_{k},v_{k+1})$ for $k=1,2,\ldots ,n$ with $v_{n+1}\equiv v_{1}$, and let this set of arcs be $A_{1}$. Take $f(a)=f_{1}$ for $a\in A_{1}$.

• Take arcs of $(v_{k+1},v_{k})$ for $k=1,2,\ldots ,n$ with $v_{n+1}\equiv v_{1}$, and let this set of arcs be $A_{2}$. Take $f(a)=f_{2}$ for $a\in A_{2}$.

Fig. 26

Type-2 clustered f-network: $n=6$

A type-2 clustered f-network consists of two cycles that have the “opposite” direction in the sense of the associated arcs. Figure 26 shows the underlying directed graph for a type-2 clustered f-network with $n=6$. Although the class might seem fairly special, we could generalize the associated results beyond the class, but this is beyond the scope of this study.²³

Observation 8

Type-2 clustered f-network$\langle V,A,f\rangle$ is closed.

Furthermore, we have the following closed-cycle decomposition. $\langle V,A,f\rangle =\langle V, A_{1},f_{1}\rangle +\langle V, A_{2},f_{2}\rangle$, where $A_1$ and $A_2$ are vertex-twisted.

The following result explicitly shows the quantitative implications of the property of vertex-twisted regarding this class of network.

Theorem 9

For a given type-2 clustered f-network$N^{f}=\langle V,A,f\rangle$ with $f_{1}\ge f_{2}$ in its construction, we have:

• i) $x^{max}(N^{f})=(n-1)f_{1}+f_{2}=(n-1)(f_{1}+f_{2})-(n-2)f_{2}$.

• ii) Furthermore, for the case of $f_{1}>f_{2}$, if the above value is realized with sequences on A, then $r^{atwi}(A_{1},s)=n-1$.

Proof

See Appendix A.6. $\square$

The theorem is interpreted to reveal the following two features.

• Non-proportional feature

  For a given type-2 clustered f-network $N^f$ with $f_{1}>f_{2}$, take another type-2 clustered f-network $\tilde{N}^f$ with $f_{1}>f_{2}+m$; then, we have

  • i) if $f_1>f_2+m$, then, $x^{max}(\tilde{N}^f)=x^{min}(N^f) + m$, while

  • ii) if $f_1<f_2+m$, then, $x^{max}(\tilde{N}^f)=x^{min}(N^f)+(f_2-f_1)+ (n-1)(m-f_1)$.

This states that the marginal effect on the min-circulation against an increase in flow regarding cycle $A_2$ is 1 until $m< f_1-f_2$; but once $m>f_1-f_2$, the marginal effect becomes $n-2$.

• Regime-change feature

  For a given type-2 clustered f-network $N^f=\langle V,A,f\rangle$ with $f_{1}>f_{2}$, let sequence$s^*$ on A attain the min-circulation. Take another type-2 clustered f-network $\tilde{N}^f$ with $f_{1}>f_{2}+m$; then, we have

  • i) if $f_1>f_2+m$, then, $s^*$ attains the max-circulation also for $\tilde{N}^f$, while

  • ii) if $f_1<f_2+m$, then, $s^*$ no longer attains the max-circulation for $\tilde{N}^f$.

6.2 Networks with small-world Structure

We construct an f-network with a small-world structure by the rewiring procedure, originally proposed by Watts and Strogatz (1998) for the construction of their WS model. In the face of directionality of an f-network, we rewire in a fully connectivity-preserving manner, as proposed by Maslov et al. (2003), where both the out-degree and in-degree are preserved. Furthermore, the closed property is to be preserved.

First, we start with type-1 clustered f-network$\langle V,A,f\rangle$ where $f(a)\ge f(a')$ for every $a\in A_{1}, a'\in A_{2}$ in its construction. Follow the procedure below, for appropriate ratio p ($0\le p\le 1$).

• Choose $\frac{|V|}{2}p$, an odd number of arcs from $A_{2}$, such that there are no two arcs whose vertex constitutes an arc.

• Randomly let the chosen arcs be repaired with each other; then, rewire by exchanging the end vertices while preserving each flow (e.g. a pair $(v_{a},v_{b}), (v_{c},v_{d})$ becomes $(v_{a},v_{d}), (v_{c},v_{b})$, and the flow for each old pair is preserved for each new pair).

Figure 27 shows an example of this rewiring procedure. According to the following Theorem 10, the synchronization factor characterized by the arc-twisted property and that by the vertex-twisted property are sufficiently preserved by the rewiring.

Theorem 10

For a type-1 clustered f-network $N^{f}$, denote its rewired f-network with p as $N^{f}(p)$. Then, $x^{min}(N^{f}(p)) \ge f_{1} + f_{2} + ( (n-2) - np )f_{2}$.

Proof

Suppose we have already executed rewiring with k pairs. Observe that rewiring partitions the original cycle formed by $c_{2}$ into several cycles; here, we denote the number of cycles as $k'$. When we further execute rewiring with respect to an additional pair of arcs, the rewiring occurs either among one of the cycles, or between two of them. In the former case, one more cycle is added, and the total number of cycles is $k'+1$. The latter case always lets the two cycles become one, which makes the total number of cycles $k'-1$. Focusing on how the residual amount is affected by this, in either case, the min-circulation decreases at most by $f_{2}$. $\square$

Fig. 27

Example of rewiring for type-1 clustered f-network. Notes: The left network constitutes the type-1 clustered f-network shown in Fig. 25. Rewiring the f-network with $p=\frac{1}{3}$, regarding a pair of arcs $(v_2,v_{11})$ and $(v_8,v_5)$, we derive the network shown on the right side of the figure, which includes a pair of rewired arcs $(v_2,v_5)$ and $(v_8,v_{11})$

Next, we similarly rewire type-2 clustered f-network$\langle V,A,f\rangle$ where $f(a)\ge f(a')$ for every $a\in A_{2}, a'\in A_{2}$ in its construction. Follow the procedure below, for appropriate ratio p ($0\ge p\ge 1$).

• Choose |V|p, an odd number of arcs from $A_{2}$, such that there are no two arcs whose vertex constitutes an arc.

• Randomly let the chosen arcs be repaired with each other; then, rewire by exchanging the end vertices while preserving each flow (e.g. a pair $(v_{a},v_{b}), (v_{c},v_{d})$ becomes $(v_{a},v_{d}), (v_{c},v_{b})$, and the flow for each old pair is preserved for each new pair).

Figure 28 shows an example of this rewiring procedure. According to the following Theorem 11, the synchronization factor characterized by the vertex-twist property is sufficiently preserved by the rewiring.

Theorem 11

For a type-2 clustered f-network $N^{f}$, denote its rewired f-network with p as $N^{f}(p)$. Then, $x^{max}(N^{f}(p)) \le (n-1)(f_{1} + f_{2}) - ( (n-2) - np )f_{2}$.

Proof

The proof is shown similarly to that of Theorem 10. $\square$

Fig. 28

Example of rewiring for type-2 clustered f-network. Notes: The left network constitutes the type-1 clustered f-network shown in Fig. 26. Rewire the f-network with $p=\frac{1}{3}$, regarding a pair of arcs $(v_2,v_1)$ and $(v_5,v_4)$; then, the network shown on the right side of the figure includes a pair of rewired arcs $(v_2,v_4)$ and $(v_5,v_1)$

6.3 Discussion

For both the rewiring procedures, a clustered structure appropriately defined²⁴ would only be locally affected, while the average path length would be affected as much as that in the case of the WS model when n is sufficiently large relative to p. This implies that a small-world structure would emerge with appropriate p. In this sense, Theorems 10 and 11 indicate that the effects of the twist properties can be preserved under a small-world structure. As it is argued that real-world payment networks have a small-world structure, our twist properties have significance when applied to real-world payment networks.

7 Concluding Remarks

In this study, we introduced a graph-theoretic framework intended to capture interbank settlements in an RTGS system. We analyzed the lower bound and upper bound of the required liquidity for a given payment network, by offering corresponding minimization and maximization graph problems. We showed our characterization for a general class of payment network by introducing two graph properties—arc-twisted and vertex-twisted. We further showed that these “twist” properties are sources of the non-linear effect on the required liquidity against an increase of the amount of obligation, illustrating the effects for networks with clustered and small-world structures.

In existing models of financial networks, liquidity is usually discussed by implicitly or explicitly assuming simultaneous settlements. This assumption tends to underevaluate overall liquidity needs, considering that sequential settlement is prevalent in reality. Thus, the types of models in the existing literature are not particularly suitable for a discussion of liquidity regulations in which a sufficient level of liquidity requirements is the focus. Our framework enables to discuss liquidity needs explicitly by considering the sequential nature of settlements, and thus, has potential to contribute significantly to the issue. It remains for our future work to enrich the model for the sake of those applications.

Appendix

1.1 Proof of Lemma 2

For an e-covered $\langle V,A,f,s,p\rangle$ on a closed $\langle V,A,f\rangle$, we derive a set of e-covered fsp-networks for some closed-cycle decomposition of $\langle V,A,f\rangle$ by executing the unbundling procedure for each $v\in V$, which proceeds as follows.

Let $A_v^I=\left\{ (v',v)\right\} _{v'\in V}$ and $A_v^O=\left\{ (v,v')\right\} _{v'\in V}$ denote the incoming arcs to vertex v and the outgoing arcs to v, respectively. Note that $argmin _{a\in A_v^I}s(a)$ denotes the arc whose sequence is the smallest within the incoming arcs regarding vertex v. We similarly use the notation of argmax.

• 0. Initially, let $A_{v,work}^{I}=A_{v}^{I}$, $A_{v,work}^{O}=A_{v}^{O}$, $f_{work}=f$.

• 1. We update them until $A_{v,work}^{I}=A_{v,work}^{O}=\emptyset$.

  Take $a_{min}^{I},a_{max}^{I} \in A_{v,work}^{I}$, $a_{min}^{O} \in A_{v,work}^{O}$ such that $a^{I}_{min}= argmin _{a\in A^{I}_{v,work}}s(a)$, $a^{I}_{max}=argmax _{a\in A^{I}_{v,work}}s(a)$, $a^{O}_{min}=argmin _{a\in A^{O}_{v,work}}s(a)$.

• 2a. If $s(a_{min}^{I})<s(a_{min}^{O})$, then let the arcs be a pair with the same amount of flow$min\left\{ f_{work}(a_{min}^{I}), f_{work}(a_{min}^{O})\right\}$.

  For the center vertex of the paired arc, endow potential 0, and let the sequence on the pair of arcs be consistent with the original sequence on $\langle V,A,f\rangle$.

  Update $f_{work}(a_{min}^{I}):=f_{work}(a_{min}^{I})-min\left\{ f_{work}(a_{min}^{I}), f_{work}(a_{min}^{O})\right\}$, and $f_{work}(a_{min}^{O}): f_{work}(a_{min}^{O})-min\left\{ f_{work}(a_{min}^{I}), f_{work}(a_{min}^{O})\right\}$.

  Remove $a_{min}^{I}$ from $A_{v,work}^{I}$ if $f_{work}(a_{min}^{I})=0$, and remove $a_{min}^{O}$ from $A_{v,work}^{O}$ if $f_{work}(a_{min}^{O})=0$.

  Go back to step 1 if either $A_{v,work}^{I}$ or $A_{v,work}^{O}$ is not empty; otherwise, end the procedure.

• 2b. If $s(a_{min}^{I})>s(a_{min}^{O})$, then let the arcs be a pair with the same amount of flow$min\left\{ f_{work}(a_{max}^{I}), f_{work}(a_{min}^{O})\right\}$.

  For the center vertex of the paired arc, endow potential$min\big \{f_{work}(a_{max}^{I}), f_{work}(a_{min}^{O})\big \}$, and let the sequence on the pair of arcs be consistent with the original sequence on $\langle V,A,f\rangle$.

  Update $f_{work}(a_{max}^{I}):=f_{work}(a_{max}^{I})-min\left\{ f_{work}(a_{max}^{I}), f_{work}(a_{min}^{O})\right\}$, and $f_{work}(a_{min}^{O}):= f_{work}(a_{max}^{O})-min\left\{ f_{work}(a_{max}^{I}), f_{work}(a_{min}^{O})\right\}$.

  Remove $a_{max}^{I}$ from $A_{v,work}^{I}$ if $f_work(a_{max}^{I})=0$, and remove $a_{min}^{O}$ from $A_{v,work}^{O}$ if $f_work(a_{min}^{O})=0$.

  Go back to step 1 if either $A_{v,work}^{I}$ or $A_{v,work}^{O}$ is not empty; otherwise, end the procedure.

After the above unbundling procedure for each $v\in V$, we let consecutive arcs be arbitrarily connected to each other with each same flow and relevant potential so as to form a closed-cycle decomposition. Then, we can always connect consecutive pairs by taking an appropriately small unit of flow attached when necessary. Furthermore, by attaching an appropriate sequence for each derived decomposed f-network that is consistent with the original sequence, each derived connected fsp-network is to be e-covered by construction. Figure 30 shows our unbundling procedure for the example shown in Fig. 29.

Fig. 29

Before the unbundling procedure

Fig. 30

Unbundling procedure for Fig. 29

1.2 Proof of Theorem 2

Lemma 2 ensures that our search for fsp-networks on the basis of closed-cycle decomposed f-networks always includes fsp-networks that realize the min-circulation. What remains to be shown is that we correctly choose those fsp-networks by minimizing the circulation for closed-cycle decomposed f-networks. This is ensured by the following lemma.

Lemma 3

Given a closed f-network $N^{f}=\langle V,A,f\rangle$, for any closed-cycle decomposition $N^{f}=\sum _{c\in C}\langle V^{c},c,f^{c}\rangle$, if $\langle V^{c},c,f^{c},s^{c},p^{c} \rangle$ is e-covered for every $c\in C$, and we can take $s:V\rightarrow \left\{ 1,2,\ldots ,|A|\right\}$ which is consistent with $\left\{ s^{c}\right\} _{c\in C}$, then $\langle V,A,f,s,p\rangle = \sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$ is covered.

Proof

As long as $\left\{ s^{c}\right\} _{c\in C}$ is consistent with s, it is straightforward that combining covered fsp-networks always gives a covered fsp-network. $\square$

The lemma states that our search on the basis of closed-cycle decomposed f-networks never lets us find smaller circulation than the “true” min-circulation. Combining Lemmas 2 and 3, we end our proof.

1.3 Proof of Theorem 3

Our proof is similar to that for Theorem 2. Lemma 2 ensures that our search for fsp-networks on the basis of closed-cycle decomposed f-networks always includes fsp-networks that realize the max-circulation. Since we confine our focus to the cases in which combined fsp-networks become e-covered, our search on the basis of closed-cycle decomposed f-networks never lets us reach a larger circulation than the “true” max-circulation. This ends our proof.

1.4 Proof of Theorem 4

Lemma 4 provides our proof of the theorem, regarding both min and max-circulation.

Lemma 4

(E-covered decomposition with undominated closed-cycle decomposition)

Given a closed f-network $N^{f}=\langle V,A,f\rangle$, take an arbitrary e-covered fsp-network $N^{fsp}=\langle V,A,f,s,p\rangle$.

Then, we always take some e-covered decomposition $N^{fsp}=\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$ with undominated closed-cycle decomposition $\left\{ \langle V^{c},c,f^{c}\rangle \right\} _{c\in C}$.

Proof

For the given $N^{fsp}$, take an e-covered decomposition $\left\{ \langle V^{c},c,f^{c},s^{c},p^{c}\rangle \right\} _{c\in C}$ with a closed cycle decomposition $\left\{ \langle V^{c},c,f^{c}\rangle \right\} _{c\in C}$. We consider to take an undominated closed cycle decomposition by transforming the closed cycle decomposition in a manner stated below. We show that, for the derived undominated closed cycle decomposition, we can take an e-covered decomposition of the given $N^{fsp}$.

For a given closed cycle decomposition, we consider transformation such that for a vertex, taking different pairs of the incoming arcs and the outgoing arcs to form another closed cycle decomposition. For the sake of our formal statement of the transformation, we prepare notations; for a vertex $v\in V$, denote $A_{v}^{I}=\left\{ (v',v)\right\} _{v'\in V}$, and $A_{v}^{O}=\left\{ (v,v')\right\} _{v'\in V}$.

First, when either $A^{I}_{v}$ or $A^{O}_{v}$ is singleton, Lemma 5 ensures that any combination between $A^{I}_{v}$ and $A^{O}_{v}$ that can generate another closed-cycle decomposition maintains the e-covered property under the same s and p. Now, we proceed to the case in which each of $A^{I}_{v}$ and $A^{O}_{v}$ is not singleton. Under the supposed closed-cycle decomposition, if any two cycles both commonly include v but have no common arc, then we only need to combine the two cycles into one punctured cycle in order to derive an undominated closed-cycle decomposition. Lemma 6 ensures that the derived cycles are necessarily e-covered under the same s and p. Then, suppose that there exists an undominated closed-cycle decomposition with some other combination between $A^{I}_{v}$ and $A^{O}_{v}$ for each $v\in V$. Some repetition of the procedure stated in Lemma 7 ensures that we can always take some undominated closed-cycle decomposition with the original combination between $A^{I}_{v}$ and $A^{O}_{v}$. This means that we can take some undominated closed-cycle decomposition under the same s and p that constitutes the same e-covered fsp-network for which the original undominated closed-cycle decomposition is another e-covered decomposition. $\square$

Lemma 5

(Invariance of e-covered property: singleton $A^{I}_{v}$ or $A^{O}_{v}$)

For a closed f-network $N^{f}=\langle V,A,f\rangle$, take a closed-cycle decomposition $N^{f}=\sum _{c\in C}\langle V^{c},c, f^{c}\rangle$ such that it constitutes some e-covered decomposition for some e-covered $N^{fsp}=\langle V,A,f,s,p\rangle$ as $N^{fsp}=\langle V,A,f,s,p\rangle =\sum _{c\in C}\langle V^{c},c, f^{c},s^{c},p^{c}\rangle$. Then, for any $v\in V$ such that either $A^{I}_{v}$ or $A^{O}_{v}$ is singleton, take another closed-cycle decomposition $\left\{ \langle V^{c},c,f^{c}\rangle \right\} _{c\in C'}$ by transforming it such that the combination between $A^{I}_{v}$ and $A^{O}_{v}$ is different.

Then, we can always take an e-covered decomposition $\langle V,A,f,s,p\rangle =\sum _{c\in C'}\langle V^{c},c, f^{c},s^{c},p^{c}\rangle$

Proof

Under given closed-cycle decomposition $N^{f}=\sum _{c\in C}\langle V^{c},c, f^{c}\rangle$, suppose that $A^{I}_{v}$ or $A^{O}_{v}$ is singleton. Then, any sequences on $A^{I}_{v}\cup A^{O}_{v}$ uniquely determines the relative order between any pair of arcs $a,a'$ where $a\in A^{I}_{v}$ and $a'\in A^{O}_{v}$. $\square$

Lemma 6

(Invariance property of e-covered decomposition by letting cycles be punctured)

For a closed f-network $N^{f}=\langle V,A,f\rangle$, take arbitrary e-covered $N^{fsp}=\langle V,A,f,s,p\rangle$ and some e-covered decomposition $N^{fsp}=\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$.

Then, if there exist any two cycles $c,c'\in C$ that constitute a punctured cycle $c''\notin C$, we always take another closed-cycle decomposition that includes the punctured cycle, and it still constitutes an e-covered decomposition for the same $\langle V,A,f,s,p\rangle$.

Proof

Take some e-covered decomposition $N^{fsp}=\sum _{c\in C}\langle V^{c},c,f^{c},s^{c},p^{c}\rangle$. When there exist K cycles $\left\{ c_{k}\right\} _{k=1,\ldots ,K}$ with flow$\left\{ f^{c_{k}}\right\} _{k=1,\ldots ,K}$ each includes some $v\in V$, denote the relevant arcs as $A^{I}_{v,k}\equiv c_{k}\cap A^{I}_{v}$, $A^{O}_{v,k}\equiv c_{k}\cap A^{O}_{v}$.

Take two cycles $c_{k},c_{k'}\in C$ that constitute a punctured cycle $c_{K+1}\notin C$. Take another closed-cycle decomposition with $c_{K+1}$ with some flow$f^{c_{K+1}}\le min(f^{c_{k}}, f^{c_{k'}})$. Let $\langle V^{c_{K+1}}, c_{K+1}, f^{c_{K+1}}, s^{c_{K+1}},p^{c_{K+1}}\rangle$ be e-covered under the same s on A. We always have $p^{c_{K+1}}(v)\le p^{c_{k}}(v)+ p^{c_{k'}}(v)$ from Lemma 8. Suppose that $p^{c_{K+1}}(v)< p^{c_{k}}(v)+ p^{c_{k'}}(v)$. Then, for the original decomposition to be e-covered, the redundant amount somehow needs to be absorbed by some other cycles within $C_{v}$ with respect to v. Again, this contradicts Lemma 8 with respect to other relevant cycles not to be transformed. Thus, $p^{c_{K+1}}(v)= p^{c_{k}}(v)+ p^{c_{k'}}(v)$, which ensures invariance of the e-covered property under our transformation. $\square$

Lemma 7

(Invariance of undominated closed-cycle decomposition)

For a closed $N^{f}=\langle V,A,f\rangle$, take an undominated closed-cycle decomposition $N^{f}=\sum _{c\in C}\langle V^{c},c, f^{c}\rangle$. For an arbitrary $v\in V$ such that $|A^{I}_{v}|>1$ and $|A^{O}_{v}|>1$, let $C_{v}\subset C$ denote the set of cycles that include v. Let $C_{v}=\left\{ c_{1},c_{2}..,c_{K}\right\}$ with $\sum _{k=1}^{K}f^{c_{k}}\equiv F_{v}$, and let $A^{I}_{v,k}\equiv c_{k}\cap A^{I}_{v}$ and $A^{O}_{v,k}\equiv c_{k}\cap A^{O}_{v}$.

Take another combination between $A^{I}_{v}$ and $A^{O}_{v}$ by combining some $a^{I}_{v,k}\in A^{I}_{v,k}$ and $a^{O}_{v,k'}\in A^{O}_{v,k'}$, and also combine $a^{I}_{v,k'}\in A^{I}_{v,k'}$ and $a^{O}_{v,k}\in A^{O}_{v,k}$. Further, take an arbitrary amount of flow$f'\le min (f^{c_{k}}, f^{c_{k'}})$ for each combination.

Then, we can always take another undominated closed-cycle decomposition with this new combination between $A^{I}_{v}$ and $A^{O}_{v}$.

Proof

For two cycles $c_{k},c_{k'}\in C$ where neither is a subset of the other, if they have some common $v\in V$, we can always take some arc $a\in c_{k}\cap c_{k'}$ as ensured by Lemma 9. Take a path from a to $a^{I}_{v,k}$, and $a^{O}_{v,k'}$ to a, and merge two paths to take a cycle and denote it as $c_{K+1}$. Furthermore, take its counterpart path from a to $a^{I}_{v,k'}$, and $a^{O}_{v,k}$ to a each , and merge them to take a cycle $c_{K+2}$. Attach flow$f'$ on both $c_{K+1}$ and $c_{K+2}$, and remove the same amount $f'$ from each of the original two cycles $c_{k},c_{k'}$ as $f^{c_{k}}=f^{c_{k}}-f'$ and $f^{c_{k'}}=f^{c_{k'}}-f'$. The derived set of closed-cycles constitutes a new closed-cycle decomposition. From its construction, the sum of flow for the derived cycles is the same as $F_{v}$, which shows that the derived closed-cycle decomposition is also undominated. $\square$

Lemma 8

(Invariance of covered property by merge of vertices)

For a closed $\langle V,A,f\rangle$, take an e-covered $\langle V,A,f,s,p\rangle$. Let $v,v'\in V$ merge into a single $v''$ that maintains relevant flow, sequence, and potential, to have another fsp-network $\langle V',A',f',s',p'\rangle$.

Then, $\langle V',A',f',s',p'\rangle$ is always covered.

Proof

From the definition of the e-covered property, for any $v\in V$, at any point of its outflow there remains a sufficient amount of funds. It is straightforward that merging these two vertices preserves the covered property. $\square$

Lemma 9

(Property of undominated closed-cycle decomposition)

For a closed f-network $N^{f}=\langle V,A,f\rangle$, take an undominated closed-cycle decomposition $N^{f}=\sum _{c\in C}\langle V^{c},c, f^{c}\rangle$. Then, we have for any two $c,c'\in C$ where neither is a subset of the other. Then, $V^{c}\cap V^{c'}\ne \emptyset$ iff $c\cap c' \ne \emptyset$.

Proof

It is immediate that $V^{c}\cap V^{c'}\ne \emptyset$ if $c\cap c' \ne \emptyset$. For the opposite part, suppose that under some undominated closed-cycle decomposition, there exist two cycles $c,c'$ with $\langle V^{c},c, f^{c}\rangle$ and $\langle V^{c'},c', f^{c'}\rangle$ where $V^{c}\cap V^{c'}\ne \emptyset$ but $c\cap c'= \emptyset$. Then, we always take another closed-cycle decomposition by letting the cycles combine to take $\langle V^{c}\cup V^{c'}, c\cup c', min\left\{ f^{c},f^{c'}\right\} \rangle$, which dominates the original closed-cycle decomposition. This contradicts our supposition. $\square$

1.5 Proof of Theorem 8

We provide our proof from a rather general perspective, focusing not only on type-1 clustered networks but also on clustered networks in which each cluster forms a tree, whose definition is stated below. When each cluster is captured by a tree, we show that a certain monotonicity enables us to examine min-circulation.

1.5.1 Defluent Partition

First, we prepare terminologies in order to formally describe the relevant monotonicity. The key terminology is defluent. Monotonicity implied by defluent refers to how flow bifurcates, which lies in the monotonicity implied by tree with regard to how arcs connect to each other. Figure 31 helps clarify the following terminologies.

We start by defining tree. First consider a graph that is not directed, which we denote as $\langle V,E\rangle$ where each $e\in E$ is an unordered pair of vertices denoted as $e=\left\{ v,v'\right\}$ with some $v,v'\in V$. We allow multiple edges for the same pair of vertices. We say that $\langle V,E\rangle$ has a cycle if there exists a sequence of vertices such that every two consecutive vertices are included as a different edge and the same vertex can be shown more than once in the sequence. For a directed graph $\langle V,A\rangle$, we can take its underlying undirected graph $\langle V,E\rangle$ by replacing each ordered pair with an unordered pair. Now, we call a directed graph $\langle V,A\rangle$ a tree if it is connected and its underlying undirected graph $\langle V,E\rangle$ has no cycle. Note that if $\langle V,A\rangle$ is a tree, then it has no cycle on the basis of a directed graph, but the opposite is not necessarily true, since our definition of tree does not allow even a cycle on the basis of an undirected graph to exist. For tree$\langle V,A\rangle$, we call each vertex $v\in V$ that has no arc that starts at v a leaf.

A tree$\langle V,A\rangle$ is called a rooted tree if there is one vertex $v\in V$ designated as the root such that for any other vertex $v'\in V\setminus v$, there is a sequence of vertices from v to $v'$ where every two consecutive vertices $v_{k},v_{k'}$ are included as a different arc as $(v_{k},v_{k'})\in A$.

A tree$\langle V,A\rangle$ is called a trunked tree if (1) it is a rooted tree, and (2) there is only one arc $(v,v')$ designated as the trunk such that it starts at the root $v\in V$.

Fig. 31

Examples of defluent and relevant notions. Each of the left and right f-networks is defluent. The underlying directed graph for the left f-network is a trunked tree whose root is $v_{a}$, trunk is $(v_{a},v_{b})$, and leaves are $v_{d}$, $v_{e}$, and $v_{f}$. Height is 0 for the leaves, 1 for $v_{c}$, 2 for $v_{b}$, and 3 for $v_{a}$. For the right f-network, the underlying directed graph is not itself a tree, but the directed graph on the left is its trunked tree representation that is hatcheled on $v_{d}$ by adding $v_{f}$

For a rooted tree, we define the height of each vertex within the tree. First we prepare the terminology length of a path. The length of path$A'$ is the number of arcs $|A'|$. Now, for a rooted tree$\langle V,A\rangle$, the height of a vertex $v\in V$ is the maximum length of the path to the leaves.

We define tree to obey common usage. Since the definition is too strict for our purpose, we argue whether $\langle V,A\rangle$ has trunked tree representation or not. In order to define trunked tree representation, we prepare the terminology of hatchel. Directed graph $\langle V,A\rangle$ is hatcheled into $\langle V',A' \rangle$ when we can take $\langle V',A'\rangle$ through the following procedure. For every $v\in V$ that has no arc that starts at v, when there exist $n>1$ multiple arcs that end at v, add $n-1$ vertices. Then, for each of the arcs except arbitrary ones , replace v with each of the added vertices such that each arc ends at each different vertex either at v or at some added vertex. For derived $\langle V',A'\rangle$, any vertex that has no arc that starts at itself has no two arcs that end at itself.

Now, we say that directed graph $\langle V,A\rangle$ has trunked tree representation$\langle V',A'\rangle$ when (1) $\langle V,A\rangle$ is hatcheled into $\langle V',A'\rangle$, and (2) $\langle V',A'\rangle$ is a trunked tree. For f-network $\langle V,A,f\rangle$, when $\langle V,A\rangle$ has trunked tree representation$\langle V',A'\rangle$, $\langle V',A',f'\rangle$ is its associated f-network when (1) $f'(a)=f(a)$ for any $a\in A\cap A'$, and (2) for each replacement $a\in A$ with $a'\in A'$ by the procedure of hatchel, $f'(a')=f(a)$.

We proceed to define monotonicity regarding flow bifurcation. $\langle V,A,f\rangle$ is defluent when (1) $\langle V,A\rangle$ has trunked tree representation$\langle V',A'\rangle$, and (2) for its associated $\langle V',A',f'\rangle$, for any $v\in V'$ that is neither root nor leaf, flow is balanced as $\sum _{v'\in V'}f(v,v')= \sum _{v'\in V'}f(v',v)$.

We argue partial monotonicity by examining a specific class of decomposition called defluent partition. For $N^{f}=\langle V,A,f\rangle$, decomposition$\left\{ N^{f}_{k}=\langle V_{k},A_{k},f_{k}\rangle \right\} _{k=1,2,\ldots ,K}$ is partition when (1) for every $k=1,2,\ldots , K$, $\langle V_{k},A_{k}\rangle$ is connected, and (2) for any two $N^{f}_{k}, N^{f}_{k'}$, we have $A_{k}\cap A_{k'}=\emptyset$.

Finally, a partition for $\langle V,A,f\rangle$ is a defluent partition when (1) each partitioned f-network is defluent, and (2) any two partitioned f-networks have no common vertex that is neither root nor leaf within either of the defluents.

For f-network $N^{f}=\langle V,A,f\rangle$, when we take defluent partition$\left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K}$, we obtain the set of edge vertices denoted as $V^{edge}(\left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K})\subset V$; each vertex is the root for the partitioned f-network in the sense that each vertex is the root for each trunked tree representation.

For any f-network, there exists some defluent partition since a partition into each arc is itself a defluent partition.

Theorem 12

(Defluent partition)

For a closed f-network $N^{f}=\langle V,A,f\rangle$, take an arbitrary defluent partition$\left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K}$ with the set of edge vertices $V^{edge}(\left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K})$. Then, the following problem attains the same value with $x^{min}(N^{f})$.

$$\begin{aligned} \begin{aligned} min_{s,p}&\sum _{v\in V}p(v)\\ \hbox {s.t., }&\langle V,A,f,s,p\rangle \hbox { is e-covered, and}\\&p(v)=0\hbox { for every }v\in V\setminus V^{edge}\left( \left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K}\right) . \end{aligned} \end{aligned}$$

Proof

For our input $N^{f}=\langle V,A,f\rangle$, take an arbitrary e-covered $\langle V,A,f,s,p\rangle$, which attains the min-circulation $x^{min}(N^{f})$.

For a partitioned f-network $N^{f}_{k}=\langle V_{k},A_{k},f_{k}\rangle$, denote a set of vertices $V_{k}^{i}$ with $i=0,1,\ldots$ where each $V_{k}^{i}$ contains vertices that have heighti within its rooted tree. First find $p(v)>0$ for $v\in V^{1}_{k}$. When we find such v with $(v',v)$, then we always take an arc $a'=(v,v'',n)\in A$ such that $s(a')<s(a)$ with some $n=0,1,\ldots$. Now take another sequence$s':A\rightarrow \left\{ 1,2,\ldots ,A\right\}$ that lets $s'(a')>s'(a)$ while endowing the same ordering with the sequences for $A\setminus a'$. Take associated e-covered $\langle V,A,f,s',p'\rangle$; then, we have $p'(v)=p(v)-f(a')$ and $p'(v'')\le p(v'')+f(a')$. The former is true since there is only one arc that ends at v, while the latter is true since there is only one arc that starts at $v''$. In addition, we have $p'(v''')=p(v''')$ for any $v'''\in V\setminus v, v''$. It leads to $\sum _{v\in V}p'(v) \le \sum _{v\in V}p(v)$. Furthermore, since $\sum _{v\in V}p(v)=x^{min}p(v)$, we have $\sum _{v\in V}p'(v)=x^{min}(N^{f})$.

Fig. 32

Example for defluent partition. Notes: For the f-network on the left, the three f-networks on the right constitute its defluent partition with the set of edge vertices $\left\{ v_{d},v_{f},v_{b}\right\}$

For each of the vertices within $V^{1}_{k}$, execute this procedure of replacing the sequence. When completed for $V^{1}_{k}$, we proceed to $V^{2}_{k}$. For this case, when we replace the sequence regarding vertex $v\in V^{2}_{k}$ and arc $(v,v')\in V$, we also maintain the ordering within each trunked tree with trunk $(v,v')$ and its leaves so that the potential is different only within the edge vertices $V^{edge}(\left\{ N^{f}_{k}\right\} _{k=1,2,\ldots ,K})$. When finished for $V^{2}_{k}$, we proceed to $V^{3}_{k},V^{4}_{k},\ldots$ until we reach each root. Such replacement of a sequence always realizes the min-circulation with the associated e-covered fsp-network, while letting $p(v'')=0$ for every vertex except for root and leaves. By executing the procedure for every partitioned defluent, we derive the statement in the theorem (Fig. 32). $\square$

1.5.2 Proof of Theorem 8

We prove the theorem using defluent partition.

Proof

For our given f-network with some n, take a defluent partition$N^{f}=\sum _{k=1}^{n}N^{f}_{k}$ with $N^{f}_{k}=\langle V_{k},A_{k},f_{k}\rangle$, which consists of $V_{k}= \left\{ v_{2k-1},v_{2k},v_{2k+1},v_{2k-3} \right\}$, $A_{k}= \left\{ (v_{2k-1},v_{2k}), (v_{2k},v_{2k+1}), (v_{2k}, v_{2k-3}) \right\}$, $f_{k}(a_{k})=f(a_{k})$ for every $a_{k}\in A_{k}$, where we let $v_{-i}=v_{2n-i}$ and $v_{2n+i}=v_{i}$ for $i=0,1,2$. For our defluent partition, the set of edges is $V^{edge}=\left\{ v_{2k-1}\right\} _{k=1,2,\ldots , n}$.

From Theorem 12, we only need to examine e-covered $\langle V,A,f,s,p\rangle$ where $p(v_{2k-1})\ge 0$ while $p(v_{2k})=0$ for $k=1,2,\ldots n$. Take such a sequences and associated e-covered $\langle V,A,f,s,p\rangle$; then, take another sequence$s'$ with its associated e-covered $\langle V,A,f,s',p'\rangle$ where $s'$ is derived from s as follows. Let $s'( (v_{2k}, v_{2k+1}) )=s'( (v_{2k-1}, v_{2k}) )+1$, and $s'( (v_{2k},v_{2k-3}) ) = s'( (v_{2k-1},v_{2k}) )+2$ for every $k=1,2,\ldots n$, while $s'$ preserves the ordering of s on $\left\{ (v_{2k-1}, v_{2k}) \right\} _{k=1,2,\ldots , n}$. Observe that it satisfies $p'(v_{2k-1})\ge 0$, $p'(v_{2k})=0$ for $k=1,2,\ldots n$. Then, we have $\sum _{v\in V}p'(v)\le \sum _{v\in V}p(v)$. It is immediate that given the ordering among $\left\{ (v_{2k-1}, v_{2k}) \right\} _{k=1,2,\ldots , n}$ and $p'(v_{2k-1})\ge 0$, $p'(v_{2k})=0$ for $k=1,2,\ldots n$, the ordering on each $(v_{2k}, v_{2k+1})$, $(v_{2k},v_{2k-3})$ should be set as early as possible for $k=1,2,\ldots n$ in order to minimize circulation.

For such sequence$s'$, take sequence$s''$ and associated e-covered $\langle V,A,f,s'',p''\rangle$ so that it further satisfies $s( (v_{2k-1}, v_{2k}) ) < s( (v_{2k+1}, v_{2k+2}) )$ while preserving the ordering within each $\left\{ (v_{2k-1},v_{2k}), (v_{2k},v_{2k+1}), (v_{2k}, v_{2k-3}) \right\}$ for $k=1,2,\ldots ,n$. Note that we have $r^{atwi}(c,s'')=1$. Now we have $\sum _{v\in V} p''(v)=(f^{c}+f^{c'}) +(n-2)*f^{c'} \le \sum _{v\in V} p(v)$. This is because if there exists one pair of arcs $(v_{2m-1},v_{2m})$ and $(v_{2m'-1}, v_{2m'})$ with some $m < m'\in \left\{ 1,2,\ldots ,n\right\}$ such that $s'((v_{2m-1},v_{2m})) > s((v_{2m'-1}, v_{2m'}))$, then $\sum _{v\in V} p''(v)+ (f^{c}-f^{c'})\le \sum _{v\in V} p(v)$. When there exists more than one such pair, the above relation is still satisfied. Note that when $f^{c}=f^{c'}$, we have $\sum _{v\in V} p''(v)= \sum _{v\in V} p(v)$, which means that the min-circulation can be attained with any $r^{atwi}(c,s')\in \left\{ 1,2,\ldots ,n\right\}$. $\square$

1.6 Proof of Theorem 9

First, we prove the case of $f_{1}=f_{2}$ for type-2 clustered f-network $\langle V,A,f\rangle$ with $|V|=n$. We observe that under any e-covered fsp-network $\langle V,A,f,s,p\rangle$, $p(v)\in \left\{ 0,f_{1},2f_{1}\right\}$ for any $v\in V$. We show that max-circulation is $nf_{1}$ in the following steps. Denote $V=\left\{ v_{1},v_{2},\ldots ,v_{n}\right\}$ with $v_{n+1}\equiv v_{1}$ as defined in its construction, such that every two consecutive vertices constitute a cycle by themselves.

Lemma 10

If $\langle V,A,f,s,p\rangle$ attains the max-circulation, then, we do not have $p(v_{k})=2f_{1}$ and $p(v_{k+1})=2f_{1}$ at the same time for $k=1,2,\ldots ,n$.

Proof

Suppose that $p(v_{k})=2f_{1}$; then $s((v_{k},v_{k+1}))<s((v_{k+1},v_{k}))$, which necessarily lets $p(v_{k+1})\le f_{1}$. $\square$

For the next Lemma 11, we prepare the following notation. For type-2 clustered networks, for two $v_{k},v_{k'}$, we denote $V_{k},V_{k'}$ such that they constitute a partition $V=v_{k}\cup V_{1}\cup v_{k}\cup V_{2}$ and each of $V_{1}$ and $V_{2}$ is connected.

Lemma 11

When $\langle V,A,f,s,p\rangle$ attains the max-circulation, if there exists $v_{k}, v_{k'}$ such that $p(v_{k})=p(v_{k'})=2f_{1}$, then, there exists $v_{k''}\in V_{k}$ and $v_{k'''}\in V_{k'}$ such that $p(v_{k''})=p(v_{k'''})=0$.

Proof

For $p(v_{k})=2f_{1}$, both out-arcs need be settled before either of the in-arcs such that $s((v_{k},v_{k+1}))<s((v_{k+1},v_{k}))$, and $s((v_{k},v_{k-1}))<s((v_{k-1},v_{k}))$. As shown in the previous lemma, $p(v_{k+1})\le f_{1}$, $p(v_{k-1})\le f_{1}$. When we also have $p(v_{k'})=2f_{1}$ with $k'\ne k$, then, proceeding from both vertices to endow a potential on each passed vertex as $f_{1}$, we need to attain some vertex $v_{k''}$ both of whose neighbors have endowed potential$f_{1}$. Thus, for $v_{k''}$, both in-arcs are settled before both out-arcs, which necessarily lets $p(v_{k''})=0$. This completes our proof. $\square$

Suppose that there are i vertices that are endowed potential$2f_{1}$. Combining Lemmas 10 and 11, we know that $0\le i\le \frac{n}{2}$. When $i=0$, each vertex can be endowed at most $f_{1}$, which lets $sum_{v\in V}p(v)\le nf_{1}$. Further suppose that each is actually endowed with $f_{1}$potential. When we let each one vertex be endowed with $2f_{1}$potential, there need to be at least two vertices on both sides that need to be endowed with 0 potential. We know that this never increases the circulation. This ends our proof for the case of $f_{1}=f_{2}$.

Now, it is almost straightforward to show the case of $f_{1}>f_{2}$. The above proof shows that max-circulation is now attained in the direction with $r^{atwi}(A_{1},s)=n-1$ with $x^{max}(N^{f})=(n-1)f_{1}+f_{2}$.

1.7 Results Relevant to Rotemberg (2011)

We follow the notation of Rotemberg (2011) with regard to its target class of network.

The next corollary shows that Rotemberg (2011) treats one of the simplest classes of f-network with no arc-twisted cycles.

Corollary 1

(Case of Rotemberg (2011): min-circulation)

For a closed f-network $N^{f}=\langle V,A,f\rangle$ that is in a class of $C^{K}_{N}$ with flowz²⁵, we have $x^{min}_{N^{f}}= z$.

Proof

Since $C^{K}_{N}$ is based on a Euler graph, we can take a cycle c that consists of all the arcs. Furthermore, since the flow for each arc equals z, we can take a closed-cycle decomposition with a unique undominated cycle c with flow$f(c)=z$. Since a Euler graph has no arc-twisted cycles, the min-circulation is realized with c, and the derived value is z. $\square$

The next corollary shows that Rotemberg (2011) treats one of the simplest classes of f-network with no vertex-twisted cycles.

Corollary 2

(Case of Rotemberg (2011): max-circulation)

For a closed f-network $N^{f}=\langle V,A,f\rangle$ which is in the class of $C^{K}_{N}$ with flowz, suppose that N / (K!) is an integer. Then, we have $x^{max}_{N^{f}}= z \sum _{k=1}^{K} k*(\frac{N}{k}-1)$

Proof

When N / (K!) is an integer, there exists no vertex-twisted cycles within $C^{np}_{G}$ for any associated graph G, where $C^{np}_{G}$ denotes the set of non-punctured cycles for G. Observe that we can take a set of cycles $C\subseteq C^{np}_{G}$ such that C constitutes a closed cycle decomposition with constant flow z for each cycle, and $|C|=\sum _{k=1}^{K}k$, for which there are k number of cycles for each $|c|=\frac{N}{k}$, for $k=1,2,\ldots , K$. Since there is no vertex-twisted relation between the cycles in $C^{np}_{G}$, we take a sequence whereby the circulation for each cycle c with $|c|=\frac{N}{k}$ is $z(\frac{N}{k}-1)$. Thus, the sequence attains the circulation stated in this corollary. We easily confirm that the circulation equals the max-circulation for the given f-network, observing that any combination of the cycles within C is not dominated by non-punctured cycles. $\square$