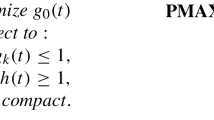Quasi-Newton approaches to interior point methods for quadratic problems

Abstract

Interior point methods (IPM) rely on the Newton method for solving systems of nonlinear equations. Solving the linear systems which arise from this approach is the most computationally expensive task of an interior point iteration. If, due to problem’s inner structure, there are special techniques for efficiently solving linear systems, IPMs demonstrate a reduced computing time and are able to solve large scale optimization problems. It is tempting to try to replace the Newton method by quasi-Newton methods. Quasi-Newton approaches to IPMs either are built to approximate the Lagrangian function for nonlinear programming problems or provide an inexpensive preconditioner. In this work we study the impact of using quasi-Newton methods applied directly to the nonlinear system of equations for general quadratic programming problems. The cost of each iteration can be compared to the cost of computing correctors in a usual interior point iteration. Numerical experiments show that the new approach is able to reduce the overall number of matrix factorizations.

1 Introduction

Let us consider the following general quadratic programming problem

$$\begin{aligned} \begin{array}{ll} \min &{} \frac{1}{2} x^T Q x + c^T x \\ \text{ s. } \text{ t. } &{} A x = b \\ &{} x \ge 0, \end{array} \end{aligned}$$

(1)

where $x, c \in \mathbb {R}^n$, $b \in \mathbb {R}^m$, $Q \in \mathbb {R}^{n \times n}$ and $A \in \mathbb {R}^{m \times n}$. We will suppose that the rows of A are linearly independent. Define function $F: \mathbb {R}^{2n + m} \rightarrow \mathbb {R}^{2n + m}$ by

$$\begin{aligned} F(x, \lambda , z) = \begin{bmatrix} - Q x + A^T \lambda + z - c \\ A x - b \\ X Z e \end{bmatrix}, \end{aligned}$$

(2)

where $X, Z \in \mathbb {R}^{n \times n}$ are diagonal matrices defined by $X = {{\,\mathrm{diag}\,}}(x)$ and $Z = {{\,\mathrm{diag}\,}}(z)$, respectively, and e is the vector of ones of appropriate size. First order necessary conditions for (1) state that, if $x^* \ge 0$ is a minimizer, then there exist $z^* \in \mathbb {R}^n$, $z^* \ge 0$, and $\lambda ^* \in \mathbb {R}^m$ such that $F(x^{*}, {\lambda }^{*}, z^{*}) = 0$.

Primal-Dual IPMs try to solve (1) by solving a sequence of relaxed constrained nonlinear equations in the form of

$$\begin{aligned} F({x, \lambda , z}) = \begin{bmatrix} 0 \\ 0 \\ \mu e \end{bmatrix}, \quad x, {z} > 0, \end{aligned}$$

(3)

where $\mu \in \mathbb {R}$ is called the barrier parameter, which is associated with the logarithmic barrier applied to the inequalities $x \ge 0$ used to derive the method [14, 30]. As $\mu \rightarrow 0$ more importance is given to optimality over feasibility. Systems of type (3) are not easy to solve. When $\mu = 0$, they can be solved by general algorithms for bounded nonlinear systems [10, 19]. In this case, a suitable merit function, usually $\Vert F(x)\Vert$, has to be used to select the step-sizes. IPMs try to stay near the solution of (3), called the central path, and reduce $\mu$ at each iteration. Instead of solving (3) exactly, one step of the Newton method is applied. Thus, given an iterate $(x^{k}, {\lambda }^{k}, z^{k})$, in the interior of the bound constraints, i.e. $x^k, z^k > 0$, the next point is given by

$$\begin{aligned} (x^{k + 1}, {\lambda }^{k + 1}, z^{k + 1}) = (x^{k}, {\lambda }^{k}, z^{k}) + (\alpha _P \Delta {x}^k, \alpha _D \Delta {\lambda }^k, \alpha _D \Delta {z}^k), \end{aligned}$$

(4)

where $(\Delta {x}^k, \Delta {\lambda }^k, \Delta {z}^k)$ is computed by solving some Newton-like systems

$$\begin{aligned} J(x^{k}, {\lambda }^{k}, z^{k}) \begin{bmatrix} \Delta {x}^k\\ \Delta {\lambda }^k\\ \Delta {z}^k\end{bmatrix} = v, \end{aligned}$$

(5)

where $v \in \mathbb {R}^{2n + m}$ and $J : \mathbb {R}^{2n + m} \rightarrow \mathbb {R}^{(2n + m) \times (2n + m)}$ is the Jacobian of F, defined by

$$\begin{aligned} J(x, \lambda , z) = \begin{bmatrix} -Q&A^T&I \\ A&0&0 \\ Z&0&X \end{bmatrix}. \end{aligned}$$

(6)

Standard predictor-corrector algorithms solve (5) twice: first the affine scaling predictor is computed for $v = - F(x^{k}, {\lambda }^{k}, z^{k})$ and then the corrector step is computed using $v = \begin{bmatrix} 0&0&\sigma _k \mu _k e \end{bmatrix}^T$, with $\sigma _k \in (0, 1)$, $\mu _k = {x^k}^T z^k / n$. Additional correctors can be computed in one iteration to further accelerate convergence, such as second order correctors [22] or multiple centrality correctors [13]. Scalars $\alpha _P$ and $\alpha _D$ are selected such that $x^{k + 1} > 0$ and $s^{k + 1} > 0$, respectively.

The most expensive task during an interior point (IP) iteration is the resolution of (5). The coefficient matrix $J(x, \lambda , z)$ is known as unreduced matrix and has dimension $(2n + m) \times (2n + m)$, but its nice structure allows efficient solution techniques to be used. The most common approaches for solving the linear system in IPMs are to work with augmented system or normal equations. If we eliminate $\Delta z$ in (5), we have the augmented system for which we can solve directly using matrix factorizations or compute adequate preconditioners and solve iteratively by Krylov subspace methods. If matrix Q is easily invertible, or $Q = 0$ (linear programming problems), it is possible to further eliminate $\Delta x$ and solve the normal equations by Cholesky factorization or by Conjugate Gradients, depending on the size of the problem. For both approaches it is known that computing good preconditioners or computing the factorization can be most expensive part of the process. A comprehensive discussion about the solution of linear systems arising in IPMs is carried out in [4]. Therefore (5) can be solved several times for the same $J(x^{k}, {\lambda }^{k}, z^{k})$ with different right-hand sides, in a classical predictor-corrector approach [22] or in the multiple centrality correctors framework [3, 14]. In this work we will extensively use the fact that the backsolves in (5) are less expensive than computing a good preconditioner or factorization.

Although $J(x, \lambda , z)$ is unsymmetric, under reasonable assumptions Greif, Moulding and Orban showed that it has only real eigenvalues [18]. Based on those results, Morini, Simoncini and Tani [25] developed preconditioners for the unreduced matrix and compared the performance of interior point methods using unreduced matrices and augmented systems. The authors observed that the use of augmented systems resulted in more robust and efficient algorithms, due to smaller dimensions of the involved matrices.

It is well known that the unreduced matrix has advantages, when compared to augmented system and normal equations. First, small changes of variables x or z result in small changes in $J(x, \lambda , z)$. Second, J is the Jacobian of F, so it is possible to approximate it by building models or evaluating F on some extra points. These two characteristics are explored in this work, while avoiding the drawbacks presented in [25].

Since J is the Jacobian of F, it is natural to ask if it can be approximated by evaluating F in some points. Function F is composed by two linear and one nonlinear functions. Therefore, the only part of J which may change during iterations is the third row. Moreover, it can be efficiently stored by just storing A, Q, x and z. Since computing and storing J is inexpensive, the only reason to use an approximation B of J is if system (5), using $B_k$ instead of $J(x^{k}, {\lambda }^{k}, z^{k})$, becomes easier to solve. That is where quasi-Newton methods and low rank updates become an interesting tool in interior point methods.

Quasi-Newton methods are well known techniques for solving large scale nonlinear systems or nonlinear optimization problems. The main motivation is to replace the Jacobian used by the traditional Newton method by its good and inexpensive approximation. Originally, they were useful to avoid computing the derivatives of F, but they have become popular as a large scale tool, since they usually do not need to explicitly build matrices and enjoy superlinear convergence. Classical references for quasi-Newton methods are [6, 21] for nonlinear equations and [26] for unconstrained optimization.

In the review [21] about practical quasi-Newton methods for solving nonlinear equations, Martínez suggests that there is room for studying such techniques in the interior point context. The author points to the work of Dennis Jr., Morshedi and Turner [7] which applies quasi-Newton techniques to make the projections in Karmarkar’s algorithm cheaper. The authors write the interpolation equations associated with the linear system in interior point iterations and describe a fast algorithm to compute updates and also to update an already existing Cholesky factorization. When solving general nonlinear programming problems by IPMs, a well known approach is to replace the Hessian of the Lagrangian function by low rank approximations [26].

In 2000, Morales and Nocedal [24] used quasi-Newton arguments to show that the directions calculated by the Conjugate Gradient algorithm can be used to build an automatic preconditioner for the matrix under consideration. The preconditioner is a sequence of rank-one updates of an initial diagonal matrix. Such approach is efficient when solving a sequence of linear systems with the same (or a slowly varying) coefficient matrix. Based on those ideas, a limited memory BFGS-like preconditioner for positive definite matrices was developed in [16] and was specialized for symmetric indefinite matrices in [17]. Recently, Bergamaschi et al. [2] developed limited-memory BFGS-like preconditioners to KKT systems arising from IP iterations and described their spectral properties. The approach was able to reduce the time for solving a sequence of KKT systems by Preconditioned Conjugate Gradient algorithm, but the approximation deteriorates as the number of interior point iterations increase. Also, extra linear algebra has to be performed to ensure orthogonality of the vectors used to build the updates.

In all works, with exception of [7], the main focus was to use low rank updates of an already computed preconditioner such that new preconditioners are constructed in an inexpensive way and reduce the overall time taken by the algorithm. In the present work, our main objective is to work directly with nonlinear equations and use low rank secant updates for computing the directions in the IP iterations. We use least change secant updates, in particular Broyden updates, and replace the Newton system (5) by an equivalent one. Some properties of the method are presented and extensive numerical experiments are performed. The main features of the proposed approach are:

• Low rank approximations are matrix-free and use only vector multiplications and additions;

• The quasi-Newton method for solving (5) can be easily inserted into an existing IPM;

• The number of factorizations is reduced for small and large instances of linear and quadratic problems;

• When the cost of the factorization is considerably higher than the cost of the backsolves, the total CPU time is also decreased.

In Sect. 2 we discuss the basic ideas of quasi-Newton methods, in particular the Broyden method, which is extensively used in the work. In Sect. 3 we show that, if the initial approximation is good enough, least change secant updates preserve most of the structure of the true coefficient matrix and a traditional IP iteration can be performed with the cost of computing correctors only. New low rank secant updates, which are able to exploit the sparsity of J are also discussed. In Sect. 4 we describe the aspects of a successful implementation of a quasi-Newton interior point method. In Sect. 5 we compare our approach with a research implementation of the primal-dual IPM for solving small- and medium-sized linear and quadratic problems. Finally, in Sect. 6 we draw the conclusions and mention possible extensions of the method.

Notation Throughout this work we use $F_k$ and $J_k$ as short versions of vector $F(x^{k}, {\lambda }^{k}, z^{k})$ and matrix $J(x^{k}, {\lambda }^{k}, z^{k})$, respectively. The vector e denotes the vector of ones of appropriate dimension. Given vectors a, b and c, we use the simplified notation of the composed vector $\begin{bmatrix} a&b&c \end{bmatrix}^T$ instead of $\begin{bmatrix} a^T&b^T&c^T \end{bmatrix}^T$.

2 Background for quasi-Newton methods

Quasi-Newton methods can be described as algorithms which use approximations to the Jacobian in the Newton method in order to solve nonlinear systems. The approximations are generated using information from previous iterations. Suppose that we want to find ${\bar{x}}\in \mathbb {R}^N$ such that $F({\bar{x}}) = 0$, where $F : \mathbb {R}^N \rightarrow \mathbb {R}^N$ is continuously differentiable. Given the current point ${\bar{x}}^k$ at iteration k, Newton method builds a linear model of F around ${\bar{x}}^k$ in order to find ${\bar{x}}^{k + 1}$. Now, suppose that ${\bar{x}}^k$ and ${\bar{x}}^{k + 1}$ have already been calculated and let us create a linear model for F around ${\bar{x}}^{k + 1}$:

$$\begin{aligned} M_{k + 1}({\bar{x}}) = F({\bar{x}}^{k + 1}) + B_{k + 1} ({\bar{x}}- {\bar{x}}^{k + 1}). \end{aligned}$$

(7)

The choice $B_{k + 1} = J_{k + 1}$ results in the Newton method for iteration $k + 1$. In secant methods, $B_{k + 1}$ is constructed such that $M_{k + 1}$ interpolates F at ${\bar{x}}^k$ and ${\bar{x}}^{k + 1}$, which gives us the secant equation

$$\begin{aligned} B_{k + 1} s_k = y_k, \end{aligned}$$

(8)

where $s_k = {\bar{x}}^{k + 1} - {\bar{x}}^k$ and $y_k = F({\bar{x}}^{k + 1}) - F({\bar{x}}^k)$. When $s_k \ne 0$ and $N > 1$ there are more unknowns than equations and several choices for $B_{k + 1}$ exist [5, 21].

Let $B_k$ be the current approximation to $J_k$, the Jacobian of F at ${\bar{x}}^k$ (it can be $J_k$ itself, for example). One of the most often used simple secant approximations for unsymmetric Jacobians is given by the Broyden “good” method. Given $B_k$, a new approximation $B_{k + 1}$ to $J_{k + 1}$ is given by

$$\begin{aligned} B_{k + 1} = B_k + \frac{(y_k - B_k s_k) s_k^T}{s_k^T s_k}. \end{aligned}$$

(9)

Matrix $B_{k + 1}$ is the closest matrix to $B_k$, in Frobenius norm, which satisfies (8). The update of the Broyden method belongs to the class of least change secant updates, since $B_{k + 1}$ is a rank-one update of $B_k$. As we are interested in solving a linear system, it may be interesting to analyze matrix $B_{k+1}^{-1} = H_{k + 1}$, which is obtained by the well known Sherman-Morrison-Woodbury formula:

$$\begin{aligned} H_{k + 1} = H_k + \frac{(s_k - H_k y_k) s_k^T H_k}{s_k^T H_k y_k} = \left( I + \frac{u_k s_k^T}{\rho _k} \right) H_k, \end{aligned}$$

(10)

where $u_k = s_k - H_k y_k$ and $\rho _k = s_k^T H_k y_k$. We can see that $H_{k + 1}$ is also a least change secant update of $H_k$. To store $H_{k + 1}$, one needs first to compute $H_k y_k$ and then store one scalar and two vectors. Storing $u_k$ is more efficient than storing $H_k s_k$ when $H_{k + 1}$ is going to be used more than once. According to (10), the cost of computing $H_{k + 1} v$ is the cost of computing $H_k v$ plus one scalar product and one sum of vectors times a scalar. After $\ell$ updates of an initial approximation $B_{k - \ell }$, current approximation $H_{k}$ is given by

$$\begin{aligned} H_{k} = \left( I + \frac{u_{k - 1} s_{k - 1}^T}{\rho _{k - 1}} \right) H_{k - 1} = \left[ \prod _{j = 1}^{\ell } \left( I + \frac{u_{k - j} s_{k - j}^T}{\rho _{k - j}} \right) \right] H_{k - \ell }. \end{aligned}$$

(11)

Instead of updating $B_k$ and then computing its inverse, the Broyden “bad” method directly computes the least change secant update of the inverse:

$$\begin{aligned} H_{k + 1} = H_k + \frac{(s_k - H_k y_k) y_k^T}{y_k^T y_k} = H_k V_k + \frac{s_k y_k^T}{\rho _k}, \end{aligned}$$

(12)

where $V_k = \left( I - \frac{y_k y_k^T}{\rho _k} \right)$ and $\rho _k = y_k^T y_k$. Similarly to $B_{k + 1}$ in (10), $H_{k + 1}$ given by (12) is the closest matrix of $H_k$, in the Frobenius norm, such that $H_{k + 1}^{-1}$ satisfies (8). The cost of storing $H_{k + 1}$ is lower than that of (10), since vectors $s_k$ and $y_k$ have already been computed. The cost of calculating $H_{k + 1} v$ is higher: it involves one scalar product, two sums of vector times a scalar and $H_k v$. After $\ell$ updates of an initial approximation $H_{k - \ell }$, current approximation $H_{k}$ is given by

$$\begin{aligned} \begin{aligned} H_{k}&= H_{k - 1} V_{k - 1} + \frac{s_{k - 1} y_{k - 1}^T}{\rho _{k - 1}} \\&= H_{k - \ell } \left( \prod _{j = k - \ell }^{k - 1} V_{j} \right) + \sum _{i = 1}^{\ell } \left( \frac{s_{ k - i} y_{ k - i}^T}{\rho _{ k - i}} \prod _{j = k - i + 1}^{k - 1} V_{j} \right) \end{aligned} \end{aligned}$$

(13)

Approach (13) has some advantages over (11). First, it does not need to compute $u_k$ for constructing the update. When $H_{k - \ell }$ is not easy to obtain, this is a costly operation. Second, unlike (11), matrices $V_{j}$ depend solely on $y_{j}$ and $s_{j}$ for all $j = 1, \dots , \ell$, so it is possible to replace the initial approximation $H_{k - \ell }$ by different matrices without updating the whole structure. Third, the computation of $H_{k} v$ can be efficiently implemented in a scheme similar to the BFGS update described in [26], as we show in Algorithm 1. Unfortunately, the Broyden “bad” method is known to behave worse in practice than the “good” method [6]. To avoid the extra cost of computing $H_{k} y_{k}$ in (10) it is common to compute a Cholesky or LU factorization of $B_{k - \ell }$ and work directly with (9). Rank-one updates of the LU factorization can be efficiently implemented [11]. The computational cost of the important operations for approaches (11) and (13) is summarized in Table 1.

Table 1 Comparison between Broyden “good” and “bad” updates with respect the cost of storing/updating, the cost of computing $H_k v$ and the cost of updating the initial approximation $H_{k - \ell }$

The class of rank-one least change secant updates can be generically represented by updates of the form

$$\begin{aligned} B_{k + 1} = B_k + \frac{(y_k - B_k s_k) w_k^T}{w_k^T s_k}, \end{aligned}$$

(14)

where $w_k^T s_k \ne 0$. Setting $w_k = s_k$ defines the Broyden “good” method and $w_k = B_k^T y_k$ defines the Broyden “bad” method. Several other well known quasi-Newton methods fit in update (14), such as the Symmetric Rank-1 update used in nonlinear optimization, which defines $w_k = y_k - B_k s_k$. See [5, 6] for details on least change secant updates.

3 A quasi-Newton approach for IP iterations

According to the general description of primal-dual IPMs in Sect. 1, we can see that, at each iteration, they perform one Newton step associated with the nonlinear system (3), for decreasing values of $\mu$. Each step involves the computation of the Jacobian of F and the solution of a linear system (5).

Our proposal for this work is to perform one quasi-Newton step to solve (3), replacing the true Jacobian $J(x, \lambda , z)$ by a low rank approximation B. The idea might seem surprising at first glance, since, for quadratic problems, $J(x, \lambda , z)$ is very cheap to evaluate. In this section we further develop the quasi-Newton ideas applied to interior point methods and show that they might help to reduce the cost of the linear algebra when solving (1).

It is important to note that F and J discussed in Sect. 2 will be given by (2) and (6), respectively, in the interior point context, which highlights the importance of using the unreduced matrix in our analysis. Therefore, variable ${\bar{x}}$ in Sect. 2 is given by $(x, \lambda , z)$ and, consequently, $N = 2n + m$.

3.1 Initial approximation and update

Suppose that $k \ge 0$ is an interior point iteration for which system (5) was solved and ${\begin{bmatrix} x^{k + 1}&{\lambda }^{k + 1}&z^{k + 1} \end{bmatrix}^T}$ was calculated, using any available technique. Usually, solving (5) involves an expensive factorization or the computation of a good preconditioner associated with $J_k$. Most traditional quasi-Newton methods for general nonlinear systems compute $B_k$ by finite differences or use a diagonal matrix as the initial approximation. According to Sect. 2, it is necessary to have an initial approximation of $J_k$ in order to generate approximation $B_{k + 1}$ of $J_{k + 1}$ by low rank updates. Most of traditional quasi-Newton methods for general systems compute $B_k$ by finite differences or use a diagonal matrix. Since $J_k$ has already been computed, we will define it as $B_k$, i.e., the perfect approximation to $J_k$. It is clear that, in such case, $H_k = J_k^{-1}$ is the approximation to $J_k^{-1}$.

In order to compute $B_{k + 1}$, vectors $s_k$ and $y_k$ in secant equation (8) have to be built:

$$\begin{aligned} s_{k}= & {} \begin{bmatrix} s_{k,x} \\ s_{k,\lambda } \\ s_{k,z} \end{bmatrix} = \begin{bmatrix} x^{k + 1} - x^k \\ \lambda ^{k + 1} - \lambda ^k \\ z^{k + 1} - z^k \end{bmatrix} \nonumber \\ y_{k}= & {} \begin{bmatrix} y_{k,c} \\ y_{k,b} \\ y_{k,\mu } \end{bmatrix} = F(x^{k + 1}, {\lambda }^{k + 1}, z^{k + 1}) - F(x^{k}, {\lambda }^{k}, z^{k})\nonumber \\= & {} \begin{bmatrix} - Q s_{k,x} + A^T s_{k,\lambda } + s_{k,z} \\ A s_{k,x} \\ X^{k + 1} Z^{k + 1} e - X^{k} Z^{k} e \end{bmatrix}. \end{aligned}$$

(15)

The use of $J_k$ as the initial approximation ensures that the first two block elements of $B_k s_k - y_k$ are zero. This is a well known property of low rank updates given by (14) when applied to linear functions (see [6, Ch. 8]). In Lemma 1 we show that rank-one secant updates maintain most of the good sparsity structure of approximation $B_k$ when its structure is similar to the true Jacobian of F.

Lemma 1

Let J be the Jacobian of F given by (2). If the least change secant update $B_{k + 1}$ for approximating $J_{k + 1}$ is computed by (14) using $w_k^T = \begin{bmatrix} a_k&b_k&c_k \end{bmatrix}^T$, $a_k, c_k \in \mathbb {R}^n$, $b_k \in \mathbb {R}^m$, and $B_{k}$ is defined by

$$\begin{aligned} B_{k} = \begin{bmatrix} - Q&A^T&I \\ A&0&0 \\ M^1_{k}&M^2_{k}&M^3_{k} \end{bmatrix} \end{aligned}$$

then

$$\begin{aligned} B_{k + 1} = \begin{bmatrix} - Q&A^T&I \\ A&0&0 \\ M^1_{k + 1}&M^2_{k + 1}&M^3_{k + 1} \end{bmatrix}, \end{aligned}$$

where $M^i_{k + 1}$ is a rank-one update of $M^i_{k}$, for $i = 1, 2, 3$. In addition, if $M^2_k = 0$ and $b_k = 0$, then $M^2_{k + 1} = 0$.

Proof

By the definition of $s_k$ and $y_k$ in (15) it is easy to see that $y_k - B_k s_k = \begin{bmatrix} 0&0&u_k \end{bmatrix}^T$, where

$$\begin{aligned} u_k = (X^{k + 1} Z^{k + 1} - X^k Z^k) e - M^1_{k} s_{k, x} - M^2_{k} s_{k,\lambda } - M^3_{k} s_{k,z}. \end{aligned}$$

Using the secant update (14), we have that the first two rows of $B_k$ are kept the same and

$$\begin{aligned} \begin{aligned} M^1_{k + 1}&= M^1_k + u_k a_k^T / (w_k^T s_k) \\ M^2_{k + 1}&= M^2_k + u_k b_k^T / (w_k^T s_k) \\ M^3_{k + 1}&= M^3_k + u_k c_k^T / (w_k^T s_k). \end{aligned} \end{aligned}$$

It is easy to see that $M^2_{k + 1} = 0$ when $M^2_k = 0$ and $b_k = 0$. $\square$

By Sect. 2 we know that Broyden “good” and “bad” updates are represented by specific choices of $w_k$ and, therefore, enjoy the consequences of Lemma 1. Unfortunately, not much can be said about the structure of the “third row” of $B_{k + 1}$. When $B_k = J_k$, the diagonal structure of blocks $Z^k$ and $X^k$, as well as the zero block in the middle, are likely to be lost. However, if we select $w_k^T = \begin{bmatrix} s_{k,x}&0&s_{k,z} \end{bmatrix}^T$, then, by Lemma 1, the zero block is kept in $B_{k + 1}$. The update given by this choice of $w_k$ is a particular case of Schubert’s quasi-Newton update for structured and sparse problems [29]. This update minimizes the distance to $B_k$ on the space of the matrices that satisfy (8) and have the same block sparsity pattern of $B_k$ [5]. Using the Sherman–Morrison–Woodbury formula, we also have the update for $H_k$:

$$\begin{aligned} H_{k + 1} = \left( I - \frac{(H_k y_k - s_k) w_k^T}{w_k^T H_k y_k} \right) {H_k}, \end{aligned}$$

which only needs an extra computation of $H_k y_k$ to be stored. There is no need to store $w_k$, since it is composed by components of $s_k$. We can say that this approach is inspired by the Broyden “good” update.

On the other hand, if we use $w_k^T = \begin{bmatrix} 0&y_{k, b}&y_{k, \mu } \end{bmatrix}^T B_k$, then we still have $M^2_{k + 1} = 0$ by Lemma 1 and, in addition, we are able to remove the calculation $H_k y_k$ in the inverse. This approach is inspired by the Broyden “bad” update and results in the following update

$$\begin{aligned} H_{k + 1} = H_k + \frac{(s_k - H_k y_k) \begin{bmatrix} 0&y_{k, b}&y_{k, \mu } \end{bmatrix}^T }{y_{k, b}^T y_{k, b} + y_{k, \mu }^T y_{k, \mu }}. \end{aligned}$$

(16)

Up to the knowledge of the authors, this update has not been theoretically studied in the literature.

Lemma 1 also justifies our choice to work with approximations of $J^{-1}$ rather than J. After $\ell > 0$ rank-one updates, if $B_{k} u = v$ is solved by factorizations and backsolves, it would be necessary to perform $\ell$ updates on the factorization of initial matrix $B_{k - \ell }$, which could introduce many nonzero elements. A clear benefit of defining $B_{k - \ell } = J_{k - \ell }$ is that computing $H_{k} v$ uses the already calculated factorizations/preconditioners for $B_{k - \ell }$, which were originally used to solve (5) at iteration $k - \ell$. Step 3 of Algorithm 1 is an example of low rank update (13). Clearly, we do not explicitly compute $H_{k - \ell } v$, but instead solve the system $B_{k - \ell } u = v$.

3.2 Computation of quasi-Newton steps

Having defined how quasi-Newton updates are initialized and constructed, we now have to insert the approximations in an interior point framework. Denoting ${\begin{bmatrix} x^{0}&{\lambda }^{0}&z^{0} \end{bmatrix}^T}$ as the starting point of the algorithm, at the end of any iteration k it is possible to build a rank-one secant approximation of the unreduced matrix to be used at iteration $k + 1$. Let us consider iteration k, where $k \ge 0$ and $\ell \ge 0$. If $\ell = 0$, then, by the previous subsection, $B_{k - \ell } = B_k = J_k$ and the step in the interior point iteration is the usual Newton step, given by (5). If $\ell > 0$, we have a quasi-Newton step, which can be viewed as a generalization of (5), and is computed by solving

$$\begin{aligned} B_k \begin{bmatrix} \Delta {x}^k\\ \Delta {\lambda }^k\\ \Delta {z}^k\end{bmatrix} = v \end{aligned}$$

(17)

or, equivalently, by performing $H_k v$. All the other steps of the IPM remain exactly the same.

When $\ell > 0$, the cost of solving (17) depends on the type of update that is used. In general, it is the cost of solving system $J_{k - \ell } r = q$ (or, equivalently, $J_{k - \ell }^{-1} q$) plus some vector multiplications and additions. However, since $J_{k - \ell }$ has already been the coefficient matrix of a linear system at iteration $k - \ell$, it is usually less expensive than solving for the first time. That is one of the main improvements that a quasi-Newton approach brings to interior point methods.

When the Broyden “bad” update (13) is used together with defining $B_{k - \ell } = J_{k - \ell }$ as the initial approximation, it is possible to derive an alternative interpretation of (17). Although this update is known to have worse numerical behavior when compared with the “good” update (10), this interpretation can result in a more precise implementation, which is described in Lemma 2.

Lemma 2

Assume that $k, \ell \ge 0$ and $H_{k}$ is the approximation of $J_{k}^{-1}$ constructed by $\ell$ updates (13) using initial approximation $H_{k - \ell } = J_{k - \ell }^{-1}$. Given $v \in \mathbb {R}^{2n + m}$, the computation of $r = H_k v$ is equivalent to the solution of

$$\begin{aligned} J_{k - \ell } r = v + \begin{bmatrix} 0 \\ 0 \\ \sum \limits _{i = 1}^{\ell } \alpha _i \left( Z^{k - \ell } s_{k - i, x} + X^{k - \ell } s_{k - i,z} - y_{k - i, \mu } \right) \end{bmatrix}, \end{aligned}$$

where $\displaystyle \alpha _i = \frac{y_{k - i}^T \prod _{j = k - i + 1}^{k - 1} V_{j}}{\rho _{k - i}} v$, for $i = 1, \dots , \ell$.

Proof

Using the expansion (12) of Broyden “bad” update, the definition of $\alpha _i$ and the fact that $H_{k - \ell } = J_{k - \ell }^{-1}$, we have that

$$\begin{aligned} \begin{aligned} r&= H_k v = H_{k - \ell } \left( \prod _{j = k - \ell }^{k - 1} V_{j} \right) v + \sum _{i = 1}^{\ell } \left( \frac{s_{ k - i} y_{ k - i}^T}{\rho _{ k - i}} \prod _{j = k - i + 1}^{k - 1} V_{j} \right) v \\&= J_{k - \ell }^{-1} \left( \prod _{j = k - \ell }^{k - 1} V_{j} \right) v + \sum _{i = 1}^{\ell } \alpha _i s_{k - i} \\&= J_{k - \ell }^{-1} \left( v - \sum _{i = 1}^{\ell } \alpha _i y_{ k - i} \right) + \sum _{i = 1}^{\ell } \alpha _i s_{k - i}. \end{aligned} \end{aligned}$$

(18)

Last equality comes from the definition of $\alpha _i$ and the definition of $V_{k}$ in (12), applied recursively. One step of this recursion is given by

$$\begin{aligned} \begin{aligned} \left( \prod _{j = k - \ell }^{k - 1} V_{j} \right) v&= V_{k - \ell } \left( \prod _{j = k - \ell + 1}^{k - 1} V_{j} \right) v = \left( I - \frac{y_{k - \ell } y_{k - \ell }^T}{\rho _{k - \ell }} \right) \left( \prod _{j = k - \ell + 1}^{k - 1} V_{j} \right) v \\&= \left( \prod _{j = k - (\ell - 1)}^{k - 1} V_{j} \right) v - \alpha _\ell y_{k - \ell }. \end{aligned} \end{aligned}$$

When $i = 1$, we assume that $\prod _{j = k - i + 1}^{k - 1} V_{j}$ results in the identity matrix, therefore $\alpha _1 = y_{k - 1}^T v / \rho _{k - 1}$. Multiplying from the left both sides of equality (18) by $J_{k - \ell }$ , we obtain

$$\begin{aligned} J_{k - \ell } r = v + \sum _{i = 1}^{\ell } \alpha _i \left( J_{ k - \ell } s_{k - i} - y_{k - i} \right) . \end{aligned}$$

By Lemma 1 and definition (15), the first two components of $J_{k - \ell } s_{k - i} - y_{k - i}$ are zero, for all i, which demonstrates the lemma.$\square$

Lemma 2 states that only the third component of the right-hand side actually needs to be changed in order to compute Broyden “bad” quasi-Newton steps at iteration k. This structure is very similar to corrector or multiple centrality correctors in IPMs and reinforce the argument that the cost of computing a quasi-Newton step is lower than the Newton step. It is important to note that scalars $\alpha _i$ are the same as the ones computed at step 2 of Algorithm 1.

3.3 Dealing with regularization

Rank-deficiency of A, near singularity of Q or the lack of strict complementarity at the solution may cause matrix J, the augmented system or the normal equations to become singular near the solution of (1). As the iterations advance, it becomes harder to solve the linear systems. Regularization techniques address this issue by adding small perturbations to J in order to increase numerical accuracy and convergence speed, without losing theoretical properties. A common approach is to interpret the perturbation as the addition of weighted proximal terms to the primal and dual formulations of (1). Saunders and Tomlin [28] consider fixed perturbations while Altman and Gondzio [1] consider dynamic ones, computed at each iteration. Friedlander and Orban [9] add extra variables to the problem, expand the unreduced system and, after an initial reduction, arrive in a regularized system similar to [1]. In all these approaches, given reference points ${\hat{x}}$ and ${\hat{\lambda }}$, the regularized matrix ${\hat{J}}$

$$\begin{aligned} {{\hat{J}}}(x, \lambda , z) = \begin{bmatrix} - Q - R_p&A^T&I \\ A&R_d&0 \\ Z&0&X \end{bmatrix}, \end{aligned}$$

(19)

where diagonal matrices $R_p \in \mathbb {R}^{n \times n}$ and $R_d \in \mathbb {R}^{m \times m}$ represent primal and dual regularization, respectively, can be viewed as the Jacobian of the following function

$$\begin{aligned} {\hat{F}}(x, \lambda , z) = \begin{bmatrix} A^T \lambda - Q x - R_p (x - {\hat{x}}) - c \\ A x + R_d (\lambda - {\hat{\lambda }}) - b \\ X Z e \end{bmatrix}. \end{aligned}$$

Any choice is possible for reference points ${\hat{x}}$ and ${\hat{\lambda }}$. However, in order to solve the original Newton system (5) and make use of the good properties of the regularization (19) at the same time, they are usually set to the current iteration points $x^k$ and $\lambda ^k$, respectively, which annihilates terms $R_p (x - {\hat{x}})$ and $R_d (\lambda - {\hat{\lambda }})$ on the right-hand side of (5) during affine scaling steps.

Matrix ${\hat{J}}$ given by (19) now depends on $R_p$ and $R_d$ in addition to x and z. The regularization terms $R_p$ and $R_d$ do not need to be considered as variables, but if new regularization parameters are used, a new factorization or preconditioner needs to be computed. Since this is one of the most expensive tasks of the IP iteration, during quasi-Newton step k the regularization parameters are not allowed to change from those selected at iteration $k - \ell$, where the initial approximation was selected. That is a reasonable decision, as the system that is actually being solved in practice has the coefficient matrix from iteration $k - \ell$. The fact that the regularization terms are linear in ${\hat{F}}$ implies, by Lemma 1, that the structure of (19) is maintained during least change secant updates.

The reference points have no influence in ${\hat{J}}$, but they do influence the function ${\hat{F}}$. Suppose, as an example, that $\ell = k$, i.e., the initial approximation for quasi-Newton is the Jacobian at the starting point ${\begin{bmatrix} x^{0}&{\lambda }^{0}&z^{0} \end{bmatrix}^T}$, and only quasi-Newton steps are taken in the interior point algorithm. If we use $x^0$ and $\lambda ^0$ as the reference points and the algorithm converges, the limit point could be very different from the true solution, as initial points usually are far away from the solution, especially for infeasible IPMs. If we update the reference points at each quasi-Newton iteration, as it is usually the choice in literature [1, 9], we eliminate their effect on the right-hand side of (17) during affine scaling steps. By (7), $B_{k + 1}$ is the Jacobian of a linear approximation of ${\hat{F}}$ which interpolates ${\begin{bmatrix} x^{k}&{\lambda }^{k}&z^{k} \end{bmatrix}^T}$ and ${\begin{bmatrix} x^{k + 1}&{\lambda }^{k + 1}&z^{k + 1} \end{bmatrix}^T}$. As the regularization parameters are fixed during quasi-Newton iterations, the reference points can be seen as simple constant shifts on ${\hat{F}}$, with no effect on the Jacobian. Therefore, the only request is that ${\hat{F}}$ has to be evaluated at points ${\begin{bmatrix} x^{k}&{\lambda }^{k}&z^{k} \end{bmatrix}^T}$ and ${\begin{bmatrix} x^{k + 1}&{\lambda }^{k + 1}&z^{k + 1} \end{bmatrix}^T}$ using the same reference points, when calculating $y_k$ by (15). The effect of changing the reference points at each iteration in practice is the extra evaluation of ${\hat{F}}$ at the beginning of iteration k.

4 Implementation

The quasi-Newton approach can easily be inserted into an existing interior point method implementation. In this work, the primal-dual interior point algorithm HOPDM[12] was modified to implement the quasi-Newton approach. Algorithm 2 describes the steps of a conceptual quasi-Newton primal-dual interior point algorithm.

The most important element of Algorithm 2 is $\ell$, the memory size of the low rank update, which controls if the iteration involves Newton or quasi-Newton steps. At step 1 several systems (17) might be solved, depending on the IPM used. HOPDM implements the strategy of multiple centrality correctors [3], which tries to maximize the step-size at the iteration. HOPDM also implements the regularization strategy (19). Note in (17) that we do not have to care how the systems are solved, only how to implement the matrix-vector multiplication $H_k v$ efficiently.

Step 3 is the most important step in a quasi-Newton IP algorithm, since it decides whether or not quasi-Newton steps will be used in the next iteration. Several possible strategies are discussed in this section, as well as some implementation details.

Bound constraints

$$\begin{aligned} l \le x \le u, \quad l, u \in \mathbb {R}^n \end{aligned}$$

can be considered in the general definition (1) of a quadratic programming problem by using slack variables. HOPDM explicitly deals with bound constraints and increases the number of variables to $4n + m$. When bound constraints are considered, function F is given by

$$\begin{aligned} F(x, t, \lambda , z, w) = \begin{bmatrix} A^T \lambda - Q x + z - w - c \\ A x - b \\ x + t - u \\ X Z e \\ T W e \end{bmatrix} \end{aligned}$$

and the Jacobian J is

$$\begin{aligned} J(x, t, \lambda , z, w) = \begin{bmatrix} -Q&0&A^T&I&-I \\ A&0&0&0&0 \\ I&I&0&0&0 \\ Z&0&0&X&0 \\ 0&W&0&0&T \end{bmatrix}. \end{aligned}$$

Note that, in this case, l is eliminated by proper shifts, u represents upper shifted constraints and t represents slacks. All the results and discussions considered so far can be easily adapted to the bound-constrained case. Therefore, in order to keep notation simple, we will refer to the more general and simpler formulation (1) and work in the $(2n + m)$-dimensional space.

4.1 Storage of $H_{k}$ and computation of $H_{k} v$

When solving quadratic problems, the Jacobian of function F used in a primal-dual interior point method is not expensive to compute and has an excellent structure, which can be efficiently explored by traditional approaches. Therefore, there is no point in explicitly building approximation matrix $B_{k}$ (or $H_{k}$) since, by Lemma 1, they would be denser. For an efficient implementation of the algorithm only the computation $H_{k} v$ has to be performed in (17). To accomplish this task, we store

• Initial approximation $J_{k - \ell }$ and

• Triples $(s_{k - i}, u_{k - i}, \rho _{k - i})$ or $(s_{k - i}, y_{k - i}, \rho _{k - i})$ , $i = 1, \dots , \ell$, if updates are based on Broyden “good” or “bad” method, respectively.

In order to store $J_{k - \ell }$ we have to store vectors $x^{k - \ell }$ and $\lambda ^{k - \ell }$, since all other blocks of J are constant. If regularization is being used, vectors $R_p$ and $R_d$ used at iteration $k - \ell$ are also stored. The reference points are not stored. The most important structure to store is the factorization or the preconditioner computed when solving (17) at iteration $k - \ell$ for the first time. Without this information, the computation of $H_k v$ would have the same computational cost of using the true matrix $J_{k}$. Data is stored at step 3 of Algorithm 2, whenever it has been decided to store quasi-Newton information and $\ell = 0$.

Regarding the triples, they are composed of two $(2n + m)$-dimensional vectors and one scalar. Storing $y_{k - i}$ is the most expensive part in Broyden “bad” updates, since function F has to be evaluated twice. In Broyden “good” updates the computation of $u_{k - i}$ is the most expensive, due to the computation of $H_{k - i} y_{k - i}$.

The implementation of an algorithm to compute $H_k v$ depends on the selected type of low rank update. Algorithm 1 is an efficient implementation of the general Broyden “bad” update (13). If the structure described by Lemma 1 is being used, then all vector multiplications are performed before the solution of the linear system, as described by Algorithm 3. Both algorithms can be easily modified to use updates of the form $w_k^T = \begin{bmatrix} a_k&b_k&c_k \end{bmatrix}^T B_k$ in the generic update (14). The only changes are the storage of an extra vector and the computation of scalars $\alpha _i$ at step 2. The implementation of the sparse update (16) is straightforward and there is no need to store extra information. Algorithm 3 uses a little extra computation, since vector q is discarded after the computation of all $\alpha _i$. On the other hand, there is no need to store blocks $s_{k - i,\lambda }$, $i = 1, \dots , \ell$.

Algorithm 4 describes the steps to compute $H_{k} v$ when Broyden “good” update (10) is considered. Note that a linear system is first solved, then a sequence of vector multiplications and additions is applied. The algorithm is simpler and more general than Algorithm 1, but it has to be called more often in an interior point algorithm: to compute the steps (step 1 in Algorithm 2) and to compute $H_{k} y_{k}$, needed to build $u_{k}$ (step 3 in Algorithm 2). Algorithm 4 is very general and can be easily modified to consider any least change secant update of the form (14) without extra storage requirements, although not necessarily in an efficient way.

4.2 Size of $\ell$

The cost of computing $H_k v$ increases as the quasi-Newton memory $\ell$ increases. In addition, it was observed that the quality of the approximation decreases when the quasi-Newton memory is large [2]. In our implementation of Algorithm 2, we also observed the decrease in the quality of the steps when $\ell$ is too large. The decrease of the barrier parameter $\mu _k = {x^k}^T z^k / n$ for different bounds on $\ell$ is shown in Fig. 1, for problem afiro, the smallest example in Netlib test collection. In this example, Newton steps were allowed after $\ell _\mathrm {max}$ quasi-Newton iterations, where $\ell _\mathrm {max} \in \{0, 5, 20, 100, 200\}$. The maximum of 200 iterations was allowed.

We can see that if the Jacobian is only evaluated once ($\ell _\mathrm {max} = 200$) then the method is unable to converge in 200 iterations. As the maximum memory is reduced, the number of iterations to convergence is also reduced. On the other hand, the number of (possibly expensive) Newton steps is increased. When $\ell _\mathrm {max} = 0$, i.e., no quasi-Newton steps, the algorithm converges in 7 iterations. We take the same approach as [2] and define an upper bound $\ell _\mathrm {max}$ on $\ell$ in the implementation of Algorithm 2. When this upper bound is reached, we set $\ell$ to 0, which, by (17), results in the computation of a Newton step. The verification is performed at step 3 of Algorithm 2. This approach is also known as quasi-Newton with restarts [20] and differs from usual limited-memory quasi-Newton [26], where only the oldest information is dropped.

Fig. 1

Small bounds for $\ell$ reduce the number of iterations, but increase the necessity of evaluating and factorizing the Jacobian. The circles represent iterations where Newton steps were calculated

4.3 The quasi-Newton steps

The behavior of consecutive quasi-Newton steps depicted in Fig. 1 reminds us that it is important to use the true Jacobian in order to improve convergence of the method. However, we would like to minimize the number of times the Jacobian is evaluated, since it involves expensive factorizations and computations. Unfortunately, to use only the memory bound as a criterion to compute quasi-Newton steps is not a reasonable choice. When $\ell _\mathrm {max} = 100$, for example, the algorithm converges in 110 iterations, but it spends around 60 iterations without any improvement. As the dimension of the problem increases, this behavior is getting even worse. We can also see that the choice $\ell _\mathrm {max} = 20$ is better for this problem, as the algorithm converges in 31 iterations, computing only two times the Cholesky factorization of the Jacobian.

The lack of reduction is related to small step-sizes $\alpha _P^k$ and $\alpha _D^k$. Our numerical experience with quasi-Newton IP methods indicates that the quasi-Newton steps often are strongly attracted to the boundaries. The step-sizes calculated for directions originated from a quasi-Newton predictor-corrector strategy are almost always small and need to be fixed. Several strategies have been tried to increase the step-sizes of those steps:

• (i) Perturb complementarity pairs $x_i z_i$ for which the relative component-wise direction magnitude

  $$\begin{aligned} \frac{|\left[ \Delta {x}^k\right] _i|}{x_i^k}\quad \text {or}\quad \frac{|\left[ \Delta {z}^k\right] _i|}{z_i^k},\quad i = 1, \dots , n \end{aligned}$$

  (20)

  is high and then recompute quasi-Newton direction;

• (ii) Use multiple centrality correctors [3];

• (iii) Gentle reduction of $\mu$ on quasi-Newton iterations, by setting $\mu _k$ to

  $$\begin{aligned} 0.5 (x^k)^T z^k / n\quad \text {and}\quad 0.9 (x^k)^T z^k / n \end{aligned}$$

  for predictor and corrector steps, respectively.

Note that the terms in (i) are the inverses of the maximum step-sizes allowed by each component.

The motivation of strategy (i) is the strong relation observed between components of the quasi-Newton direction which are too large with respect their associated variable and components which differ too much from the respective component of the Newton direction for the same iteration, i.e.,

$$\begin{aligned} \frac{\left| \left[ {\Delta {x}^k}^{(N)} - {\Delta {x}^k}^{(QN)} \right] _i \right| }{x^k_i}\quad \text {and}\quad \frac{\left| \left[ {\Delta {z}^k}^{(N)} - {\Delta {z}^k}^{(QN)} \right] _i \right| }{z^k_i}, \end{aligned}$$

(21)

for $i = 1, \dots , n$. We display this relation in Fig. 2a for one iteration on linear problem GE. Positive spikes represent the component-wise relative magnitude of quasi-Newton steps (20) for each component of variables x and z. The higher the spikes, the smaller the step-sizes are. Negative spikes represent the component-wise relative error between the Newton and quasi-Newton directions (21). The lower the spikes, the larger the relative difference between Newton and quasi-Newton components. To generate this figure, the problem was solved twice and, at the selected iteration, the Newton step and quasi-Newton step were saved. Only negative quasi-Newton directions were considered in the figure. It is possible to see in Fig. 2a that very few components are responsible for the small step-sizes. Interestingly, most of those blocking components are associated with components of the quasi-Newton direction which differ considerably from the Newton direction. In order to implement the perturbation, the component in the pair associated with a large value in (20) was set to $0.2 \mu / \max \{x_i, z_i\}$. Then, the quasi-Newton step is computed again. As “large”, we defined to be greater or equal 20. Unfortunately, numerical experiments showed that the perturbation of variables or setting the problematic components of the computed direction to zero has the drawback of increasing the infeasibility and cannot be performed at many iterations.

Fig. 2

Relation between small step-sizes for quasi-Newton steps (positive spikes) and large relative errors when compared with Newton step (negative spikes) for one iteration on linear problem GE. High positive spikes represent blocking components of the quasi-Newton direction. The errors when only a simple predictor-corrector direction is used are displayed in a. The effect of using strategy (ii) to improve step-sizes is shown in b

To test the impact of each strategy on the quality of the steps, four linear and three quadratic programming problems were selected: afiro, GE, stocfor3, finnis, AUG2DQP, BOYD1 and POWELL20. The tests were performed as follows. Given an iteration k of a problem, we run algorithm HOPDM allowing only Newton steps up to iteration $k - 1$. At iteration k only one of each approach is applied: Newton step, quasi-Newton step, or one of the discussed strategies (i), (ii) or (iii). Only one affine-scaling predictor and one corrector were allowed, except for strategy (ii), where multiple centrality correctors were used at iteration k. We repeated this procedure for k from 2 up to the total number of iterations that the original version of HOPDM needed to declare convergence.

The average of the sum of the step-sizes for each problem and for each approach is shown in Table 2. We can see that quasi-Newton steps are considerably smaller than Newton steps. All improvement strategies are able to increase, on average, the sum of the step-sizes. Strategy (i) has the drawback of increasing the infeasibility and has a huge impact on the convergence of the algorithm. Strategy (iii) is simple and efficient to implement but has worse results when compared to strategy (ii), based on multiple centrality correctors. Strategy (ii) has the ability to improve quasi-Newton directions in almost all iterations and has the drawback of extra backsolves. Similar behavior was observed in [3]. The effect of strategy (ii) is shown in Fig. 2b. Step-sizes are increased, but the new quasi-Newton direction is slightly different from the Newton direction for the same step. Strategy (ii) was selected as the default one in our implementation.

Table 2 Average of the sum $\alpha _P^k+ \alpha _D^k$ for improvement strategies (i), (ii) and (iii) on selected linear and quadratic programming problems

In order to perform as few Newton steps as possible, step 3 of Algorithm 2 has to be carefully implemented. Clearly, the first basic condition to try a quasi-Newton step at iteration $k + 1$, $k \ge 0$, is to check if there is available memory to store it at iteration k.

Criterion 1

(Memory criterion) If $\ell \le \ell _\mathrm {max}$.

Our experience shows that quasi-Newton steps should always be tried, since they are cheaper than Newton steps. This means that a quasi-Newton step is always tried (but not necessarily accepted) after a Newton step in the present implementation. As shown in Fig. 1, using only Criterion 1 can lead to slow convergence and slow convergence is closely related to small step-sizes. Therefore, in addition to Criterion 1 we tested two criteria, which cannot be used together. In Sect. 5 we compare those different acceptance criteria.

Criterion 2

($\alpha$criterion) If iteration k is a quasi-Newton iteration and

$$\begin{aligned} \alpha _P^k+ \alpha _D^k\ge \varepsilon _\alpha . \end{aligned}$$

Criterion 3

(Centrality criterion) If iteration k is a quasi-Newton iteration and

$$\begin{aligned} {x^{k + 1}}^T z^{k + 1} \le \varepsilon _c \left( {x^k}^T z^k \right) . \end{aligned}$$

5 Numerical results

Algorithm 2 was implemented in Fortran 77 as a modification of the primal-dual interior point algorithm HOPDM[12], release 2.45. The code was compiled using gfortran 4.8.5 and run in a Dell PowerEdge R830 powered with Red Hat Enterprise Linux, 4 processors Intel Xeon E7-4660 v4 2.2GHz and 512GB RAM. The modifications discussed in Sects. 3 and 4 have been performed in order to accommodate the quasi-Newton strategy. The main stopping criteria have been set to Mehrotra and Li’s stopping criteria [3, 23]:

$$\begin{aligned} \frac{\mu }{1 + |c^T x|} \le \varepsilon _\mathrm {opt}, \quad \frac{\Vert b - Ax\Vert }{1 + \Vert b\Vert } \le \varepsilon _P, \quad \frac{\Vert c - {Q x }- A^T \lambda - z\Vert }{1 + \Vert c\Vert } \le \varepsilon _D, \end{aligned}$$

(22)

where $\mu = x^T z / n$. By default, in HOPDM parameters are defined to $\varepsilon _\mathrm {opt} = 10^{-10}$, $\varepsilon _P = 10^{-8}$ and $\varepsilon _D$ is set to $10^{-8}$ for linear problems and to $10^{-6}$ for quadratic problems. In addition to (22), successful convergence is also declared when lack of improvement is detected and $\mu / (1 + |c^T x|) \le 10^3 \varepsilon _\mathrm {opt}$. Besides several performance heuristics, HOPDM implements the regularization technique [1] and the multiple centrality correctors strategy [3].

For solving linear systems (17), sparse Cholesky factorization of normal equations or $LDL^T$ factorization of the augmented system is automatically selected on initialization. HOPDM also has a matrix-free [15] implementation and the present approach is fully compatible with it. We recall that how the linear system is solved is not important to the proposed approach, as long as we are able to save information for future use. The unreduced matrix is used only to compute the quasi-Newton updates.

According to Algorithm 2, once a quasi-Newton step is computed, it is used to build point ${\begin{bmatrix} x^{k + 1}&{\lambda }^{k + 1}&z^{k + 1} \end{bmatrix}^T}$. However, in practice, if such step is considered “bad”, it is also possible to discard it, setting $\ell = 0$, compute the exact Jacobian and perform the Newton step at this iteration. The idea is to avoid quasi-Newton steps which might degrade the quality of the current point. Preliminary experiments using linear programming problems from Netlib collection were performed, in order to test several possibilities for $\ell _\mathrm {max}$ in Criterion 1 and to select between Criterias 2 and 3. In addition we also verified the possibility to reject quasi-Newton steps, instead of always accepting them. The selected combination uses $\ell _\mathrm {max} = 5$ and Criterion 3 with $\varepsilon _c = 0.99$. Rejecting quasi-Newton steps has not led to reductions in the number of factorizations and has the drawback of more expensive iterations, therefore, the steps are always taken. As mentioned in Sect. 4, the multiple centrality correctors strategy (ii) is used to improve quasi-Newton directions.

A key comparison concerns the type of low rank update to be used. Three implementations were tested:

U1 :

General Broyden “bad” algorithm, described by Algorithm 1;

U2 :

Sparse Broyden “bad” algorithm, described by Algorithm 3 using update (16) inspired by Schubert’s update [29];

U3 :

General Broyden “good” algorithm, described by Algorithm 4.

Four test sets were used in the comparison: 96 linear problems from Netlib,¹ 10 medium-sized linear problems from Maros-Mészáros misc library,² 39 linear problems from the linear relaxation of Quadratic Assignment Problems (QAP)³ generated by Terry Johnson’s code⁴ and 138 convex quadratic programming problems from Maros-Mészáros qpdata library.⁵ In order to compare algorithms in large test sets, performance profiles were used [8]. A problem is declared solved by an algorithm if the obtained solution ${\begin{bmatrix} x^{*}&{\lambda }^{*}&z^{*} \end{bmatrix}^T}$ satisfies (22). Number of factorizations or total CPU time (in seconds) are used as performance measures.

Using the default HOPDM values for (22), implementations U1, U2 and U3 are able to solve 269, 275 and 271 problems, respectively, out of 283. The cases where HOPDM fails to converge are detailed in Table 3. There were three different cases of failure: the algorithm reached the maximum of 200 iterations, a sub-optimal solution was found or the problem was declared primal infeasible. Sub-optimal solutions occur when there is no improvement in the last 5 iterations, but the values used to check condition (22) are acceptable. We observed that there were many cases where sub-optimal solutions were found, thus we relaxed the parameters in (22), multiplying them by a factor of $10^2$, and solved again 19 problems where at least one implementation failed. It is possible to see in Table 3 that the sub-optimal cases were eliminated after the relaxation. The resulting performance profiles are shown in Fig. 3, using number of factorizations and CPU time as performance measures.

Table 3 Summary of the failure cases for implementations U1, U2 and U3, before and after relaxation of (22)

Update U2 is the most efficient, since it solves 208 problems using the smallest number of factorizations and 135 problems using the smallest CPU time, while U1 solves 174 and 123 and U3 solves 121 and 83, respectively. In addition, updates U2 and U3 are the most robust implementations, being able to solve 281 out of 283 problems. Therefore, U2 was used as the default update in this work. Update U2 has performed particularly well on quadratic problems, which explains the difference in efficiency between updates.

Fig. 3

Performance profiles comparing 3 Broyden updates: Broyden “bad” given by Algorithm 1 (U1), structured Broyden “bad” by Algorithm 3 (U2) and Broyden “good” by Algorithm 4 (U3)

Based on the preliminary results, the default implementation of Algorithm 2, denoted qnHOPDM from now on, uses update U2 for solving (17) and computing the step, strategy (ii) to improve quasi-Newton directions and Criteria 1 and 3 to decide when to use quasi-Newton at step 3. By default, HOPDM uses multiple centrality correctors, which were shown to improve convergence of the algorithm [3]. We implemented two versions of Algorithm 2: with (qnHOPDM-mc) and without (qnHOPDM) multiple centrality correctors for computing Newton steps. Since we are using strategy (ii), multiple correctors are always used for quasi-Newton steps. Each implementation was compared against its respective original version: HOPDM-mc and HOPDM.

In the first round of tests only the QAP collection was excluded from the comparison, which gives 244 problems from Netlib and from Maros-Mészáros linear and quadratic programming test collection. The performance profiles using number of factorizations and CPU time as performance measures are shown in Fig. 4. Comparisons between the implementation of HOPDM without multiple centrality correctors and qnHOPDM are given by Fig. 4a, b. The comparison of implementations HOPDM-mc and qnHOPDM-mc is displayed in Fig. 4c, d.

Fig. 4

Performance profiles for the comparison between the quasi-Newton IPM and HOPDM without (a and b) and with (c and d) multiple centrality correctors for Newton steps in 244 linear and quadratic programming problems

Similarly to the previous comparison, using default parameters, 5 problems were not solved by qnHOPDM or HOPDM without multiple centrality correctors, while 7 problems were not solved by qnHOPDM-mc or HOPDM-mc. Criteria (22) was relaxed in the same way on these problems. Using this approach, HOPDM is able to solve all the 244 problems, qnHOPDM solves 242, HOPDM-mc solves 243 and qnHOPDM-mc solves 242. The quasi-Newton implementations are able to successfully reduce the number of factorizations, as shown in Fig. 4a, c. We can see in Fig. 4a that from all 242 problems considered solved by qnHOPDM, in 237 it uses less factorizations than HOPDM without multiple centrality correctors. On the other hand, for about 150 problems, qnHOPDM uses at least twice as much CPU time as HOPDM (Fig. 4b). The behavior of the implementations using multiple centrality correctors in the Newton step is similar, but HOPDM-mc has improved efficiency results. The problems where qnHOPDM reduces both factorizations and CPU time when compared to HOPDM without centrality correctors are highlighted in Table 4. The only problem which qnHOPDM-mc uses strictly less CPU time than HOPDM-mc is the quadratic programming problem cont-101.

Table 4 Problems where the quasi-Newton implementation qnHOPDM used strictly less CPU time than HOPDM

Our last comparison considers 39 medium-sized problems from the QAP collection. These problems are challenging, since they are sparse, but their Cholesky factorizations are very dense. Performance profiles were once more used for comparing the implementations. As the algorithm approaches the solution, the linear systems become ill conditioned. The difficulty of barrier methods for solving the linear relaxation of QAPs was also observed in [27]. Therefore, using default HOPDM values for parameters in (22) the number of problems solved is 21 (HOPDM), 31 (qnHOPDM), 25 (HOPDM-mc) and 35 (qnHOPDM-mc). Clearly the quasi-Newton approach benefits from using matrices that are not too close to the solution. From the 39 problems, 19 were solved again using relaxed parameters for the comparison between HOPDM and qnHOPDM, and 14 were solved again for the comparison between HOPDM-mc and qnHOPDM-mc. The results are shown in Fig. 5. Quasi-Newton IPM is the most efficient and robust algorithm in terms of CPU time for both implementations, solving all 39 problems. Without multiple centrality correctors (Fig. 5a), HOPDM has a poor performance and is not able to solve any problem using less CPU time than qnHOPDM. When multiple centrality correctors are allowed (Fig. 5b), HOPDM-mc is able to solve only 10 problems using less or equal CPU time than qnHOPDM-mc.

Clearly, the efficiency of qnHOPDM is due to the decrease in the number of factorizations, as shown in Table 5. In this table we display the number of factorizations (F) and CPU time (CPUt) for each problem and each algorithm in all QAP test problems considered. When no multiple centrality correctors are allowed at Newton steps, qnHOPDM displays the biggest improvements, being the fastest solver in all problems. The results are more competitive when multiple centrality correctors are allowed, but qnHOPDM-mc was the most efficient in 29 problems while HOPDM-mc was the most efficient in 10 problems.

Fig. 5

Performance profiles for the comparison between quasi-Newton IPM and HOPDM [(without (a) and with (b) multiple centrality correctors] on the QAP test collection. CPU time was used as performance measure

Table 5 Numerical results for the QAP collection. For each algorithm the number of Cholesky factorizations (F) and CPU time (CPUt) is displayed

6 Conclusions

In this work we discussed a new approach to IPM based on rank-one secant updates for solving quadratic programming problems. The approach was motivated by the multiple centrality correctors, which provide many possible points where the function F can be evaluated in order to build a good approximation of J. Instead of using several points, the present approach uses only the new computed point in order to build a low rank approximation to the unreduced matrix at the next iteration. The computational cost of solving the quasi-Newton linear system can be compared with the cost of computing one corrector, as all the factorizations and preconditioners have already been calculated.

It was shown that rank-one secant updates maintain the main structure of the unreduced matrix. Also, several aspects of an efficient implementation were discussed. The proposed algorithm was implemented as a modification of algorithm HOPDM using the Broyden “bad” update, modified to preserve the sparsity structure of the unreduced matrix. The implementation was compared with the original version of HOPDM and was able to reduce the overall number of factorizations in most of the problems. However, only in the test set containing linear relaxations of quadratic assignment problems, the reduction in the number of factorizations was systematically translated into the reduction of the CPU time of the algorithm. This suggests that the proposed algorithm is suitable for problems where the computational cost of the factorizations is much higher than the cost of the backsolves.