Surface-Layer Flux–Gradient Relationships over Inclined Terrain Derived from a Local Equilibrium, Turbulence Closure Model

Abstract

Derivation of surface-layer flux–gradient relationships from a local-equilibrium, turbulence-closure model for a forced flow over inclined terrain is presented. Results are shown as a generalization of Monin–Obukhov universal functions respesenting non-dimensional wind and temperature gradients.

1 Introduction

The Monin–Obukhov surface-layer similarity theory (Obukhov 1946, 1971; Monin and Obukhov 1954; hereafter MOST) has been proven successful as a framework for establishing flux–gradient relationships in the atmospheric surface layer over flat and uniform terrain. Such relationships have great practical importance; for example, virtually all three-dimensional models used in numerical weather prediction utilize bulk schemes for calculating surface fluxes based on MOST, as their vertical grid spacing is grossly insufficient for resolving explicitly the large variability of main flow variables near the ground.

Universal functions of MOST can either be derived from turbulence models or determined from field data (e.g. Zilitinkevich and Chalikov 1968; Businger et al. 1971). While the performance of early theoretical models (KEYPS, Kazanski and Monin 1956) was rather poor, the second-order Reynolds-stress modelling provided solutions consistent with field data (e.g. Lewellen and Teske 1973; Mellor 1973; Prenosil 1979). Nevertheless, simpler empirical methods dominated. While admitting this fact, we would like to point out that the alternative theoretical approach offers advantages over the empirical one, such as a broader generality, self-consistency, and a prospect for consistency with the turbulence parametrization as used in the numerical model.

Although MOST assumptions seem rather restrictive with respect to real conditions wide application of MOST in atmospheric modelling has been very succesful. Perhaps this success is owed to sufficient accuracy in estimating relatively large fluxes that control the dynamics of atmospheric flows. However, with grid spacing of numerical weather prediction models approaching 1 km, our focus shifts to microscale problems, particularly in complex terrain where slope effects associated with stable equilibrium come into play. Hence, questions arise: are the slope effects important for influencing the exchange between the atmosphere and the underlying surface? If so, under what circumstances do slope effects become important? And finally, what modifications to existing algorithms are necessary to account for these effects?

While the empirical approach to these questions seems to be a natural path, it may not be easy to establish proper relationships. First, two new relevant parameters appear—wind direction with respect to the slope and terrain inclination angle. Second, while MOST is primarily designed for externally driven flows (volume forces acting in the flow direction within the surface layer are neglected) it does not apply to density-driven flows that develop over inclined terrain. It is then difficult to separate the density-driven component of the flow along the surface from the shear-driven component that is handled by MOST. Although there is a bulk of experimental results, most of the data come from field studies of katabatic flows (e.g. Horst and Doran 1983; van den Broeke 1997; Oerlemans et al. 1999). One of the few exceptions is the study by Park and Park (2006). However, this study is focused on turbulence statistics rather than flux calculations, and is limited to unstable conditions. An alternative approach to derive the desired relationships from a Reynolds-stress model is taken here. Of particular interest to this study is the work presented by Denby (1999), who successfully simulated katabatic flows over glaciers and ice caps with a one-dimensional, high resolution, second-order turbulence closure model transformed into slope coordinates. While Denby’s work confirms the feasibility of a one-dimensional framework to slope flows the demand for a high density vertical grid near the surface precludes its use in most of the present three-dimensional numerical models.

One might wonder whether the approach taken here is feasible. Indeed, in katabatic flows the wind maximum can be found at heights as low as 1 m (Denby 1999). Also, density-driven flows are not steady. Therefore, the presented method does not include a mechanism of density flow formation for modelling katabatic flows with insufficient vertical resolution. The underlying assumption for practical application is a possibility of separation of scales of motions so that the density-driving mechanism can be handled in resolvable scales while the transfer described by the solutions presented here would be treated as a subgrid process.

2 The Model

The turbulence model adopted herein stems from the Mellor–Yamada Level-2 model (Mellor 1973; Mellor and Yamada 1974, 1982) widely used in applications such as numerical weather prediction (e.g. Janjić 1990; Gerrity et al. 1994; Saito et al. 2007), mesoscale atmospheric research (e.g. Sušelj and Sood 2010; Foreman and Emeis 2012), ocean modelling (e.g. Blumberg and Mellor 1987; Kantha and Clayson 1994; Burchard and Bolding 2001), and global atmospheric models (e.g. Sirutis and Miyakoda 1990). Here, we follow a modification of this model by Nakanishi (2001); the model equations for horizontally homogeneous conditions over flat terrain in a conventional coordinate frame are listed in the Appendix 1.

2.1 Slope Coordinates

For sloping terrain, one might consider a two-dimensional Cartesian coordinate system, with its $XZ$ vertical plane containing the wind vector, the $X$-axis pointing in the wind direction, parallel to the slope, and the $Z$-axis perpendicular to the $X$-axis. Although not precise, the $X$ direction will be termed tangent, and the $Z$ direction termed normal in the following. This setting provides an exact transformation for pure downslope or upslope flows; for a general case, it should be treated as a simplification whose validity needs to be established. The transformation rules are summarized in Appendix 2.

Transformation of the model Eqs. 44–50 is accomplished by applying the transformation rules (56a, 56b) and substituting velocity components from (55a, 55b). In the following, however, we shall drop tildes, since now all the coordinates are expressed in the slope system unless explicitly stated. The model equations read

$$\begin{aligned} {\overline{u^{\prime 2}}}&= 6\,A_1 (1-C_2) \,\frac{\ell }{q}\,\beta \sin \alpha \,\,{\overline{u^{\prime }\theta ^{\prime }}} + \gamma _1 {q^2} \nonumber \\&+ 2\,A_1 C_2 \,\frac{\ell }{q}\, \beta \left( \sin \alpha \,\,\overline{u^{\prime }\theta ^{\prime }} + \cos \alpha \,\,\overline{w^{\prime }\theta ^{\prime }}\right) -6\,A_1 \,\frac{\ell }{q}\,{\overline{u^{\prime }w^{\prime }}}\, \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}, \end{aligned}$$

(1)

$$\begin{aligned} {\overline{v^{\prime 2}}}&= \gamma _1 q^2 + {2\,A_1\,C_2} \,\frac{\ell }{q} \,\beta \left( \sin \alpha \,\,\overline{u^{\prime }\theta ^{\prime }} + \cos \alpha \,\,\overline{w^{\prime }\theta ^{\prime }}\right) ,\end{aligned}$$

(2)

$$\begin{aligned} {\overline{w^{\prime 2}}}&= 6 A_1 (1-C_2)\,\beta \cos \alpha \,\, {\overline{w^{\prime }\theta ^{\prime }}}\frac{\ell }{q}\, +\gamma _1 q^2 \nonumber \\&+ 2 A_1 C_2 \,\frac{\ell }{q}\, \beta \left( \sin \alpha \,\,\overline{u^{\prime }\theta ^{\prime }} + \cos \alpha \,\,\overline{w^{\prime }\theta ^{\prime }}\right) , \end{aligned}$$

(3)

$$\begin{aligned} {\overline{u^{\prime }w^{\prime }}}&= - 3A_1 \frac{\ell }{q} \,\left( \overline{w^{\prime 2}} - C_1 q^2 \right) \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}} \nonumber \\&+ 3A_1 \frac{\ell }{q}\, \left( 1-C_2\right) \,\beta \left( \cos \alpha \,{\overline{u^{\prime }\theta ^{\prime }}} + \sin \alpha \, {\overline{w^{\prime }\theta ^{\prime }}} \right) , \end{aligned}$$

(4)

$$\begin{aligned} \overline{u^{\prime }\theta ^{\prime }}&= - 3 A_2 \,\frac{\ell }{q}\,\left[ \overline{u^{\prime }w^{\prime }}\, \frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}} + (1-C_5)\,\overline{w^{\prime }\theta ^{\prime }}\, \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}} \right] \nonumber \\&+ {3 A_2} (1-C_3) \,\frac{\ell }{q} \,\beta \sin \alpha \,\, \overline{\theta ^{\prime 2}}, \end{aligned}$$

(5)

$$\begin{aligned} \overline{w^{\prime }\theta ^{\prime }}&= - 3 A_2 \,\frac{\ell }{q}\,\overline{w^{\prime 2}}\, \frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}} + 3 A_2 (1-C_3)\, \frac{\ell }{q}\, \beta \,\overline{\theta ^{\prime 2}}, \end{aligned}$$

(6)

$$\begin{aligned} \overline{\theta ^{\prime 2}}&= - B_2\,\frac{\ell }{q}\,\overline{w^{\prime }\theta ^{\prime }} \,\frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}}, \end{aligned}$$

(7)

$$\begin{aligned}&-{\overline{u^{\prime }w^{\prime }}}\, \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}+ \beta \left( \sin \alpha \,\,\overline{u^{\prime }\theta ^{\prime }} + \cos \alpha \,\,\overline{w^{\prime }\theta ^{\prime }}\right) - \frac{q^3}{B_1\ell } = 0. \end{aligned}$$

(8)

In the above equations, $\alpha$ is the slope inclination along the wind direction, $x$ and $z$ denote coordinates of the slope coordinate system, $U$ is the wind speed (assumed parallel to the surface), $\Theta$ is the potential temperature, $u^{\prime }$, $v^{\prime }$ and $w^{\prime }$ are the fluctuation velocity components in slope coordinates; $\beta$ is the buoyancy parameter, $\theta ^{\prime }$ is the potential temperature fluctuation, $\ell$ is the turbulence master-length scale, the overbar represents Reynolds averaging, and $q^2$ is twice the turbulent kinetic energy (TKE), that is, $\overline{u^{\prime 2}}+\overline{v^{\prime 2}}+\overline{w^{\prime 2}}$. $A_1$, $A_2$, $B_1, B_2, C_1, C_2, C_3$ and $C_5$ are the model constants, and $\gamma _1=\frac{1}{3}-\frac{2A_1}{B_1}$.

While the basic set of prognostic equations for second-order statistical moments is systematically derived from conservation equations, the formulation of the turbulent master-length scale $\ell$ applied in closure hypotheses rests largely on heuristic arguments. Mellor and Yamada (1982) recognized this as the possibly largest outstanding weakness of this class of models. Numerous formulations of the turbulence master-length scale $\ell$ have been proposed in the past, mainly regarding stable stratification (e.g. Grisogono 2010). However, some limitations were found to be helpful in ensuring physical realizability in rapidly growing turbulence (e.g. Janjić 2001). Since the avoidance of branching threads seems to be justified by a preliminary character of this study, a simple wall-effect parametrization, $\ell =\kappa z$ has been chosen here, at the cost of a certain limitation of the model applicability range.

For $\alpha =0$, these equations reduce to the conventional surface-layer system, given in Appendix 1. The physical effects behind this transformation, are

• the gravitational force splits now into two components, one acting along the $Z$ axis, and the other acting along the slope. Note a new term in the downslope heat flux budget Eq. 5.

• the master-length scale is proportional to the distance from the surface (or to its projection onto the $Z$ axis), not to the height

2.2 Equilibrium Parameters and the TKE Budget

In the slope coordinate system, we assume scaling the dimensionless wind and temperature profiles with the $z$ coordinate and corresponding velocity and temperature scales $u_*$ and $T_*$,

$$\begin{aligned} \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}\left( \frac{\kappa z}{u_*}\right)&= \phi _m, \end{aligned}$$

(9)

$$\begin{aligned} \frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}}\left( \frac{\kappa z}{T_*}\right)&= \phi _h, \end{aligned}$$

(10)

where the scales $u_*$ and $T_*$ are defined by

$$\begin{aligned} u_*^2&= -{\overline{u^{\prime }w^{\prime }}}, \end{aligned}$$

(11)

$$\begin{aligned} T_*&= -\frac{\overline{w^{\prime }\theta ^{\prime }}}{u_*}. \end{aligned}$$

(12)

Note that the fluctuations in velocity are expressed as components $u^{\prime }$ and $w^{\prime }$ in the slope system, so that $\overline{u^{\prime }w^{\prime }}$ expresses a tangential surface stress rather than a vertical momentum flux. Further, we introduce

$$\begin{aligned} \ell _n=\frac{\ell }{\kappa z} \end{aligned}$$

(13)

and

$$\begin{aligned} q_n=\frac{q}{u_*}. \end{aligned}$$

(14)

From the TKE budget Eq. 8, using Eqs. 9 and 13,

$$\begin{aligned} \phi _m + \frac{\kappa z \beta \overline{u^{\prime }\theta ^{\prime }}}{u_*^3} \sin \alpha + \frac{\kappa z \beta \overline{w^{\prime }\theta ^{\prime }}}{u_*^3} \cos \alpha = \frac{q^3}{B_1\ell } \, \frac{\kappa z}{u_*^3}. \end{aligned}$$

(15)

Let us now introduce

$$\begin{aligned} \zeta _x=\frac{z}{L_x} = - \frac{\kappa z \beta \overline{u^{\prime }\theta ^{\prime }}}{u_*^3}, \end{aligned}$$

(16)

and

$$\begin{aligned} L_x = - \frac{u_*^3}{\kappa \beta \overline{u^{\prime }\theta ^{\prime }}}. \end{aligned}$$

(17)

Further, we use

$$\begin{aligned} \zeta _z=\frac{z}{L_z} = - \frac{\kappa z \beta \overline{w^{\prime }\theta ^{\prime }}}{u_*^3} \end{aligned}$$

(18)

and

$$\begin{aligned} L_z = - \frac{u_*^3}{\kappa \beta \overline{w^{\prime }\theta ^{\prime }}}. \end{aligned}$$

(19)

Now the TKE budget can be rewritten as

$$\begin{aligned} \phi _m - \zeta _x \sin \alpha - \zeta _z \cos \alpha = q_n^3 \ell _n^{-1} {B_1^{-1}} \end{aligned}$$

(20)

or

$$\begin{aligned} q_n^3=\frac{q^3}{u_*^3} = B_1 \ell _n \left( \phi _m - \zeta _x \sin \alpha - \zeta _z \cos \alpha \right) . \end{aligned}$$

(21)

This tempts us to denote

$$\begin{aligned} \zeta _s = \zeta _x \sin \alpha + \zeta _z \cos \alpha \end{aligned}$$

(22)

so that $\zeta _s$ corresponds to the Obukhov parameter $\zeta$ as defined using the vertical component of the turbulent heat flux (Fig. 1). However, for an inclined surface, $\zeta _s$ is not equivalent to $\zeta$, as the friction velocity used here, $u_*={\left| \overline{u^{\prime }w^{\prime }}\right| }^{1/2}$, is a tangential stress rather than a vertical momentum flux. Note also that the vertical heat flux is not just a vector sum of the downslope and normal components, as a non-zero horizontal flux may exist.

Fig. 1

Slope coordinate system and components of the vertical heat flux

Similarly, the flux Richardson number may be expressed now as

$$\begin{aligned} R_{Fs} = \frac{\beta \left( \sin \alpha \overline{u^{\prime }\theta ^{\prime }} + \cos \alpha \overline{w^{\prime }\theta ^{\prime }}\right) }{\displaystyle {\overline{u^{\prime }w^{\prime }}} \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}} \end{aligned}$$

(23)

hence

$$\begin{aligned} R_{Fs} = \frac{\kappa z \beta \left( \overline{u^{\prime }\theta ^{\prime }} \sin \alpha + \beta \overline{w^{\prime }\theta ^{\prime }} \cos \alpha \right) }{u_*^3 \phi _m} = \frac{\zeta _s}{\phi _m} \end{aligned}$$

(24)

so that we have again

$$\begin{aligned} q_n^3= B_1 \ell _n \zeta _s ~ \frac{1-R_{Fs}}{R_{F_s}} = B_1 \ell _n \left( \phi _m-\zeta _s\right) . \end{aligned}$$

(25)

2.3 Non-Dimensional Form of Model Equations

With the annotations introduced in the previous subsection, Eqs. 1–8 can be transformed into a non-dimensional form

$$\begin{aligned}&\frac{\overline{w^{\prime 2}}}{q^2} = \gamma _1 - \frac{2 A_1}{B_1} \, \frac{C_2 \zeta _s + 3 (1-C_2) \zeta _z \cos \alpha }{\phi _m-\zeta _s}, \end{aligned}$$

(26)

$$\begin{aligned}&\frac{\overline{u^{\prime 2}}}{q^2} = \gamma _1 + \frac{2 A_1}{B_1} \frac{3\phi _m - C_2\zeta _s -3\, (1-C_2) \zeta _x\,\sin \alpha }{ \phi _m - \zeta _s}, \end{aligned}$$

(27)

$$\begin{aligned}&q_n \ell _n \left[ \left( \frac{\overline{w^{\prime 2}}}{q^2} - C_1 \right) \phi _m +\left( 1-C_2\right) \, (\sin \alpha \, \zeta _z + \, \cos \alpha \, \zeta _x)\, {q_n^{-2}}\right] = \frac{1}{3A_1}, \end{aligned}$$

(28)

$$\begin{aligned}&\frac{\zeta _x}{\zeta _z} = {-3A_2 \frac{\ell _n}{q_n}} \left[ \phi _h \left( 1+B_2 (1-C_3) \frac{\ell _n}{q_n} \zeta _z \sin \alpha \right) +\left( 1-C_5\right) \phi _m \right] , \end{aligned}$$

(29)

$$\begin{aligned}&{\ell _n}{q_n}\left[ \frac{\overline{w^{\prime 2}}}{q^2} \phi _h - \left( 1-C_3\right) q_n^{-2} \zeta _z \frac{\overline{\theta ^{\prime 2}}}{T_*^2} \right] = \frac{1}{3A_2}, \end{aligned}$$

(30)

$$\begin{aligned}&\frac{\overline{\theta ^{\prime 2}}}{T_*^2} = B_2 \ell _n q_n^{-1} \phi _h. \end{aligned}$$

(31)

Comparison with the horizontal flow case $(\alpha =0)$ shows that the controlling equilibrium parameter $\zeta$ is now replaced by two parameters $\zeta _x$ and $\zeta _z$ linked by the downwind heat flux budget Eq. 29.

2.4 Solution Procedure

Taking $\ell _n=1$, let us rewrite the equation system (26–31) as

$$\begin{aligned}&\left[ \gamma _1 - C_1 - \frac{2 A_1}{B_1} \, \frac{C_2 \zeta _s + 3 (1-C_2) \zeta _z \cos \alpha }{\phi _m-\zeta _s} \right] \phi _m \nonumber \\&\quad +\left( 1-C_2\right) \, (\sin \alpha \, \zeta _z + \, \cos \alpha \, \zeta _x)\, {q_n^{-2}} = \frac{1}{3\,A_1\, q_n}, \end{aligned}$$

(32)

$$\begin{aligned}&\frac{\zeta _x}{\zeta _z} = {-3A_2 {q_n^{-1}}} \left[ \phi _h \left( 1+B_2 (1-C_3) {q_n^{-1}} \zeta _z \sin \alpha \right) +\left( 1-C_5\right) \phi _m \right] , \end{aligned}$$

(33)

$$\begin{aligned}&\left[ \gamma _1 - \frac{2 A_1}{B_1} \, \frac{C_2 \zeta _s + 3 (1-C_2) \zeta _z \cos \alpha }{\phi _m-\zeta _s} \right] \,\phi _h \nonumber \\&\quad - B_2\,\left( 1-C_3\right) \, q_n^{-3} \, \zeta _z \,\phi _h = \frac{1}{3A_2 \, {q_n}}, \end{aligned}$$

(34)

where

$$\begin{aligned} \Gamma _s = {\frac{\phi _m}{\zeta _s}-1} = \frac{\phi _m-\zeta _s}{\zeta _s} \end{aligned}$$

(35)

so that

$$\begin{aligned} q_n= B_1^{1/3} \Gamma _s^{1/3}\zeta _s^{1/3}. \end{aligned}$$

(36)

For a further reduction, we introduce the following annotations:

$$\begin{aligned}&a=\gamma _1 B_1;\,\,b=2 A_1 C_2;\,\,c=6 A_1 (1-C_2);\,\,d=B_1 C_1; \nonumber \\&e=3A_2 \left( 1-C_2\right) ;\,\,f=\left( 1-C_5\right) ;\,\, \displaystyle g_1=\frac{B_1^{2/3}}{3 A_1};\,\,g_2=\frac{B_1^{2/3}}{3 A_2} \nonumber \\&g_3=\frac{B_1^{1/3}}{3 A_2};\,\,h_1=B_2 \left( 1-C_3\right) ;\,\,h_2=B_2 B_1^{-1/3} \left( 1-C_3\right) ; \nonumber \\&\displaystyle h_3 = B_1^{1/3}\,\left( 1-C_2\right) , \,\,r=\frac{\zeta _x}{\zeta _s},\end{aligned}$$

(37)

$$\begin{aligned}&\chi =\frac{\zeta _z}{\zeta _s}, \end{aligned}$$

(38)

so that

$$\begin{aligned} \zeta _z&= \chi \, \zeta _s = \frac{\zeta _s}{\cos \alpha } - r\,\zeta _s \, \tan \alpha , \end{aligned}$$

(39)

$$\begin{aligned} \chi&= \frac{1}{\cos \alpha } - r\, \tan \alpha . \end{aligned}$$

(40)

With the above, Eqs. 32–36 reduce to a closed set of non-linear algebraic equations

$$\begin{aligned}&(a-d-b\Gamma _s^{-1}- c \chi \,\Gamma _s^{-1} \cos \alpha ) \, \phi _m \nonumber \\&\quad +{h_3\, (\chi \, \sin \alpha + \,r \, \cos \alpha )\, \Gamma _s^{-2/3}\zeta _s^{1/3}} = \frac{g_1}{\Gamma _s^{1/3}\zeta _s^{1/3}}, \end{aligned}$$

(41)

$$\begin{aligned}&\frac{g_3 \, r}{\chi } = {- \Gamma _s^{-1/3}\zeta _s^{-1/3}} \left[ \phi _h \left( 1+h_2 \Gamma _s^{-1/3}\zeta _s^{2/3} \chi \,\sin \alpha \right) +\left( 1-C_5\right) \phi _m \right] , \end{aligned}$$

(42)

$$\begin{aligned}&(a\, - b \Gamma _s^{-1}\, - c \chi \,\Gamma _s^{-1} \, \cos \alpha - h_1 \, \chi \, \Gamma _s^{-1}) \,\phi _h = \frac{g_2}{\Gamma _s^{1/3}\zeta _s^{1/3}}, \end{aligned}$$

(43)

with three unknowns, $\Gamma _s$, $r$ and $\phi _h$. The simplest one-point iterative method ${\mathbf {x}}^{(k+1)}=f({\mathbf {x}}^{(k)})$ converges only in a very narrow range of $\zeta _s$, hence other methods are necessary. In this study, a first-order iterative Newton method was used; the necessary details are given in Appendix 3.

3 Results

For this study, we adopted a set of model constants recommended by Nakanishi (2001), viz.

$$\begin{aligned}&\left( A_1,\, A_2,\,B_1,\,B_2\right) = \left( 1.18, 0.665, 24.0, 15.0\right) , \\&\left( C_1,\,C_2,\,C_3,\,C_5\right) = \left( 0.137, 0.65, 0.294, 0.2\right) . \end{aligned}$$

Figure 2 displays dimensionless (scaled) normal components of gradients of wind velocity and potential temperature for downslope flows ($\alpha \le 0$), while the corresponding gradients for upslope flows ($\alpha \ge 0$) are shown in Fig. 3. It is seen that the terrain inclination has virtually no effect on dimensionless temperature gradients and little effect on the dimensionless wind-speed gradient under unstable conditions (at least in the stability interval considered here, $-2 < \zeta _s \le 0$). On the other hand, slope effects under stable conditions are pronounced.

Fig. 2

Dimensionless gradients of wind velocity and potential temperature for downslope flows ($\alpha \le 0$)

Fig. 3

Dimensionless normal components of gradients of wind velocity and potential temperature for upslope flows ($\alpha \ge 0$)

Under stable stratification, scaled normal components of wind-speed and temperature gradients diminish with surface steepness. Interestingly, the non-dimensional wind-speed gradient appears to assume a linear dependence while the dimensionless temperature gradient exhibits some curvature, particularly for larger slope inclinations. In upslope flows, opposite effects are observed: dimensionless gradients of wind speed and temperature grow with the terrain inclination angle. Over steep slopes, the growth rate of the non-dimensional temperature gradient soon becomes rapid and the model breaks down. Apparently, this breakdown is related to the vanishing of the turbulent heat flux’s normal component (Fig. 4). As can be seen from Eq. 6 this may happen not only in adiabatic conditions (where both the potential temperature gradient and the potential temperature variance are null), but also at certain conditions under stable stratification where the two terms on the right-hand side of (6) may cancel each other.

Fig. 4

Ratio of tangential to normal components of the turbulent heat flux as a function of stability parameter $\zeta _s$, for various terrain inclination angles: top upslope flows ($\alpha \ge 0$); bottom downslope flows ($\alpha \le 0$)

A key to explaining these tendencies lies in the role of the tangential component of the turbulent heat flux. As can be seen from Eq. 8, this component is related to a buoyant production of the TKE. Let us consider upslope flow under stable stratification; inspection of the tangential heat-flux budget, Eq. 5, shows that both of the two terms in square brackets are negative (thus the entire expression containing the terms in square brackets is positive), and the remaining term (containing the potential temperature variance) is also positive. Therefore, all the terms contribute to the growth of the tangential heat flux. Indeed, as can be seen from Fig. 4 (upper panel), the tangential component of heat flux is several times greater than the normal component [in agreement with wind-tunnel measurements (Arya 1975) and field data Wyngaard et al 1971]. The ratio of tangential to normal components increases (in terms of absolute values) with growing stability and inclination. This, in turn, increases the TKE (Fig. 5). As can be seen from Eq. 29, both of these increases correspond to the increase of dimensionless temperature and wind-speed gradients.

Fig. 5

Doubled turbulent kinetic energy, scaled with the kinematic surface stress as a function of stability parameter $\zeta _s$, for various terrain inclination angles: top upslope flows ($\alpha \ge 0$); bottom downslope flows ($\alpha \le 0$)

Qualitative analysis of the relations in downslope flows is more difficult, as the individual terms in the tangential heat-flux budget equation, Eq. 5, are not of the same sign and partially cancel each other. While the sign of the result can hardly be predicted by this argumentation, it is evident that the tangential heat flux should have a smaller value than in an upslope flow under comparable forcing. This is corroborated by calculations presented in the bottom panel of Fig. 4. While the tangential component is still larger than the normal one, its role in the TKE budget is currently marginal; over steeper terrain, we now see a relative reduction of TKE now. Consequently, dimensionless temperature and wind-speed gradients should assume smaller values than in upslope winds.

Figure 5 displays the value of the $q_n^2 = q^2 / u_*^2$ function, that is the doubled TKE normalized by kinematic surface stress. One may note that the slope influences agree, at least in qualitative terms with the field results presented by Park and Park (2006) (compare their Fig. 12) for unstable stratification. This agreement may seem encouraging, although more extensive experimental evidence is necessary to validate the theoretical predictions presented here.

4 Summary and Conclusions

Perspectives of the inclusion of terrain inclination effects into the surface-layer flux–gradient relationships have been theoretically investigated with a local-equilibrium, second-order turbulence model. The aim of the present study was twofold: first, to propose a methodological approach to the inclusion of slope effects into the MOST; second, to assess the possible outcome of such an extension, at least in qualitative terms.

The approach taken here rests on the following simplifications and assumptions:

• the external forcing is sufficient to maintain homogeneity along the slope so that a single-column framework may be applied;

• further, the MOST assumptions are imposed, with the exception of the requirement that the underlying surface be horizontal;

• consequently, the results can only be applicable to the region where gravitational/buoyancy forces can be neglected in the budget of the downslope momentum component. In other words, existence of a turbulent sublayer where the mean motion is primarily shear-driven and the turbulence is driven by both the shear and buoyancy is postulated;

• the wall proximity effects are parametrized via the master-length scale as dependent on the distance from the inclined surface, while the buoyancy effect act along the vertical;

• as a result of the flow’s time evolution, a quasi-stationary regime is reached through a process of self-adaptation of the profiles and forcing, and the potential temperature gradient assumes a direction perpendicular to the surface;

• the influence of the crosswind component of the topographical slope is neglected, i.e. the theory is strictly applicable to pure downslope or upslope winds.

Obviously, these simplifications may seem restrictive. On the other hand, the current modelling practice mainly rests on utilizing empirical MOST flux–gradient relationships where slope effects are not taken into account.

Corresponding to the aforementioned goals, we have opted for a widely applied, relatively simple turbulence closure model, thereby postponing the issue of optimal model choice to subsequent studies. The results presented here should be seen as preliminary and interpreted in qualitative terms rather than quantitative.

Calculations show that the classic MOST profiles may be used with almost no modification under unstable equilibrium, with simple geometric adjustments to account for the direction of the surface stress and for scaling the distance to the surface. However, in stable conditions, a modification of the universal functions $\varphi _m(\zeta )$ and $\varphi _h(\zeta )$ is also necessary. Such a modification can be quite simple for downslope winds over gently or moderately sloping terrain. However, the model results for upslope flows over steep terrain point to a more complex behaviour that may involve realizability limitations of the model. A further clarification of this issue is necessary, with the use of alternative turbulence closures, in particular the newly developed models that avoid the limitation of the gradient Richardson number (Zilitinkevich et al 2007), large-eddy simulation studies and analyses of field data.

Appendices

Appendix 1: The Turbulence Model

The turbulence model adopted for this study is an extension of the Mellor–Yamada model introduced by Nakanishi (2001). With the usual local equilibrium approximations for a constant-flux layer, the set of relevant equations can be written as

$$\begin{aligned}&\displaystyle {\overline{u^{\prime 2}}} = \gamma _1 {q^2} + 2 A_1 C_2 \frac{\ell }{q} \beta \overline{w^{\prime }\theta ^{\prime }} - 6 A_1 \frac{\ell }{q} {\overline{u^{\prime }w^{\prime }}} \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}},\end{aligned}$$

(44)

$$\begin{aligned}&\displaystyle {\overline{v^{\prime 2}}} = \gamma _1 {q^2} + 2 A_1 C_2 \frac{\ell }{q} \beta \overline{w^{\prime }\theta ^{\prime }},\end{aligned}$$

(45)

$$\begin{aligned}&\displaystyle {\overline{w^{\prime 2}}} = \gamma _1 {q^2} + 2 A_1 \left( 3 - 2 C_2\right) \frac{\ell }{q} \beta \overline{w^{\prime }\theta ^{\prime }},\end{aligned}$$

(46)

$$\begin{aligned}&\displaystyle {\overline{u^{\prime }w^{\prime }}} = 3A_1 \frac{\ell }{q} \left[ - \left( \overline{w^{\prime 2}} - C_1 q^2 \right) \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}+ \left( 1-C_2\right) \beta \overline{u^{\prime }\theta ^{\prime }}\right] ,\end{aligned}$$

(47)

$$\begin{aligned}&\displaystyle \overline{u^{\prime }\theta ^{\prime }} = 3A_2 \frac{\ell }{q}\left( - \overline{u^{\prime }w^{\prime }} \frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}} -\left( 1-C_5\right) \overline{w^{\prime }\theta ^{\prime }} \frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}} \right) ,\end{aligned}$$

(48)

$$\begin{aligned}&\displaystyle \overline{w^{\prime }\theta ^{\prime }} = 3A_2 \frac{\ell }{q}\left( - \overline{w^{\prime 2}} \frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}} + \left( 1-C_3\right) \beta \overline{\theta ^{\prime 2}} \right) ,\end{aligned}$$

(49)

$$\begin{aligned}&\displaystyle \overline{\theta ^{\prime 2}} = -B_2 \frac{\ell }{q} \overline{w^{\prime }\theta ^{\prime }}\frac{\,\mathrm {d}{\Theta }}{\,\mathrm {d}{z}},\end{aligned}$$

(50)

$$\begin{aligned}&\displaystyle q^2 = B_1 \frac{\ell }{q} \left( -\overline{u^{\prime }w^{\prime }}\frac{\,\mathrm {d}{U}}{\,\mathrm {d}{z}}+ \beta \overline{w^{\prime }\theta ^{\prime }} \right) . \end{aligned}$$

(51)

Symbols used here are explained in Sect. 2.

Appendix 2: Coordinate Transformation

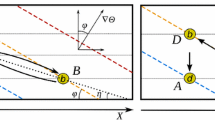
Let us consider two Cartesian coordinate systems as shown in Fig. 1. Contravariant coordinates of an arbitrary vector ${\mathbf {V}}$ can be expressed by

$$\begin{aligned} {\mathbf {V}} = V^i {\mathbf {e}}_i = \widetilde{V}^i \widetilde{{\mathbf {e}}}_i \end{aligned}$$

(52)

where ${\mathbf {e}}_i$ and $\widetilde{{\mathbf {e}}}_i$ denote bases of these systems.

In our case, $V^1=x$ and $V^2=z$ are the horizontal and vertical coordinates, and $\widetilde{V}^1=\tilde{x}$, and $\widetilde{V}^2=\tilde{z}$ are coordinates of ${\mathbf {V}}$ in the slope coordinate system. The coordinate transformation (rotation) is given by,

$$\begin{aligned} \tilde{x}&= x \cos \alpha + z \sin \alpha , \end{aligned}$$

(53a)

$$\begin{aligned} \tilde{z}&= - x \sin \alpha + z \cos \alpha , \end{aligned}$$

(53b)

and

$$\begin{aligned} x&= \tilde{x} \cos \alpha - \tilde{z} \sin \alpha , \end{aligned}$$

(54a)

$$\begin{aligned} z&= \tilde{x} \sin \alpha + \tilde{z} \cos \alpha . \end{aligned}$$

(54b)

In particular, for the velocity vector

$$\begin{aligned} u&= \tilde{u} \cos \alpha - \tilde{w} \sin \alpha , \end{aligned}$$

(55a)

$$\begin{aligned} w&= \tilde{u} \sin \alpha + \tilde{w} \cos \alpha . \end{aligned}$$

(55b)

The transformation of partial derivatives is obtained by applying the chain rule to Eqs. 54a, 54b

$$\begin{aligned} \frac{\partial {}}{\partial {x}}&= \cos \alpha \,\frac{\partial {}}{\partial {\tilde{x}}} -\sin \alpha \,\frac{\partial {}}{\partial {\tilde{z}}}, \end{aligned}$$

(56a)

$$\begin{aligned} \frac{\partial {}}{\partial {z}}&= \sin \alpha \,\frac{\partial {}}{\partial {\tilde{x}}} + \cos \alpha \,\frac{\partial {}}{\partial {\tilde{z}}}. \end{aligned}$$

(56b)

Appendix 3: Numerical Solution

The non-linear equation set,

$$\begin{aligned} \varvec{\Phi }(\mathbf {x})=\mathbf {0} \end{aligned}$$

(57)

is solved using an iterative, first-order Newton method,

$$\begin{aligned} \varvec{\Phi }^{\prime }(\mathbf {x}^{(k)})(\mathbf {x}^{(k+1)}-\mathbf {x}^{(k)})+\varvec{\Phi }(\mathbf {x}^{(k)})=0. \end{aligned}$$

(58)

In the above, $\mathbf {x}$ denotes the vector of unknowns, the superscripts represent the iteration step number, and the $\varvec{\Phi }^{\prime }$ denotes the Jacobi matrix, containing partial derivatives of functions $\varvec{\Phi }^{\prime }(\mathbf {x})$ representing the equations, with respect to all their arguments $(\mathbf {x})$. This method requires all the $\varvec{\Phi }(\mathbf {x})$ functions to be given, as well as all the components of the Jacobi matrix. The $\varvec{\Phi }(\mathbf {x})$ functions are

$$\begin{aligned} \Phi _1&= [a\,\Gamma ^{1/3} - (b + c \chi \, \cos \alpha + h_1 \, \chi ) \, \Gamma _s^{-2/3}] \,\phi _h - {g_2}{\zeta _s^{-1/3} },\end{aligned}$$

(59)

$$\begin{aligned} \Phi _2&= (a-d)\Gamma _s^{4/3} \,\zeta _s -(b+ c \chi \,\cos \alpha ) \Gamma _s^{1/3}\,\zeta _s \nonumber \\&+ (a-d)\Gamma _s^{1/3}\, \zeta _s -(b+ c \chi \,\cos \alpha ) \Gamma _s^{-2/3} \, \zeta _s \nonumber \\&+{h_3\, \left[ \chi \, \sin \alpha + \,r \, \cos \alpha \right] \, \Gamma _s^{-1/3}\zeta _s^{1/3}} - {g_1} \zeta _s^{-1/3}, \end{aligned}$$

(60)

$$\begin{aligned} \Phi _3&= g_3 \,\Gamma _s^{1/3}\, r + \phi _h \zeta _s^{-1/3}{\chi } + h_2 \Gamma _s^{-1/3} \zeta _s^{1/3} \phi _h {\chi }^2 \,\sin \alpha \nonumber \\&+ f \zeta _s^{2/3}{\chi } (\Gamma _s+1). \end{aligned}$$

(61)

Note that $\chi =\chi (r)$, and

$$\begin{aligned} \frac{\partial {\chi }}{\partial {r}}=-\tan \alpha \end{aligned}$$

(62)

so that the Jacobi matrix elements can be written as

$$\begin{aligned} \frac{\partial {\Phi _1}}{\partial {\Gamma _s}}&= \frac{1}{3} a \,\phi _h \Gamma _s^{-2/3} + \frac{2}{3} (b+c\,\chi \,\cos \alpha + h_1\,\chi )\,\phi _h \, \Gamma _s^{-5/3}, \end{aligned}$$

(63)

$$\begin{aligned} \frac{\partial {\Phi _1}}{\partial {r}}&= c \, \Gamma _s^{-2/3}\,\phi _h \, \sin \alpha + h_1 \phi _h \Gamma _s^{-2/3} \tan \alpha , \end{aligned}$$

(64)

$$\begin{aligned} \frac{\partial {\Phi _1}}{\partial {\phi _h}}&= a \,\Gamma _s^{1/3} - (b+c\,\chi \,\cos \alpha + h_1\,\chi )\,\Gamma _s^{-2/3}, \end{aligned}$$

(65)

$$\begin{aligned} \frac{\partial {\Phi _2}}{\partial {\Gamma _s}}&= \frac{4}{3} a \, \Gamma _s^{1/3}\,\zeta _s + \frac{1}{3} a \,\Gamma _s^{-2/3}\,\zeta _s - \frac{1}{3} (b+c\,\chi \,\cos \alpha )\,\Gamma _s^{-2/3} \,\zeta _s \nonumber \\&+ \frac{2}{3} (b+c\,\chi \,\cos \alpha )\,\Gamma _s^{-5/3} \,\zeta _s - \frac{4}{3} \hbox {d} \, \Gamma _s^{1/3} \,\zeta _s - \frac{1}{3} \hbox {d} \, \Gamma _s^{-2/3} \,\zeta _s \nonumber \\&- \frac{1}{3} h_3\, r \, \Gamma _s^{-4/3}\zeta _s^{1/3}, \end{aligned}$$

(66)

$$\begin{aligned} \frac{\partial {\Phi _2}}{\partial {r}}&= c \,\zeta _s \, (\Gamma _s^{1/3}+\Gamma _s^{-2/3})\, \sin \alpha + h_3\,\Gamma _s^{-1/3}\zeta _s^{1/3} (-\tan \alpha \sin \alpha + \cos \alpha ), \end{aligned}$$

(67)

$$\begin{aligned} \frac{\partial {\Phi _2}}{\partial {\phi _h}}&= 0, \end{aligned}$$

(68)

$$\begin{aligned} \frac{\partial {\Phi _3}}{\partial {\Gamma _s}}&= \frac{1}{3} g_3 \, \Gamma _s^{-2/3}\, r -\frac{1}{3} h_2 \Gamma _s^{-4/3} \zeta _s^{1/3}{\chi }^2 \phi _h \sin \alpha + f\, \chi \, \zeta ^{2/3} , \end{aligned}$$

(69)

$$\begin{aligned} \frac{\partial {\Phi _3}}{\partial {r}}&= g_3 \, \Gamma ^{1/3}\, \nonumber \\&-[\phi _h \zeta _s^{-1/3} + 2\,\chi \, h_2 \Gamma _s^{-1/3} \zeta _s^{1/3} \phi _h \,\sin \alpha + f \zeta _s^{2/3}(\Gamma _s+1)] \tan \alpha \end{aligned}$$

(70)

$$\begin{aligned} \frac{\partial {\Phi _3}}{\partial {\phi _h}}&= \zeta _s^{-1/3} \chi + h_2 \Gamma _s^{-1/3} \zeta _s^{1/3} \, {\chi }^2 \,\sin \alpha . \end{aligned}$$

(71)