1 Introduction

Ground motion models (GMM) represent key-elements in applied seismology as they mathematically describe the effect of earthquakes at the site, given a scenario event defined in terms of at least magnitude and distance. They are also basic ingredients in probabilistic and deterministic seismic hazard analyses, also used for loss and risk assessment, as well as in many tools for civil protection planning and engineering applications, like shaking scenarios and Shakemaps (Worden et al. 2018). The main drawback of these models rely in the fact that they represent extreme simplifications of the earthquake process and also because they are typically calibrated on limited data that are available only in high-seismicity areas of the world and then applied as global averages without considering the specific location, thus invoking common ergodic assumption (Anderson and Brune 1999). The use of the ergodic hypothesis typically leads to large uncertainty associated with the ground motion predictions (Stafford 2014), which strongly impacts on the results of hazard analysis and related products, as highlighted in the literature (Bommer et al. 2010).

For these reasons, in the last years, a strong effort has been made by the research community to reduce ground motion variability and move towards regionalised models at smaller scale. The most acknowledged and advanced strategy to this aim is based on the relaxation of the ergodic assumption; a shift that is nowadays possible thanks to the increasing availability of records consequent to the growing of seismic networks worldwide. A fully nonergodic approach is based on the principle that wherever many records at each station from multiple earthquakes are available, it is possible to identify the systematic contributions of variability into event-, source-, site- and path- effects, through a statistical decomposition technique (Al-Atik et al. 2010). It is estimated that about 60–70% of the aleatory variance in ergodic GMM is due to these systematic effects (Abrahamson et al. 2019).

Examples of recent fully nonergodic models, conducted either with continuous or spatial regionalization approaches, can be found in Landwehr et al. (2016), Baltay et al. (2017), Parker et al. (2022), Kuehn et al. (2019), Abrahamson et al. (2019), Sgobba et al. (2019), Lanzano et al. (2021), Sung et al. (2022), Lavrentiadis et al. (2021; 2022), Liu et al. (2022) among the others. All these models are associated with random-terms that act as adjustments of the median prediction, while moving part of the aleatory variability into epistemic uncertainty (Al-Atik et al. 2010; Anderson and Uchiyama 2011). These studies have been typically developed in highly sampled regions such as California or Italy. In this latter country, the occurrence of the last seismic sequences in 2016–2017 in Central Italy, has enhanced a lot the Italian datasets allowing to gather geophysical, geological and seismological information that have driven to a fruitful activity of empirical modeling in this region. In detail, this exceptional set of information has produced many studies in the area that went into detailed parametrization of the regional geology (Chiaraluce et al. 2017; Buttinelli et al. 2021; Di Bucci et al. 2021) and prediction of ground motion at the site (Bindi et al. 2018a, b; Morasca et al. 2019; Lanzano et al. 2020; Felicetta et al. 2018; Sgobba et al. 2021; Lanzano et al. 2021; Castro et al. 2022; Colavitti et al. 2022).

In this work, we want to further exploit the mine of data and seismological parameters in Central Italy, to complement the nonergodic model calibrated by Sgobba et al. (2021) for spectral accelerations (SA), with a new ad-hoc GMM based on Fourier Amplitude Spectra (FAS) by using a set of fully consistent physical information to predict the ground motion parameters and capture more epistemic uncertainty. In doing this, we consider that the aim of setting seismological constraints to ground motion can be achieved more appropriately in terms of FAS compared to response spectral accelerations SA, because FAS are more closely related to the physics, as also highlighted by Bora et al. (2015) and Bindi et al. (2018c). Hence, our study is conducted in terms of a GMM-FAS similarly to Bora et al. (2015) and Bayless and Abrahamson (2019), who proposed a physically-consistent approach for developing FAS predictions easily adjustable to different seismological conditions. Yet, compared to those works, we here investigate the relationships between the systematic terms of uncertainty of the FAS-GMM and the physical parameters related to the source rupture and site response gathered from independent analyses, under a complete nonergodic framework. An advantage linked to the inclusion of more physical constraints in the predictions consists in the opportunity to assess the impact of a boosted parametrization on the aleatory variability reduction. The final purpose is to define a methodological framework for calibrating a model of FAS that, once converted in spectral intensities, could be used to generate non-ergodic and physics-based empirical shaking scenarios (e.g. Sgobba and Pacor 2023; Sgobba et al. 2021; Abrahamson et al. 2019) for civil protection purposes or that could be also exploited to produce expeditive simulations of ground-motion time series.

The paper is outlined as follows: we first develop a nonergodic FAS-GMM on 69 ordinates of the Fourier spectrum including only source and attenuation scaling terms and related to reference rock sites. Then we correlate the repeatable terms of variability with a suite of region-specific spectral parameters (i.e. stress-drop, shear-wave velocity in the top 30 m and high-frequency attenuation kappa) obtained from a non-parametric generalized inversion technique (GIT) developed on the same dataset by Morasca et al. (2023). Finally, we re-parametrise the original model including the additional explanatory variable through a stepwise regression approach and then compare the prediction performance and uncertainty contributions among the two model versions.

2 Dataset

The collection of records used in this study is composed of both accelerometric and velocimetric three components waveforms of events located in Central Italy and occurred between 2009 and 2018 including the latest major seismic sequences that occurred in the area of study, i.e. the 2009 L’Aquila seismic sequence and the 2016–2017 Amatrice-Visso-Norcia sequence.

This dataset was originally developed in the framework of the seismic microzonation study carried out in Central Italy after the 2016 Mw 6.0 Amatrice earthquake (Priolo et al. 2020), but it was also extensively used to study the temporal and spatial variability of the ground motion in the area (Bindi et al. 2018b; Sgobba et al. 2021).

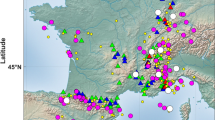
It consists of more than 30,000 waveforms relative to about 450 earthquakes in the magnitude range 3.2–6.5 (local magnitude for M < 4.5 and moment magnitude for M ≥ 4.5) recorded by about 460 stations within 250 km from the epicenters (Fig. 1a).

Fig. 1
figure 1

a Map of the study-area with the spatial distribution of events and stations.; b Scatter plot of the dataset records as a function of magnitude and source-to-site distance; c Map showing the source-to-site paths in the study-area

Full size image

The magnitude-distance distribution plot (Fig. 1b) shows that the region is highly sampled in the distance and magnitude ranges [0–100] km and [3.2–4.5], respectively. The large amount of records at short distances and for small events is due to the stations belonging to the temporary networks installed during the seismic sequences. This high number of stations and events in such a relatively small area has allowed us to sample a relevant number of ray-paths (Fig. 1c), which is a requirement to apply a fully nonergodic approach.

On this dataset, we analyze the Fourier amplitude spectra (FAS) of S-wave windows band-pass filtered with a variable high-pass corner frequency depending on the signal-to-noise ratio. The time windows used to calculate the spectral amplitudes were selected using a distance dependent energy criterion. The FAS are smoothed using the Konno and Ohmachi (1998) algorithm (the smoothing parameter b was set to 40). Details about the data selection and processing are provided by Pacor et al. (2016), Bindi et al. (2017), and Colavitti et al. (2022).

3 Base model

As the aim of the work is to assess the median and variability of a GMM-FAS including regional seismological parameters, we perform two calibrations: the first one allows us to develop a nonergodic base model including basic dependencies and scaling terms; then a second calibration is developed to include the additional explanatory variables.

The functional form, adopted frequency-by-frequency for the base model is:

$${log}_{10}Y={a}_{0}+{F}_{M}\left(M\right)+{F}_{R}\left(M,R\right)+\delta {B}_{e}+{\delta S2S}_{s}+\delta L2{L}_{r}+\delta P2{P}_{p}+\delta {W}_{0}$$
(3.1)

where fixed- and random- effects can be identified. The fixed part is composed by the term a, which is the offset of equation and the magnitude FM(M) and distance FR(M,R) scalings that are treated adopting standard dependencies, as follows:

$${F}_{M}\left(M\right)={b}_{1}\left({M}_{w}-{M}_{h}\right)\,\,\,\,for\,\,\,\, {M}_{w}\le {M}_{h} ; {b}_{2}\left({M}_{w}-{M}_{h}\right)\,\,otherwise$$
(3.2)
$${F}_{R}\left(M,R\right)= \left[{c}_{1}\left({M}_{w}-{M}_{h}\right)+{c}_{2} \right] {log}_{10}\frac{\sqrt{{R}^{2}+{h}^{2}}}{{R}_{ref}} +{c}_{3}\left(\sqrt{{R}^{2}+{h}^{2}} -{R}_{ref} \right)$$
(3.3)

In particular, we assume a non-linear magnitude scaling through a stepwise linear function (\({F}_{M}\) term) and the distance scaling is composed by a geometrical spreading (including a magnitude dependent term) and the anelastic attenuation terms (\({F}_{R}\) term).

The explanatory variables are the moment magnitude Mw and the source-to-site distance R. In detail, for the strongest events (M > 5.5), R is the Joyner and Boore distance (RJB), computed from the fault geometries published in the ITalian ACcelerometric Archive (ITACA) database (Russo et al. 2022), whereas for smaller events the epicentral distance Repi is assumed for R. It is worth to note that we do not include the focal depth among the parameters, because the dataset refers to an homogeneous tectonic regime (extensional) characterized by events with roughly constant depths (< 20 km), normally distributed (mean 9.3 km; standard deviation 3.1 km), as also stated by Sgobba et al. (2021), with reference to the spectral acceleration-based model calibrated on the same dataset. Note also that the functional form lacks a site-response scaling term (typically dependent on the shear wave velocity \({V }_{S,30}\)), so that all the unmodelled site effects turn out in the corresponding random-terms \({\delta S2S}_{s}\).

In Eqs. (3.2) and (3.3), some parameters are fixed in a first stage by nonlinear regression, i.e. the hinge magnitude Mh = 5.0, the reference distance Rref = 1 km and the pseudo-depth h = 6 km. The reference magnitude Mref is instead frequency-dependent estimated from a preliminary non-linear regression; it varies between 5.45 (at frequency f ~ 1 Hz) and 3.3 (at frequency f ~ 7.5 Hz).

The sites adopted for model calibration come from the study of Lanzano et al. (2020), who identified a set of 36 recording stations in Italy installed on rock and classified as “reference sites” that are intended as out-cropping rock or stiff soils that show a flat, unamplified response over a frequency range of engineering interest (Lanzano et al. 2022a). These sites have been identified on the basis of a multi-criteria ranking approach including several proxies that influence the site response, i.e., (i) the outcropping geology, (ii) the installation features, (iii) the shear wave velocity VS,30 according to EC8 (CEN, 2003), (iv) the site topography, (v) the horizontal-to-vertical spectral ratios obtained from noise measurements or recordings and (vi) the repeatable site term obtained from residual analysis (δS2Ss) and that can be considered as the empirical amplification function of each station (Priolo et al. 2020; Lanzano et al. 2020; Paolucci et al. 2021).

In the present study, with respect to the initial 36 stations identified according to the above criteria, a further selection is performed on the basis of the high-frequency attenuation κ0 parameter extracted from the analysis of the Fourier Spectra (named κ0-FAS). The κ0-FAS are estimated as the semi-logarithmic frequency decay of the S-waves of FAS (Ktenidou et al. 2014), by using the semi-automatic procedure described in Lanzano et al. (2022a). The final set of 6 reference stations is listed in Table 1 and include five stations with κ0-FAS < 0.015 s, namely LSS, MNF, SLO, SNO and SDM, plus a sixth station (NRN), which shows a δS2Ss trend very similar to the average of the 5 selected sites, although it does not have an estimate of κ0-FAS.

Table 1 List of reference rock sites used for model calibration
Full size table

The random terms of Eq. (3.1) include some corrective factors related to the systematic source, propagation, and site effects related to event e, source-region r, site s and path p. The random effects are the repeatable terms of variability that are introduced to remove the ergodic assumption, namely:

  • between-event \(\delta {B}_{e}\): represents the average deviation away from the median prediction of the GMM for any event; it shows a clear dependence on earthquake stress-drop (Bindi et al. 2017);

  • location-to-location \(\delta L2{L}_{r}\): represents the variability term related to the source region due to different releases of radiated energy; indeed, regions with different average stress drops can be identified on smaller scales (Baltay et al. 2019). In this work, this term is estimated via the clustering approach adopted by Sgobba et al. (2021) with reference to a non-ergodic SA-GMM calibrated on the same dataset adopted herein. The clustering is based on the following criteria: (1) seismogenic setting (considering the source zones identified by the database of seismogenic sources, DISS 3.2.1 catalog - DISS Working Group 2018); (2) similarity in the stress drop values associated with the events of each cluster; (3) space–time aggregation based on Reasenberg’s algorithm (Reasenberg 1985): the earthquakes are counted within a time window of 10-days bins and assuming a Poisson distribution. Following these criteria, the events are aggregated within polygonal source areas and identified as follows: cluster #1 (area of L’Aquila, southernmost), #2 (area of Amatrice-Norcia in the middle), and #3 (area of Muccia, farther North). In the rest of the region we considered a background seismicity with a mean value of the location term equal to zero. A map of the clusters is reported in Fig. 2a;

  • site-to-site \({\delta S2S}_{s}\): defines the systematic bias of ground motions recorded at each station s with respect to the reference rock motion predicted by the fixed-effect part of the model on the basis of the 6 reference sites listed above;

  • path-to-path \(\delta P2{P}_{p}\): defines the variability from one source-to-site path to another due to differences in travel paths across heterogeneous geological layers or main structural discontinuities. The path terms are estimated by dividing the whole region into squared cells (0.2°-spaced) - Fig. 2b that allow to capture the spatial distribution of the attenuation behavior (cell-specific attenuation). The adopted cell size is a compromise value between the available data and the desired spatial resolution given the size of the region, in line with the approach of Dawood and Rodriguez-Marek (2013), Sgobba et al. (2021) and Sung et al (2022). Moreover, we have verified that the observed variability in the paths ranges from 10 to 100 km, but in most cases is larger than 20 km, which is in line with the adopted grid size.

Fig. 2
figure 2

a Source-regions identification based on clusters after Sgobba et al (2021): #1 (main event: L’Aquila 06/04/2009 - 01:36 UTC), #2 (main event: Amatrice 24/08/2016 - 01:32 UTC) and #3 (main event: Muccia 10/04/2018 - 03:11 UTC); b map of stations overlapped to the reference grid adopted for path sampling. The cells numbering identifies the sample paths from the source clusters to the sites falling in each cell of the grid

Full size image

The regression coefficients a, b1, b2, c1, c2 and c3 of Eqs. (3.2) and (3.3) are obtained via linear mixed-effects regressions (Stafford 2014; Bates et al. 2015) and are available frequency-by-frequency together with the values of Mref (see “Data availability” section). All the terms in the functional show a p-value (test of the statistical significance of the explanatory variables, Wasserstein and Lazar 2016) lower than 0.05, indicating a significant correlation between the predictor and the response variable.

4 Additional explanatory variables

The base FAS-model defined before is described by a simple equation dependent on basic explanatory variables mainly including magnitude and source-to-site distance scaling. This means that all the unmodelled effects related to source, site and path are not included in the median model but are centered in the random-terms, which act as adjustments of the FAS predictions. In order to parametrise these terms and move further epistemic uncertainty from the aleatory variability, we adopt the strategy to add constraints by using the physical parameters made available by Morasca et al (2023) from a non-parametric Generalized Inversion Technique (GIT, Andrews 1986; Castro et al. 1990; Oth et al. 2013; Bindi and Kotha 2020). The latter is a data-driven approach useful to resolve source, path and site contributions from the observed FAS that hence has the advantage to derive region-specific spectral parameters for the analyzed events, i.e. seismic moment, corner frequency, stress-drop, source and site kappa values and quality factor.

Starting from the same dataset of almost 460 events used in this study, Morasca et al (2023) selected the FAS corresponding to 283 stations and simultaneously inverted the FAS to isolate the three different factors (source, path and site) by solving an overdetermined linear system in the least-squares sense:

$$log_{10} FAS_{es} \left( {f,R_{es} ,M_{e} } \right) = log_{10} Source_{e} \left( {f,M_{e} } \right) + log_{10} Path_{es}\left( {f,R_{es} } \right) + log_{10} Site_{s} (f)$$
(3.4)

where f is the frequency (analyzed in a range 0.5–25 Hz), Res represents the hypocentral distance between the event e and the station s and M is the magnitude associated to the event e.

In the non-parametric approach applied by Morasca et al (2023), no a priori models are assumed to isolate the different terms. This implies the necessity of a second step to extract the source and path parameters from the non-parametric solutions by fitting them a posteriori. To estimate the source parameters for each earthquake, the authors assumed the Brune (1970) model, while non-parametric attenuation functions were fitted assuming a standard model including a distance-dependent bi-linear geometrical spreading and a frequency-dependent attenuation term accounting for source-to-site distance, propagation medium properties, high-frequency attenuation described by the kappa (κ0-GIT) parameter, and the regional Quality factor (Qr). All the physical parameters obtained by Morasca et al. (2023) are available at the link https://shake.mi.ingv.it/central-italy/ where the moment magnitude, corner frequency, stress-drop, kappa source and seismic moment are available for each analyzed event together with the amplification functions of each station.

In addition to the parameters derived from the GIT of Morasca et al (2023) on Central Italy - hereafter called M-GIT - we also consider the most common site proxy, that is the shear wave velocity in the uppermost 30 m, \({V}_{S,30}\), as discussed in the next section.

In the following, we illustrate how the random effects of the empirical FAS model are investigated and parameterized: we first evaluate the statistical correlation of the random-effects on the site and seismological parameters get from GIT and, where found relevant, we incorporate them in the regression as additional explanatory variables.

Details on the application of the M-GIT are described in the Morasca et al (2023); we just highlight here that the inversion is performed in such a way that its results are consistent with those from the FAS base model, due to: (i) the correspondence of the original datasets used in both the analyses, though only 283 stations were considered for GIT, each sampling at least 10 events, to obtain more robust inversions; (ii) the adoption of a common reference motion: this is an a priori constraint required by GIT to solve the system of linear equations. Namely, the same 6 reference stations introduced in Sect. 3 were adopted both for the calibration of the base empirical FAS model and the GIT analyses. Owing to this consistency, we assume that the random-terms from the empirical FAS model and the outcomes of the M-GIT are inherently related, so we attempt to capture the underlying seismological connections due to the source and geophysical properties in order to parametrise the model variability and adjust the FAS predictions.

4.1 Source parameters

Among the random-terms of the empirical FAS model, the between-event δBe and the location-to-location δL2Lr are the components related to the source physics due to energy radiation and tectonic setting. Indeed, it is well established that ground motion at high-frequency depends on earthquake stress drop Δσ (e.g., Boore 1983; Bindi et al. 2017; ; Baltay et al. 2019), which reflects in the between-event variability. Also the determination of the location-to-location terms δL2Lr associated to event clusters (Sgobba et al. 2021) allows us to capture the variations in the Δσ within the Central Italy region, i.e. a given cluster produces earthquakes that are characterized, on average, by higher or lower stress drops. Therefore, also the sum of the event and location terms (i.e., the total source-related random components δL2Lr + δBe) can be considered related to the stress-drop parameter, which is thus assumed a candidate predictor variable.

Both stress-drop and other source parameters are here extracted by model fitting of the non-parametric source spectra based on M-GIT (an ω2-model Brune’s model is assumed, Brune 1970). Namely, the non-parametric analysis allows the extraction of event-specific values of Δσ and the high-frequency source parameter \({\kappa }_{source}\), whose distributions are shown in Fig. 3a and b, respectively. This parameter \({\kappa }_{source}\) is defined as the average slope of the source spectra that accounts for the high-frequency attenuation effects close to the fault (e.g. Oth et al. 2011; Bindi et al. 2018c; Bindi et al. 2017) although its correlation with event and location variability is less studied in the literature. The median values of distribution are approximately equal to 0.15 log10 for Δσ distribution (1.5 MPa) and to 20 ms for the \({\kappa }_{source}\). Both Δσ and \({\kappa }_{source}\) values are reported in the “Data availability” section.

Fig. 3
figure 3

Histograms of a stress-drop Δσ and b \({\kappa }_{source}\) inferred from non-parametric M-GIT analysis

Full size image

We thus compare the inversion-based estimates of Δσ and \({\kappa }_{source}\) with the total source-related random components at each frequency (Fig. 4).

Fig. 4
figure 4

\({\delta B}_{e}\) plus \({\delta L2L}_{r}\) versus \(\Delta \sigma\) for a f = 1 Hz; b f = 24 Hz and versus \({\kappa }_{source}\) for c f = 1 Hz; d f = 24 Hz. The box plots represent the median trend with the central circular marker and the edge of each box shows the corresponding 25th and 75th percentiles

Full size image

Figure 4 shows that for low frequencies (e.g. f = 1 Hz, Fig. 4a), the trend is weak with values of \({\delta B}_{e}\)+ \({\delta L2L}_{r}\) close to zero throughout the stress drop range (from 0.1 up to 100 MPa), denoting poor or absent correlation. At high-frequency (e.g. f = 24 Hz, Fig. 4b), the data show a trend that increases as the stress-drop values increase up to about 2 MPa and then it flattens out.

An opposite behavior can be noted for \({\delta B}_{e}\)+\({\delta L2L}_{r}\) against the \({\kappa}_{source}\) parameter at high-frequency (negative correlation), Fig. 4d, whereas at low-frequency (Fig. 4c) the trend is weaker.

In light of above, it can be stated that stress drop \(\Delta \sigma\) and \({\kappa}_{source}\) values are anti-correlated as also illustrated, in Fig. 5 where we show the frequency-dependent Pearson’s correlation coefficient computed between the terms \({\delta B}_{e}\)+\({\delta L2L}_{r}\) versus stress drop \(\Delta \sigma\) and versus \({\kappa}_{source}\).

Fig. 5
figure 5

Correlation coefficient between \({\delta B}_{e}\)+\({\delta L2L}_{r}\) versus stress drop \(\mathrm{{\Delta}{\sigma}}\) (blue dots) and \({\delta B}_{e}\)+\({\delta L2L}_{r}\) versus \({\kappa }_{source}\)(red dots) as a function of frequency

Full size image

Regarding the stress drop, the correlation coefficient \(\rho\) is negative for frequencies lower than 1 Hz, then rising to positive values around 0.3 for higher frequencies. Concerning the correlation between \({\delta B}_{e}\) + \({\delta L2L}_{r}\) and \({\kappa}_{source}\), it assumes small positive values (< 0.2) for frequencies below 2.5 Hz, and then falls to negative values as the frequency increases, reaching a value of −0.45 for f = 25 Hz.

Summarizing, it appears that the correlation of the source-based random terms \({\delta B}_{e}\)+ \({\delta L2L}_{r}\) with both the parameters is stronger at high-frequency (above about 5 Hz), as expected from physics-based considerations, albeit opposite for \(\Delta \sigma\) and \({\kappa}_{source}\), and thus we consider these two parameters significant to further parametrise the FAS predictive model.

4.2 Site parameters

In this section, we investigate on the site-to-site random terms δS2Sscomputed with respect to the mean site response of the 6 reference rock sites and whose dependencies can be studied to improve the site description of the final calibration. The statistical dependency is evaluated against geophysical proxies describing the effect of local site response due to deep and shallow geology, not already included as explanatory variables in the base FAS model: (i) the shear wave velocity in the uppermost 30 m, \({V}_{S,30}\) (Borcherdt 1994) and (ii) the near-site high-frequency attenuation parameter \({\kappa }_{0}\) (Anderson and Hough 1984; Ktenidou et al. 2014). \({V}_{S,30}\) is chosen as it provides quantitative and synthetic description of the subsurface structure (first 30 m in depth) that is most accessible to geotechnical investigations. It is also the most common explanatory variable typically included in ground motion models, as well as an easy and low-cost parameter to evaluate site response classification (e.g., Rodriguez-Marek et al. 2001; Abrahamson et al. 2008; Pitilakis et al. 2013).

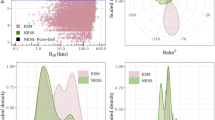
Herein, the values of \({V}_{S,30}\)(m/s) are taken from direct in-situ measurements of the S-wave velocity profile (provided by the Engineering Strong-Motion database, ESM https://esm-db.eu/; Luzi et al. 2020; Lanzano et al. 2021) and the Italian database (ITACA). For stations where a measurement is not available, an estimate of \({V}_{S,30}\) is provided from the empirical correlation with the topographic slope, according to Wald and Allen (2007) relationship, on the basis of slope measurements from high-resolution digital elevation models (DEM) of Italy (Mascandola et al. 2021). An histogram plot of these estimates of \({V}_{S,30}\) is shown in Fig. 6a which denotes a log-normal distribution with a median value of about 900 m/s.

Fig. 6
figure 6

Histograms of: a \({V}_{S,30}\) inferred from slope (Wald and Allen 2007) and b \({\kappa }_{0}\) from non-parametric GIT analysis

Full size image

Following the taxonomy proposed by Ktenidou et al. (2014), the values of \({\kappa }_{0}\) used for the model calibration are obtained from the amplification functions extracted from the M-GIT analysis according to the procedure by Drouet et al. (2011). The average site amplification of the 6 reference stations was assumed flat and equal to one in the M-GIT computation (Morasca et al. 2023), which is equivalent to assuming, on average, \({\kappa }_{0}\)=0 for the reference sites. As a result, the \({\kappa }_{0}\) estimates from the amplification functions suffer from this assumption and need to be corrected with the mean value of \({\kappa }_{0}\) (0.012 s) of the reference rock sites obtained from an independent computation on the observed FAS (\({\kappa }_{0}\)-FAS in Table 1). The corrected values of \({\kappa }_{0}\) from GIT (\({\kappa }_{0}\)-GIT in Table 1), in the following simply named \({\kappa }_{0}\), are provided in the “Data availability” section and reported in Table 1 for the 6 reference rock sites.

The histogram of \({\kappa }_{0}\) is shown in Fig. 6b where it follows an approximately normal distribution with a median value at 0.02 s.

We then examine the dependencies of δS2Ss both with the \({V}_{S,30}\) and \({\kappa }_{0}\) (Fig. 7) for low- and high- frequencies. The site empirical terms δS2Ss exhibit a dependence on the \({V}_{S,30}\) (anti-correlation) which is more evident at low-frequency (Figs. 7 and 8c) than at high-frequency (Figs. 7 and 8d), as also found by other authors (see Bergamo et al. 2020) who evidenced that this proxy shows larger correlation with site amplification in the low-to-intermediate frequency range. On the contrary, a negative correlation between the site terms and \({\kappa }_{0}\) is more pronounced at high-frequency (Figs. 7 and 8b) than at low-frequency (Figs. 7 and 8a).

Fig. 7
figure 7

Correlation coefficient between \({\delta S2S}_{s}\) versus \({\kappa }_{0}\)(blue dots) and \({V}_{S,30}\)(red dots) as a function of frequency

Full size image
Fig. 8
figure 8

Scatter plot of the site-to-site residuals δS2Ssversus \({\kappa }_{0}\) for a f = 1 Hz; b f = 24 Hz and \({V}_{S,30}\) at c f = 1 Hz; d f = 24 Hz

Full size image

5 Regression approach

The assumed functional form of the advanced model is consistent with the one proposed by Bora et al. (2015), so that it is formalized as follows:

$${\text{log}}_{{{1}0}} {\text{Y}} = {\text{a}}_{{1}} + {\text{F}}_{{\text{M}}}^{\prime } \left( {{\text{M}},\Delta \sigma } \right) + {\text{F}}_{{\text{S}}} \left( {{\text{V}}_{{{\text{S}},{3}0}} ,\kappa_{0} } \right) + {\text{F}}_{{\text{R}}} \left( {{\text{R}},{\text{M}}} \right) + \delta {\text{B}}_{{\text{e}}}^{\prime } + \delta {\text{S2S}}_{{\text{s}}}^{\prime } + \delta {\text{L2L}}_{{\text{r}}}^{\prime } + \delta {\text{P2P}}_{{\text{p}}}^{\prime } + \delta {\text{W}}_{{0}}^{\prime }$$
(5.1)

The source scaling FM is modified as:

$${\text{F}}_{{\text{M}}}^{\prime } \left( {{\text{M}}, \, \Delta \sigma } \right) = {\text{ b}}_{1}^{\prime } *\left( {{\text{M}}_{{\text{w}}} - {\text{M}}_{{\text{h}}} } \right)*\left( {{\text{M}}_{{\text{w}}} < {\text{M}}_{{\text{h}}} } \right) \, + {\text{ b}}_{2}^{\prime } *\left( {{\text{M}}_{{\text{w}}} - {\text{M}}_{{\text{h}}} } \right)*\left( {{\text{M}}_{{\text{w}}} > {\text{M}}_{{\text{h}}} } \right) + {\text{b}}_{3}^{\prime } {\text{log}}_{{{1}0}} \left( {\Delta \sigma /\Delta \sigma_{{{\text{ref}}}} } \right) + {\text{b}}_{4}^{\prime } \left( {\kappa_{source} - \kappa_{source, ref} } \right)$$
(5.2)

where \({\text{F}}_{{\text{M}}}^{\prime }\) explicits the logarithmic dependence on stress drop Δσ, scaled to a reference value of Δσref = 1.5 MPa, corresponding to the central value of the interval of the stress drops estimated from M-GIT; the dependence on κsource is, instead, linear and the reference value is \({\kappa }_{source,ref}\)=0.02 s. The site-effect term is introduced in the parametrized model as:

$$\begin{aligned} {\text{F}}_{{\text{S}}}^{\prime } \left( {{\text{V}}_{{{\text{S}},{3}0}} ,\kappa_{0} } \right) & = {\text{d}}_{1}^{\prime } {\text{log}}_{{{1}0}} \left( {{\text{V}}_{0} /{\text{V}}_{{{\text{S}},{3}0,{\text{ref}}}} } \right) + {\text{d}}_{2}^{\prime } \left( {\kappa_{0} - \, \kappa_{{0,{\text{ref}}}} } \right)\quad {\text{where}}\quad {\text{V}}_{0} = {\text{V}}_{{{\text{S}},{3}0}} \;\;{\text{for}}\;\;{\text{ V}}_{{{\text{S}},{3}0}} \le {15}00\;{\text{m/s}} \\ & \quad {\text{otherwise }}\;\;{\text{V}}_{0} = {15}00\;{\text{m/s}} \\ \end{aligned}$$
(5.3)

where we introduce the logarithmic scaling with VS,30 and consider a reference shear wave velocity VS,30,ref = 900 m/s. The scaling with κ0 is linear and the reference value is κ0,ref = 0.012 s.

The values of VS,30ref and κ0,ref are chosen to be representative of reference rock motion in Central Italy, and assumed as the average of the measured values of VS,30 and the values of κ0 obtained from the GIT for the 6 reference sites in Table 1.

The distance scaling FR (R, M) remains unchanged compared to the base model, since we did not calibrate a specific relation between the path terms δP2Pp and the parameters related to the propagation terms derived from the non-parametric M-GIT analysis. This has meant the inability to introduce in the parametrization an additional proxy describing the effect of anisotropic attenuation due to crustal heterogeneities over the study-area.

Finally, in Eq. (5.1), the terms δB′e, \(\delta S2S_{s}^{\prime }\), \(\delta L2L_{{\text{r}}}^{\prime }\), \(\delta P2P_{p}^{\prime }\) , \(\delta W_{0}^{\prime }\) are the random terms of the advanced model, homologous to the base model.

A schematic summary of the explanatory parameters for the basic and advanced models is shown in Fig. 9.

Fig. 9
figure 9

Schematic representation of model coefficients in base and advanced models (the additional seismological parameters are denoted in bold)

Full size image

In a preliminary stage of the analysis, we consider a first trial model including all the explanatory variables of Eq. (5.1) in a standard one-stage regression process. We apply this approach to explore the potential trade-off effects between the various terms of the model, which are well-known effects in the regression problems. This is a more relevant issue when the number of parameters in a regression increases, as in the present case; indeed, more complex models, while often associated with improved prediction capabilities, are also affected by larger trade-offs among the parameters that make it hard to resolve the individual contributions in the predictive equation.

Results of the one-stage trial regression analysis can be found in the “Data availability” section. In Fig. 10 we report the correlation matrix of the model parameters to investigate potential trade-offs and then assess the most convenient strategy of parametrization.

Fig. 10
figure 10

Correlation matrix of the parameterized model at: a f = 1 Hz (low-frequency) and b f = 24 Hz (high-frequency)

Full size image

The matrix of the parameterized model evidences that there is a negligible correlation among the different groups of coefficients, which are associated to different physical effects (i.e. group bn: source-related; group cn: attenuation-related; group dn: site-related), as it can be noted in the example of Fig. 10 both at low- (Fig. 10a) and high-frequency (Fig. 10b). Yet, the source terms are affected by mutual trade-off (negative correlation) particularly among stress-drop (b3), kappa source (b4) and magnitude scaling for M < Mh (b1), as expected. A small cross-correlation is obtained between \({V}_{S,30}\) (d1) and site \({\kappa }_{0}\) (d2): these two terms indeed mainly affect the model amplitudes in different frequency ranges, as shown before. Instead, a very strong correlation exists at high frequency (Fig. 10b) as well-known, between the geometrical spreading (c1 and c2) and the anelastic attenuation (c3) so they should be always considered as two components of the same attenuation model (Bindi and Kotha 2020).

5.1 Stepwise parametric regression

In order to prevent the observed trade-off effects among the coefficients of the different contributions, we adopt a stepwise regression technique similar to the one proposed by Bayless and Abrahamson (2019). In this way, the choice of the predictive variables is carried out with a step-by-step procedure by which at each step, a new variable is considered for addition to the set of base explanatory variables, thus in order to constrain different components of the model using the data relevant to each piece (Bayless and Abrahamson 2018).

The procedure is repeated including the additional dependencies with the seismological and geophysical parameters for a total of 7 steps (Table 2) in order to build-up the base and the final advanced models, as described in the next section. At the end of each step, we also apply a smoothing on the coefficients, which is performed to get smoothed spectra and better constrain the model to more physical behavior (Abrahamson et al. 2014).

Table 2 Linear regression steps
Full size table

Table 2 shows the regression steps of the base model (i.e. without including the additional parameters) and the advanced model (i.e. including the additional parameters). For the base model (from step #1 to #3), we first constrain the magnitude scaling and the frequency-dependent geometrical spreading using data up to 80 km to isolate the effects of the geometric attenuation from the anelastic one, thus leaving the parameters a0, b1, b2, c2 and the random terms free in the regression; then the c2 coefficient is finally estimated and smoothed after the regression (step #1). Once fixed c2, in step #2, the magnitude-dependent geometric spreading and the anelastic attenuation are introduced by regressing also the terms c1 and c3, respectively so the coefficients b1, b2, c1 and c3 are finally estimated and smoothed. Note that here the c3 is forced to assume non-positive values in order to avoid unphysical increasing of ground motion at large distances (R > 80 km). At the end (step #3), the intercept a0 of the functional and the random terms are estimated along with the corresponding standard deviations.

The same approach is used for the advanced model, (from step #4 to step #7) where we estimate the additional terms d1, b3, d2, b4, a1 and random terms by sequential stages. Note that the step model is built in such a way that the advanced model is a specialization of the base model; in fact, for this purpose, the coefficients of the advanced model (b1, b2, c1, c2, and c3) are the same of the base model, so the former is calibrated assuming that the scaling with magnitude and distance of the latter are still valid. In addition, the reference values for the site parameters in the calibration (VS,30,ref and κ0,ref) are assumed as representative of the 6 reference sites in Table 1. In this way, if any of the additional terms of the advanced model were null, the returned predictions would be close to those provided by the base model. All the model coefficients are reported in the “Data availability” section.

The stepwise regression is also performed via a mixed-effects regression, thus considering the random-terms δB’e, δS2S′s, δL2L′r and δP2P′p introduced in the base model that are zero-mean normally distributed random variables with variances \({\tau }^{2}\), \({\phi }_{S2S}^{2}\), \({\tau }_{L2L}^{2}\), \({\phi }_{P2P}^{2}\), respectively. These residual components allow us to calculate the repeatable terms and associated variability of event, site, source-area, and path and compare them to those obtained from the base model to evaluate the effectiveness of the parameterization.

The plot of the raw and smoothed coefficients is reported in Fig. 11. One could note that the intercept value undergoes small variation when passing from the base model to the advanced one – i.e. the difference between the regression coefficient a0 and a1 (denoted by δa) is negligible especially below 10 Hz. Conversely, the corresponding offset obtained from the one-step regression (a′ in Fig. 11) shows a sensibly different trend compared to a0. This observation confirms that the stepwise approach allows to redistribute the model variability on the random terms and associated uncertainty rather than on the fixed-coefficients and thus it does not produce biased spectral shapes compared to the base model version.

Fig. 11
figure 11

Offset values of base and advanced models

Full size image

In Fig. 12 (on the top), the coefficients b1 and b2 related to the magnitude scaling respectively for small earthquakes (⁠Mw < Mh⁠) and stronger earthquakes (⁠Mw > Mh⁠) tend to mainly affect the low-frequency range, whereas b3 increases as frequency increases, thus reflecting the greatest relevance of the stress-drop parameter at high-frequencies.

Fig. 12
figure 12

Raw and smoothed regression coefficients of base and advanced model. The error bars denote the standard deviation of the coefficients

Full size image

Another aspect concerns the complementary trends of d1 and d2 (site effects), which are dominant in different frequency bands (Fig. 12 on the bottom). The former mainly act at low-frequency depending on the shear wave velocities at shallow depth, in line with the findings by Bergamo et al (2020) that show a good correspondence of VS,30 with site amplification across the whole 1.7–6.7 Hz band.

Instead, the coefficient d2 prevails at high-frequency being dependent on κ0. Namely, d2 is forced to zero up to 5 Hz to limit the contribution of the site attenuation parameter at high-frequency. The same approach is adopted to constrain the b4 term that leads to linear effect of \({\kappa }_{source}\) only in the high-frequency range starting from about 5 Hz. For similar reasons, the c3 coefficient of the apparent anelastic term is constrained to be non-positive up to about 3 Hz to avoid unrealistic effects, such as the enhancement of the ground motion from a certain distance onward, which is also a common assumption (e.g. Lanzano et al. 2021). The c1 and c2 coefficients (Fig. 12 in the middle) vary in the interval 0 to 0.15 and − 1.5 to − 2, respectively over the entire period range, with a typical trend observed in the geometrical spreading terms of the empirical models. Figure 12 also reveals that the coefficients of the stepwise regression and those related to the one-step calibration are quite similar, and that the only coefficients that show remarkably different trends are c1, c2 and c3, confirming that a strong trade-off exists between these terms.

Greater uncertainties are observed for the coefficient b2 (related to magnitude scaling at high magnitudes) due to poorer constraint to data in this range and d1 (VS,30 scaling), probably as a consequence of the uncertainty of the VS,30 estimates.

To assess the impact of the additional seismological terms on the variability’s reduction, we compare the individual uncertainty contributions of the base model against the advanced one (i.e. the parameterized model of Eq. (5.1)).

Figure 13 shows that the between event component \(\left(\tau \right)\)-Fig. 13a - is significantly reduced in the advanced model with respect to the base model at high-frequencies, from about 0.25 to 0.08 log10 units for f > 20 Hz (total gain of 68%). Also the standard deviation associated to the location term - \(\left({\tau }_{L2L}\right)\) Fig. 13b - vanishes at all frequencies except at f > 10 Hz, thus indicating that the variability contribution due to the source region is completely captured in the range 1–10 Hz by the introduction of the stress drop and \({\kappa }_{source}\) in the modelling.

Fig. 13
figure 13

Standard deviations of the random-effects terms of the nonergodic models against frequencies for: a between-event \(\left(\uptau \right)\) and location-to-location \(\left({\uptau }_{\mathrm{L}2\mathrm{L}}\right)\); b site-to-site \(\left({\phi }_{\mathrm{S}2\mathrm{S}}\right)\) and path-to-path \(\left({\phi }_{\mathrm{P}2\mathrm{P}}\right)\); c aleatory \(({\phi }_{0})\) and total sigma \(\left(\upsigma \right)\)

Full size image

The introduction of the geophysical variables (VS,30 and site kappa) have also a relevant impact on the site-to-site variability \(\left({\phi }_{S2S}\right)\) as plotted in Fig. 13c, which shows a reduction compared to the counterpart contribution of the base model, particularly at high-frequency over 10 Hz (e.g. about 35% at 25 Hz). The parameterized model shows no difference in the path-term variability \(\left({\phi }_{P2P}\right)\) - Fig. 13d, due to the lack of a path-specific proxy of crustal properties in the model description. A small reduction of variability is still observed as a result of the mutual trade-off between path and site effects, so that the introduction of the additional site parameters also reflects on the propagation terms. The remaining aleatory variability \(\left({\phi }_{0}\right)\) of the parameterized model (Fig. 13e) is substantially equal to that of the base model, whereas the total sigma \((\sigma )\) associated with the logarithmic FAS at each frequency, computed from the vectorial combination of all uncertainty contributions \(\sigma =\sqrt{{{\sigma }_{0}^{2 }+\tau }^{2}+{\tau }_{L2L}^{2}+{\phi }_{S2S}^{2}+{\phi }_{P2P}^{2}}\), shows a stable trend with frequencies and an appreciable reduction at f > 30–40 Hz. As we can observe in Fig. 13f, this reduction reaches a maximum value of 0.4 log10 units at the highest frequency, due to the fact that the source and site parameters mainly affect the high-frequency range.

We point out that these values of sigma are relatively low compared to the most typical ones published in the literature (Akkar et al. 2014; Bora et al.; 2014, 2015). This aspect indeed is one of the technical obstacles associated with GMM-FAS models as discussed in Bora et al. (2014). Our findings demonstrate a beneficial effect of the parametrization in constraining the uncertainty, which may be a result of the strategic combination of both an effective physical description of the ground motion through the introduced parameters and the application of a fully nonergodic framework for modelling.

6 Predictive scenarios

The median estimates of the FAS model (fixed-effects) are here shown to reproduce a set of predictive scenarios with varying magnitude and distance (Fig. 14). The overall trends for different magnitudes are similar to those obtained by Bayless and Abrahamson (2019) and reproduce the decreasing in the corner frequency with increasing magnitude as expected from theoretical source spectra with double-corner frequencies ω−2 model (Brune 1970) (Fig. 14a). Also the trend with distance is well captured by the median model, where is evident a stronger fall-off rate at high-frequency of the curve corresponding to 120 km in the range where c3 is higher in absolute value, confirming that the trend is controlled by the anelastic attenuation at larger distances (Fig. 14b).

Fig. 14
figure 14

Median FAS model at distance 20 km and varying magnitudes (a) and for Mw6.0 and varying distances (b)

Full size image

Other FAS scenarios are provided in Fig. 15 where the additional site and seismological parameters are allowed to vary while the other parameters are kept fixed. Variation in the Δσ (Fig. 15a) produces a significant effect both on the median prediction estimates and on the shape of the spectra; i.e., higher stress drop leads to greater FAS in the high-frequency range (according to b3 increasing with frequency), as well as an increase in the higher corner frequency due to the theoretical scaling laws that link stress drop and corner frequency (Boore 1983). Note that in these examples we fixed all the other parameters to the mean values of each corresponding distribution; this causes the base model to coincide with the advanced model corresponding to the mean value of the stress drop (i.e. the curve corresponding to 1.5 MPa - Fig. 14a). This observation also clarifies that the advanced model leads back to the base one in case all the additional parameters are set to the mean values, as a result of the stepwise regression approach.

Fig. 15
figure 15

Median FAS model with varying \(\mathrm{{\Delta}{\sigma}}\) a, \({\kappa }_{source}\)(b), \({\mathrm{V}}_{\mathrm{s}30}\)c and \({\upkappa }_{0}\) (d)

Full size image

The increasing \({\kappa }_{source}\) (Fig. 15b) and \({\kappa }_{0}\) at site (Fig. 15d) causes the FAS to drop proportionally in the high frequency range (> 5 Hz) as the respective parameter increases, consistently with the trend of b3 and d2 respectively, so without any effect at lower frequencies. This dependency of the FAS from the high-frequency attenuation parameter follows a well-known and expected trend as observed by other authors (Lanzano et al. 2022a among the others).

In contrast, variations of VS,30 (Fig. 15c) show a pronounced effect on FAS at low frequencies and negligible at high frequencies. Even in this case, it can be noted that for values close to the average reference rock site condition in Italy (namely VS,30 = 1100 m/s and \({\kappa }_{0}\)=15 ms) and average source properties (Δσ = 1.5 MPa and \({\kappa }_{source}\)=20 ms), the advanced model returns to the base one.

7 Conclusions

In this work we have proposed a new FAS model for Central Italy constrained to seismological and geophysical parameters with the aim to better capture the underlying physics related to different energetic values of the source and different attenuation scaling due to the crustal properties and geological features of the region. Compared to other approaches, the proposed model takes advantage from the application of a fully nonergodic framework that provides improvements in terms of median predictions and in the constraining of the associated standard deviation.

Our study shows that the incorporation of additional proxies in the regression, such as the stress drop, the VS,30 and the high-frequency source and site kappa parameters, available thanks to the dense collection of data sampled in the area of the seismic sequences occurred in 2016–2017 in Central Italy, allows to capture a significant part of ground motion variability, whose reduction varies to a different extend with the frequency.

Moreover, the use of a stepwise regression technique has not only allowed to prevent the potential trade-offs arising from the inclusion of additional parameters, but it also represents a convenient and flexible strategy of parametrization to obtain the FAS predictions. Hence, the advanced model is built with a modular approach so it can be adopted even when any of the additional parameters is lacking, thus returning predictions close to those provided by the base model. This aspect has the advantage of providing a unique regression model that could be used in different contexts depending on the type and amount of parameters at disposal, so returning in a more complex functional shape with increased accuracy when all the physical parameters are known or, alternatively, with a simpler form when the physical data are missing. In particular, when the model is used in its advanced form for predictive purposes, the source parameters (stress drop and kappa source) could be derived from specific studies conducted on the source area and then used as input parameters with the corresponding variability to be handled as epistemic model uncertainty. Furthermore, it should be noted that, as a result of the regression analysis, the kappa term and the stress drop are highly correlated at lower frequencies, so a simplified version of the advanced model could be considered by including only one of these two terms for the source.

Results have shown that the impact of such a parametrization on the between-event variability, compared to the base model, only including dependency on magnitude and distance, corresponds to a reduction of about 68% at high-frequencies. Also the standard deviation associated to the location term goes to zero at almost all frequencies, indicating that the variability contribution due to the source region is completely captured under 10 Hz by the introduction of Δσ and \({\kappa }_{source}\) in the regression.

Finally, the inclusion of the variables VS,30 and \({\kappa }_{0}\) has also a relevant impact on the site-to-site variability, which shows a reduction of about 35% compared to the counterpart contribution of the base model, particularly at high-frequency.

Unchanged values of the remaining aleatory variability indicate that all the effects captured by the advanced parametrization concern only repeatable effects related to the source and site that are quantified as random-terms in the nonergodic base model. Other non-systematic physical phenomena, such as those linked to rupture directivity, slip distribution, radiation pattern etc. are not accounted for here and will deserve further analysis, for instance using the same approach implemented by Colavitti et al (2022) to model directivity on the same target area, therefore to combine those findings with the present parameterization and get a more comprehensive modelling.

With regard to the total variability of the advanced model (0.35–0.45 log10 units), we observe similar or even lower values (especially at high-frequency) with respect to those available in the literature, such as: 0.28–0.5 log10 for the parameterised model of Bora et al. (2015); 0.3–0.52 log10 for Bayless and Abrahamson (2019); 0.35–0.65 log10 units for Kotha et al. (2022); 0.41–0.61 log10 for the model of Sung et al. (2022) for France.

Finally, we suggest that the final FAS model could be coupled with Random Vibration Theory (RVT, Crandall and Mark 1963) methods to convert the median nonergodic predictions into pseudo-spectral accelerations and then used to generate physics-based shaking scenarios, as well as to produce expeditive simulations of ground-motion time series which may help to improve the coverage of recorded data in near-source region and increase understanding of the spatial features of ground shaking within this boundary.