1 Introduction

Availability of reliable numerical models is a key aspect in the seismic assessment of existing unreinforced masonry (URM) buildings. The assessment outcome can significantly affect both the design of strengthening interventions at the local level and the mitigation policies carried out by the public administrations at the territorial scale.

Computer programs constitute one of the essential tools used by analysts and engineers involved in such process. In engineering practice, analysts carry out blind predictions, since the real structural response of a building is unknown and the software (SW) reliability and adherence to the actual structural behaviour are difficult to evaluate. Moreover, unless the analysts are fully aware of the properties and limitations of the different software packages, the wide variety of available programs can lead to a potential scattering in the expected results (e.g. Marques and Lourenço 2011).

Available results of shaking table tests on prototypes are no doubt very useful, since they provide a detailed knowledge of both model and input, necessary to reduce the uncertainties on the modelling phase (Benedetti et al. 1998; Benedetti and Magenes 2001; Magenes et al. 2010a; Magenes et al. 2014; Senaldi et al. 2014; Mazzoni et al. 2010; Guerrini et al. 2019; Van de Lindt et al. 2019). However, the tested prototypes are typically simplified when compared to the actual structures because of lab limitations, instrumentation needs, geometric and material irregularities in real structures often due to structural changes over time, particularly in masonry structures.

In this context, data from Ambient Vibration Tests (AVTs) and from permanent monitoring systems can be very useful to support seismic assessment procedures, since they define a target for the numerical model calibration (Dolce et al. 2017; Astorga et al. 2020). The comparison with instrumental data and experimental modal information actually represent one of the tools to investigate and evaluate the reliability of numerical models and of different modelling approaches, at least at stages with little or no damage.

For existing masonry buildings, the Equivalent Frame Model (EFM) approach has gained a widespread use and is available in a number of programs for both practice and research. It is quite simple and computationally efficient particularly for nonlinear analyses. The reliability and effectiveness of this modelling strategy has been documented through numerical simulations of actual URM buildings damaged by earthquakes (Morandi et al. 2019; Marino et al. 2019; Cattari et al. 2021a; Brunelli et al. 2021).

In this context, the aim of this paper is dual: on the one hand, the paper intends to verify the reliability of five selected SWs that used the EFM approach by comparing the results of linear and nonlinear analyses for the blind prediction of a benchmark case study; on the other hand, for two of these SWs, the study intends to check the capability of the EFM to reproduce the actual seismic response of the structure, once the numerical models have been refined thanks to available data from AVTs and recordings from a permanent monitoring system.

The Benchmark Structure (labelled BS6) is a 2-story masonry building (Sect. 2), whose geometry and structural details are inspired by the town hall of Pizzoli (AQ, Italy). The case study is part of an ongoing research program that started in 2014 and involves several Italian Universities (Italian Network of Seismic Laboratories–ReLUIS—funded by the Italian Department of Civil Protection DPC). The specific contents of this paper fall in the "URM nonlinear modelling–Benchmark project” (Cattari and Magenes 2021). The building has been instrumented with a permanent monitoring system since 2009 by the Osservatorio Sismico delle Strutture of DPC (OSS—Dolce et al. 2017) and was hit by the 2016/2017 Central Italy earthquake sequence.

The five Equivalent Frame (EF) structural models used for comparison were developed with five different SWs: 3Muri Release 10.9.1.7 (distributed by S.T.A. DATA and developed by Lagomarsino et al. 2013); Aedes.PCM Release 2018.2.4.0; ANDILWall (Manzini et al. 2006) and Pro_SAM (2Si, 2020), both based on the SAM-II solver developed by Magenes et al. (2006), the former no longer in distribution and substituted by the latter, distributed by 2Si; CDS (CDMa Win Release 2018/a); MIDAS\Gen 2018, based on the hinge formulation proposed in Spacone and Camata (2007) and Spacone et al. (2008).

In the first research task (Sect. 3), the analyses were performed as a blind prediction, without any preliminary calibration of the models and using commonly made assumptions for the material properties’ selection and modelling choices. This was done in order to ease the interpretation of the differences in the obtained results and to limit their potential scattering. The comparison involved both the intrinsic characteristics of the building (masses and periods) and the significant parameters of the structural response (such as pushover curves and parameters that describe the equivalent bi-linear curves). In the second task, two of the above-mentioned EFMs were calibrated in the linear elastic range using data on the dynamic identification available from OSS (Sect. 4). The two models were then validated (Sect. 5) using different nonlinear constitutive laws in order to simulate the structure’s cyclic response during the 2016/2017 Central Italy earthquake. Within the aim of this validation, the recorded and numerical results were compared both at the global scale (in terms of dynamic hysteretic curves and occurred damage) and at the local scale (in terms of accelerations and floor spectra).

2 Case study description and modelling criteria

2.1 Geometry and structural details

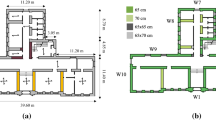
The building dates back to around 1920. It is a simple structure, regular in elevation and with a C-shaped floor plan, whose dimensions are about 38 × 12.5 m (Fig. 1a-b). It has two levels, a basement (neglected in the model) and a non-habitable attic (modelled as an equivalent load) characterized by a pavilion roof (Fig. 1c) composed of RC joists and hollow clay units and a 3 cm thick slab. The total height of the building is approximately 8.6 m. The walls are made of regular stone masonry and the horizontal floors consist of small iron beams and hollow clay units capped with a RC slab (Fig. 1d). With respect to the original configuration of the Pizzoli’s town hall, a few simplifications were introduced in the “URM nonlinear modelling—Benchmark project” and are described in the Annex I-Benchmark Structures input data (BS Form n°6) in Cattari and Magenes (2021). The annex also contains the complete set of input data on geometry, materials, loads and constructive details assumed in the analyses and necessary to model BS6.

Fig. 1
figure 1

a 3D view of the Pizzoli’s town hall (Cattari et al. 2018a); b Floor plans and walls’ thickness; c Section cut A-A; d Floor detail

Full size image

Four different structural models were analysed. Each model is intended to focus on different critical aspects related to the modelling of masonry buildings, such as the interaction between the structural elements (i.e. piers and spandrels) and the effects induced by the tension resisting elements coupled to the spandrels, considering the strength criteria in the Italian Building Code (NTC 2018). The four configurations are:

  • Case A: spandrels not coupled to any tension resisting horizontal element at floor level. This model should induce a “weak spandrel-strong pier” behaviour. The presence of an effective architrave is assumed, while the contribution of other factors that can produce an equivalent tensile strength on spandrels is neglected;

  • Case B: spandrels with horizontal steel tie rods (ϕ24 mm) placed at the floor level;

  • Case C: spandrels coupled with RC ring beams (4ϕ12 longitudinal rebars and ϕ6 two leg stirrups at 250 mm spacing, whose values are for example consistent with the minimum reinforcement requirements for new buildings in NTC 2018);

  • Case D: piers coupled by beams with infinite axial stiffness and restrained against the rotation in order to induce a “shear-type” behaviour.

It should be noted that Case C is the most consistent one with the actual configuration of the building. Since in-situ investigations detected a full thickness RC ring beam, the spandrels were modelled with two separate elements, one above and one below the ring beam. The same modelling approach for the spandrels was assumed for all four cases.

The mechanical properties used in the numerical models during the blind predictions (Sect. 3) are reported in Table 1. They were selected based on the values proposed in the Commentary of the Italian Technical Code (MIT 2019) and confirmed by experimental tests available in the literature (Vanin et al. 2017 and Krzan et al. 2015). Starting from the median values of the range proposed by MIT 2019 for the masonry typology found in the building (namely, “cut stone masonry with good bond pattern”), the following corrective coefficients were applied: k1 = 1.3, to account for the presence of a good mortar; k2 = 1.1, to account for the presence of brick layers in the stone masonry; k3 = 1.3, in order to account for the effective transversal connection. While k2 and k3 increase the strength parameters only, k1 is applied to both the strength and the stiffness characteristics. The masonry elastic moduli in Table 1 refer to the initial elastic condition. In order to use parameters representative of a cracked condition, the elastic parameters were divided by two, consistently with what is usually suggested by Codes (e.g.: NTC 2018, EC8-32005) and found in experimental data (e.g., Vanin et al. 2017).

Table 1 Material mechanical properties
Full size table

All SWs used in this study model the response of the structural elements through non-linear frame elements with “zero-length” lumped plasticity through a bi-linear elastic-perfectly plastic constitutive law with a limitation of the maximum (ultimate) displacement. The in-plane shear strength of the masonry panels was computed according to the diagonal cracking criterion by Turnšek and Cačovic (1971), with the modification introduced by Turnšek and Sheppard (1980). The flexural strength was estimated through the criterion found in the Building Codes, which neglects the tensile strength of the masonry and assumes a rectangular stress block at the compressed toe. The panels’ strength was assumed as the minimum between the shear and flexural strengths. The ultimate deformation limits for the shear and flexural failure modes were set to 0.40% and 0.60%, respectively.

In order to reduce both the SWs influence and the analyst’s arbitrariness in the model definition, the modelling process used the following common assumptions: geometry (such as wall thickness, as illustrated in Fig. 1b), elements’ distribution, value and distribution of loads associated with the horizontal diaphragms, strength criteria and materials’ mechanical properties.

Rigid horizontal diaphragms were assumed for all floors in the blind predictions. The roof structural elements were not explicitly modelled, but an equivalent load was applied. As for the masses of the structural elements, all SWs consider the translation masses lumped in the nodes and neglect the rotational masses.

All cases follow the same equivalent frame idealization of piers and spandrels following the criteria proposed by Lagomarsino et al. (2013). A discussion on the model sensitivity to the different assumptions on the piers’ effective heights is reported in Cattari et al. (2021b), Manzini et al. (2021) and Ottonelli et al. (2021). Moreover, in all cases “perfect” coupling between orthogonal walls was assumed. This assumption intends to simulate both a good wall-to-wall connection and the “so-called” flange effect. All SWs assume, by default, a kinematic coupling between incident walls: this is obtained through the direct condensation of the vertical degree of freedom in the case of 3Muri and with the use of rigid elements for the other SWs (ANDILWall-Pro_SAM, CDS,  Aedes.PCM and MIDAS\Gen). The assumption of perfect coupling was consistent with the available data on geometry and constructive details and with the post-earthquake damage survey, which suggested that a box behaviour could be guaranteed. In Ottonelli et al. (2021) the sensitivity of the results to the effectiveness of the wall-to-wall connection is investigated, while Cattari et al. (2021b) focuses on the modelling of the wall-to-wall connection in the EFM.

Finally, the out-of-plane contribution of the walls was neglected.

2.2 Overview on the available data from OSS monitoring system

The case-study structure has been instrumented since 2009 with a permanent accelerometric monitoring system suitable for recording both strong-motion earthquakes and low vibrations and tremors, with accelerations from 10−4 to 2 g (Spina et al. 2019). The sensor layout is shown in Fig. 2a. Some accelerometers are bi-axial and were placed at different levels of the structure. One three-axial sensor was placed at the foundation level in order to measure the seismic input applied to the structure. This latter instrument is important to evaluate the amplification effects of the floor accelerations with respect to the ground/base excitation.

Fig. 2
figure 2

a Sensor layout; b Epicentres of the 2016/2017 Central Italy earthquake near the Pizzoli’s town hall

Full size image

Table 2 reports the recordings made available by OSS (Cattari et al. 2018a and Cattari et al. 2019) and used in this paper, arranged in a chronological order and distinguished in mainshocks (E in the table) or ambient noise (AN). Table 2 also provides the UTC date/time and the Peak Ground Acceleration (PGA) in the building X and Y directions (as shown in Fig. 2a). All mainshocks refer to the Central Italy 2016/2017 earthquake sequence, whose epicentres are identified in Fig. 2b.

Table 2 Available recordings used in the paper
Full size table

More specifically, this paper reports:

  • the results of the dynamic identification performed using the available ambient measurements (AN in Table 2), used as target to calibrate the structural models in the elastic range (Sect. 4);

  • the recordings of the of August 24, 2016, October 26, 2016, October 30, 2016 and January 18, 2017 mainshocks, used for the validation of the EFMs of the Pizzoli’s town hall (Sect. 5). After the last shock, the structure showed a moderate damage as described in Sect. 5.4.

2.3 Building dynamic identification

Two dynamic identifications of the structure were available in literature, one by Spina et al. (2019) and the other by Sivori et al. (2021). They both used the ambient vibration data acquired for one hour by the accelerometers of the OSS monitoring system, with a sampling frequency of 250 Hz. The first test used the Operational Modal Analyses (OMA) techniques, while the second employed the frequency domain decomposition technique with a frequency resolution of 0.05 Hz.

The two methods provided very similar results on the first three modes (Fig. 3), both in terms of frequencies and modal shapes. In Sivori et al. (2021) two higher modes were also identified.

Fig. 3
figure 3

a Dynamic identifications comparison in terms of frequencies and b MAC (see Eq. (1) in Sect. 3.1) for the first three modes identified

Full size image

In the following Sections, reference to the dynamic identification by Sivori et al. (2021) is made.

Figure 4 shows a 3D representation of the eigenvectors of the first three identified modal shapes.

Fig. 4
figure 4

Simplified 3D representation of the modal displacements at the monitored points for the first three identified modes

Full size image

The blue dots indicate the modal displacements of the monitored points on the schematic building 3D view. Modes 1 and 3 are translational modes (f1 = 4.55 Hz and f3 = 6.55 Hz, in Y and X direction respectively), while mode 2 is a torsional mode (f2 = 5.70 Hz). Two higher modes are identified at frequencies equal to f4 = 9.05 Hz and f5 = 12.25 Hz. These results are consistent with those obtained by other Research Units (RU) involved in the ReLUIS project by DPC in 2017 and 2018 (Task 4.1 “Analysis of buildings monitored by Osservatorio Sismico delle Strutture”), performed using different output-only techniques both in the frequency and time domains (Cattari et al. 2018a; Cattari et al. 2019).

3 Blind predictions

This Section presents the results of the blind predictions carried out on BS6 with the five SWs, all of which use the EFM approach. The structural models use same modeling assumptions and mechanical parameters reported in Sect. 2.1.

In the following paragraphs, the parameters considered in the comparison of the numerical results (hereinafter referred to as SPs, Significant Parameters) are: (i) masses and parameters representative of the dynamic structural response (Sect. 3.1); (ii) global pushover curves and parameters that describe the equivalent bi-linear curve (equivalent stiffness Ks, yield base shear Vy and ultimate displacement du, as defined in MIT (2019) (Sect. 3.2)). The stiffness Ks was evaluated at a base shear level equal to 70% of the maximum base shear, the displacement du at a base shear drop of 20% the maximum value, and the yield base shear Vy imposing the equivalence of the areas under the capacity curve and the equivalent bi-linear idealization up to du. In all tables and figures, the numerical results are reported and commented without any explicit reference to the adopted software, each being associated anonymously to randomly assigned label and color (consistently with URM nonlinear modelling–Benchmark project, though only a subset of five SWs is considered in this paper—SW1, SW2, SW3, SW5 and SW6).

3.1 Masses and modal analysis: comparison among models and with available experimental data

Table 3 summarizes the total masses computed by the five SWs and the variation percentage with respect to the reference value found from hand calculations using the building geometry, masses and materials. In all cases a good consistency of the SWs’ estimates with the hand calculation is observed, with maximum variation of 4%. The main source for this slight difference lies in the different methods implemented by the SWs for the geometric model generation.

Table 3 Masses computed by the five SWs and reference value evaluated from hand calculations for the configurations A and C
Full size table

The dynamic SPs computed from modal analysis (mainly modal periods, shapes and participation masses) by the different SWs are presented. For the three configurations (Cases A, B and C), all SWs report a first translational mode in the Y direction (mode 1 in Fig. 5) and a second translational mode in the X direction (mode 3 in Fig. 5). Axes are identified in Fig. 2a. A torsional mode between modes 1 and 3 (mode 2 in Fig. 5) is also found. It should be recalled that all modal analyses were carried out using values of masonry E and G reduced by 50%.

Fig. 5
figure 5

Percentage variation of the modal periods with respect to the mean values for the first three modes: a Case A and b Case C

Full size image

Figure 5 illustrates the percentage variation in the periods computed by the different SWs with respect to the mean value across the five SWs. The mean values are reported in parenthesis below the x-axis of the plots of Fig. 5. The results are compared for configurations A (Fig. 5a) and C (Fig. 5b).

Table 4 reports for Case C the modal participation masses in the X and Y directions for the first three modes. Mode 1 is mainly translational in the Y direction, mode 3 is translational in the X direction and mode 2 is mainly torsional. It has to be specified that, regarding mode 2, the values of participant masses indicated with 0 are very low but non null.

Table 4 Modal participation masses for the first three modes for Case C
Full size table

The displacements of the mode shapes at level 2, reported at significant points (indicated in Fig. 6a) are shown in Fig. 6b–d. Since no significant differences were found between Cases A and C, Fig. 6b–d show the first three modal shapes obtained by the five SWs only for the Case C. Figure 6 shows that the predicted modal shapes are almost identical, being the lines almost overlapped.

Fig. 6
figure 6

a Locations of significant points used to plot the mode shapes; b-c-d Modal shapes and undeformed configuration (in grey) at the second level for Case C

Full size image

Finally, for Case C only, that best represents the actual building, the numerical results are compared with the target experimental ones.

Figure 7 presents the comparison in terms of percentage error between periods and the MAC (Modal Assurance Criterion) indexes (Allemange and Brown, 1982) obtained by the five SWs. The latter can be interpreted as a normalized scalar product among vectors, computed as:

$${\text{MAC}} \left( {n,\;e} \right) = \frac{{\left| {\left\{ {\psi_{e} } \right\}^{T} \left\{ {\psi_{n} } \right\}} \right|^{2} }}{{\left( {\left\{ {\psi_{e} } \right\}^{T} \left\{ {\psi_{e} } \right\}} \right)\left( {\left\{ {\psi_{n} } \right\}^{T} \left\{ {\psi_{n} } \right\}} \right)}}$$
(1)

where subscripts n and e refer to the numerical and experimental values, respectively. As \(\left\{ {\psi_{n} } \right\}\) approaches \(\left\{ {\psi_{e} } \right\}\), MAC tends to 1 thus providing a measure of the correlation between numerical and experimental modal shapes.

Fig. 7
figure 7

a Percentage variation of the periods calculated by the five SWs with respect to the experimentally identified target period (TID); b-c-d-e–f MAC index computed for each SW comparing numerical and experimental modal shapes

Full size image

The variations in modal periods were computed with respect to the experimentally identified target periods presented in Sect. 2.3 (TID in Fig. 7a). The MAC values (Fig. 7b–f) are plotted only when they are larger than 0.50.

The matching between numerical (obtained through blind predictions) and experimental modes is quite good, with maximum variations lower than 13.5% for the modal periods and significant values of MAC (higher than 0.90 for the first three modes, except for SW3).

3.2 Nonlinear static analyses: comparison among models

Nonlinear static analyses were performed in the ± X and ± Y directions. The accidental eccentricities were neglected.

Two different load patterns were used, one proportional to the masses and one proportional to the product of the mass matrix times the first mode shape (considered linear along the height). This leads to eight analyses for each configuration. Figure 8 shows the global pushover curves obtained with the different SWs for Cases A, B, C and D, applying a load distribution proportional to masses (“Uniform”) in the + X and + Y directions.

Fig. 8
figure 8

Pushover curves in the + X and + Y directions computed with all five SWs for configurations A, B, C and D (using mass proportional load pattern)

Full size image

Three SWs adopt the Newton–Raphson convergence criterion, while two SWs the event-to-event approach. In general, the trend of the pushover curves from Case A to Case C is the same already observed for the other benchmark structures (Ottonelli et al. 2021 and Manzini et al. 2021). More specifically, it is possible to note from Case A to C an increase in the initial elastic stiffness and in the maximum base shear and a reduction in the ultimate displacement capacity. This trend can be seen in Table 5 that reports the mean values (of the five SWs’ responses) of the parameters of the equivalent elastic-perfectly plastic curve obtained following the criteria discussed in Sect. 3. Such mean values have also been used to calculate the percentage variation of Vy, Ks and du obtained with the five SWs and presented in Fig. 9.

Table 5 Mean values of parameters defining the bilinear curves obtained from the different SWs for Cases A, B, C, D
Full size table
Fig. 9
figure 9

Percentage variation of the three parameters defining the equivalent bilinear curves for configurations A, B, C and D in the + X and + Y directions with a mass proportional load pattern

Full size image

Figure 9 shows that the most pronounced differences are observed in the + Y direction, while in the + X direction the results are less scattered. Moreover, in general the SWs provide a good agreement when configurations are close to the shear-type idealization (Case D), while the scatter increases in the configurations with weak spandrels (Case A). It is interesting to observe that the highest percentage variations concern du. This is due to the fact that the different SWs—given the lack of clear definitions in Design Codes—use different approaches to compute the angular deformation demands on structural elements, that are then compared with the collapse thresholds specified in Sect. 2.1. The main issue is whether the rotation and the rigid body motion is subtracted in the evaluation of the deformation demand on the pier. For the ideal static scheme of fixed rotations at both pier ends, the definition of this parameter is unique and equal to the ratio between the horizontal relative displacement at the end sections and the effective height of the panel (drift ratio on the effective height). Conversely, when the pier end nodes rotate, different assumptions are made by different SWs. For example, in 3Muri and ANDILWall-Pro_SAM the angular deformation is defined as the drift ratio on the effective height subtracting the rotation at the end sections, while in MIDAS\Gen, Aedes.PCM and CDS the angular deformation is computed in terms of drift ratio on the effective height.

However, the results of the blind prediction shown in Fig. 8 and Fig. 9 are generally satisfactory, with limited percentage variations with respect to the mean of the five SWs. More specifically:

  • The scatter in Ks is lower than 27% and 12% and with an average value of 10% and 4% for Case A and C, respectively;

  • The scatter in Vy is lower than 27% and 24% and with an average value of 9% and 7% for Case A and C, respectively;

  • The scatter in du is lower than 42% and 15% and with an average value of 16% and 11% for Case A and C, respectively.

4 Refinement of EF models: calibration in the elastic range through dynamic identification

This Section presents the calibration in the elastic range of two of the analysed EFMs with reference to the configuration C, which was the most similar to the real building. The target was the modal parameters identified using the ambient vibration measurements (in the following tables and figures referred to as “experimental”). The two SWs are 3Muri and MIDAS\Gen.

The refinement of models’ calibration in the elastic range was carried out acting: on the masonry stiffness properties (more specifically on the Young Modulus E and the Shear Modulus G), for both SWs; also on the stiffness of the diaphragms, in the case of 3Muri. It should be pointed out that other sources that can contribute to the increased frequencies measured in AVT results, such as the explicit modelling of structural and non-structural elements (Soti et al. 2020) or the impact of the mass distribution and of non-structural elements (Mugabo et al. 2019), were neglected. Actually, the role of the non-structural elements can be relevant particularly in structures less massive and less stiff than masonry buildings. Thus, this assumption is considered appropriate.

As far as the EFM developed in MIDAS\Gen concerns, it used rigid diaphragms (similarly to the model used for the blind prediction): this is why the model refinement only focused on the masonry stiffness properties. In order to match measured and computed frequencies, the values of E and G were slightly increased with respect to those used in the blind prediction, by obtaining at the end of the calibration process: E = 2550 MPa and G = 840 MPa. These values are in agreement with those found in experimental tests on historic stone masonry panels (Magenes et al. 2010b, 2010c) and improve the fitting with the experimental frequencies (with percentage error lower than 7% for the first three modes).

In the case of 3Muri, to act also on the stiffness of diaphragms allowed to improve the fitting with the recorded data also in terms of modal shapes. This was made possible since in 3Muri the diaphragms are modelled as 3 − or 4-node elastic orthotropic membrane finite elements, whose mechanical properties are Young modulus E1eq along the principal direction, Young modulus E2eq along the perpendicular direction, Poisson ratio v, and shear modulus Geq (Lagomarsino et al. 2013).

In particular, in this case, the calibration followed an iterative technique based on the use of parametric analyses, in order to estimate the effects of the different uncertainties and identify those that mostly affect the global response. The results of the numerical modal analyses were compared with the measured data (Sect. 2.3) in terms of fundamental periods and modal shapes by computing the percentage error in the modal periods (err%) and the MAC index between experimental and numerical modal shapes.

The sensitivity of the dynamic response is assessed with respect to: (i) uncertainties connected to the stiffness of the diaphragms; and (ii) properties associated with the masonry stiffness. Accordingly, the parameters considered in the parametric analyses are: (i) the horizontal diaphragms’ shear modulus Geq, the parameter that most affects the tangential stiffness (by coupling the walls and thus redistributing the seismic forces) both in linear and nonlinear range; and (ii) the stiffness properties of the masonry elements (E and G).

The uncertainties connected to Geq and the relative ratio between Geq and G are the parameters that mostly affect the variation of the modal shapes. While the parametric analysis on the influence of the variation of Geq aimed at improving the fitting with the measured modal shapes, the study on the effects of the masonry stiffness properties aimed at improving the fitting of the modal periods. The proper choice of diaphragm stiffness is a complex issue, particularly for existing URM buildings where the simplified assumption of in-plane rigid behaviour is often violated. At present, few publications are available for estimating the stiffness properties for horizontal diaphragms. A model-based structural identification procedure has been recently proposed by Sivori et al. (2021) to analytically assess the diaphragm’s inertial and elastic properties based on experimental modal analyses. The latter procedure (hereinafter referred to as “literature procedure”) was used in the present work to assess the optimal value of Geq. Table 6 summarizes the initial and calibrated values derived from this procedure.

Table 6 (a) Initial (b) and calibrated values of Geq (for diaphragms) and E and G (for masonry elements) derived from the proposed procedure
Full size table

The initial values of Geq = 12,500 MPa was assumed as representative of a rigid diaphragm corresponding to the contribution of the 16 cm thick RC slab, as determined from the available data on geometry and construction details (Sect. 2.1), whereas the initial values of the masonry stiffness are those proposed by MIT 2019 (Sect. 2.1).

In order to assess the sensitivity of the dynamic response to Geq, four different values were considered: Gstart = Gs = 12,500 MPa, Gs/3, Gs/8 (value proposed in the literature procedure), and Gs/100. These values can be justified by considering the uncertainties related to the stiffness properties of the RC slabs (due to the concrete strength class and to the preservation state probably affected by creep and/or cracking) and to the effectiveness of the wall-to-floor connection. While the variability of the material properties of the floors is usually limited, the variation of Geq due to a different wall-to-floor connection can be very high. For these reasons, the parametric analysis performed with Gs/3 is more consistent with the stiffness property of well-connected RC slab, while the analysis performed with Gs/100 is closer to the configuration with very poor wall-to-floor connection. Figure 10 shows the MAC indexes obtained under the different assumptions on the shear stiffness Geq.

Fig. 10
figure 10

MAC indexes for different values of the diaphragm shear stiffness Geq: a Gs, b Gs/8, c Gs/3 and d Gs/100

Full size image

The results of Fig. 10 indicate that a lower value of the diaphragm shear stiffness Geq (Fig. 10 b and c) guarantees a better fitting with the experimental results in terms of modal shape; however, if the value of Geq evaluated with the above-mentioned literature procedure is assumed, the fitting with the measured data is good for the higher modes too (Fig. 10b). Finally, Fig. 10d shows that the modelling with flexible diaphragms leads to poor fitting, with a non-diagonal MAC matrix and lower values on the first three modes. The latter result confirms that the assumption of Geq = Gs/100 does not apply to the building under consideration that has effective wall-to-floor connections. Based on the results of Fig. 10, the value for the shear stiffness of the diaphragms proposed in literature (Table 6b) was assumed for the subsequent analyses, since it guarantees to obtain the highest MAC indexes up to the fifth mode (Fig. 10b), with values included in the range 0.96–0.98 for the first three modes. Finally, Table 7 compares the measured and numerical modal periods obtained using Geq = Gs/8 and shows that the differences are small.

Table 7 Comparison between measured and numerical modal periods, assuming the value of the diaphragm shear stiffness evaluated from the literature procedure (Geq = Gs/8)
Full size table

In order to further improve the fitting between measured and numerical results in terms of modal periods, the values of E and G were slightly increased, starting from the initial values used in the blind prediction and obtaining the values presented in Table 6b. Figure 11 compares experimental and updated numerical results in terms of frequencies (Fig. 11a) and MAC index (Fig. 11b).

Fig. 11
figure 11

Calibrated model: a comparison between measured and numerical frequencies (errors expressed on the x-axis in brackets); b MAC indexes

Full size image

The calibrated model presents a very good fitting with the experimental target both in terms of frequencies (with errors on the first four modes lower than 7%) and deformed shapes (with MAC index on the first four modes between 0.95 and 0.99).

5 Validation of EF models: nonlinear dynamic analyses and comparison with data recorded from the Central Italy 2016/2017 earthquake sequence

After calibration of the two EF structural models in the elastic field (Sect. 4), their validation in the nonlinear range was provided by simulating the dynamic response recorded during the mainshocks of the 2016/2017 Central Italy earthquake sequence. Nonlinear dynamic analyses (NLDA) were carried out using, as input, the three components of the accelerograms recorded by the monitoring system at the building base (sensors n. 15, 16 and 17 of Fig. 2a) during the mainshocks of August 24, 2016, October 26, 2016, October 30, 2016 and January 18, 2017. The accelerograms were applied in sequence, in order to evaluate the possible effects of damage accumulation on the building. The NLDAs were carried out assuming for the masonry panels the constitutive laws described in Sect. 5.1. The analyses used the Newmark integration method with dt = 0.004 s. Rayleigh damping was used with 3% viscous damping at T1 and Tsec, where T1 is the first period from the modal analysis and Tsec is the period computed assuming a ductility equal to 4 (i.e. Tsec = 2T1). The period Tsec is intended to represent the expected evolution of the structural response in the nonlinear range, in order to avoid an overestimation of the viscous damping in nonlinear dynamic analyses. No convergence problem was reported.

5.1 Modelling of the cyclic nonlinear response

The programs used for the nonlinear dynamic analyses of the building were 3Muri (through its research version Tremuri) and MIDAS\Gen.

The model geometry developed in the 3Muri software package was transferred to the research version Tremuri since Tremuri allows a wider range of constitutive laws for nonlinear dynamic analyses (Cattari et al. 2018b; Cattari and Lagomarsino, 2013; Penna et al. 2014). In the present case, the constitutive law used to describe the nonlinear cyclic response of the masonry panels is the piecewise-linear model proposed by Cattari and Lagomarsino (2013) and shown in Fig. 12a). This law simulates the nonlinear response up to very severe damage levels (from 1 to 5) through progressive strength degradation, defined in terms of residual strength (βi) corresponding to assigned drift values (θi). The hysteretic response is formulated through a phenomenological approach that, thanks to a proper setting of specific coefficients (ci with i = 1,…,4), allows to capture in a simple manner the differences among the various possible failure modes (i.e. flexural, shear or hybrid flexural-shear type) and the different response of piers and spandrels. The elastic phase is described according to the beam theory defined through the elastic Young (E) and shear (G) moduli. Progressive degradation is computed in an approximate way by a secant stiffness by assigning a proper ratio (kr) between initial (kel) and secant (ksec) stiffness, where the maximum strength is attained.

Fig. 12
figure 12

a Piecewise-linear constitutive law and b parameters used for masonry panels in Tremuri for NLDA

Full size image

The strength parameters used in the analyses are presented in Table 8. These parameters were defined on the basis of available data on materials and constructive details and are compatible with the values proposed by the Italian Technical Code (MIT 2019) for the examined masonry typology, as described in Sect. 2.1. As for the other parameters (βi, θi and ci), the assumed drifts are consistent with those proposed in the technical literature (CNR-DT 212/2013) and are also supported by the experimental evidence for existing masonry typologies (Vanin et al. 2017). Finally, in order to properly describe the different stiffness degradation as a function of the assigned ratio kr between the elastic (kel) and cracked (ksec) stiffness, the values of kr = 1.7 and kr = 2 were assumed for shear and flexural failure modes, respectively. These parameters take into account the different spread of damage in the panel and, as a consequence, the resulting stiffness degradation.

Table 8 Mechanical properties assumed in the structural models
Full size table

As for the EFM developed with the MIDAS\Gen software, it makes use of the Takeda tri-linear hysteretic model to describe the nonlinear flexural and diagonal shear cyclic behavior of piers and spandrels (Takeda et al. 1970). The Takeda’s model is defined as shear-drift curve (V-θi), as reported in Fig. 13. The constitutive response is defined by three branches associated with two damage levels DL3 and DL5 and is calibrated following the Italian guidelines CNR-DT212/2013. The values of Vy in Fig. 13 represent the element shear or flexural capacity (depending on the failure mechanism), while θ2 is the elastic drift calculated in cracked condition. The cracked stiffness Kc is assumed equal to 50% the elastic gross stiffness. The softening branch (stiffness K4) depends on the element drift θ5 and on the β5 coefficient that represents the capacity loss at the damage level DL5.

Fig. 13
figure 13

a Takeda’s trilinear model and b parameters used for masonry panels in MIDAS\Gen for NLDA

Full size image

The \(K_{{{\text{un2}}}}\) parameter is the unloading stiffness of the outer loop and depends on the cracked stiffness Kc, on the maximum deformation θmax in the zone to which the unloading point belongs, on the drift θ2, and on a constant α = 0.4. The mechanical parameters used in the EFM developed with the MIDAS\Gen software were defined on the basis of experimental tests performed on historic stone masonry panels (Magenes et al. 2010b, c).

Table 8, Figs. 12 and 13 summarize all the parameters used for the two EFMs.

5.2 Comparison between recorded and simulated accelerograms

A first comparison between recorded and numerical data is made in terms of accelerations recorded by sensors and corresponding acceleration floor spectra. The sensor location is shown in Fig. 2a. In all the following figures, the data directly recorded or derived from the monitoring system are referred to as “experimental” and labeled “exp”. Similarly to the blind prediction, in the following Sections all the numerical results are anonymously reported, without any explicit reference to the specific software. Figure 14 compares the accelerations computed by the two SWs for the seismic event of the January 18, 2017, which was the most significant one on the building. The numerical results are plotted in red, while the recorded ones are in black. Four sensors are considered in the figure: sensors 6 and 13, placed in the X direction at the first and at the second level, respectively, and sensors 7 and 14, placed in the Y direction at the first and at the second level, respectively.

Fig. 14
figure 14

Comparison between recorded and numerical accelerations computed with the two SWs used in the validation: a SWa and b SWb

Full size image

Figure 15 shows the comparison between the recorded (continuous graphs) and numerical (dashed graphs) acceleration floor spectra at the sensors located along the same Vertical Alignment (VA) at the two levels (identified in Fig. 2a). The results are reported for the two EFMs. It should be pointed out that in Fig. 15 VA4 comprises sensors 2–3 at the first level and 8–9 at the second one, even though strictly speaking they are not aligned along the same vertical axis.

Fig. 15
figure 15

Comparison between recorded (continuous graphs) and numerical (dashed graphs) acceleration floor spectra for software: a SWa and b SWb

Full size image

The results show quite a good match between recorded and numerical data, more specifically for software SWb in both directions and for software SWa in the Y direction. Figure 15 indicates that both SWs correctly reproduce the amplification of the seismic action provided by the filtering effect of the main structure on various parts of the building and at different levels. The effectiveness of both models in capturing the acceleration demand is particularly relevant from the engineering point of view, since such models constitute the main tool for the seismic assessment of both structural and non-structural components.

A very good agreement can be observed for all sensors for SWb, while in the SWa the results are slightly overestimated, particularly in the X direction where the numerical model amplifies the input response spectrum at a period that is slightly lower than the recorded one. This is consistent with the results obtained at the global scale, which will be provided in Sect. 5.3.

The results are sensitive to the choice of the damping coefficient used in the nonlinear dynamic analyses, whose definition is always affected by uncertainties. Figure 16 illustrates, for three sensors, the floor spectra obtained with SWa assuming a damping coefficient equal to 5% (continuous red plot) and 3% (dashed red plot). It is clear that the numerical acceleration floor spectra better fit the recorded ones in terms of maximum amplification when a damping coefficient equal to 5% is assumed.

Fig. 16
figure 16

Sensitivity of the results of SWa to the damping coefficient: 3% (dashed red plot) vs 5% (continuous red plot). The floor spectra of the recorded data are plotted in black

Full size image

In order to quantify the effects of the model’s calibration described in Sect. 4, the floor spectra obtained from SWa (with a damping coefficient equal to 3%) are compared with those computed with the same model before the refinement of Sect. 4. Figure 17 shows these results. The dashed red plot refers to the floor spectra obtained from the NLDA carried out with the calibrated model, while the continuous red plot refers to the results of the blind model (NC in the figure stands for “not calibrated”).

Fig. 17
figure 17

Comparison of the floor spectra obtained with SWa (with 3% damping coefficient): before (continuous red plot) and after (dashed red plot) the model calibration of Sect. 4. The floor spectra of the recorded data are plotted in black

Full size image

It is possible to notice that a slight improvement of the fitting with the experimental floor spectra (in black in Fig. 17) are obtained for sensors 7 and 14, even if the overall results are substantially confirmed. This was probably because the model has fitted quite well the experimental target already before its calibration in the elastic field. This result is also encouraging because it demonstrates that the results obtained under a blind prediction (as usually done in the engineering practice) already provide satisfactory results in structures rather simple like the examined one.

5.3 Comparison of the activated inertial forces

The two models’ validation was further investigated by checking the main parameters affecting the seismic global response. Figure 19 shows the results in terms of dynamic hysteretic curves (inertial forces V vs. top displacement d) obtained with the two SWs by applying in sequence the mainshocks recorded during the 2016/2017 earthquake sequence.

The experimental curve was estimated defining an equivalent M-DOF system for the building (where M is equal to the number of stories) and computing V as the sum of the product of the recorded accelerations (ai) and the corresponding masses (mi). The masses were estimated on the basis of the influence area attributed to each sensor, as illustrated in Fig. 18a. The top displacement d was computed as the average displacement of the nodes on the top level weighted on the pertinent mass. The displacement was obtained with a double integration of the recorded accelerations. Figure 18b indicates that the structural response has just exceeded the linear-elastic range, as appears evident by comparing the cyclic and the pushover curve obtained by nonlinear static analyses (NLSA). This result is consistent with the moderate damage observed after the earthquake, as reported in Sect. 5.4.

Fig. 18
figure 18

a Influence areas attributed to each sensor for the evaluation of the masses; b Recorded hysteretic curve (in black) compared with the numerical one (in red), as obtained from SWa from the NLDA. The graph also shows the pushover curve for SWa from NLSA with a mass proportional load pattern (dotted red plot)

Full size image

Figure 19 shows a close-up of the hysteretic curves obtained with the two EFMs. For software SWa, in the X direction the numerical response provides an initial stiffness slightly higher than the recorded one, consistently with the results presented in Sect. 5.2. Overall, the comparison presented in Fig. 19 confirms that the numerical results fit quite well the recorded ones at a global scale too.

Fig. 19
figure 19

Comparison between recorded and numerical V-d hysteretic curves in the X and Y directions for: a SWa and b SWb

Full size image

5.4 Comparison between actual and simulated damage

Finally, a comparison between observed and simulated damage was carried out. After the earthquake, particularly after the mainshock of January 18, 2017, the building exhibited a moderate/low level of damage that was mainly concentrated in the masonry piers parallel to the Y-direction. Figure 20 shows the damage pattern of the four facades, identified in Fig. 1b.

Fig. 20
figure 20

adapted from Cattari and Magenes (2021)

Damage reported on the main façades identified in Fig. 1b, according to the damage survey carried out by the Task 4.1—Workgroup on June 26, 2017 (Cattari et al. 2018a)—figure

Full size image

Considering wall 2 (identified in plan in Fig. 1b), Fig. 21 compares: (a) the damage pattern surveyed after the January 18, 2017 earthquake; (b) the damage numerically simulated with SWb; and (c) the damage obtained with SWa. The colour legends used to indicate the damage level and the failure modes are reported in Sect. 5.1 (Figs. 12a and 13a).

Fig. 21
figure 21

Comparison, for wall 2, between: a observed damage; b damage simulated with SWb; c damage simulated with SWa

Full size image

As shown in Fig. 21a, the damage surveyed in June 2017 on wall 2 was moderate and was concentrated in the piers at both levels and was characterized by the presence of: (i) pseudo-horizontal cracks (associated with a flexural mode) and diagonal cracks (associated with a shear failure mechanism) at the first level; (ii) horizontal cracks at the top of the lateral piers (probably associated to a flexural mode) and pseudo-vertical cracks in the second level central pier.

As for the damage simulated with software SWb (Fig. 21b), after the seismic event of the August 24, 2016, flexural damage is found at the top edge of the masonry piers at the centre and on the right side at the second level (yellow hinges in Fig. 21b). Shear mode was detected from the analyses in the central masonry spandrel at the second level (yellow hinges in Fig. 21b). No damage was found at the first level, where the masonry piers remain in the linear-elastic range (see the blue and green hinges in Fig. 21b). Moreover, from the damage pattern simulated using all the seismic events in sequence, in addition to the above-mentioned level of damage, flexural modes at the base of the masonry piers of the second level were also found in the numerical results.

The damage pattern simulated with software SWa (Fig. 21c) is quite similar to that evaluated with SWb, both in terms of damage level (which is light and corresponds to DL1-DL2-DL3 according to the legend presented in Fig. 12a) and type of the activated mechanisms (with a prevailing flexural behaviour in the masonry piers). However, unlike SWb, SWa is also able to catch the damage occurred in the piers of the first level. In this case too, the simulated damage highlights a prevailing flexural behaviour of the piers, even if, in the actually observed damage pattern, both pseudo-horizontal and shear diagonal cracks were detected. Furthermore, in both SWs damage accumulation is not significant. From these results it appears that in general both numerical models are capable of accurately capturing the occurred damage, both in terms of failure modes and damage levels.

6 Conclusions

The research activities presented in this paper were developed in two phases.

The first phase studied the reliability of five selected software programs based on the EFM approach through a blind prediction, which is consistent with the approach commonly used by professional engineers. Modal and nonlinear static analyses were performed with the five programs on different models of a 2-story masonry building with rigid diaphragms, inspired by the town hall of Pizzoli (AQ, Italy). This building was instrumented in 2009 and was later hit by the 2016–2017 Central Italy earthquake sequence. Four structural configurations were considered, according to different assumptions on the in-plane coupling effect between walls. No preliminary calibration of the models was performed, but common assumptions on materials and modelling were made. The results of the modal analyses were found to be consistent with the data of AVTs, although with slightly larger values of the modal periods. The nonlinear static analyses provided results with rather limited variations between the different software in terms of stiffness, base shear and displacement capacity of the pushover curves. Comparison of the results of the five software programs also provided interesting outcomes regarding the impact of the model uncertainties (e.g., Alam and Barbosa 2018; De Falco et al. 2017).

In the second phase of the study, two of the EFMs developed in the first phase were calibrated in the elastic range using the results of available AVTs by varying the elastic properties of the masonry and of the floor stiffness, in order to attain a good correspondence with the recorded data. The two refined models were then validated in the nonlinear range by simulating the dynamic response during the mainshocks of the 2016/2017 Central Italy earthquake using proper cyclic constitutive laws. The numerical response was compared with the recorded data in terms of dynamic hysteretic curves, damage, floor acceleration histories and floor spectra. The results were found to be satisfactory, since the analyses showed the capability of both models to very well capture the recorded floor acceleration demands and the actual damage level of the building.

A future step of this research could examine the bias and standard deviation between blind prediction modeling and calibrated/experimental results. However, the present study provides a first comparison with the nonlinear dynamic analysis performed on a non-calibrated EF model. This was done in order to quantify the effect of the model’s calibration, pointing to the importance of data from dynamic identification tests. In the case considered here, a slight improvement of the fitting with the recorded target was obtained, though the overall results were substantially confirmed. AVTs data were essential for refining the numerical models since they allowed to verify the assumptions made in the blind predictions and to address the most proper modelling choices in the validation phase. Moreover, such data represent a fundamental tool, especially for the calibration of models characterized by complex geometry or influenced by many modelling uncertainties (as discussed in Cattari et al. 2021a; Brunelli et al. 2021). This paper clearly shows the importance of having information from permanent monitoring systems, useful for an effective validation of the structural response in the linear and nonlinear range.

Finally, even though further research is certainly needed, the results of this study once again confirm that EFMs represent a reliable and efficient modelling strategy for the seismic assessment of existing masonry buildings, given their capability to capture properly the elastic stiffness, lateral strength, floor acceleration demand and damage pattern of real structures.