1 Introduction

After the discovery of general relativity in 1915 by Einstein, it’s become an important tool for understanding and explaining the gravitational system. In particular, obtaining a singularity free interior solution for compact astrophysical objects is an important issue in relativistic astrophysics for the past two and a half decades. At some points, we usually refer compact objects as a collection of different types of high density objects like white dwarfs, neutron stars and quark stars, that form at the end of their stellar evolution. Therefore, in order to study the structure of such stars form microscopic composition and properties of dense matter in an extreme condition is one of the most fundamental problems in modern astrophysics. However, in spite of the fact that such extreme densities nuclear matter may consist not only of leptons and nucleons but also consists of some mesons, hyperons, baryon resonances as well as strange quark matter (SQM), in their different forms and phases at the time of stellar evolution. Indeed, works reviewed by different authors demonstrate the difficulties associated with constructing solutions for obtaining a comprehensive description of compact objects.

From the above description one can easily understand that obtaining a reliable description of dense compact object is not an easy task, though there are several theoretical investigations, laboratory experiments as well as observation tests have been performed during the last few decades. But the observational data form compact stars may soon provide some information about largest uncertainties in nuclear physics that rely heavily on the equations of state (EoS) at nuclear and supranuclear densities. In general, this could be achieved by estimating their mass and radius [2,3,4] which depends on EoS [5,6,7,8]. The motivation to undertake such a task was initiated by the discovery of the pulsar PSR J1614-2230 that produced hot spots on the surface of compact stars [9] led to several interpretative problems such as neutron stars (NSs) and quark stars (QSs). However, this pulsar profile does not depend only on the stellar mass and radius, but also depends on several other features like moment of inertia, quadrupole moment and higher multi-pole moments etc. According to recent observation there are many compact objects, namely, X-ray burster 4U 1820-30, X-ray pulsar Her X-1, X-ray sources 4U 1728-34, PSR 0943+10 and RX J185635-3754, whose masses and radii are not compatible with the standard neutron star models. The problem is that we still have lack of information about the nuclear matter density, so theoretical studies hints that pressure is likely to be anisotropic within the stellar radii, i.e., the radial pressure and the tangential pressure. The search for anisotropic superdense star was initiated by Bowers and Liang [10] and then a number of articles appeared related with this in [11,12,13,14,15,16,17,18,19].

The search for an exact solutions of Einstein field equations for static isotropic and anisotropic astrophysical objects are excellent testbeds with growing interest to mathematician as well as physicists. However, most of the exact interior solutions for both isotropic and anisotropic cases do not satisfy the general physical required conditions of the stellar systems. Therefore, exact solutions of Einstein–Maxwell field equations are also important in relativistic astrophysics. The conjecture is the obtained solution may be utilized to model for a charged relativistic star, which is constructed by matching the Reissner–Nordstr\(\ddot{\text {o}}\)m exterior spacetime at the boundary. In this context one can avoid the gravitational collapse of a spherically symmetric distribution of matter, because of gravitational attraction is counterbalanced by the repulsive Coulomb force in addition to the pressure gradient. In connection to this, Ivanov [46] and Sharma et al. [27] showed that due presence of the electric field affects the nature of luminosities, redshifts and maximum masses of relativistic star. Later on, Mafa Takisa and Maharaj [59] have proposed an exact solution for charged anisotropic polytropic spheres. Imposing different equation of state some of these charged solutions have studied in [8, 20,21,22,23,24].

The simplest known procedure is that can be added for constructing a static charged perfect fluid interior solution for compact objects are either to prescribe a metric ansatz or an equation of state relating pressure and density. In the present article we consider a well known ansatz for one of the metric functions, namely, Vaidya and Tikekar [1], who prescribed an ansatz for the geometry of the t = constant hypersurface. The main important feature is that the solution characterizes a class of static spherically symmetric perfect fluid configuration and provides an exact solution of Einsteins equations. In an attempt to generate exact solutions of the Einstein–Maxwell field equations, Komathiraj and Maharaj [25] have used Vaidya and Tikekar ansatz with a specified form of the electric field intensity. In a recent treatment Naveen and Bijalwan [31, 32] have obtained a charged perfect fluid model with generalized electric intensity for all K except for \(0< K < 1\) and extending this point of view Kumar and Gupta [33, 34] obtained another solution for \(0<K<1\). Following this technique, a large number of solutions have been studied in [26,27,28,29,30]. In the present problem we focus on a charged fluid sphere starting with Vaidya and Tikekar [1] metric potential and investigate the physical features of the model in connection with some standard observed mass and radius of compact stars as proposed in [35].

The paper is organized as follows: following a brief introduction in Sect. 1, then we formulate the general relativistic formulation of Einstein–Maxwell system of equations for a relativistic stellar model in Sect. 2. Paying particular attention to solve the system of equations analytically, we assume a particular form of metric potential, namely, Vaidya–Tikekar to generate exact solutions and obtain the expression for energy density and pressure in the same section. Then, we match the interior charged fluid to the exterior Reissner–Nordstr\(\ddot{\text {o}}\)m line element in Sect. 3. Next, in Sect. 4, we have discussed briefly some physical features of the proposed model maintaining the regularity condition and obtained results are compared with observational data. Finally in Sect. 5, we give a brief discussion.

2 Einstein field equations

In this work, we consider the static spherically symmetric spacetime for seeking solution of a compact stellar object, that can be written in Schwarzschild coordinates as

$$\begin{aligned} ds^{2} = e^{\nu (r)}dt^{2}-e^{\lambda (r)}dr^{2} -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(1)

where the unknowns \(\nu (r)\) and \(\lambda (r)\) are both metric functions in terms of radial coordinate, which yet to be determined by solving the field equations.

The most important question that arise is the matter distribution inside a compact star. Here, we consider the case of a charged gravitating object with isotropic pressures. Then the energy momentum tensor \(T^{i}_{j}\) will include the terms from Maxwell’s equation \(E^{i}_{j}\), and the complete form of energy-momentum tensor is

$$\begin{aligned} T^{i}_{j}+E^{i}_{j}= & {} \bigg [(c^{2}\rho +p)u^{i}u_{j}-p\delta ^{i}_{j}\nonumber \\&+\dfrac{1}{4\pi }\bigg (-F^{im}F_{jm} +\dfrac{1}{4}\delta ^{i}_{j}F_{mn}F^{mn}\bigg )\bigg ], \end{aligned}$$
(2)

where \(u_j\) and \({\delta ^i_j}\) stand for 4-velocity of the fluid and the metric tensor, respectively. Generally first component standards for energy momentum tensor; e.g. for a perfect fluid we have \(\left[ (c^{2}\rho +p)u^{i}u_{j}-p\delta ^{i}_{j}\right] \), where \(\rho \) is the matter density and p is the isotropic pressure of the fluid. The basic argument to assume the perfect fluid implies that the flow of matter is adiabatic, no heat flow, radiation, or viscosity is present [36]. The second term associate with electromagnetic stress-energy tensor from the Maxwell’s field equation and hence they will follow the relation \(\left[ \sqrt{-g}F^{i j}\right] _{,j}=4\pi j^{i}\sqrt{-g}\), where \(F_{ij}\) denotes the skew symmetric electromagnetic field tensor and \(j^{i}\) is the four-current density.

Now, accomplishing the effects due to the electric field and pressure isotropy, and using the metric (1) with stress tensor given in Eq. (2), the Einstein field equation, \(G^{\mu }_{\nu }\) = -\(\kappa \left[ T^{\mu }_{\nu }+E^{\mu }_{\nu }\right] \), where \(G^{\mu }_{\nu }=R^{\mu }_{\nu }-\dfrac{1}{2}R\delta ^{i}_{j}\), provides the following relationships

$$\begin{aligned} \dfrac{\lambda '}{r}e^{-\lambda }+\dfrac{(1-e^{-\lambda })}{r^{2}}= & {} \kappa \rho +\dfrac{q^{2}}{r^{4}}, \end{aligned}$$
(3)
$$\begin{aligned} \dfrac{\nu '}{r}e^{-\lambda }-\dfrac{(1-e^{-\lambda })}{r^{2}}= & {} \kappa p-\dfrac{q^{2}}{r^{4}}, \end{aligned}$$
(4)
$$\begin{aligned} \bigg (\dfrac{\nu ''}{2}-\dfrac{\lambda '\nu '}{4}+ \dfrac{\nu '^{2}}{4}+\dfrac{\nu '-\lambda '}{2r}\bigg )e^{-\lambda }= & {} \kappa p+\dfrac{q^{2}}{r^{4}}, \end{aligned}$$
(5)

with \( \kappa = 8\pi \) (geometrized units \(G = c = 1\)) and prime denotes the differentiation with respect to the radial coordinate. The total charge inside a radius r is given by

$$\begin{aligned} q(r)= & {} r^{2}\sqrt{-F_{14}F^{14}}=r^{2}F^{41}e^{(\lambda +\nu )/2}\nonumber \\= & {} 4\pi \int _{0}^{r}\sigma r^{2}e^{\lambda /2}dr. \end{aligned}$$
(6)

Also \( F_{14}\) is only non-vanishing component of the skew-symmetric electromagnetic tensor i.e., \( F_{14}= -F_{41}\). Equations (3)-(5) are invariant under the transformation \(q(r) = - q(r) \) and \(\sigma = -\sigma \). Here, we exclusively deal with the positive square root of \(q^2\).

Note that Eqs. (3)–(5) provide three independent equations, with five unknown quantities i.e. \( \nu , \lambda , \rho ( r), p(r)\) and q(r) which we have to solve simultaneously to obtain our results. As, obtaining explicit solutions to the Einstein field equations is a difficult tusk due to highly nonlinearity of the equations. Thus, we will reduce the number of unknown functions by assuming a well known form of metric potential [1]

$$\begin{aligned} e^{\lambda }=\dfrac{K(1+Cr^{2})}{K+Cr^{2}},\quad 0<K<1, \end{aligned}$$
(7)

where \(C =-K/R^2\), and K & R are two parameters which characterize the geometry of the star. Our choice of Vaidya–Tikekar ansatz is physically well motivated and has been studied for uncharged superdense stars by Tikekar [37], and Maharaj and Leach [38]. This facilitated the model in an interesting geometric meaning as deviation from sphericity of 3-space geometry. It may also be noted that metric potential restricts the geometry of the 3-dimensional hypersurfaces t = const. to be spheroidal and when \(K = 0\) the hypersurfaces t = const. become spherical.

The solution of EFEs (3)–(5), is in a different but equivalent form if we introduce \(Cr^{2}=x \) and \( e^{\nu }=Z^{2} \) as a new variables. After a little bit algebraic calculation we have

$$\begin{aligned}&\dfrac{(K-1)(3+x)}{K(1+x)^{2}}-\dfrac{q^{2}C}{x^{2}}=\dfrac{\kappa c^{2}\rho }{C}, \end{aligned}$$
(8)
$$\begin{aligned}&Z''-Z'\Bigg (\dfrac{\sqrt{C}K}{\sqrt{x}(K+x)}+ \dfrac{\sqrt{xC}}{(1+x)}\Bigg )+\dfrac{C}{(\sqrt{K+x})} \nonumber \\&\quad \times \Bigg (\dfrac{(K-1)x}{(1+x)}-2q^{2}CK(1+x) \Bigg )Z= 0,\end{aligned}$$
(9)
$$\begin{aligned}&\dfrac{(K+x)}{\sqrt{xC}K(1+x)}\dfrac{2Z'}{Z}+ \dfrac{(1-K)}{K(1+x)}+\dfrac{q^{2}C}{x^{2}}= \dfrac{\kappa p}{C}, \end{aligned}$$
(10)

where prime denotes differentiation with respect to the variable x. Furthermore, to transform the field equations in a more convenient form we introduce another variables defined by

$$\begin{aligned} Y=\sqrt{\dfrac{K+x}{1-K}},\quad \text {and}\quad Z=(1+Y^{2})^{1/4}\Phi , \end{aligned}$$
(11)

and plugging the values of Y and Z into the Eq. (9), we get

$$\begin{aligned} \dfrac{d^{2}\Phi }{dY^{2}}+\chi \Phi =0 \end{aligned}$$
(12)

where for notational simplicity we use

$$\begin{aligned} \chi= & {} -\dfrac{1}{(1+Y^{2})}\nonumber \\&\times \,\Bigg (K-1-2K q^{2}\dfrac{(1+x^{2})C}{x^{3}}+\dfrac{2-3Y^{2}}{4(1+Y^{2})^{2}}\Bigg ). \end{aligned}$$
(13)

In order to solve the second order differential equation (12) more easily, we have chosen \( \chi =-2\beta ^{2}/(Y^{2}\beta ^{2}+b)\), where \( \beta \) is a positive constant, and comparing with Eq. (13) leads to defining the total charge of the system as

$$\begin{aligned} \dfrac{q^{2}}{x^{2}}= & {} \dfrac{x}{2CK(1+x)^{2}}\nonumber \\&\times \,\bigg [K-1+ \dfrac{2-3Y^{2}}{4(1+Y^{2})^{2}}+ \dfrac{2\beta ^{2}(1+Y^{2})}{(Y^{2}\beta ^{2}+b)}\bigg ]. \end{aligned}$$
(14)

Moreover, using the value of \( \chi \) from (13) into the Eq. (12), which yields

$$\begin{aligned} (Y^{2}\beta ^{2}+b)\dfrac{d^{2}\Phi }{dY^{2}}-2\beta ^{2}\Phi =0 , \end{aligned}$$
(15)

Now, comparing Eq. (15) with a known standard differential equation

$$\begin{aligned} P_{0}\dfrac{d^{2}Y}{dX^{2}}+P_{1}\dfrac{dY}{dX}+P_{2}X = R, \end{aligned}$$
(16)

which leads to the following relations \( P_{0} = Y^{2}\beta ^{2}+b,~~ P_{1}=0,~~ P_{2} = -2\beta ^{2},~~R=0\).

Thus it is clear that the differential equation is exact and rearranging the terms one can write this in a conventional form \(P_{2}-\dfrac{dP_{1}}{dY}+\dfrac{d^{2}P_{0}}{dY^{2}}=0\). Hence the primitive of the given equation is

$$\begin{aligned}&P_{0}\dfrac{d\Phi }{dY}+(P_{1}-P'_{0})\Phi =\int R dY +A,\nonumber \\&\quad \implies \dfrac{d\Phi }{dY}-\dfrac{2Y\beta ^{2}+1}{Y^{2}\beta ^{2}+b}\Phi =\dfrac{A}{Y^{2}\beta ^{2}+b}, \end{aligned}$$
(17)

where A and b stands for arbitrary constants. Finally, the differential equation (17) leads to the following expression

$$\begin{aligned} \Phi (Y)= & {} (Y^{2}\beta ^{2}+b)\dfrac{A}{2\,\beta \,b^{3/2}} \bigg [\arctan \bigg (\dfrac{Y\beta }{\sqrt{b}}\bigg )\nonumber \\&\quad +\dfrac{1}{2}\sin 2\bigg (\arctan \bigg (\dfrac{Y\beta }{\sqrt{b}}\bigg )\bigg )\bigg ]+B(Y^{2}\beta ^{2}+b),\nonumber \\ \end{aligned}$$
(18)

Now, using the relation (11) for Z, which yields

$$\begin{aligned} Z= & {} A(1+Y^{2})^{1/4}\nonumber \\&\times \,\Bigg [(Y^{2}\beta ^{2}+b)\dfrac{1}{\beta \, b^{3/2}}H(Y)+B(Y^{2}\beta ^{2}+b)\Bigg ], \end{aligned}$$
(19)

where

$$\begin{aligned} H(Y)= & {} \bigg [\dfrac{1}{2}\arctan \bigg (\dfrac{Y\beta }{\sqrt{b}}\bigg )+\dfrac{1}{4}\sin 2\\&\quad \times \, \bigg (\arctan \bigg (\dfrac{Y\beta }{\sqrt{b}}\bigg )\bigg )\bigg ]. \end{aligned}$$

In addition, taking into account Eqs. (14) and (19) into Eqs. (8)–(10), it is straightforward to achieve the following nonzero components of field equations

$$\begin{aligned} \dfrac{\kappa c^{2}\rho }{C}= & {} \dfrac{(K-1)(3+x)}{K(1+x)^{2}}-\dfrac{x}{2K(1+x)^{2}}\nonumber \\&\quad \times \,\bigg [K-1+\dfrac{2-3Y^{2}}{4(1+Y^{2})^{2}} +\dfrac{2\beta ^{2}(1+Y^{2})}{(Y^{2}\beta ^{2}+b)}\bigg ], \end{aligned}$$
(20)
$$\begin{aligned} \dfrac{\kappa p}{C}= & {} \dfrac{Y^{2}x}{K(1+Y^{2})} \left[ \dfrac{ \dfrac{N1\times N2}{(1-K)}+N3}{N4\times N1}\right] \nonumber \\&\quad -\dfrac{1}{K(1+Y^{2})}+ N6, \end{aligned}$$
(21)

where,

$$\begin{aligned}&N1=\dfrac{1}{\beta b^{3/2}}\left[ \dfrac{1}{2}\arctan \bigg ( \dfrac{Y}{\sqrt{b}}\beta \bigg )\right. \\&\left. \quad \qquad +\dfrac{1}{4}\sin 2\bigg (\arctan \bigg ( \dfrac{Y}{\sqrt{b}}\beta \bigg )\bigg )\right] +\dfrac{B}{A},\\&N2=\dfrac{(Y^{2}\beta ^{2}+b)}{2(1+Y^{2})^{3/4}}+ 2\beta ^{2}(1+Y^{2}) ^{1/4},\\&N3=\dfrac{(1+Y^{2})^{1/4}}{2b(1-K)Y}\left[ 1+\cos 2\bigg (\arctan \bigg ( \dfrac{Y}{\sqrt{b}}\beta \bigg )\bigg )\right] ,\\&N4=(1+Y^{2})^{1/4}(Y^{2}\beta ^{2}+b),\\&N6=\dfrac{x}{2K(1+x)^{2}} \bigg [K-1+\dfrac{2-3Y^{2}}{4(1+Y^{2})^{2}}\\&\quad \quad \quad \quad +\dfrac{2\beta ^{2}(1+Y^{2})}{(Y^{2}\beta ^{2}+b)}\bigg ]. \end{aligned}$$
Fig. 1
figure 1

The energy density, pressure, charge and density-pressure in their normalized forms as a function of the radial coordinate are shown on the panels from top to bottom for the compact star candidates SAX J1808.4-3658, 4U 1538-52 and Her X-1. For plotting, we choose the values of physical parameters and constants are as follows: (i) \(K = 0.0032, b = 0.01, C_1 = - 0.00099\), \( \beta ^{2} \) = 1.006 \(M = 0.9 M_{\odot }\), and \(R = 7.951 Km\) for SAX J1808.4-3658 (Table 1), (ii)\( K = 0.0033, b = 0.05, C_1 = -0.001\), \(\beta ^{2}\) = 4.82, \(M = 0.87 M_{\odot }\) and \(R = 7.866 Km\) for 4U 1538-52 (Table 2), (iii) \(K = 0.034, b = 0.09, C_1=-0.01\), \(\beta ^{2}\) = 0.835, \(M = 0.85 M_{\odot }\) and \(R = 8.1 Km\) for Her X-1 (Table 3)

Full size image

With the purpose of determining the non-zero components, we are in a position to determine the internal structure of compact stars. For compact star described by electrically charged fluid (within a certain radius) should comply with the following requirements throughout the interior radius:

  • The energy density and pressure should be positive and regular within the radius.

  • \( (d\rho /dr)_{r=0}=0 \) and \( (d^{2}\rho /dr^{2})_{r=0}<0, \) so that gradient of density \( d\rho /dr \) is negative within \( 0<r < R \).

  • \( (dp/dr)_{r=0}=0 \) and \( (d^{2}p/dr^{2})_{r=0}< 0, \) so that pressure gradient dp / dr is negative within \( 0< r < R \).

The above three conditions imply that pressure and density should be maximum at the center and monotonically decreasing towards the surface, which is clear from Fig. 1. We are concerned here with charged isotropic case and according to Thirukkanesh and Maharaj [60] charge distributions are singular at the origin, whereas the electric field does not vanish. That means, at the origin all our sources have vanishing electric field and finite proper charge density. From Fig. 1, it is clear that the charge will increase with the increasing charge fraction.

3 Boundary conditions

At this stage the interior solution is smoothly connected to the vacuum exterior Reissner–Nordstr\(\ddot{\text {o}}\)m metric at the junction surface at radius \(r = R\). It is important to note that these three constants A, b and \(\beta \) are fixed by suitable junction conditions imposed on the internal and external metrics at the hyper-surface. The exterior metric is given by

$$\begin{aligned} ds^{2}= & {} \bigg ( 1-\dfrac{2M}{r}+\dfrac{Q^{2}}{r^{2}}\bigg )dt^{2} -\bigg (1-\dfrac{2M}{r}+\dfrac{Q^{2}}{r^{2}}\bigg )^ {-1}dr^{2}\nonumber \\&\quad -r^{2}(d\theta ^{2}+\sin ^{2}\theta d\phi ^{2}), \end{aligned}$$
(22)

where M is the total gravitational mass of the fluid distribution and is defined by

$$\begin{aligned} M=\zeta (R)+\xi (R), \end{aligned}$$
(23)

with the definition \(\zeta (R) = \dfrac{\kappa }{2}\int _{0}^{R}\rho r^{2}dr\), \(\xi (R)= \dfrac{\kappa }{2} \int _{0}^{R}r\sigma qe^{\lambda /2}dr\) and \(Q = q(R)\) represents, the mass within the sphere, the mass equivalence of the electromagnetic energy of distribution and Q is the total charge inside the sphere as suggested in [39]. To do the matching properly, at the boundary surface \(r = R,\) we start by imposing the junction condition that the metric should be continuous [40]. Thus, by joining the interior metric function \(g_{rr}\) = \(e^{\lambda }\) and \(g_{tt}\) = \(e^\nu \) with the metric coefficient of the exterior Reissner–Nordstr\(\ddot{\text {o}}\)m spacetime given in (22), we obtain the following conditions by using the continuity

$$\begin{aligned} e^{\lambda }= & {} 1-\dfrac{2M}{R}+\dfrac{Q^{2}}{R^{2}},\quad \text {and}\quad y^{2}=1-\dfrac{2M}{R}+\dfrac{Q^{2}}{R^{2}},\end{aligned}$$
(24)
$$\begin{aligned} p(R)= & {} 0,\quad \text {and}\quad q(R)=Q. \end{aligned}$$
(25)

Now, using the conditions (24) and (25), we can fix the values of arbitrary constants. We being here, for some particular values of M and R, and the corresponding values of constant coefficients A, b and \(\beta \) are determined. We use three configurations of stellar bodies, i.e., SAX J1808.4-3658, 4U 1538-52 and Her X-1 of masses 0.87M(\( M_{\odot } \)), 0.85M(\( M_{\odot } \)), and 0.9M(\( M_{\odot } \)), respectively. Some possibilities of such types are tabulated in Table 4.

Table 1 Values of the model parameters \(K= 0.0032, C_1 = - 0.00099,\) \(\beta ^{2} = 1.006, b = 0.01, z_o = 0.02399, z_s = 0.01595\)
Full size table
Table 2 Values of the model parameters \( K = 0.0033, C_1 = -0.001, \) \(\beta ^{2} = 4.83, b = 0.05, z_o = 0.307064, z_s = 0.197225\)
Full size table
Table 3 Values of the model parameters \( K = 0.034, C_1 = -0.01, \) \(\beta ^{2} = 0.835, b = 0.09, z_o = 0.284819, z_s = 0.184272\)
Full size table
Fig. 2
figure 2

We have plotted different forces, namely, gravitational \((F_g)\), hydrostatic \((F_h)\) and electric forces \((F_e)\), respectively, to describe the equilibrium condition for charged fluid sphere. The result shows that gravitational force is dominated by hydrostatic and electric forces to maintain the equilibrium condition. We follow the same procedure for finding solutions as given in Fig. 1

Full size image

We will demonstrate here the interior and surface gravitational redshift \(z_s\) of these compact sources by using the definition \(z_s\) = \(\Delta \lambda /\lambda _{e}\) = \(\frac{\lambda _{0}-\lambda _{e}}{\lambda _{e}}\), where \(\lambda _{e}\) is the emitted wavelength at the surface of a nonrotating star and \(\lambda _{0}\) is the observed wavelength received at radial coordinate r. Thus, one of these quantities is defined according to

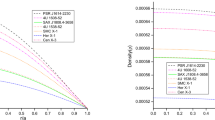
$$\begin{aligned} z_s = -1+\arrowvert g_{tt}(r) \arrowvert ^{-1/2} = -1+\left( 1-\frac{2M}{R}+\dfrac{Q^{2}}{R^{2}}\right) ^{-1/2}, \end{aligned}$$
(26)

where \(g_{tt}(r)\) = \(e^{\nu (R)}\) =\(\left( 1-\frac{2M}{R}+\dfrac{Q^{2}}{R^{2}}\right) \) is the metric function. Note that interior redshift should decrease with the increase of radius and less than the universal bounds, found when different energy conditions holds. In the isotropic case gravitational redshift for perfect fluid spheres is given by \(z_{s}<\) 2 [41, 42]. For an anisotropic star, this value admits higher redshifts, \(z_{s}\) = 3.84, as given in Refs. [43, 44], but in the presence of cosmological constant provides a significant increase up to \(z_{s} \le \) 5 [45], which is consistent with the bound \(z_{s} \le \) 5.211 obtained by Ivanov [46]. In Tables 1, 2 and3, we tabulated the calculated values of the center and surface redshift for the compact objects SAX J1808.4-3658, 4U 1538-52 and Her X-1 by taking the same values which we have used for graphical representation in Fig. 1.

4 Physical features and stability analysis of compact objects

To gain some insight into the electrically charged fluid stellar model, we perform some analytical calculations and study physical properties of the interior fluid sphere. The structure of charged spheres are analyzed by plotting several figures and studied equilibrium conditions under different forces. The obtained solution in this paper is used to study relativistic compact stellar objects within specified observational constraint.

4.1 Tolman–Oppenheimer–Volkoff (TOV) equations

To address the question, how gravitational and other different fluid forces counteract with increasing electrostatic repulsion when the pressure gradient tend to vanish towards the boundary and charged fluid becomes more diluted.This situation may be illustrated by considering the hydrostatic equilibrium under different forces. This can be easily achieved by adapting generalized Tolman–Oppenheimer–Volkoff (TOV) equation [47, 48] in the presence of charge, as prescribed by Ponce de Leon [49] is

$$\begin{aligned} -\frac{M_G(\rho +p)}{r^2}e^{\frac{\lambda -\nu }{2}}-\frac{dp}{dr}+ \sigma \frac{q}{r^2}e^{\frac{\lambda }{2}} =0, \end{aligned}$$
(27)

where \(M_G = M_G(r)\) is the effective gravitational mass inside a sphere of radius r and \(q = q(r)\) is given by (14). The expression for the effective gravitational mass is given by

$$\begin{aligned} M_G(r)=\frac{1}{2}r^2 \nu ^{\prime }e^{(\nu - \lambda )/2}. \end{aligned}$$
(28)

Now, plugging the value of \(M_G(r)\) in Eq. (27), we get

$$\begin{aligned} -\frac{\nu '}{2}(\rho +p)-\frac{dp}{dr}+\sigma \frac{q}{r^2}e^{\frac{\lambda }{2}} =0, \end{aligned}$$
(29)

As a result Eq. (29) gives the information about the stellar equilibrium configuration for charged relativistic fluid, subject to the gravitational \((F_g)\), hydrostatic \((F_h)\) and electric forces \((F_e)\), respectively, which leads to

$$\begin{aligned} F_g(r)= & {} -\frac{\nu '}{2}(\rho +p)=\dfrac{Z'}{8\pi Z}(\rho +p), \end{aligned}$$
(30)
$$\begin{aligned} F_h(r)= & {} -\frac{dp}{dr}\nonumber \\= & {} -\dfrac{1}{8\pi }\left[ {\dfrac{N}{(N1.N4)^{2}} -\dfrac{2\sqrt{Cx}}{K(1+Y^{2})^{2}}+M3.M4+M5.M6}\right] , \end{aligned}$$
(31)
$$\begin{aligned} F_e(r)= & {} \sigma \frac{q}{r^2}e^{\frac{\lambda }{2}}= \frac{1}{8\,\pi \,r^4}\,\frac{dq^2}{dr}\nonumber \\= & {} \dfrac{1}{16\pi } \left[ \dfrac{\sqrt{Cx}[\beta ^{2}(4-3K+x)-3b(1-K)]}{4(1-K)^{2}(1+Y^{2})^{7/4}}\nonumber \right. \\&\quad \left. +\dfrac{\beta ^{2}\sqrt{Cx}}{(1-K)(1+Y^{2})^{3/4}}\right] . \end{aligned}$$
(32)

We represent the profile of the hydrostatic equilibrium for compact star candidates SAX J1808.4-3658, 4U 1538-52 and Her X-1 in Fig. 2. Note that, the whole system is counterbalanced by the components of gravitational force \((F_g)\), hydrostatic force \((F_h)\) and electric force \((F_e)\) and the system attains a static equilibrium.

4.2 Stability analysis

Now, we are interested in analysing the speed of sound propagation \(v^2_s \), which is given by the expression \(v^2_s = dp/ d\rho \). In natural the velocity of sound is less than the velocity of light. Here one can consider the speed of light is \(c = 1\), so the sound speed is always less than unity. At this stage we investigate the sound speed for charged fluid matter, and for stable equilibrium configurations this should belongs to the interval \(0< v^{2}=\frac{dp}{d\rho } < 1\), as in Ref. [50] for a subliminal sound speed. We take Eqs. (20) and (21) for obtaining an explicit solution, which is

$$\begin{aligned} \dfrac{dp}{c^{2}d\rho }=\dfrac{\dfrac{N}{(N1.N4)^{2}} -\dfrac{2\sqrt{Cx}}{K(1+Y^{2})^{2}}+M3.M4+M5.M6}{\bigg (N7-N8-N9\bigg )}, \end{aligned}$$
(33)
Fig. 3
figure 3

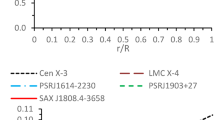
We have plotted the velocity of sound against r / R for the compact star candidates SAX J1808.4-3658, 4U 1538-52 and Her X-1 inside the stellar interior by employing the same values of the constants as mentioned in Fig. 1

Full size image

where we use for notational simplicity

$$\begin{aligned} N= & {} (N1.N4).M1.(N1.N2+N3)\\&\quad +M7\bigg [(N1.N2)\bigg (M8.N2+N1(M8+M9)\\&\quad +M10.M11+M12.M13\bigg )\\&\quad -(N1.N2+N3)(M14.N4+N1.M15)\bigg ],\\&\quad \text {with}\\ M1= & {} \dfrac{4\sqrt{Cx}}{K(1+Y^{2})^{2}},\\ M3= & {} \dfrac{\sqrt{Cx}(1-x)}{K(1+x)^{3}},\\ M4= & {} \bigg [K-1+\dfrac{2-3Y^{2}}{4(1+Y^{2})^{2}}+\dfrac{2\beta ^{2}(1+Y^{2})}{(Y^{2}\beta ^{2}+b)}\bigg ],\\ M5= & {} \dfrac{x}{2K(1+x)^{2}},\quad M6=\dfrac{5(K-1)\sqrt{Cx}}{2K(1+x)^{2}}\\&\quad -\dfrac{-2\beta ^{2}}{(Y^{2}\beta ^{2}+b)}\dfrac{2\sqrt{Cx}}{K(1-K)}\\&\quad -\dfrac{(1+Y^{2})}{K}\dfrac{4\sqrt{Cx}\beta ^{4}}{(1-K)(Y^{2}\beta ^{2}+b)^{2}},\\ M7= & {} \dfrac{Y^{2}}{K(1+Y^{2})},\\ M8= & {} \dfrac{\sqrt{Cx} [\beta ^{2}(4-3K+x)-3b(1-K)]}{4(1-K)^{2} (1+Y^{2})^{7/4}},\\ M9= & {} \dfrac{\beta ^{2}\sqrt{Cx}}{(1-K)(1+Y^{2})^{3/4}},\\ M10= & {} \dfrac{\sqrt{Cx}(K-2-x)}{4b(1-K)^{3/2}(K+x) ^{3/2}(1+Y^{2})^{3/4}},\\ M11= & {} 1+\cos 2\bigg (\arctan \bigg ( \dfrac{Y}{\sqrt{b}}\beta \bigg )\bigg ),\\ M12= & {} \dfrac{(1+Y^{2})^{1/4}}{2b(1-K)Y},\\ M13= & {} \dfrac{-4\sqrt{Cx} \beta }{b(1-K)+(K+x)\beta ^{2}}\sin 2\bigg (\arctan \bigg ( \dfrac{Y}{\sqrt{b}}\beta \bigg )\bigg ),\\ M14= & {} \dfrac{2\sqrt{Cx}}{(1-K)(1+Y^{2})^{3/4}}[1/4(Y^{2}\beta ^{2}+b) +\beta ^{2}(1+Y^{2})],\\ M15= & {} \dfrac{\sqrt{cx}}{2Yb(b(1-K)+(K+x)\beta ^{2})}\\&\quad \times \left[ 1+\cos 2\bigg (\arctan \bigg (\dfrac{Y}{\sqrt{b}} \beta \bigg )\bigg )\right] ,\\ N8= & {} M3.M4,\\ N9= & {} M5.M6, N7=\dfrac{2\sqrt{Cx}(1-K)(5+x)}{K(1+x)^{3}}. \end{aligned}$$
Fig. 4
figure 4

Curves are plotted for the NEC, WEC, and SEC for the compact objects SAX J1808.4-3658, 4U 1538-52 and Her X-1. For the purposes of this calculation, we use the same values as given in Fig. 1

Full size image
Fig. 5
figure 5

Behaviour of redshift and adiabatic constant vs. fractional radius r / R for SAX J1808.4-3658, 4U 1538-52 and Her X-1. For plotting we have employed data set values of physical parameters and constants which are the same as used in Fig. 1

Full size image

Due to complexity of the above expression we use graphical representation to represent it more conveniently. Using the expressions for all the terms in this formula, we have plotted Fig. 3. From Fig. 3, it is clear that the velocity of sound lies within the proposed interval and the speed of sound is less than the speed of light. Our investigation shows that our proposed model for charged perfect fluid star satisfies both energy and stability condition.

Table 4 The numerical values of the masses–radius (M / R) and surface density \((\rho _{S})\) for the compact star candidates
Full size table

4.3 Energy conditions

To clarify the question of whether the present model satisfies all the energy conditions within the framework of general relativity or not. Clearly, such configurations depend on the relationship between matter density and pressure obeying certain restrictions. In connection with that, energy conditions are essential tools to understand many theorems of classical general relativity -such as the singularity theorems of stellar collapse. Basic definitions are given for instance in [51, 52]. Among them, we will be particularly interested in the (i) Null energy condition (NEC), (ii) Weak energy condition (WEC) and (iii) Strong energy condition (SEC). Such conditions have the following inequalities

$$\begin{aligned} \rho (r)+p \ge 0, \end{aligned}$$
(34a)
$$\begin{aligned} \rho (r)+ \frac{q^2}{8 \pi r^4} \ge 0,\end{aligned}$$
(34b)
$$\begin{aligned} \rho +p+\frac{q^2}{4 \pi r^4} \ge 0, \end{aligned}$$
(34c)
$$\begin{aligned} \rho +3\,p +\frac{q^2}{4 \pi r^4}\ge 0. \end{aligned}$$
(34d)

Inequalities (34) hold automatically for the sources considered here. The weak energy condition imposes the requirement of a positive energy density as measured by a distant observer. Using this inequalities one can easily justify the nature of energy conditions for the specific stellar configuration as shown in Fig. 4, satisfying the energy conditions for our proposed model.

4.4 Relativistic adiabatic index and stability

So far we have considered stars in both hydrostatic equilibrium and speed of sound. But an important question that remains to be answered is whether these centenarians are enough for stable analysis. As another application is the adiabatic index. Using this one can incorporate all the basic characteristics of an equation of state on the instability formulae. In the case of an EOS of neutron star matter, the adiabatic index \(\gamma \), varies from 2 to 4 and for an anisotropic compact star will be stable if \(\gamma > 4/3\) [53]. For an adiabatic perturbation, the adiabatic index \(\gamma \), can be expressed in the form [54]

$$\begin{aligned} \gamma =\left( \left( \dfrac{c^{2}\rho +p}{p}\right) \left( \dfrac{dp}{c^{2}d\rho }\right) \right) > 4/3. \end{aligned}$$
(35)

Starting with Eqs. (20), (21) and (35), one can easily justify the adiabatic index and stable configuration for the specific stellar configuration SAX J1808.4-3658, 4U 1538-52 and Her X-1. A graphical analysis also provides the dependence of the average adiabatic index in Fig. 5, which is the requirement for a stable configuration. Finally, it should be noted that the adiabatic index which we consider in Eq. (35), is a local characteristic of a specific EOS and depends on interior fluid density. For further reference we refer our reader to follow [55].

5 Conclusion

The main point we wish to make is that a general solution of the Vaidya–Tikekar model for a spherically symmetric superdense star has been carried out, and it is found a physically valid solution. The sphere contains a charged perfect fluid matter and the exterior spacetime is represented by the Reissner–Nordstr\(\ddot{\text {o}}\)m metric. We also intend to study more closely the physical features of compact stars, generating an exact solution, and competed with number of specific astronomical objects. We summarize the obtained results for the stellar configuration as follows:

  1. 1.

    Regularity conditions The energy density and pressure are finite and positive inside the star. The central density \(\rho _{0}= \left( 3C(K-1)\right) /K > 0\) and central pressure \( p_{r}(r=0)>0\), which shows that the density and pressure are positive inside the star.

  2. 2.

    Generalized TOV equation We consider the generalized TOV equation for describing the equilibrium condition subject to gravitational (\(F_g\)), hydrostatic (\(F_h\)) and electric forces (\(F_e\)), respectively and we observe from Fig. 2, that gravitational force is balanced by the joint action of hydrostatic and electric forces to attain the required stability of the model. However, the effect of electric force is less than the hydrostatic force.

  3. 3.

    Causality condition In addition, we have shown that within the stellar object the speed of sound is less than the speed of light i.e. \(0< (dp/c^{2}d\rho )<1 \) for different values of \(0< K <1\) (see Tables 1, 2 and 3 for more detail results). However, one can see from Fig. 3 that the sound speed is increasing monotonically towards the surface of the star.

  4. 4.

    Energy conditions The configuration of the charged fluid sphere satisfies the null energy condition (NEC), weak energy condition (WEC) and strong energy condition (SEC), simultaneously inside the star as displayed in Fig. 4.

  5. 5.

    Surface Redshift We have also studied another impotent feature is the surface redshift of stellar structure. A general feature of the behavior is that it attend maximum value at the center and monotonically decreasing towards the boundary, which we can see from Fig. 5 (left panel). The numerical values corresponding to center and surface redshift for the SAX J1808.4-3658, 4U 1538-52 and Her X-1 are enlisted in Tables 1, 2 and 3.

  6. 6.

    Stability condition We have also considered the adiabatic index to gain some useful information in an extreme condition, and for stable configuration of compact objects. The variation of adiabatic index throughout the star is shown in Fig. 5 (right panel) and it is found the adiabatic index \(\gamma>\) 4/3 throughout the stellar interior. These are presented in the Tables 1, 2 and 3.

  7. 7.

    Mass–radius ratio As an another important aspect is the upper bound of mass-radius relation together with the Buchdahl limit for perfect fluid satisfying the inequality \(R\le \) (9/8) \(R_S\) = (9/4) G M/\(c^2\) [41]. For an electrically charged compact configuration, the Buchdahl limit is certainly increase. It has been found that Buchdahl limit for charged stars in [56,57,58]. In our case the obtained mass-radius ratio fall within the bounds as proposed for charged spheres (see Table 4 for more). In Tables 1, 2 and 3, where various symbols have been used \( CR^2=C_1, z_o=\) central redshift and

In conclusion, we will investigate other forms of metric potentials that could exhibit more general behavior and to make observationally distinguish between these compact objects.