1 Introduction

Resuspension of sediments has diverse consequences to the aquatic environment. One of these is the increased consumption of dissolved oxygen in the river water phase. A low oxygen concentration in river and estuarine systems is critical for fish populations (Thiel et al. 1995; Miller et al. 2002; Rong et al. 2016) as well as for the trophic interaction (Breitburg et al. 1997). The sediment oxygen demand (SOD) is defined as the rate of oxygen consumption, biologically or chemically, on or in the sediment at the bottom of a water body (Veenstra and Nolen 1991). This definition usually refers to the diffusion-controlled flux of oxygen into the sediment–water interface and to the fluxes of reduced compounds out of the sediment (Steinsberger et al. 2019). However, if sediment resuspension occurs, large amounts of oxygen-consuming compounds are suddenly released, and the rates of oxygen consumption are no longer controlled by diffusion. In this case, the SOD can be described as the sum of different processes controlled by the oxygen supply, the biochemical processes taking place and the properties of the resuspended sediments. In the case of a resuspension, the sediment thus shows its oxygen consumption potential (OCP). In the scientific literature, the SOD of sediments predominantly focusses on immobile sediments and thus excludes the OCP. Barcelona (1983) and Rong and Shan (2016) divided the SOD into chemical oxidation of reduced iron, manganese, and sulphur, and into biochemical oxidation of ammonium and nitrite to nitrate, in addition to the mineralisation of organic matter. In natural rivers, SOD can account for more than 50% of the total oxygen consumption (Rutherford et al. 1991; Matlock et al. 2003) besides respiration and the degradation of organic carbon in the water phase. Therefore, it is crucial to examine the total oxygen demand caused by sediments and to understand the share of involved processes.

In the upper part of the Elbe estuary with the Port of Hamburg and all its harbour basins, a strong decline in dissolved oxygen concentrations in the water phase is frequently observed during the summer months (Bergemann et al. 1996; Schroeder 1997; Schöl et al. 2014). In order to explain this decline in oxygen, previous studies have concentrated rather on the oxygen-consuming processes within the water phase than on the influence of the sediments. Thereby, this decline is mainly attributed to algal respiration and carbon degradation (Schroeder 1997) as well as zooplankton grazing (Schöl et al. 2014). Schroeder (1997) postulated that nitrification and sediment processes are of minor relevance, while Sanders et al. (2017) found a substantial amount of nitrification in the Hamburg area in spring and summer. Kerner (2000) also concluded that microbial oxygen consumption coupled with the degradation of freshly transported, organic material from the upper stream controls the oxygen concentration in the warmer seasons. However, the influence of the biogeochemical sediment composition on the oxygen consumption during a resuspension event within the Hamburg area is still unknown.

Various physical processes lead to sediment resuspension when the bottom shear stress is high enough to transport sediment particles into the water column (Almroth et al. 2009). This critical shear stress can be exceeded by natural forces such as tidal currents, wind, and biological activities (Sanford et al. 1991; Graf and Rosenberg 1997), or by human activities such as shipping and dredging (Cappuyns et al. 2006). For instance, sediment must be dredged regularly in port areas to keep the shipping channel navigable. For the Port of Hamburg, this amounts to 1.7 to 6 million tonnes of dry matter per year (2010–2018; Hamburg Port Authority, unpublished data).

To our knowledge, there are only a few studies that quantify the effect of such activities on the oxygen balance of water bodies, as, for example, the work of Bianucci et al. (2018) who investigated the influence of hurricane-induced sediment resuspension. Likewise, many numerical models that calculate biochemical processes within the water phase exclude the resuspension of sediments and its effect on oxygen and nutrient dynamics (Moriarty et al. 2018). To further address this gap, two sampling campaigns in the Hamburg Port were performed to investigate the spatial variability and temporal dynamics of sediments. This study aims to (i) derive the OCP of sediments from characteristic sediment parameters such as total organic carbon (TOC), total nitrogen (Ntotal), water content, or particle size distribution; (ii) quantify the SOD of resuspended sediments; and (iii) to analyse the physical and chemical properties of sediments in the upper Elbe estuary. The contribution of major oxygen-consuming processes to the overall OCP of these sediment samples was estimated in the laboratory. Based on the results, a model was developed that enables to predict the OCP of sediments from common characteristics to foster the transfer of our results to other applications. In summary, the aim of the study is to understand the individual sub-processes that lead to oxygen consumption during resuspension and to derive a simple prognosis model for future practical application. The particular research questions were:

  1. 1.

    Which biochemical processes control the OCP of sediments during a seven-day resuspension event?

  2. 2.

    What is the share of the main biochemical processes compared to the total OCP of sediments?

  3. 3.

    Which sediment properties control the OCP?

  4. 4.

    Can the OCP of sediments be predicted by using sediment parameters?

2 Material and Methods

2.1 Study Site and Sampling

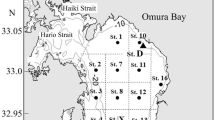
The upper Elbe estuary (Germany), characterised by fresh water from the middle Elbe, stretches from the weir Geesthacht (stream-km 586) 46 km downstream to Wedel (stream-km 541) and includes the large area of the Port of Hamburg. Between stream-km 609 and 626, the Elbe forms an inland delta with the Northern Elbe and the Southern Elbe as its major branches (Fig. 1). With the start of the trafficability for ocean vessels at about stream-km 619 (Southern Elbe) and stream-km 624 (Northern Elbe), the depth of the fairway and the harbour basins has been increased to 15 m.

Fig. 1
figure 1

source Germany map: https://d-maps.com)

Sampling locations within the upper Elbe estuary and the Port of Hamburg. Big black dots represent the sampling locations between stream-km (small dots) 589 (P1) and 643 (P21) for the analysis of the spatial variability. P10 refers to the access area of the Hansahafen for the analysis of the seasonal dynamic (

Full size image

Two sampling campaigns were carried out. The first campaign aimed at obtaining a large number of sediments with varying sediment properties regarding TOC, Ntotal, or particle size distribution. For this purpose, samples were taken at 21 locations in the Hamburg area between 2017-06-30 and 2017-07-04. The sites were located in the fairway, in the entrance area and end area of the different harbour basins, and in the upper stream. The second sampling campaign aimed to investigate the seasonal changes in sediment properties and their influence on the OCP. Sampling took place monthly at one location in the Port of Hamburg, from December 2016 to November 2018, except for August 2017 and July and October 2018, when no samples could be taken. This location is characterised by a sedimentation rate of up to 9 cm day−1 (HPA, unpublished data), which is among the highest in the area of Hamburg harbour. It is therefore assumed that the upper sediment layer reflects the current environmental conditions and their fluctuations.

Since dredging activities, e.g. water injection, frequently cause near-surface sediments as well as deeper sediments to be resuspended, one sample of a near-surface layer L1 (0–20 cm) and one sample of a deeper layer L2 (40–60 cm) were analysed. Sampling took place from a ship with a core sampler (Frahm-Lot, length 80 cm, inner diameter 10 cm). For correct sampling, we only used cores that contained at least 60 cm of sediment and some supernatant water. As a single core did not provide enough material per layer for the laboratory tests, the sediment sample was created from three parallel core samples that were about 1 to 10 m apart from each other. To prevent oxidation processes before analyses, the following precaution measures were performed: On the ship, material from the core samples was filled into airtight jars (1 L volume) immediately. In the laboratory, mixed samples were prepared from the parallel samples and the respective layers in a glove box under nitrogen atmosphere. This procedure was carried out for the first sampling campaign and the first eight sampling dates (until May 2017) of the second campaign. For the second sampling campaign, two replicates were carried out per sampling date, resulting in sample A and B. Later, a new core design was used that eliminated the need to fill samples into airtight vessels on the ship. The new cores consist of three segments, the top one with a height of 40 cm and the two lower segments, each with a height of 20 cm. These core segments made it possible to take samples out of the core first in the laboratory by disassembling the cores and taking the sample material from the individual core segments under a nitrogen atmosphere. Each homogenised sample was divided into two subsamples and stored in completely filled airtight jars at 4 °C until measurement started. The first subsample was used to determine the OCP, and the airtight jar was opened only for this purpose. The second subsample was used to extract the pore water and to determine the sediment solid parameters. Due to stronger consistency, at the locations 2, 6, 17, and 18 no samples could be taken from the lower layer.

2.2 Sediment Characterisation

The pore water was extracted through centrifugation at 2816 rcf (relative centrifugal force) for 30 min. Afterwards, it was vacuum filtered through a 0.45 µm cellulose acetate filter under a nitrogen atmosphere. Ammonium was measured photometrically (Photometer DR5000, Hach, USA) using the indophenol blue method (DIN 38,406–5) within three days after sampling. Sulphate, nitrate, and nitrite were analysed with an ion chromatograph (Metrohm, Germany) according to DIN EN ISO 10304-1. Dissolved iron and manganese were analysed with a flame atomic absorption system AA280FS (Agilent, USA) as given by DIN 38406-32 and DIN 38406-33.

For the analysis of solid parameters, mixed samples were dried at 105 °C and ground for analysis of carbon and nitrogen content. Total carbon (TC) and Ntotal were determined by dry combustion using a Vario MAX cube analyser (Elementar Analysensysteme GmbH, Germany) (DIN ISO 10694). Inorganic carbon (IC) was determined after acidification with 42.5% phosphoric acid according to Luther-Mosebach et al. (2018). TOC was obtained by difference between TC and IC. The grain size fraction < 20 µm was estimated by the sedimentation method (DIN ISO 11277). Gravimetric water content was determined by drying the sediment samples at 105 °C.

Chlorophyll concentrations were measured as an indicator for the biomass of algae. Therefore, 50 mL of the homogenised samples from the upper sediment layer (0–20 cm depth) were freeze-dried. The samples were extracted with 90% acetone, and the concentrations of chlorophyll-a and pheophytin-a were determined according to Lorenzen (1967). The chlorophyll value given in this study represents the sum of the chlorophyll-a concentration and its degradation product pheophytin-a.

2.3 Oxygen Consumption

The OCP of sediments during resuspension was measured with the respirometer BSB-digi O2 (Selutec, Germany) at 20 °C ± 0.5 °C. The respirometer measures the power consumption for electric oxygen production, which is necessary to compensate for the uptake of oxygen and thus the internal pressure in the chamber is kept constant. A vessel with 1 M sodium hydroxide solution placed in the chamber headspace absorbed the CO2 produced by the mineralisation and thus removed it from the air phase of the chamber. For further information, see Young et al. (1965), Montgomery (1967), and Young and Baumann (1976). Of the fresh sediment, 30 g were bottled (500 mL) under a nitrogen atmosphere to avoid oxidation processes and 200 mL of oxygen saturated, demineralised water were added. The suspension was stirred at 300 revolutions per minute. OCP was measured continuously for 168 h to identify the fast and slow biochemical processes involved in oxygen consumption. Data were recorded in 0.5-h intervals. Using the cumulative oxygen consumption curves, the oxygen consumption rate and the total OCP after 168 h were calculated. Three parallel measurements were taken per sample. However, some incubations failed during the experiments. Therefore, the indicated errors are the minimum and maximum of the measured values as given in the figures. All runs were made in the absence of light. Immediately after each experiment, the supernatant water was filtered and analysed for nutrient concentration. To determine the share of the mineralisation compared to the total consumption, the CO2 adsorbed in NaOH was quantified by titration with 0.1 M HCl solution and phenolphthalein as an indicator. The absorbed CO2 was calculated 1 to 1 into oxygen consumption. Parallel to the samples, blank values were measured with demineralised water, which were subtracted from the samples. For five samples (1 L1, 2 L1, 4 L1 and L2, and 8 L2) the CO2 formation could not be determined because the CO2 production exceeded the sorption capacity of the NaOH. For these samples, the proportion of the mineralisation was calculated using a fitting of the cumulative oxygen consumption curves for the period from hour 100 to hour 168. Based on our results, the oxygen consumption during this time period is characteristic of the mineralisation of organic material. By extrapolation of the fitting to the whole period of 168 h, the proportion of mineralisation in the total oxygen consumption was calculated.

In two additional sets of incubation experiments, the effect of ammonium on OCP was analysed. Therefore, one sediment sample (location 10, sampling 2018-06-22) was incubated with and without an addition of ammonium. Experiment A had an additional ammonium concentration in the suspension of 978 µmol L−1 and experiment B of 1,911 µmol L−1. Initially, the suspension was prepared with 250 mL of demineralised water of which 50 mL was sampled to determine the initial ammonium concentration. Per experiment, we measured six replicates with and six replicates without the addition of ammonium. After 24, 48, and 168 h, two incubations were stopped and the remaining ammonium concentration in the suspension was analysed. Due to a failure of the respirometer the last samples of experiment A were stopped after 138 h. However, in this experiment, the jar in which the sample was stored had to be opened several times during the period of both experiments. This allowed oxygen to enter, which led to different curves between the two tests and the samples without ammonium addition.

2.4 Calculation of Oxidation Reactions

The oxygen consumption was calculated stoichiometrically based on the change in concentration of the involved compounds in the pore water after sampling and after the incubation. The oxidation reactions are given in Eqs. (1–6) (mineralisation, nitrification in two steps, and the oxidation of iron, manganese, and hydrogen sulphide, respectively). Equation (6) stands for the oxygen consumption during the formation of sulphate. Because sulphur can be present in different compounds (FeS and FeS2, Schippers and Jorgensen 2001) and sulphate can be the product of different oxidation reactions, we assume that two moles of oxygen were consumed per mole of formed sulphate. The oxygen consumption due to the oxidation of other metals is neglected here, as we did expect only a very small contribution to the total oxygen demand.

$${\text{C}}_{6} {\text{H}}_{12} {\text{O}}_{6} + 6{\text{ O}}_{2} { } \to 6{\text{ CO}}_{2} + 6{\text{ H}}_{2} {\text{O}}$$
(1)
$${\text{NH}}_{4}^{ + } + 1.5{\text{ O}}_{2} { } \to {\text{NO}}_{2}^{ - } + {\text{ H}}_{2} {\text{O}} + 2{\text{ H}}^{ + }$$
(2)
$${\text{NO}}_{2}^{ - } + 0.5{\text{ O}}_{2} { } \to {\text{NO}}_{3}^{ - }$$
(3)
$${\text{2Fe}}^{2 + } + 0.5{\text{ O}}_{2} + 2{\text{ H}}_{2} {\text{O}} \to {\text{ Fe}}_{2} {\text{O}}_{3} + 4{\text{ H}}^{ + }$$
(4)
$${\text{Mn}}^{2 + } + 0.5{\text{ O}}_{2} + {\text{ H}}_{2} {\text{O}} \to {\text{ MnO}}_{2} + 2{\text{ H}}^{ + }$$
(5)
$${\text{MeS}} + { }2{\text{ O}}_{2} \to {\text{ SO}}_{4}^{2 - } + { }2{\text{ H}}^{ + }$$
(6)

Spearman correlation analyses were performed between the sediment parameter (TOC, Ntotal, TOC/Ntotal, Chlorophyll) and the measured and calculated OCP. The result is the Spearman correlation coefficient (rsp) was calculated using the software OriginLab (Pro) (Version 2019b).

2.5 Development of an Oxygen Consumption Model

In order to develop a model for the calculation of oxygen consumption we used the following approach: (i) The cumulative oxygen consumption curves of the samples from the spatial investigation were divided into three superposed processes with differing kinetics. These were the biochemical oxidation of reduced compounds, nitrification, and mineralisation. For each sample, these processes were fitted in a stepwise approach (see results section). (ii) The resulting function parameters of all samples were correlated with the sediment properties. This resulted in six linear or nonlinear regression equations between sediment properties and function parameters. Using the sediment properties, we were able to calculate the six parameters per sample, which allowed us to calculate the temporal dynamic of the three oxygen-consuming processes. For all samples the normalised root mean squared error (NRSME) between measured and modelled oxygen consumption was calculated. Here, the NRMSE was normalised by dividing the root mean squared error by the difference between the maximum and minimum observed values. (iii) To validate our model the samples from the second campaign were used. To quantify how well a model fits the data, the adjusted R2 (Adj. R2) was used. This differs from the normal R2 in that the Adj. R2 takes the number of predictors in the model into account. More information can be found on the homepage of the OriginLab (Pro) software (www.originlab.com).

3 Results

3.1 Characterisation of the Sediments

The samples from the spatial sampling campaign had a strong variability in their sediment composition (Table 1). Location 7 had the lowest TOC content with 0.2% d.wt. and location 4 the highest with 6.3% d.wt. TOC values showed a high positive correlation with the grain size fraction < 20 µm (rsp = 0.780; p < 0.01). A high variability was also found in the Ntotal content. The TOC/Ntotal ratio of all samples varied between 7.2 and 10 for the top layer and between 8.2 and 10.9 for the bottom layer. In general, the lower layers had higher TOC/Ntotal ratios than the upper ones. Chlorophyll was measured only for the upper layer and showed a strong variability among the different sites.

Table 1 Sediment properties for both campaigns
Full size table

The samples from the seasonal sampling campaign showed less variation in their composition. Here, the maximum values for TOC, Ntotal, chlorophyll, and the grain size fraction < 20 µm were found during the summer months concomitantly with the lowest TOC/Ntotal ratio.

3.2 Oxygen Consumption Potential

During the incubation of resuspended sediment samples for 168 h, the cumulative oxygen consumption curves and more noticeably the oxygen consumption rates reflect different phases of oxygen consumption (Fig. 2). All samples showed the highest oxygen consumption during the first hours and at least one sharp decrease in the oxygen consumption rate. Afterwards, the rate was often nearly constant for several hours before the rate dropped a second time. Figure 2a gives a typical example of the measured oxygen consumption (sample 6 L1). Here, after 16 h and 39% of the measured oxygen consumption, the first bend point was reached. After another 42 h with nearly constant oxygen consumption rate, the second decrease began. At this moment, 72% of the measured oxygen consumption has been measured. From 58 to 168 h the oxygen consumption rate was low and slightly further decreasing, forming a curved course of the cumulative consumption. This pattern applied to most of the measured oxygen consumption curves. However, some samples showed three decreases in the rates or even an increase in the rate after the first drop (Fig. 2b). After six hours (26% of OCP) the oxygen consumption rate decreased. The rate remained constant for a few hours and then increased. After 35 h (59% of OCP), the rate dropped again and remained almost constant for about 25 h, with a lower rate than in the previous phase. After 65 h (81% of OCP) the rate flattened for the third time.

Fig. 2
figure 2

Cumulative oxygen consumption (square) during a 168 h incubation period and the respective oxygen consumption rates (circle) for locations 6 L1 (a) and 13 L2 (b). The error bars indicate the standard deviation (n = 3)

Full size image

In order to determine the influence of nitrification on the oxygen consumption rate, two incubation experiments were carried out with different amounts of ammonium addition (Fig. 3). As expected from Eqs. (2) and (3), the samples with additional ammonium displayed (i) a higher oxygen consumption than preparations without additional ammonium and (ii) a later occurrence of the second decrease in the oxygen consumption curve. After the second decrease, no remaining ammonium was detected in the samples (Table 2). These results indicate that nitrification has a strong influence on the oxygen consumption and that the second phase in the consumption curve is controlled by nitrification.

Fig. 3
figure 3

Cumulative oxygen consumption during 168 h of incubation of samples with (dashed line) and without (dotted line) additional ammonium. a Additional ammonium concentration in suspension of 978 µmol L−1 and b additional ammonium concentration in suspension of 1911 µmol L−1

Full size image
Table 2 Ammonium concentrations in sediment suspensions from an experiment to determine the influence of ammonium on oxygen consumption
Full size table

3.3 Stoichiometric Analysis and Correlations

Based on the measured change in concentration of nitrate, sulphate, iron, manganese, and the formed CO2, the total oxygen consumption was calculated stoichiometrically according to Eqs. (1) to (6). The oxygen consumptions of the individual processes were summed up to compare the total with the measured oxygen consumption (Fig. 4). Between calculated and measured oxygen consumption, a high correlation exists (rsp = 0.960). There is no general trend in over- or underestimation of the calculated oxygen consumption.

Fig. 4
figure 4

Comparison of the stoichiometric calculation of the oxygen consumption (height of column) and the measured oxygen consumption (circle) for the two layers (L1 and L2) of the spatial sampling campaign. The samples were sorted according to their Ntotal content. The calculated consumption consists of the proportion of carbon dioxide formed (mineralisation), the sulphate formation, the nitrification, and iron and manganese oxidation. + the proportion of mineralisation in the total consumption was calculated. Numbers in brackets indicate the sample, and numbers without brackets indicate the Ntotal content (% d.wt.). The error bars display the min and max values for the replicates (n = 2 to 3)

Full size image

There is a high variability in oxygen consumption with respect to the different processes. In most cases, the mineralisation had the highest proportion of oxygen consumption after 168 h. The oxygen consumption due to the formation of sulphate and nitrate varies between 5.3% and 57.6% and between 1.2% and 40.5%, respectively. However, this is very different according to the individual sites and layers. Dissolved iron and manganese oxidation showed only a very small contribution (< 0.5%) to the total oxygen consumption, which is due to their low concentration in the pore water. Therefore, the processes of sulphate formation, nitrification, and mineralisation are sufficient to describe the oxygen consumption.

Location 4 L1 shows the highest measured oxygen consumption after 168 h (0.967 mmol O2 g d.wt.−1) with the largest influence of mineralisation, high rates of nitrification, and minor rates of sulphur oxidation. This is the sample with the highest content of TOC (6.3% d.wt.) and the lowest TOC/Ntotal ratio (7.2). In contrast, location 7 L1 shows the lowest oxygen consumption (0.005 mmol O2 g d.wt.−1). Here, the TOC content is very low as well (0.2% d.wt.). This relationship corresponds to the results of the Spearman correlation analysis (Fig. 5). The total measured oxygen consumption correlates highly with TOC (rsp = 0.939), Ntotal (rsp = 0.946), and chlorophyll (rsp = 0.960). Also, chlorophyll and Ntotal are strongly correlated with each other (rsp = 0.923). The chlorophyll concentration varies between 1.7 µg g d.wt.−1 and 1100.9 µg g d.wt.−1. The locations with the four highest OCPs also show the four highest sediment chlorophyll concentrations.

Fig. 5
figure 5

Above the diagonal: Scatter plots for the measured and calculated oxygen consumption and the sediment composition of the spatial analysis. Below the diagonal: Results of a Spearman correlation analysis between the measured (O2 meas.) and calculated (O2 calc.) oxygen consumption, the sediment composition, and the chlorophyll concentration (Chl.). All parameters tested are significantly correlated with each other (p < 0.05)

Full size image

3.4 Development of an Oxygen Consumption Model

Within the studied time frame of 168 h after resuspension, three sub-processes can describe the cumulative oxygen consumption of sediments during resuspension. Sub-process 1 comprises the rapid chemical and microbial oxidation of dissolved iron, manganese, and hydrogen sulphide as well as solid sulphur compounds such as iron monosulphides, elemental sulphur, or pyrite. The second sub-process reflects the nitrification of ammonium to nitrate via nitrite. The third sub-process is the mineralisation of organic matter. As supported by the analysed course of oxygen consumption, we can describe sub-processes 1 and 3 by a first-order exponential degradation function. And, as visualised in Fig. 2, nitrification can be described by a constant rate (zero-order kinetic) and a given time period.

Based on these considerations, the model development started with an adaptation of the corresponding functions to the measured OCP curves. This was done in three steps:

  1. a.

    For every sample \(i\) the data of cumulative oxygen consumption after the second drop in rate were fitted with an exponential degradation function (Eq. 7), resulting in the parameters \(A_{i}\) and \(t_{i}\). The resulting function was differentiated (Eq. 8) to result in \(A_{i}^{*}\). The constants \(A_{i}^{*}\) and \(t_{i}\) were regarded to describe the kinetics of mineralisation of every sample for the whole studied period (168 h). From the measured oxygen consumption rates, the calculated fitted mineralisation was subtracted.

    $$y_{{i;{\text{min}}}} = y_{{0i;{\text{min}}}} + A_{i} *e^{{\left( {\frac{ - x}{{t_{i} }}} \right)}}$$
    (7)
    $$r_{{i;{\text{min}}}} = A_{i}^{*} *e^{{\left( {\frac{ - x}{{t_{i} }}} \right)}}$$
    (8)
    $$A_{i}^{*} = A_{i} *\left( {\frac{ - 1}{{t_{i} }}} \right)$$
    (9)

    where \(y_{{i;{\text{min}}}}\) = calculated cumulative mineralisation of sample \(i\) at time \(x\) (mmol O2 g d.wt.−1), \(y_{{0i;{\text{min}}}}\) = offset of sample \(i\) (mmol O2 g d.wt.−1), \(r_{{i;{\text{min}}}}\) = calculated rate of mineralisation of sample \(i\) at time \(x\) (mmol O2 g d.wt.−1 h−1), \(A_{i}\) = amplitude of sample \(i\) (mmol O2 g d.wt.−1), \(A_{i}^{*}\) = amplitude of sample \(i\) (mmol O2 g d.wt.−1 h−1), \(x\) = time (h), \(t_{i}\) = degradation rate constant (h−1).

  2. b.

    For each sample, the remaining curves of the oxygen consumption rates were analysed for the mean rate of nitrification. Based on Eq. (10) the oxygen consumption due to nitrification was calculated. For the period from 0 to \(D_{i}\) the resulting nitrification rate \(R_{i}\) (mmol O2 g d.wt−1 h−1) was again subtracted from the remaining measuring values.

    $$r_{{i;{\text{nit}}}} = R_{i} *D_{i}$$
    (10)

    where \(r_{{i;{\text{nit}}}}\) = calculated cumulative nitrification of sample \(i\) at time \(x\) (mmol O2 g d.wt.−1), \(R_{i}\) = calculated rate of nitrification of sample \(i\) at time \(x\) (mmol O2 g d.wt.−1 h−1), \(D_{i}\) = calculated duration of nitrification of sample \(i\) (h).

  3. c.

    Finally, the remaining cumulative oxygen consumption curve was handled as in step a. An exponential degradation function (Eq. 11) was fitted to the data, resulting in the parameters \(B_{i}\), \(s_{i}\), and \(B_{i}^{*}\), which were regarded as a description of the fast chemical oxidation processes.

    $$y_{{i;{\text{chem}}}} = y_{{0i;{\text{chem}}}} + B_{i} *e^{{\left( {\frac{ - x}{{s_{i} }}} \right)}}$$
    (11)
    $$r_{{i;{\text{chem}}}} = B_{i}^{*} *e^{{\left( {\frac{ - x}{{s_{i} }}} \right)}}$$
    (12)

    where \(r_{{i;{\text{chem}}}}\) = calculated rate of fast chemical oxidation of sample \(i\) at time \(x\) (mmol O2 g d.wt.−1 h−1), \(y_{{0i;{\text{chem}}}}\) = offset of sample \(i\) (mmol O2 g d.wt.−1), \(B_{i}\) = amplitude of sample \(i\) (mmol O2 g d.wt.−1), \(B_{i}^{*}\) = amplitude of sample \(i\) (mmol O2 g dw−1 h−1), \(s_{i}\) = chemical oxidation rate constant (h−1).

In total, with the curve-fitting process for each sample six independent fitting parameters were derived (\(B_{i}\), \(s_{i}\), \(R_{i}\), \(D_{i}\), \(A_{i}\), \(t_{i}\)), of which two were always necessary to quantify the kinetics of the three sub-processes. These fitting parameters were correlated to the sediment properties TOC, Ntotal, TOC/Ntotal ratio, particle fraction < 20 µm, and total chlorophyll. Five samples had to be excluded from the correlation analysis because they had either a high sand content (7 L1 and 18 L1), an outstanding chlorophyll content (2 L1 and 4 L1), or an irregular oxidation dynamic resulting in a negative \(t_{i}\) (19 L2).

The best correlations were observed for Ntotal and TOC (Table 3). The parameters \(A_{i}^{*}\) and \(B_{i}^{*}\) showed a rSp > 0.698 (p < 0.05) for TOC and Ntotal. The degradation rate constant \(t_{i}\) did not significantly correlate to the sediment properties but had a higher correlation with the parameter \(A_{i}\) (rsp > 0.606). The nitrification rate \(R_{i}\) and the pool of nitrification (\(R_{i} *D_{i}\)) significantly correlated to Ntotal and TOC. The duration \(D_{i}\), however, did not significantly correlate to the studied sediment properties.

Table 3 Results of a Spearman correlation analysis between the sediment properties (TOC and Ntotal) and the fitted functions parameters of the oxidation consumption model
Full size table

Univariate regression functions among the six model variables and the significantly correlating sediment properties were used to derive estimated variables (Table 4). For \(A^{*}\), \(R\),\(B^{*} ,\) and \(R*D\), linear regression was used with Ntotal as proxy, as it has a better correlation with the OCP than TOC. For the rate constant \(t\) and \(s\), linear regression was used with the estimated function parameters \(A_{e}\) and \(B_{e}\) as proxies, respectively (Table 4). The nitrification duration variable \(D_{i}\) was calculated from the pool \((R_{i} *D_{i}\)) and the rate. Based on the derived regression functions and known sediment properties, the corresponding function parameters can be calculated and thus also estimate the oxygen consumption for each step in time.

Table 4 Estimated function parameters and the linear and nonlinear functions fitted to the correlation, their goodness of fit, and the variable used for correlation
Full size table

Figure 6 compares the measured cumulative oxygen consumption values with the estimated values according to the equations of Table 4 after 3, 24, and 168 h for all samples. These times were chosen because they reflect respective sub-processes (chemical oxidation [3 h], nitrification [24 h], and mineralisation [168 h]), as shown before. Linear regressions show a good fit with an Adj. R2 > 0.840 for all three periods. The slope varies between 1.152 (3 h) and 0.697 (168 h), which leads to a slight underestimation or overestimation of oxygen consumption by the model. This is particularly evident in the samples with a high chlorophyll content and an oxygen consumption > 0.8 mmol O2 g d.wt.−1, where the model strongly underestimates the consumption after 168 h.

Fig. 6
figure 6

Comparison between the measured oxygen consumption after 3 h (a), 24 h (b), and 168 h (c) and the calculated oxygen consumption for all samples of the data set “spatial analysis”

Full size image

In 28 of the 38 samples, the NRMSE is below 0.2 after 168 h and in 13 samples below 0.1 (Fig. 7). Among the three selected times, the 3 h-values showed the highest deviations between the model and the measured consumption, with a mean NRMSE of 0.17 ± 0.11 (sample 7 L1 excluded). For the sandy sample 7 L1 the oxygen consumption was strongly overestimated by the model and therefore showed the largest error (NRMSE > 0.5). The mean NRMSE after 24 h was 0.12 ± 0.11. In most cases the NRMSE was smaller than after 3 h. For those samples where this was not the case, the consumption rate due to nitrification or the duration was over- or underestimated by the model. After 168 h, the mean NRMSE was 0.14 ± 0.10.

Fig. 7
figure 7

Normalised root mean squared error (NRMSE) between the calculated and measured oxygen consumption curves from the spatial sampling campaign for the upper (L1) and lower (L2) layer. *no sample exists for the lower layer

Full size image

3.5 Validation of the Oxygen Consumption Model

The oxygen consumption curves of 82 samples from the temporal analysis campaign were used to validate the model. Oxygen consumption was calculated from Ntotal of the samples, and Fig. 8 compares the measured oxygen consumption with the calculated one. The results show a good fit for the summer samples (April to August). After 3 h and 24 h the summer samples show a lower scatter and a steeper slope (Fig. 8) compared to the winter samples (September to March), which show a slope of 0.488 after 3 h (Adj. R2 = 0.321) and a slope of 0.771 after 24 h (Adj. R2 = 0.497). After 168 h the winter samples show a steeper slope (0.920) but also a larger dispersion (Adj. R2 = 0.610). The fit improves with increasing resuspension time.

Fig. 8
figure 8

Comparison between the measured oxygen consumption after 3 h (a), 24 h (b), and 168 h (c) and the calculated oxygen consumption for all samples of the data set “temporal analysis”. The samples are divided into summer samples (April to August) and winter samples (September to March). The regression line refers to the summer samples

Full size image

Comparing the calculated NRMSE values for the year 2018 (Fig. 9), it is also evident that the model provides better predictions for the summer samples than for the winter samples. The NRMSE is higher for the winter samples and has a mean value of 0.27 ± 0.20 (3 h), 0.36 ± 0.24 (24 h), and 0.22 ± 0.09 (168 h). In the summer samples the average calculated error is 0.15 ± 0.06 (3 h), 0.10 ± 0.09 (24 h), and 0.09 ± 0.09 (168 h). The NRMSE values between summer and winter differ significantly (p < 0.01) for the 24 and 168 hourly values. The difference for the 3 h values is not significant at a significance level of p = 0.069.

Fig. 9
figure 9

Normalised root mean squared error (NRMSE) between the calculated and measured oxygen consumption curves from the temporal sampling campaign for the upper (L1) and lower (L2) layer. Letters A and B indicate the replicates

Full size image

The difference between summer and winter is also reflected in the measured oxygen consumption, where the sediments show the highest OCP between May and August (Fig. 10). Figure 10 shows that the assumptions made about the sub-processes can also be applied to the data set “temporal analysis”. For the year 2018 a high correlation exists (rsp = 0.967) between the calculated and measured oxygen consumption, and there is no general trend in over- or underestimation of the calculated oxygen consumption.

Fig. 10
figure 10

Comparison of the stoichiometric calculation of the oxygen consumption (height of column) and the measured oxygen consumption (circle) for the temporal analysis. Shown are the respective replicates (A and B) for the upper layer. The calculated consumption consists of the proportion of carbon dioxide formed (mineralisation), the sulphate formation, the nitrification, and iron and manganese oxidation. + the proportion of mineralisation in the total consumption was calculated. The error bars display the min and max values for the replicates (n = 2 to 3)

Full size image

For the data set “temporal analysis” the measured and calculated oxygen consumption and the sediment properties are correlated significantly with each other (p < 0.05) with one exception between TOC and TOC/Ntotal ratio (p = 0.07) (Fig. 11). Chlorophyll shows the highest correlation with the measured oxygen consumption. TOC (rsp = 0.752) and Ntotal (rsp = 0.839) correlate highly with the OCP even though the data of the temporal analysis show a larger scattering compared to the spatial analysis. Additionally, at the temporal analysis, Ntotal shows a higher correlation to the OCP than TOC.

Fig. 11
figure 11

Above the diagonal: Scatter plots for the measured and calculated oxygen consumption and the sediment composition of the temporal analysis. Below the diagonal: Results of a Spearman correlation analysis between the measured (O2 meas.) and calculated (O2 calc.) oxygen consumption, the sediment composition, and the chlorophyll concentration (Chl.). All parameters tested are significantly correlated (p < 0.05) with each other with one exception: The correlation between the TOC and the TOC/Ntotal ratio (p = 0.07)

Full size image

4 Discussion

Two sampling campaigns were carried out in the Hamburg Port Area to investigate the factors influencing the OCP of Elbe sediments and the biogeochemical processes that contribute to oxygen consumption. To control potential storage effects, we measured OCP of some samples repeatedly and found not significant temporal change in OCP. Thus, we concluded that our results can be extrapolated to the in situ situation.

The OCP of sediments in the Hamburg area of the river Elbe shows a high correlation to the sediment parameter Ntotal, TOC, and the chlorophyll content and is attributable to three main processes: sulphate formation, nitrification, and the mineralisation of organic matter. These processes differ in their kinetics and available substrate pools. Upon depletion of the respective substrates, sulphate formation and nitrification eventually cease, and a distinct decrease in the oxygen consumption rate is observed. By contrast, the aerobic degradation of organic matter is a still ongoing process at the end of the measurement period of seven days. Using this knowledge, a prognosis model was developed that can be used to calculate the oxygen consumption potential of Hamburg port sediments.

4.1 Sediment Composition

The sediment composition is substantially more variable spatially than temporally. The structure of the upper estuary with shallow waters and the deep fairway, harbour basins, and channels results in different flow velocities and sedimentation rates. This corresponds to the varying properties of the sediments at the respective locations with regard to grain size composition, TOC, and origin of the particulate matter. Tidal influence is known to transport marine particles into the upper estuary up to approximately stream-km 620 (Weilbeer 2014; Reese et al. 2019). The smaller variability within the sediment composition from the data set “temporal analysis” can be attributed to the fact that the samples were taken from one single site. Here the sediment properties are controlled only by seasonal parameters such as temperature, organic matter input, and flow velocities, which had a smaller impact on the variation than the spatial parameters (Table 1).

4.2 OCP and Stoichiometric Analysis

Sediment resuspension results in an increased release of nutrients into the water phase (Kristensen et al. 1992; Wainright and Hopkinson 1997; Gibson et al. 2015). Even thin sediment layers in the range from a few mm to cm are sufficient to affect the water column substantially (Tengberg et al. 2003; Blackburn 1997). This frequently leads to an increased oxygen consumption in the water column, due to the oxidation of reduced inorganic and organic products from anaerobic processes in the sediment (Sloth et al. 1996; Almroth et al. 2009).

Due to the release of these products, the oxygen consumption during resuspension is subject to various processes (chemical and microbial oxidation, nitrification, and carbon mineralisation of organic matter). These processes vary in their reaction rates and in their influence on oxygen consumption, depending on the concentration of the educts. The cumulative oxygen consumption curves and rates (Fig. 2) clearly show that the rates decrease at distinct times. These decreases are explained by the depletion of the respective oxidation substrates. Therefore, the OCP can be divided into three phases, whereby these phases are dominated by different processes.

The first phase includes the chemical and microbial oxidation of dissolved iron and manganese and reduced sulphur compounds. Due to the experimental design, we cannot distinguish between spontaneous chemical oxidation and oxidation by microbes of the respective educts. Barcelona (1983) showed in his 24 h experiments that more than half of the SOD took place in the first half hour and attributed this to chemical oxidation processes. The oxidation of reduced sulphur compounds such as pyrite (FeS2), iron sulphide (FeS), and hydrogen sulphide (H2S) is subject to different reaction rates. Richards et al. (2018) estimated oxidation rates for acid-volatile sulphide (AVS) between 8 and 21 mmol S kg−1 d−1, which are three orders of magnitudes higher than those for hydrogen sulphide (6 to 26 µmol S kg−1 d−1). Morse (1991) concluded from his experiments that the oxidation of pyrite is characterised by a daily to monthly time scale, whereby the rates depend on the particle size so that smaller particles are oxidised faster. Sulphate formation is therefore a process that can have a high influence on the measured oxygen consumption, both within the first hours and over a longer term. Although the sulphate release may take place over a longer period of time, the results show that the second flattening of the cumulative oxygen curve is initiated by the end of nitrification and that sulphate formation and chemical oxidation no longer dominate. Therefore, the first phase can be attributed to the chemical oxidation of dissolved iron and manganese and the oxidation of reactive sulphur compounds.

As shown in Fig. 3, the second phase is characterised by nitrification, with the required ammonium coming in equal parts from the pore water, the loosely bound fraction, and the tightly bound fraction (Morin and Morse 1999). Some samples showed three decreases in the oxygen consumption rates (Fig. 2b). One explanation for this could be the coupled process of nitrification. According to Ossenbruggen et al. (1996) and Brouwer et al. (1998) this so-called double tailing occurs when stage two of nitrification (conversion of nitrite to nitrate) is slower than stage one of nitrification (conversion of ammonium to nitrite). The increase in the rate after the first drop can be attributed to bacterial growth and thus to a higher conversion rate (Wainright 1987; Sloth et al. 1996). Oxygen consumption by nitrification therefore depends not only on ammonium concentration but also on the activity and density of microorganisms.

The third phase is dominated by the mineralisation of organic substances. The mineralisation rate is determined by the composition and degradability of the organic matter. Fresh algal biomass shows a higher degradability than older, recalcitrant biomass (Arndt et al. 2013) that often has a terrestrial origin. Therefore, this algal biomass is remineralised at higher rates and can enhance the oxygen consumption more than sediments with only refractory organic matter. This relationship is highlighted by the high correlations between the sediment chlorophyll concentration and the oxygen consumption. The third phase shows the lowest consumption rate but has the highest consumption potential in relation to a long-term resuspension due to the storage of TOC. Therefore, the relative effect of carbon mineralisation on the oxygen consumption is lowest at the beginning and increases with time.

The high correlation between Ntotal and chlorophyll can be explained by the accumulation of dead algal biomass that contains chlorophyll and labile, organic N-compounds. As a result, the sediment chlorophyll content is a suitable proxy for the enrichment of the sediment with organic N- and C- compounds by fresh algal biomass. This is also reflected in TOC/Ntotal ratios that are close to the theoretical C: N ratio of fresh plankton biomass of 6.6 in high chlorophyll sediment (Redfield 1934; Meyers 1994).

The aim of the model development was to enable the prognosis of oxygen consumption of resuspended sediments based on easily available sediment properties. The chlorophyll content showed the strongest correlation to the OCP, but it is not a typical parameter that is determined by standard methods. Therefore, this parameter was excluded from the search for proxies. Within the available standard properties, Ntotal showed the strongest relation to the 168 h oxygen consumption and to the chlorophyll content. The correlation between TOC and Ntotal and oxygen consumption differed only slightly in the spatial analysis. In the temporal analysis, however, Ntotal showed a higher correlation with the OCP than TOC.

In the comparison of the calculated and measured oxygen consumption, the model was able to predict the oxygen consumption reasonably well. The deviations show in most cases a NRMSE less than 0.2. However, in some samples the oxygen consumption was substantially over- or underestimated. This can have various origins. The functional parameters for the calculation of the mineralisation were adjusted based on the last phase of the cumulative oxygen consumption curve. In some cases, the consumption rate did not decrease consistently due to mineralisation. This can be explained by the composition of the organic matter. If the organic matter consists of a fast (fresh) and a slow (recalcitrant) degradable fraction, the rate may decrease during mineralisation when the fast degradable fraction is depleted. Likewise, nitrogen tailing and bacterial growth are not included as parameters in the model, although their inclusion may lead to an improved estimation. The model was calibrated using the samples from the spatial analysis, which were taken in summer. The calculation of the oxygen consumption curves based on the nitrogen contents from the temporal analysis showed the largest deviations in winter, when the overall OCP is lower. In summer, however, the consumption could be predicted with small deviations (NRMSE = 0.09). Seasonal processes, such as the type and composition of the microorganisms and their activity, the quality of the organic matter, and its TOC/Ntotal ratio, are not included in the model, which may be a reason for the larger deviation in winter months. If necessary, a calibration of the model with oxygen consumption curves from the winter months could improve the fitting. However, the model is well suited to assess the OCP of sediments under resuspension in the critical summer months with ecologically relevant high values. It must be taken into account that the tests were carried out under laboratory conditions, and the sediment was kept in suspension for 168 h. Therefore, further investigations are needed to determine the influence of resuspended sediments more precisely. This includes determining the resuspension time of suspended sediments under in situ conditions and how strong the difference is between the oxygen consumption of sediments before and during a resuspension event.

5 Conclusion

The sediments within the upper Elbe estuary show a strong spatial variability in their composition and OCP. This high variability makes it difficult to estimate the effects of resuspension on the oxygen balance and nutrient release, for example, due to maintenance measures such as water injection dredging. We have shown that the seven-day oxygen consumption is strongly dependent on the chlorophyll, Ntotal, and TOC content, so future studies should focus on these factors. The OCP can be described by sulphate formation, nitrification, and mineralisation, whereby these three processes show different reaction kinetics. The developed prognosis model calculates the oxygen consumption by using a single sediment parameter. The model shows the best adjustment in the months which are known for their critical oxygen supply. As the OCP of sediments can be calculated for any resuspension duration, the model can thus become a working tool when it comes to the question of whether or not maintenance measures can be carried out in the case of critical oxygen concentrations.