Abstract
We study the problem of scheduling container transport in synchromodal networks considering stochastic demand. In synchromodal networks, the transportation modes can be selected dynamically given the actual circumstances and performance is measured over the entire network and over time. We model this problem as a Markov Decision Process and propose a heuristic solution based on Approximate Dynamic Programming (ADP). Due to the multi-period nature of the problem, the one-step look-ahead perspective of the traditional approximate value-iteration approach can make the heuristic flounder and end in a local-optimum. To tackle this, we study the inclusion of Bayesian exploration using the Value of Perfect Information (VPI). In a series of numerical experiments, we show how VPI significantly improves a traditional ADP algorithm. Furthermore, we show how our proposed ADP–VPI combination achieves significant gains over common practice heuristics.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The interest of Logistic Service Providers (LSPs) in intermodal transport has increased due to its potential savings in cost (Kordnejad, 2014) and emissions (Craig et al., 2013) compared to road transport. However, economical and environmental benefits are not alone the precursors of a change from road to intermodal transport. The organization and synchronization of the various transportation services in an intermodal network can further ease or impede this change. Increasingly, LSPs are opting for cooperation and integration approaches among different processes for planning and controlling intermodal transport (SteadieSeifi et al., 2014). In this paper, we focus on one of those approaches: synchromodal transport.
In intermodal transport, mode choice decisions are made predominately by the shippers and transportation modes are booked in advance by the LSPs (Khakdaman et al., 2020). Synchromodal transport is a form of intermodal transport with so-called mode-free booking flexibility, which provides LSPs with network-wide real-time control to maximize the overall efficiency while satisfying agreed conditions such as time, costs, emissions, etc. (Riessen et al., 2015a). In synchromodal transport, any service (transportation mode with specific attributes such as schedule, duration, capacity, cost, etc.) and any transfer (change from one service to another in an intermodal terminal) can be used for any shipment (Riessen et al., 2015a). This increased flexibility allows LSPs to select, or to change, the next part of a shipment’s route as late as possible, with the possibility of including the latest information about the transportation network. As a result, there are more consolidation options throughout the network and throughout time than in traditional intermodal transport, making the optimization more challenging.
In this paper, we study the problem of scheduling containers in a synchromodal network with the objective of maximizing performance over a multi-period horizon. Containers are characterized by a destination, release-day and due-day. The number of containers that will arrive each period of the horizon and their characteristics are uncertain, but there is probabilistic information about their arrival (which may vary between periods of the horizon). On the supply side, we consider that all available services and transfers are fixed, but not necessarily the same for each period of the horizon. We consider that a single network-wise LSP decides over all services and transfers even if they are not its own. In general, the complexity of synchromodal transport lies in the relation between the possible decisions, and their effect on the performance over time. At any given period of the horizon (which we refer to as day in the remainder of this paper), there are three possibilities for scheduling the transport of containers. The scheduler can, for each possible combination of containers, either (i) transport them to their destination today, (ii) transport them to intermodal terminals using a service available today, or (iii) postpone their transportation to another day. Part of the impact of these scheduling options on the performance can be measured immediately (e.g., transportation costs, revenue, holding costs, CO\(_2\) emissions, capacity utilization). However, another part of their impact occurs on a posterior moment. For example, transporting a container to its destination today reduces the number of containers to be considered for consolidation in the future; transporting a container to an intermodal terminal defines the future services that can be used for transporting it; and postponing a shipment may reduce its feasible transportation options due to its time-window, or may saturate the network. The future impact of each scheduling option is dependent on posterior decisions, as well as the containers that will arrive in the future. It is therefore essential to estimate the impact of current scheduling decisions on the future performance, and to anticipate on it.
The objective of our investigation is threefold: (i) to model the scheduling of synchromodal transport as a stochastic optimization problem, (ii) to design a solution approach that handles the uncertainty and the time relations among parameters and variables in synchromodal scheduling, and (iii) to explore the use of our approach under various network configurations and demand patterns. Following our objective, the contribution of our work is threefold. First, we model the scheduling problem as a Markov Decision Process (MDP), which maximizes the expected reward over time. Second, we design an algorithm for the MDP model using the framework of Approximate Dynamic Programming (ADP) and incorporate Bayesian learning, through the concept Value of Perfect Information (VPI), to cope with the exploration versus exploitation tradeoff in ADP. Third, we characterize how traditional value-iteration based ADP designs can make the algorithm flounder and end in a local-optimum, and we analyze how VPI elements can help the algorithm to overcome those problems. More specifically, we describe, test, and show the benefits of various modifications to the VPI concept in ADP.
The remainder of this paper is organized as follows. We begin by examining the relevant literature about scheduling synchromodal transport in Sect. 2. We formulate an MDP model for our problem in Sect. 3. Subsequently, we present a common ADP approach to solve this MDP in Sect. 4. Next, we extend the ADP approach using the VPI concept in Sect. 5. In Sect. 6, we test our approach under different network settings and discuss the results. We finalize in Sect. 7 with our main conclusions and insights for further research.
2 Literature review
In this section, we review literature related to scheduling synchromodal transport. First, we perform a brief literature review specifically on scheduling problems in synchromodal transport. Since this literature is scarce, we subsequently focus our review on scheduling problems arising in dynamic and flexible inter/multi-modal transport. We briefly review the problem characteristics and proposed solutions of relevant intermodal transport studies, and identify their shortcomings with respect to synchromodality. For an in-depth review of the scheduling problems arising in intermodal transport, we refer the reader to Caris et al. (2013), SteadieSeifi et al. (2014), and del Mar Agamez-Arias and Moyano-Fuentes (2017). Third, we focus on literature using Approximate Dynamic Programming (ADP), a suitable approach for solving large-scale transportation problems with stochastic demand, and inspect its necessary changes when applied to our problem. We finalize this section with our contribution statement.
Scheduling problems in synchromodality deal with flexibility in mode choice and with decisions based on real-time information (SteadieSeifi et al., 2014). These characteristics require that there is coordination between multiple network actors and an overview of transportation supply and demand in the network for its scheduling (del Mar Agamez-Arias and Moyano-Fuentes, 2017), and that a balance between demand and supply is made every time new information becomes known (Riessen et al., 2015a). Most studies on scheduling synchromodal transport consider re-planning once new information becomes known without explicitly incorporating the effect of real-time information in advance. For example, Behdani et al. (2016) and Riessen etal. (2015b) determine the schedules of transportation modes and the assignment of containers to the various modes assuming deterministic demand. They take a reactive approach and assume that re-planning can be done by solving the model again once the new information becomes known. Studies that explicitly consider re-planning (e.g., due to new demand or disruptions), such as Zhang and Pel (2016) and Mes and Iacob (2016), have taken a more proactive approach towards re-planning but also do not explicitly anticipate on future real-time information. Similarly, Lemmens et al. Lemmens et al., (2019) propose a heuristic decision rule to support real-time switching between transport modes, and Larsen et al. (2020) propose a method to learn the ideal departure times of barges for real time co-planning between a barge and a truck operator. The same authors also propose a method for simultaneous and real-time planning of container transport and vehicle routes using model predictive control (Larsen et al., 2021). Guo et al. (2020) investigates a dynamic shipment matching problem using a rolling horizon approach to handle newly arrived shipment requests. Most closely related to our work in the area of synchromodal transport planning is the work of Yee et al. (2021), who explicitly includes future real-time information, also by modelling the problem as an MDP. Their model allows adaptations to the modal choice based on real-time travel time information. However, their focus is on stochastic travel times under known demand whereas we focus on consolidation opportunities of unknown demand.
Scheduling problems in intermodal transport that are closely related to synchromodal transport can be categorized into two groups: (i) those that include dynamic and flexible assignment of containers to services and (ii) those that include anticipatory decisions on information that becomes known over time. In the first group, problems fall under the intermodal scheduling family of Dynamic Service Network Design (DSND). In DSND methods, shipments are assigned to transportation services and modes in a network where at least one feature varies over time (SteadieSeifi et al., 2014). Graph theory and (integer) linear programming methods are commonly used to model DSND problems due to their time-space nature. However, these methods have limitations for large and complex time-evolving problems (Wieberneit, 2008), which are common to synchromodality (Riessen et al., 2015a). To tackle these limitations, decomposition algorithms (Ghane-Ezabadi and Vergara, 2016), receding horizons (Li et al., 2015), and model predictive control (Nabais et al., 2015), have been combined with DSND models in the literature. One disadvantage of combining these constructs with DSND models is that the relation between stochastic information and the decisions is harder to include. This may explain why the majority of DSND studies considers deterministic demand only (SteadieSeifi et al., 2014) although the need to incorporate uncertainty in demand has been recognized (Lium et al., 2009).
In the second group, most studies have been about extending DSND models with stochastic demand to anticipate on new information that becomes known over time. For example, Lium etal. (2009) and Crainic etal. (2014) have used scenario generation methods to create schedules that are robust to the various demand realizations. However, the resulting schedule does not adapt to new information dynamically as other methods do. Adapting dynamically means new schedules depend on the information that became know. Methods such as two-stage stochastic programming (Lo et al., 2013; Bai et al., 2014) and ADP (Dall’Orto et al., 2006; Pérez Rivera and Mes, 2015), which include re-planning with the new information that became known, have been shown to have benefits over static decisions. However, when considering synchromodal scheduling, some limitations arise. In two-stage stochastic programming, explicit probabilistic formulations and computational complexity limit the size of problem instances that can be solved. In ADP, the design and validation of the approximation algorithm is problem specific. Nevertheless, ADP might reduce the computational complexity while providing a close-to-optimal solution and has been shown to work well in the scheduling of intermodal transport (Pérez Rivera and Mes, 2016, 2017) and single-mode transportation problems (Simao et al., 2009; Ghiani et al., 2012; Ulmer et al., 2017; van Heeswijk et al., 2017). Although ADP seems to be an ideal candidate to fill the gap in the literature about anticipatory scheduling of synchromodal transport, our problem requires more than its mere application.
In transportation problems such as ours, the complexity of the network could make the application of ADP difficult (Powell et al., 2012). To begin with, the multi-period traveling times are a known issue to traditional ADP algorithms in transportation problems (Godfrey and Powell, 2002). Furthermore, when transportation services have multiple attributes (in our case, different capacities, durations, costs, revenues, beginning and ending locations), the design of the Value Function Approximation (VFA) and its learning-phase play a crucial role in ADP (Simao et al., 2009). In the design of the VFA, additional methods to the common post-decision state in ADP, such as aggregation of post-decision attributes (Bouzaiene-Ayari et al., 2016) and sampling (Goodson et al., 2016), may be necessary. In the learning phase of the VFA, a fundamental challenge that arises is the exploration versus exploitation problem (Powell, 2011). The problem consists on whether to let ADP make the best decision according to its current estimate of the VFA (exploit) or let it make a different decision that may lead to an improvement of the VFA (explore).
The exploration versus exploitation dilemma has been widely studied in the reinforcement learning (Sutton and Barto, 1998) and optimal learning communities (Powell and Ryzhov, 2012). The dilemma arises when a machine/agent tries to maximize its rewards by interacting with its environment through a series of actions. A widely studied optimization problem facing this dilemma is the so-called multi-armed bandit problem (Macready and Wolpert, 1998; Vermorel and Mohri, 2005). Two approaches that have been applied to this problem, and the exploration versus exploitation dilemma, are evolutionary algorithms (Črepinšek et al., 2013) and Bayesian learning methods (Macready and Wolpert, 1998; Strens, 2000). Bayesian learning methods usually rely on the concept of value of information (Dearden et al., 1999), which appears under different names, among which expected improvement and knowledge gradient (Ryzhov et al., 2019). Although many real-life problems can be modeled as multi-armed bandit problems or solved using evolutionary algorithms and Bayesian learning methods, there are several difficulties to translate these approaches to a transportation problem and to an ADP method as a solution approach. Among those difficulties we find the so-called “physical” state where decisions depend on the state of our physical resources, such as containers and barges, and the correlation of values of alternative decisions (e.g., economies of scale in adding more containers to a barge) (Ryzhov et al., 2019). These difficulties are incorporated by Ryzhov et al. (2019) assuming an infinite horizon, whereas our problem deals with a finite horizon. To the best of our knowledge, the application of Bayesian learning techniques within finite horizon ADP has not been studied before. Nevertheless, ADP can benefit from a translation of the knowledge on Bayesian learning to deal with the exploration versus exploitation dilemma (Powell, 2011; Ryzhov et al., 2019).
Overall, we observed in the literature that DSND models and methods provide a useful base for synchromodal scheduling with some additional work. We believe that our contribution to DSND methods and synchromodal scheduling has three focus points. First, we formulate an MDP model and design a solution method based on ADP that incorporates stochastic demand as well as the complex time and performance evolution of the transportation network. Second, we explore the use of new exploration strategies for ADP based on Bayesian exploration using the value of perfect information, and provide design and validation insights. Third, we compare our ADP designs against a benchmark heuristic, under different problem characteristics.
3 Markov decision process model
In this section, we formulate the problem of scheduling synchromodal transport as a Markov Decision Process (MDP). We begin by introducing the notation and all required input parameters (Sect. 3.1); a complete overview of the mathematical symbols used throughout this paper is provided in “Appendix A”. Subsequently, we formulate the elements of the MDP model: stages, states, decisions, transitions, and objective function (Sect. 3.2). Finally, we examine the relations between the various elements of our model and identify challenges that these relations bring for heuristic approaches to solve the model (Sect. 3.3).
3.1 Notation
We consider a finite horizon \({\mathcal {T}}\) of \(T^\text {max}\) days, i.e., \({\mathcal {T}}=\left\{ 0,1,2,\ldots ,T^\text {max}-1\right\} \). A finite-horizon formulation allows us to support decisions in the real-world for a given state, and include up-to-date information within our MDP regarding the finite period that lies ahead. For example, we may include information about the expected reduced capacity of inland vessels due to low water levels on some days within the horizon, or an increase in the number of containers from a given day onward due to the release of a vessel blocking the Suez Canal. On the contrary, an infinite horizon formulation requires stationary or cyclic information, e.g., the relatively lower intensity of container arrivals on a Monday. Hence, a finite horizon formulation makes it easier to use the MDP for re-planning purposes once the information changes, which is a key characteristic of synchromodality. To cope with the end-effects of a finite horizon problem, i.e., zero costs at the end of the horizon irrespective of the state of the system, we include a cost component depending on the containers left in the system at the end of the horizon (see Sect. 6.1). Although our approach can easily be used in a rolling-horizon fashion, we limit ourselves to finding a single decision policy to be used for the whole planning horizon. Note that, although we refer to a period in the horizon as a “day”, time can be discretized in any arbitrary interval as long as all time-dependent parameters are measured in that same interval.
The transportation network is represented by a time-dependent directed graph \(G_t=({\mathcal {N}}_t,{\mathcal {A}}_t)\), as it is usually done in DSND models. Nodes \({\mathcal {N}}_t\) denote locations where services begin or end, and arcs \({\mathcal {A}}_t\) denote the services running from one location to another. To ease the formulation, we categorize nodes into three types: (i) origin nodes \({\mathcal {N}}^\text {O}_t\), (ii) destination nodes \({\mathcal {N}}^\text {D}_t\), and (iii) intermodal terminal nodes \({\mathcal {N}}^\text {I}_t\), such that \({\mathcal {N}}_t={\mathcal {N}}^\text {O}_t\cup {\mathcal {N}}^\text {D}_t\cup {\mathcal {N}}^\text {I}_t\); and we index all nodes in \({\mathcal {N}}_t\) by i, j, and d. In this categorization, the sets of origin and destination nodes represent the possible starting and ending locations of a shipment, respectively, and are mutually exclusive with the set of intermodal terminals nodes. This separation of nodes applies to our model, but not necessarily to our problem. We further elaborate on this assumption, and how to overcome it, in “Appendix B”.
Each day t, new containers with different characteristics arrive to the network. Each container that arrives has a known origin \(i\in {\mathcal {N}}^\text {O}_t\), destination \(d\in {\mathcal {N}}^\text {D}_t\), release-day \(r\in {\mathcal {R}}_t\), and time-window \(k\in {\mathcal {K}}_t\). The release-day denotes the number of days in which a container will be released after its arrival. The set \({\mathcal {R}}_t=\left\{ 0,1,2,\ldots ,R^\text {max}_t\right\} \) ranges from immediate release to \(R^\text {max}_t\) days before release. The time-window denotes the number of days in which a container must be at its destination after it has been released. The set \({\mathcal {K}}_t=\left\{ 0,1,2,\ldots ,K^\text {max}_t\right\} \) ranges from the same day a container is released to \(K^\text {max}_t\) days after it is released. Although shipments are unknown before they arrive, there is probabilistic knowledge about their arrival in each origin \(i\in {\mathcal {N}}^\text {O}_t\). In between two consecutive days \(t-1\) and t, for origin \(i\in {\mathcal {N}}^\text {O}_t\), a total of \(f\in {\mathbb {N}}\) containers arrive with probability \(p^\text {F}_{f,i,t}\). A container that arrives between days \(t-1\) and t in origin \(i\in {\mathcal {N}}^\text {O}_t\) has destination \(d\in {\mathcal {N}}^\text {D}_t\) with probability \(p^\text {D}_{d,i,t}\), release-day \(r\in {\mathcal {R}}_t\) with probability \(p^\text {R}_{r,i,t}\), and time-window \(k\in {\mathcal {K}}_t\) with probability \(p^\text {K}_{k,i,t}\).
In a similar fashion to the categorization of nodes, we categorize arcs into three types: (i) arcs between an origin and an intermodal terminal node \({\mathcal {A}}^\text {O}_t=\{(i,j)|i\in {\mathcal {N}}^\text {O}_t\) and \(j\in {\mathcal {N}}^\text {I}_t\}\), (ii) arcs between two intermodal terminal nodes \({\mathcal {A}}^\text {I}_t=\{(i,j)|i,j\in {\mathcal {N}}^\text {I}_t\}\), and (iii) arcs between an origin or an intermodal node, and a destination \({\mathcal {A}}^\text {D}_t=\{(i,d)|i\in {\mathcal {N}}^\text {O}_t\cup {\mathcal {N}}^\text {I}_t\) and \(d\in {\mathcal {N}}^\text {D}_t\}\). For services beginning at an origin or ending at a destination (i.e., \({\mathcal {A}}^\text {O}_t\) and \({\mathcal {A}}^\text {D}_t\)), we assume there is unlimited capacity every day. In other words, we assume that the pre- and end-haulage operations of our synchromodal network are not restrictive. However, for each service between two intermodal terminals (i.e., \({\mathcal {A}}^\text {I}_t\)), we consider there is a maximum capacity of \(Q_{i,j,t}\) containers and a transportation duration of \(L^\text {A}_{i,j,t}\) days. In addition to the duration and capacity of each service, we consider that for each location \(i\in {\mathcal {N}}_t\), there is a transfer duration of \(L^\text {N}_{i,t}\) days, which includes all handling operations, and we assume unlimited handling capacity. Consequently, the total time required for the service between two intermodal terminal nodes is given by \(M_{i,j,t}=L^\text {N}_{i,t}+L^\text {A}_{i,j,t}+L^\text {N}_{j,t}\). Finally, we consider that between any two nodes, there is at most one arc (i.e., one service between two locations) and that all service durations are at least one (i.e., \(M_{i,j,t}\ge 1\forall (i,j)\in {\mathcal {A}}_t\)). Relaxations of these assumptions are given in “Appendix B”.
With respect to the objective, we define a generic reward function \(R_t(\cdot )\) to capture the immediate reward (i.e., reward at day t) of transporting a container in the network. Note that we use the common terminology of rewards to denote the profits given by the revenues received from transporting containers minus the transportation costs (both fixed costs for using certain services and variable costs per container). For each arc \((i,j)\in {\mathcal {A}}_t\), or service between i and j, we include three components in the reward function: (i) a revenue \(A_{i,j,d,t}\) per container with destination d, (ii) a setup cost \(B_{i,j,t}\) independent of the number of containers using the service, and (iii) a variable cost \(C_{i,j,d,t}\) per container with destination d. These components can also have a value of zero to model different financial conditions such as receiving the entire revenue of a shipment at the beginning of transportation (i.e., \(A_{i,j,d,t}=0\forall i\notin {\mathcal {N}}^\text {O}_t\)) or constant cost for reserved space in a service (i.e., \(B_{i,j,t}>0\) and \(C_{i,j,d,t}=0\) for the reserved service (i, j)).
3.2 Formulation
The stages at which decisions are made in our MDP model correspond to the days in the horizon, i.e., \(t\in {\mathcal {T}}\). The state of the system \(S_t\in {\mathcal {S}}\) is modeled as the vector of all containers, and their characteristics, that are present at each node and each arc of the network (i.e., containers available at a location or traveling to a location) at stage t. In the state vector, we denote containers at location \(i\in {\mathcal {N}}^\text {O}_t\cup {\mathcal {N}}^\text {I}_t\), that have destination \(d\in {\mathcal {N}}^\text {D}_t\), release-day \(r\in {\mathcal {R}}'_t\), and time-window \(k\in {\mathcal {K}}_t\) with the integer variable \(F_{i,d,r,k,t}\). Hence, the state is given by (1).
Note that we use a different set \({\mathcal {R}}'_t\) for the release-day r to model containers that are being transported to location i using \(F_{i,d,r,k,t}\) in a computationally efficient way. We define \({\mathcal {R}}'_t=\left\{ 0,1,2,\ldots ,\max {\left\{ R^\text {max}_t,\max _{(i,j)\in {\mathcal {A}}^\text {I}_t}{M_{i,j,t}}\right\} }\right\} \) and use a virtual time-window to model containers that are en route. For example, if a container is being transported to location i using a service that departs on Monday and arrives at i on Thursday, then this container will be modeled in the state of Tuesday as a container that will be available at i in two days, i.e., a container with release-day \(r=2\). Furthermore, if the container has a deadline of Friday, its time-window on Tuesday will be \(k=1\), i.e., one day after it arrives, or, in terms of our virtual time-windows, it is virtually released. So, on Tuesday, instead of modeling the container that is already released and being transported with \(r=0\) and \(k=3\), we model it with \(r=2\) and \(k=1\). We further elaborate on the use of virtual time-windows to capture the evolution of the network later on in this section.
At every stage, the planner decides which of the released containers (i.e., \(r=0\)) to transport using a given service and which ones to postpone. Remind that if the planner decides to transport a container, only the route to the first destination is fixed, which may be an intermodal terminal or its final destination. We model the decision with the vector \(x_t\) consisting of all containers that will be transported at stage t, as shown in (2a). We denote the number of containers that will be transported from location i to j, having destination \(d\in {\mathcal {N}}^\text {D}_t\) and time-window \(k\in {\mathcal {K}}_t\), with the integer variable \(x_{i,j,d,k,t}\). Naturally, the decision \(x_t\) is bounded by the feasible decision space \({\mathcal {X}}_t\) described by constraints (2b) to (2f).
Constraints (2b) ensure that, for every origin and intermodal terminal, only containers that are released can be transported. Constraints (2c) guarantee that containers whose time-window is as long as the duration of direct trucking are transported using this service. Note that with this constraint, we assume that trucking to a destination is faster than going via an intermodal terminal, i.e., \(L^A_{i,d,t}< \min _{j\in {\mathcal {N}}^\text {I}_t}{\left\{ M_{i,j,t}+L^A_{j,d,t}\right\} },\forall (i,d)\in {\mathcal {A}}^\text {D}_t\). Equation (2d) ensure that containers are not transported to a terminal j if the fastest “intermodal” route to their destination after arriving at that terminal (whose duration we denote with \({\widetilde{M}}_{j,d,t'}\), with \(t'=t+M_{i,j,t}\)) is longer than the corresponding time-window. This strict definition of transportation options means that two trucking services cannot be used sequentially. The value of \({\widetilde{M}}_{j,d,t'}\) is case dependent: (i) if a container is at an origin (i.e., \(i\in {\mathcal {N}}^\text {O}_t\)), then \({\widetilde{M}}_{j,d,t'}\) includes the duration of the shortest service from terminal j to terminal \(j'\) and the duration of trucking from \(j'\) to the destination d; (ii) if a container is at an intermodal terminal (i.e., \(i\in {\mathcal {N}}^\text {I}_t\)) then \({\widetilde{M}}_{j,d,t'}=M_{j,d,t}\) since the intermodal service \((i,j)\in {\mathcal {A}}^\text {I}_t\) already accounts for the intermodal part. Constraints (2e) ensure that the capacity of each service is not exceeded. Finally, constraints (2f) define the domains of the variables.
After making a decision \(x_{t-1}\) and before entering the state \(S_{t}\), exogenous information on new shipments arrives. We denote the number of new containers with origin \(i\in {\mathcal {N}}^\text {O}_t\), destination \(d\in {\mathcal {N}}^\text {D}_t\), release day \(r\in {\mathcal {R}}_t\), and time-window \(k\in {\mathcal {K}}_t\) that arrive in between two consecutive stages \(t-1\) and t with the integer variable \({\widetilde{F}}_{i,d,r,k,t}\). Hence, we model this exogenous information with the vector \(W_{t}\), as seen in (3).
The transition from state \(S_{t-1}\) to state \(S_t\) depends on (i) the decision \(x_{t-1}\), (ii) the exogenous information \(W_t\), and (iii) the various time relations involving shipments and services. We capture this transition using the function \(S^M\), as seen in (4). First, and most naturally, decisions shift containers from one location to another through time. However, this shift can take longer than one stage, i.e., when a service duration spans more than one day. To avoid remembering decisions of services spanning more than one day (i.e., earlier decisions than \(x_{t-1}\)), we use the virtual time-windows. As exemplified before, virtual time-windows increase the release-day and reduce the time-window of containers that are transported using a service with a duration longer than one day, i.e., \(M_{i,j,t}>1\). Second, the exogenous information increases the number of containers of a certain type that are present in the network. Third, various time relations apply to different types of containers. For example, released containers that are not transported remain at the same location and their time-window decreases. To capture all these relations, \(S^M\) categorizes container variables \(F_{i,d,r,k,t}\) into seven equations, as shown in (4b) to (4h).
Equation (4b) define containers that are released (i.e., \(r=0)\) at an origin (i.e, \(i\in {\mathcal {N}}^\text {O}_t\)), and with a time-window smaller than \(K^\text {max}_t\) (i.e., \(k+1\in {{\mathcal {K}}_t}\)), as the sum of two types of containers from the previous stage at that origin with the same destination: (i) containers with a time-window of one stage longer that were not transported (i.e., \(F_{i,d,0,k+1,t-1}-\sum _{j\in {\mathcal {A}}_t}{x_{t-1,i,j,d,k+1}}\)), and (ii) containers that had a release-day of one (i.e., \(F_{i,d,1,k,t-1}\)) meaning that they would be released at the current stage, in addition to the newly arriving containers in between the stages that had the same characteristics (i.e., \({\widetilde{F}}_{t,i,d,0,k}\)). Equation (4c) define containers that are released, at an origin, and have the maximum time-window as the sum of containers with a release-day of one and the newly arriving containers with the same characteristics. Equation (4d) define containers that are released, at an intermodal terminal, and with a time-window smaller than the maximum one, as the result of three types of containers from the previous stage at that terminal with the same destination: (i) containers with a time-window of one stage longer that were not transported, (ii) containers that had a release-day of one, and (iii) inbound containers from all locations j whose service duration was one period (i.e., \(M_{j,i,t}=1\)) and whose time-window was the service duration longer (i.e., a reduced time-window from \(k+M_{j,i,t}\) to k) at the moment of the decision \(x_{t-1}\) (i.e., \(\sum _{j\in {\mathcal {A}}_t|M_{j,i,t}=1}{x_{t-1,j,i,d,k+M_{j,i,t}}}\)). Equation (4e) define containers at an origin node that are still not released and do not have the maximum release-day, as the sum of two types of containers from the previous stage at that origin with the same destination and time-window: (i) containers with a release-day of one period longer and (ii) new arriving containers that had the same characteristics. Containers of the previous type that have the maximum release-day are the result of only the new arriving containers with the same characteristics, as shown in (4f). Equation (4g) define containers that are at an intermodal terminal and that are not released but do not have the maximum release-day, as the sum of two types of containers from the previous stage at that terminal: (i) containers with the same time-window and with a release-day of one period longer, and (ii) containers sent in the decision of the previous stage, from all other locations to that terminal, whose service duration equals the release-day plus one period and whose time-window was a service duration longer. Finally, containers at an intermodal terminal with the maximum release-day of the virtual time-windows are the result of inbound containers to that location following the virtual time-windows reasoning, as shown in (4h).
The immediate rewards of a decision \(R_t\left( x_t\right) \) resemble the profits as given by the revenues minus costs, see (5a). Remind that \(A_{i,j,d,t}\) and \(C_{i,j,d,t}\) are the revenue and variable cost of using service \((i,j)\in {\mathcal {A}}_t\) for one container with destination d, respectively, and that \(B_{i,j,t}\) is the setup cost for using the aforementioned service independent of the number of containers.
Since the decision \(x_t\) depends on the state, and the state is partially random, the objective is to find a policy that maximizes the expected discounted reward over the planning horizon. We denote a policy with \(\pi \in \varPi \), and define it as a function that determines a decision \(x_{t}^{\pi }\in {\mathcal {X}}_t\) for each possible state \(S_t\in {\mathcal {S}}\). Thus, the objective can be expressed as shown in (6), where \(\gamma _t\) is the discount factor balancing the impact of future and present rewards and \(S_0\) is the initial state of the system.
The optimal expected rewards can be estimated using a set of recursive equations and Bellman’s principle of optimality, as shown in (7). These equations can be solved backwards, from the end of the horizon towards the beginning. In (7a), the state \(S_{t+1}\) is partially random and partially the result of decision \(x_t\). Using the transition function \(S^M\), we can express \(S_{t+1}\) as a function of the current state, decision, and a realization of the exogenous information, as shown in (7b). Assuming that the possible realizations of the exogenous information \(\varOmega _{t+1}\) (i.e., \(W_{t+1}\in \varOmega _{t+1}\)) are finite, and defining \(p^{\varOmega _{t+1}}_\omega \) as the probability of realization \(\omega \in \varOmega _{t+1}\), we can recursively solve our MDP as shown in (7c). The solution to these last equations yield the optimal policy \(\pi ^*\). However, solving these equations is challenging for various reasons. In the following, we elaborate further on those solution challenges.
3.3 Solution challenges
As with most MDP models, ours suffers from the so-called three curses of dimensionality (Powell, 2011). Equation (7c) hold for the entire state space \({\mathcal {S}}\), decision space \({\mathcal {X}}_t\), and exogenous information space \(\varOmega _t\), which grow larger with an increasing size of the transportation network and demand parameters. Another challenge arises due to the interaction among the model’s reward function, transition function, and the finite horizon; and the need for heuristic/approximation solution methodologies. In the transportation industry, the revenue is usually received at a single point in time (e.g., at the pick-up or at the delivery) while the costs for the entire route are accrued in several points in time depending on the route. Although this is not an issue for the MDP model, it may result in strange behavior of heuristic approaches. When revenue is received at the pick-up, heuristics might prefer to pick up a container as soon as possible, to receive the revenue, and then take it to the closest location and leave it there in order to avoid costs. In the opposite case, when the revenue is received at the delivery, heuristics might prefer to take a container to its destination, as soon as possible, to receive the revenue, and avoid longer transportation options which might be cheaper. Consequently, the “greedy” nature of heuristics may lead to a poor performance in our finite horizon look-ahead model.
Although our MDP model brings various solution challenges, its components (e.g., transition function, decision constraints, exogenous information) can be used within the ADP framework to design a heuristic solution for them. We elaborate on this design, and how to overcome the challenges, in the following section.
4 Approximate dynamic programming solution
To solve the MDP model from the previous section, we use ADP. Here, the solution to the Bellman’s Equations in (7) is approximated using simulation, along with other optimization and statistical techniques, in an iterative manner. As the main contribution of this work relates to the inclusion of Bayesian learning in ADP to cope with the exploration versus exploitation tradeoff, we use the standard approximate value iteration form of ADP, see Powell (2011). In this section, we describe this traditional ADP design combined with the use of basis functions and \(\epsilon \)-greedy exploration, which has been used successfully for other intermodal transportation problems (Pérez Rivera and Mes, 2017).

The ADP algorithm consists of various parts of the MDP model, such as the state, decision, and transition function, as shown in Algorithm 1. The algorithm runs for a number of iterations N and hence has all its variables indexed with n, as shown in Line 2. The overall idea of ADP is to replace the expectation of future rewards in (7a) with an approximation \({\overline{V}}_t^n\) and to update this approximation over the iterations. At the end, the algorithm yields the approximation of the last iteration, for all stages, as shown in Line 15. Thus, the output of ADP is a policy, based on the approximation \(\left[ {\overline{V}}_t^N\right] _{\forall t\in {\mathcal {T}}}\) of the expected rewards, in a similar way to the MDP.
The approximation \({\overline{V}}_t^n\) is a function of the so-called post-decision state \(S_t^{x,n}\). The post-decision state is the state of the system after a decision has been made but before the new exogenous information becomes known and the next stage state is realized, i.e., \({{S}}_t^{n,x} = S^{M,x}\left( {{S}}_{t}^{n},{{x}}_{t}^{n}\right) \). The transition \(S^{M,x}\) to the post-decision state works in a similar way as the transition function \(S^M\), see (4), with the only difference that no exogenous information is considered, i.e., all \({\widetilde{F}}_{i,d,r,k,t}\) variables are omitted in (4b) to (4h). To update the approximation \({\overline{V}}_t^n\), the algorithm simulates the use of its resulting policy for all stages. In contrast to backwards dynamic programming, ADP moves forward in the stages, as shown in Line 4. In each stage, the optimality equations in (7) are transformed into one single equation (using \({\overline{V}}_t^n\)), as shown in Line 7. Furthermore, the decision that attains the maximum reward \({\widehat{v}}_t^n\), as well as its corresponding post-decision state, are stored as shown in Lines 5 and 6. To advance to the next stage \(t+1\), the algorithm uses a sample from \(\varOmega _{t+1}\), obtained through a Monte Carlo simulation, and the transition function \(S^M\) defined in (4), as shown in Line 8. After all stages are processed, a function \(U^n_{t-1}\) is used to update the approximation in a backward manner, as seen in Lines 11 to 13. This function uses the information stored throughout the stages. The entire procedure is repeated N times.
The benefit of having the approximation \({\overline{V}}_t^n\) in ADP is two-fold. First, it avoids enumerating all possible realizations of the exogenous information \(\varOmega _{t}\). Second, it allows the optimality equation in Line 7 to be solved for one state at a time. These two benefits eliminate two of the curses of dimensionality. However, the large decision space must be tackled separately. For this, we propose the use of a restricted decision space \({\mathcal {X}}_t^\text {R}\) by adding more constraints to the feasible decision space \({\mathcal {X}}_t\) described by constraints (2b) to (2f). The restricted decision space as defined in (8), works with four additional constraints to the feasible decision space. First, containers that are not urgent (i.e., \(k>L^A_{i,d,t}\)) cannot use direct trucking to their destination (8b). Second, all containers of the same type, i.e., having the same location, destination, and time-window, must be transported together (8c and 8d). To achieve this, we use the binary variable \(x_{i,j,d,k,t}^{\text {R}}\), which gets a value of 1 if containers at location i with destination d and time-window k are sent using service \((i,j)\in {\mathcal {A}}^\text {I}_t\) and 0 otherwise, and the binary parameter \(M_{i,j,d,k,t}^\text {R}\), which gets a value of 1 if the fastest intermodal route for containers at location i with destination d and time-window k, going through terminal j, is longer than the container’s time-window (i.e., \(k<M_{i,j,t}+{\widetilde{M}}_{j,d,t'}\)). Third, we consider that all containers that arrive at an origin and have the same destination must be either transported to the same intermodal terminal or postponed (8e). To achieve this, we use the binary variable \(x_{j,d,t}^{\text {R}}\), which gets a value of 1 if the intermodal terminal j is chosen for containers with destination d and 0 otherwise. Naturally, we assume with this last restriction that there is at least one terminal to which containers from all origins can be brought to. Note that, if computational resources allow, the restrictions on the policy can be omitted.
For the approximation \({\overline{V}}_t^n(S_t^{x,n})\), we make use of basis functions. The overall idea of basis functions is to quantify characteristics of a post-decision state that explain the expected future rewards to a certain degree. We denote the basis function of a characteristic \(b\in {\mathcal {B}}_t\) with \(\phi _{b,t}:S^{x,n}_{t}\rightarrow {\mathbb {R}}\) and the degree (i.e., weight) with which it explains the future rewards by \(\theta ^n_{b,t}\in {\mathbb {R}}\). We introduce the vectors \(\phi _t\left( S^{x,n}_{t}\right) \) and \(\theta ^{n}_{t}\) containing the basis functions and weights for all \(b\in {\mathcal {B}}\), respectively. The approximated future rewards are the result of the product between all basis functions and their weights, as shown in (9).
At each stage t, the set of characteristics \({\mathcal {B}}_t\) counts two types of containers per location-destination pair: (i) containers whose time-window is shorter than the duration of the shortest intermodal path of the entire network, which we denote as \(\psi \), as shown in (10a), and (ii) containers whose time-window is at least the duration of the shortest intermodal path of the entire network, as shown in (10b). Furthermore, we also count the total number of containers going to each destination, independent of their current location, release-day, or time-window, as shown in (10c). Finally, we add a constant as shown in (10d). We have a total number of characteristics \(\left| {\mathcal {B}}_t\right| =2\left( \left| {\mathcal {N}}^\text {O}_t\right| +\left| {\mathcal {N}}^\text {I}_t\right| \right) \times \left| {\mathcal {N}}^\text {D}_t\right| +\left| {\mathcal {N}}^\text {D}_t\right| +1\). To index them, we use the functions b, \(b''\), and \(b'''\), with range \([1,\ldots ,\left| {\mathcal {B}}_t\right| ]\).
The weights \(\theta ^{n}_{b,t}\) depend on iteration n and stage t. The idea is that, throughout the iterations, the observed rewards for each stage can be used to update the weights, and thus the approximation \({\overline{V}}_t^n(S_t^{x,n})\). For the updating function \(U^n_{t-1}\), we use recursive least squares for non-stationary data, see Powell (2011).
The ADP design presented before uses the so-called exploitation decision strategy. Exploitation decisions are those that take us to the best post-decision state given our estimate of the downstream rewards at that iteration, as seen in Line 5 of Algorithm 1. If these estimates are far from good, the post-decision state they take us too can also be far from optimal, and since the estimates are updated with the post-decision state we saw (i.e., using the basis functions), we might end-up in a chain reaction for the worse. A different approach to make decisions, which aims to avoid such cycles during the learning phase of ADP, is to consider exploration decisions. In analogy to local search heuristics, exploration decisions can be seen as moves that prevent ADP from getting stuck in local optima. The benefit of making exploration decisions in our basis functions approach is that we may observe post-decision state characteristics we had not seen before (i.e., basis function values different than zero), or not that often, and therefore improving the approximation of the downstream rewards. One way to consider exploration decisions is the \(\epsilon \)-greedy strategy (Powell, 2011). In this strategy, a fraction \(\epsilon \) of the decisions through the iterations should be exploration ones. To implement this, we need to update Line 5 in Algorithm 1 such that a random decision from \({\mathcal {X}}_t^\text {R}\) is chosen with probability \(\epsilon \).
Although exploration decisions may take us to possibly better post-decision states, we also run the risk of deteriorating our approximation and thus making worse exploitation decisions. This is caused by updating the weights of basis functions that we have already seen (and for which we may have reasonable values) using values resulting from possibly far-from-optimal decisions. Although one could update the approximation using the exploitation decision rather than the exploration one (known as off-policy updating), in a finite horizon problem this results in a larger propagation of errors across the stages since the observed post-decision states (and hence the value of the basis functions we use for updating our approximation) depend on the exploration decision and not the exploitation one. In the following section, we introduce a different exploration strategy that aims to balance the trade-off between visiting relatively unknown post-decision states and the risk of deteriorating the current approximation using ideas from Bayesian exploration and implementing them into a hybrid ADP design.
5 ADP with Bayesian exploration
As argued in the previous section, a traditional ADP design as shown in Algorithm 1, works for many applications. However, some problems require a more balanced tradeoff between exploration and exploitation. Exploration decisions have the potential to improve our approximation when the approximation is not good. Exploitation decisions have the potential to improve our approximation further once the approximation is reasonably good. Since there is uncertainty on whether we already have a good approximation, the balance between exploration and exploitation decisions can be seen as a stochastic optimization sub-problem. A way to quantify the uncertainty and balance this tradeoff is through Bayesian exploration, using the concept of Value of Perfect Information (VPI), as proposed in Ryzhov etal. (2019). Although this technique has been recently applied successfully to infinite horizon problems, applying it to finite horizon problems such as ours comes with several challenges. As far as we know, this has not been considered before. In this section, we introduce the general idea of Bayesian exploration and subsequently present the challenges and possible modifications to apply it to finite horizon problems in what we call a hybrid ADP design. For in-depth explanation of Bayesian exploration we refer the reader to Powell and Ryzhov (2012).
During the early iterations of the ADP algorithm, there is a lot of uncertainty about the approximation of the downstream rewards. As the algorithm progresses, and more post-decision states are observed, this uncertainty is reduced. However, if the same post-decision states are observed over and over again, there could be a bias towards these post-decision states just because we have good estimates about their downstream rewards. The general idea of Bayesian exploration is to prevent such a bias in the algorithm by making decisions that will provide information about which post-decision states are actually better than the ones we thought were best. In contrast to the way of making decisions in \(\epsilon \)-greedy exploration, in Bayesian exploration we make the decision that provides the maximum value of exploration \(v_{t}^{E,n}\) at stage t and iteration n, as shown in (11). In (11), \(K_{t}^{n}\) represents the knowledge about the uncertainty in the approximation of the downstream rewards. We now describe \(v_{t}^{E,n}\) and \(K_{t}^{n}\) in more detail.
In the VPI concept applied to ADP, the value of exploration \(v_{t}^{E,n}\) of a decision \(x_t^n\) is defined as the expected improvement in the approximated downstream reward that arises from visiting the post-decision state corresponding to \(x_t^n\). It is defined as “expected” because the true value of the approximation is considered to be a random variable for which we have an initial distribution of belief (Powell and Ryzhov, 2012). The best estimate of the mean of this random variable at iteration n and stage t is \({\overline{V}}_{t}^{n}({{S}}_{t}^{n,x})\). Recall that in our basis function design, \({\overline{V}}_{t}^{n}({{S}}_{t}^{n,x})\) is the scalar product of the values of the basis functions for post-decision state \({{S}}_{t}^{n,x}\) and the weights. Thus, the variance of \({\overline{V}}_{t}^{n}({{S}}_{t}^{n,x})\) is dependent on the weights \(\theta ^{n}_{t}\) and the basis functions \(\phi _t\). We define \(C^{n}_{t}\) as the \(\left| {\mathcal {B}}_t\right| \) by \(\left| {\mathcal {B}}_t\right| \) covariance matrix at iteration n and stage t. The uncertainty knowledge \(K_{t}^{n}\) of the approximated downstream rewards is defined as the tuple shown in (12).
The value of exploration of a decision should be larger for those decisions that lead us to choosing a better decision in future iterations, given that we are at the same state in the same stage, than for the decision that we currently think is the best. Furthermore, the value of exploration should decrease as we explore though the iterations since the uncertainty of the estimated downstream rewards is also reduced with increasing number of observations. Eventually, when we are confident of discriminating between optimal and non-optimal decisions, only exploitation decisions should be made in order to improve the approximation \({\overline{V}}_t^n(S_t^{x,n})\). To achieve this, VPI [as applied by Ryzhov et al. (2019) in the context of infinite horizon ADP] builds upon the notion of the value of information in reinforcement learning systems (Dearden et al., 1999) and defines \(v_{t}^{E,n}\) using the elements of \(K_{t}^{n}\) as shown in (13). In (13), the function f quantifies the knowledge gain of an exploration decision based on the initial belief distribution, and is defined using \(f(z)=z\varPhi (z)+\varphi (z)\) where \(\varPhi \) is the cumulative distribution function and \(\varphi \) the probability density function of the standard normal distribution. Furthermore, \(\sigma _{t}^{2,n}(S_{t}^{x,n})\) represents the prior variance of \({\overline{V}}_{t}^{n}({{S}}_{t}^{n,x})\) and is computed as shown in (13c). For a comprehensive description and derivation of (13), we refer the reader to Ryzhov et al. (2019).
In (13), we observe that the larger the uncertainty \(\sigma _{t}^{2,n}(S_{t}^{x,n})\) about the impact of decision \(x_{t}^{n}\), the larger the value of exploration is. Besides the uncertainty, the difference between the approximated downstream rewards of decision \(x_{t}^{n}\) (given by \({\overline{V}}^{x,n}_{t}\left( S_{t}^{x,n}\right) \)) and the best decision of the remaining feasible decisions \(y_t^n\in {\mathcal {X}}_t|y_t^n\ne x_t^n\) (given by \({\overline{V}}^{x,n}_{t}\left( S_{t}^{y,n}\right) \)) is considered. The larger this difference is, the lower the value of exploration \(v_{t}^{E,n}\) corresponding with decision \(x_{t}^{n}\) becomes. Thus, the definition of \(v_{t}^{E,n}(K_{t}^{n},S_{t}^{n},x_t^n)\) in (13) has the desired characteristic of reducing the risk of deteriorating our approximation through exploration decisions. To implement it, Line 5 in Algorithm 1 must be replaced by (11). In addition, the covariance matrix \(C^{n}_{t}\) must be initialized for all stages \(t\in {\mathcal {T}}\) before Line 2 in Algorithm 1. Since it is difficult to define an initial distribution of belief about the true value of the approximation, the covariance matrix is usually initialized with a large number \(\chi ^\text {C}\) on the diagonal and with zero on its other entries (Ryzhov and Powell, 2011). This initialization resembles the case of no prior knowledge about the relation between between the weights of the basis functions.
The approximation and the belief about its distribution must be updated after each iteration. To update the approximated downstream rewards (i.e., update the weights of the basis functions), we use (14) where \({\widehat{v}}_t^n\) is the value of the exploration decision in (11), as calculated in Line 7 in Algorithm 1, and \(\sigma ^{2,\text {E}}\) is a noise term due to the measurement error. This updating procedure is identical to the analogous recursive least squares method (Ryzhov et al., 2019), and considers the difference between approximated and observed downstream rewards as well as the current uncertainty knowledge through the covariance matrix. Naturally, besides using the observed rewards, the observed basis functions can be used to update the covariance matrix. Remind that, with increasing number of observations of a post-decision state \(S^{x,n}_{t}\) (i.e., observed basis functions), the uncertainty about the approximated downstream rewards of that post-decision state decreases. We update the covariance matrix as shown in (15), again using the noise term \(\sigma ^{2,\text {E}}\). To implement these updating methods, we replace Line 12 in Algorithm 1 with (14) and (15).
In the updating procedure explained above, we use the downstream rewards from the exploration decisions. This differs from Ryzhov etal. (2019), where the approximated downstream rewards of the exploitation decision are being used instead of the exploration decision. This off-policy updating as used by Ryzhov et al. (Ryzhov et al., 2019) is less appropriate for finite horizon problems, especially in combination with backwards updating (Sutton and Barto, 1998; Sutton et al., 2009). This minor adjustment might require additional modifications to prevent exploration decisions affecting our approximation in a negative way. Therefore, we propose to be slightly more conservative in three aspects of exploration: (i) the definition of “gain” in the value of exploration, i.e., \(\delta (S_{t}^{x,n})\) defined in (13b), (ii) the use of the value of exploration in making decisions, i.e., \(x_t^{n*}\) defined in (11), and (iii) the updates resulting from exploration decisions using the noise term \(\sigma ^{2,\text {E}}\) as shown in (14) and (15). In the following subsections, we elaborate on each of these aspects.
5.1 The gain in value of exploration
To be more conservative with the value of exploration \(v_{t}^{E,n}\), we can incorporate more aspects of the exploitation decision. The first aspect we note is the exclusion of the direct rewards \(R_t\left( {{x}}_t^n\right) \) in the calculation of the value of exploration of decision \(x_t^n\), as shown in (13). On the one hand, it is reasonable to use only the expected downstream rewards \({\overline{V}}^{x,n}_{t}\left( S_{t}^{x,n}\right) \) in (13) because the post-decision state corresponding to decision \(x_{t}^n\) and its basis functions might be observed without, or with different, direct rewards in a later iteration. Remind that different states and different decisions at stage t might still lead to the same post-decision state and thus the same basis function values. On the other hand, if observing basis function values would always involve direct rewards (as in the “online” use of ADP which we describe at the end of the next section), it makes sense to include them in the value of exploration. Thus, we can add \(R_t\left( \cdot \right) \) to (13b), as seen in (16).
5.2 The exploration decision
Although the idea from the previous modification decreases the value of exploration for decisions with relatively low direct rewards, the exploration decision itself, as given by (11), is still solely based on the value of exploration. Another way to be conservative with the exploration decisions is to directly include, in addition to the value of exploration, some aspects of the exploitation decision (i.e., Line 5 in Algorithm 1). Naturally, there are many forms to include these aspects. We propose three forms of doing so.
First, we can include the approximated downstream reward when making a decision as proposed by Dearden et al. (Dearden et al., 1999) and shown in (17). This modification overcomes the disadvantage of making decisions that are far-from-optimal with respect to downstream rewards due to solely focusing on the value of exploration. Nevertheless, if \(v_{t}^{E,n}\ll {\overline{V}}^{x,n}_{t}\) we might explore only seldom and therefore converge to a “locally optimal” policy.
Second, both the direct and the approximated downstream rewards can be added to the value of exploration when making a decision as proposed by Ryzhov et al. (2019) and shown in (18). This modification ensures that towards the last iterations, when the value of exploration is approximately the same for many decisions, the exploitation decision is chosen. Exploitation in the last iterations will improve the downstream estimates if the policy learned is close to optimal. However, in this approach we need to be even more careful that the value of exploration is scaled properly, i.e., \(v_{t}^{E,n}\sim \left( R_{t}\left( S_{t}^{n},x_{t}\right) +{\overline{V}}^{x,n}_{t}\right) \), such that we actually do some exploration.
Third, we use the same rationale of the second modification but with a tighter control over the amount of exploration throughout the iterations. To achieve that in early iterations decisions are made according to traditional VPI exploration, i.e., (11), and in later iterations follows pure exploitation, i.e., Line 5 in Algorithm 1, we introduce a weight \(\alpha ^n\in [0,1]\), as shown in (19). This iteration-dependent weight is close to one in early iterations and close to zero in later ones.
The idea of exploring using the traditional VPI exploration decision in (11) is suitable as long as we are able to improve our approximation and it does not “cost” anything. However, some of the applications for which the idea was introduced have costs associated with exploration. This can happen, for instance, if the algorithm uses real-life observations of the exogenous information, or if the simulation of the exogenous information is so expensive that there is a limit on the number of iterations in ADP. This is the so-called “online” use of ADP (Ryzhov et al., 2019), and for this case, the proposed modification in (18) seems reasonable. Although in our problem we use the “offline” version of ADP, which means we first learn the approximation without making real costs and then use the approximation to make decisions in real-life, we still suffer from exploration due to our on-policy strategy. This issue brings us to our last proposed modification: to be more conservative with updates resulting from exploration decisions.
5.3 The update of the approximation
The last modification we propose deals with the updates resulting from exploration decisions. Specifically, we propose adjusting the noise term \(\sigma ^{2,\text {E}}\) in the updating Eqs. (14) and (15). The general idea is that the higher this noise term is, the less the observed error (i.e., difference between the approximated downstream rewards and the observed ones) affects the approximations, since the difference can be partly attributed to “noise”. Noise, in our context, has two causes: (i) fluctuations in the downstream rewards due to realizations of the random demand, and (ii) changes in the policy due to the changing approximation \({\overline{V}}_t^n(S_t^{x,n})\). Typically, this noise term is assumed known and constant across all stages in an infinite horizon problem. In our problem, however, this would mean that \(\sigma ^{2,\text {E}}=\eta ^\text {E}\forall t\in {\mathcal {T}}\), where \(\eta ^\text {E}\) is the problem specific noise. This is not desirable as we explain below.
Suppose that we are at the same state and stage at iterations n and \(n+1\) in the ADP algorithm. Although in both situations the feasible decision space is the same, decision \(x_{t}^{n+1,*}\) might differ from decision \(x_{t}^{n,*}\) because, from iteration n to iteration \(n+1\), either the approximation \({\overline{V}}_t^n(S_t^{x,n})\) changed or the uncertainty knowledge \(K_{t}^{n}\) used to make exploration decisions changed. Typically, the noise resulting from these differences will be smaller in later iterations as the policy has converged. Furthermore, in a finite horizon problem with backward updates, changes in decisions at later stages would accumulate to earlier stages of the horizon, meaning that at early stages noise would be larger than at later stages. To account for this decreasing nature of noise across the stages in the horizon, or across the iterations in our ADP algorithm, we propose three forms of modifying the noise term \(\sigma ^{2,\text {E}}\).
First, we can let the noise term \(\sigma _{t}^{2,\text {E}}\) depend on the stage t as a linearly decreasing function of the constant noise term \(\eta ^\text {E}\), as shown in (20). The noise term \(\eta ^\text {E}\) must, nevertheless, be tuned for the problem.
Second, to deal with the noise due to changes in the policy across the iterations, as well as stages, we can let the noise term depend on the uncertainty \({\sigma _{t}^{2,n}(S_{t}^{x,n})}\) about the impact of a decision, as shown in (21). The logic behind this modification is that, if we choose a decision that leads us to a highly uncertain post-decision state (i.e., high variance of the approximated downstream rewards of that post-decision state), then the resulting observation will have a lesser impact on our update. In VPI, the decision to visit a highly uncertain post-decision state is likely to be an exploration decision, and these decisions we typically want to contribute less since they can be far from optimal.
Third, we can combine the two previous ideas, as shown in (22). This is the most conservative of our proposals to modify the update of the approximation.
To recap, we proposed several modifications in three aspects of the exploration decisions to decrease the risk of negatively affecting our approximation. We proposed these modifications because a straightforward application of Bayesian exploration within a finite horizon ADP not necessarily provides the best results. In the following section, we investigate which of the \(2\times 4\times 4=32\) combinations (the original plus 31 modifications) work best, and study the performance of ADP with Bayesian exploration compared to traditional ADP and other heuristics.
6 Numerical experiments
To evaluate the performance of our ADP designs, with and without Bayesian exploration, we carry out two types of experiments: tuning and benchmark experiments. In the tuning experiments, we test several input parameters, such as the exploration probability \(\epsilon \) and the noise term \(\eta ^\text {E}\). Furthermore, we test the 32 possible VPI modifications. Our goal in these experiments is to provide insights into the relation of these parameters and their performance. We describe these experiments in detail and present their results in Sect. 6.2. In the benchmark experiments, we compare our ADP approach with a benchmark heuristic under different time-window settings. Our goal is to study the relation between time-window characteristics and the gains or losses of using ADP over using the benchmark heuristic. We describe these experiments and present their results in Sect. 6.3. We end with a discussion on advantages and limitations of our approach in Sect. 6.4. But first, we present our experimental design in Sect. 6.1.
6.1 Experimental design
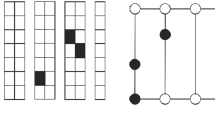
To test our ADP algorithms, we use three synchromodal network configurations and a planning horizon of \(T^\text {max}=50\) days. These three networks, and their settings, are based on the intermodal consolidation network typologies suggested by Macharis and Bontekoning (2004), Woxenius (2007), and Caris et al. (Caris et al., 2013). Each network increases in amount of consolidation opportunities (i.e., more services or terminals) compared to the previous one, as shown in Figs. 1, 2 and 3. In these figures, the axes denote the distance (in km) between the locations in the network, Q the capacity of each service in number of containers, and \(L^A\) the duration of each service in days. The duration of truck connections is one day. We consider transfer time not to be restrictive in any terminal in the network, i.e., \(L^N_{i,t}=0\), for all terminals i.
All networks span an area of \(1000\times 500\) km, and have the same locations for origins and destinations. The distances between the origins and the destinations range from 800 to 1044 km, and the distances between terminals close to the origin and terminals close to the destinations range from 500 to 854 km, to resemble distances that make consolidation for the long-haul desirable in Europe according to Woxenius (2007). We use a cost structure comparable to the one proposed by Bierwirth et al. (2012) and Janic (2007) to represent internal and external costs of intermodal transportation networks, and especially, to incorporate the differences in costs due to economies of scale of various transportation modes. For each day t in the horizon, the setup cost \(B_{i,j,t}\) ranges between 169 and 425 for barges and trains and the variable cost \(C_{i,j,d,t}\) ranges between 37 and 868 for barges, trains, and trucks. Further details of this cost structure are given in “Appendix C”. For each day, the revenue \(A_{i,j,d,t}\) is 868 for each container picked up at its origin, independent of its origin or destination, and 0 otherwise. This entails that the entire revenue is received at the beginning of transportation (i.e., first mile), and afterwards only costs are incurred for each container.
The number of containers that arrives at each origin, and their destination, varies according to the probability distributions shown in “Appendix D”. The time-window, upon arrival, is fixed to \(r=0\) and \(k=6\) for all containers (i.e., \(p^\text {R}_{0,i,t}=1\) and \(p^\text {K}_{6,i,t}=1\) for all origins i). This means that containers can immediately be transported, or postponed at most 2 days for a long-haul intermodal service to be feasible.
The initial state \({{S}}_0\) for each network contains six containers, one container of each of the following characteristics: \(F_{0,11(12),0,6,0}\), \(F_{1,10(11),0,6,0}\), \(F_{2,10(11),0,6,0}\), \(F_{3,9(10),0,4,0}\), \(F_{4,11(12),0,5,0}\), and \(F_{5,11(12),0,1,0}\) (note that destinations in Network 3 are displayed between parenthesis). This initial state contains “average” containers on the origins plus a few containers in the network. Our choice of 50 days in the planning horizon ensures a limited effect of the initial state in the rewards for the entire horizon. To avoid unnecessary postponement of transport till the end of the horizon, we include an end-effect (i.e., costs after day 50) by estimating the costs to send all containers remaining in the network using the benchmark heuristic (see Sect. 6.3).
6.2 Tuning experiments
In our tuning experiments, we test the various modifications of our ADP design with Bayesian exploration and compare them to our ADP design with epsilon-greedy exploration. To make the comparison fair, we test several input values for the tunable parameters of each of the two designs, under the same conditions. Before presenting the results, we first describe the conditions under which we test our designs and the input values we use for the tunable parameters.
As described in Sect. 5, we are interested in the offline use of ADP, which is to first learn the approximation of downstream rewards within a simulated environment, and then use the approximation to make real-life decisions. For this reason, we measure performance in two ways: (i) the learned approximation of downstream rewards after running the ADP algorithm, which we call learned rewards, and (ii) the realized rewards of using the approximation for making decisions in a simulation. The two of them are related to the MDP model’s objective function in (6), the first relates to the optimal expected discounted rewards, and the second one relates to the policy that obtains these rewards. Although related, these two performance measurements are not necessarily the same. The basis function weights that our ADP algorithms learn can be far from the optimal rewards, but the resulting policy can be close to the optimal policy.
For each ADP design, we use \(N=50\) iterations and common random numbers, i.e., containers that arrive during each day of each iteration are the same across tested designs. To test the resulting policy of each ADP design, we use 50 simulation runs of the planning horizon and, again, common random numbers that differ from those used in the learning phase.
For the ADP design with \(\epsilon \)-greedy exploration, we test three values of \(\lambda =\left\{ 0.01,0.1,1\right\} \) within the recursive least squares method for non-stationary data, and test four values of the probability of exploration \(\epsilon =\left\{ 0,0.3,0.6,0.9\right\} \). Remind that \(\epsilon =0\) means only exploitation decisions, while \(\epsilon =1\) means only exploration decisions. Furthermore, we test two ways of initializing the weights of the basis functions: (i) \(\theta ^{0}_{b,t}=0\) for all characteristics \(b\in {\mathcal {B}}\) and days \(t\in {\mathcal {T}}\), and (ii) \(\theta ^{0}_{\left| {\mathcal {B}}\right| ,t}={\beta \left( T^\text {max}-t\right) }/{T^\text {max}}\) for the constant basis function and \(\theta ^{0}_{b,t}=0\) for all other characteristics \(b\in {\mathcal {B}}|b\ne \left| {\mathcal {B}}\right| \) and days \(t\in {\mathcal {T}}\). The first initialization represents a case where we have no knowledge about the weights of the approximated rewards, and the second one represents a case where we have an estimate of the magnitude of the total downstream rewards \(\beta \). In our case, \(\beta \) is defined as the rewards attained by the benchmark heuristic (see Sect. 6.3): \(\beta =38,036\) for Network 1, \(\beta =33,445\) for Network 2, and \(\beta =33,889\) for Network 3.
For the ADP design with Bayesian exploration, we initialize the basis function weights using the second option described before. We test four values of the noise term \(\eta ^\text {E}=\left\{ 10^2,10^4,10^6,10^8\right\} \). For the initial covariance matrix, we test four values for the diagonal \(\chi ^\text {C}=\left\{ 10,10^2,10^3,10^4\right\} \). We base our settings on Ryzhov et al. (2019), who recommend that \(\eta ^\text {E}>\chi ^\text {C}\) and that their ratio is of the order 10 or \(10^2\). For the weight \(\alpha ^n\) in modification (19), we test \(\alpha ^n=\left\{ 1/n,10/(n+9),100/(n+99)\right\} \). We test all the parameters described above for each of the 32 combinations of VPI modifications that we proposed in Sect. 5.
Testing all tunable parameters and modifications of our two ADP designs for the three experimental networks results in more than 3500 experiments. Each experiment provides the learned and the realized rewards of ADP. Before discussing the details of the relation between ADP performance and the tunable parameters/modifications, we limit ourselves to present the results of the best parameters and modifications from Table 1, which consists of (i) the result for the tuned value of \(\epsilon \), \(\lambda \), and \(\beta \) for the ADP design with \(\epsilon \)-greedy exploration, and (ii) the tuned value of \(\eta ^\text {E}\), \(\chi ^\text {C}\), and \(\alpha ^n\), and the best combination of modifications in Sect. 5 for the ADP design with Bayesian exploration. Note that we use the abbreviation BF to refer to the basis functions approach.
In Table 1, we observe the maximum realized rewards over all settings of the tunable parameters and VPI modifications, and their corresponding learned reward, for each ADP design. Two observations stand out. First, using VPI instead of the traditional \(\epsilon \)-greedy strategy for exploration significantly improves the realized rewards. In fact, the policy resulting from the \(\epsilon \)-greedy strategy, although better in most cases than exploitation only (i.e., BF), ends up in costs. Second, the accuracy of the approximation (i.e., difference between learned and realized rewards) varies per network for the traditional designs, but is more consistent for the BF+VPI design. BF+VPI underestimates the rewards by at most 9,088 whereas the traditional designs overestimate the rewards by at most 45,305.
Next, we analyze the tuning of the noise and Bayesian-belief related parameters. In Fig. 4 (left), we provide a comparison of different ratios \(\eta ^\text {E}/\chi ^\text {C}\). From this figure, we can gather important insights for the ratio \(\eta ^\text {E}/\chi ^\text {C}\): (i) realized rewards and accuracy initially seem to improve with an increasing ratio, (ii) in the area where the ratio results in the best performance (in our case \(10^4\)), we also find the smallest difference with the learned rewards, and (iii) for even larger ratios, realized rewards rapidly decrease, even though the learned rewards remain the same. In line with Ryzhov et al. (2019), we observe that with ratios of \(10^2\) through \(10^4\), VPI works best on average over all modifications.
Finally, we analyze the performance of our VPI modifications. In Fig. 4 (right), we show the average realized rewards (over all networks) as a function of the decision and noise modifications explained in Sects. 5.2 and 5.3, respectively. We exclude from our analysis the modification to the gain in value of exploration using the direct rewards (Sect. 5.1), since this performed significantly worse than the original definition of the value of exploration, for all decision and noise modifications. The superscript E1 represents the original noise and decision definition in VPI, meaning that the upper corner corresponds to the original VPI design. We observe that the modifications of how to make a decision have a larger impact than the modifications to the noise used when updating the approximation. Overall, including the downstream rewards in addition to the value of exploration when making decisions (i.e., \(x_t^\text {E2}\)) and letting the noise depend only on the post-decision state of the given stage and iteration (i.e., \(\sigma _t^\text {E3}\)) are the best modifications tested for our problem. It seems that including the downstream rewards instead of the direct rewards helps the algorithm avoid the aforementioned greedy behavior. It also seems that considering the uncertainty of the post-decision state instead of a constant noise term when updating pays off. Using modifications \(x_t^\text {E2}\) and \(\sigma _t^\text {E3}\) for our BF+VPI design, we continue to our benchmark experiments.
6.3 Benchmark experiments
In our benchmark experiments, we compare the realized rewards of our best ADP design (i.e., BF + VPI with the modifications \(x_t^\text {E2}\) and \(\sigma _t^\text {E3}\)) against a Benchmark Heuristic (BH). The objective is to compare the use of the learned ADP policy against a simpler but effective scheduling heuristic. For this, we use a rule-of-thumb BH as used by practitioners and for which competitive performance has been shown compared to a typical ADP implementation (Pérez Rivera and Mes, 2016). This BH aims to use the intermodal services efficiently, i.e., consolidating as many containers as possible in a service once the setup costs for using that service can be covered. The BH consists of fours steps: (i) define the shortest and second shortest path for each container to its final destination, considering only variable costs for services between terminals, (ii) calculate the savings between the shortest and second shortest path and define these as savings of the first intermodal service used in the shortest path, (iii) sort all containers in non-decreasing time-window length, i.e., closest due-day first, and (iv) for each container in the sorted list, check whether the savings of the first intermodal service of its shortest path are larger than the setup cost for using this service; if so, use this service for the container, if not, postpone the transportation of the container. The pseudo-code for this heuristic can be found in “Appendix F”.
Using the three networks from the previous section plus additional time-window distributions, we set up our experiments as follows. For each network, we replicate ten times the process of learning the ADP weights and simulating the use of the resulting policy. The BH is also replicated ten times, using common random numbers with the corresponding ADP part, such that differences arise due to the scheduling differences and not the arriving containers. Identical to the tuning experiments of the previous section, one replication of the ADP process consists on running the ADP algorithm for 50 iterations and simulating the entire planning horizon 50 times. For the networks with different time-window distributions, we re-tune the noise parameters, since they are dependent on the inherent uncertainty of the problem. Here we fix the best ratio \(\eta ^\text {E}/\chi ^\text {C}\) found, i.e., \(10^4\), but increase the values of \(\eta ^\text {E}\) and \(\chi ^\text {C}\).
Table 2 shows the average realized rewards, over the ten replications, using the same networks from the tuning experiments of the previous section. We observe that, for Network 1, ADP performs slightly better than the benchmark heuristic, but not with a significant difference. In Networks 2 and 3, however, ADP performs significantly better than the heuristic. The differences in performance of both the BH and ADP across the networks seem to indicate that the larger the complexity of the network is, the lower the average realized rewards are, but up to a certain extent (we come back to this later).
In the experiments above, all containers that arrive are immediately released and have a time-window length of six days. With this time-window length, containers can be postponed at most 2 days for a long-haul intermodal service to be feasible. However, the length and uncertainty of the time-windows may affect the performance of an ADP algorithm (Pérez Rivera and Mes, 2017). To test this, we design three distributions for Release-Days (RD) and three distributions for Time-Window (TW) lengths, as shown in Tables 7 and 8 in “Appendix D”. Each distribution is categorized as short, medium, or long. Short RD means that 60% of the containers are released immediately while long RD means that 60% of the containers are released two days after arriving. Short TW means that 60% of the containers must be at their destination within 4 days after being released while long RD means that 60% of the containers have a time-window length of 6 days. We follow the same procedure as before, with ten replications. To reduce computation time and provide a fair comparison, both ADP and BH work with the restricted decision space. Relative results are shown in Fig. 5 and absolute results in Table 9 (see “Appendix E”).
As can be expected, the longer the distribution of time-window length, the larger the realized rewards are for both scheduling methods in each network, independent of the release-day. This happens because both methods are able to postpone transport and anticipate on better consolidation opportunities. Furthermore, with larger time-windows the difference between ADP and BH increases, as ADP can better anticipate on future consolidation opportunities. For small time-windows in Network 3, we see that the heuristic outperforms ADP. Actually, it is to be expected that ADP is less useful when there are short time-windows since postponement may directly result in using the expensive alternative mode (i.e., truck). In other words, anticipatory decisions do not make sense in such a problem. With respect to RD distributions, we observe that for each TW distribution, the gains of ADP are larger in the case of short RD. There are two possible reasons for this: (i) the basis functions do not include any feature about release-days, so it is difficult (impossible) to learn among post-decision containers with different release-days, (ii) when there are short release-days, rewards and costs are observed earlier, which improves the learning of the feature weights. These two reasons hint that the design of the approximation itself (i.e., the choice of basis functions) in transportation problems such as ours should take into account the time when rewards and costs are realized and their constraints.
In general, our experiments show that including VPI in ADP improves its performance compared to traditional designs, and that this new design can lead to substantial gains over a benchmark heuristic for various problem settings. However, they also showed that a “one-size fits all” ADP solution is hard to achieve, and some tuning is necessary. In the following section, we reflect upon our results and discuss their implications.
6.4 Discussion
In our tuning experiments, we observed differences between the learned and realized rewards for most ADP designs. We observed that in the traditional ADP designs, a large learned reward did not necessarily results in a good policy. Most of the times, the learned rewards were positive while the realized rewards were negative. When looking for causes of the mismatch between learned and realized rewards, one can argue that problem characteristics such as the cost structure (i.e., revenue received at the beginning of transportation) and restricted decision space (i.e., some post-decision states are not attainable) have a strong influence on the mismatch. Nevertheless, we observe that through the inclusion of VPI, ADP is able to tackle these issues and significantly improves the results of traditional designs, both in learned and realized rewards. Specifically, we observed that during the learning phase, combining downstream rewards with the value of exploration in VPI was the best way of making exploration decisions, and that incorporating the uncertainty of a post-decision state when updating was the best way to update the approximation. More generally, our results indicate that the inclusion of VPI in ADP helps to balance the uncertainty in objective value across time, which particularly plays a role in problems with delayed rewards and costs, resulting in a more challenging exploration versus exploitation dilemma. However, a major disadvantage of this ADP+VPI combination is the effort required for tuning and calibration as well as the increase in computation time per iteration of ADP (which might be negated by a faster convergence).
A limitation of our experiment is the use of a restricted decision space. When comparing the performance of ADP with restricted decision space with the benchmark heuristic without restrictions on the decisions, ADP will often be outperformed. Nevertheless, we have seen that if we consider the restricted decision space to be part of the problem, ADP outperforms the benchmark heuristic drastically. These improved gains provide an indication of the gains that are possible if restrictions in the decision space of ADP would be removed. However, removing restrictions in the decision space can make it more computationally complex, which in turn can make exploration in the ADP learning phase more challenging.
To provide an indication of the computation times, the ADP learning phase for BF and BF+VPI, per replication consisting of 50 iterations, took roughly half an hour, 2 hours, and 15 hours for networks 1, 2, and 3, respectively, on average across all replications, modifications and settings of the noise parameters. The computation times of the simulation phase are roughly the same (also per replication consisting of 50 iterations). Removing the restrictions on the decision-space results in computation times that are roughly 10 times higher. Note that this might still be feasible in practice as the time-consuming training phase of ADP can be performed offline and easily be parallelized. The addition of VPI did not result in a significant increase in computation time compared to a pure exploitation strategy. However, ADP + \(\epsilon \)-greedy resulted in roughly 40% lower computation times as we not always had to enumerate all possible decisions. The balance between the computationally complex decision space, the computational demands of a more advanced exploration strategy (such as VPI), and the restricted decision space, needs further research. We distinguish two promising directions. First, restricting the policy during early iterations of ADP and then removing the restrictions in later iterations may overall result in a better policy learned with reasonable time. Second, using a heuristic decision policy rather than restrictions might also result in a better policy with less computational burden.
7 Conclusions
In this paper, we formulated an MDP model for the anticipatory scheduling of containers in a synchromodal transportation network, and designed a heuristic solution based on ADP. We used the traditional constructs of basis functions and \(\epsilon \)-greedy exploration, as well as methods from Bayesian exploration, specifically VPI. We described how the one-step look-ahead perspective of the traditional ADP design can make the algorithm flounder and end in a local-optimum, and how the ADP algorithm can escape this local-optimum and at the same time improve the solution by using the value of exploration from VPI. We proposed various modifications to VPI, which appeared to be beneficial for finite horizon ADP designs.
In a series of numerical experiments, we evaluated our ADP designs and our proposed modifications to VPI and provided insight into which modifications and tunable settings work best. We showed how VPI significantly improves the traditional \(\epsilon \)-greedy strategy, as long as exploring and updating in VPI is done slightly more conservative than in the original application of VPI in infinite horizon problems. We exemplified how ADP and VPI achieve significant gains in scheduling synchromodal transport compared to a benchmark heuristic under different demand patterns. Finally, we reflected on the limitations of our study and possible ways to tackle these limitations. Further research about the reduction of the decision space and the robustness of VPI settings in finite horizon problems is necessary for ADP to achieve the best performance in the scheduling of containers in a synchromodal transportation network considering demand uncertainty and performance over time.
References
Bai, R., Wallace, S. W., Li, J., & Chong, A. Y. L. (2014). Stochastic service network design with rerouting. Transportation Research Part B: Methodological, 60, 50–65. https://doi.org/10.1016/j.trb.2013.11.001.
Behdani, B., Fan, Y., Wiegmans, B., & Zuidwijk, R. (2016). Multimodal schedule design for synchromodal freight transport systems. European Journal of Transport & Infrastructure Research, 16(3), 424.
Bierwirth, C., Kirschstein, T., & Meisel, F. (2012). On transport service selection in intermodal rail/road distribution networks. Business Research, 5(2), 198–219. https://doi.org/10.1007/BF03342738.
Bouzaiene-Ayari, B., Cheng, C., Das, S., Fiorillo, R., & Powell, W. B. (2016). From single commodity to multiattribute models for locomotive optimization: A comparison of optimal integer programming and approximate dynamic programming. Transportation Science, 50(2), 366–389. https://doi.org/10.1287/trsc.2014.0536.
Caris, A., Macharis, C., & Janssens, G. K. (2013). Decision support in intermodal transport: A new research agenda. Computers in Industry, 64(2), 105–112. https://doi.org/10.1016/j.compind.2012.12.001.
Craig, A. J., Blanco, E. E., & Sheffi, Y. (2013). Estimating the CO2 intensity of intermodal freight transportation. Transportation Research Part D: Transport and Environment, 22, 49–53. https://doi.org/10.1016/j.trd.2013.02.016.
Crainic, T. G., Hewitt, M., & Rei, W. (2014). Scenario grouping in a progressive hedging-based meta-heuristic for stochastic network design. Computers & Operations Research, 43, 90–99. https://doi.org/10.1016/j.cor.2013.08.020.
Črepinšek, M., Liu, S. H., & Mernik, M. (2013). Exploration and exploitation in evolutionary algorithms: A survey. ACM Computing Surveys, 45(3), 1–35. https://doi.org/10.1145/2480741.2480752.
Dall’Orto, L. C., Crainic, T. G., Leal, J. E., & Powell, W. B. (2006). The single-node dynamic service scheduling and dispatching problem. European Journal of Operational Research, 170(1), 1–23. https://doi.org/10.1016/j.ejor.2004.06.016.
Dearden, R., Friedman, N., & Andre, D. (1999). In Model based Bayesian exploration (Vol. UAI–99, pp. 150–159). San Francisco, CA: Morgan Kaufmann Publishers Inc.
del Mar, Agamez-Arias A., & Moyano-Fuentes, J. (2017). Intermodal transport in freight distribution: A literature review. Transport Reviews. https://doi.org/10.1080/01441647.2017.1297868.
Ghane-Ezabadi, M., & Vergara, H. A. (2016). Decomposition approach for integrated intermodal logistics network design. Transportation Research Part E: Logistics and Transportation Review, 89, 53–69. https://doi.org/10.1016/j.tre.2016.02.009.
Ghiani, G., Manni, E., & Thomas, B. W. (2012). A comparison of anticipatory algorithms for the dynamic and stochastic traveling salesman problem. Transportation Science, 46(3), 374–387. https://doi.org/10.1287/trsc.1110.0374.
Godfrey, G. A., & Powell, W. B. (2002). An adaptive dynamic programming algorithm for dynamic fleet management, ii: Multiperiod travel times. Transportation Science, 36(1), 40–54. https://doi.org/10.1287/trsc.36.1.40.572.
Goodson, J. C., Thomas, B. W., & Ohlmann, J. W. (2016). Restocking-based rollout policies for the vehicle routing problem with stochastic demand and duration limits. Transportation Science, 50(2), 591–607. https://doi.org/10.1287/trsc.2015.0591.
Guo, W., Atasoy, B., van Blokland, W. B., & Negenborn, R. R. (2020). A dynamic shipment matching problem in hinterland synchromodal transportation. Decision Support Systems, 134, 113289. https://doi.org/10.1016/j.dss.2020.113289.
Janic, M. (2007). Modelling the full costs of an intermodal and road freight transport network. Transportation Research Part D: Transport and Environment, 12(1), 33–44. https://doi.org/10.1016/j.trd.2006.10.004.
Khakdaman, M., Rezaei, J., & Tavasszy, L. (2020). Shippers’ willingness to delegate modal control in freight transportation. Transportation Research Part E: Logistics and Transportation Review, 141, 102027.
Kordnejad, B. (2014). Intermodal transport cost model and intermodal distribution in urban freight. Procedia: Social and Behavioral Sciences,125, 358–372. https://doi.org/10.1016/j.sbspro.2014.01.1480
Larsen, R. B., Atasoy, B., & Negenborn, R. R. (2020). Learning-based co-planning for improved container, barge and truck routing. In E. Lalla-Ruiz, M. Mes, & S. Voß (Eds.), Computational logistics (pp. 476–491). Cham: Springer International Publishing.
Larsen, R. B., Atasoy, B., & Negenborn, R. R. (2021). Model predictive control for simultaneous planning of container and vehicle routes. European Journal of Control, 57, 273–283. https://doi.org/10.1016/j.ejcon.2020.06.003.
Lemmens, N., Gijsbrechts, J., & Boute, R. (2019). Synchromodality in the physical internet—Dual sourcing and real-time switching between transport modes. European Transport Research Review. https://doi.org/10.1186/s12544-019-0357-5.
Li, L., Negenborn, R. R., & Schutter, B. D. (2015). Intermodal freight transport planning a receding horizon control approach. Transportation Research Part C: Emerging Technologies, 60, 77–95. https://doi.org/10.1016/j.trc.2015.08.002.
Lium, A. G., Crainic, T. G., & Wallace, S. W. (2009). A study of demand stochasticity in service network design. Transportation Science, 43(2), 144–157. https://doi.org/10.1287/trsc.1090.0265.
Lo, H. K., An, K., & Hua Lin, W. (2013). Ferry service network design under demand uncertainty. Transportation Research Part E: Logistics and Transportation Review, 59, 48–70. https://doi.org/10.1016/j.tre.2013.08.004.
Macharis, C., & Bontekoning, Y. (2004). Opportunities for OR in intermodal freight transport research: A review. European Journal of Operational Research, 153(2), 400–416. https://doi.org/10.1016/S0377-2217(03)00161-9.
Macready, W. G., & Wolpert, D. H. (1998). Bandit problems and the exploration/exploitation tradeoff. IEEE Transactions on Evolutionary Computation, 2(1), 2–22.
Mes, M. R. K., & Iacob, M. E. (2016). Synchromodal transport planning at a logistics service provider. In H. Zijm, M. Klumpp, U. Clausen, & T. M. Hompel (Eds.), Logistics and supply chain innovation: Bridging the gap between theory and practice (pp. 23–36). Cham: Springer International Publishing.
Nabais, J., Negenborn, R., BenÃtez, R. C., & Botto, M. A. (2015). Achieving transport modal split targets at intermodal freight hubs using a model predictive approach. Transportation Research Part C: Emerging Technologies, 60, 278–297. https://doi.org/10.1016/j.trc.2015.09.001.
Pérez Rivera, A., & Mes, M. (2015). Dynamic multi-period freight consolidation. In F. Corman, S. Voß, & R. R. Negenborn (Eds.), Computational logistics: 6th international conference, ICCL 2015, September 23–25, 2015, Proceedings, lecture notes in computer science (Vol. 9335, pp. 370–385). Delft: Springer International Publishing.
Pérez Rivera, A., & Mes, M. (2016). Service and transfer selection for freights in a synchromodal network. In A. Paias, M. Ruthmair, & S. Voß (Eds.), Proceedings (pp. 227–242). Cham: Springer International Publishing. https://doi.org/10.1007/978-3-319-44896-1_15
Pérez Rivera, A., & Mes, M. (2017). Anticipatory freight selection in intermodal long-haul round-trips. Transportation Research Part E: Logistics and Transportation Review, 105, 176–194. https://doi.org/10.1016/j.tre.2016.09.002.
Powell, W. B. (2011). Approximate dynamic programming: Solving the curses of dimensionality (2nd ed.). New York: Wiley.
Powell, W. B., & Ryzhov, I. O. (2012). Optimal learning. New York: Wiley. https://doi.org/10.1002/9781118309858.
Powell, W. B., Simao, H. P., & Bouzaiene-Ayari, B. (2012). Approximate dynamic programming in transportation and logistics: A unified framework. EURO Journal on Transportation and Logistics, 1(3), 237–284.
Riessen, B., Negenborn, R. R., & Dekker, R. (2015a). Synchromodal container transportation: An overview of current topics and research opportunities. In F. Corman, S. Voß, & R. R. Negenborn (Eds.), Computational logistics: 6th international conference, ICCL 2015, Delft, September 23–25, 2015, Proceedings of synchromodal container transportation: An overview of current topics and research opportunities, lecture notes in computer science (pp. 386–397). Cham: Springer. https://doi.org/10.1007/978-3-319-24264-4_27
Riessen, B. V., Negenborn, R. R., Dekker, R., & Lodewijks, G. (2015b). Service network design for an intermodal container network with flexible transit times and the possibility of using subcontracted transport. International Journal of Shipping and Transport Logistics, 7(4), 457–478. https://doi.org/10.1504/IJSTL.2015.069683.
Ryzhov, I. O., & Powell, W. B. (2011). Bayesian active learning with basis functions. In IEEE symposium on adaptive dynamic programming and reinforcement learning (ADPRL) (pp. 143–150), winner, best paper, IEEE international symposium on adaptive dynamic programming and reinforcement learning.
Ryzhov, I. O., Mes, M. R., Powell, W. B., & van den Berg, G. A. (2019). Bayesian exploration for approximate dynamic programming. Operations Research, 67(1), 198–214. https://doi.org/10.1287/opre.2018.1772.
Simao, H. P., Day, J., George, A. P., Gifford, T., Nienow, J., & Powell, W. B. (2009). An approximate dynamic programming algorithm for large-scale fleet management: A case application. Transportation Science, 43(2), 178–197. https://doi.org/10.1287/trsc.1080.0238.
SteadieSeifi, M., Dellaert, N., Nuijten, W., Woensel, T. V., & Raoufi, R. (2014). Multimodal freight transportation planning: A literature review. European Journal of Operational Research, 233(1), 1–15. https://doi.org/10.1016/j.ejor.2013.06.055.
Strens, M. (2000). A Bayesian framework for reinforcement learning. In ICML (pp. 943–950).
Sutton, R. S., & Barto, A. G. (1998). Introduction to reinforcement learning (1st ed.). Cambridge, MA: MIT Press.
Sutton, R. S., Maei, H. R., Precup, D., Bhatnagar, S., Silver, D., Szepesvári, C., & Wiewiora, E. (2009). Fast gradient-descent methods for temporal-difference learning with linear function approximation (Vol. ICML –09, pp. 993–1000), New York, NY.
Ulmer, M. W., Mattfeld, D. C., & Köster, F. (2017). Budgeting time for dynamic vehicle routing with stochastic customer requests. Transportation Science Articles in Advance, 52, 20.
van Heeswijk, W. J. A., Mes, M. R. K., & Schutten, J. M. J. (2017). The delivery dispatching problem with time windows for urban consolidation centers. Transportation Science Articles in Advance, 53, 203.
Vermorel, J., & Mohri, M. (2005). Multi-armed bandit algorithms and empirical evaluation. In J. Gama, R. Camacho, P. B. Brazdil, A. M. Jorge & L. Torgo (Eds.), 16th European conference on machine learning machine learning: ECML 2005 (pp. 437–448), Porto, Portugal, October 3–7, 2005. Proceedings. Berlin: Springer. https://doi.org/10.1007/11564096_42
Wieberneit, N. (2008). Service network design for freight transportation: A review. OR Spectrum, 30(1), 77–112. https://doi.org/10.1007/s00291-007-0079-2.
Woxenius, J. (2007). Generic framework for transport network designs: Applications and treatment in intermodal freight transport literature. Transport Reviews, 27(6), 733–749. https://doi.org/10.1080/01441640701358796.
Yee, H., Gijsbrechts, J., & Boute, R. (2021). Synchromodal transportation planning using travel time information. Computers in Industry, 125, 103367. https://doi.org/10.1016/j.compind.2020.103367.
Zhang, M., & Pel, A. (2016). Synchromodal hinterland freight transport: Model study for the port of Rotterdam. Journal of Transport Geography, 52, 1–10. https://doi.org/10.1016/j.jtrangeo.2016.02.007.
Acknowledgements
This research has been partially funded by the Dutch Institute for Advanced Logistics, DINALOG, under the project SynchromodalIT.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
A Notation
In this appendix, we present all mathematical notation used throughout the paper. Table 3 provides an overview of all sets, and Table 4 contains all variables, parameters, and functions used.
B Modeling assumptions
To simplify the formulation of the MDP model in Sect. 3, we made several assumptions. These assumptions apply to our model, but not necessarily to our problem. In this Appendix, we briefly describe the possible modifications to the MDP model such that each assumption or condition can be bypassed.
The first condition we impose in our model is the separation between origin, intermodal, and destination nodes. If an intermodal terminal is also an origin or destination, a duplicate node can be included in the set of origins or destinations and their related parameters can be changed accordingly. The second assumption in our model relates to the unlimited capacity for the services beginning at an origin or ending at a destination node. In other words, we assume that the pre- and end-haulage operations of our synchromodal network are not restrictive. If there is a restriction, this must be added to the decision space and, in case of penalization, the transition function must be changed accordingly. The third assumption is related to having at most one service between two terminals. To allow for multiple services, duplicate intermodal nodes can be added, and services need to be modified accordingly. However, this modification is more than just altering the arcs, it involves: (i) modifying the transition function such that the same containers appear/disappear in the duplicated nodes and (ii) modifying the decision space constraints such that service capacities going to/from the duplicated nodes are respected and such that no more than the existing containers (i.e., not duplicated) can be transported.
C Cost and network settings
To model the costs and the effects of container consolidation (i.e., setup costs), we use the costs per km presented in Bierwirth et al. (2012) and the model with which they were calculated originally in Janic (2007). This cost model was developed for internal and external costs of intermodal and road transportation networks, and the logic behind it is that costs decrease non-linearly with distance and at different rates depending on the transport mode. The variable cost (i.e., euro per km) for truck is \(5.46d^{-0.278}\), for train is \(0.58d^{-0.26}\), and for barge is \(0.46d^{-0.26}\), where d is the distance between two locations. For the fixed or setup cost (i.e., euro per service independent of the number of containers) of a service for the train is \(q((1560^{0.74})/q+40)\) and for barge is \(0.8q((1560^{0.74})/q+40)\), where q is the capacity of the service. We refer the reader to Janic (2007) for a thorough explanation on the cost model. In the next paragraph, we describe the consolidation opportunities and challenges of making decisions in each network.
Network 1 represents the so-called point-to-point topology (Macharis and Bontekoning, 2004). Although there are no transfers in this network, there are three consolidation opportunities for each origin, namely the two train and barge services. The complexity of the decisions in this network is two-fold: (i) the restrictions imposed by the capacity of each service and (ii) the relation between the transportation duration with the time-windows. Network 2 represents the so-called collection-distribution topology (Macharis and Bontekoning, 2004). In this network, there are four additional services, and new transfers connected to the central terminals, compared to Network 1. The new consolidation opportunities bring two additional challenges to those of Network 1, the trade-off of using truck against truck-and-train to (i) bring a container from its origin to the start of the long-haul and (ii) bring a container from the end of the long-haul to its destination. Network 3 represents the so-called hub-and-spoke network topology (Macharis and Bontekoning, 2004). In this network, there is one additional terminal, four additional services, and new transfers connected to the new terminal, compared to Network 2. The number of paths a container can take from its origin to its destination significantly increases, and thus the complexity of the decisions increases as well.
D Experimental probability distributions
The probability distributions used for the experiments can be found in Table 6, Table 7, and Table 8.
E Absolute results of the benchmark experiments
The absolute results of the benchmark experiments can be found in Table 9.
F Benchmark heuristic

Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rivera, A.E.P., Mes, M.R.K. Anticipatory scheduling of synchromodal transport using approximate dynamic programming. Ann Oper Res (2022). https://doi.org/10.1007/s10479-022-04668-6
Accepted:
Published:
DOI: https://doi.org/10.1007/s10479-022-04668-6