Impacts of synergies on software project scheduling

Abstract

The adequate allocation of human resources is one of the most important success factors in software projects. Although project teams can be regarded as complex systems in which a team’s performance is highly influenced by the interdependencies among team members, the allocation methods applied to date have focused only on individual skills and consider project teams as units of isolated workers. The existing software project scheduling problem (SPSP) is extended to (1) consider different skills and efficiencies of employees and (2) examine the pairwise synergies between them, as well as to (3) handle the flexible structure of the project that is used in flexible management, such as agile project management. To better understand the impact of synergies on the project’s cost, the solutions of the traditional and extended SPSP versions are analyzed and compared on the generated project networks. The results show not only that this factor has a highly significant impact but also that the project cost strongly depends on the structural parameters of the synergy network (e.g., topology, network size and degree centrality). Among these parameters, a low degree of centrality and some topologies, most notably star and circular networks, obtained the highest reduction in the projects’ total cost.

1 Introduction

The tasks of allocating human resources and scheduling play a critical role in the success of software development projects and, consequently, in competition in the IT industry (Nan and Harter 2009). To reduce development costs and beat the market, companies have to make reliable project plans; however, efficient allocation of workers is a uniquely difficult and challenging problem, particularly for medium- to large-scale projects (see, e.g., Minku et al. 2013). For instance, in China alone, more than 40% of software projects were unsuccessful due to incoherent planning of project tasks and human resources (Ding and Jing 2003).

In the literature on software development, the common issue of resource allocation and task scheduling is referred to as the software project scheduling problem (SPSP) (see, e.g., Vega-Velázquez et al. 2018), which is a special kind of multiskill resource-constrained project scheduling problem (MS-RCPSP) (Myszkowski et al. 2019; Tirkolaee et al. 2019). The efficiency of solving this problem is usually related to several factors. On the one hand, the development process should be as short as possible, thus allowing the allocation of resources to other profitable processes as soon as possible. On the other hand, the associated cost should be minimal. This multiobjective nature makes planning even more complicated and, as a result of the increasing size of software projects, makes manual scheduling almost impossible (Shen et al. 2018).

Research on this topic has intensified rapidly in recent years; however, due to the abovementioned reasons, such research has mostly focused on the technical improvements of computer-aided planning. Even though human aspects are an important factor in the success of software projects and should be a key research area within the field of software project planning, existing studies have only explored the human properties of task selection and scheduling to a limited extent (Shen et al. 2018).

In this study, we extend the traditional SPSP with pairwise synergies between employees and present a novel matrix-based approach that can handle employees’ interdependencies, their different skills and efficiencies, and provide support for agile software development.¹ Then, we analyze and compare the solutions of the traditional and the extended SPSP versions on projects from generated project networks² to evaluate the impact of synergies on their costs. It will be shown that this factor has a highly significant impact that is strongly influenced by the structural parameters of the synergy networks (e.g., topology, network size and degree centrality).

The rest of this paper is organized as follows. Section 2 presents a review of the studies of both the scheduling process of the software projects and the synergy of workers. Sections 3 and 4 introduce the extended SPSP and the hybrid genetic algorithm proposed to solve this problem. Sections 5 and 6 present the steps of the calculation and its results. Section 7 shows the threats to validity. Finally, Sect. 8 concludes the paper, and Sect. 9 states the limitations.

2 Related works

In this section, we briefly review the main features of the software project scheduling problem. Then, we present several studies of how employee interactions can affect teams’ performance and consequently the allocation process itself.

2.1 Combination of task scheduling and personnel allocation

Many approaches to task scheduling (see, e.g., Hartmann and Briskorn 2010; Weglarz et al. 2011) and resource allocation (see, e.g., Pentico 2007) have been proposed in the literature; however, the integration between these fields has not been as comprehensively studied (Fernandez-Viagas and Framinan 2014). Generally, there is still no consensus on the name of this joint problem (see, e.g., Fernandez-Viagas and Framinan 2014); however, in the software development literature, it is referred to as the software project scheduling problem and has been extensively studied (see, e.g., Hapke et al. 1994; Xiao et al. 2013; Luna et al. 2014; Rezende et al. 2019).

The two major goals that arise when scheduling a software project are reducing both its cost and duration; however, these goals are in conflict with each other (see, e.g., Alba and Chicano 2007; Myszkowski et al. 2019). Similar to other problems with multiple objectives, a general SPSP has no single solution and instead has a Pareto-optimal set (Deb 2001). In this set, every point is optimal in the sense that neither the duration nor the cost objectives can be improved without worsening the other objective.

To solve a multiobjective problem, Coello et al. (2006) and Myszkowski et al. (2019) propose several metaheuristics, while Chicano et al. (2011) and Luna et al. (2014) compare the accuracy and scalability of several of these algorithms specifically for the case of SPSP. Chicano et al. (2011) and Luna et al. (2014) observe that the algorithm called Pareto archived evolution strategy (PAES) (Knowles and Corne 2000) has the best scalability and obtains the best approximate Pareto sets, while the most widely used nondominated sorting genetic algorithm II (NSGA-II) (Deb et al. 2002) and strength Pareto evolutionary algorithm 2 (SPEA2) (Zitzler et al. 2001) are examples of the least accurate solvers in general.³

While cross-validation of solvers and other technical aspects of SPSP have been extensively explored in the literature, significantly fewer studies consider the definition of the problem itself. In this paper, we focus on two possible approaches to extending the traditional SPSP. First, a general form of SPSP assumes fixed logic plans; however, applying flexible dependencies and using task priorities instead of fixed occurrences will result in more flexible project plans consistent with the agile approach. Despite the existence of agile project scheduling algorithms (see, e.g., Kosztyán 2015), to date, SPSP has not yet been extended to incorporate this feature. Second, while software development projects and particularly those that are software development projects using the agile approach (Wysocki 2011) place a greater emphasis on teamwork than the traditional methods (Nerur et al. 2005), in SPSP, employees are regarded as independent resources. This by definition assumes that the best (i.e., the most skilled) workers will perform tasks within the shortest timespan and with the highest quality; however, none of the extensions address the interdependence of resources.

2.2 Project team as a complex system

Although it is simpler to predict a team’s outcome based on the aggregate skills of its members, employees’ interdependencies may have a comparable or greater effect on team performance (Hsu et al. 2016). More specifically, interdependencies are sources of synergies between team members (see, e.g., Larson 2010; Hackman 1983); consequently, they have a significant—favorable or unfavorable—effect on team performance (see, e.g., Hackman 1983). In the relevant literature, there are numerous studies that help identify the sources of synergies.

During recent decades, researchers have investigated the personalities of team members as an important factor in cooperation (see, e.g., Hogan et al. 1988; Smith-Jentsch et al. 1996; Barry and Stewart 1997). According to Larson (2007), in diverse groups, joint work is more effective than in homogeneous groups, and diverse groups should perform better than even their best individual members. Moreover, cooperative interaction among members should benefit the performance of diverse groups but impair the performance of homogeneous groups. Whereas considering personalities is useful in general, purely personality-based allocation strategies provide weaker predictions than do strategies based on individual knowledge, abilities or skills (see, e.g., Schmitt et al. 1984; Hunter et al. 1990).

Formal and informal relationships between employees are also important sources of synergy. To investigate the social structure or, more generally, interdependence among group members, researchers use sociometry (Moreno 1960; Sorenson 1971). Although we have limited information on how the structural properties of a network affect collective performance, several studies reported in the literature have focused on this issue (see, e.g., Sparrowe et al. 2001; Ahuja et al. 2003; Cummings and Cross 2003). Based on Ahuja et al. (2003), centrality indicators of the social network are stronger direct predictors of performance than are individual characteristics, e.g., functional role, status or communication role.⁴ Sparrowe et al. (2001) observed that groups with decentralized structures performed better at complex tasks than the groups with centralized structures, and as stated in Cummings and Cross (2003), structural deficiencies of the leaders, more hierarchical structure and greater core-periphery discrepancies were negatively related to performance.

2.3 Summary and research questions

Based on the reviewed studies related to the practice and theories of human resource allocation, we can state that most approaches regard a project team as a complex system; nevertheless, none of the applied methods can handle the synergy among employees. Working together can result in either favorable or unfavorable synergy that affects the performance or outcome of a project. We know little about synergy, particularly in project environments where poorly balanced teams can cause a project to fail. According to the reviewed studies, integrated structures perform better than do other structures; however, we also know that in the case of complex tasks, decentralized structures can outperform other structures. In this study, a novel synergy-based method is presented, and the following research questions (RQs) are subsequently answered:

• $\mathbf {RQ}_{1}:$ Which indicators influence the effect of synergy on the project cost?

• $\mathbf {RQ}_{2}:$ Which structures of synergy networks increase/decrease the projects’ costs the most?

To answer the research questions, SPSP must be extended to handle flexible project plans to model agile projects and consider interdependencies between human resources to handle pairwise synergies between employees.

3 Formal description of the synergy-based SPSP

This section contains a formal description of SPSP, as well as that of its extension, i.e., SSPSP. Unlike other reported studies of this topic, for clarity and flexible planning, we use a matrix-based method to define the problem.

The proposed matrix-based method is an extension of the multidomain mapping (MDM) method (see Danilovic and Browning 2007). The original MDM version allows several domains that can interact with one another; however, the original MDM only handles fixed dependencies and task occurrences (see, e.g., Danilovic and Browning 2007; Browning 2014). Contrary to the original method, the proposed synergy mapping model (SMM) considers flexible dependencies and supplementary task completions to support the synergy-based software project scheduling problem (SSPSP).

Since SSPSP is an extension of SPSP, it is based on a combination of the agile approach and sociometric graphs. Formulating the problem, we extend the notation of Alba and Chicano (2007) and Luna et al. (2014). Since the problem is solved via the proposed multidomain matrix-based method, the necessary domains (submatrices) are also specified.

3.1 Notation

First, we give the mathematical definitions necessary for stating our problem as well as the solution algorithm. Here, we extend the formulation proposed by Alba and Chicano (2007) and Luna et al. (2014); however, our model considers the different skills and efficiencies of employees, as well as the synergy between them.

Briefly: We are given a set of employees with $\pm$ synergies among them and possessing certain (individual) levels of some skills or (skill) efficiencies to solve certain tasks that require certain levels of these skills. We must decide which tasks should be done (possibly not all of them) and their order, and we must distribute (allocate) the employees (possibly as part time) to solve the chosen tasks, fulfilling several other requirements and achieving some optimum [see Eqs. (31)–(34) for details]. The set of all of these decisions made by the algorithm is called a project scenario.

Fig. 1

Synergy mapping model (SMM)

All the data are stored in a large matrix called the SMM matrix, containing several blocks that we call domains, as shown in Fig. 1.

In detail:

• $E=\left\{ e_{1},\ldots ,e_{m}\right\}$ is the set of employees ($m\in {\mathbb {N}}^+$).

• ${\mathbf {Y}}$ is called the synergy domain in the proposed SMM. It is a symmetric m by m matrix of nonnegative real numbers ( ${\mathbf {Y}}\in \left( {\mathbb {R}}^{+}\right) ^{m\times m}$), denoting the synergies among the employees as (for $i,j=1,2,\ldots ,m$):

  • $[{\mathbf {Y}}]_{i,j}>1$ represents positive (or favorable) synergy,

  • $[{\mathbf {Y}}]_{i,j}=1$ represents neutral synergy,

  • $0<[{\mathbf {Y}}]_{i,j}<1$ represents negative (or unfavorable) synergy between employees $e_{i}$ and $e_{j}$, and $[{\mathbf {Y}}]_{i,i}=1$ and $[{\mathbf {Y}}]_{i,j}=[{\mathbf {Y}}]_{j,i}$ are assumed.⁵

• For any subset $\varepsilon \subseteq E$, we let:

  $$\begin{aligned} {\overline{Y}}_{\varepsilon }:=\left\{ \begin{array}{ll} 1 &{}\quad \text {if}\, |\varepsilon |\le 1\\ \root \eta \of {\prod \limits _{e_i,e_j\in \varepsilon , ~ i<j } ~[{\mathbf {Y}}]_{i,j}}\quad \text {where }\eta =\frac{|\varepsilon |\cdot \left( |\varepsilon |-1\right) }{2} &{}\quad \text {if}\quad |\varepsilon |>1 \end{array} \right. \end{aligned}$$

  (1)

  the (geometric) mean of synergies among the employees in $\varepsilon$.

• The synergy domain (Y) of the SMM can be represented by a social network where nodes are employees and weighted edges are negative or positive synergies between them (see Fig. 1). The notations of the structural parameters of this social network are summarized in Table 1.

• $S=\left\{ \sigma _{1},\ldots ,\sigma _{s}\right\}$ is the set of skills, the names of certain working abilities⁶ ($s\in {\mathbb {N}}$).

• Each employee may have a set of skills, i.e., person $e_{i}$ has skills $S\left( e_{i}\right) :=\left\{ \sigma _{1}^{\left( i\right) },\ldots ,\sigma _{\rho _{i} }^{\left( i\right) }\right\} \subseteq S$.

• The proposed model also handles skill efficiencies: $\ell \left( e_{i},\sigma _{k}\right) \ge 0$ is the (skill) efficiency of $e_{i}$ in $\sigma _{k}$ ($1\le i\le m$, $1\le k\le s$); clearly, $\sigma _{k}\in S\left( e_{i}\right) \iff 0<\ell \left( e_{i},\sigma _{k}\right)$.⁷ These efficiencies can be added, e.g., $e_{i_{1}}$ and $e_{i_{2}}$ working together achieve efficiency in $\sigma _{k}$ skill:

  $$\begin{aligned}{}[{\mathbf {Y}}]_{i_{1},i_{2}}\cdot \left( \ell \left( e_{i_{1}},\sigma _{k}\right) +\ell \left( e_{i_{2}},\sigma _{k}\right) \right) . \end{aligned}$$

  (2)

  For a larger set $\varepsilon \subseteq E$, we can only use the approximate formula:

  $$\begin{aligned} \ell \left( \varepsilon ,\sigma _{k}\right) :={\overline{Y}}_{\varepsilon }\cdot \sum _{e_i\in \varepsilon }\ell \left( e_{i},\sigma _{k}\right) \text {.} \end{aligned}$$

  (3)

  (Note that this formula will be modified by the matrix ${\mathbf {O}}$ later.)

• ${\mathbf {S}}$ is the m by s matrix $[{\mathbf {S}}]_{i,k}:=\ell \left( e_{i},\sigma _{k}\right)$ that we call the skill domain in the SMM matrix.

• $A=\left\{ a_{1},\ldots ,a_{n}\right\}$ is the set of tasks (or activities) to be performed ($n\in {\mathbb {N}}$).   $A^{c} \subseteq A$ is the subset of mandatory (or compulsory) tasks, and $A^{-}:=A\smallsetminus A^{c}$ is the set of supplementary tasks. Supplementary tasks can be removed from the project or postponed to a later project if they cannot be implemented due to constraints.

• The algorithm will choose which supplementary tasks will be carried out, but it must perform each compulsory task. The final set of tasks to be carried out is denoted by $A^{c(O)}$; clearly, $A^{c}\subseteq A^{c(O)}\subseteq A$ must hold.

• Among all of the tasks, we have dependencies $\prec ,\thicksim ,\bowtie$ with the following meanings. For any $i,j\le n$, $i\ne j$:

  • $a_{i}\prec a_{j}$ means a strict (or required) dependency: $a_{j}$ must not be started unless $a_{i}$ has been completed,

  • $a_{i}\thicksim a_{j}$ means no dependency: the starting time of $a_{j}$ is not affected by $a_{i}$,

  • $a_{i}\bowtie a_{j}$ means an uncertain (or flexible) dependency: the algorithm must turn each $a_{i}\bowtie a_{j}$ into either (i) $a_{i}\prec a_{j}$ or $a_{j}\prec a_{i}$ or (ii) $a_{i}\thicksim a_{j}$. In case (i), we say that the dependency $a_{i}\bowtie a_{j}$ is included in the project; in case (ii), it is excluded.

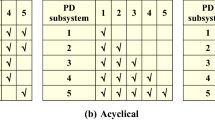
• Clearly, $\prec$ is a partial order that excludes cycles⁸ such as $a_{1}\prec a_{2}\prec \ldots \prec a_{1}$, while $\bowtie$ and $\thicksim$ are symmetric relations.

• ${\mathbf {A}}$ is called the logic domain in the SMM. It is the n by n matrix storing the above information as⁹:

  • $[{\mathbf {A}}]_{i,i}=1 \iff$ $a_{i}$ is mandatory,

  • $0<[{\mathbf {A}}]_{i,i}<1\iff$ $a_{i}$ is supplementary (score value or relative priority of $a_{i}$),

  • $[{\mathbf {A}}]_{i,j}=1 \iff$ $a_{i}\prec a_{j}$,

  • $[{\mathbf {A}}]_{i,j}=0 \iff$ $a_{i}\thicksim a_{j}$,

  • $0<[{\mathbf {A}}]_{i,j}<1\iff$ $a_{i}\bowtie a_{j}$ (score value or relative priority of $a_{i}\bowtie a_{j}$). (The values $[ {\mathbf {A}}]_{i,j}$ will also be called probabilities in constraint ${\mathbf {C}}_{5}$.)

• The algorithm must modify the elements of ${\mathbf {A}}$ such that $0<[{\mathbf {A}}]_{i,i}<1$ and $0<[{\mathbf {A}}]_{i,j}<1$ (and leave the others unchanged), where the final matrix is denoted by ${\mathbf {A}}({\mathbf {O}})$, which contains only the 0 and 1 entries.

• The set of skills that are required to perform activity $a_{j}$ is denoted by   $S\left( a_{j}\right) :=\left\{ \sigma _{1}^{\left( j\right) },\ldots ,\sigma _{\rho _{j} }^{\left( j\right) }\right\} \subseteq S$ $(j=1,2,\ldots ,n)$.

• More specifically, if the minimum amount of skill of $\sigma _{k}$ required for $a_{j}$ is a nonnegative real number $L\left( a_{j},\sigma _{k}\right) \in {\mathbb {R}}$, then we must have¹⁰$\sigma _{k}\in S\left( a_{j}\right) \iff 0<L\left( a_{j},\sigma _{k}\right)$.

• ${\mathbf {W}}$ is the n by s matrix storing L, i.e., $[{\mathbf {W}}]_{j,k}:=L\left( a_{j},\sigma _{k}\right)$, where ${\mathbf {W}}$ is called the skilled work domain (in SMM), and its elements $w_{j,k}=[{\mathbf {W}} ]_{j,k}$ are called skilled work elements.

• ${\mathbf {M}}$ is an m by n matrix, called the matching domain, where $[{\mathbf {M}}]_{i,j}\in [0,1]$ is the maximal (allowed) ratio of the working time of employee $e_{i}$ allocated to (working on) task $a_{j}$.¹¹

• The solution of the SSPSP, which must be determined by the algorithm, is an n by m matrix (of nonnegative real numbers), denoted by ${\mathbf {O}}$, where the element $[{\mathbf {O}}]_{j,i}>0$ represents the (final) allocation of employee $e_{i}$ to activity $a_{j}$.

• The value $[{\mathbf {O}}]_{j,i}$ is the proposed ratio of the working time of $e_{i}$ allocated to $a_{j}$; clearly, $[{\mathbf {O}}]_{j,i}=0$ means no allocation. $[{\mathbf {O}}]_{j,i}\le [{\mathbf {M}}]_{i,j}$ and $\sum _{j=1}^{n}[{\mathbf {O}}]_{j,i}\le 1$ must hold for each $j=1,2,\ldots ,n$ and $i=1,\ldots ,m$, while $\sum _{j=1}^{n}[M]_{i,j}\le 1$ are not required for any $i=1,\ldots ,m$.

• $[{\mathbf {O}}]_{j,i}$ will sometimes be denoted by $a_{j}^{e_{i}}$.

• The duration of activity $a_{j}$ is denoted by $a_{j}^{dur}({\mathbf {O}})$. This depends on resources modified by the synergy factor, as calculated in Eqs. (10) and (11). The starting time of $a_{j}$ is $a_{j}^{start}({\mathbf {O}})$, and the finishing time is¹²$a_{j}^{end}({\mathbf {O}})=a_{j}^{start}({\mathbf {O}})+a_{j}^{dur}({\mathbf {O}})$ [see Eq. (12)].

• The duration of the project is denoted by $p_{dur}$ or TPT (the total project time), and its cost is $p_{cost}$ or TPC (the total project cost).

• Each employee $e_{i}$ can be allocated partially or entirely to the project, where the total of $e_{i}^{w}:=\sum _{j=1}^{n}[ {\mathbf {O}}]_{j,i}$, not exceeding its maximum value $e_{i}^{maxw}:=\sum _{j=1}^{n}[{\mathbf {M}}]_{i,j}$. Clearly, $0\le e_{i}^{w}\le 1$ by $\sum _{j=1}^{n}[{\mathbf {O}}]_{j,i}\le 1$. (See the matching domain (${\mathbf {M}}$) in Fig. 1.)

• The monthly salary of employee $e_{i}$ is denoted by $e_{i}^{salary}$.

Table 1 Analyzed centrality and proximity metrics

3.2 Formalism related to project duration

Assume that the algorithm has already fixed all of the supplementary tasks and flexible dependencies (stored in ${\mathbf {A}}$ and in ${\mathbf {A}}\left( {\mathbf {O}}\right)$), as well as the allocations of $e_{i}$ to $a_{j}$ (stored in ${\mathbf {O}}$). In the following, the algorithm has already decided that all of the $a_{j}$ mentioned below are compulsory.

We note that Alba and Chicano (2007) assumed that there was no change in the allocation of a certain employee to a certain activity while it was being performed.

The total effort that is allocated to $a_{j}$ ($j=1,2,\ldots ,n$) is:

$$\begin{aligned} A_{j}:=\sum _{i=1}^{m}a_{j}^{e_{i}} =\sum _{i=1}^{m} [{\mathbf {O}}]_{j,i}\text {.} \end{aligned}$$

(4)

For any task $a_{j}$ ($j=1,\ldots ,n$), let:

$$\begin{aligned} \varepsilon _{j}:=\left\{ e_i \in E : 0<[{\mathbf {O}}]_{j,i}\right\} \end{aligned}$$

(5)

be the set of employees who are effectively working on¹³ (allocated to) $a_{j}$.

Since we measure the (skill) efficiencies, which must be summed separately, we have to consider all the skills separately. For any skill $\sigma _{k}$, the amount of work on $\sigma _{k}$ that team $\varepsilon _{j}$ completes in $a_{j}$ is (without synergies)¹⁴:

$$\begin{aligned} A_{j}^{w}\left( k\right) :=\sum _{i=1}^{m}\left( [{\mathbf {S}} ]_{i,k}\cdot [{\mathbf {O}}]_{j,i}\right) =\sum _{e_i\in \varepsilon _{j}}\ell \left( e_{i},\sigma _{k}\right) \cdot \left[ {\mathbf {O}}\right] _{j,i}\text {.} \end{aligned}$$

(6)

Considering the synergies, the adjusted amount of work done in skill $\sigma _{k}$ is:

$$\begin{aligned} A_{j}^{w,adj}\left( k\right) :={\overline{Y}}_{\varepsilon _{j}}\cdot A_{j}^{w}\left( k\right) \text {.} \end{aligned}$$

(7)

Since task $a_{j}$ requires $L\left( a_{j},\sigma _{k}\right) = \left[ {\mathbf {W}}\right] _{j,k}$ amount of skill $\sigma _{k}$, the required time (duration) for completing $\sigma _{k}$ in $a_{j}$ by $\varepsilon _{j}$ , without synergies is:

$$\begin{aligned} a_{j,k}^{dur}\left( {\mathbf {O}}\right) =\dfrac{L\left( a_{j},\sigma _{k}\right) }{A_{j}^{w}\left( k\right) }=\dfrac{\left[ {\mathbf {W}}\right] _{j,k}}{\sum _{i=1}^{m}\left( [{\mathbf {S}}]_{i,k}\cdot [{\mathbf {O}}]_{j,i}\right) }\text {,} \end{aligned}$$

(8)

and the adjusted required time (with synergies) is:

$$\begin{aligned} a_{j,k}^{dur,adj}\left( {\mathbf {O}}\right) =\dfrac{L\left( a_{j},\sigma _{k}\right) }{A_{j}^{w,adj}\left( k\right) }=\dfrac{\left[ {\mathbf {W}}\right] _{j,k}}{{\overline{Y}}_{\varepsilon _{j}}\cdot \sum _{i=1}^{m}\left( [ {\mathbf {S}}]_{i,k}\cdot [{\mathbf {O}}]_{j,i}\right) }\text {.} \end{aligned}$$

(9)

Assuming that each $e_{i}$ uses all of his or her skills simultaneously:

$$\begin{aligned} a_{j}^{dur}\left( {\mathbf {O}}\right) =\max \limits _{\sigma _k\in S\left( a_{j}\right) } \left\{ a_{j,k}^{dur}\left( {\mathbf {O}}\right) \right\} \end{aligned}$$

(10)

and (with synergies):

$$\begin{aligned} {\widetilde{a}}_{j}^{dur}\left( {\mathbf {O}}\right) :=a_{j}^{dur,adj}\left( {\mathbf {O}}\right) =\max \limits _{\sigma _k\in S\left( a_{j}\right) }\left\{ a_{j,k}^{dur,adj}\left( {\mathbf {O}}\right) \right\} \text {.} \end{aligned}$$

(11)

Of course, completing $a_{j}$ requires all necessary skills to be covered.¹⁵

This value is used to calculate the ending times of the activities $a_{j}^{end}({\mathbf {O}})=a_{j}^{start}({\mathbf {O}})+{\widetilde{a}}_{j}^{dur}( {\mathbf {O}})$, where:

$$\begin{aligned} a_{j}^{start}({\mathbf {O}}) \ge \left\{ \begin{array}{ll} 0&{}\quad \text {if} \ \not \exists \text { }a_{i}\in A\text {, }a_{i}\prec a_{j} \\ \max \{a_{i}^{end}({\mathbf {O}}):a_{i}\prec a_{j}\}&{}\quad \text {otherwise} \end{array}. \right. \end{aligned}$$

(12)

At this point, we also note that the referenced studies have not addressed the cases in which an activity cannot be started because there are no available resources for performing that activity, even though all of its prerequisite activities have been finished. Moreover, we assume that the starting time of the project is 0. (Clearly, $a_{i}$ and the former $\bowtie$ in Eq. (12) and hereinafter are decided by the algorithm to be carried out and converted to $\prec$.)

The values calculated above enable calculating the duration of the project ($p_{dur}$) as follows:

$$\begin{aligned} \text {TPT}:=p_{dur}=\max \{a_{j}^{end}({\mathbf {O}}):j=1,\ldots ,n\}. \end{aligned}$$

(13)

We must emphasize that the values $a_{j}^{start}({\mathbf {O}})$ in Eq. (12) and TPT in Eq. (13) are minimal: no algorithm can start $a_{j}$ and finish the project earlier than in Eqs. (12) and (13), so they can be denoted by $a_{j}^{start}({\mathbf {O}})_{\min }$ and $\hbox {TPT}_{\min }$. However, in practice, it is possible that some activities cannot be started at $a_{j}^{start}({\mathbf {O}})_{\min }$ (e.g., because of the lack of human resources). Therefore, our algorithm is allowed to schedule some (even all) tasks $a_{j}$ later than $a_{j}^{start}({\mathbf {O}})_{\min }$, as described by:

$$\begin{aligned} a_{j}^{start}({\mathbf {O}})_{ALG}\ge a_{j}^{start}({\mathbf {O}})_{\min }, \end{aligned}$$

(14)

where $a_{j}^{start}({\mathbf {O}})_{ALG}$ is the real starting time for the task $a_{j}$. Clearly, ${\widetilde{a}}_{j}^{dur}({\mathbf {O}} )_{ALG}={\widetilde{a}}_{j}^{dur}({\mathbf {O}})_{\min }$, $a_{j}^{end}( {\mathbf {O}})_{ALG}=a_{j}^{start}({\mathbf {O}})_{ALG}+{\widetilde{a}}_{j}^{dur}( {\mathbf {O}})_{ALG}$ and:

$$\begin{aligned} a_{j}^{start}({\mathbf {O}})_{ALG}\ge \left\{ \begin{array}{ll} 0&{}\quad \text {if} \ \not \exists \text { }a_{i}\in A\text {, }a_{i}\prec a_{j} \\ \max \{a_{i}^{end}({\mathbf {O}})_{ALG}:a_{i}\prec a_{j}\}&{}\quad \text {otherwise} \end{array} \right. \end{aligned}$$

(15)

must also hold.¹⁶

We also require:

$$\begin{aligned} \text {TPT}_{ALG}\ge \text {TPT}_{\min } \text {.} \end{aligned}$$

(16)

We call the sequence (of real numbers):

$$\begin{aligned} (a_{1}^{start}({\mathbf {O}})_{ALG},\ldots ,a_{n}^{start}({\mathbf {O}})_{ALG}) \end{aligned}$$

(17)

scheduled start time sequence (SST). Clearly, an SST must be determined by the algorithm. In the following, we omit the subscripts $\min$ and ALG, and we always mean ALG, unless stated otherwise.

Figure 1 presents several networks, such as a single project (see the logic domain, A and the project graph on the bottom right corner of Fig. 1), a synergy network (see the synergy domain, S and the synergy graph in the top left corner of Fig. 1), possible matches between employees and tasks (see the matching domain, M and the employee-task matching graph in the top right corner of Fig. 1), and the output domain (O). The skill domain (S) represents the skill efficiency, while the amount of required (skilled) work is specified in the skilled work domain (W). A prerequisite for project success is that the required skills are available. The proposed matrix-based model only represents the required available skills. The goal is to assign employees to tasks to achieve a good feasible solution with respect to the composite objective function [see Eq. (34)] and constraints (see ${\mathbf {C}}_{1}$-${\mathbf {C}}_{8}$ in Sect. 3.4).

3.3 Formalism related to the project cost

The cost of the project (TPC, $p_{cost}$) can be calculated as the sum of the salaries of employees that are paid for their dedication to the project. Since positive synergy reduces and negative synergy increases the duration $a_{j}^{dur}$ to ${\widetilde{a}}_{j}^{dur}$, the project cost can be calculated with and without the synergy effect, obtaining $\hbox {TPC}_{{syn}}$ and $\hbox {TPC}_{{nosyn}}$, respectively. Formally:

$$\begin{aligned}&\text {TPC}_{syn}=\text {TPC}:=p_{cost}=\sum _{i=1}^{m}\sum \limits _{j=1}^{n}(e_{i}^{salary}\times [{\mathbf {O}}]_{j,i}\times {\widetilde{a}}_{j}^{dur}({\mathbf {O}})), \end{aligned}$$

(18)

$$\begin{aligned}&\text {TPC}_{nosyn}:=\sum _{i=1}^{m}\sum \limits _{j=1}^{n}(e_{i}^{salary}\times [{\mathbf {O}}]_{j,i}\times a_{j}^{dur}({\mathbf {O}})). \end{aligned}$$

(19)

3.4 Constraints

While a solution to the SSPSP is calculated, several constraints must be taken into account and satisfied. First, we list these constraints, and then, we explain each of them in detail.

• ${\mathbf {C}}_1$: Each activity must be performed by at least one human resource.

• ${\mathbf {C}}_2$: The set of skills that an activity requires must be a subset of the union of skills of the employees who perform this activity.

• ${\mathbf {C}}_{3}$: There must not be any human resource who exceeds his or her maximum dedication (allocation) to the project (roughly, $e_{i}^{w}:=\sum _{j=1}^{n}[{\mathbf {O}}]_{j,i}\le e_{i}^{maxw}$ for $i=1,\ldots ,m$).

There are two new constraints: the first specifies the set of implemented tasks, and the second considers both the (skill) efficiencies and the synergies among employees.

• ${\mathbf {C}}_{4}$: The score of the project scenario (total project score, TPS; see Eq. (33)) is greater than a specified (score) constraint $C_{s}$.

• ${\mathbf {C}}_{5}$: The probability of the project structure is greater than a specified (probability) constraint $C_{p}$.

The following three additional constraints are the constraints of the project plan:

• ${\mathbf {C}}_{6}$: Overwork is allowed up to a certain level (roughly: $E^{w}=\sum _{i=1}^{m} e_{i}^{w} \le K^{w}$ for some constant $K^{w}$, with minor exceptions).

• ${\mathbf {C}}_{7}$: The total project cost (TPC) must be less than the cost constraint $(C_{c}).$

• ${\mathbf {C}}_{8}$: The duration of the project (the total project time, TPT) must be less than the time constraint $(C_{t}).$

In our model, a complex objective (target) function is specified. The goal is to specify the most likely project structure and a resource allocation scheme that minimizes the project duration in the most desired project scenario.

Now, we describe ${\mathbf {C}}_{1}$-${\mathbf {C}}_{8}$ in detail.

• ${\mathbf {C}}_{1} :$ for each $a_{j}\in A^{c(O)}$,

  $$\begin{aligned} \varepsilon _{j}:=\left\{ e_{i}\in E:0<[{\mathbf {O}}]_{j,i} \right\} \ne \emptyset . \end{aligned}$$

  (20)

• ${\mathbf {C}}_{2} :$ for each $a_{j}\in A^{c(O)}$,

  $$\begin{aligned} S\left( a_{j}\right) \subseteq \bigcup \limits _{ e_i \in \varepsilon _{j} }S\left( e_{i}\right) . \end{aligned}$$

  (21)

• ${\mathbf {C}}_{3} :$ Since several tasks cannot be solved simultaneously, the rate of the allocation of $e_{i}$ may vary with time. Therefore, we create a function $e_{i}^{work}(\tau )$ (for $0\le \tau \le p_{dur}$) that determines how much work by employee $e_{i}$ is dedicated (allocated) to the project for all of the parallel activities at time $\tau$:

  $$\begin{aligned} e_{i}^{work}(\tau ):=\sum _{\{j~|~a_{j}^{start}\le \tau \le a_{j}^{end},~a_{j}\in A^{c(O)}\}}[{\mathbf {O}}]_{j,i}. \end{aligned}$$

  (22)

  (Here, we mean $a_{j}^{start}({\mathbf {O}})_{ALG}\le \tau \le a_{j}^{end}({\mathbf {O}})_{ALG}$, according to SST of the algorithm.) Therefore, $C_{3}$ is:

  $$\begin{aligned} e_{i}^{work}(\tau ) \le e_{i}^{maxw} \quad \text {for} ~ i=1,\ldots ,m ~ \text {and} ~ \tau . \end{aligned}$$

  (23)

For ${\mathbf {C}}_{4}$ to ${\mathbf {C}}_{6}$, we need to define some additional terminology and notation.¹⁷

Let the score values of the implemented activity $a_{i}\in A^{c(O)}$ be ${\mathbb {S}}_{i}:=[{\mathbf {A}}]_{i,i}$ and the score values of the omitted one $(a_{i}\in A\backslash A^{c(O)})$ be ${\mathbb {S}} _{i}:=1-[{\mathbf {A}}]_{i,i}$ ($i=1,2,\ldots ,n$).

The probability $p_{i,j}$ of the (input) dependency $a_{i}\bowtie a_{j}$ for $a_{i},a_{j}\in A^{c(O)}$ is $p_{i,j}:=[{\mathbf {A}}]_{i,j}$ if that dependency will be included in the project plan (i.e., changed to $a_{i}\prec a_{j}$),¹⁸ and $p_{i,j}:=1-[ {\mathbf {A}}]_{i,j}$ if not (i.e., changed to $a_{i}\thicksim a_{j}$).

The proposed model allows decision-makers to omit several supplementary activities from this project and allocate them to the next project (or the next sprint), i.e., $A^{c}\subseteq A^{c(O)}\subseteq A$.

For ${\mathbf {C}}_{4}$ through ${\mathbf {C}}_{6}$, we are given the (suitable) constants (positive real numbers) $C_{s}$, $C_{p}$, $C_{c}$, $C_{t}$, $K^{w}$ and $\epsilon ^{K}$.

• ${\mathbf {C}}_{4}$:

  $$\begin{aligned} \text {TPS}:=\root n \of {\prod _{i=1}^{n}{\mathbb {S}}_{i}}~\ge ~C_{s}. \end{aligned}$$

  (24)

• ${\mathbf {C}}_{5}$:

  $$\begin{aligned} \sum _{a_{i},a_{j}\in A^{c(O)},~i\ne j}p_{i,j}\ge C_{p}. \end{aligned}$$

  (25)

For ${\mathbf {C}}_{6}$, first, we construct the function $overwork(\tau )$ for $0\le \tau \le p_{dur}$ as:

$$\begin{aligned} overwork(\tau ):=\left\{ \begin{array}{ll} \sum _{i=1}^{m} e_{i}^{work}(\tau ) - K^{w} &{}\quad \text {if} \ \sum _{i=1}^{m} e_{i}^{work}(\tau ) > K^{w} \\ 0&{}\quad \text {otherwise} \end{array} \right. \text {,} \end{aligned}$$

(26)

and the total overwork $p_{over}$ of the project:

$$\begin{aligned} p_{over}:=\int \limits _{\tau =0}^{\tau =p_{dur}}overwork(\tau )d\tau \text {.} \end{aligned}$$

(27)

Now, we set:

• ${\mathbf {C}}_{6}$:

  $$\begin{aligned} p_{over} < \epsilon ^{K}. \end{aligned}$$

  (28)

• ${\mathbf {C}}_{7}$:

  $$\begin{aligned} \text {TPC}:=p_{cost}\le C_{c}. \end{aligned}$$

  (29)

• ${\mathbf {C}}_{8}$:

  $$\begin{aligned} \text {TPT}:=p_{dur}\le C_{t}. \end{aligned}$$

  (30)

Next, we must find $\hbox {TPT}_{\min }$, $\hbox {TPC}_{\min }$ and $\hbox {TPS}_{\max }$. The minimum $\hbox {TPT}_{\text {min}}$ is reached if all of the uncertain tasks and flexible dependencies are omitted from the project (i.e., $A^{c(O)}=A^{c}$ and each $\bowtie$ is changed to $\thicksim$) and if the maximum number of employees is dedicated (allocated) to the activities (i.e., $[{\mathbf {O}}]_{j,i}=[{\mathbf {M}}]_{i,j}$).

Similarly, $\hbox {TPC}_{\text {min}}$ is reached if all of the uncertain tasks are omitted (i.e., $A^{c(O)}=A^{c}$), whereas TPC reaches its maximum $\hbox {TPC}_{\max }$ if all of the tasks are completed (i.e., $A^{c(O)}=A$) (see Kosztyán and Szalkai 2018, 2020 and Kosztyán et al. 2019 for details).

Now, we state the objective functions that we seek to optimize simultaneously [in Eq. (34)] using the algorithm:

$$\begin{aligned}&\text {TPT}\rightarrow \min , \end{aligned}$$

(31)

$$\begin{aligned}&\text {TPC}\rightarrow \min , \end{aligned}$$

(32)

and

$$\begin{aligned} \text {TPS}\rightarrow \max . \end{aligned}$$

(33)

These objective (target) functions can be considered a multiobjective problem or a composite objective (target) function and can be specified as follows (here, $C_{s}$, $C_{p}$ , $C_{c}$ and $C_{t}$ are given reasonable constants):

$$\begin{aligned} z:=1-\root 3 \of {\left( \frac{C_{t}-\text {TPT}}{C_{t}-\text {TPT}_{\min }} \right) *\left( \frac{C_{c}-\text {TPC}}{C_{c}-\text {TPC}_{\min }}\right) *\left( \frac{\text {TPS}-C_{s}}{\text {TPS}_{\max }-C_{s}}\right) } \rightarrow \min , \end{aligned}$$

(34)

assuming the constraints ${\mathbf {C}}_{1}-{\mathbf {C}}_{8}$.

Finally, similar to most of the SPSP literature, we assume constant skills of the human resources for simplicity. However, several studies address improvements in human skills, and our model can also be extended to take this into account. For example, Chang et al. (2008) introduce an employee experience and training model that accounts for the learning speed of employees and the time interval of training when calculating the improvement in employee skills. The model in Chang et al. (2008) influences how quickly employees can perform a specific task.

3.5 Summary of notations

The notations are summarized as follows:

• $E=\left\{ e_{1},\ldots , e_{m}\right\}$ = employees, $e_{i}\in E$,

• $[{\mathbf {Y}}]_{i,j}$ = synergy between $e_{i}$ and $e_{j}$,

• ${\overline{Y}}_{\varepsilon }= \root \eta \of {\prod \nolimits _{e_i,e_j\in \varepsilon , ~ i<j } ~[{\mathbf {Y}}]_{i,j}}$ geometric mean of synergies [see Eq. (1)],

• $S=\left\{ \sigma _{1},\ldots ,\sigma _{s}\right\}$ = skills, $\sigma _{k}\in S$,

• $S\left( e_{i}\right) :=\left\{ \sigma _{1}^{\left( i\right) },\ldots ,\sigma _{\rho _{i} }^{\left( i\right) }\right\}$ = skills of $e_{i}$ , $S\left( e_{i}\right) \subseteq S$,

• $[{\mathbf {S}}]_{i,k}=\ell \left( e_{i},\sigma _{k}\right)$ = the efficiency of $e_{i}$ in $\sigma _{k}$, $\ell \left( \varepsilon ,\sigma _{k}\right) :={\overline{Y}}_{\varepsilon }\cdot \sum _{e_i\in \varepsilon }\ell \left( e_{i},\sigma _{k}\right)$,

• $A=\left\{ a_{1},\ldots ,a_{n}\right\}$ = tasks (activities), $a_{j}\in A$,

  • $A^{c}=$ mandatory (compulsory), given, $A^{-}=A\smallsetminus A^{c}$ supplementary,

  • $A^{c(O)}=$ compulsory tasks decided by the algorithm, $A^{c}\subseteq A^{c(O)}\subseteq A$,

  • $a_{i}\prec a_{j}$ strict (or required) dependency, $a_{i}\thicksim a_{j}$ no dependency,

  • $a_{i}\bowtie a_{j}$ uncertain (or flexible) dependency,

• ${\mathbf {A}}$ = input matrix:

  • $[{\mathbf {A}}]_{i,i}=1\iff a_{i}$ is mandatory,

  • $0<[{\mathbf {A}}]_{i,i}<1\iff a_{i}$ is supplementary,

  • $[{\mathbf {A}}]_{i,j}=1\iff$ $a_{i}\prec a_{j}$,

  • $[{\mathbf {A}}]_{i,j}=0\iff$ $a_{i}\thicksim a_{j}$,

  • $0<[{\mathbf {A}}]_{i,j}<1\iff$ $a_{i}\bowtie a_{j}$,

• ${\mathbf {A}}({\mathbf {O}})=$ ${\mathbf {A}}$ as modified by the algorithm,

• $S\left( a_{j}\right) :=\left\{ \sigma _{1}^{\left( j\right) },\ldots ,\sigma _{\rho _{j} }^{\left( j\right) }\right\}$ = skills required to $a_{j}$, $S\left( a_{j}\right) \subseteq S$,

• $[{\mathbf {W}}]_{j,k}=w_{j,k}=L\left( a_{j},\sigma _{k}\right) =$ the minimum amount of skilled work $\sigma _{k}$ required to $a_{j}$,

• $[{\mathbf {M}}]_{i,j}$ = the maximal (allowed) ratio of the working time of $e_{i}$ allocated to $a_{j}$,

• $[{\mathbf {O}}]_{j,i}$ = the (proposed) working time ratio of $e_{i}$ allocated to $a_{j}$,

• $a_{j}^{e_{i}}:=[{\mathbf {O}}]_{j,i}$,

• $A_{j}:=\sum _{i=1}^{m} a_{j}^{e_{i}}$ = the total effort allocated to $a_{j}$ (in terms of human resources),

• $\varepsilon _{j}:=\left\{ e_{i}\in E:0<a_{j}^{e_{i}}\right\}$,

• $e_{i}^{w}:=\sum \limits _{j=1}^{n}[{\mathbf {O}}]_{j,i}\le e_{i}^{maxw}:=\sum _{j=1}^{n}[ {\mathbf {M}}]_{i,j}$,

• $a_{j}^{dur}({\mathbf {O}})$ = duration of $a_{j}$; see Eq. (10),

• ${\widetilde{a}}_{j}^{dur}({\mathbf {O}})$ = adjusted duration of $a_{j}$; see Eq. (11),

• $a_{j}^{end}({\mathbf {O}})=a_{j}^{start}({\mathbf {O}})+ {\widetilde{a}}_{j}^{dur}({\mathbf {O}})$,

• $a_{j}^{start}({\mathbf {O}})_{\min }$ = minimal starting time of $a_{j}$; see Eq. (12),

• $a_{j}^{start}({\mathbf {O}})$ = $a_{j}^{start}({\mathbf {O}})_{ALG}$ = the scheduled starting time, SST, decided by the algorithm,

• SST = $\left( a_{1}^{start}({\mathbf {O}})_{ALG}~,~...~,a_{n}^{start}( {\mathbf {O}})_{ALG}\right)$; see Eq. (17),

• TPT $=p_{dur}$ = total project duration; see Eq. (13 ),

• $\hbox {TPC}_{syn}=~$TPC $=p_{cost}$ = total project cost with synergies; see Eq. (18),

• $\hbox {TPC}_{{nosyn}}$ = total project cost without synergies; see Eq. (19),

• $e_{i}^{work}(\tau )$ = how much $e_{i}$ is allocated to the project at time $\tau$; see Eq. (22),

• ${\mathbb {S}}_{i}$ = score values of $a_{i}$,

• $p_{i,j}$ = probability of the dependency $a_{i}\bowtie a_{j}$,

• TPS = total project score; see Eq. (24),

• $overwork(\tau )$ = general overwork at time $\tau$; see Eq. (26),

• $p_{over}$ = the total overwork of the project; see Eq. (27),

• z = the composite objective function to be minimized; see Eq. (34).

4 Proposed hybrid genetic algorithm

Since SPSP is NP-hard (Xiao et al. 2013), which is a special case of synergy-based SPSP, the SSPSP is also NP-hard. There are exact methods that can solve small instances of SPSP to optimality (Vega-Velázquez et al. 2018); however, these methods are not practical for larger instances, and their resolution requires other kinds of techniques such as metaheuristics (Yang 2010). Thus, a metaheuristic method of solving it is proposed. This section provides an overview of this algorithm.

Although most variables of the objective (target) function (i.e., dedications to activities and the scheduled start time of activities, referred to as SST) are continuous (with real variables), the model also contains several binary variables, namely, decisions regarding task/dependency exclusion/inclusion. Therefore, a mixed-integer genetic algorithm is used to seek a good feasible solution. All of the default operators (i.e., crossover, mutation, and selection) of the genetic algorithm must be modified because an excluded task has no dependency, duration, or cost demands.

The results of the genetic algorithm are refined using a Nelder-Mead minimization (NMM) method. The NMM optimization function continues the optimization after the termination of the GA. The NMM function can refine only the real values, such as the values of the output matrix (O) and the scheduled start time (SST) of activities. The MATLAB Global Optimization toolbox is used to implement the hybrid genetic algorithm; however, the standard mutation, crossover and selection function as well as the hyperparameters must be modified.

Generally, the sets of excluded/included flexible task occurrences and flexible task dependencies (see the logic domain $(\mathbf {A)}$), the values of allocations (see the output domain $({\mathbf {O}})$) and the scheduled start time (SST) for all tasks must be specified. After the final specification, the resulting matrix ${\mathbf {A}}^{\prime }$ contains only values $\{0,1\}$, where $[{\mathbf {A}}]_{ii}=1$ ($[{\mathbf {A}}]_{ii}=0$) means that task $a_{i}$ will be included in (excluded from) the project. Nevertheless, if a task is excluded from the project, the dependencies of the (excluded) tasks and all the (time/cost/resource) requirements are also excluded from the project.

4.1 Genetic algorithm parameters

Fitness function In our case, the fitness function is a composite function [see Eq. (34)]. We seek the elements of the output matrix $({\mathbf {O}}\in {\mathbb {R}} _{+}^{n\times m})$, the decision results of the flexible dependencies and supplementary task occurrences that are represented in the final logic domain ${\mathbf {A}}^{\prime }\in \{0,1\}^{n\times n}$, and the scheduled start time for all activities such that we can satisfy the resource constraint. It is assumed that a potential solution to a problem may be represented as a set of parameters/values. These values (known as genes) are joined together to form a vector (referred to as a chromosome, shown in Fig. 2). In genetic terminology, the set of values represented by a particular chromosome is referred to as an individual.

Fig. 2

Structure of a chromosome

If u is the number of uncertain tasks + dependencies, m is the number of employees, and n is the number of activities, then a chromosome vector with $u+(m+1)n$ elements can be constructed. For ease of use, the first part of the chromosome is the decision part, and the numbers are binary values. The second part is the output, which codes the output matrix row by row. In this part, the values are real and positive within the interval of [0,${\mathbf {e}}^{maxw}$]. The last part is the scheduling part, where the values are also real and positive. The fitness of an individual depends on its chromosome and is evaluated by the fitness function. During the reproductive phase, individuals are selected from the population and are recombined, producing offspring that compose the next generation. Parents are then randomly selected from the population using a scheme that favors fitter individuals. After two parents have been selected, their chromosomes are recombined, typically using the mechanisms of crossover and mutation. The latter is usually applied to some individuals to guarantee population diversity.

Population In the first step, a number of possible solutions must be generated. First, the elements of the logic domain ${\mathbf {A}}^{\prime }$ will be generated because if $[{\mathbf {A}}^{\prime }]_{ii}=0$, then $[{\mathbf {O}}]_{ij:=1,2...,m}:=0$, i.e., activity $a_{i}\in A$ will be excluded from the project; therefore, the excluded task has no time, cost or resource requirements. Since an excluded task has no dependencies, $[{\mathbf {A}}^{\prime }]_{ji}=[{\mathbf {A}}^{\prime }]_{ij}:=0$ if $[{\mathbf {A}}^{\prime }]_{ii}=0.$ We denote the initial population by $P_{0}$ and the population of the Gth generation by $P_{G}$.

Selection mechanism One of the main operators in a genetic algorithm is the selection operator. First, feasible solutions must be selected by a tournament. Because we usually have many feasible solutions, we use a tournament selection mechanism. In this case, each parent is determined by choosing a random number of tournament players and then choosing the best individual from that set to be a parent. The tournament size must be at least 2. In our case, we set the tournament size to 10. We denote the set of selected chromosomes in the Gth generation by $S_{G}$.

Elite count This is a positive integer specifying how many individuals in the current generation are guaranteed to survive to the next generation. It was set to 5% in our work, which means there were 5% so-called elite children in every generation.

Crossover fraction The crossover fraction specifies the fraction of each population (other than elite children) that consists of crossover children. A crossover fraction of 1 means that all of the children other than elite individuals are crossover children, while a crossover fraction of 0 means that all of the children are mutation children. The best results were obtained when we set this parameter to 0.8. This means that 80% of the selected children (excluding elite children) were children used in the crossover function (so-called crossover children), and 20% of the selected children (excluding elite children) were used in the mutation function (so-called mutation children).

Crossover operator We used the (fractioned) selected chromosomes. Since a chromosome has a binary or decision part and two continuous parts, two kinds of crossover functions must be combined. For the continuous parts, the arithmetic crossover function is used. Such a function creates children that are the weighted arithmetic mean of the two parents (i.e., depending on the fitness function). For the continuous part (called recombined), this crossover function can be very effective. At the same time, this crossover mechanism cannot be used for the binary or decision parts of the chromosome. In this case, a uniform crossover function is used. However, the parents may be infeasible; thus, here, we assume that the feasible parents’ genes are 10 times as dominant. In other words, a gene is ten times more likely to originate from feasible parents than from infeasible parents.¹⁹ After the set of children chromosomes has been determined, the requirements of the excluded tasks and their task dependencies must be eliminated (set to 0). We denote the set of recombined children chromosomes in the Gth generation by $C_{G}(S_G)$.

Mutation operator The mutation is a two-step process, in which the first step is general and is carried out for all parts of the chromosome. In the first step, the algorithm selects a fraction of the vector entries of an individual for mutation, where each entry has a probability rate of being mutated. According to the results of the settings, this rate is specified as 0.01. In the second step, although the same mechanism is used when the mutation operator is implemented, the two parts of the chromosomes must be distinguished. In this case, the adaptive feasible mutation function is used. The mutation operator chooses a direction and step length that satisfy the bounds and linear constraints. In the presence of constraints, directions that are adaptive with respect to the preceding successful or unsuccessful generation are randomly generated. After the mutation operator is used, the requirements of the excluded tasks and their task dependencies must be eliminated (set to 0). We denote the set of mutated chromosomes in the Gth generation by $M_{G}(S_G)$.

Next generation The mutated and crossover individuals are considered together with the old population, and the best $N=100$ individuals are selected for the next generation.

Stopping criteria A genetic algorithm terminates if we reach the maximum number of generations (set at 100 in this case) or if the average relative change in the best fitness function value over generations is less than or equal to the function tolerance (1E-8).

5 Calculation steps

The purpose of the simulation is to determine the parameter(s) that influence(s) the (changes in) project duration and the cost demands of the project while considering the synergies between the employees. The simulation process is separated into two stages.

• Stage 1: Specifying problem sets.

• Stage 2: Solving problems.

5.1 Specify problem sets

A problem set contains the following:

• (1) SMM matrices that numerically represent the synergy-based software scheduling problem,

• (2) Minimum ($\delta _{\min }$) and maximum ($\delta _{\max }$) values of the possible synergies between two members,²⁰ and

• (3) Constant ratios (see Sect. 5.1.2).

5.1.1 Specification of SMM matrix

To determine the SMM matrices, first, the logic and skill domains of the SMM matrices are generated by the iMOPSE project generator (Myszkowski et al. 2019).

The aim of the selection and generation of the initial project plans is to meet the expectations for (IT) software project plans to the greatest extent possible, particularly the features of agile projects. Therefore, the following selection criteria were defined:

$\hbox {CR}_1$:

Since Tavares et al. (1999) and Vanhoucke (2012) showed that software projects usually contain more parallel tasks, in the case of selected project structures, the number of parallel tasks should be greater than the number of serial tasks.²¹ Nevertheless, several agile methods, such as the KANBAN and SCRUMBAN methods, limit the number of parallel work-in-progress (WIP) tasks and allow only 3–5 WIP tasks. Therefore, in the simulation, the number of WIP tasks must be lower than 5.

$\hbox {CR}_2$:

Projects are usually separated into smaller autonomous subprojects (so-called sprints) (see, e.g., Dingsøyr et al. 2012) that should be completed within 2-5 weeks; therefore, the number of tasks is limited and should not be greater than 50.

Therefore, the number of tasks was 30 and 50 ($N_a$), and the number of employers (resources) was 10. The other parameters were selected as the default values with a minimal task duration = 1, maximal task duration = 8, minimal resource skill type = 1, and maximal resource skill type = 9 (the number of skills is $N_{sk}$). Ten projects that fulfilled criteria $\hbox {CR}_1$ and $\hbox {CR}_2$ were selected from the generated project networks.

Nevertheless, these project networks cannot be used directly. Neither known project generators—such as ProGen (Kolisch and Sprecher 1997), RanGen I (Demeulemeester et al. 2003), and II (Vanhoucke et al. 2008) or iMOPSE (Myszkowski et al. 2019)—nor open project data sources—such as PSPLIB (Kolisch and Sprecher 1997) and MMLIB (Peteghem and Vanhoucke 2014)—distinguish mandatory and supplementary tasks or consider strict and flexible dependencies. Therefore, there are no score values linked to task completion or task dependencies. Thus, to simulate project flexibility, $ff \times 100$% (where $ff:={0.10,0.15,0.20}$) of the matrix values are reduced from 1 to a lower value in the range of [0.5,1.0], causing them to represent either uncertain tasks or flexible dependencies.

The original database does not contain synergies between the employees, which therefore must be specified to follow a sociometric structure (see Fig. 5. The default value of synergy between two employees is 1 and is known as neutral synergy. For given sociometric structures (see Fig. 5 in Sect. 6), the synergy values (weights of synergy networks) can be either greater or less than 1. Values $\delta _{\min }:=\{-0.3,-0.1,\ldots ,0.2\}, \delta _{\max }:=\delta _{\min }+0.1$ represent the minimum and maximum differences between the generated and neutral synergies, respectively.

5.1.2 Calculate constraints

After SMM matrices are generated, the constraints are calculated. The ratio of the project score is $C_{s\%}=\frac{C_{s}-\text {TPS}_{\min }}{{\text {TPS}_{\max }}-{\text {TPS}_{\min }}}:=\{0.6,0.8.,1.0\}$. In addition to the score constraints, both cost ($C_{c}:=\{1.00,1.25,1.50\}\cdot \text {TPC}_{\min }$) and time ($C_{t}:=\{1.00,1.25,1.50\}\cdot \text {TPT}_{\min }$) are calculated. As a result, a set of $n_{C_{t}\%}\times n_{C_{c}\%}\times n_{C_{s}\%}\times n_{ff\%}\times n_{s_{\max }}\times n_{n}\times n_{proj}= 3^5\times 2 \times 144 =69,984$ SMM matrices and constraints are generated, where $n_{C_{t}\%}, n_{C_{c}\%}, n_{C_{s}\%}$ are the numbers of time, cost and score constraints, respectively; $n_{ff\%}$ is the number of flexible parameters; $n_{s_{\max }}$ is the number of $s_{\max }$ values; $n_{n}$ is the number of task numbers (30, 50); and $n_{proj}$ is the number of selected project structures.

5.2 Solve problems

In stage 2, the problem sets are solved by the proposed hybrid genetic algorithm, where the objective (target) function is Eq. (34). Given this complex target function, in addition to the maximization of the project scores, the project duration, project cost, and thus the resource demands must be reduced simultaneously. The project durations (TPT), project costs (TPC), and total project scores (TPS) are calculated for every problem set both considering and ignoring synergies, obtaining $\hbox {TPX}_{\text {syn}}$ and $\hbox {TPX}_{\text {nosyn}}$, respectively. The differences between TPX_nosyn and TPX_syn are calculated, and the cost differences observed in the results are studied. In this study, both positive (or favorable) and negative (or unfavorable) synergistic effects are considered. A positive $\Delta$TPC = TPC_nosyn-TPC_syn means that the positive synergy effect is greater than the negative synergy effect.

6 Results

In this section, we answer the stated research questions ($\mathbf {RQ}_{1}$, $\mathbf {RQ}_{2}$) by analyzing 69, 984 optimization results. The analysis is based on the following research model (see Fig. 3).

Fig. 3

Research model

This model is focused on three cases: the case of SPSP, in which synergies are ignored (M1), the case of SSPSP, in which synergies are considered (M2), and the difference between these two approaches (M3). Since the cost of the project is a function of the duration and the employees’ salary, in the main text, ${TPC}_{nosyn}$, ${TPC}_{syn}$ and $\Delta TPC$ are considered the only dependent variables. To derive a complete picture of the operation of the proposed method, we also perform calculations for the project durations in the Appendices (see Appendices B and C).²²

• $\mathbf {RQ}_{1}:$ Which indicators influence the effect of synergy on the project cost?

To answer this question, the regression tree ensemble model of the MATLAB regression learner app (MathWorks 2019b) is employed.²³ Fig. 4 shows the relative importance of the independent variables/predictors for all three cases.²⁴

Fig. 4

Relative importance of the various predictors

In the case of the SPSP (see Fig. 4—M1), the size of the project ($N_a$) and the various skills of employees ($N_{sk}$) are the main factors impacting project costs; however, if synergies between two employees are considered (see Fig. 4—M2), the principal effect is due to the average pairwise synergy (AvgSyn) itself. In this case, changes in the time, score and cost constraints ($C_{t\%},C_{s\%},C_{c\%}$) and flexibility (ff) also influence the project cost, while the previously important size ($N_{a}$) and skills ($N_{sk}$), as well as degree of centrality ($C_D$), have only a small impact on the cost.

Model 3 answers $\mathbf {RQ}_{1}$ by specifying the parameters that explain the cost differences of these two approaches. According to this model, the project size has the highest explanatory power of 47%, followed by the average synergy (AvgSyn—35%) and the structural parameter (${C}_{D}$ – 16%).

These results have two main implications. First, the synergy-related parameters have a stvery strong effect on projects’ costs even though, based on the current parameterization of our model, the interdependence of two employees can only change their performance by up to 30% (see Sect. 5). Second, the high impact of the structural parameter ($C_{D}$) appears to be consistent with the relevant literature (see Sect. 2.2). These statements emphasize the impact of the interdependencies between employees on (software) project scheduling; in other words, they highlight the importance of the SSPSP approach.

• $\mathbf {RQ}_{2}:$ Which structures of synergy networks increase/decrease the projects’ costs the most?

To answer this question, we examine how $\Delta$TPC (see Fig. 3—M3) is influenced by the sociometric structure and how their relation changes based on the structural parameter (${C}_{D}$; the respective results are shown in shades of gray) or how project flexibility (ff—Cases 1–3) varies (see Fig. 5).

Fig. 5

Effect of sociometric structures on the project cost

Figure 5 shows that structures with a low degree of centrality ($C_{D}$) generally lead to a greater reduction in the project cost; however, the veracity of this statement depends on the topology of the sociometric network. Although we observe that the flexibility of the project (ff) has a negligible effect on $\Delta$TPC (see Fig. 4), we find that the chain and full graph networks are highly sensitive, even to insignificant changes of this parameter (see Fig. 5 Cases 1-3). In some cases involving these topologies, we observe that $\hbox {TPC}_{\text {syn}}$ is greater than $\hbox {TPC}_{\text {nosyn}}$, resulting in a negative $\Delta$TPC. This finding is contrary to that of Sparrowe et al. (2001) since in this model, decentralized networks (such as circle and full graph networks) are unable to reduce costs by an amount greater than that of the centralized networks (such as star and sociometric star networks). Furthermore, in the case of networks randomly containing favorable and unfavorable synergies, the most decentralized topology (the full graph) leads to the worst results because of its high sensitivity to negative synergies.

7 Threats to validity

Internal validity threats in our case study can be due to the randomness of the results obtained from the simulation and GA, as well as a lack of treatment of several variables such as synergy structures for the optimization. To avoid such a threat, different actions were taken:

• First and foremost, we carefully calibrated the number of generations, elite count, crossover fraction, mutation rate and population size needed by the GA. The chosen values were determined to ensure that further changes did not significantly affect the results. Hyperparameters were then used where the convergence was best.

• Similarly, we calibrated the number of iterations required by the entire approach. As described in detail in Section 4, further increases over 50 iterations do not produce improvements in our fitness function; nevertheless, the maximum iterations are specified to 100 (see Sect. 4).

• To avoid the effect of randomness on the results, GAs were executed 40 times, and we verified that the obtained fitness function value at the last stage does not change among the iterations.

• Finally, Nelder-Mead optimization was used to refine the continuous part of the chromosome.

Regarding the external validity, our approach and the obtained results can be extended to non-IT project structures. We applied $\hbox {CR}_1$ and $\hbox {CR}_2$ (see Sect. 5.1.1) to select project structures that are specific to IT projects merely because flexible approaches are still only widely used in IT projects. However, with the proliferation of flexible approaches, this study may also be interesting for projects with different structures.

Construct validity threats may be due to the simplifications of the software project process. To mitigate this threat, all small social network structures were explored, which can be reviewed in the literature. Software projects are generated by the iMOPSE generator (Myszkowski et al. 2019). The selection criteria (see $\hbox {CR}_1$ and $\hbox {CR}_2$ in Sect. 5.1.1) were then followed. Therefore, considering the available literature regarding the structure of IT projects, the generated project structure characterizes the features of an IT project.

To improve the conclusion validity, the optimization results are analyzed by a highly robust method, the so-called regression tree ensemble model of the MATLAB regression learner app (MathWorks 2019b). During the calculation, 10-fold cross-validation was used, and hyperparameters were tuned by Bayesian optimization.²⁵ In addition, large-scale simulation increases the validity of the conclusion.

8 Conclusions

In this paper, the traditional software project scheduling problem is extended with different employee skill efficiencies and pairwise synergies between them—which can influence their performance during project implementation—as well as with flexible structure of the project—which is used in flexible management such as agile project management. Using simulations based on the new approach, we search for project indicators that have the largest influence on changes in project costs. The main results of the study are as follows. Based on the proposed simple model, (1) the costs of projects are extremely sensitive to the interdependencies of resources; (2) synergy networks with a low degree of centrality significantly reduce the project costs, and (3) synergy networks with a full graph topology are most sensitive to unfavorable synergies (e.g., conflicts). Since the impact of positive or negative pairwise synergies and the structure of sociometric networks can also be modeled, the proposed method can be a novel element in risk analysis tools, particularly in the context of human resource-critical projects.

9 Limitations and directions for future research

To simplify the model, the simulations we performed were based on only pairwise synergies; nevertheless, we believe that the importance of resource interdependencies may motivate researchers to explore this aspect in greater detail and to test our statements in practice. The presented simple model disregards several important human factors that could affect our results (e.g., employees may prefer working in groups with a decentralized sociometric structure). In our study, we focused on single projects; however, such software projects are usually pursued in a multiproject environment. Therefore, the next paper will address the impacts of synergy effects in software projects in a multiproject environment.

Appendices

Appendices

1.1 Appendix A Correlation of independent variables

See Appendix Table 2.

Table 2 Kendall rank correlation of independent variables

1.2 Appendix B Predictor importance in additional models

See Appendix Fig. 6.

Fig. 6

Relative importance of the various predictors (dependent variables are related to time)

Appendix C Supplementary information

See supplementary information files.