Abstract
For a scheduling problem to minimize the makespan on three uniform parallel machines we present a parametric analysis of the quality of a schedule with at most one preemption compared to the global optimal schedule with any number of preemptions. A tight bound is derived as a function of the relative speeds of the machines, provided that two of the machines have the same speed.
Similar content being viewed by others
1 Introduction
In parallel machine scheduling, we are given the jobs of set \(N=\left\{ J_{1},J_{2},\ldots ,J_{n}\right\} \) and m parallel machines \(M_{1}\), \( M_{2},\ldots ,M_{m}\). If a job \(J_{j}\in N\) is processed on machine \(M_{i}\) alone, then its processing time is known to be \(p_{ij}\). There are three main types of scheduling systems with parallel machines: (i) identical parallel machines, for which the processing times are machine-independent, i.e., \(p_{ij}=p_{j}\); (ii) uniform parallel machines, which have different speeds, so that \(p_{ij}=p_{j}/s_{i}\), where \(s_{i}\) denotes the speed of machine \(M_{i};\) and (iii) unrelated parallel machines, for which the processing time of a job depends on the machine assignment.
In this paper, we focus on the problem of minimizing the makespan, i.e., the maximum completion time across all m machines. For a schedule S, the makespan is denoted by \(C_{\max }(S)\). In a non-preemptive schedule, each job is processed on the machine it is assigned to without interruption. In a preemptive schedule, the processing of a job on a machine can be interrupted at any time and then resumed either on this or on any other machine, provided that the job is not processed on two or more machines at a time. For an instance of a scheduling problem on parallel machines, let \( S_{\left( q\right) }^{*}\) and \(S_{p}^{*}\) denote an optimal schedule with at most q preemptions, and an optimal preemptive schedule which uses an unlimited number of preemptions, respectively. We will refer to schedules with an unlimited number of preemptions as simply preemptive. The case \(q=0\) corresponds to a non-preemptive schedule, and an optimal non-preemptive schedule is denoted by \(S_{np}^{*}.\)
The number of preemptions in an optimal schedule \(S_{p}^{*}\) need not exceed \(m-1\) in the case of identical machines and \(2\left( m-1\right) \) in the case of uniform machines, as proved by McNaughton (1959) and Gonzalez and Sahni (1978), respectively.
If any number of preemptions is allowed, then even in the most general settings with unrelated machines an optimal schedule can be found in polynomial time. Finding an optimal non-preemptive schedule is an NP-hard problem, even on two identical parallel machines. See a focused survey by Chen (2004) on parallel machine scheduling with the makespan objective for details and references.
For \(m\ge 3\), the problem of finding an optimal preemptive schedule with at most \(q\le m-2\) preemptions on identical parallel machines is NP-hard due to Shchepin and Vakhania (2008). For \(m\ge 3\) uniform machines, the problem of finding an optimal schedule with the number of preemptions q such that q is even and \(q\le 2\left( m-3\right) \) is shown to be NP-hard by Shachnai et al. (2005). Soper and Strusevich (2018) prove that finding an optimal schedule with at most one preemption on two unrelated parallel machines is NP-hard. On the other hand, it is shown by Soper and Strusevich (2018) that on two uniform machines an optimal schedule with at most one preemption can be found in polynomial time; we reproduce the corresponding algorithm in Sect. 2.2.
Consider an instance of a scheduling problem to minimize the makespan \( C_{\max }\) on m parallel machines (identical, uniform or unrelated). For the corresponding problem, we measure the quality of a schedule with a limited number of preemptions by an upper bound \(\rho _{m}^{\left( q\right) } \) on the ratio \(C_{\max }(S_{\left( q\right) }^{*})/C_{\max }(S_{p}^{*})\). The bound \(\rho _{m}^{\left( q\right) }\) determines what can be gained regarding the maximum completion time if instead of at most q preemptions any number of preemptions is allowed. More formally, in order to determine the exact value of \(\rho _{m}^{\left( q\right) }\) for a particular problem it has to be demonstrated that the inequality
holds for all instances of the problem at hand. To establish tightness of the bound \(\rho _{m}^{\left( q\right) }\), instances of the problem have to be exhibited, for which (1) holds as equality.
Most of the known results in this area address the situation of \(q=0\), i.e., are aimed at comparing an optimal non-preemptive schedule with an optimal preemptive schedule, regarding the makespan objective. The value \(\rho _{m}^{\left( 0\right) }\) is often called the power of preemption. Some of the results on determining \(\rho _{m}^{\left( 0\right) }\) are reviewed below. Among the results on the power of preemption measured with respect to objective functions other than the makespan, here we mention the recent studies on the single machine problem to minimize the weighted completion time by Epstein and Levin (2016) and on the problem on uniform parallel machines to minimize the total completion time by Epstein et al. (2017).
For the makespan objective, if the machines are identical parallel, then it is known that \(\rho _{m}^{\left( 0\right) }=2-2/\left( m+1\right) \), as independently proved by Braun and Schmidt (2003) and Lee and Strusevich (2005). It is shown in Rustogi and Strusevich (2013) that the value of \(\rho _{m}^{\left( 0\right) }\) can be reduced for some instances that contain jobs with fairly large processing times.
According to Woeginger (2000), for m uniform parallel machines \(\rho _{m}^{\left( 0\right) }=2-1/m\). In Soper and Strusevich (2014b), the necessary and sufficient conditions under which the global bound of \(2-1/m\) is tight are given. If the makespan of an optimal preemptive schedule \(S_{p}^{*}\) is equal to the ratio of the total processing time of \(r<m\) longest jobs over the total speed of r fastest machines, it is shown in Soper and Strusevich (2014b) that the tight bound on the power of preemption \(\rho _{m}^{\left( 0\right) } \) is \(2-1/\min \{r,m-r\}\).
For unrelated parallel machines, a tight bound \(\rho _{m}^{\left( 0\right) }=4\) on the power of preemption is established in Correa et al. (2012).
For uniform machines, several papers conduct a parametric analysis of the power of preemption. For example, an analysis of \(\rho _{2}^{\left( 0\right) }\) with respect to the speed of the faster machine is independently performed in Jiang et al. (2014) and Soper and Strusevich (2014a). For \(m=3\), a similar analysis is contained in Soper and Strusevich (2014a), provided that the machine speeds take at most two values, 1 and \(s\ge 1\); in other words, either there are two fast machines with speed s and one slow machine with speed 1 or there are two slow machines with speed 1 and one fast machine with speed s. Notice that the difference between the problem in this paper and the one studied in Soper and Strusevich (2014a) is that in the latter paper an optimal preemptive schedule is compared with an optimal schedule with no preemption.
Several publications compare optimal schedules with a limited number of preemptions to optimal preemptive schedules. For identical machines, Braun and Schmidt (2003) prove that \(\rho _{m}^{\left( q\right) }=\left( 2m\right) /\left( m+q+1\right) \), where \(0\le q\le m-1\), and that this bound is tight. For the problem on m uniform parallel machines, Soper and Strusevich (2018) show that \(\rho _{m}^{\left( 1\right) }=2-2/m\), where \(m\ge 3\).
Jiang et al. (2014) perform a parametric analysis of a single preemption for two uniform machines with speeds \(s^{\prime }\) and \(s^{\prime \prime }\), where \( s^{\prime }\ge s^{\prime \prime }\), from which it follows that
This function attains its maximum value of 9 / 8 when \(s^{\prime }=2s^{\prime \prime }\).
In this paper, we focus on the problem on three uniform parallel machines. The bound \(\rho _{3}^{\left( 1\right) }=\frac{4}{3}\) follows from Soper and Strusevich (2018) and holds as a global bound for all instances, irrespective of relative speeds of the machines. The main purpose of this paper is to perform a parametric analysis of the value \(\rho _{3}^{\left( 1\right) }\). Although we establish bounds on \(\rho _{3}^{\left( 1\right) }\) with respect to arbitrary speeds on the machines, as a rule we are only able to demonstrate the tightness of these bounds, provided that there are either two fast machines or two slow machines.
The problem that we address may arise in producing schedules for multi-processor systems. We limit our analysis, at least as far as the tightness of the derived bounds is concerned, to the situations in which the speeds of the processors have two values, 1 (slow) and \(s\ge 1\) (fast). Uniform machines with two distinct values of machine speeds are often used in attempts either to improve bounds of approximation algorithms or to demonstrate tightness of those bounds; see Gonzalez et al. (1977) as an example. Besides, having s as a parameter, allows performing a thorough parametric analysis, as is done for the problem of minimizing the makespan on two uniform machines when no preemption is allowed (see Mireault et al. (1997)) or a single preemption is allowed (see Jiang et al. (2014), Soper and Strusevich (2014a)). For these problems, as well as for the problems on three uniform machines in Soper and Strusevich (2014a) and in this paper, the results of the parametric analysis allow the user to perform an appropriate speed scaling in order to achieve a certain guaranteed performance.
The single-parameter analysis performed in Soper and Strusevich (2014a) and in this paper for three uniform machines requires considerable technical efforts, which give an estimate of a possible difficulty of extending a similar analysis to a larger number of machines. The latter can be seen as a goal for further research.
An additional interest in considering the three-machine problem with at most one preemption is due to (i) \(m=3\) is the smallest number of machines for which finding a schedule with at most one preemption is NP-hard, and (ii) for \(m=3\) allowing at most one preemption leads to the smallest loss of quality of the makespan compared to the global preemptive schedule.
The remainder of this paper is organized as follows. Section 2 presents two main tools that are used as subroutines in the subsequent parts of the paper. A tight bound on the quality of a schedule with a single preemption is derived as a function of the relative speeds of the machines in Sects. 3 and 4.
2 Main ingredients
We start this section by introducing a classification of the instances of the problem on m uniform parallel machines, based on the shape of the optimal preemptive schedule \(S_{p}^{*}\).
In our analysis of the quality of schedules with a single preemption on three uniform parallel machines we rely on two tools: (i) a polynomial-time algorithm for finding an optimal schedule with a single preemption on two uniform parallel machines, and (ii) a parametrized partition algorithm that splits a set of jobs into two subsets with required properties. These two tools are discussed in the remainder of this section.
2.1 Class distinction
An instance I of the problem with n jobs and m uniform parallel machines is defined by the list \(\mathcal {L}_{n}=\left( p_{1},p_{2},\ldots ,p_{n}\right) \) of the processing times of the jobs and the list \(\mathcal {M} _{m}=\left( s_{1},s_{2},\ldots ,s_{m}\right) \) of the machine speeds. In what follows, we assume that both lists are non-increasing. In other words, the jobs are numbered in accordance with the LPT rule (6) and the machines are numbered in non-increasing order of their speeds, i.e., \( s_{1}\ge s_{2}\ge \cdots \ge s_{m}.\)
Feasible non-preemptive and preemptive schedules for an instance \(I=\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \) are denoted by \(S_{np}\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \) or \(S_{np}\left( I\right) \), and by \(S_{p}\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \) or \(S_{p}\left( I\right) \), respectively; the corresponding optimal non-preemptive and preemptive schedules are denoted by \(S_{np}^{*}\left( \mathcal {L}_{n}, \mathcal {M}_{m}\right) \) or \(S_{np}^{*}\left( I\right) \) and by \( S_{p}^{*}\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \) or \(S_{p}^{*}\left( I\right) ,\) respectively. The reference to an instance may be omitted if it is clear which instance is being discussed.
For our analysis, we need precise expressions for the makespan of the preemptive schedules. The fastest algorithm for finding an optimal preemptive schedule on uniform parallel machines is due to Gonzalez and Sahni (1978) and requires \(O(n+m\log m)\) time.
Given an instance \(I=\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \), for each u, \(1\le u\le m\), define the total speed of the u fastest machines \(S_{u}=\sum _{i=1}^{u}s_{i}\). Besides, define the set of the u longest jobs \(H_{u}=\left\{ 1,2,\ldots ,u\right\} \).
Define \(m^{\prime }=\min \left\{ n,m-1\right\} \) and
It is well-known (see, e.g., Brucker (2007)) that for an optimal preemptive schedule \(S_{p}^{*}\left( I\right) \) the makespan is equal to
Definition 1
An instance \(I=\left( \mathcal {L}_{n},\mathcal {M}_{m}\right) \) is said to belong to Class r, \(1\le r\le m,\) if \(C_{\max }\left( S_{p}^{*}\left( I\right) \right) =T_{r}=\max \left\{ T_{u}|1\le u\le m\right\} .\)
In the case of three machines, we will distinguish between three classes
Given an instance of the problem on three uniform machines, we determine its class by computing the values \(T_{r}\), \(1\le r\le 3,\) and the value of r associated with the largest \(T_{r}\) defines the class of the instance. In the case of ties, an instance may belong to more than one class; however, for our purposes instances of Class 3 are harder to handle and we assume without loss of generality that the ties are broken in favour of the smaller r.
Clearly \(T_{m}=p\left( N\right) /S_{m}\) is a lower bound on \(C_{\max }(S_{p}^{*}\left( I\right) )\) even when simultaneous execution of jobs is allowed, since it is the average machine load, i.e., the time for processing all jobs, provided all machines are continuously busy.
For an instance I, a schedule \(S_{\left( 1\right) }\left( I\right) \) with exactly one preemption is defined by
- (i):
-
a job \(J_{k}\in N\) which is processed with preemption on two machines \(M_{k^{\prime }}\) and \(M_{k^{\prime \prime }}\) such that \(1\le k^{\prime }<k^{\prime \prime }\le m\); the actual processing times of job \( J_{k}\) on these machines are equal to \(x_{k}/s_{k^{\prime }}\) and \( y_{k}/s_{k^{\prime \prime }}\), where \(x_{k}+y_{k}=p_{k};\)
- (ii):
-
a partition of set \(N\backslash \left\{ J_{k}\right\} \) into m subsets \(N_{1}\), \(N_{2},\ldots ,N_{m},\) where the jobs of set \(N_{i}\) are assigned to be processed on machine \(M_{i}\), \(1\le i\le m\).
Notice that even in an optimal schedule some of the subsets \(N_{i}\) can be empty, since it may be counterproductive to assign jobs to very slow machines. For a particular instance, it might be optimal not to preempt any job, in which case a schedule \(S_{\left( 1\right) }\left( I\right) \) is defined by a partition of set N into m subsets \(N_{1}\), \(N_{2},\ldots ,N_{m}\). If there is a preempted job \(J_{k}\) in schedule \(S_{\left( 1\right) }\left( I\right) \) then the jobs assigned to machines \(M_{k^{\prime }}\) and \( M_{k^{\prime \prime }}\) must be arranged in a such a way that the two portions of job \(J_{k}\) do not overlap.
2.2 Single preemption on two uniform parallel machines
The algorithm that finds an optimal schedule with at most one preemption on two uniform parallel machines is used throughout this paper as a subroutine. This is why below we present it in a generic way, so that the two machines are denoted by \(M^{\prime }\) and \(M^{\prime \prime }\), while their speeds are \(s^{\prime }\) and \(s^{\prime \prime }\), respectively, where \(s^{\prime }\ge s^{\prime \prime }\). Assume that the jobs are numbered in accordance with the LPT rule, i.e., in non-increasing order of their processing times
For a non-empty subset \(R\subseteq N\), define
and for completeness define \(p\left( \varnothing \right) =0\).
For two uniform parallel machines, instances can only be of either Class 1 or Class 2, i.e., \(C_{\max }\left( S_{p}^{*}\right) =\max \left\{ p_{1}/s^{\prime },T_{2}\right\} ,\)where
As follows from Gonzalez and Sahni (1978), if there is no restriction on the number of preemptions, then an optimal preemptive schedule \(S_{p}^{*}\) can be found in \(O\left( n\right) \) time.
The algorithm below finds an optimal schedule with at most one allowed preemption. It is developed by Soper and Strusevich (2018).
Algorithm Q2Pr1
- Step 1. :
-
Compute \(T_{2}\) by (7). If
$$\begin{aligned} p_{1}<s^{\prime }T_{2}, \end{aligned}$$go to Step 2; otherwise, output a non-preemptive schedule \(S_{\left( 1\right) }\) with job \(J_{1}\) on machine \(M^{\prime }\) and the other jobs on machine \(M^{\prime \prime }\) and stop.
- Step 2. :
-
Scanning the jobs in the order of their numbering, find job \(J_{k}\) such that
$$\begin{aligned} \sum _{j=1}^{k-1}p_{j}<s^{\prime }T_{2},~\sum _{j=1}^{k}p_{j}\ge s^{\prime }T_{2}. \end{aligned}$$ - Step 3. :
-
Compute
$$\begin{aligned} x_{k}=s^{\prime }T_{2}-\sum _{j=1}^{k-1}p_{j},~y_{k}=p_{k}-x_{k}. \end{aligned}$$If
$$\begin{aligned} \frac{y_{k}}{s^{\prime \prime }}>\frac{1}{s^{\prime }}\sum _{j=1}^{k-1}p_{j}, \end{aligned}$$go to Step 4; otherwise, output the following schedule \(S_{\left( 1\right) }\) (see Fig. 1a): on \(M^{\prime }\) the jobs \(J_{1},\ldots ,J_{k-1}\) are processed in any order, followed by a part of job \(J_{k}\) for \( x_{k}/s^{\prime }\) time units; on \(M^{\prime \prime }\) process a part of job \(J_{k}\) for \(y_{k}/s^{\prime \prime }\) time units, followed by an arbitrary sequence of jobs \(J_{k+1},\ldots ,J_{n}\). Stop.
- Step 4. :
-
For job \(J_{k}\), compute the values \(\tilde{x}_{k}\) and \( \tilde{y}_{k}\) such that
$$\begin{aligned} \frac{\tilde{y}_{k}}{s^{\prime \prime }}=\frac{1}{s^{\prime }} \sum _{j=1}^{k-1}p_{j},~\tilde{x}_{k}=p_{k}-\tilde{y}_{k}. \end{aligned}$$Output the following schedule \(S_{\left( 1\right) }\) (see Fig. 1b): on \(M^{\prime }\) the jobs \(J_{1},\ldots ,J_{k-1}\) are processed in any order, followed by a part of job \(J_{k}\) for \(\tilde{x}_{k}/s^{\prime }\) time units; on \(M^{\prime \prime }\) process a part of job \(J_{k}\) for \(\tilde{y}_{k}/s^{\prime \prime }\) time units, followed by an arbitrary sequence of jobs \(J_{k+1},\ldots ,J_{n}\). Stop.
Soper and Strusevich (2018) show that Algorithm Q2Pr1 finds an optimal schedule and it requires \(O\left( n\right) \) time, provided that the LPT numbering of the jobs is available. Obtaining such a numbering can be seen as a preprocessing stage. Thus, the overall time complexity of Algorithm Q2Pr1 is \(O\left( n\log n\right) \).
On several occasions in this paper, we demonstrate that certain bounds are tight by exhibiting instances of the problem for which inequalities similar to (1) hold as equalities. In the analysis of such instances, we quite often need the value of the makespan for a schedule found by Algorithm Q2Pr1 applied to two jobs of equal duration.
Notice that for schedule \(S_{\left( 1\right) }\) found in Step 4, we have that \(\tilde{y}_{k}=\frac{s^{\prime \prime }}{s^{\prime }} \sum _{j=1}^{k-1}p_{j}\) and \(\tilde{x}_{k}=p_{k}-\frac{s^{\prime \prime }}{ s^{\prime }}\sum _{j=1}^{k-1}p_{j}\), so that we deduce that \( \sum _{j=1}^{k-1}p_{j}+\tilde{x}_{k}=\left( \frac{s^{\prime }-s^{\prime \prime }}{s^{\prime }}\right) \sum _{i=1}^{k-1}p_{j}+p_{k}\). This implies that
Lemma 1
Let \(S_{\left( 1\right) }\) be a schedule found by Algorithm Q2Pr1 applied to the instance that contains two jobs \(J_{1}\) and \( J_{2}\) such that \(p_{1}=p_{2}=w\). Then
Proof
For the instance under consideration, Algorithm Q2Pr1 will output schedule \(S_{\left( 1\right) }\) found in Step 4. Applying (8) with \(k=2\), we obtain
and (9) follows. \(\square \)
2.3 Parametric partition algorithm
Below, we present and analyze Procedure Split, which is used as a subroutine in the algorithms presented in Sect. 4. Although the procedure is used in this paper as an auxiliary tool, it is of interest in its own right and is applicable if one needs a partition with some prescribed properties. Such partitions are often required in approximation scheduling algorithms. For example, a simplified version of Procedure Split has been used in Soper and Strusevich (2014a) for the single-parameter analysis of the power of preemption on three uniform machines.
Procedure Split
Input: An integer \(r\ge 3\), a set of jobs \(N=\left\{ J_{1},J_{2},\ldots ,J_{n}\right\} \) with normalized processing times, \( p\left( N\right) =1\), numbered in the LPT order (at least for the \(r-1\) longest jobs) and with \(p_{j}\le \frac{2}{r+1}\) for all \(j\in N\)
Output: A partition of set N into two subsets \( H^{\prime }\) and \(H^{\prime \prime }\) such that \(p(H^{\prime })\le \frac{2}{ r+1}\) and \(p(H^{\prime \prime })\le 1-\frac{1}{r}\)
- Step 1.:
-
Scanning the jobs in the order of their numbering, determine the job \(J_{u}\), \(u>1\), such that
$$\begin{aligned} \sum _{j=1}^{u}p_{j}\le \frac{2}{r+1},\text { }\sum _{j=1}^{u}p_{j}+p_{u+1}> \frac{2}{r+1} \end{aligned}$$and define
$$\begin{aligned} U:=\left\{ J_{1},\ldots ,J_{u}\right\} . \end{aligned}$$(10)If
$$\begin{aligned} p(U)\ge \frac{1}{r} \end{aligned}$$(11)define
$$\begin{aligned} H^{\prime }:=U,~H^{\prime \prime }=N\backslash U; \end{aligned}$$and go to Step 4. Otherwise go to Step 2.
- Step 2.:
-
Scanning the jobs in the order of their numbering, consider the sum \(\sum _{j=1}^{r-1}p_{j}\). If
$$\begin{aligned} \sum _{j=1}^{r-1}p_{j}\ge 1-\frac{2}{r+1} \end{aligned}$$(12)then define \(U:=\left\{ J_{1},\ldots ,J_{r-1}\right\} \),
$$\begin{aligned} H^{\prime \prime }:=U,~H^{\prime }=N\backslash U \end{aligned}$$and go to Step 4. If
$$\begin{aligned} p_{r-2}+p_{r-1}\ge \frac{1}{r} \end{aligned}$$(13)then define \(V:=\left\{ J_{r-2},J_{r-1}\right\} \) and
$$\begin{aligned} H^{\prime }:=V,~H^{\prime \prime }=N\backslash V \end{aligned}$$and go to Step 4. Otherwise go to Step 3.
- Step 3.:
-
Continue scanning the jobs until the first job \(J_{u}\) is reached such that
$$\begin{aligned} \sum _{j=1}^{u}p_{j}\ge 1-\frac{2}{r+1} \end{aligned}$$Define \(U:=\left\{ J_{1},\ldots ,J_{u}\right\} \)
$$\begin{aligned} H^{\prime \prime }:=U,~H^{\prime }=N\backslash U. \end{aligned}$$ - Step 4.:
-
Stop.
The running time of Procedure Split is O(n).
Lemma 2
Procedure Split finds a required partition.
Proof
In Step 1,
and under the condition (11) we have that
as required.
We come to Step 2 if the inequality \(p\left( U\right) <\frac{1}{r}\) holds for set U defined in Step 1 by (10). In fact, \(p_{1}<\frac{1}{r }\), i.e., the duration of each job is less than \(\frac{1}{r}\). This implies that
If (12) holds, then we may set \(H^{\prime \prime }=\left\{ J_{1},\ldots ,J_{r-1}\right\} \) and \(H^{\prime }=N\backslash H^{\prime \prime }\) since
as required.
If (12) does not hold, then it follows from
that the sum of the two smallest processing times \(p_{r-2}+p_{r-1}\) does not exceed \(\frac{2}{r+1}\). Thus, if \(p_{r-2}+p_{r-1}\ge \frac{1}{r}\), we have
as required.
We come to Step 3 with \(p_{r-2}+p_{r-1}<\frac{1}{r}\), which implies that \( p_{r-1}\) and the processing time \(p_{j}\) of each job \(j\ge r\) is smaller then \(\frac{1}{2r}.\) Thus, for job \(J_{u}\), \(u\ge r\), found in Step 3, we deduce
where the last inequality holds for all \(r\ge 3.\)
Thus,
as required. \(\square \)
In this paper, Procedure Split is used in Sect. 4 and is applied with \(r=4\).
3 Single parameter analysis for three uniform machines: Classes 1 and 2
The remainder of this paper focuses on the case of three uniform machines, i.e., we consider instances \(I=\left( \mathcal {L}_{n},\mathcal {M}_{3}\right) \). We perform a class-based analysis, for each form of the optimal preemptive schedule, considering Classes 1 and 2 first and then the more intricate Class 3. Our results give tight bounds for each class as a function of a single parameter equal to the relative speeds of the machines.
In this section, we consider instances of the problem with three uniform machines that belong either to Class 1 or 2; see Definition 1. The Class 3 instances are studied in Sect. 4.
We create heuristic schedules with at most one preemption, that will deliver an upper bound on \(\rho _{3}^{\left( 1\right) }\) as a function of the speeds of the three machines. Although most of the presented arguments hold for arbitrary speeds, similarly to Soper and Strusevich (2014a) we derive our final conclusion for the models with two fast machines (\(s_{1}=s_{2}=s\ge s_{3}=1\) ) and for those with two slow machines (\(s_{1}=s\ge s_{2}=s_{3}=1\)). This will allow us to deliver the bound on \(\rho _{3}^{\left( 1\right) }\) as a function of a single parameter s and to prove its tightness.
Consider instances of the form \(I=\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) of the problem with three uniform machines \(M_{1},M_{2}\) and \( M_{3}\) that belong to either Class 1 or Class 2. As above, it is assumed that the jobs are numbered in accordance with (6), while for the machines \(s_{1}\ge s_{2}\ge s_{3}\) holds.
For an instance \(I=\left( \mathcal {L}_{n},\mathcal {M}_{3}\right) \) of Class r, \(r\in \left\{ 1,2\right\} \), let \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~r\right) \) denote the ratio of the makespan that is optimal for schedules with at most one preemption to the optimal makespan for preemptive schedules for instances of that class. We derive an upper bound on \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~r\right) \) as a function \(\Phi \left( s_{1},s_{2},s_{3}\right) \) of the machine speeds.
The algorithm below takes as input an instance \(I=\left( \mathcal {L}_{n}, \mathcal {M}_{3}\right) \) of either Class 1 or Class 2, and finds a schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) with at most one preemption.
Algorithm Q3Pr1CL1&2
- Step 1. :
-
If a given instance \(I=\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) belongs to Class 1, go to Step 2; otherwise, go to Step 3.
- Step 2. :
-
Find schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{n}, \mathcal {M}_{3}\right) \) in which job \(J_{1}\) is assigned to be processed on machine \(M_{1}\), while the remaining jobs are scheduled by Algorithm Q2Pr1 on machines \(M^{\prime }=M_{2}\) and \(M^{\prime \prime }=M_{3}\). Go to Step 4.
- Step 3. :
-
Find schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{n}, \mathcal {M}_{3}\right) \) in which jobs \(J_{1}\) and \(J_{2}\) are scheduled by Algorithm Q2Pr1 on machines \(M^{\prime }=M_{1}\) and \(M^{\prime \prime }=M_{2}\), while the remaining jobs are processed non-preemptively in any order on machine \(M_{3}\). Go to Step 4.
- Step 4. :
-
Stop.
Algorithm Q3Pr1CL1&2 is analyzed below. Part of the analysis is based on the parametric bound (2) developed in Jiang et al. (2014) for two uniform machines.
Theorem 1
For an instance \(I=\left( \mathcal {L}_{n},\mathcal {M}_{3}\right) \) of Class r, \(1\le r\le 2\), Algorithm Q3Pr1CL1&2 takes \(O\left( n\log n\right) \) time and finds a schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{n}, \mathcal {M}_{3}\right) \) such that
where
Proof
First, note that the running time of Algorithm Q3Pr1CL1&2 is determined by the running time of Algorithm Q2Pr1, and is therefore \(O\left( n\log n\right) \).
For a given instance of Class r, \(r\in \left\{ 1,2\right\} \), define the lists \(\mathcal {L}_{r}\) and \(\mathcal {M}_{r}\), that contain the r longest jobs and the r fastest machines, respectively. Also define the lists \( \mathcal {L}_{r}^{\prime }\) and \(\mathcal {M}_{r}^{\prime }\) obtained from the lists \(\mathcal {L}_{n}\) and \(\mathcal {M}_{3}\) by the removal of the r longest jobs and the r fastest machines, respectively. In other words, \( \mathcal {L}_{r}^{\prime }=\left( p_{r+1},\ldots ,p_{n}\right) \) and \( \mathcal {M}_{r}^{\prime }=\left( s_{r+1},\ldots ,s_{3}\right) \).
By definition of a Class r instance, we have that
For schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) found by Algorithm Q3Pr1CL1&2, we have that
It follows that
For instances of Class 1, Step 2 of Algorithm Q3Pr1CL1&2 guarantees that
i.e.,
Since the remaining jobs are scheduled on machines \(M_{2}\) and \(M_{3}\) optimally with at most one preemption, we have that \(C_{\max }\left( S_{\left( 1\right) }^{H}\left( \mathcal {L}_{1}^{^{\prime }},\mathcal {M} _{1}^{^{\prime }}\right) \right) =C_{\max }\left( S_{\left( 1\right) }^{*}\left( \mathcal {L}_{1}^{^{\prime }},\mathcal {M}_{1}^{^{\prime }}\right) \right) \), so that
where the last inequality follows from (2) applied to the machines with speeds \(s^{\prime }=s_{2}\) and \(s^{\prime \prime }=s_{3}\). Thus, (14) holds for \(r=1\), since \(\left( 2s_{2}^{2}+s_{2}s_{3}-s_{3}^{2}\right) /2s_{2}^{2}\ge 1\).
Applying (15) to the instances of Class 2, notice that
since the machine environment \(\mathcal {M}_{2}^{^{\prime }}\) consists only of machine \(M_{3}\), so that \(C_{\max }\!\left( S_{p}^{*}\left( \mathcal {L} _{2}^{^{\prime }},\mathcal {M}_{2}^{^{\prime }}\right) \right) =C_{\max }\left( S_{\left( 1\right) }^{H}\left( \mathcal {L}_{2}^{^{\prime }},\mathcal { M}_{2}^{^{\prime }}\right) \right) \).
Step 3 of Algorithm Q3Pr1CL1&2 guarantees that
and due to (2) applied with \(s^{\prime }=s_{1}\) and \( s^{\prime \prime }=s_{2}\), we conclude that
Thus, (14) holds for \(r=2.\) \(\square \)
Figure 2 illustrates \(\Phi \left( s_{1},s_{2},s_{3}\right) \) as a function of the speed ratio: \(s_{2}/s_{3}\) for \(r=1\) or \(s_{1}/s_{2}\) for \( r=2\). The maximum of the function is \(\frac{9}{8}\), attained for the ratio equal to 2. That value provides a global numerical bound on \(\rho _{3}^{\left( 1\right) }\) for the instances of Classes 1 and 2.
Lemma 3
Bound (14) is tight for instances of Class 2.
Proof
Take a Class 2 instance given by a set of three jobs with \(\mathcal {L}_{3}=\left( p,p,p\frac{2s_{3}}{s_{1}+s_{2}}\right) \) and \(\mathcal {M}_{3}=\left( s_{1},s_{2},s_{3}\right) \). It follows that \( C_{\max }\left( S_{p}^{*}\left( \mathcal {L}_{3},\mathcal {M}_{3}\right) \right) =C_{\max }\left( S_{p}^{*}\left( \mathcal {L}_{2},\mathcal {M} _{2}\right) \right) =2p/\left( s_{1}+s_{2}\right) \). Let \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{3},\mathcal {M}_{3}\right) \) be the schedule found by Algorithm Q3Pr1CL1&2. The algorithm schedules the identical jobs \(J_{1}\) and \(J_{2}\) on machines \(M_{1}\) and \(M_{2}\) and the remaining job on machine \(M_{3}\). It follows that schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L} _{2},\mathcal {M}_{2}\right) \) is in fact an optimal schedule \(S_{\left( 1\right) }^{*}\left( \mathcal {L}_{2},\mathcal {M}_{2}\right) \) for processing the two longest jobs on the two fastest machines with at most one preemption. We deduce from (9) applied with \(s^{\prime }=s_{1}\) , \(s^{\prime \prime }=s_{2}\) and \(w=p\) that
Furthermore,
and therefore \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~2\right) = \frac{\left( 2s_{1}-s_{2}\right) \left( s_{1}+s_{2}\right) }{2s_{1}^{2}}= \frac{2s_{1}^{2}+s_{1}s_{2}-s_{2}^{2}}{2s_{1}^{2}}=\Phi \left( s_{1},s_{2},s_{3}\right) \), as required. \(\square \)
Lemma 4
Bound (14) is tight for instances of Class 1 with two distinct values of speed.
Proof
Consider a Class 1 instance given by a set of three jobs such that \(\mathcal {L}_{3}=\left( p,p\frac{s_{2}+s_{3}}{2s_{1}},p \frac{s_{2}+s_{3}}{2s_{1}}\right) \) and \(\mathcal {M}_{3}=\left( s_{1},s_{2},s_{3}\right) \). It follows that \(C_{\max }\left( S_{p}^{*}\left( \mathcal {L}_{3},\mathcal {M}_{3}\right) \right) =C_{\max }\left( S_{p}^{*}\left( \mathcal {L}_{1},\mathcal {M}_{1}\right) \right) =p/s_{1}\). Algorithm Q3Pr1CL1&2 creates the heuristic schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{3},\mathcal {M}_{3}\right) \) by scheduling job \( J_{1} \) on machine \(M_{1}\) and the two remaining identical jobs on machines \( M_{2}\) and \(M_{3}\) in accordance with Algorithm Q2Pr1. It follows from (9) applied with \(s^{\prime }=s_{2}\), \(s^{\prime \prime }=s_{3}\) and \(w=p\frac{s_{2}+s_{3}}{2s_{1}}\) that
Thus, \(C_{\max }\left( S_{\left( 1\right) }^{H}\left( \mathcal {L}_{3}, \mathcal {M}_{3}\right) \right) =C_{\max }\left( S_{\left( 1\right) }^{H}\left( \mathcal {L}_{1}^{\prime },\mathcal {M}_{1}^{\prime }\right) \right) \), and therefore
Bound (14) is tight for the instance under consideration if schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{3},\mathcal {M} _{3}\right) \) is in fact an optimal schedule with at most one preemption. However, unlike for the Class 2 instances discussed in Lemma 3, this does not happen for all combinations of speeds. To demonstrate this, assume that \(s_{1}=s\), \(s_{2}=\frac{s}{2}\) and \(s_{3}=1\). It follows that
However, for such an instance an optimal schedule with exactly one preemption can be found by splitting job \(J_{3}\) between machines \(M_{1}\) and \(M_{3}\). In this schedule \(S_{\left( 1\right) }^{*}\left( \mathcal {L} _{3},\mathcal {M}_{3}\right) \), jobs \(J_{1}\) and \(J_{2}\) are processed without preemption on machines \(M_{1}\) and \(M_{2}\), respectively. Job \(J_{3}\) is processed in the time interval \(\left[ 0,p/s\right] \) on machine \(M_{3}\) and then starting from time p / s on machine \(M_{1}\), so that the makespan of this schedule becomes
It is easily seen that \(\frac{5s-2}{4s^{2}}<\left( s+2\right) \frac{s-1}{ s^{3}}\) for \(2<s<4\).
Still, bound (14) is tight if there are two different values of speeds only, i.e., either \(s_{1}=s>s_{2}=s_{3}=1\) (two slow machines) or \( s_{1}=s_{2}=s>s_{3}=1\) (two fast machines).
In the former case, the smallest makespan of p / s is achieved for a non-preemptive schedule, and that cannot be improved by allowing any number of preemptions, so that \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class} ~1\right) \) becomes equal to 1, which complies with (14).
In the latter case, schedule \(S_{\left( 1\right) }^{H}\left( \mathcal {L}_{3}, \mathcal {M}_{3}\right) \) is in fact an optimal schedule with a single preemption, which implies that \(\rho _{3}^{\left( 1\right) }\left( \mathrm { Class}~1\right) =\frac{2s_{2}^{2}+s_{2}s_{3}-s_{3}^{2}}{2s_{2}^{2}}=\) \(\Phi \left( s_{1},s_{2},s_{3}\right) \), as required. Note that for two slow machines \(s_{2}=s_{3}\), the bound \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~1\right) \) becomes equal to 1.
Notice that the example above demonstrates that for the Class 2 instances the bound (14) is tight for arbitrary machines speeds, in particular for instances with two fast and two slow machines. \(\square \)
Since our main intention is to perform a single parameter analysis of the quality of schedules with at most one single preemption on three uniform parallel machines, below we formulate the results of this section in terms of the instances with two fast machines and with two slow machines.
Corollary 1
For the instances of the problem with two fast machines (\( s_{1}=s_{2}=s>1=s_{3})\) the following bounds
hold and are tight. For the instances of the problem with two slow machines ( \(s_{1}=s>1=s_{2}=s_{3})\) the following bounds
hold and are tight.
The fact that the bound \(\rho _{3}^{\left( 1\right) }\) is equal to 1 for some classes of instances complies with the fact that for those instances the optimal preemptive schedule requires at most one preemption.
4 Single parameter analysis for Class 3 instances on three uniform machines
It remains to consider instances of Class 3, i.e., instances for which \( C_{\max }\left( S_{p}^{*}\left( I\right) \right) =T_{3}\). Our analysis is presented in two subsections, starting with instances for which the ratio between the fastest and the slowest speeds is limited to 2 and followed by instances with larger relative speeds.
4.1 Limited relative machine speeds \(s_{2}\le s_{1}\le 2s_{3}\)
Temporarily assume that the feasibility of schedules with a single preemption is ignored, i.e., simultaneous processing of pieces of the same (preempted) job on different machines is allowed. Let C be the makespan of an optimal schedule of this type. Comparing C with the optimal makespan \( C_{\max }\left( S_{p}^{*}\left( I\right) \right) =T_{3}\), define an upper bound \(\Phi \left( s_{1},s_{2},s_{3}\right) \) such that the inequality \(C\le \Phi \left( s_{1},s_{2},s_{3}\right) T_{3}\) holds across all instances of Class 3. Obtaining the required heuristic schedule simplifies to an appropriate split of the jobs into two sets, and an allocation of one of these sets to be processed on a single machine, and placing the other on the remaining pair of machines, using the preemption to share the load appropriately between the pair. The splitting of the jobs is performed by Procedure Split defined and analyzed in Sect. 2.3.
During the analysis of the Class 3 instances we will assume that the jobs of any instance have normalized processing times, \(p\left( N\right) =1\), so that \(T_{3}=\frac{1}{s_{1}+s_{2}+s_{3}}.\) Define
Algorithm OneSplit below partitions the set of jobs into two subsets \(N_{u}\) and \(N_{v,w}\) such that for some triple \(\left( u,v,w\right) \) of the machine indices 1, 2 and 3 the inequalities
hold, provided that \(s_{2}\le 2s_{3}\). In what follows, without loss of generality we assume that \(v<w\), i.e., \(\left( u,v,w\right) \) is one of the triples \(\left( 1,2,3\right) ,\) \(\left( 2,1,3\right) \) or \(\left( 3,1,2\right) \).
Algorithm OneSplit
Input: An instance \(I=\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) of Class 3, with normalized processing times, \(p\left( N\right) =1\), numbered in the LPT order and a set of speeds satisfying \( s_{3}\le s_{2}\le s_{1}\le 2s_{3}\)
Output: Subsets \(N_{u}\) and \(N_{v,w}\) that satisfy (17) and (18) for some triple \(\left( u,v,w\right) \)
- Step 1.:
-
Compute \(T_{3}\) and \(\Phi T_{3}\). If \(p_{1}>2/5\) then output \( N_{1}=\left\{ J_{1}\right\} \) and \(N_{2,3}=N\backslash \left\{ J_{1}\right\} \) and stop. Otherwise, run Procedure Split with \(r=4\), to produce two sets of jobs \(H^{\prime }\) and \(H^{\prime \prime }\) satisfying \(p(H^{\prime })\le \frac{2}{5}\) and \(p(H^{\prime \prime })\le \frac{3}{4}\).
- Step 2.:
-
Identify a triple \(\left( u,v,w\right) \in \left\{ \left( 1,2,3\right) ,\left( 2,1,3\right) ,\left( 3,1,2\right) \right\} \) such that \( p(H^{\prime })\in \big [ 1-\Phi T_{3}\left( s_{v}+s_{w}\right) ,\Phi T_{3}s_{u}\big ] \) and output \(N_{u}=H^{\prime }\), \(N_{v,w}=H^{\prime \prime }\).
Lemma 5
Algorithm OneSplit splits the jobs of set N into two subsets \(N_{u}\) and \(N_{v,w}\) such that (17) and (18) hold for some triple \(\left( u,v,w\right) \).
Proof
For a partition \(N_{1}\) and \(N_{2,3}\) found in Step 1, we deduce that
since \(\Phi \ge 1\) and our instance is of Class 3, so that \(\frac{p_{1}}{ s_{1}}\le T_{3}\). It follows from \(p\left( N_{1}\right) =p_{1}>2/5\) that \( p\left( N_{2,3}\right) <\frac{3}{5}\). Using the fourth term in the right-hand side of (16), we derive
The right-hand side of the above inequality decreases in \(s_{2}\), so that \( s_{2}\le 2s_{3}\) implies \(\Phi T_{3}\left( s_{2}+s_{3}\right) \ge \frac{3}{ 5}\), as required by (18). Thus, the lemma holds for \(\left( u,v,w\right) =\left( 1,2,3\right) \).
We carry out Step 2 if \(p_{1}\le 2/5\), so that the conditions for running Procedure Split are satisfied and the two sets of jobs \(H^{\prime }\) and \( H^{\prime \prime }\) will be found with \(p(H^{\prime })\le \frac{2}{5}\) and \( p(H^{\prime \prime })\le \frac{3}{4}\). This additionally bounds \( p(H^{\prime })\) from below, since \(p(H^{\prime })=1-p(H^{\prime \prime })\ge \frac{1}{4}.\)
If for some triple \(\left( u,v,w\right) \) we have that \(p\left( H^{\prime }\right) \in \left[ 1-\Phi T_{3}\left( s_{u}+s_{v}\right) ,\Phi T_{3}s_{w} \right] \) then the lemma holds for such a triple. Thus, we need to prove that such a triple always exists.
Consider the three intervals \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \), \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \), \(\left[ 1-\Phi T_{3}\left( s_{2}+s_{3}\right) ,\Phi T_{3}s_{1}\right] \). It is straightforward to check that the right endpoint of each interval is no less than its left endpoint, since \(\Phi \ge 1\), so that the intervals are well defined. We can consider the intervals in the natural order:\(\ \left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \), \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \), \(\left[ 1-\Phi T_{3}\left( s_{2}+s_{3}\right) ,\Phi T_{3}s_{1}\right] \), since in this sequence the right endpoints of the intervals are nondecreasing, as are their left endpoints.
We show that the value \(p\left( H^{\prime }\right) \) such that \(\frac{1}{4} \le p(H^{\prime })\le \frac{2}{5}\) belongs to at least one of these intervals.
Using each of the components of \(\Phi \) in the order of their appearance in the right-hand side of (16), we deduce that
-
the right endpoint of \(\left[ 1-\Phi T_{3}\left( s_{2}+s_{3}\right) ,\Phi T_{3}s_{1}\right] \) is no less than 2 / 5 since \(\Phi T_{3}s_{1}\ge \frac{2}{5};\)
-
the left endpoint of \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \) is at most 1 / 4 since \(\Phi T_{3}\left( s_{1}+s_{2}\right) \ge \frac{3}{4};\)
-
the intervals \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \) and \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \) overlap since \(\Phi T_{3}s_{3}\ge 1-\Phi T_{3}\left( s_{1}+s_{3}\right) \) due to \(\Phi T_{3}\left( s_{1}+2s_{3}\right) \ge 1;\)
-
the intervals \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \) and \(\left[ 1-\Phi T_{3}\left( s_{2}+s_{3}\right) ,\Phi T_{3}s_{1}\right] \) overlap since \(\Phi T_{3}s_{2}\ge 1-\Phi T_{3}\left( s_{2}+s_{3}\right) \) due to \(\Phi T_{3}\left( 2s_{2}+s_{3}\right) \ge 1.\)
Suppose that \(p\left( H^{\prime }\right) \) belongs to neither the interval \( \left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \) nor to \(\left[ 1-\Phi T_{3}\left( s_{2}+s_{3}\right) ,\Phi T_{3}s_{1}\right] \); otherwise, the lemma holds either for \(\left( u,v,w\right) =\left( 3,1,2\right) \) or for \(\left( u,v,w\right) =\left( 1,2,3\right) \), respectively. This is only possible if the two intervals do not intersect and
However, since each of these two intervals intersects with \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \), we obtain that
so that \(p\left( H^{\prime }\right) \in \left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \), and the lemma holds for \( \left( u,v,w\right) = \left( 2,1,3\right) \). \(\square \)
Algorithm OneSplit is used as a splitting procedure in the following algorithm for finding a schedule with a single preemption.
Algorithm Q3Pr1CL3Lim
Input: An instance \(I=\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) of Class 3, with its jobs having normalized processing times, \( p\left( N\right) =1\), numbered in the LPT order
Output: A schedule \(S_{(1)}^{H}\) with at most one preemption
- Step 1.:
-
If \(p_{1}\ge p_{2}>\Phi T_{3}s_{2}\) then define \(\left( u,v,w\right) =\left( 3,1,2\right) \), \(N_{v,w}=\left\{ J_{1},J_{2}\right\} \), \(N_{u}=N\backslash \left\{ J_{1},J_{2}\right\} \) and go to Step 4; otherwise go to Step 2.
- Step 2.:
-
If \(p_{2}>\Phi T_{3}s_{3}\) then define \(\left( u,v,w\right) =\left( 2,1,3\right) \), \(N_{u}=\left\{ J_{2}\right\} \), \(N_{v,w}=N\backslash \left\{ J_{2}\right\} \) and go to Step 4; otherwise go to Step 3.
- Step 3.:
-
Run Algorithm OneSplit that outputs sets \(N_{u}\) and \(N_{v,w}\) for a triple of indices \(\left( u,v,w\right) \).
- Step 4.:
-
Run Algorithm Q2Pr1 to find a schedule \(S_{v,w}\) for processing the jobs of set \(N_{v,w}\) on machines \(M^{\prime }=M_{v}\) and \( M^{\prime \prime }=M_{w}\), provided that at most one preemption is allowed. Create the following schedule \(S_{(1)}^{H}\): schedule the jobs of set \(N_{u}\) nonpreemptively on machine \(M_{u}\) and process the remaining jobs in accordance with schedule \(S_{v,w}\). Stop.
In the analysis below, the following notation is used. For schedule \( S_{\left( 1\right) }^{H}\) found by Algorithm Q3Pr1CL3Lim that is associated with a triple \(\left( u,v,w\right) \) of indices, let \(C_{u}=p\left( N_{u}\right) /s_{u}\) denote the makespan of processing the jobs of set \( N_{u} \) non-preemptively on machine \(M_{u}\), while \(C_{v,w}\) denotes the makespan of processing the jobs of set \(N_{v\,,w}\) with a single preemption on machines \(M_{v}\) and \(M_{w}\). Thus, \(C_{\max }\left( S_{\left( 1\right) }^{H}\right) =\max \left\{ C_{u},C_{v,w}\right\} \).
Lemma 6
For schedule \(S_{(1)}^{H}\) associated with the sets \( N_{1,2}\) and \(N_{3}\) found in Step 1 of Algorithm Q3Pr1CL3Lim the following bound
holds, where \(\Phi \) is defined by (16).
Proof
Since in Step 1, we have that \(p_{1}\ge p_{2}\ge \Phi T_{3}s_{2}\), it follows from (16) that
which implies that \(\frac{p\left( N\backslash \left\{ J_{1},J_{2}\right\} \right) }{s_{3}}\le \frac{1}{2s_{2}+s_{3}}\le \Phi T_{3}\). Therefore, \( C_{3}\le \Phi T_{3}\) as required. According to (8), the processing of jobs \(J_{1}\) and \(J_{2}\) will complete at time
If \(C_{1,2}=\frac{p_{1}}{s_{1}}=T_{1}\) then \(C_{1,2}\le T_{3}\le \Phi T_{3} \), since we deal with instances of Class 3 (and not of Class 1) and \( \Phi \ge 1\). Further, since we are considering instances of Class 3 (and not of Class 2), it follows from \(T_{2}=\frac{p_{1}+p_{2}}{s_{1}+s_{2}}\le T_{3}=\frac{1}{s_{1}+s_{2}+s_{3}}\) that \(p_{1}\le \frac{s_{1}+s_{2}}{ s_{1}+s_{2}+s_{3}}-p_{2}\), which implies that \(p_{2}\le \frac{s_{1}+s_{2}}{ 2\left( s_{1}+s_{2}+s_{3}\right) }\) due to \(p_{2}\le p_{1}\). We deduce
This proves the lemma. \(\square \)
Lemma 7
For schedule \(S_{(1)}^{H}\) associated with the sets \( N_{u}\) and \(N_{v,w}\) found either in Step 2 or in Step 3 of Algorithm Q3Pr1CL3Lim the following bound
holds, where \(\Phi \) is defined by (16).
Proof
We only need to analyze the instances for which \( p_{2}\le \Phi T_{3}s_{2}.\) Since for any triple \(\left( u,v,w\right) \) we have that \(v\le 2\), it follows that \(p_{2}\le \Phi T_{3}s_{v}\).
In our proof, we need to distinguish between the following three options: the sets \(N_{u}\) and \(N_{v,w}\) are found
- Option 1::
-
in Step 2 of Algorithm Pr1CL3Lim, so that \(\Phi T_{3}s_{3}<p_{2}\le \Phi T_{3}s_{2}\) and \(\left( u,v,w\right) =\left( 2,1,3\right) \), \(N_{u}=\left\{ J_{2}\right\} \), \(N_{v,w}=N\backslash \left\{ J_{2}\right\} \);
- Option 2::
-
by running Step 1 of Algorithm OneSplit, so that \(p_{1}> \frac{2}{5},\) \(p_{2}\le \Phi T_{3}s_{3}\) and \(\left( u,v,w\right) =\left( 1,2,3\right) \), \(N_{u}=\left\{ J_{1}\right\} \), \(N_{v,w}=N\backslash \left\{ J_{1}\right\} \);
- Option 3::
-
by running Step 2 of Algorithm OneSplit, so that \(p_{1}\le \frac{2}{5},p_{2}\le \Phi T_{3}s_{3}\) and \(p\left( N_{u}\right) \in \left[ 1-\Phi T_{3}\left( s_{v}+s_{w}\right) ,\Phi T_{3}s_{u}\right] \).
First, we prove that \(C_{u}\le \Phi T_{3}\). For Option 1, the inequality \( C_{u}=p_{2}/s_{2}\le \Phi T_{3}\) follows immediately. For Options 2 and 3, set \(N_{u}\) is found by Algorithm OneSplit, so that (17) holds due to Lemma 5.
From now on, we focus on establishing an upper bound on \(C_{v,w}\). Let \( p=\max \left\{ p_{j}|J_{j}\in N_{v,w}\right\} \) denote the duration of the longest job in set \(N_{v,w}\), and \(\sigma =\left( \sigma \left( 1\right) ,\sigma \left( 2\right) ,\ldots \right) \) be the sequence of indices for jobs of set \(N_{v,w}\) taken in the LPT order, so that \(p_{\sigma \left( 1\right) }=p\). Adapting (8), the makespan \(C_{v,w}\) can be written as
where in the last term the preempted job \(J_{\sigma \left( k\right) }\), such that \(\sigma \left( k\right) \ge 2\), is identified by Algorithm Q2Pr1.
We start with the case that \(C_{v,w}\) is determined by the average load on machines \(M_{v}\) and \(M_{w}\). Again, for Options 2 and 3, set \(N_{v,w}\) is found by Algorithm OneSplit, so that (18) holds due to Lemma 5 and \(C_{v,w}\le \Phi T_{3}\). For Option 1, it follows from \( \Phi T_{3}s_{3}<p_{2}\le \Phi T_{3}s_{2}\) that \(p\left( N_{u}\right) =p_{2}\in \left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2} \right] \), since the intervals \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{2}\right) ,\Phi T_{3}s_{3}\right] \) and \(\left[ 1-\Phi T_{3}\left( s_{1}+s_{3}\right) ,\Phi T_{3}s_{2}\right] \) overlap; see the proof of Lemma 5. Thus, for Option 1, we deduce that \(p\left( N_{u}\right) \in \left[ 1-\Phi T_{3}\left( s_{v}+s_{w}\right) ,\Phi T_{3}s_{u}\right] \), so that
and the lemma holds.
Now we look at the case that \(C_{v,w}=\frac{p}{s_{v}}\), so that schedule \( S_{v,w}\) is non-preemptive and its makespan is determined by the duration of processing the longest job in set \(N_{v,w}\) on the fastest machine \(M_{v}\). For Option 1, \(p=\max \left\{ p_{j}|J_{j}\in N_{1,3}\right\} =p_{1}\) and if \( C_{v,w}=C_{1,3}=\frac{p_{1}}{s_{1}}\), we obtain \(\frac{p_{1}}{s_{1}} =T_{1}\le T_{3}\le \Phi T_{3}\). For Option 2, clearly \(p=p_{2}\). For Option 3, set \(N_{v,w}\) is found by Procedure Split run with \(r=4\). It follows from Step 1 of that procedure that either job \(J_{1}\) belongs to set \(N_{u}\) and therefore \(p\le p_{2}\), or \(p\le p_{1}\le \frac{1}{4}\).
It follows from (16) that
since \(s_{2}\le s_{1}\le 2s_{3}\). This guarantees that \(\Phi T_{3}s_{3}\ge \frac{1}{4}\) for all speeds of the range under consideration. If \(p\le p_{2}\) then the inequality \(p_{2}\le \Phi T_{3}s_{v}\) ensures \( C_{v,w}\le \Phi T_{3}\). Alternatively, \(p\le \frac{1}{4}\) and we have that
We are now left to consider the case that \(C_{v,w}\) is given by the third term in the right-hand side of (20). It can be derived that \( C_{\max }\left( S_{v,w}\right) \) does not exceed the actual processing time of the preempted job \(J_{\sigma \left( k\right) }\) on the slower machine, i.e., \(C_{v,w}\le \frac{p_{\sigma \left( k\right) }}{s_{w}}\). Since (8) implies that job \(J_{\sigma \left( k\right) }\) is at most the second longest in set \(N_{v,w}\), it follows that \( p_{\sigma \left( k\right) }\le p_{2}\). In the case of Options 2 and 3, the condition \(p_{2}\le \Phi T_{3}s_{3}\) implies that
so that we only need to consider Option 1. If \(p_{\sigma \left( k\right) }\le \frac{1}{4}\) then we apply (21) to deduce
In the remainder of this proof, we assume \(p_{\sigma \left( k\right) }>\frac{ 1}{4}\), i.e., job \(J_{\sigma \left( k\right) }\), as the second longest job of set \(N_{1,3}\) is job \(J_{3}\).
It is clear that \(p_{1}\le \left( 1-p_{2}-p_{3}\right) \le \left( 1-2p_{3}\right) \), and \(p_{3}\le \frac{1}{3}\). We deduce
Since \(p_{3}\le \frac{1}{3}\) and \(s_{1}\le 2s_{3}\) for the range of speeds under consideration, we finally derive
as required. \(\square \)
Lemmas 6 and 7 together provide a global upper bound on \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \). We now use this to provide tight bounds for the cases of two slow and two fast machines.
We first notice that the component of \(\Phi \) given by \(\frac{ s_{1}+s_{2}+s_{3}}{s_{1}+2s_{3}}\) is dominated by \(\frac{\left( 2s_{1}-s_{3}\right) \left( s_{1}+s_{2}+s_{3}\right) }{3s_{1}^{2}}\) found in Lemma 7 since \(\frac{\left( 2s_{1}-s_{3}\right) }{3s_{1}^{2} }\ge \frac{1}{s_{1}+2s_{3}}\) if \(\left( s_{1}-2s_{3}\right) \left( s_{3}-s_{1}\right) \ge 0\). The latter condition holds for \(s_{3}\le s_{1}\le 2s_{3}\), the speed range of interest. Hence we define \(\tilde{\Phi } \) to be \(\Phi \) with the component \(\frac{s_{1}+s_{2}+s_{3}}{s_{1}+2s_{3}}\) removed.
Corollary 2
For schedule \(S_{(1)}^{H}\) on two slow machines \((2\ge s_{1}=s\ge 1=s_{2}=s_{3})\) found by Algorithm Q3Pr1CL3Lim the bound
holds and this bound is tight.
Proof
For the case of two slow machines, \(T_{3}=\frac{1 }{s+2}\) and we derive from (16) that
If the makespan of schedule \(S_{(1)}^{H}\) is dominated by preemptive processing, then the expressions given in Lemma 6 and in Lemma 7, respectively, simplify as
Since \(\frac{s+1}{2}>\frac{s+2}{3}\) for \(s\ge 1\), it follows that in the two expressions above the first one dominates the second. On other other hand, we can compare \(\frac{\left( 2s-1\right) \left( s+1\right) }{2s^{2}}\) with the second and the third components of \(\tilde{\Phi }\). We see that \( \frac{\left( 2s-1\right) \left( s+1\right) }{2s^{2}}\le \frac{3\left( s+2\right) }{4\left( s+1\right) }\le \tilde{\Phi }\) for \(s\le \root 3 \of {2}\), while \(\frac{\left( 2s-1\right) \left( s+1\right) }{2s^{2}}\le \frac{s+2}{3} \le \tilde{\Phi }\) for \(\left( s-1\right) \left( 2s^{2}-3\right) \ge 0\), which holds if \(s\ge \sqrt{\frac{3}{2}}\). Since for each \(s\in \left[ 1,2\right] \) either \(s\le \root 3 \of {2}= 1.\, 259\,9\ldots \) or \(s\ge \sqrt{\frac{3}{2}}= 1.\, 2247\ldots \), we deduce that \(\frac{\left( 2s-1\right) \left( s+1\right) }{ 2s^{2}}\le \tilde{\Phi }\), so that \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \le \tilde{\Phi }\). The break-points are easily seen to be as in (22).
Figure 3 shows the graph of \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \), as a function of \(s\in \left[ 1,2\right] \).
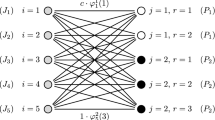
Tight instances are represented by five jobs of equal length for \(1\le s\le \frac{8}{7}\), four jobs of equal length for \(\frac{8}{7}\le s\le \frac{5}{4}\) and three jobs of equal length for \(\frac{5}{4}\le s\le 2\); see rows 1–3 of Table 1. In this table, the column labelled \(S_{\left( 1\right) }^{*}\) shows the assignment of the jobs to the machines; if a job appears in two of the columns labelled \(M_{1}\), \(M_{2}\) or \(M_{3}\), then the job is processed on the corresponding machines with a single preemption.
Schedule \(S_{(1)}^{*}\) for the instances in Table 1: a row 1, b row 2
For the instance in row 1 of Table 1, we have that \(\tilde{ \Phi }=\frac{2\left( s+2\right) }{5s}\). The schedule shown in Fig. 4a assigns two jobs to the fast machine \(M_{1}\) and processes the remaining three jobs on two slow machines with a single preemption of job \(J_{4}\). Notice that \(\frac{2}{5s}>\frac{3}{10}\) for \(s< \frac{4}{3}\). This schedule is in fact an optimal schedule for the instance. Indeed, with a single preemption, we need to schedule four full jobs and two parts of the fifth job on three machines. In any case, there will be a machine that processes at least two full jobs, so that the makespan cannot be smaller than \(\frac{2}{5s}\).
For the instance in row 2, we have that \(\tilde{\Phi }=\frac{3(s+2)}{4\left( s+1\right) }\). The schedule shown in Fig. 4b processes three jobs on machines \(M_{1}\) and \(M_{2}\), while machine \(M_{3}\) processes a single job. The preempted job \(J_{2}\) is processed on \(M_{2}\) in the time interval \(\left[ 0,\frac{2-s}{4\left( s+1\right) }\right] \), where \( \frac{2-s}{4\left( s+1\right) }<\frac{1}{4s}\) for all s. Job \(J_{2}\) is also processed on machine \(M_{1}\) in the time interval \(\left[ \frac{1}{4s}, \frac{3}{4(s+1)}\right] \). There is no overlap in the processing of this job. Machine \(M_{2}\) performs \(\frac{2-s}{s+1}\) of the job, while machine \( M_{1}\) performs \(\frac{2s-1}{s+1}=1-\frac{2-s}{s+1}\) of the job, i.e., job \( J_{2}\) is processed in full. Since \(\frac{3}{4(s+1)}\ge \frac{1}{4}\) for \( s\le 2\), the makespan of this schedule is equal to \(\frac{3}{4(s+1)}\), which is the average machine load for processing three jobs on two non-identical machines, i.e., this schedule is the best schedule, provided that the fast machine is involved in the processing of the preempted job. In the alternative class of schedules, exactly one job is processed on machine \( M_{1}\), while the remaining three jobs are processed with a single preemption on machines \(M_{2}\) and \(M_{3}\), similarly to the schedule shown in Fig. 4a. However, the makespan of the latter schedule is equal to \(\frac{3}{8}\ge \frac{3}{4(s+1)}\). Thus, the schedule in Fig. 4b is optimal.
For the instance in row 3, we have that \(\tilde{\Phi }=\frac{s+2}{3}\). Consider a schedule in which each machine receives exactly one job, which is processed with no preemption. The makespan of the resulting schedule is \( \frac{1}{3}\). If no job is processed in full on a slow machine, then the average load of the fast and a single slow machine is equal to \(\frac{1}{s+1} \), which is no less than \(\frac{1}{3}\) for \(s\le 2\).
This completes the proof. \(\square \)
Corollary 3
For schedule \(S_{(1)}^{H}\) on two fast machines \(\left( 2\ge s_{1}=s_{2}=s\ge 1=s_{3}\right) \) found by Algorithm Q3Pr1CL3Lim the bound
holds and this bound is tight.
Proof
For the case of two fast machines, \(T_{3}=2s+1\) and we derive from (16) that
where the last equality holds since \(\frac{2}{5s}\) dominates the other components for \(s\le 2\).
If the makespan of schedule \(S_{(1)}^{H}\) is dominated by preemptive processing, then the expressions given in Lemma 6 and in Lemma 7, respectively, simplify as
Thus,
and the break-point is easily seen to be as in (23).
Figure 5 shows the graph of \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \), as a function of \(s\in \left[ 1,2\right] \) .
Tight instances consist of five jobs of equal length for \(1\le s\le \frac{5 }{4}\), and of three jobs of equal length for \(\frac{5}{4}\le s\le 2\); see rows 4–5 of Table 1.
For the instance in row 4 of Table 1, we have that \(\tilde{ \Phi }=\frac{2\left( 2s+1\right) }{5s}\). The schedule shown in Fig. 6a assigns two jobs to each of the fast machines \(M_{1}\) and \(M_{2}\), while the fifth job is processed on \(M_{3}\). The makespan of this schedule is \(\frac{2}{5s}\ge \frac{1}{5}\) for \(s\le 2\). This schedule is in fact an optimal schedule for the instance. Indeed, with a single preemption, we need to schedule four full jobs and two parts of the fifth job on three machines. In any case, there will be a machine that processes at least two full jobs, so that the makespan cannot be smaller than \(\frac{2 }{5s}\).
For the instance in row 5, the schedule shown in Fig. 6b assigns one job to be processed non-preemptively on each fast machine \( M_{1}\) and \(M_{2}\), while job \(J_{3}\) is processed with a single preemption: on the slow machine \(M_{3}\) in the time interval \(\left[ 0,\frac{1}{3s} \right] \) and on machine \(M_{1}\) in the interval \(\left[ \frac{1}{3s},\frac{ 2s-1}{3s^{2}}\right] \). There is no overlap in the processing of this job. Machine \(M_{3}\) performs \(\frac{1}{s}\) of the job, while machine \(M_{1}\) performs \(\frac{s-1}{s}=1-\frac{1}{s}\) of the job, i.e., job \(J_{3}\) is processed in full. If machine \(M_{3}\) processes at least one full job, then it completes no earlier than time \(\frac{1}{3}\), which is no less than \( \frac{2s-1}{3s^{2}}\) for all \(s\ge 1\). If \(M_{3}\) processes no jobs at all, then the three jobs are to be processed on two identical fast machines \( M_{1} \) and \(M_{2}\), which implies the makespan of at least \(\frac{1}{2s}\), the latter value being no less than \(\frac{2s-1}{3s^{2}}\) for \(s\le 2\). Thus, the schedule in Fig. 6b is an optimal schedule \(S_{\left( 1\right) }^{*}\). \(\square \)
Schedule \(S_{(1)}^{*}\) for the instances in Table 1: a row 4, b row 5
4.2 Unlimited relative machine speeds (\(s_{1}\ge 2s_{3}\))
In this section, we assume that \(s_{1}\ge 2s_{3}\). The analysis of the value of \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \) is focused on the instances of the three-machine problem with either two fast or two slow machines. For these situations, we derive tight upper bounds on the value \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) \).
The algorithm below schedules all jobs with at most one preemption on the first two machines, the slowest machine \(\,M_{3}\) is not used at all.
Algorithm Q3Pr1CL3UnLim
Input: An instance \(I=\left( \mathcal {L}_{n},\mathcal {M} _{3}\right) \) of Class 3, with its jobs having normalized processing times, \( p\left( N\right) =1\), numbered in their LPT order; among the three machines there are either two fast \(\left( s_{1}=s_{2}=s\ge 2\text {, }s_{3}=1\right) \) or two slow \(\left( s_{1}=s\ge 2\text {, }s_{2}=s_{3}=1\right) \)
Output: A schedule \(S_{(1)}^{H}\) with at most one preemption
- Step 1.:
-
Create schedule \(S_{(1)}^{H}\) in which all jobs are scheduled in accordance with Algorithm Q2Pr1 on machines \(M^{\prime }=M_{1}\) and \( M^{\prime \prime }=M_{2}\). Stop.
Lemma 8
For schedule \(S_{(1)}^{H}\) found in Step 1 of Algorithm Q3Pr1CL3UnLim, the inequality
holds for two slow machines, while the inequality
holds for two fast machines. Both bounds are tight.
Proof
Algorithm Q2Pr1 will produce a schedule with the makespan equal to the maximum of one of three expressions similarly to (20), i.e.,
The second expression \(\frac{p_{1}}{s_{1}}\) cannot dominate, since \(\frac{ p_{1}}{s_{1}}=T_{1}\le T_{3}=\frac{1}{s_{1}+s_{2}+s_{3}}<\frac{1}{ s_{1}+s_{2}}\) for Class 3 instances.
In the case of two fast machines, in order to create schedule \(S_{(1)}^{H}\), two identical machines of speed s are used and \(C_{\max }\left( S_{(1)}^{H}\right) =\frac{1}{s_{1}+s_{2}}=\frac{1}{2s}\) for any Class 3 instance. Hence, \(\rho _{3}^{\left( 1\right) }\left( \mathrm {Class}~3\right) =\frac{C_{\max }\left( S_{(1)}^{H}\right) }{T_{3}}=\frac{2s+1}{2s}\) as claimed. This function is decreasing and attains its maximum of \(\frac{5}{4}\) at \(s=2\); see Fig. 7.
For two slow machines, the makespan \(C_{\max }\left( S_{(1)}^{H}\right) \) is given by either the average machine load on the two machines \(\frac{1}{ s_{1}+s_{2}}=\frac{1}{s+1}\), or is defined by the total actual processing time of the preempted job \(J_{k}\). In the latter case, the third expression of (24) for the two slow machines simplifies to
If \(k=2\), then in schedule \(S_{(1)}^{H}\) the jobs \(J_{1}\) and \(J_{2}\) are scheduled exactly as in the schedule analyzed in Lemma 6. Thus, (19) holds, which for the two slow machines simplifies to
If for the preempted job \(J_{k}\) we have that \(k\ge 3\), then substituting \( \sum _{i=1}^{k-1}p_{j}\le 1-p_{k}\) and \(p_{k}\le 1/k\) into (25) gives
The right-hand side expression above achieves its maximum for \(k=3\), which implies
Hence
It is easily checked that \(\frac{\left( 2s-1\right) \left( s+1\right) }{ 2s^{2}\left( s+2\right) }\le \frac{3s-2}{3s^{2}}\) for \(s\ge 1\) and \(\frac{1 }{s+1}\le \frac{3s-2}{3s^{2}}\) for \(s\ge 2\), so that \(\frac{3s-2}{3s^{2}}\) dominates, and
as claimed. The maximum value of \(\rho _{3}^{\left( 1\right) }\left( \mathrm { Class}~3\right) \) for the two slow machines is 4 / 3, which is attained at \( s=2;\) see Fig. 7. Notice that this maximum value is equal to the global bound \(2-2/m\), since \(m=3\).
For both situations, the tightness of the bounds is provided by the instance with three identical jobs, \(p_{1}=p_{2}=p_{3}=\frac{1}{3}\). In the schedules discussed below the slow machine \(M_{3}\) is assigned no jobs.
In the case of two fast machines, the schedule shown in Fig. 8a processes the jobs on two identical machines of speed s with a single preemption, which gives the makespan of \(\frac{1}{2s}\). This schedule is in fact an optimal schedule for the instance. Indeed, if machine \(M_{3}\) processes a full job, then that job would complete at time \(\frac{1}{ 3}>\frac{1}{2s}\) for \(s\ge 2\). If there is a job which is processed with preemption on \(M_{3}\) and on one of the fast machines, then we get a schedule shown in Fig. 6b, with the makespan \(\frac{ 2s-1}{3s^{2}}\ge \frac{1}{2s}\) for \(s\ge 2\).
In the case of two slow machines, consider the schedule shown in Fig. 8b, in which two full jobs are processed on machine \(M_{1}\), and job \(J_{3}\) is processed with a single preemption, on the slow machine \( M_{2}\) in the time interval \(\left[ 0,\frac{2}{3s}\right] \) and on machine \( M_{1}\) in the interval \(\left[ \frac{2}{3s},\frac{3s-2}{3s^{2}}\right] \). There is no overlap in the processing of this job. Machine \(M_{2}\) performs \( \frac{2}{s}\) of the job, while machine \(M_{1}\) performs \(\frac{s-2}{s}=1- \frac{2}{s}\) of the job, i.e., job \(J_{3}\) is processed in full. If a slow machine processes at least one full job, then it completes no earlier than time \(\frac{1}{3}\), which is no less than \(\frac{3s-2}{3s^{2}}\) for \(s\ge 2\) . Thus, the schedule in Fig. 8b is an optimal schedule \(S_{\left( 1\right) }^{*}\). \(\square \)
5 Conclusion
In this paper, for the problem on three uniform machines to minimize the makespan we have performed a parametric analysis of the quality of a schedule with at most one preemption compared to the optimal preemptive schedule. We have derived tight bounds in terms of a single parameter, the relative speed of the machines, for the cases of two fast and two slow machines, respectively.
We hope that Procedure Split, simple as it, may appear useful as part of various scheduling algorithms that require partitioning of jobs into two subsets with prescribed properties.
For the general problem on \(m\ge 3\) uniform machines, it is an interesting research goal to deduce a quality measure of schedules on uniform machines, provided any fixed number of preemptions \(2\le q\le 2\left( m-1\right) \) is allowed. Possible extensions may also include an objective function other than the makespan and/or a more general machine environment, e.g., unrelated parallel machines.
References
Braun, O., & Schmidt, G. (2003). Parallel processor scheduling with limited number of preemptions. SIAM Journal on Computing, 32, 671–680.
Brucker, P. (2007). Scheduling algorithms (5th ed.). Berlin: Springer.
Chen, B. (2004). Parallel machine scheduling for early completion. In J. Y.-T. Leung (Ed.), Handbook of scheduling: Algorithms, models and performance analysis (pp. 9-175–9-184). London: Chapman & Hall/CRC.
Correa, J. R., Skutella, M., & Verschae, J. (2012). The power of preemption on unrelated machines and applications to scheduling orders. Mathematical Operations Research, 37, 379–398.
Epstein, L., & Levin, A. (2016). The benefit of preemption for single machine scheduling so as to minimise total weighted completion time. Operations Research Letters, 44, 772–774.
Epstein, L., Levin, A., Soper, A. J., & Strusevich, V. A. (2017). Power of preemption for minimizing total completion time on uniform parallel machines. SIAM Journal on Discrete Mathematics, 31, 101–123.
Gonzalez, T. F., Ibarra, O. H., & Sahni, S. (1977). Bounds for LPT schedules on uniform processors. SIAM Journal on Computing, 6, 155–166.
Gonzalez, T. F., & Sahni, S. (1978). Preemptive scheduling of uniform processor systems. Journal of the ACM, 25, 92–101.
Jiang, Y., Weng, Z., & Hu, J. (2014). Algorithms with limited number of preemptions for scheduling on parallel machines. Journal of Combinatorial Optimization, 27, 711–723.
Lee, C.-Y., & Strusevich, V. A. (2005). Two-machine shop scheduling with an uncapacitated interstage transporter. IIE Transactions, 37, 725–736.
McNaughton, R. (1959). Scheduling with deadlines and loss functions. Management Science, 6, 1–12.
Mireault, P., Orlin, J. B., & Vohra, R. V. (1997). A parametric worst case analysis of the LPT heuristic for two uniform machines. Operations Research, 45, 116–125.
Rustogi, K., & Strusevich, V. A. (2013). Parallel machine scheduling: Impact of adding extra machines. Operations Research, 61, 1243–1257.
Shachnai, H., Tamir, T., & Woeginger, G. J. (2005). Minimizing makespan and preemption costs on a system of uniform machines. Algorithmica, 42, 309–334.
Shchepin, E., & Vakhania, N. (2008). On the geometry, preemptions and complexity of multiprocessor and shop scheduling. Annals of Operations Research, 159, 183–213.
Soper, A. J., & Strusevich, V. A. (2014a). Single parameter analysis of power of preemption on two and three uniform machines. Discrete Optimization, 12, 26–46.
Soper, A. J., & Strusevich, V. A. (2014b). Power of preemption on uniform parallel machines. In 17th international workshop on approximation algorithms for combinatorial optimization problems (APPROX’14)/18th international workshop on randomization and computation (RANDOM’14). Leibniz international proceedings in informatics (LIPIcs) (Vol. 28, pp. 392–402). https://doi.org/10.4230/LIPIcs.APPROX-RANDOM.2014.392.
Soper, A. J., & Strusevich, V. A. (2018). Power of a single preemption on uniform parallel machines. Discrete Applied Mathematicshttps://doi.org/10.1016/j.dam.2018.03.007. (in Press).
Woeginger, G. J. (2000). A comment on scheduling on uniform machines under chain-like precedence constraints. Operations Research Letters, 26, 107–109.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Soper, A.J., Strusevich, V.A. Parametric analysis of the quality of single preemption schedules on three uniform parallel machines. Ann Oper Res 298, 469–495 (2021). https://doi.org/10.1007/s10479-018-2952-6
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-2952-6