1 Introduction

Fault diagnosis of analog circuits is an important problem in the design and testing of electronic devices [1–22]. Generally, fault diagnosis includes detecting faulty circuits, locating faulty parameters and evaluating their values. If a faulty parameter is drifted from its tolerance range but does not lead to some topological changes, the fault is said to be soft or parametric. If a fault is open circuit or short circuit, it is called hard or catastrophic. In integrated circuits physical imperfections, such as near–opens or near–shorts may occur as spot defects [7, 10, 21, 22]. The methods dedicated to soft fault diagnosis usually exploit the simulation after test approach, where circuit simulations take place after any testing. They are based on measurements of the voltages at accessible points of the circuit, leading to equations with the tested parameters as unknown variables.

In current CMOS technology the global variations of parameters are measured by dedicated test structures included in the wafer. However, the problem is how to identify the random local variations of the process parameters. The local variations are due to fabrication or due to aging phenomenon. They affect the components across the die independently. Examples of local variations in ICs include local geometrical deformations, such as variations in the channel length and width, the oxide thickness, etc.

Many concepts and methods focused on parametric fault diagnosis are presented in references [1–3, 5, 9, 11, 13, 16–20]. Most of the works, dealing with soft fault diagnosis of analog circuits, address only the case when just one parameter is faulty. Fewer papers are devoted to the multiple fault diagnosis, where several parameters can be faulty. In real circuits the test equations, that express the measured voltages in terms of the parameters are nonlinear and cannot be presented in explicit analytical form. These equations may actually have multiple solutions, which means that several sets of the parameter values meet the test. To find the multiple solutions the parametric homotopy [17], the simplicial homotopy [18], or the block relaxation method [19] were proposed. To determine the actual solution a new efficient approach was proposed in Ref. [20] as follows. Two tests of the circuit are arranged, one used to find the solutions and the other to check if the obtained solution is the actual one. To compute the solution the extended systematic search method was developed [20]. In this paper the Nelder–Mead optimization method is applied with the objective function properly modified during the computation process and similarly as in [20] the obtained result is checked using the validation test. If the obtained solution passes this test the algorithm terminates, otherwise another solution is calculated and verified. The procedure is carried out as long as the solution which meets the validation test is obtained.

2 Diagnostic tests

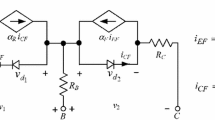
Let us consider a nonlinear DC circuit, with \(n\) parameters \(x_{1} ,\; \ldots ,\;x_{n}\) considered as potentially faulty, having one or more input nodes accessible for excitation and one output node accessible for measurement. We connect to the output node a resistor \(R_{\text{o}}\) and apply DC voltage sources to the input nodes (see Fig. 1). We choose \(n\) sets of the input voltage values and read the corresponding values of the output voltage. They are labelled \(v_{\text{o}}^{\left( 1\right)} ,\; \ldots ,\;v_{\text{o}}^{\left( n \right)}\) and used to form vector \({\mathbf{v}}^{{\left( {\text{o}} \right)}} = \left[ {v_{\text{o}}^{\left( 1\right)} \cdots \;v_{\text{o}}^{\left( n \right)} } \right]^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}\), where \({\text{T}}\) means transposition. Each of the voltages is a function of the circuit parameters \(x_{1} ,\; \ldots ,\;x_{n}\), \(v_{\text{o}}^{\left( j \right)} = \tilde{g}_{j} \left( {\mathbf{x}} \right)\), where \({\mathbf{x}} = \left[ {x_{1} \cdots \;x_{n} } \right]^{{{\kern 1pt} {\text{T}}}}\) is the vector consisting of the parameters considered as potentially faulty. Thus, it holds

Fig. 1
figure 1

Diagnostic test

Full size image
$${\mathbf{v}}^{{\left( {\text{o}} \right)}} = {\tilde{\mathbf{g}}}\left( {\mathbf{x}} \right) ,$$
(1)

where \({\tilde{\mathbf{g}}}\left( {\mathbf{x}} \right) = \left[ {\tilde{g}_{1} \left( {\mathbf{x}} \right) \cdots \;\tilde{g}_{n} \left( {\mathbf{x}} \right)} \right]^{{{\kern 1pt} {\text{T}}}}\). Equation (1) can be rewritten in the compact form

$${\mathbf{g}}\left( {\mathbf{x}} \right) = {\mathbf{0}} ,$$
(2)

where \({\mathbf{g}}\left( {\mathbf{x}} \right) = \left[ {g_{1} \left( {\mathbf{x}} \right) \cdots \;g_{n} \left( {\mathbf{x}} \right)} \right]^{{{\kern 1pt} {\text{T}}}} = {\tilde{\mathbf{g}}}\left( {\mathbf{x}} \right) - {\mathbf{v}}^{{\left( {\text{o}} \right)}}\), and named a test equation.

The diagnostic method developed in Sect. 3 requires two tests arranged using the above–described approach. As a result the voltages \(\hat{v}_{\text{o}}^{\left( 1\right)} ,\; \ldots ,\;\hat{v}_{\text{o}}^{\left( n \right)}\) are measured in the circuit as depicted in Fig. 1, but driven by different sets of the input voltage sources, forming vector \({\hat{\mathbf{v}}}^{{\left( {\text{o}} \right)}} = \left[ {\hat{v}_{\text{o}}^{\left( 1\right)} \cdots \;\hat{v}_{\text{o}}^{\left( n \right)} } \right]^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}\). The first test leading to Eq. (2) will be named a principal test (PT), whereas the second one will be named a validation test (VT).

Unfortunately, in real electronic circuits the function \({\mathbf{g}}\left( {\mathbf{x}} \right)\) cannot be presented in explicit analytical form. However, the values of \(\tilde{g}_{i} \left( {\mathbf{x}} \right)\) \(i = 1,\; \ldots ,\;n\), for given \({\mathbf{x}}\), can be found by performing the analyses of the circuits driven by the sources as in the test, with the parameters being the elements of vector \({\mathbf{x}}\).

3 Fault diagnosis algorithm

An algorithm that allows finding actual values of the parameters \(x_{1} ,\; \ldots ,\;x_{n}\) is developed in this section. The algorithm solves the PT Eq. (2) and verifies the obtained solutions applying the VT. Its core is the Nelder–Mead optimization method [23–25]. The algorithm takes into consideration the possibility of existing several solutions of the nonlinear Eq. (2). Each of the solutions is a set of the parameters that meet the PT.

Since the algorithm exploits the Nelder–Mead method, a background of this method as well as the version that is used in this paper is described below. The Nelder–Mead method is designed to solve the unconstrained optimization problem of minimizing given nonlinear function \(f\left( {\mathbf{x}} \right) :R^{n} \to R\). In this paper the method is adapted to solve Eq. (2). For this purpose the function

$$f\left( {\mathbf{x}} \right) = \sqrt {\alpha_{1} g_{1}^{2} \left( {\mathbf{x}} \right) + \; \cdots \; + \alpha_{n} g_{n}^{2} \left( {\mathbf{x}} \right)}$$
(3)

is formed, where \(\alpha_{1} ,\; \ldots ,\;\alpha_{n}\) are coefficients equal to zero or one. If all the coefficients are equal to one the function \(f\left( {\mathbf{x}} \right)\) will be called a complete function, otherwise a reduced function. The complete function is identical to the Euclidean norm of \({\mathbf{g}}\left( {\mathbf{x}} \right)\), i.e., \(f\left( {\mathbf{x}} \right) = \left\| {{\kern 1pt} {\mathbf{g}}\left( {\mathbf{x}} \right){\kern 1pt} } \right\|_{{{\kern 1pt} 2}}\). The Nelder–Mead method uses only the function values at some points in \(R^{n}\) and does not require gradients at the points. This is why this method is very useful to solve Eq. (2), with \({\mathbf{g}}\left( {\mathbf{x}} \right)\) not given in explicit analytical form. The Nelder–Mead method is simplex–based [23–25]. An m-simplex is a figure formed by \(m + 1\) independent points, written as \(S = \left\{ {{\mathbf{x}}^{0} ,\; \ldots ,\;{\mathbf{x}}^{m} } \right\}\), where \({\mathbf{x}}^{i} = \left[ {x_{1}^{{{\kern 1pt} i}} \cdots \;x_{n}^{{{\kern 1pt} i}} } \right]^{{{\kern 1pt} {\kern 1pt} {\text{T}}}}\), \(i = 0,\;1,\;\; \ldots ,\;m\), are called vertices. It is a convex hull of the \(m + 1\) independent points \({\mathbf{x}}^{i}\) \(\left( {i = 0,\;1,\;\; \ldots ,\;m} \right)\). For example, 2-simplex is a triangle (see Fig. 2).

Fig. 2
figure 2

Exemplary 2-simplex

Full size image

The method exploits simplices having \(n + 1\) vertices \(S = \left\{ {{\mathbf{x}}^{0} ,\; \ldots ,\;{\mathbf{x}}^{n} } \right\}\). The corresponding function values at these vertices are labeled \(f^{0} = f\left( {{\mathbf{x}}^{0} } \right)\,,\; \ldots ,\;f^{n} = f\left( {{\mathbf{x}}^{n} } \right)\). At any stage of the computation process the method generates a new simplex, aimed at decreasing the function values at its vertices. To construct this simplex one or more new points are searched comparing their function values with those at the vertices. Generally the method terminates when the simplex becomes sufficiently small, or the simplex is flat or degenerated [24]. The crucial point of the Nelder–Mead method is creating an adjusted simplex to the current simplex \(S\). In this paper the approach described in [23] is adopted. Choose the indices \(h\), \(s\), \(l\), of the worst, second worst, and the best vertex of \(S\) so that \(f^{h} = \mathop { \hbox{max} }\limits_{i} f^{i}\), \(f^{s} = \mathop { \hbox{max} }\limits_{i \ne h} f^{i}\), \(f^{l} = \mathop { \hbox{min} }\limits_{i} f^{i}\). Calculate the centroid \({\mathbf{c}}\) of the side opposite to the worst vertex \(h\), \({\mathbf{c}} = \frac{1}{n}\sum\limits_{i \ne h} {{\mathbf{x}}^{i} }\) and find the reflection point \({\mathbf{x}}^{r} = {\mathbf{c}} + \left( {{\mathbf{c}} - {\mathbf{x}}^{h} } \right)\) as well as \(f^{r} = f\left( {{\mathbf{x}}^{r} } \right)\) (see Fig. 3).

Fig. 3
figure 3

Basic simplex operations

Full size image

If \(f^{l} \le f^{r} < f^{s}\) choose \({\mathbf{x}}^{r}\) as the new vertex of the adjusted simplex. Otherwise, continue the procedure depending on whether \(f^{r} < f^{l}\) or \(f^{r} \ge f^{s}\).

  • If \(f^{r} < f^{l}\), compute the point \({\mathbf{x}}^{e} = {\mathbf{c}} + \gamma \left( {{\mathbf{x}}^{r} - {\mathbf{c}}} \right)\) and \(f^{e} = f\left( {{\mathbf{x}}^{e} } \right)\). If \(f^{e} < f^{r}\) choose \({\mathbf{x}}^{e}\) as the new vertex, otherwise, choose \({\mathbf{x}}^{r}\) as a new vertex.

  • If \(f^{r} \ge f^{s}\), compute a point \({\mathbf{x}}^{c}\) using the following approach.

  • If \(f^{r} < f^{h}\), compute \({\mathbf{x}}^{c} = {\mathbf{c}} + \beta \left( {{\mathbf{x}}^{r} - {\mathbf{c}}} \right)\) and \(f^{c} = f\left( {{\mathbf{x}}^{c} } \right)\). If \(f^{c} \le f^{r}\), choose \({\mathbf{x}}^{c}\) as the vertex, otherwise, perform a shrink operation as described below.

  • If \(f^{r} \ge f^{h}\), compute \({\mathbf{x}}^{c} = {\mathbf{c}} + \beta \left( {{\mathbf{x}}^{h} - {\mathbf{c}}} \right)\) and \(f^{c} = f\left( {{\mathbf{x}}^{c} } \right)\). If \(f^{c} \le f^{h}\), choose \({\mathbf{x}}^{c}\) as the vertex. Otherwise, perform a shrink operation.

Shrink operation: Compute \(n\) new vertices \({\mathbf{x}}^{i} = {\mathbf{x}}^{l} + \delta \left( {{\mathbf{x}}^{i} - {\mathbf{x}}^{l} } \right)\), for \(i = 0,\; \ldots ,\;n\), \(i \ne l\), (see Fig. 4).

Fig. 4
figure 4

Shrink operation

Full size image

3.1 Note

The coefficients \(\gamma\), \(\beta\), \(\delta\) are chosen as proposed in Ref. [25]: \(\gamma = 1 + \frac{2}{n}\), \(\beta = 0.75 - \frac{1}{2n}\), \(\delta = 1 - \frac{1}{n}\).

As the initial simplex we choose the regular one using the procedure described in Ref. [24].

It should be emphasized that the function \(f\left( {\mathbf{x}} \right)\) is not given in explicit analytical form. In consequence, to find the value of the complete function \(f\left( {\mathbf{x}} \right)\) at given \({\mathbf{x}}\), \(n\) analyses of the circuit must be performed applying the sources as in PT. This is time consuming process. The time is shrunk if \(f\left( {\mathbf{x}} \right)\) is the reduced function. Since the Nelder–Mead method requires large number of the values of \(f\left( {\mathbf{x}} \right)\) at various points \({\mathbf{x}}\), the reduced function is exploited at some stages of the algorithm proposed in this paper. Moreover, for different reduced functions the method searches for the solution (a set of the parameters) in different directions. This observation is used to find a new solution, when the obtained one does not pass the VT.

4 Sketch of the algorithm

  1. 1.

    Pick the required measurement accuracy of the voltages \(v_{\text{o}}^{\left( 1\right)} ,\; \ldots ,\;v_{\text{o}}^{\left( n \right)}\) and \(\hat{v}_{\text{o}}^{\left( 1\right)} ,\; \ldots ,\;\hat{v}_{\text{o}}^{\left( n \right)}\), the tolerance \(\varepsilon_{1}\) such that the inequality \(\left\| {{\kern 1pt} {\mathbf{g}}\left( {\mathbf{x}} \right){\kern 1pt} } \right\|_{{{\kern 1pt} 2}} < \varepsilon_{1}\) is a good approximation of \(\left\| {{\kern 1pt} {\mathbf{g}}\left( {\mathbf{x}} \right){\kern 1pt} } \right\|_{{{\kern 1pt} 2}} = 0\), the tolerance \(\varepsilon_{2}\) used in Step 4, a maximum number of the generated simplices \(M\), and the side \(a\) of the initial regular simplex.

  2. 2.

    Arrange two diagnostic tests, PT and VT, and form the vectors \({\mathbf{v}}^{{\left( {\text{o}} \right)}}\) and \({\hat{\mathbf{v}}}^{{\left( {\text{o}} \right)}}\) consisting of the measured voltages.

  3. 3.

    Create the reduced function \(f\left( {\mathbf{x}} \right)\) specified by Eq. (3) with \(\alpha_{1} = \; \cdots \; = \alpha_{n - 1} = 1\), \(\alpha_{n} = 0\) and apply the Nelder–Mead method. If during the process a simplex is obtained so that the value of \(f\left( {\mathbf{x}} \right)\) at the best vertex is <\(100\varepsilon_{2}\), the computation process is modified as follows. The obtained \({\mathbf{x}}\) is considered as an approximate solution. Next the complete function \(f\left( {\mathbf{x}} \right)\) is created by setting \(\alpha_{1} = \; \cdots \; = \alpha_{n} = 1\), a new regular simplex is constructed around this best vertex and the procedure is continued. If during the process a vertex, at which the value of \(f\left( {\mathbf{x}} \right)\) is less than \(\varepsilon_{1}\) appears, the parameters \(x_{1} ,\; \ldots ,\;x_{n}\) corresponding to this vertex meet the PT. Otherwise, go to Step 5.

  4. 4.

    Check if the obtained parameters satisfy the VT. For this purpose analyse the circuit with these parameters, driven by the sources as in VT, find the voltages labelled \(\tilde{v}_{\text{o}}^{\left( 1\right)} ,\; \ldots ,\;\tilde{v}_{\text{o}}^{\left( n \right)}\) and form vector \({\mathbf{r}} = \left[ {r_{1} \cdots \;r_{n} } \right]^{{{\kern 1pt} {\text{T}}}}\), where \(r_{j} = \tilde{v}_{\text{o}}^{{\left( {\text{j}} \right)}} - \hat{v}_{\text{o}}^{{\left( {\text{j}} \right)}}\), \(j = 1,\; \ldots ,\;n\). If \(\left\| {{\kern 1pt} {\mathbf{r}}{\kern 1pt} } \right\|_{{{\kern 1pt} 2}} = \sqrt {r_{1}^{2} \; + \cdots + \;r_{n}^{2} } \le \varepsilon_{2}\), the parameters are the actual ones. In such a case the algorithm terminates. Otherwise, they are virtual and we proceed to Step 5.

  5. 5.

    Modify the function \(f\left( {\mathbf{x}} \right)\) by setting \(\alpha_{n - 1} = 0\), \(\alpha_{1} = \; \cdots \; = \alpha_{n - 2} = \alpha_{n} = 1\) and repeat the steps 3–4 adapted to this case.

This procedure can be continued if the actual parameters have not been found, by setting in succession \(\alpha_{n - 2} = 0,\; \cdots ,\;\alpha_{1} = 0\). In any case the remaining coefficients are equal to one and the number of the generated simplices cannot exceed maximum value \(M\).

4.1 Note

If at any stage of the algorithm the small or the flat simplex [24] appears, the set of the coefficients \(\alpha_{1} ,\; \ldots ,\;\alpha_{n}\) is changed as described in step 5. If the degenerated simplex [24] appears, a new regular simplex is created around the best vertex of this simplex and the process is continued.

5 Numerical examples

The proposed algorithm has been implemented in the joined environments: DELPHI and IsSPICE 4, and tested numerically using MOS circuits designed in nanometer technology. The calculations were executed on PC with the processor Intel Core (TM) i7-2600. To illustrate effectiveness of the algorithm we consider three exemplary circuits designed in nanometer technology. In all the examples the transistors are characterized by the BSIM 4.6 model implemented in IsSPICE 4, Level 14 [26]. The nominal values of the channel lengths of the transistors are indicated in Figs. 5, 6 and 7, whereas the nominal values of the oxide thicknesses are \(\left( {TOX} \right)_{\text{p}} = \left( {TOX} \right)_{\text{n}} = 1.4\,{\text{nm}}\). The other quantities are as follows: \(XL = 5\,{\text{nm}}\), \(XW = 15\,{\text{nm}}\). The discussed in this section soft faults are variations in the channel length \(\Delta L\) and in the oxide thickness \(\Delta TOX\), considered separately for NMOS and PMOS transistors.

Fig. 5
figure 5

Bias two-stage operational amplifier

Full size image
Fig. 7
figure 6

A rail–to–rail input buffer

Full size image

5.1 Example 1

Let us consider the bias two–stage op–amp shown in Fig. 5 [27]. To arrange the diagnostic tests (PT and VT) the input voltages \(V_{{S_{1} }}\) and \(V_{{S_{2} }}\) as well as the output voltage \(V_{\text{o}}\) are selected. It is assumed that the measurement accuracy of \(V_{\text{o}}\) is 1 μV, \(M = 2000\), \(\varepsilon_{1} = 10^{ - 6}\), \(\varepsilon_{2} = 10^{ - 5}\), \(a = 0.05\), the output resistance \(R_{\text{o}} = 10\;{\text{k}}\varOmega\). At the preliminary stage of the diagnosis process the sensitivities of the voltage \(V_{\text{o}}\) due to variations of the parameters \(L\) and \(TOX\) of all the transistors, for different values \(V_{{S_{1} }}\) and \(V_{{S_{2} }}\), are calculated. The analysis shows that the sensitivities of \(V_{\text{o}}\) due to the parameters of the transistors M6 and M7 are approximately 100 times smaller than due to the parameters of the other transistors. Thus, deviations of the parameters of transistors M6 and M7 have slight influence on the tested voltage \(V_{\text{o}}\) and they cannot be diagnosed in real conditions. In the sequel we consider the soft faults of the following parameters:

  • the channel lengths and the oxide thicknesses of PMOS transistors M1, M2, M3,

  • the channel lengths and the oxide thicknesses of NMOS transistors M4, M5, M8, M9.

On the basis of sensitivity analyses and numerical experiments the following sets of the values of \(V_{{S_{1} }}\) and \(V_{{S_{2} }}\) have been chosen to perform of the PT and VT.

$$\begin{array}{*{20}c} {\text{PT}} & {\text{VT}} \\ \begin{aligned} V_{{S_{1} }} = 1.30\;{\text{V}}\,\,V_{{S_{2} }} = 1.25\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.10\;{\text{V}}\,\,V_{{S_{2} }} = 0.95\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.55\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.80\;{\text{V}}\,\,V_{{S_{2} }} = 0.65\;{\text{V,}} \hfill \\ \end{aligned} & \begin{aligned} V_{{S_{1} }} = 1.20\;{\text{V}}\,\,V_{{S_{2} }} = 0.90\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.90\;{\text{V}}\,\,V_{{S_{2} }} = 0.70\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.70\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.60\;{\text{V}}\,\,V_{{S_{2} }} = 0.40\;{\text{V}} .\hfill \\ \end{aligned} \\ \end{array}$$

All the four sets are exploited to test the parameters of the four NMOS transistors M4, M5, M8, M9 and the first three of them are used to test the parameters of the three PMOS transistors M1, M2, M3.

The results of different multiple soft fault diagnoses are summarized in Tables 1, 2, 3, 4. They comprise three sets of the simultaneous variations of all the channel lengths in NMOS transistors M4, M5, M8, M9 (Table 1), and in PMOS transistors M1, M2, M3 (Table 2), three sets of the simultaneous variations of all the oxide thicknesses in NMOS transistors M4, M5, M8, M9 (Table 3) and in PMOS transistors M1, M2, M3 (Table 4). In all the cases the obtained values of the parameters are very close to their actual values.

Table 1 Results of the fault diagnosis of the channel lengths in NMOS transistors M4, M5, M8, M9
Full size table
Table 2 Results of the fault diagnosis of the channel lengths in PMOS transistors M1, M2, M3
Full size table
Table 3 Results of the fault diagnosis of the oxide thicknesses in NMOS transistors M4, M5, M8, M9
Full size table
Table 4 Results of the fault diagnosis of the oxide thicknesses in PMOS transistors M1, M2, M3
Full size table

In this example the transistors M6 and M7 cannot be tested, because their parameters have very slight influence on the output voltage. Numerical experiments show that even in some idealized circumstances, under very high accuracy of the measurements of \(V_{\text{o}}\), equal to 0.01 μV, and \(M = 5000\) some determined parameters of these transistors can be erroneous and the CPU time long. Some exemplary results conforming this statement are included in Table 5.

Table 5 Results of the fault diagnosis of all NMOS transistors under the measurement accuracy 0.01μV
Full size table

5.2 Example 2

Figure 6 shows the CMOS circuit, being the voltage reference, designed in nanometer technology [27]. The measurement accuracy and the constants of the computation process are the same as in Example 1. To arrange the diagnostic tests the input voltage \(V_{{S_{1} }}\) and the output voltage \(V_{\text{o}}\) are selected. At the preliminary stage of the diagnosis process the sensitivities of the output voltage due to variations of the parameters \(L\) and \(TOX\) of all the transistors, for different values \(V_{{S_{1} }}\), are calculated. The analysis reveals that the sensitivities due to the parameters of the transistors M1, M2, M6, M7, and M8 are 100–100,000 times smaller than due to the parameters of the other transistors. Thus, they cannot be tested. This is why we perform the fault diagnosis of the parameters of transistors M3, M4, M5, M9, M10, and M11, separately for the PMOS (M3, M4, M5) and NMOS (M9, M10, M11) ones. On the basis of sensitivity analyses and numerical experiments the following values of \(V_{{S_{1} }}\) have been chosen to perform of the PT and VT.

Fig. 6
figure 7

Voltage reference circuit

Full size image
$$\begin{array}{*{20}c} {\text{PT}} & {\text{VT}} \\ \begin{aligned} V_{{S_{1} }} = 0.45\;V, \hfill \\ V_{{S_{1} }} = 0.60\;V, \hfill \\ V_{{S_{1} }} = 0.70\;V, \hfill \\ \end{aligned} & \begin{aligned} V_{{S_{1} }} = 0.40\;V, \hfill \\ V_{{S_{1} }} = 0.50\;V, \hfill \\ V_{{S_{1} }} = 0.80\;V. \hfill \\ \end{aligned} \\ \end{array}$$

The results of various multiple soft fault diagnoses are summarized in Tables 6, 7, 8, 9. They comprise three sets of the simultaneous variations of all the channel lengths in NMOS transistors (Table 6), in PMOS transistors (Table 7), and three sets of the simultaneous variations of all the oxide thicknesses in NMOS transistors (Table 8) and the PMOS transistors (Table 9). In all the cases the obtained values of the parameters are very close to their actual values.

Table 6 Results of the fault diagnosis of the channel lengths in NMOS transistors M9, M10, M11
Full size table
Table 7 Results of the fault diagnosis of the channel lengths in PMOS transistors M3, M4, M5
Full size table
Table 8 Results of the fault diagnosis of the oxide thicknesses in NMOS transistors M9, M10, M11
Full size table
Table 9 Results of the fault diagnosis of the oxide thicknesses in PMOS transistors M3, M4, M5
Full size table

5.3 Example 3

Let us consider the rail–to–rail input buffer [27] shown in Fig. 7. To arrange the diagnostic tests the input voltages \(V_{{S_{1} }}\), \(V_{{S_{2} }}\) and \(V_{{S_{3} }}\) as well as the output voltage \(V_{\text{o}}\) are selected. The constants of the computation process are the same as in Example 1, \(R_{\text{o}} = 100\;{\text{k}}\varOmega\). Sensitivity analyses of the output voltage due to variations of the parameters \(L\) and \(TOX\) of the transistors reveal that all the transistors can be tested.

The following sets of the values of the input voltages have been chosen.

$$\begin{array}{*{20}c} {\text{PT}} & {\text{VT}} \\ \begin{aligned} V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V}}\,\,V_{{S_{3} }} = 0.35\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V}}\,\,V_{{S_{3} }} = 0.42\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V}}\,\,V_{{S_{3} }} = 0.45\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.30\;{\text{V}}\,\,V_{{S_{2} }} = 0.80\;{\text{V}}\,\,V_{{S_{3} }} = 0.70\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.30\;{\text{V}}\,\,V_{{S_{2} }} = 0.80\;{\text{V}}\,\,V_{{S_{3} }} = 0.75\;{\text{V,}} \hfill \\ \end{aligned} & \begin{aligned} V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.30\;{\text{V}}\,\,V_{{S_{3} }} = 0.25\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.40\;{\text{V}}\,\,V_{{S_{3} }} = 0.40\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 1.00\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V}}\,\,V_{{S_{3} }} = 0.45\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.80\;{\text{V}}\,\,V_{{S_{2} }} = 0.40\;{\text{V}}\,\,V_{{S_{3} }} = 0.40\;{\text{V,}} \hfill \\ V_{{S_{1} }} = 0.80\;{\text{V}}\,\,V_{{S_{2} }} = 0.50\;{\text{V}}\,\,V_{{S_{3} }} = 0.50\;{\text{V}} .\hfill \\ \end{aligned} \\ \end{array}$$

Some results of multiple soft fault diagnosis are summarized in Tables 10, 11. The obtained values of the parameters are very close to their actual values.

Table 10 Results of the fault diagnosis of the channel lengths in NMOS and PMOS transistors
Full size table
Table 11 Results of the fault diagnosis of the oxide thicknesses in NMOS and PMOS transistors
Full size table

6 Conclusion

The method developed in this paper allows effective diagnosing multiple soft faults of the process parameters in small and middle–size ICs designed in nanometer technology. The method does not require access to internal nodes of the circuit. The set of the parameter values is obtained by solving nonlinear equations, not given in explicit analytical form, that may have more than one solution. The proposed approach, whose core is the Nelder–Mead optimization method, is capable of finding the multiple solutions and select the actual one. Numerical examples reveal that the accuracy of the determined parameter values is very good. The method does not allow testing the transistors whose parameters have slight influence on the output voltage. This is why the fault diagnosis process should be preceded by the sensitivity analyses.

The proposed method has been compared with the methods recently published in references [18] and [20] devoted to similar problem. They will be named M2016, M2014 and M2015, respectively.

At first we concentrate on the methods M2016 and M2014. To perform the comparison, method M2014 has been implemented to allow diagnosing CMOS circuits designed in nanometer technology, comprising the transistors characterized by the model BSIM 4.6. All 30 fault diagnoses included in Tables 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 providing the results found by method M2016, have been performed using method M2014 with the same diagnostic tests and the assumed measurement accuracy and the parameters \(\phi\), \(\xi\), \(k_{ \hbox{max} }\) as in [18] (Example 1). On the basis of these experiments the following conclusion can be drawn. Method M2014 is very sensitive to the tests and in numerous cases several tries must be taken to select the proper one. Moreover, sometimes this method requires more than one measurement node. In the great majority of cases method M2014 is more time consuming than method M2016. To be specific, let us consider in detail Example 1. For the diagnoses included in Tables 1, 2, 3 the results given by method M2014 are very similar to the ones provided by method M2016 (see Tables 12, 13, 14). In all cases, except one, method M2014 consumes more CPU time which is 1.48–6.64 times longer. For the cases presented in Tables 4, 5 method M2014 fails. However, it is possible to arrange another tests so that the method works and gives correct results. Unfortunately, the tests relating to the diagnoses indicated in Table 5 requires access to two measurement nodes.

Table 12 Results of the fault diagnosis of the channel lengths in NMOS transistors M4, M5, M8, M9 given by method M2014
Full size table
Table 13 Results of the fault diagnosis of the channel lengths in PMOS transistors M1, M2, M3 given by method M2014
Full size table
Table 14 Results of the fault diagnosis of the oxide thicknesses in NMOS transistors M4, M5, M8, M9 given by method M2014
Full size table

Method M2015 comprises very large class of circuits, including bipolar and CMOS ones, designed in micrometer and submicrometer technologies. In Ref. [20] the MOS transistors designed in nanometer technology are characterized by PSP103.1 model introduced into DELPHI environment. Thanks to this the circuit analyses are executed using a dedicated program written in DELPHI, that considerably improves the computation process and makes the method sound. To compare with M2016 the method M2015 was implemented including BSIM 4.6 modeled MOS transistors and circuit analyses were performed in IsSPICE 4. Method M2015 requires numerous sensitivity analyses that in this case must be performed using the brute–force incremental approach. In consequence this method needs large computing power and consumes much CPU time. Thus, method M2016 is less universal than M2015 but, in the case of CMOS circuits with BSIM 4.6 modeled transistors, faster and easier to implement. To be specific, all the cases presented in Tables 1, 2, 3, 4 were retaken using method M2015 with \(h = 0.05\). The method gives the results very close to the ones provided by M2016, but the CPU time is 7–45 times longer.